Featured Application
Accuracy of additively manufactured implants for clinical surgery.
Abstract
In craniomaxillofacial surgical procedures, an emerging practice adopts the preoperative virtual planning that uses medical imaging (computed tomography), 3D thresholding (segmentation), 3D modeling (digital design), and additive manufacturing (3D printing) for the procurement of an end-use implant. The objective of this case study was to evaluate the cumulative spatial inaccuracies arising from each step of the process chain when various computed tomography protocols and thresholding values were independently changed. A custom-made quality assurance instrument (Phantom) was used to evaluate the medical imaging error. A sus domesticus (domestic pig) head was analyzed to determine the 3D thresholding error. The 3D modeling error was estimated from the computer-aided design software. Finally, the end-use implant was used to evaluate the additive manufacturing error. The results were verified using accurate measurement instruments and techniques. A worst-case cumulative error of 1.7 mm (3.0%) was estimated for one boundary condition and 2.3 mm (4.1%) for two boundary conditions considering the maximum length (56.9 mm) of the end-use implant. Uncertainty from the clinical imaging to the end-use implant was 0.8 mm (1.4%). This study helps practitioners establish and corroborate surgical practices that are within the bounds of an appropriate accuracy for clinical treatment and restoration.
1. Introduction
Additive manufacturing (AM), non-technically known as three-dimensional (3D) printing, is a process in which material is added and joined typically on a layer-by-layer principle to make products using digital data of a 3D model [1]. AM is a rapidly evolving technology [2], which originated in early 1980s [3]. To this end, it differs from the conventional manufacturing methodologies, i.e., subtractive and formative manufacturing. AM has been widely implemented in the medical industry [4], and it has gained clearance for more than 80 AM medical devices such as maxillofacial implants and a knee joint replacement system from the United States Food and Drug Administration (FDA) [2]. Substantial AM growth is enabled by its economical lot-size-one that allows for unprecedented geometrical freedom [5] in one build cycle using minimal set-up because it is a general-purpose digital technology which is not constrained by patient-specific tooling [6,7,8]. Further, it enables a unique supply chain with increased communication and responsiveness [9] that complements the state of urgency in the medical field.
The powder bed fusion (PBF) technique is one of the seven AM processes in which thermal energy is used to selectively fuse regions of the powder bed [1]. When this method is applied to fabricate metallic parts, it is typically known as direct metal laser sintering (DMLS), selective laser melting (SLM), and electron beam melting (EBM) depending on the power source and the machine manufacturer. This method has been widely implemented to manufacture custom-made and patient-specific implants from metal alloys, particularly titanium [10,11,12,13,14,15,16,17]. Implants seem to be one of the most utilized applications of additive manufacturing in the head and neck area in hospitals [18]. Further, it is increasingly fulfilling the demand for porous titanium that can facilitate osseointegration through the independent adjustment of the mechanical properties and porosity in terms of size and distribution [19,20,21,22,23].
A classification for medical applications of AM was established by Tuomi et al. [24,25], which comprises medical models for planning, medical aids, tools for medical devices, inert implants, and bio-manufacturing. Akmal et al. [26] have extended the classification of custom-made inert implants to intelligent implants containing patient-specific digital data and drug delivery systems. The advent of preoperative virtual planning, based on medical imaging, segmentation, implant modeling, and manufacturing [27] in particular with AM techniques, has enabled excellent functional and aesthetic reconstruction of different craniomaxillofacial surgical procedures including the reduction of intraoperative time [28,29,30,31,32,33].
The craniomaxillofacial, in particular the mandibular, deformities can be caused by tumor, injuries, and/or infections [34]. The reconstruction of mandibles followed by an ablative tumor surgery poses a challenge for practitioners [31]. This is due to the nature of complex 3D patient-specific geometry that is difficult to replicate. Any signs of an aberration in its structural alignment may lead to functional disturbance due to the malocclusion or temporomandibular disorders [33]. Further, difficulties may arise due to extensive bone resection, temporomandibular joint involvement, or severely distorted bony contour [33].
Evidently, the development of medical imaging, in particular computed tomography (CT) techniques, has changed the dynamics of the medical industry because it has enabled data capture from the interior and exterior of the patient-specific anatomy. This captured data is volumetric in nature comprising 3D block of smaller cuboid structures called voxels (volume element). Each voxel represents a relative X-ray attenuation [35] that is characterized by grey scale values in Hounsfield unit (HU). More specifically, the Hounsfield units represent material X-ray attenuation value relative to water. In principle, this relationship enables a calibration of CT images by means of the grey scale range. The slice-by-slice captured voxels are interpreted by stacking the slices to obtain multiple 2D representations [35]. The CT images are generally stored in 16 bits according to the international standard of digital imaging and communications in medicine (DICOM) format.
CT imaging can essentially be performed using either a fan-beam multi-slice CT (MSCT) or a cone-beam CT (CBCT) system depending on the geometry of the X-ray acquisition [35]. Further, a dual-energy CT (DECT) system provides more possibilities for the clinical applications by acquiring CT images using two different X-ray spectra [36]. Though a MSCT system may provide a higher low-contrast resolution, a reduced image noise [37], and a rapid scan time [35], a CBCT system is increasingly used in the maxillofacial surgeries owing to an acceptable image quality [38], a similar scanning time [35,37], a lower cost, and a reduced radiation dose [35,37,38,39].
Regarding the quality assurance (QA) of the CT systems, QA programs for the MSCT system are well-established. However, the QA programs for the CBCT system are still evolving and present only a few established sources, i.e., programs for high-end and large-volume CBCT systems [40], the QA program proposed by the SEDENTEXCT Project [41], and the EFOMP CBCT QA Protocol [42]. The standardized QA Phantoms including the European project-based [41], commercial [43], and low-cost alternatives [44] enable the assessment of accuracy and quality of the CT systems [40]. The composition of a Phantom varies according to the application and involves several properties, i.e., radiation type, energy range, linear attenuation coefficient, and density, which mimic water or body tissues by means of attenuating photons [45].
Though conventional 2D representations of medical images benefit from the localized analysis of different anatomical structures, a reconstruction of medical images to a 3D model enables enhanced visualization of craniomaxillofacial structures, deformities, and implant sites [37,46,47]. Further, it assists in 3D modeling of patient-specific implants, saw guides, and drill guides [34,48]. A conversion of 2D medical images (DICOM) to 3D data (standard tessellation language: STL) requires 3D thresholding techniques for segmenting different forms of tissues. There are several 3D thresholding techniques for the 3D reconstruction of medical images, namely a volume-based approach, contour-based approach, and point-cloud-based approach [49]. However, the most commonly used method is the volume-based [39] that uses a marching cubes algorithm [50]. The volume-based approach involves an elimination of all voxels consisting of the grey scale values in HU that are lower than the selected threshold value t. It includes all the voxels that are equal to or greater than t. The following binary mask M(x,y) (Equation (1)) denotes these relationships where I(x,y) depicts the grey scale values of medical images in HU [51]:
Though the collective processes of CT imaging, 3D thresholding, 3D modeling, and AM yield beneficial outcomes of surgical procedures [15,16,28,29,30,31,32,33], both academics and practitioners have noticeably understudied the potential sources of their cumulative error [52]. Each step of the process can contribute geometric error to the resulting implant [53]. Previous efforts have been made to evaluate inaccuracies through different CT systems and their protocols [37]; different CT system voltage and current [54]; various CT systems and thresholding values [39,55]; different thresholding values [54,56]; various thresholding values and software [57]; different AM processes [53,58]; and various metal AM machines [59], all of which have prompted additional verification studies that account for the whole process chain.
The aim of this study is to evaluate cumulative spatial inaccuracies [52] in the process chain of implementing AM from medical imaging involving different CT imaging protocols, 3D thresholding involving various Hounsfield units, and 3D modeling involving patient-specific geometry. The case study follows the process chain of a pre-operative virtual planning for the procurement of an end-use implant to aid practitioners in establishing appropriate clinical practices that can allow treatment and restoration. The study designs and evaluates a QA Phantom in line with sound metrological expertise to validate a MSCT system. In addition, accurate measurement techniques traceable to the SI unit [60] are adopted for the reference measurements. These include a tactile-probing coordinate measuring machine (CMM) [61] and an optical 3D coordinates measuring system which comprises a combination of the structured light [62] and stereo vision [63] techniques. The procedure offers an innovative approach for determining the inaccuracy of an end-use implant involving the whole process chain as opposed to the partial analyses in the literature involving one or few process steps.
2. Materials and Methods
This study was conducted in compliance with relevant laws and institutional guidelines of the EU Directive 2010/63/EU. No human subjects or living animals were used in this study. Figure 1 shows the process of this case study.
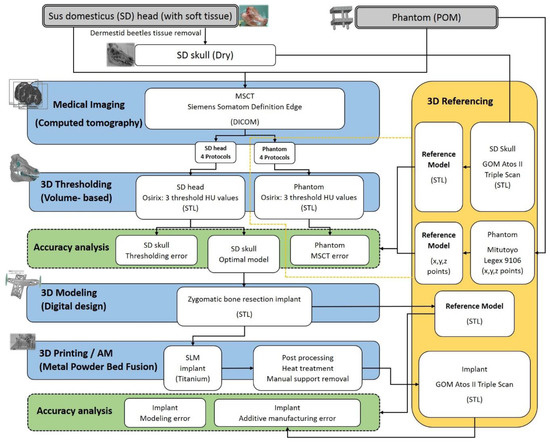
Figure 1.
The process of evaluating cumulative inaccuracies for an end-use implant.
2.1. The Sus Domesticus
This study involves a sus domesticus (SD) with an age of approximately nine months. The SD head was acquired from a conventional supplier in the food industry. The subsequent weight of the head was 9.553 kg. The head, intact with its soft tissue, was CT-scanned. After medical imaging, dermestid maculatus beetles were used to remove the soft tissue from the head to preserve a dry skull. The dry skull was covered with a plastic bag, and it was stored in a container at the room temperature to prevent dimensional changes, i.e., shrinkage, from external environmental factors such as exposure to humidity and UV. Subsequently, the dry skull was scanned and referenced using an optical 3D coordinates measuring system and a CMM, as shown in Figure 1.
2.2. The Quality Assurance Phantom
A QA Phantom was designed to verify the accuracy of the CT system in line with metrological expertise. The specific features of the Phantom allowed for measuring volumetric references of linear and angular dimensions as opposed to freeform anatomical features of the SD head. The Phantom was manufactured using conventional and precise techniques. The material of the Phantom was Polyoxymethylene (POM) due to its close representation of the bone density [64] and the bone linear attenuation coefficient [40,44]. Several studies have used POM as an appropriate Phantom material for the QA of the CT systems in the literature [40,41,65,66]. Subsequently, the Phantom was CT-scanned and referenced using the CMM, as presented in Figure 1.
2.3. Medical Imaging
A Siemens Somatom Definition Edge MSCT system was used to acquire medical images. Four different protocols of the CT system generated DICOM images of both the SD head and the Phantom, as shown in Figure 1 and Table 1. The CT imaging reconstruction kernel and image thickness were critical variables for evaluating the accuracy of the CT system. Consequently, these independent variables led to a variation in the pixels, current, and number of cuts. The CT images of the SD head are made available through an open access repository [67].

Table 1.
Parameters of multi-slice computed tomography (MSCT) imaging for the sus domesticus (SD) head and the Phantom.
2.4. 3D Thresholding
The volume-based approach of OsiriX MD (8.0.2, Pixmeo SARL, Geneva, Switzerland) software, which has been approved by the United States FDA, reconstructed the CT DICOM images to the STL format. Three individual HU values were used to segment the medical images of both the SD head and the Phantom, as shown in Figure 1. Table 2 presents the resolution, decimate resolution, and smooth iterations in addition to the HU values.

Table 2.
Three-dimensional (3D) thresholding parameters for the SD head and the Phantom.
2.5. 3D Modeling of the Implant
Assuming a case where a patient had to undergo a resection of a zygomatic bone tumor, an implant was digitally modeled to replace the deformity using 3Data Expert (11.0.0.32, Deskartes Oy, Espoo, Finland) software. The implant was designed using the right zygomatic bone projections of the SD head that were obtained from the optimal CT imaging and thresholding parameters. The resultant implant was stored in the STL format, and it was also used as a reference model, as shown in Figure 1.
2.6. Additive Manufacturing of the Implant
The computer-aided design (CAD) implant in the STL format was used to configure pre-processing parameters of AM using Materialise Magics (22.0, Materialise, Leuven, Belgium) software. During the pre-processing phase, four replicas of the implant were placed on the platform in the build chamber. The implants were oriented to create support structures for an adequate heat sink. Further, they were sliced to create contours including a laser hatch pattern and vector scanning for selectively melting the layers. The pre-processed data was used to initiate additive manufacturing, in particular for the titanium PBF using SLM Solutions 125HL (SLM Solutions Group AG, Lübeck, Germany) machine. Table 3 lists the printing parameters, and Figure 2 illustrates the printing orientation, printing location, and support structures of the implants. Subsequently, the additively manufactured implants underwent heat treatment in an argon atmosphere for stress relief. During the heat treatment process, the temperature of the chamber was increased from 20 to 800 °C at a rate of 5 °C/min, it was held at 800 °C for four hours, and eventually, it was cooled to the room temperature at the same rate. The support structures of the implants were removed by an expert using manual instruments, i.e., pliers, a saw, and an angle grinder, to yield the end-use implants. Finally, one of the implants was scanned using the optical 3D coordinates measuring system to capture the resultant geometry, as presented in Figure 1.

Table 3.
Additive manufacturing (AM) parameters for the end-use implant.

Figure 2.
The print orientation and location of four identical implants on the build platform illustrating supports in blue.
2.7. The Reference Measurements and Cumulative Error
A GOM ATOS II Triple Scan (GOM GmbH, Braunschweig, Germany) 3D coordinates measuring system and a Mitutoyo Legex 9106 (Mitutoyo Corporation, Kawasaki, Japan) CMM with tactile-probing systems were used to conduct reference measurements, as shown in Figure 1.
The optical 3D coordinates measuring system follows the structured light and stereo vision techniques built on the principle of camera-camera and camera-projector triangulation. Two calibrated reference gauge blocks were used to establish a traceability to the SI unit during the optical measurements. The measurements were performed in a room with a temperature range of 22.0–23.3 °C. The results of the measurements were compensated with the subsequent thermal expansion.
The CMM consists of a fixed bridge structure and uses the scanning and touch-trigger probing principles. The CMM is periodically verified with the interferometrically calibrated gauge blocks ensuring a maximum permissible error, E0, MPE value of 0.35 µm + L/1000 µm where L is length in mm. The CMM measurements were performed in an automated climate-controlled laboratory with a temperature stability of 20 ± 0.2 °C [68].
In this study, uncertainty was calculated according to the principles of Guide to the expression of uncertainty in measurement (GUM) [52]. Independent measurements were compared with the reference measurement of the specimens to calculate geometric variation using GOM Inspect 2018 (v2.0.1, GOM GmbH, Braunschweig, Germany) software, which is tested and certified by the National Institute of Standards and Technology (NIST) and the National Metrology Institute of Germany (PTB).
Inaccuracy of the CT system was calculated in terms of linear error in the x-, y-, and z-axis and orthogonal error in the x-y, x-z, and y-z planes. The linearity and orthogonality are estimated by establishing a coherent local coordinate system for the CT-scanned Phantom and the tactile-probed Phantom. The coherent local coordinate system enabled measurements of their deviations. The linear error in the x- and y- axis is estimated by linear regression analyses. These are conducted by measuring distance deviations from hole-to-hole center points with respect to positions in the local co-ordinate system. The linear error in z-axis is calculated by evaluating the distance deviation of the hole-to-hole center points situated in the x-z and y-z planes. It is presumed that the effects of thresholding the CT-scanned Phantom are negligible due to the custom-designed geometrical features and the selected measuring principles.
The 3D thresholding error is analyzed by relying on a mean distance deviation which is estimated by comparing surfaces of the segmented SD head and the optically scanned dry skull.
The 3D modeling error is investigated by evaluating the absolute accuracy of the modeling software.
Potential sources of error in AM are analyzed in terms of a mean distance deviation and a magnification error. The mean distance deviation is estimated by comparing the surfaces of the optically scanned implant and the nominal CAD implant. The magnification error is obtained by rescaling the optically scanned implant in the x-, y-, and z- axis scales to fit the nominal CAD implant.
In order to verify the results of the surface comparisons, mesh sensitivity analyses were performed to confirm an optimal mesh size for reference models of both the SD skull and the implant.
Finally, the combined standard uncertainty of medical imaging, 3D thresholding, 3D modeling, and AM is evaluated in terms of length-dependent (LD) and non-length-dependent (NLD) components. The worst-case error of the respective process is calculated by multiplying the LD error with the maximum length of the implant and summing the NLD error. Subsequently, the error of each process is summed to evaluate a cumulative error for the end-use implant.
3. Results
3.1. The CT Imaging Error
The custom-designed QA Phantom is shown in Figure 3. Table 4 shows the linear and orthogonal inaccuracies of the MSCT system measured with the QA Phantom. The magnification error represents the slope of the regression line, which is a dimensionless scale factor. The standard deviation of regression (Standard error) denotes the average distance between the measured deviations and the predicted deviations (regression line) in millimeters. The magnification error of the z-axis depicts the distance deviation of the hole centers with respect to the position in the local co-ordinate system. The standard deviation of the z-axis signifies the spread of the distance deviations from their average. The orthogonal error is described by the mean and standard deviations in degrees.

Figure 3.
The quality assurance Phantom for examining the MSCT imaging error.

Table 4.
Linear and orthogonal inaccuracies of the MSCT system.
3.2. The 3D Thresholding Error
Verification results of the optically scanned dry skull are presented in Table 5. The results verified that the standard STL surface, generated by GOM ATOS (Professional 2016, GOM GmbH, Braunschweig, Germany) software, contained an appropriate mesh size. The results reached steady state values from 3rd to 6th iterations. The results of the standard STL mesh size are within 0.166 % of the mean distance and 1.094 % of the standard deviation for the final iteration.

Table 5.
The mesh sensitivity analysis of the SD skull surface with respect to the segmented SD head surface.
The thresholding error, including relatively negligible CT imaging error, of the verified standard mesh size is shown in Figure 4. The legend contains a range of the distance deviations. The red color code depicts the segmented surface above the optically scanned surface, the green color code denotes the segmented surface with no deviations, and the blue color code represents the segmented surface below the optically scanned surface. In addition, the legend contains a histogram to graphically represent the frequency of the deviations. In this case, the histogram shows asymmetric deviations that skew to the left (negatively skewed).
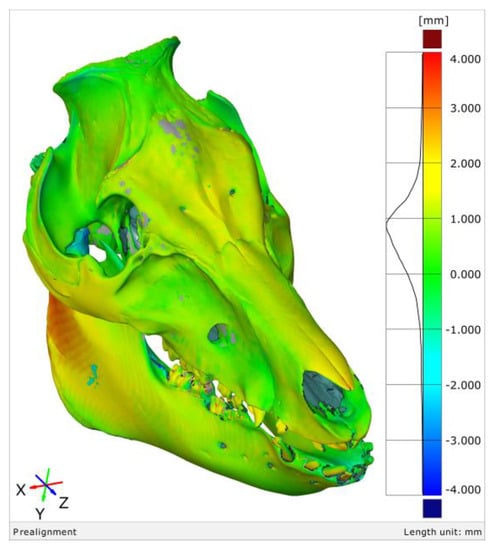
Figure 4.
The thresholding error of the segmented SD head on the dry skull with the verified mesh size.
The thresholding error of the SD head for all protocols and thresholding values is shown in Figure 5. The vertical axis shows the mean distance between the segmented SD head as a function of the CT protocols and Hounsfield units compared to the optically scanned dry skull. The horizontal axis depicts four CT protocols. The legend contains a shade plot of the thresholding values. The error bars represent a standard deviation. A maximum allowable distance of 4 mm ensured that all the data points were within the computational range of the surface comparison. The mean distance represents a central arithmetic average of all points of the surface comparison. The standard deviation evaluates the spread of the mean distance.
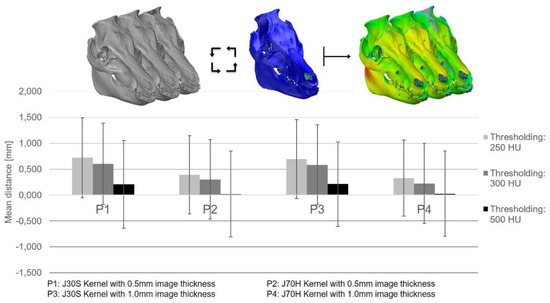
Figure 5.
The thresholding error of the segmented SD head as a function of the CT Protocols and Hounsfield units with respect to the optically scanned dry skull (blue).
According to the results shown in Figure 5, as the thresholding value increases, the mean distance decreases and the standard deviation increases. Estimating the optimal CT protocol and thresholding value based on these relationships alone was deemed trivial. To this end, Table 6 lists the additional parameters of the surface comparison results. The area of valid distance is the reference surface area that is used for the comparison. The integrated distance is the inscribed volume of the surface comparison. Finally, the integrated ABS distance describes an absolute value of the integrated distance.

Table 6.
Three-dimensional (3D) thresholding inaccuracies of the SD head intact with its soft tissue.
The results of the qualitative and quantitative analyses deduced that CT Protocol 1 and 300 HU were the optimal independent parameters for imaging the SD head because they created surfaces that were closest to the optically scanned dry skull. Subsequent thresholding error is recorded as 0.602 mm.
3.3. The 3D Modeling Error
Figure 6 shows a render of the digitally designed implant attached to the segmental resection of the right zygomatic bone. In this case, the 3D modeling error is represented by the numerical resolution of the modeling software, which is recorded as 0.0001 mm.
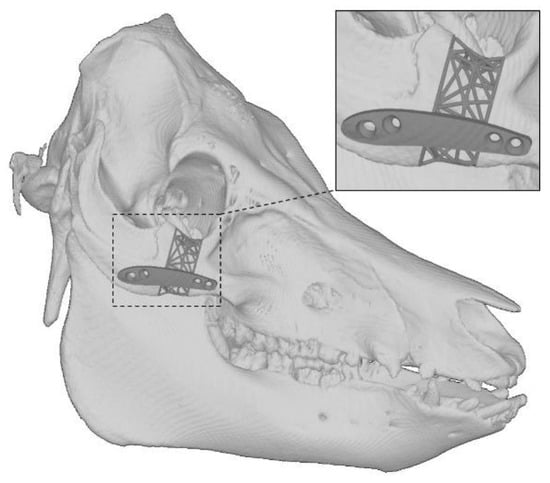
Figure 6.
The computer-aided design (CAD) implant attached to the segmental resection of the zygomatic bone.
3.4. The Additive Manufacturing Error
Figure 7 shows the additively manufactured implant with and without the support structures. Verification results of the reference (nominal CAD) implant are shown in Table 7.

Figure 7.
The additively manufactured titanium implant with the supports (right) and without the supports (left).

Table 7.
The mesh sensitivity analysis of the nominal CAD implant surface with respect to the optically scanned implant surface.
The mesh sensitivity analysis verified that the fourth iteration of the analysis reached a steady state value of 0.042 mm and 0.062 mm for the mean distance and standard deviation of the AM error, respectively. Figure 8 shows the AM error color plot of the end-use implant on the nominal CAD implant including a histogram, which shows asymmetric and positively skewed deviations.
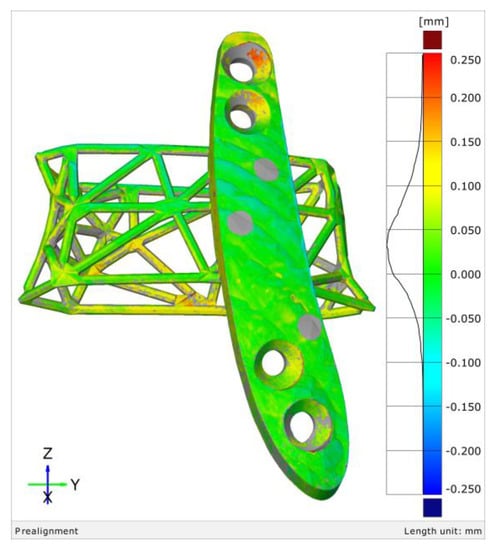
Figure 8.
The additive manufacturing error of the end-use implant on the nominal CAD implant with the verified mesh size.
A maximum allowable distance of 0.5 mm ensured that all the data points of the surfaces were within the computational range. The grey regions of the color plot depict the surface data of the end-use implant that were not captured by the optical 3D coordinates measuring system. These regions represent locations where the reference points were placed for triangulating the surface geometry. The removal of the reference point surfaces ensured that only the implant surfaces were considered for the surface comparison.
The magnification error of the additively manufactured implant was evaluated through a series of steps. Firstly, the lattices of the optically scanned implant were removed which eliminated small dimensional features. Then, the base implant was re-oriented to axially align its longest dimension with the global co-ordinate system. Finally, the absolute integrated distance of the base implant was minimized. The removal of lattices decreased the computational time and outlier contribution. The resultant magnification error is presented in Table 8. The compensation of the magnification error decreased the absolute integrated distance by a factor of 3.5 while the mean distance and standard deviations were also decreased.

Table 8.
The magnification error of the additively manufactured end-use implant with reference to the nominal CAD implant.
3.5. Uncertainty and Cumulative Error of the Implant
Uncertainty and error budget of the end-use implant is presented in Table 9.

Table 9.
The cumulative inaccuracies of the additively manufactured end-use implant.
Figure 9 shows the way in which cumulative error increases at each process step. Uncertainty of the reference measurements was significantly smaller than the uncertainty of the process chain.
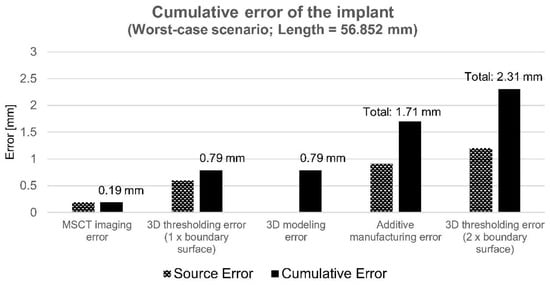
Figure 9.
The worst-case cumulative and source error of the end-use implant with a length of 56.852 mm as a function of the whole process chain.
The maximum magnification error of CT imaging is 0.000359 which resulted from CT Protocol 1 and the z-axis of the MSCT system, as shown in Table 4. CT Protocol 1 was also used to image the SD head which was used for the implant modeling process. To calculate uncertainty of this error, it is estimated to have a rectangular probability distribution. Therefore, it contributes to the LD uncertainty of CT imaging by a value of 0.000359/√3 = 0.000207. Likewise, the maximum mean orthogonal error of CT imaging is 0.114° (0.00199 rad.) which resulted from CT Protocol 1 and the x-z planes, as shown in Table 4. Uncertainty for the orthogonal error is 0.114°/√3 = 0.066° (0.00115 rad.). Considering that the angle is small, the effect of the orthogonal error for a length is the length multiplied by the angle in radians. Thus, it contributes to the LD uncertainty with a value of 0.00115. The combined LD uncertainty for CT imaging is calculated to be 0.00117 by combining the LD uncertainty of the magnification and orthogonal error.
Similarly, the maximum standard deviation is 0.0779 mm for the magnification error in Table 4. It also occurs in the z-axis of the MSCT system. The standard deviation of the orthogonal error was neglected due to its insignificant contribution to the combined standard uncertainty. Thus, the NLD standard uncertainty of CT imaging is 0.0779 mm.
Finally, the worst-case CT imaging error is 0.191 mm for the 56.852 mm long end-use implant.
The average thresholding error of the volume-based segmentation is 0.602 mm, which resulted from CT Protocol 1 and 300 HU, as shown in Table 6. In addition to CT Protocol 1, this thresholding value was used to segment the SD head which was used for the implant modeling process. If the length measurement of the implant involves two boundary surfaces, then the thresholding error is 2 × 0.602 mm = 1.2 mm. Uncertainty of the thresholding error is 0.602 mm assuming that it is not larger with a probability of 67%. Thus, it contributes to the NLD uncertainty with a value of 0.602 mm.
Consequently, the thresholding error is 0.602 mm for one boundary surface and 1.2 mm for two boundary surfaces of the implant.
The worst-case error of 3D modeling is 0.0001 mm/2 = 0.00005 mm that has a NLD uncertainty of 0.00005 mm/√3 = 0.0000289 mm.
The maximum magnification error of additive manufacturing is 0.015 that occurred in the z-axis of the implant, as shown in Table 8. It contributes to the LD uncertainty with a value of 0.015/√3 = 0.00866. The NLD uncertainty is 0.061 mm, which resulted from the standard deviation of the AM error.
Finally, the worst-case error of additive manufacturing is evaluated to be 0.914 mm for the maximum length of the end-use implant.
The combined uncertainty represents the positive square root of the combined variances that is expressed by the law of propagation of uncertainty. The implant error for each step of the process chain is calculated according to the following Equation (2):
where IEprocess depicts the implant error as combined uncertainty of a process in millimeters, uPNLD and uPLD denote the NLD [mm] and LD uncertainty associated with the process, and L represents the maximum length of the end-use implant in millimeters.
Finally, the worst-case cumulative error of the implant totals to a value of 1.71 mm for one boundary surface and 2.31 mm for two boundary surfaces. The combined standard uncertainty (uc) of the end-use implant encompassing all processes is calculated for one boundary surface condition according to the following Equation (3):
4. Discussion
This study investigated inaccuracies involved in the process chain of procuring an end-use implant. The increase in cumulative error at each step in the process chain must be considered for preplanning a surgical procedure to avoid ill-fitting implants that may cause complications during surgery.
4.1. CT Imaging
The worst-case CT imaging error emerged in the z-axis of the MSCT system and generated the second least error value compared to the other processes. The LD uncertainty of all four CT protocols ranged at an insignificant scale. The evaluation of the hole-to-hole center points of the QA Phantom ensured that the thresholding effects were minimized when estimating the CT imaging error. This is because the center points of the Phantom holes remain unchanged regardless of the thresholding effect on the hole diameter. The homogenous material of the Phantom also complemented the minimization of the thresholding effects to compute the CT imaging error. Moreover, the NLD uncertainty of CT imaging represented noise associated with the hole surfaces that were used to predict the center points. It consisted of components such as the resolution and non-linearity. This estimated error can also be negligible for most craniomaxillofacial surgical procedures.
Though the overall CT imaging error can be negligible, the impact of CT reconstruction kernel, image thickness, and Hounsfield units on the QA Phantom was evaluated quantitatively for practitioners seeking optimal results. Following a conservative conclusion, the J30S kernel with the 0.5 mm image thickness and −500 HU yielded the least amount of uncertainty for CT imaging. This is because the J70H kernel was more prone to the image noise than the J30S kernel.
The results indicated that the used MSCT system is a good candidate for AM applications, in particular for the development of an end-use implant, owing to its high accuracy. Though the calibration of the HU number is standardized in MSCT systems [40], a MSCT system from a different vendor does not have identical CT protocols and applied x-ray spectra due to different x-ray tubes, varying beam filtration, beam shaping filters, etc. in different CT scanner models. Furthermore, the soft tissue and bone have HU numbers which are outside of the calibration point of water (especially bone) and typically span a wide HU range even with a fixed scan protocol. To this end, linear and orthogonal errors calculated in this study can vary to a reasonably small extent [69]. Further, the reported error may deviate to a much larger extent when using a different type of CT system, e.g., a CBCT system, because of a lack of standardization in HU number and different CT protocols [40]. Nevertheless, a CBCT system might be an alternative when the manufacturer’s recommended protocol is used [70], but more research is needed. In principle, the developed methodology for error analysis can be extended to any type of CT system and its protocols using the tailor-made Phantom.
4.2. 3D Thresholding
The thresholding error was one of the most significant errors compared to the other processes. The thresholding error represents the edge location error considering that the LD and NLD uncertainty of the MSCT system were relatively low. This means that the volume-based segmentation overestimated the bone surfaces of the DICOM images to the STL format with a value of 0.602 mm outside the true surface. Assuming a craniomaxillofacial implant case that involves a hole into which an implant is intended to fit, then the thresholding error for the size of the implant would be 2 × 0.602 mm = 1.2 mm. Practitioners should consider that this error enables the correction of a systematic effect for the implant. The thresholding error propagates to the implant because the implant was modeled as a negative of the segmented SD head.
The variations in the thresholding value generated significantly altered SD skull geometry. The results revealed that the data loss of the skull surface was inversely proportional to the area of valid distance. Similarly, the staircase effect or the blocky coarse surfaces of the skull were directly proportional to the standard deviation, and the artefacts were directly proportional to the negative values of the integrated distance.
When excluding the J70H kernel that included the coarse skull surface comprising of data loss, the staircase effect (blocky data) with sharp edges, and a higher number of artefacts, the selection of an optimal CT reconstruction kernel delimited to the J30S kernel. Since CT Protocol 1 involved lower image thickness of 0.5 mm, it captured a slightly higher amount of the segmented SD head data than CT Protocol 3.
Though the 300 HU generated a similar and uniformly fine surface data than the 250 HU, it also contained a lower amount of inscribed volume. Comparatively, the 500 HU generated excessive artefacts.
Even though the higher sharpness enabled by the J70H kernel can be beneficial for bony structures that require a higher spatial resolution, it is also associated with accentuated noise. The optically scanned dry skull was mainly composed of smooth outer bone that was within the line of sight of the optical 3D coordinates measuring system. Thus, the results favored the J30S reconstruction kernel that generated smoother bone surfaces than the J70H kernel. The J70H kernel also exhibited properties that were more prone to the partial volume effect [39] than the J30S kernel. Though the attenuation coefficient and density of distinct matter, i.e., bone (+1000 HU), water (0 HU), and air (-1000 HU), are identifiable, the partial volume effect allocates voxels as soft tissue instead of bone at the bone-to-soft tissue boundary which results in voids and a loss of data.
The results indicated that the essential step of 3D thresholding remains as one of the critical factors that limit the accuracy of additively manufactured medical constructs. More specifically, the thresholding error was close to the imaging voxel size which has also been reported in the past using four commercially available software packages [71]. Though the use of different software can generally yield accurate geometry, discrepancies can be significant between software packages mainly due to a lack of identical array of control settings and the embedded algorithm for DICOM-to-STL conversion [71]. For example, Osirix MD, which was used in this study, is most probably related to an exact geodesic path algorithm, Dijkstra algorithm, and the fast marching method [71], whereas the Mimics software (Materialise NV, Leuven, Belgium), which is also approved by the United States FDA [72], is embedded with the adapted marching cubes algorithm with the partial volume effect for 3D imaging [73].
4.3. 3D Modeling
Uncertainty of 3D modeling was estimated to be the most insignificant in the process chain. It was derived from the arithmetic decimal places (resolution) of the software which represented the STL chordal tolerance [74]. Likewise, the rounding error that contributed to the implant budget was still the most insignificant even after assuming a worst-case scenario. The resolution of several CAD software is frequently characterized as the absolute or relative accuracy, which can be changed to a certain extent for most CAD packages.
As expected, the results indicated that the error originating from the modeling process was minimal. This error is expected to remain minimal when using different CAD software. Though the error of the process is minor, it still propagates error originating from the imaging and thresholding processes because the implant was modelled using the geometric surfaces and projections of the imaged and segmented bone. Top and bottom surfaces of the implant base are identical to the surfaces of the zygomatic bone.
4.4. Additive Manufacturing
The results indicated that uncertainty of the AM process can be the greatest in the process chain of procuring an end-use implant. Though the NLD uncertainty was reasonably low, the LD uncertainty can be the main contributor to the error budget.
The NLD uncertainty was close to two-layer thicknesses of the manufacturing process. This is most likely caused by the conglomeration of semi-fused particles (size: ~32–60 um) to the outer surface of the implant that was in contact with the surrounding powder owing to a high platform temperature of 200 °C during the build. Further, the stair-case effect [75] induced by the freeform geometry containing angled, curved, or lofted shapes (complex shapes) of the implant can also contribute to the NLD uncertainty. Considering that the machine was calibrated, and standard printing parameters were used for the standard material profile (i.e., particle size distribution and shape), this error can describe the capability of the used machine to manufacture shapes as designed when followed by a standard heat treatment process and manual support removal process.
Microstructural and mechanical anisotropy of additively manufactured metals, particularly titanium, is well understood [76,77,78,79,80]. The results of this study showed that there is also a significant amount of dimensional anisotropy. Though the maximum magnification error was generally low (1.5%) considering also the heat treatment and manual support removal, there was a significant difference of 97% and 93% for the x- and y- scale error compared to the maximum z-scale error of the implant. This is most probably caused by the cumulative effect of localized microstructural anisotropy of the freeform geometry resulting from the layer-thickness-dependent z-scale and the build-mechanism- dependent x- and y- scales of the build.
The metal PBF process is inherent to high temperature distributions as the impinging laser energy melts the metal powder. Re-solidification is highly dependent on the heat transfer capability of the melt pool, and the material is prone to residual stresses and shrinkage due to contractions caused by the physical processes. To this end, support structures are necessary for heat dissipation and anchoring the part to the platform.
Shrinkage can vary as a function of print inclination [75]. Freeform surfaces of the implant can have a fluctuating print inclination resulting in non-linear shrinkage because the microstructural morphology shifts dependency between the melt pool overlaps and the layer overlaps for resisting contractions. Since the magnification error observed in the 3D scales of the implant was positive, it means that the pre-processing software overestimated the shrinkage compensation for the standard printing parameters and material. In addition to automatic shrinkage compensation, most pre-processing software allow users to manually compensate shrinkage/expansion in 3D scale for each individual part before manufacturing.
The maximum magnification error was evaluated through multiple sources of evidence, i.e., conducting caliper measurements digitally and using a length measurement machine, however the additional methods were not reported to simplify the study.
The LD uncertainty describes the maximum magnification error of the end-use implant including the manufacturing, heat treatment, and the support removal processes. The heat treatment process is a standard procedure to cure parts and remove residual stresses. Though the manual support removal process was conducted by an expert in the field using standard tools, it may benefit from a decrease in uncertainty of human error when automated. Further, if the critical geometries are not directed on to the z-axis of the build platform that generally contain down-skin surfaces requiring support structures, the LD uncertainty can be significantly reduced by a factor of 15.
The results confirmed that the error in the metal AM process was dictated by the z-axis of the build which was also reported in a previous study using five different metal AM machines [59]. In the present study, differences of up to 80% were observed for x- and y- scales compared to the z-scale of the build. The z-scale of an AM machine is governed by the layer thickness, whereas the x- and y- scales are dependent on the size of the laser/electron beam spot and the resolution of its steering mechanism, e.g., galvanometer-based mirrors or deflection coils. Though different metal AM machines can generally create accurate geometries [59], inconsistencies remain mainly due to a lack of identical build mechanisms (i.e., laser beam, electron beam, build environment, scanning system, etc.) and process parameters (i.e., source power, layer thickness, scanning speed, scanning strategy, inert gas flow, substrate temperature, powder particle profile, etc.). When a different metal AM machine is used with the manufacturer’s recommended process parameters, the reported error may deviate with a fairly good precision of <0.14 mm, excluding the geometries that are prone to support removal error situated on the z-axis [59].
4.5. Uncertainty and Cumulative Error
Table 10 lists accuracy measurement studies [81,82,83,84,85,86,87,88,89,90,91,92] of additively manufactured constructs using various anatomical models, imaging medium and modality, measurement principles, AM technologies, and measurement instruments. Most studies have used CT imaging technology to image a dry skull. Though imaging a dry skull can account for an approximated error analysis, this is almost never the case in clinical practice and can yield unrealistic values. Several studies have imaged the skull in water to simulate close to realistic cases. However, the tissue surrounding the bone can certainly vary in density. Due to ethical concerns, only few studies have used human skull with and without soft tissue for accuracy analysis, but they can still be limited to manual contact measurements. In fact, majority of the studies have employed a contact measurement principle of repeated measurements between anatomical landmarks using calipers to estimate the overall error of the process chain. However, this principle can easily induce error in pinpointing the exact location of the freeform anatomical surface points in multiple models for linear measurements. This error was mitigated by introducing artificial reference features, i.e., grooved holes [84] or markers [58,90], into the 3D model of the specimens before manufacturing. Though this has provided an ease of pinpointing the regions of interest on the freeform geometry, the measurement principle is often laborious and is limited in terms of number of measurements. Further in literature, human error has been mitigated using CMM for data collection.

Table 10.
Cumulative error analysis of this study compared with literature.
In the present case study, the prescribed methodology aims to overcome the limitations. Principles of GUM are exploited to develop a systematic approach to evaluate overall cumulative error propagating from each process step. The use of animal model simulates a realistic case that also enables tissue removal and measurements of the dry skull to obtain a gold standard. Contact measurements are conducted on a tailor-made QA Phantom through controlled experiments that take advantage of the impeccable accuracy of the tactile-CMM. Optical measurements are conducted on freeform geometry of the dry skull and the additively manufactured implant without geometric manipulation. Subsequent mean difference is evaluated through an adequate number of measurements in the order of 500,000. The method also traces the measurements to the SI units using calibrated instruments. The prescribed methodology has potential of being a standard quality control and assurance protocol that can be applicable to various imaging, thresholding, modeling, and AM processes.
The LD and NLD components of combined uncertainty can yield a reliable measure of possible error of the end-use implant including resolution, non-linearity, and magnification error of CT imaging, segmentation error of 3D thresholding, resolution of 3D modeling, and resolution, non-linearity, and magnification error of AM including heat treatment and support removal. Further, uncertainty in terms of LD and/or NLD can also be calculated for each individual process step. The LD component allows for evaluating error as a function of length for the implant.
Worst-case cumulative error is calculated for the maximum length of the freeform implant which takes into account intricate features of the shape as a result of each process step. Evidently, a smaller dimension would yield a smaller error. Further, boundary surface plays a critical role to the length measurement of the implant which is dictated by the NLD component of thresholding.
Uncertainty results for both one and two boundary surfaces are comparable to those reported in the literature. However, when considering the worst-case cumulative error, in particular for two boundary surfaces, the error peaks compared to the reported mean differences.
4.6. Verification
The measurement instruments were calibrated using gauge blocks. Because uncertainty of the calibrated measurement instruments was insignificant compared to the combined uncertainty of the implant, it confirmed that the required accuracy for the measurements was adequate. The mesh sensitivity analyses verified the correct mesh size and the subsequent vertices that were essential to the surface comparison algorithm. This was confirmed by decreasing the maximum edge length of the mesh until steady state results were achieved. The reduction in the mesh size increased the number of triangles and their subsequent vertices. The number of mesh triangles and vertices was directly proportional to the number of measurements that were conducted for the surface comparison analysis. In this case, though the chordal length of the mesh controlled the accuracy of the intended geometry compared to the original geometry, the mesh size controlled the results of the surface comparison analysis.
4.7. Craniomaxillofacial Implants
The cumulative error pertinent to the process chain of an end-use implant can prevent patient-specific treatment and restoration owing to ill-fitting implants and complications in surgeries [93].
Though the cumulative error evaluated in the present study can be adequate for most craniomaxillofacial surgical procedures [72,94,95], a safety margin of 2.31 mm (4.1% relative) should be respected considering the worst-case error. Practitioners should also consider that the thresholding error and AM magnification error can be corrected through redesign of the implant to significantly improve the results in the future studies.
For example, the thresholding error (0.602 mm) can be compensated in the implant dimensions during the modeling process. The dominating AM magnification error in the z-axis can be manually compensated in the implant model using the pre-processing software before manufacturing, which may reduce the magnification error by a factor of 15.
Further, practitioners should avoid placing critical geometries of the implant on the z-axis, particularly to the down-skin surfaces that require addition and removal of support structures.
In addition to using standard AM process parameters and heat treatments, practitioners need to consider automating the support removal process in case it unavoidably affects critical geometries. This step should be considered before the AM process to ensure that the path of the machining tool is not obstructed by the implant material.
Through an evaluation of an increasing number of segmented anatomical parts with respect to a calibrated CT system, the thresholding error can be mitigated using regression and neural network models as a function of the HU number and software. Apart from thresholding that was performed in this study to standardize the results, practitioners should also consider manual thresholding alternatives. Though subjective and time consuming, manual thresholding may yield better STL models than the default thresholding values of the segmentation software [39]. Though not yet commercially available, advanced thresholding methods [72] are also expected to decrease the leading significance of the segmentation error. The CT images of the SD head are made available to promote future research [67].
Practitioners that require a high accuracy for the implants, e.g., the orbital floor implants [96], should respect the recommended safety margin. The prescribed correction measures can be taken if the intended processes and equipment are identical to this study or after implementing the applied methodology with the relevant processes and equipment as a quality control and assurance protocol. A lack of lower uncertainty (higher accuracy) can also be compensated with precise bone resection using additively manufactured cutting guides [97].
Moreover, it should be considered that it may not always be absolutely imperative to design the implant to fit perfectly at the initial phase. The perforation of the lingual mucosa is one of the complications related to the patient-specific implant. If the lingual foil of the implant scaffold is too high, it is prone to perforate the lingual mucosa during the postoperative healing [98]. For example, the extraction of teeth in the osteotomy line will lead to a resorption and further, remodeling of the marginal alveolar crest, which has to be considered during the planning of the implant.
A successful implementation of AM from radiologic images is a multidisciplinary task [95]. Achieving the most benefit from this technique requires a very close co-operation between all experts involved in the process.
5. Conclusions
Implementing additive manufacturing (AM) in a clinical setting, particularly for the craniomaxillofacial implants, requires tools that are sufficiently precise and accurate to conform to the patient-specific and freeform anatomical geometries considering the entire process chain. To this end, this study develops and evaluates a novel procedure for determining the cumulative spatial inaccuracies in the whole process chain of procuring an end-use implant from medical imaging, 3D thresholding, 3D modeling, and AM, as opposed to partial analyses of the process chain found in the literature. The focus on each process step enables a quality control and assurance protocol that allows for correction measures to further enhance the accuracy of an implant that may prevent treatment and restoration. The study enables practitioners and clinical researchers to establish and substantiate medical practices within the scope of an appropriate accuracy for clinical use.
Author Contributions
Conceptualization, M.S., B.H., J.P. and A.L.; methodology, J.S.A., M.S., B.H., L.T., J.P. and A.L.; software, J.S.A., M.S. and L.T.; validation, J.S.A., M.S., B.H., L.T., A.S., M.K., J.P. and A.L.; formal analysis, J.S.A. and L.T.; investigation, J.S.A., M.S., B.H., L.T., A.S. and M.K.; resources, M.S., B.H., A.S., M.K., J.P. and A.L.; data curation, J.S.A., M.S., B.H. and L.T.; writing—original draft preparation, J.S.A.; writing—review and editing, J.S.A., M.S., B.H., L.T., A.S., M.K., J.P. and A.L.; visualization, J.S.A., M.S. and T.L.; supervision, M.S., B.H., J.P. and A.L.; project administration, J.S.A., M.S., B.H. and A.L.; funding acquisition, M.S., B.H., J.P. and A.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Metrology for Additively Manufactured Medical Implants (MetAMMI) project, which received funding from the EMPIR program co-financed by the Participating States and from the European Union’s Horizon 2020 research and innovation program. The work is also part of the Academy of Finland Flagship Program, Photonics Research and Innovation (PREIN), decision 320168.
Conflicts of Interest
The authors declare no conflict of interest.
References
- ISO/TC 261 ISO/ASTM 52900:2015(E). Additive Manufacturing-General Principles-Terminology, 2nd ed.; ISO/ASTM International: Vernier, Geneva, Switzerland, 2015. [Google Scholar]
- Wohlers Associates Inc. Wohlers Report; Wohlers Associates Inc.: Fort Collins, CO, USA, 2019. [Google Scholar]
- Kruth, J.P. Material Incress Manufacturing by Rapid Prototyping Techniques. CIRP Ann. 1991, 40, 603–614. [Google Scholar] [CrossRef]
- Attaran, M. The rise of 3-D printing: The advantages of additive manufacturing over traditional manufacturing. Bus. Horiz. 2017, 60, 677–688. [Google Scholar] [CrossRef]
- Kumke, M.; Watschke, H.; Hartogh, P.; Bavendiek, A.-K.; Vietor, T. Methods and tools for identifying and leveraging additive manufacturing design potentials. Int. J. Interact. Des. Manuf. 2018, 12, 481–493. [Google Scholar] [CrossRef]
- Hague, R.; Mansour, S.; Saleh, N. Material and design considerations for rapid manufacturing. Int. J. Prod. Res. 2004, 42, 4691–4708. [Google Scholar] [CrossRef]
- Mellor, S.; Hao, L.; Zhang, D. Additive manufacturing: A framework for implementation. Int. J. Prod. Econ. 2014, 149, 194–201. [Google Scholar] [CrossRef]
- Weller, C.; Kleer, R.; Piller, F.T. Economic implications of 3D printing: Market structure models in light of additive manufacturing revisited. Int. J. Prod. Econ. 2015, 164, 43–56. [Google Scholar] [CrossRef]
- Pérès, F.; Noyes, D. Envisioning e-logistics developments: Making spare parts in situ and on demand. Comput. Ind. 2006, 57, 490–503. [Google Scholar] [CrossRef]
- Poukens, J.; Laeven, P.; Beerens, M.; Nijenhuis, G.; Sloten, J.V.; Stoelinga, P.; Kessler, P. A classification of cranial implants based on the degree of difficulty in computer design and manufacture. Int. J. Med. Robot. Comput. Assist. Surg. 2008, 4, 46–50. [Google Scholar] [CrossRef]
- Warnke, P.H.; Douglas, T.; Wollny, P.; Sherry, E.; Steiner, M.; Galonska, S.; Becker, S.T.; Springer, I.N.; Wiltfang, J.; Sivananthan, S. Rapid Prototyping: Porous Titanium Alloy Scaffolds Produced by Selective Laser Melting for Bone Tissue Engineering. Tissue Eng. Part C Methods 2009, 15, 115–124. [Google Scholar] [CrossRef]
- Salmi, M.; Tuomi, J.; Paloheimo, K.-S.; Paloheimo, M.; Björkstrand, R.; Mäkitie, A.A.; Mesimäki, K.; Kontio, R. Digital design and rapid manufacturing in orbital wall reconstruction. In Innovative Developments in Design and Manufacturing—Advanced Research in Virtual and Rapid Prototyping; CRC Press: Boca Raton, FL, USA, 2010; pp. 339–342. [Google Scholar]
- Lethaus, B.; ter Laak, M.P.; Laeven, P.; Beerens, M.; Koper, D.; Poukens, J.; Kessler, P. A treatment algorithm for patients with large skull bone defects and first results. J. Cranio-Maxillofac. Surg. 2011, 39, 435–440. [Google Scholar] [CrossRef]
- Salmi, M.; Tuomi, J.; Paloheimo, K.; Björkstrand, R.; Paloheimo, M.; Salo, J.; Kontio, R.; Mesimäki, K.; Mäkitie, A.A. Patient-specific reconstruction with 3D modeling and DMLS additive manufacturing. Rapid Prototyp. J. 2012, 18, 209–214. [Google Scholar] [CrossRef]
- Figliuzzi, M.; Mangano, F.; Mangano, C. A novel root analogue dental implant using CT scan and CAD/CAM: Selective laser melting technology. Int. J. Oral Maxillofac. Surg. 2012, 41, 858–862. [Google Scholar] [CrossRef] [PubMed]
- Mangano, F.G.; Cirotti, B.; Sammons, R.L.; Mangano, C. Custom-made, root-analogue direct laser metal forming implant: A case report. Lasers Med. Sci. 2012, 27, 1241–1245. [Google Scholar] [CrossRef] [PubMed]
- Otawa, N.; Sumida, T.; Kitagaki, H.; Sasaki, K.; Fujibayashi, S.; Takemoto, M.; Nakamura, T.; Yamada, T.; Mori, Y.; Matsushita, T. Custom-made titanium devices as membranes for bone augmentation in implant treatment: Modeling accuracy of titanium products constructed with selective laser melting. J. Cranio-Maxillofac. Surg. 2015, 43, 1289–1295. [Google Scholar] [CrossRef] [PubMed]
- Pettersson, A.B.V.; Salmi, M.; Vallittu, P.; Serlo, W.; Tuomi, J.; Mäkitie, A.A. Main Clinical Use of Additive Manufacturing (Three-Dimensional Printing) in Finland Restricted to the Head and Neck Area in 2016–2017. Scand. J. Surg. 2019, 1457496919840958. [Google Scholar] [CrossRef] [PubMed]
- Hollander, D.A.; von Walter, M.; Wirtz, T.; Sellei, R.; Schmidt-Rohlfing, B.; Paar, O.; Erli, H.-J. Structural, mechanical and in vitro characterization of individually structured Ti–6Al–4V produced by direct laser forming. Biomaterials 2006, 27, 955–963. [Google Scholar] [CrossRef] [PubMed]
- Traini, T.; Mangano, C.; Sammons, R.L.; Mangano, F.; Macchi, A.; Piattelli, A. Direct laser metal sintering as a new approach to fabrication of an isoelastic functionally graded material for manufacture of porous titanium dental implants. Dent. Mater. 2008, 24, 1525–1533. [Google Scholar] [CrossRef]
- Shibli, J.A.; Mangano, C.; D’avila, S.; Piattelli, A.; Pecora, G.E.; Mangano, F.; Onuma, T.; Cardoso, L.A.; Ferrari, D.S.; Aguiar, K.C.; et al. Influence of direct laser fabrication implant topography on type IV bone: A histomorphometric study in humans. J. Biomed. Mater. Res. Part. A 2010, 93, 607–614. [Google Scholar] [CrossRef]
- Mullen, L.; Stamp, R.C.; Brooks, W.K.; Jones, E.; Sutcliffe, C.J. Selective Laser Melting: A regular unit cell approach for the manufacture of porous, titanium, bone in-growth constructs, suitable for orthopedic applications. J. Biomed. Mater. Res. Part B Appl. Biomater. 2009, 89B, 325–334. [Google Scholar] [CrossRef]
- Mangano, F.; Chambrone, L.; van Noort, R.; Miller, C.; Hatton, P.; Mangano, C. Direct Metal Laser Sintering Titanium Dental Implants: A Review of the Current Literature. Int. J. Biomater. 2014, 2014, 461534. [Google Scholar] [CrossRef]
- Tuomi, J.; Paloheimo, K.-S.; Björkstrand, R.; Salmi, M.; Paloheimo, M.; Mäkitie, A.A. Medical Applications of Rapid Prototyping—from Applications to Classification. In Proceedings of the VR 2009 Innovative Developments in Design and Manufacturing: Advanced Research in Virtual and Rapid Prototyping, Leira, Portugal, 6–10 October 2009; Volume 4, pp. 701–704. [Google Scholar]
- Tuomi, J.; Paloheimo, K.-S.; Vehviläinen, J.; Björkstrand, R.; Salmi, M.; Huotilainen, E.; Kontio, R.; Rouse, S.; Gibson, I.; Mäkitie, A.A. A Novel Classification and Online Platform for Planning and Documentation of Medical Applications of Additive Manufacturing. Surg. Innov. 2014, 21, 553–559. [Google Scholar] [CrossRef] [PubMed]
- Akmal, J.S.; Salmi, M.; Mäkitie, A.; Björkstrand, R.; Partanen, J. Implementation of Industrial Additive Manufacturing: Intelligent Implants and Drug Delivery Systems. J. Funct. Biomater. 2018, 9, 41. [Google Scholar] [CrossRef]
- Eufinger, H.; Wehmöller, M.; Machtens, E. Individual prostheses and resection templates for mandibular resection and reconstruction. Br. J. Oral Maxillofac. Surg. 1997, 35, 413–418. [Google Scholar] [CrossRef]
- Hallermann, W.; Olsen, S.; Bardyn, T.; Taghizadeh, F.; Banic, A.; Iizuka, T. A new method for computer-aided operation planning for extensive mandibular reconstruction. Plast. Reconstr. Surg. 2006, 117, 2431–2437. [Google Scholar] [CrossRef] [PubMed]
- Hannen, E.J.M. Recreating the original contour in tumor deformed mandibles for plate adapting. Int. J. Oral Maxillofac. Surg. 2006, 35, 183–185. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.-W.; Wang, S.; Fox, B.C.; Ritman, E.L.; Yaszemski, M.J.; Lu, L. Poly(propylene fumarate) Bone Tissue Engineering Scaffold Fabrication Using Stereolithography: Effects of Resin Formulations and Laser Parameters. Biomacromolecules 2007, 8, 1077–1084. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Gui, L.; Mao, C.; Peng, X.; Yu, G. Applying Computer Techniques in Maxillofacial Reconstruction Using a Fibula Flap: A Messenger and an Evaluation Method. J. Craniofac. Surg. 2009, 20, 372–377. [Google Scholar] [CrossRef]
- Esses, S.J.; Berman, P.; Bloom, A.I.; Sosna, J. Clinical Applications of Physical 3D Models Derived From MDCT Data and Created by Rapid Prototyping. Am. J. Roentgenol. 2011, 196, W683–W688. [Google Scholar] [CrossRef]
- Abou-ElFetouh, A.; Barakat, A.; Abdel-Ghany, K. Computer-guided rapid-prototyped templates for segmental mandibular osteotomies: A preliminary report. Int. J. Med. Robot. Comput. Assist. Surg. 2011, 7, 187–192. [Google Scholar] [CrossRef]
- Zhou, L.; Shang, H.; He, L.; Bo, B.; Liu, G.; Liu, Y.; Zhao, J. Accurate Reconstruction of Discontinuous Mandible Using a Reverse Engineering/Computer-Aided Design/Rapid Prototyping Technique: A Preliminary Clinical Study. J. Oral Maxillofac. Surg. 2010, 68, 2115–2121. [Google Scholar] [CrossRef]
- Scarfe, W.C.; Farman, A.G.; Sukovic, P. Clinical Applications of Cone-Beam Computed Tomography in Dental Practice. J. Can. Dent. Assoc. 2006, 72, 6. [Google Scholar]
- Johnson, T.R.C. Dual-Energy CT: General Principles. Am. J. Roentgenol. 2012, 199, S3–S8. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.; Jacobs, R.; Hassan, B.; Li, L.; Pauwels, R.; Corpas, L.; Souza, P.C.; Martens, W.; Shahbazian, M.; Alonso, A.; et al. A comparative evaluation of Cone Beam Computed Tomography (CBCT) and Multi-Slice CT (MSCT): Part I. On subjective image quality. Eur. J. Radiol. 2010, 75, 265–269. [Google Scholar] [CrossRef]
- Lofthag-Hansen, S.; Thilander-Klang, A.; Gröndahl, K. Evaluation of subjective image quality in relation to diagnostic task for cone beam computed tomography with different fields of view. Eur. J. Radiol. 2011, 80, 483–488. [Google Scholar] [CrossRef] [PubMed]
- Van Eijnatten, M.; Koivisto, J.; Karhu, K.; Forouzanfar, T.; Wolff, J. The impact of manual threshold selection in medical additive manufacturing. Int. J. Comput. Assist. Radiol. Surg. 2017, 12, 607–615. [Google Scholar] [CrossRef] [PubMed]
- Bujtár, P.; Simonovics, J.; Zombori, G.; Fejer, Z.; Szucs, A.; Bojtos, A.; Batista, W.O.; Váradi, K.; Sándor, G.K.B. Internal or in-scan validation: A method to assess CBCT and MSCT gray scales using a human cadaver. Oral Surg. Oral Med. Oral Pathol. Oral Radiol. 2014, 117, 768–779. [Google Scholar] [CrossRef] [PubMed]
- Bamba, J.; Araki, K.; Endo, A.; Okano, T. Image quality assessment of three cone beam CT machines using the SEDENTEXCT CT phantom. Dentomaxillofac. Radiol. 2013, 42, 20120445. [Google Scholar] [CrossRef]
- De Las Heras Gala, H.; Torresin, A.; Dasu, A.; Rampado, O.; Delis, H.; Girón, I.H.; Theodorakou, C.; Andersson, J.; Holroyd, J.; Nilsson, M.; et al. Quality Control in Cone-Beam Computed Tomography (CBCT), EFOMP-ESTRO-IAEA Protocol. Phys. Med. 2017, 39, 67–72. [Google Scholar] [CrossRef]
- IEC 60601-2-44:2009+AMD1:2012+AMD2:2016 CSV. Medical Electrical Equipment—Part 2-44: Particular Requirements for the Basic Safety and Essential Performance of X-ray Equipment for Computed Tomography, 3rd ed.; International Electrotechnical Commission: Geneva, Switzerland, 2016. [Google Scholar]
- Batista, W.O.; Navarro, M.V.T.; Maia, A.F. Development and implementation of a low-cost phantom for quality control in cone beam computed tomography. Radiat. Prot. Dosim. 2013, 157, 552–560. [Google Scholar] [CrossRef]
- Homolka, P.; Nowotny, R. Production of phantom materials using polymer powder sintering under vacuum. Phys. Med. Biol. 2002, 47, N47–N52. [Google Scholar] [CrossRef]
- Kragskov, J.; Sindet-Pedersen, S.; Gyldensted, C.; Jensen, K.L. A comparison of three-dimensional computed tomography scans and stereolithographic models for evaluation of craniofacial anomalies. J. Oral Maxillofac. Surg. 1996, 54, 402–411. [Google Scholar] [CrossRef]
- Pauwels, R.; Nackaerts, O.; Bellaiche, N.; Stamatakis, H.; Tsiklakis, K.; Walker, A.; Bosmans, H.; Bogaerts, R.; Jacobs, R.; Horner, K.; et al. Variability of dental cone beam CT grey values for density estimations. Br. J. Radiol. 2013, 86, 20120135. [Google Scholar] [CrossRef] [PubMed]
- Huotilainen, E.; Salmi, M.; Lindahl, J. Three-dimensional printed surgical templates for fresh cadaveric osteochondral allograft surgery with dimension verification by multivariate computed tomography analysis. Knee 2019, 26, 923–932. [Google Scholar] [CrossRef] [PubMed]
- Chougule, V.N.; Mulay, A.V.; Ahuja, B.B. Three dimensional point cloud generations from CT scan images for bio-cad modeling. In Proceedings of the International Conference on Additive Manufacturing Technologies, Banglore, India, 7–8 October 2013; p. 5. [Google Scholar]
- Lorensen, W.E.; Cline, H.E. Marching Cubes: A High Resolution 3D Surface Construction Algorithm. Comput. Graph. 1987, 21, 7. [Google Scholar] [CrossRef]
- Sahoo, P.K.; Soltani, S.; Wong, A.K.C. A Survey of Thresholding Techniques. Comput. Vis. Graph. Image Process. 1998, 41, 233–260. [Google Scholar] [CrossRef]
- BIPM; IEC; IFCC; ILAC; ISO; IUPAC; IUPAP; OIML. Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement; Joint Committee for Guides in Metrology: Sèvres Cedex, France, 2008. [Google Scholar]
- George, E.; Liacouras, P.; Rybicki, F.J.; Mitsouras, D. Measuring and Establishing the Accuracy and Reproducibility of 3D Printed Medical Models. RadioGraphics 2017, 37, 1424–1450. [Google Scholar] [CrossRef]
- Pinto, J.M.; Arrieta, C.; Andia, M.E.; Uribe, S.; Ramos-Grez, J.; Vargas, A.; Irarrazaval, P.; Tejos, C. Sensitivity analysis of geometric errors in additive manufacturing medical models. Med. Eng. Phys. 2015, 37, 328–334. [Google Scholar] [CrossRef]
- Chen, H.; van Eijnatten, M.; Aarab, G.; Forouzanfar, T.; de Lange, J.; van der Stelt, P.; Lobbezoo, F.; Wolff, J. Accuracy of MDCT and CBCT in three-dimensional evaluation of the oropharynx morphology. Eur. J. Orthod. 2018, 40, 58–64. [Google Scholar] [CrossRef]
- Arrieta, C.; Uribe, S.; Ramos-Grez, J.; Vargas, A.; Irarrazaval, P.; Parot, V.; Tejos, C. Quantitative assessments of geometric errors for rapid prototyping in medical applications. Rapid Prototyp. J. 2012, 18, 431–442. [Google Scholar] [CrossRef]
- Huotilainen, E.; Jaanimets, R.; Valášek, J.; Marcián, P.; Salmi, M.; Tuomi, J.; Mäkitie, A.; Wolff, J. Inaccuracies in additive manufactured medical skull models caused by the DICOM to STL conversion process. J. Cranio-Maxillofac. Surg. 2014, 42, e259–e265. [Google Scholar] [CrossRef]
- Salmi, M.; Paloheimo, K.-S.; Tuomi, J.; Wolff, J.; Mäkitie, A. Accuracy of medical models made by additive manufacturing (rapid manufacturing). J. Cranio-Maxillofac. Surg. 2013, 41, 603–609. [Google Scholar] [CrossRef] [PubMed]
- Braian, M.; Jönsson, D.; Kevci, M.; Wennerberg, A. Geometrical accuracy of metallic objects produced with additive or subtractive manufacturing: A comparative in vitro study. Dent. Mater. 2018, 34, 978–993. [Google Scholar] [CrossRef] [PubMed]
- The International Bureau of Weights and Measures. The International Systems of Units (SI), 9th ed.; The International Bureau of Weights and Measures (BIPM): Sèvres Cedex, France, 2019; Available online: https://www.bipm.org/utils/common/pdf/si-brochure/SI-Brochure-9-EN.pdf (accessed on 24 April 2019).
- Sładek, J.A. Coordinate Metrology: Accuracy of Systems and Measurements; Springer Tracts in Mechanical Engineering; Springer: Berlin/Heidelberg, Germany, 2016; ISBN 978-3-662-48463-0. [Google Scholar]
- Savio, E.; De Chiffre, L.; Schmitt, R. Metrology of freeform shaped parts. CIRP Ann. 2007, 56, 810–835. [Google Scholar] [CrossRef]
- Aguilar, J.J.; Torres, F.; Lope, M.A. Stereo vision for 3D measurement: Accuracy analysis, calibration and industrial applications. Measurement 1996, 18, 193–200. [Google Scholar] [CrossRef]
- Akar, A.; Baltaş, H.; Çevik, U.; Korkmaz, F.; Okumuşoğlu, N.T. Measurement of attenuation coefficients for bone, muscle, fat and water at 140, 364 and 662keV -ray energies. J. Quant. Spectrosc. Radiat. Transf. 2006, 102, 203–211. [Google Scholar] [CrossRef]
- Lagravère, M.; Fang, Y.; Carey, J.; Toogood, R.; Packota, G.; Major, P. Density conversion factor determined using a cone-beam computed tomography unit NewTom QR-DVT 9000. Dentomaxillofac. Radiol. 2006, 35, 407–409. [Google Scholar] [CrossRef]
- Lagravère, M.O.; Carey, J.; Ben-Zvi, M.; Packota, G.V.; Major, P.W. Effect of object location on the density measurement and Hounsfield conversion in a NewTom 3G cone beam computed tomography unit. Dentomaxillofac. Radiol. 2008, 37, 305–308. [Google Scholar] [CrossRef]
- Akmal, J.S.; Salmi, M.; Hemming, B.; Teir, L.; Suomalainen, A.; Kortesniemi, M.; Partanen, J.; Lassila, A. Cumulative inaccuracies in implementation of additive manufacturing through medical imaging, 3D thresholding, and 3D modeling: A case study for an end-use implant. Mendeley Data 2020. [Google Scholar] [CrossRef]
- Lassila, A.; Kari, M.; Koivula, H.; Koivula, U.; Kortström, J.; Leinonen, E.; Manninen, J.; Manssila, J.; Mansten, T.; Meriläinen, T.; et al. Design and performance of an advanced metrology building for MIKES. Measurement 2011, 44, 399–425. [Google Scholar] [CrossRef]
- Das, M.; Ley-Zaporozhan, J.; Gietema, H.A.; Czech, A.; Mühlenbruch, G.; Mahnken, A.H.; Katoh, M.; Bakai, A.; Salganicoff, M.; Diederich, S.; et al. Accuracy of automated volumetry of pulmonary nodules across different multislice CT scanners. Eur. Radiol. 2007, 17, 1979–1984. [Google Scholar] [CrossRef]
- Liang, X.; Lambrichts, I.; Sun, Y.; Denis, K.; Hassan, B.; Li, L.; Pauwels, R.; Jacobs, R. A comparative evaluation of Cone Beam Computed Tomography (CBCT) and Multi-Slice CT (MSCT). Part II: On 3D model accuracy. Eur. J. Radiol. 2010, 75, 270–274. [Google Scholar] [CrossRef] [PubMed]
- Kang, S.-H.; Kim, M.-K.; Kim, H.-J.; Zhengguo, P.; Lee, S.-H. Accuracy Assessment of Image-Based Surface Meshing for Volumetric Computed Tomography Images in the Craniofacial Region. J. Craniofac. Surg. 2014, 25, 2051–2055. [Google Scholar] [CrossRef] [PubMed]
- Van Eijnatten, M.; van Dijk, R.; Dobbe, J.; Streekstra, G.; Koivisto, J.; Wolff, J. CT image segmentation methods for bone used in medical additive manufacturing. Med. Eng. Phys. 2018, 51, 6–16. [Google Scholar] [CrossRef] [PubMed]
- Gelaude, F.; Vander Sloten, J.; Lauwers, B. Accuracy assessment of CT-based outer surface femur meshes. Comput. Aided Surg. 2008, 13, 188–199. [Google Scholar] [CrossRef] [PubMed]
- Fadel, G.M.; Kirschman, C. Accuracy issues in CAD to RP translations. Rapid Prototyp. J. 1996, 2, 4–17. [Google Scholar] [CrossRef]
- Ullah, R.; Akmal, J.S.; Laakso, S.V.A.; Niemi, E. Anisotropy of additively manufactured AlSi10Mg: Threads and surface integrity. Int. J. Adv. Manuf. Technol. 2020. [Google Scholar] [CrossRef]
- Vilaro, T.; Colin, C.; Bartout, J.D. As-Fabricated and Heat-Treated Microstructures of the Ti-6Al-4V Alloy Processed by Selective Laser Melting. Metall. Mater. Trans. A 2011, 42, 3190–3199. [Google Scholar] [CrossRef]
- Chen, L.Y.; Huang, J.C.; Lin, C.H.; Pan, C.T.; Chen, S.Y.; Yang, T.L.; Lin, D.Y.; Lin, H.K.; Jang, J.S.C. Anisotropic response of Ti-6Al-4V alloy fabricated by 3D printing selective laser melting. Mater. Sci. Eng. A 2017, 682, 389–395. [Google Scholar] [CrossRef]
- Wu, M.-W.; Lai, P.-H.; Chen, J.-K. Anisotropy in the impact toughness of selective laser melted Ti–6Al–4V alloy. Mater. Sci. Eng. A 2016, 650, 295–299. [Google Scholar] [CrossRef]
- Popovich, A.A.; Sufiiarov, V.S.; Borisov, E.V.; Polozov, I.A.; Masaylo, D.V.; Grigoriev, A.V. Anisotropy of mechanical properties of products manufactured using selective laser melting of powdered materials. Russ. J. Non-Ferr. Met. 2017, 58, 389–395. [Google Scholar] [CrossRef]
- Calle, M.A.G.; Salmi, M.; Mazzariol, L.M.; Kujala, P. Miniature reproduction of raking tests on marine structure: Similarity technique and experiment. Eng. Struct. 2020, 212, 110527. [Google Scholar] [CrossRef]
- Barker, T.M.; Earwaker, W.J.S.; Lisle, D.A. Accuracy of stereolithographic models of human anatomy. Australas. Radiol. 1994, 38, 106–111. [Google Scholar] [CrossRef] [PubMed]
- Chang, P.S.-H.; Parker, T.H.; Patrick, C.W.; Miller, M.J. The Accuracy of Stereolithography in Planning Craniofacial Bone Replacement. J. Craniofac. Surg. 2003, 14, 164–170. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.-Y.; Choi, J.-H.; Kim, N.-K.; Kim, Y.; Lee, J.-K.; Kim, M.-K.; Lee, J.-H.; Kim, M.-J. Analysis of errors in medical rapid prototyping models. Int. J. Oral Maxillofac. Surg. 2002, 31, 23–32. [Google Scholar] [CrossRef] [PubMed]
- El-Katatny, I.; Masood, S.H.; Morsi, Y.S. Error analysis of FDM fabricated medical replicas. Rapid Prototyp. J. 2010, 16, 36–43. [Google Scholar] [CrossRef]
- Ibrahim, D.; Broilo, T.L.; Heitz, C.; de Oliveira, M.G.; de Oliveira, H.W.; Nobre, S.M.W.; dos Santos Filho, J.H.G.; Silva, D.N. Dimensional error of selective laser sintering, three-dimensional printing and PolyJet™ models in the reproduction of mandibular anatomy. J. Cranio-Maxillofac. Surg. 2009, 37, 167–173. [Google Scholar] [CrossRef]
- Nizam, A.; Gopal, R.N.; Naing, L.; Hakim, A.B.; Samsudin, A.R. Dimensional Accuracy of the Skull Models Produced by Rapid Prototyping Technology Using Stereolithography Apparatus. Arch. Orofac. Sci. 2006, 1, 60–66. [Google Scholar]
- Ono, I.; Gunji, H.; Suda, K.; Kaneko, F. Method for preparing an exact-size model using helical volume scan computed tomography. Plast. Reconstr. Surg. 1994, 93, 1363–1371. [Google Scholar] [CrossRef]
- Osman, R.B.; van der Veen, A.J.; Huiberts, D.; Wismeijer, D.; Alharbi, N. 3D-printing zirconia implants; a dream or a reality? An In-Vitro study evaluating the dimensional accuracy, surface topography and mechanical properties of printed zirconia implant and discs. J. Mech. Behav. Biomed. Mater. 2017, 75, 521–528. [Google Scholar] [CrossRef]
- Silva, D.N.; Gerhardt de Oliveira, M.; Meurer, E.; Meurer, M.I.; Lopes da Silva, J.V.; Santa-Bárbara, A. Dimensional error in selective laser sintering and 3D-printing of models for craniomaxillary anatomy reconstruction. J. Cranio-Maxillofac. Surg. 2008, 36, 443–449. [Google Scholar] [CrossRef]
- Taft, R.M.; Kondor, S.; Grant, G.T. Accuracy of rapid prototype models for head and neck reconstruction. J. Prosthet. Dent. 2011, 106, 399–408. [Google Scholar] [CrossRef]
- Van Eijnatten, M.; Rijkhorst, E.-J.; Hofman, M.; Forouzanfar, T.; Wolff, J. The accuracy of ultrashort echo time MRI sequences for medical additive manufacturing. Dentomaxillofac. Radiol. 2016, 45, 20150424. [Google Scholar] [CrossRef] [PubMed]
- Waitzman, A.A.; Posnick, J.C.; Armstrong, D.C.; Pron, G.E. Craniofacial skeletal measure-ments based on computed tomography: Part I. Accuracy and reproducibility. Cleft Palate Craniofac. J. 1992, 29, 112–117. [Google Scholar] [CrossRef]
- Stoor, P.; Suomalainen, A.; Lindqvist, C.; Mesimäki, K.; Danielsson, D.; Westermark, A.; Kontio, R.K. Rapid prototyped patient specific implants for reconstruction of orbital wall defects. J. Cranio-Maxillofac. Surg. 2014, 42, 1644–1649. [Google Scholar] [CrossRef]
- Tahmaseb, A.; Wu, V.; Wismeijer, D.; Coucke, W.; Evans, C. The accuracy of static computer-aided implant surgery: A systematic review and meta-analysis. Clin. Oral Implant. Res. 2018, 29, 416–435. [Google Scholar] [CrossRef]
- Mitsouras, D.; Liacouras, P.; Imanzadeh, A.; Giannopoulos, A.A.; Cai, T.; Kumamaru, K.K.; George, E.; Wake, N.; Caterson, E.J.; Pomahac, B.; et al. Medical 3D Printing for the Radiologist. RadioGraphics 2015, 35, 1965–1988. [Google Scholar] [CrossRef]
- Elgalal, M.; Kozakiewicz, M.; Olszycki, M.; Walkowiak, B.; Stefanczyk, L. Custom implant design and surgical pre-planning using rapid prototyping and anatomical models for the repair of orbital floor fractures. Eur. Radiol. 2009, 19, S397. [Google Scholar]
- Ciocca, L.; Marchetti, C.; Mazzoni, S.; Baldissara, P.; Gatto, M.R.A.; Cipriani, R.; Scotti, R.; Tarsitano, A. Accuracy of fibular sectioning and insertion into a rapid-prototyped bone plate, for mandibular reconstruction using CAD-CAM technology. J. Cranio-Maxillofac. Surg. 2015, 43, 28–33. [Google Scholar] [CrossRef] [PubMed]
- Stoor, P.; Suomalainen, A.; Mesimäki, K.; Kontio, R. Rapid prototyped patient specific guiding implants in critical mandibular reconstruction. J. Cranio-Maxillofac. Surg. 2017, 45, 63–70. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).