Method to Control the Deformation of Anti-Slide Piles in Zhenzilin Landslide
Abstract
1. Introduction
2. Engineering Background, Site Investigation, and Laboratory Test
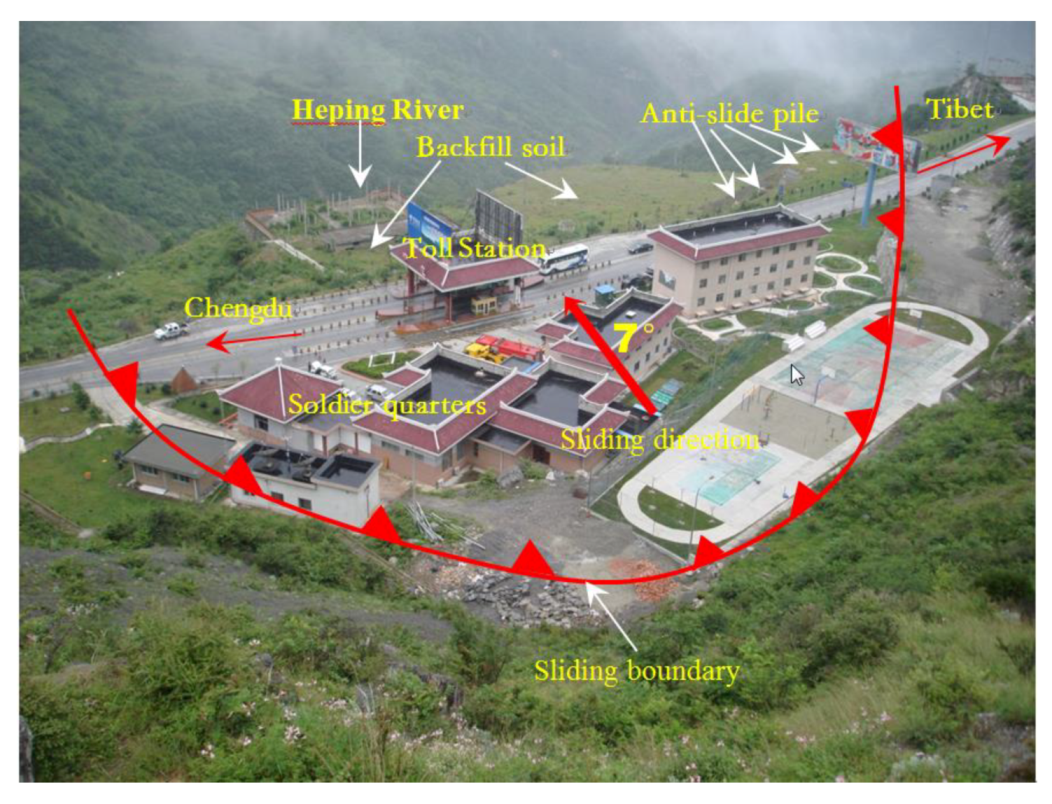
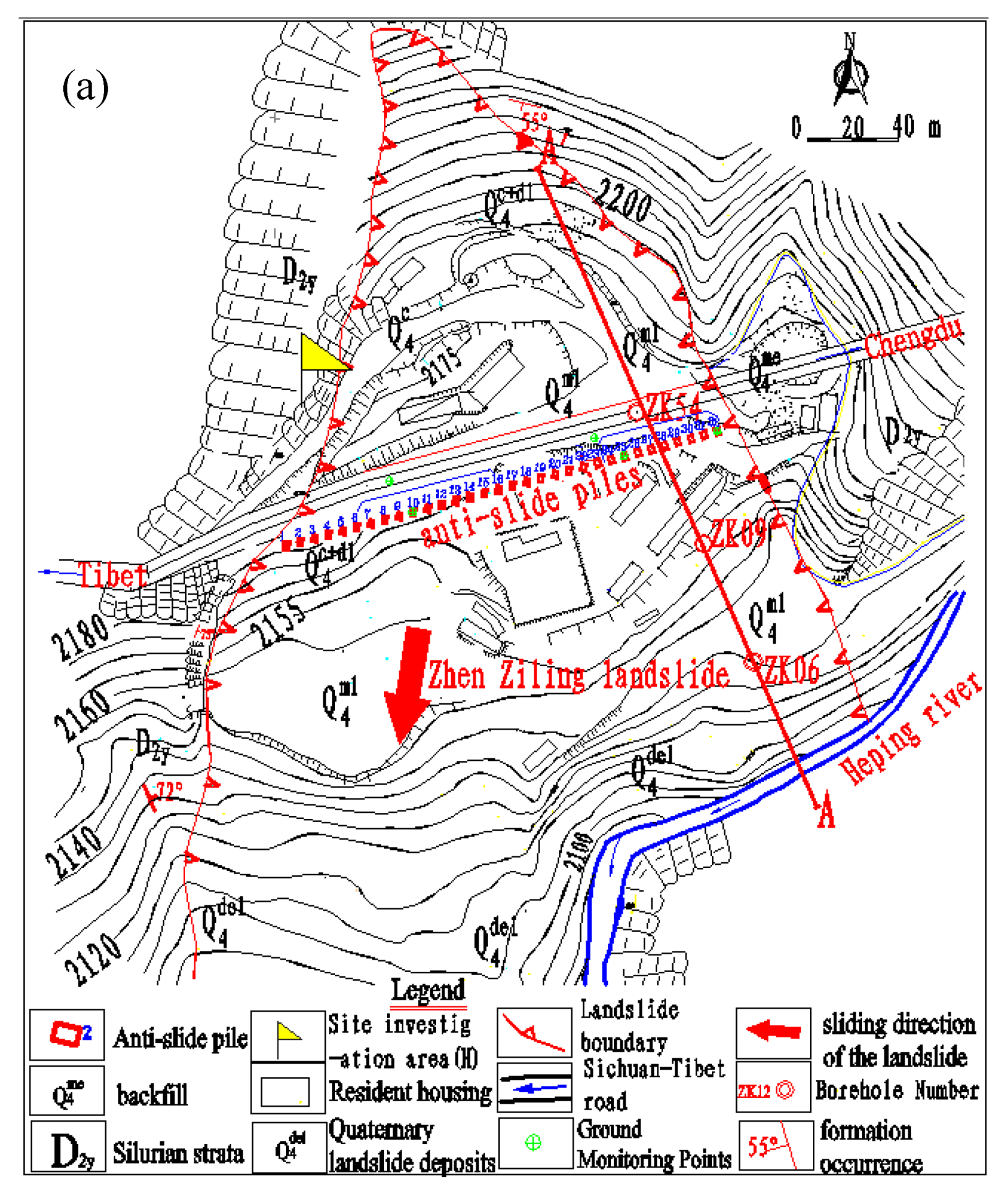
2.1. Geological Background of the Zhenzilin landslide
2.2. Landslide Stabilizing Measures
2.3. Site Investigation of Anti-Slide Pile Deformations
2.4. Laboratory Test of Sandstone and Mudstone
3. Methodology and Validation
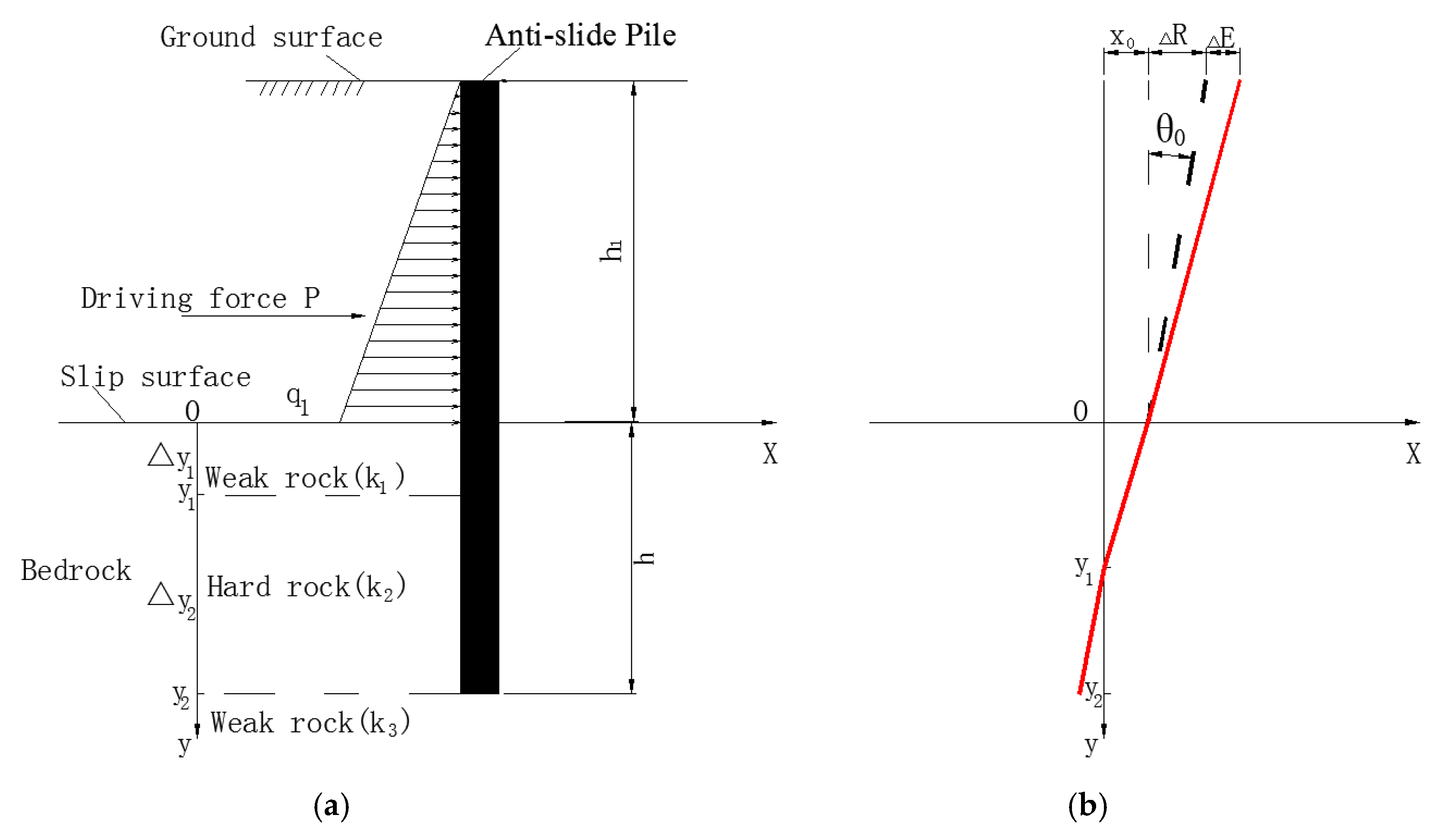
3.1. Methods for Anti-Slide Pile Calculations in Two Bedrocks with Different Strengths below the Slip Surface
3.2. Calculation Method for an Anti-Slide Pile above the Slip Surface
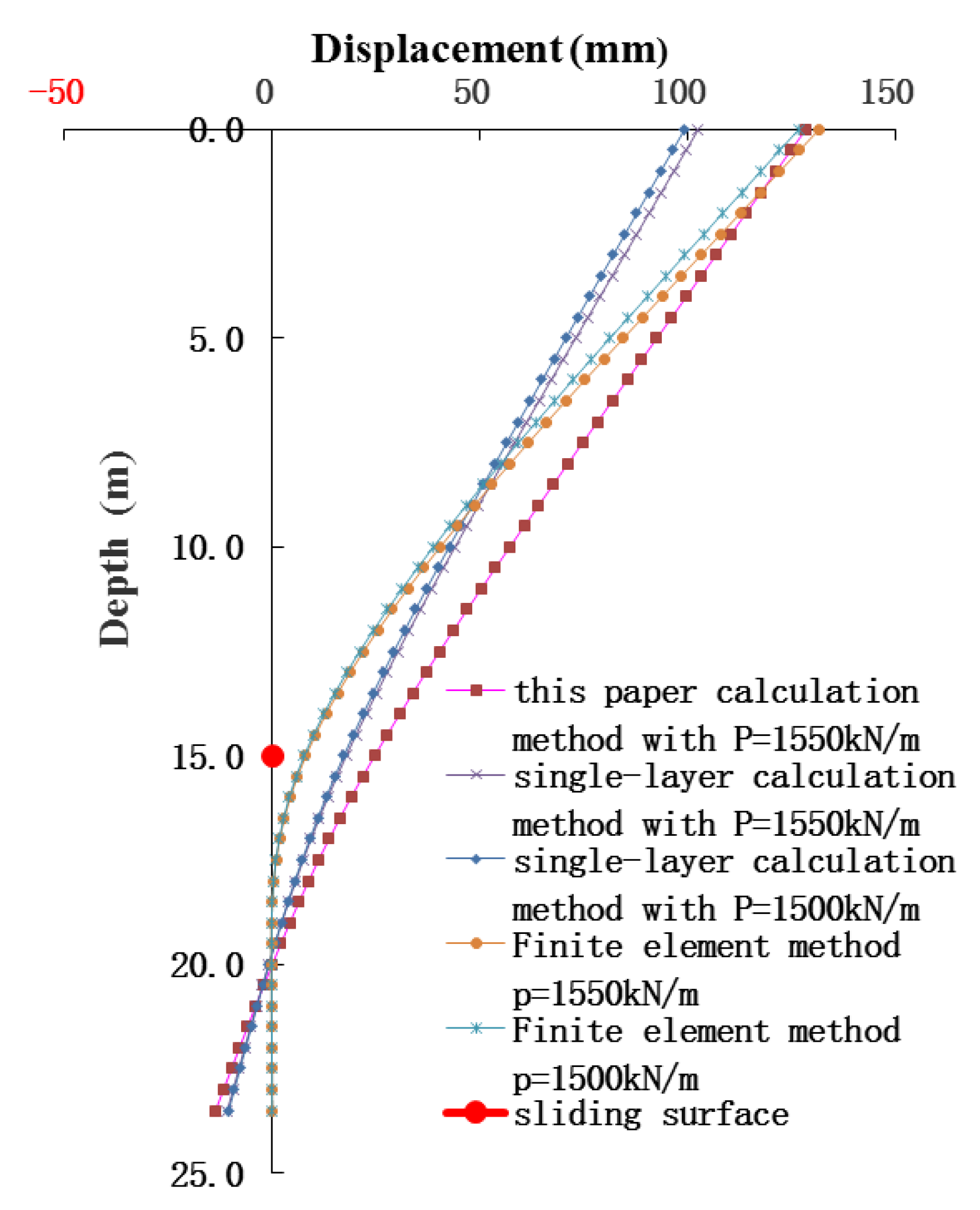
3.3. Validation of the Calculation Method for the Zhenzilin landslide
4. Influencing Factors and Control Methods of Anti-Slide Pile Deformation
4.1. Factors Influencing Anti-Slide Pile Deformation
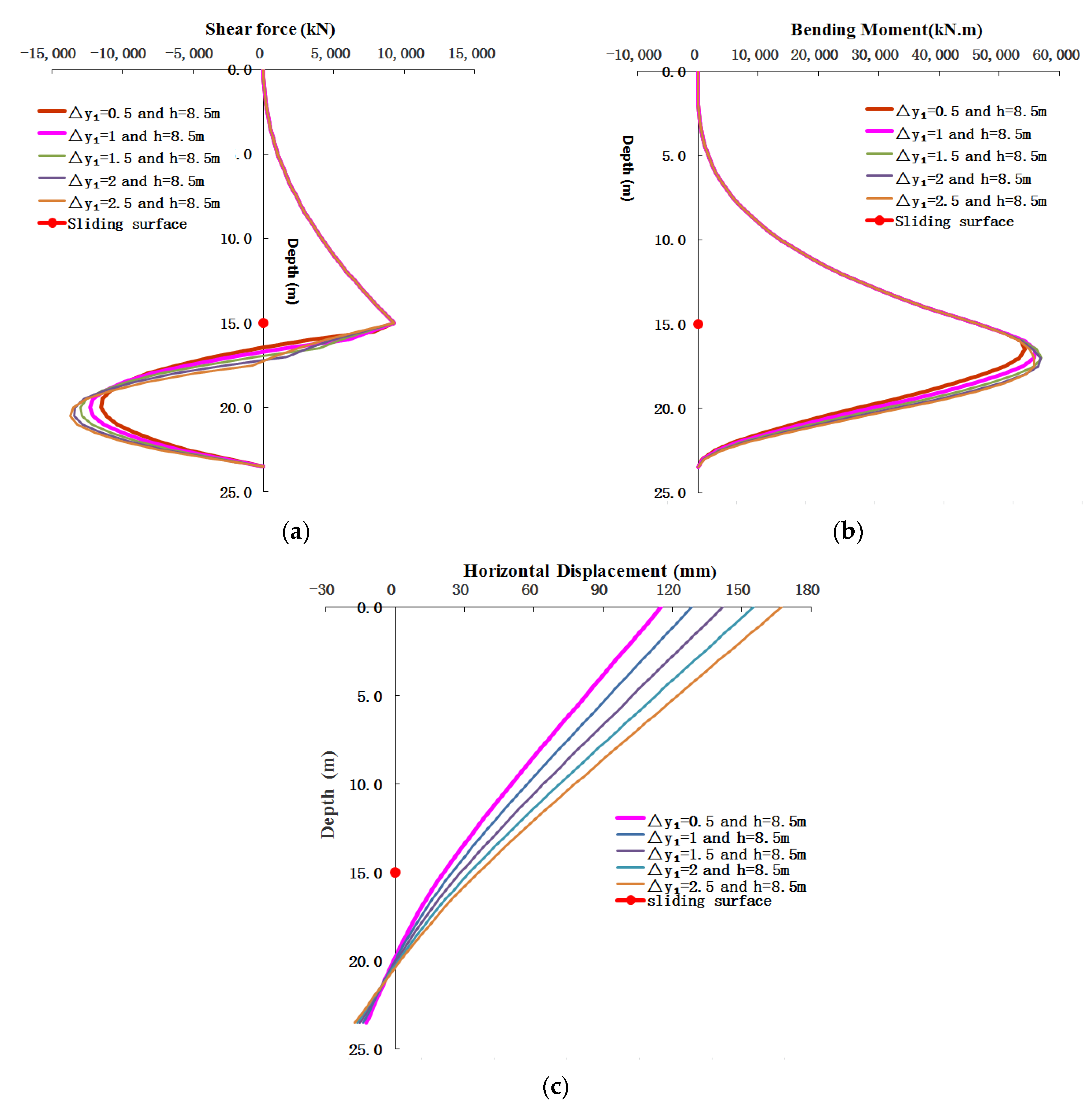
4.2. Effect of Thickness of First Weak Bedrock on the Displacement and Internal Force of the Piles
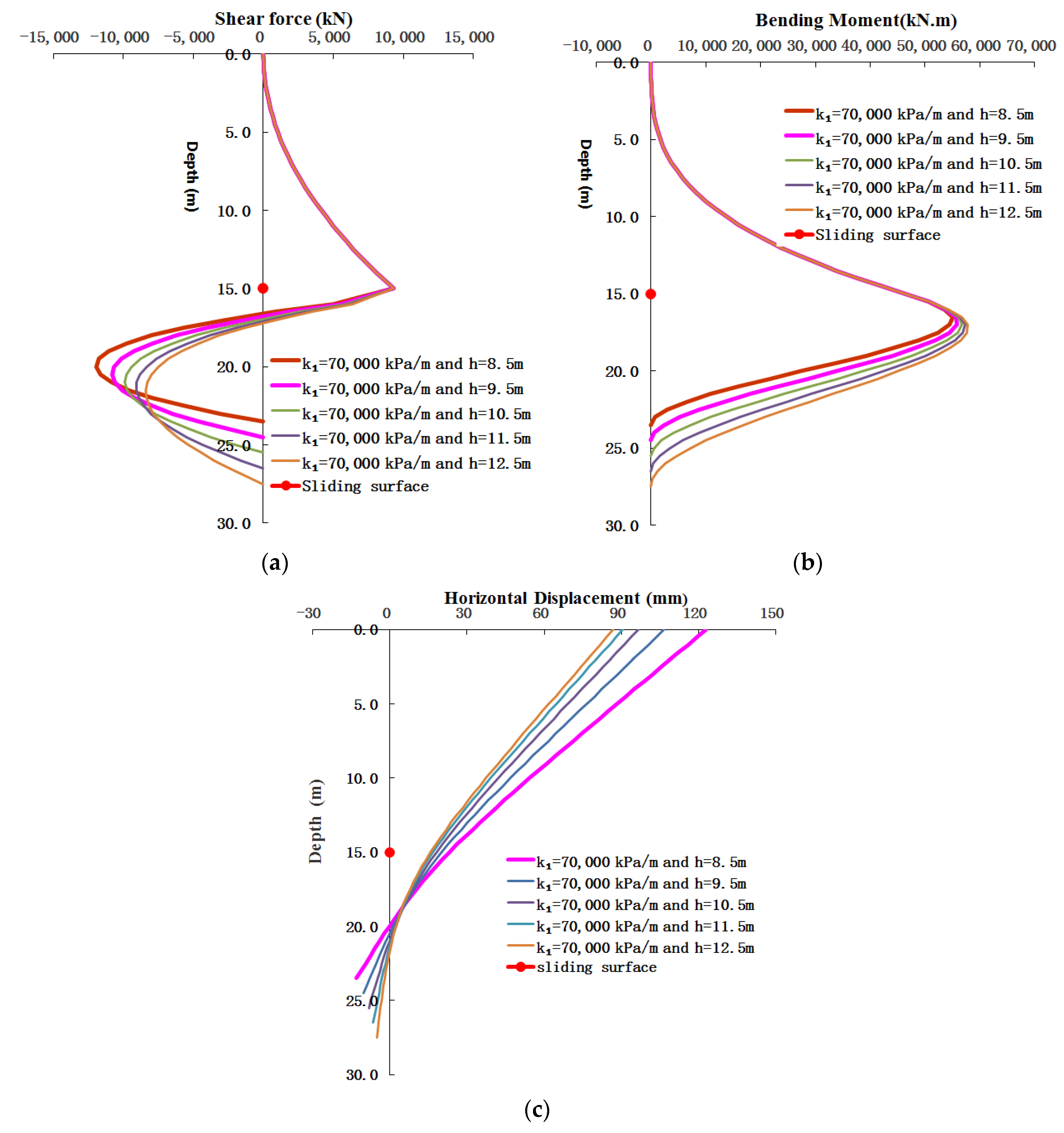
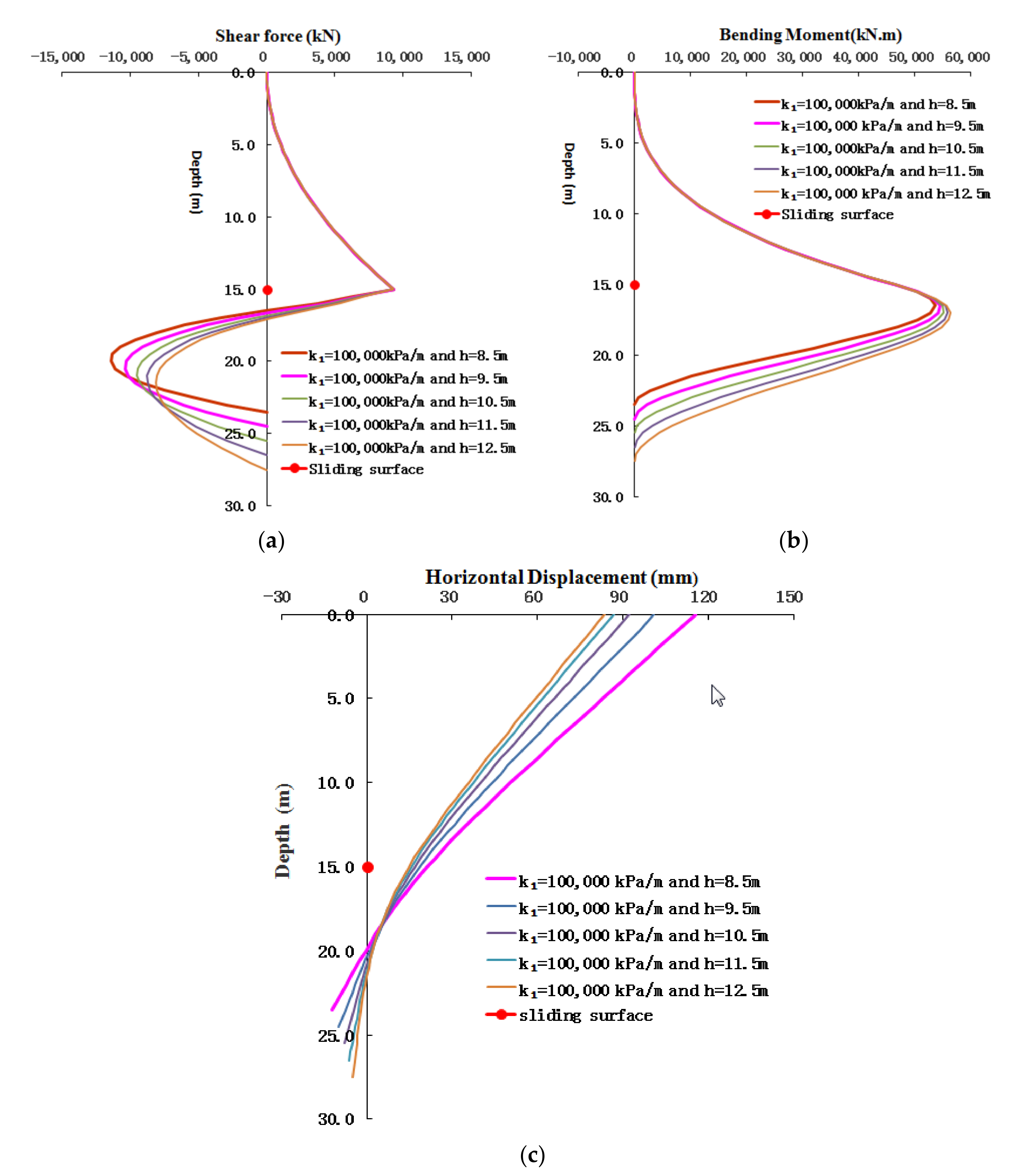
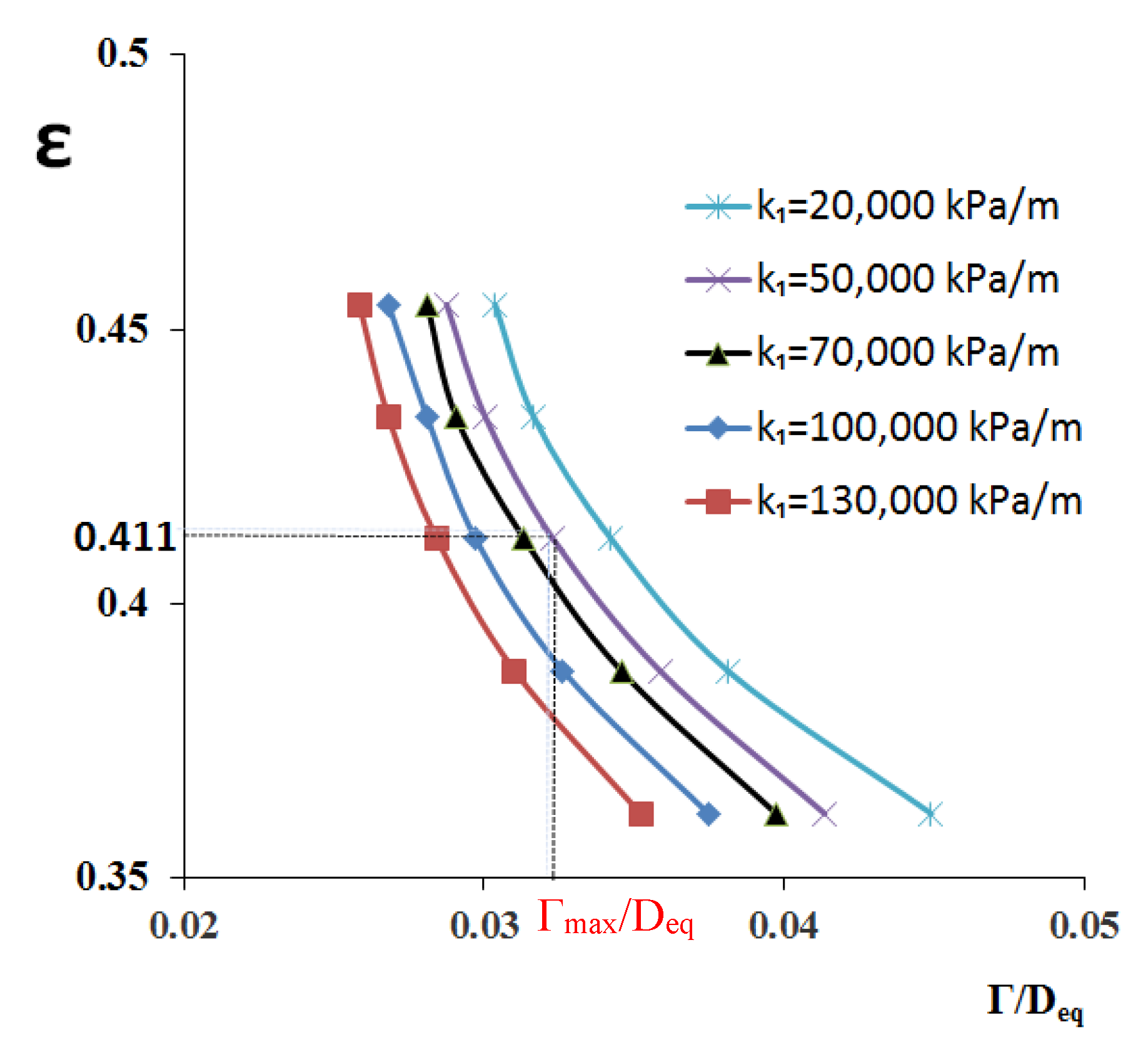
4.3. Effect of the Modulus of Subgrade Reaction for the First Weak Bedrock on the Reasonable Embedded Length
5. Discussion
5.1. Effect of the thickness of Lower Bedrock on the Deformation and Internal Forces of the Pile
5.2. Effect of Subgrade Reaction Modulus of First Weak Bedrock on the Deformation and Internal Forces of Pile
5.3. Effect of The Embedded Length on the Deformation and Internal Forces of the Pile
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jin, X.G.; Hong, W.; Zhu, L.; Wang, L.B. Study on Time-Space Motivation and Operation Mechanic of Landslide - A Case of Zhenzilin Landslide in Sichuan-Tibet Highway. Adv. Mater. Res. 2011, 243, 2811–2818. [Google Scholar] [CrossRef]
- Shen, J.H.; Wang, L.S.; Zhao, Q.H.; Jin, X.G.; Fu, R.H. The Genesis mechanism and treatment measure of Zhenzilin landslide in Erlang mountain. J. Chengdu Inst. Technol. 2000, 27, 184–188. (In Chinese) [Google Scholar]
- Kahyaoğlu, M.R.; Imançlı, G.; Özden, G.; Kayalar, A.S.; Imançli, G. Numerical simulations of landslide-stabilizing piles: A remediation project in Söke, Turkey. Environ. Earth Sci. 2017, 76, 656. [Google Scholar] [CrossRef]
- Lu, J.-F.; Zhang, X.; Wan, J.-W.; Cang, N.-R. The influence of a fixed axial top load on the dynamic response of a single pile. Comput. Geotech. 2012, 39, 54–65. [Google Scholar] [CrossRef]
- Chen, Y.-L.; Liu, G.-Y.; Li, N.; Du, X.; Wang, S.-R.; Azzam, R. Stability evaluation of slope subjected to seismic effect combined with consequent rainfall. Eng. Geol. 2020, 266, 105461. [Google Scholar] [CrossRef]
- Han, Z.; Su, B.; Li, Y.; Ma, Y.; Wang, W.; Chen, G. Comprehensive analysis of landslide stability and related countermeasures: A case study of the Lanmuxi landslide in China. Sci. Rep. 2019, 9, 12407–12412. [Google Scholar] [CrossRef]
- Li, C.; Wu, J.; Tang, H.; Hu, X.; Liu, X.; Wang, C.; Liu, T.; Zhang, Y. Model testing of the response of stabilizing piles in landslides with upper hard and lower weak bedrock. Eng. Geol. 2016, 204, 65–76. [Google Scholar] [CrossRef]
- Lirer, S. Landslide stabilizing piles: Experimental evidences and numerical interpretation. Eng. Geol. 2012, 149, 70–77. [Google Scholar] [CrossRef]
- Xiao, Z.Y.; Ji, Y.X.; Qu, Q.F.; Li, X.G. Reliability-Based Analysis and Global Optimization Design of Anchor Anti-Slide Pile. Adv. Mater. Res. 2014, 1065, 296–301. [Google Scholar] [CrossRef]
- Bo, Z.; Yun-Sheng, W.; Yu, W.; Tong, S.; Yong-Chao, Z. Retaining mechanism and structural characteristics of h type anti-slide pile (hTP pile) and experience with its engineering application. Eng. Geol. 2017, 222, 29–37. [Google Scholar] [CrossRef]
- Ito, T.; Matsui, T. Methods to Estimate Lateral Force Acting on Stabilizing Piles. Soils Found. 1975, 15, 43–59. [Google Scholar] [CrossRef]
- Abbas, J.M.; Chik, Z.H.; Taha, M.R. Single pile simulation and analysis subjected to lateral load. Electron. J. Geotech. Eng. 2008, 13, 1–15. [Google Scholar]
- Rathod, D.; Muthukkumaran, K.; Sitharam, T.G. Development of Non-dimension p–y Curves for Laterally Loaded Piles in Sloping Ground. Indian Geotech. J. 2016, 47, 47–56. [Google Scholar] [CrossRef]
- Tang, X.; Yang, M. Analysis of laterally-loaded piles in weathered rock slopes based on p-y curve method. Int. J. Geotech. Eng. 2018, 7, 1–11. [Google Scholar] [CrossRef]
- Frank, R.; Pouget, P. Experimental pile subjected to long duration thrusts owing to a moving slope. Géotechnique 2008, 58, 645–658. [Google Scholar] [CrossRef]
- Martin, G.; Chen, C.-Y. Response of piles due to lateral slope movement. Comput. Struct. 2005, 83, 588–598. [Google Scholar] [CrossRef]
- Song, Y.-S.; Hong, W.-P.; Woo, K.-S. Behavior and analysis of stabilizing piles installed in a cut slope during heavy rainfall. Eng. Geol. 2012, 129, 56–67. [Google Scholar] [CrossRef]
- Li, C.; Liu, Q.; Hu, X.; Wang, L.; MA M, E.E. Influence of composite elastic modulus and lateral load pattern on deflection of anti-slide pile head. J. Civ. Eng. Manag. 2015, 22, 382–390. [Google Scholar] [CrossRef][Green Version]
- Tang, H.; Hu, X.; Xu, C.; Li, C.; Yong, R.; Wang, L. A novel approach for determining landslide pushing force based on landslide-pile interactions. Eng. Geol. 2014, 182, 15–24. [Google Scholar] [CrossRef]
- Chenglin, L. Study on the Embedded Depth of Anti-Slide Piles. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2014. (In Chinese). [Google Scholar]
- Poulos, H. Design of reinforcing piles to increase slope stability. Can. Geotech. J. 1995, 32, 808–818. [Google Scholar] [CrossRef]
- Guo, W.; Qin, H. Thrust and bending moment of rigid piles subjected to moving soil. Can. Geotech. J. 2010, 47, 180–196. [Google Scholar] [CrossRef]
- Qin, H.; Guo, W. Response of piles subjected to progressive soil movement. Geotech. T. J. 2016, 39, 106–125. [Google Scholar] [CrossRef]
- Cai, F.; Ugai, K. Response of flexible piles under laterally linear movement of the sliding layer in landslides. Can. Geotech. J. 2003, 40, 46–53. [Google Scholar] [CrossRef]
- Wei, W.; Cheng, Y.-M. Strength reduction analysis for slope reinforced with one row of piles. Comput. Geotech. 2009, 36, 1176–1185. [Google Scholar] [CrossRef]
- Wei, B.; Fan, J.; Chen, Y.H.; Zheng, X.; Sheng, G.Q. The Analysis of Pile Deformat on Impact Factor of Pile Retaining Wall in Expansive Soil Area. Appl. Mech. Mater. 2012, 204, 230–234. [Google Scholar] [CrossRef]
- Yang, S.; Ren, X.; Zhang, J. Study on embedded length of piles for slope reinforced with one row of piles. J. Rock Mech. Geotech. Eng. 2011, 3, 167–178. [Google Scholar] [CrossRef]
- Liu, Q.S.; Liu, D.F. Study on Embedded Pile Length in Slope Reinforced. Appl. Mech. Mater. 2011, 105, 1497–1504. [Google Scholar] [CrossRef]
- Li, C.; Wang, X.; Tang, H.; Lei, G.; Yan, J.; Zhang, Y. A preliminary study on the location of the stabilizing piles for colluvial landslides with interbedding hard and soft bedrocks. Eng. Geol. 2017, 224, 15–28. [Google Scholar] [CrossRef]
- Bakri, M.; Xia, Y.Y.; Wang, H.B. Numerical Analysis of Stabilization of Slopes Overlying Bedrock Using Piles and Effect of Socketed Length of Pile on Stability. Appl. Mech. Mater. 2014, 580, 424–431. [Google Scholar] [CrossRef]
- Li, C.; Yan, J.; Wu, J.; Lei, G.; Wang, L.; Zhang, Y. Determination of the embedded length of stabilizing piles in colluvial landslides with upper hard and lower weak bedrock based on the deformation control principle. Bull. Int. Assoc. Eng. Geol. 2017, 78, 1189–1208. [Google Scholar] [CrossRef]
- Zhou, C.-M.; Shao, W.; Yin, K.-L.; Yang, Z.-J. Estimating the properties of weathered bedrock and pilerock interaction from the geological strength index. J. Mt. Sci. 2018, 15, 1757–1776. [Google Scholar] [CrossRef]
- Wang, G.X. Landslide Science and Landslide Prevention Technology; China Railway Publishing: Beijing, China, 2004; pp. 355–458. [Google Scholar]
- Standardization Administration of China. JTG E41-2005: Rules for Rock Test of Highway Engineering; Standardization Administration of China: Beijing, China, 2005. (In Chinese) [Google Scholar]
- Cong, L.; Hu, X. Triaxial rheological property of sandstone under low confining pressure. Eng. Geol. 2017, 231, 45–55. [Google Scholar] [CrossRef]
- Second Surveying and Design Institute of the National Department of Chinese Railways. Design and Computation of Anti-Slide Piles; Chinese Railway Publishing House: Beijing, China, 1983. (In Chinese) [Google Scholar]
- Madabhushi, S.P.G.; Haigh, S. Finite Element Analysis of Pile Foundations Subject to Pull-Out. Struct. Optim. 1998, 397, 131–140. [Google Scholar]
- Salim, R.R.; Abdulrazzaq, O.A. Analysis of Cast in Place Piles Using Finite Elements Method. Int. J. Appl. Eng. Res. 2017, 12, 6029–6036. [Google Scholar]
- Randolph, M.F. The response of flexible piles to lateral loading. Géotechnique 1981, 31, 247–259. [Google Scholar] [CrossRef]
- Standardization Administration of China. TB 10025/J127: Code for Design on Retaining Structures of Railway Subgrade; Standardization Administration of China: Beijing, China, 2006. (In Chinese) [Google Scholar]
- Lee, J.; Jeong, S. Experimental Study of Estimating the Subgrade Reaction Modulus on Jointed Rock Foundations. Rock Mech. Rock Eng. 2016, 49, 2055–2064. [Google Scholar] [CrossRef]
- Kog, Y.C.; Kho, C.; Loh, K.K. Tunnel Design and Modulus of Subgrade Reaction. J. Perform. Constr. Facil. 2015, 29, 04014065. [Google Scholar] [CrossRef]




| Geotechnical Classification | Moisture Contentω(%) | Density ρ (g/cm3) | Cohesion c (kPa) | Internal Friction Angle Φ (°) |
| Soil | 23.96 | 1.93 | 2.35 | 23.98 |
| Mudstone | 0.13 | 2.5 | 150 | 33 |
| Limestone | 0.1 | 2.7 | 700 | 40 |
| Geotechnical Classification | Young’s Modulus E (× 104 MPa) | Poisson’s Ratio | Natural Compressive Strength (MPa) | Saturated Compressive Strength (MPa) |
| Soil | - | - | - | - |
| Mudstone | 2 | 0.25 | 12.4 | 8.31 |
| Limestone | 5 | 0.25 | 38.59 | 59.13 |
| Influential Factors | Factors with Fixed Values | Values of Factors that Were Varied |
|---|---|---|
| h = 8.5 m | Δy1 = 0.5 m | |
| k1 = 0.5 × 105 kPa/m | Δy1 = 1 m | |
| k2 = 1.7 × 105 kPa/m | Δy1 = 1.5 m | |
| The thickness of the first weak rock (Δy1) | P = 1,550 kN/m | Δy1 = 2 m |
| Δy1 = 2.5 m | ||
| Δy1 = 1 m | k1 = 0.7 × 105 kPa/m | |
| The modulus of subgrade reaction of the first weak bedrock (k1) | k2 = 1.7 × 105 kPa/m | k1 = 1.0 × 105 kPa/m |
| P = 1,550 kN/m | k1 = 1.3 × 105 kPa/m |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Wang, P.; Qin, H.; Yue, J.; Zhang, J. Method to Control the Deformation of Anti-Slide Piles in Zhenzilin Landslide. Appl. Sci. 2020, 10, 2831. https://doi.org/10.3390/app10082831
Wang H, Wang P, Qin H, Yue J, Zhang J. Method to Control the Deformation of Anti-Slide Piles in Zhenzilin Landslide. Applied Sciences. 2020; 10(8):2831. https://doi.org/10.3390/app10082831
Chicago/Turabian StyleWang, Hao, Peng Wang, Hongyu Qin, Jianwei Yue, and Jianwei Zhang. 2020. "Method to Control the Deformation of Anti-Slide Piles in Zhenzilin Landslide" Applied Sciences 10, no. 8: 2831. https://doi.org/10.3390/app10082831
APA StyleWang, H., Wang, P., Qin, H., Yue, J., & Zhang, J. (2020). Method to Control the Deformation of Anti-Slide Piles in Zhenzilin Landslide. Applied Sciences, 10(8), 2831. https://doi.org/10.3390/app10082831





