Boiling Flow Pattern Identification Using a Self-Organizing Map

Abstract

In the paper, a self-organizing map combined with the recurrence quantification analysis was used to identify flow boiling patterns in a circular horizontal minichannel with an inner diameter of 1 mm. The dynamics of the pressure drop during density-wave oscillations in a single pressure drop oscillations cycle were considered. It has been shown that the proposed algorithm allows us to distinguish five types of non-stationary two-phase flow patterns, such as bubble flow, confined bubble flow, wavy annular flow, liquid flow, and slug flow. The flow pattern identification was confirmed by images obtained using a high-speed camera. Taking into consideration the oscillations between identified two-phase flow patterns, the four boiling regimes during a single cycle of the long-period pressure drop oscillations are classified. The obtained results show that the proposed combination of recurrence quantification analysis (RQA) and a self-organizing map (SOM) in the paper can be used to analyze changes in flow patterns in non-stationary boiling. It seems that the use of more complex algorithms of neural networks and their learning process can lead to the automation of the process of identifying boiling regimes in minichannel heat exchangers.

1. Introduction

The reduction in the size of components in cooling devices has led to a rapid increase in cooling heat flux. The miniaturization of devices requires the application of a cooling channel with a very small diameter. Using microchannels in small cooling systems can help decrease the amount of refrigerant and increase heat dissipation rates [1,2]. A flow boiling can dissipate high heat fluxes, but boiling in small channels causes problems with the control of the process. In [3,4], the occurrence of different types of the instability of two-phase flow in mini- and microchannels were noticed. The instabilities cause fluctuations in pressure drop and channel wall temperature (periodic or non-periodic). Many researchers numerically investigated the mass and heat transfer during flow boiling in various cases. Sheykhi et al. numerically analyzed the influence of channel inclination on the critical heat flux [5]. Moreover, the phase change phenomena of boiling flow inside the tube with porous medium was investigated using the Eulerian–Eulerian multi-phase Rensselaer Polytechnic Institute (RPI) [6]. Peng et al., using a molecular dynamic simulation, defined the effect of silver nanoparticles’ number on the boiling of Argon in the microchannel [7]. During boiling instabilities, the various two-phase flow patterns were observed in variously enhanced microchannels, e.g., in channels with porous walls [8], in channels with triangular corrugations [9]. Many studies report that different types of instabilities are superimposed on each other [10,11,12]. There are articles concerning flow pattern transition models [13] and flow regime mapping [14]. However, further analysis of flow patterns is still needed, especially for unstable processes [14].

The heat transfer mechanisms in mini- and microchannels are strongly related to the flow pattern dynamics. This explains the recent increase in the number of studies addressing the identification of flow patterns based on image [15,16] or signal processing [17,18]. To identify the flow patterns in air-water two-phase flow, the Kohonen self-organizing map was applied in paper [19]. However, in this paper, eight linear stochastic features were used to identify flow patterns. Therefore, the usage of linear time series analysis to study such complex signals in many cases could be insufficient, and non-linear time series analysis techniques are increasingly used for such data. In the paper [20], a multi-scale entropy was applied to identify flow regimes in pressure-difference signals. Moreover, the gas–liquid transition boundary for slug-wave and boiling wave flow was defined. Liu et al. [21] used a combination of Lyapunov stability theory and numerical analysis to investigate dynamic features of excursive instability for forced two-phase boiling flow in a horizontal channel.

In the previous paper [22], we used the combination of the windowed recurrence quantification analysis (RQA) and principal component analysis (PCA) to identify the occurrence of a dominant sequence of flow patterns. On the basis, conducted analysis to map of the dynamical properties of two-phase flow patterns was constructed. In general RQA (using the Matlab Toolbox) returns 11 coefficients. Each of them characterizes a different aspect of the considered system dynamics. A universal method of RQA coefficient selection for further analysis has not been developed. The process of two-phase flow pattern identification requires taking into consideration the combination of several coefficients at once. The PCA transfers an input set of data (RQA coefficients) into a new set of data. The coordinates of this new set of data are called the principal components. Usually, the first few components explain most of the input data variation. The principal component analysis is only a simple data transformation method. This is the reason that, instead of the PCA method, a new method of analysis of RQA results is necessary.

In the case of the PCA method, the selection of RQA coefficients was usually made by estimating the range of coefficient variation during the considered process. However, this method did not always work well. In our opinion, during the selection, we should choose coefficients, each of which distinguishes an expected feature of the system under consideration. It seems that, instead of the PCA method, it would be better to use methods based on artificial intelligence. In such a method, the classification of differences in the dynamics of pressure fluctuations would be based on the results of network learning.

Therefore, in the presented paper, a combination of a self-organizing map (SOM) with recurrence quantification analysis (RQA) was used to identify flow boiling patterns in a circular horizontal minichannel. The dynamic of the pressure-drop signal during density-wave oscillations (DWO) superimposed to the pressure drop oscillation (PDO) cycle was analyzed. To acquire images of different two-phase flow patterns in the flow boiling, a high-speed digital camera was used.

2. Materials and Methods

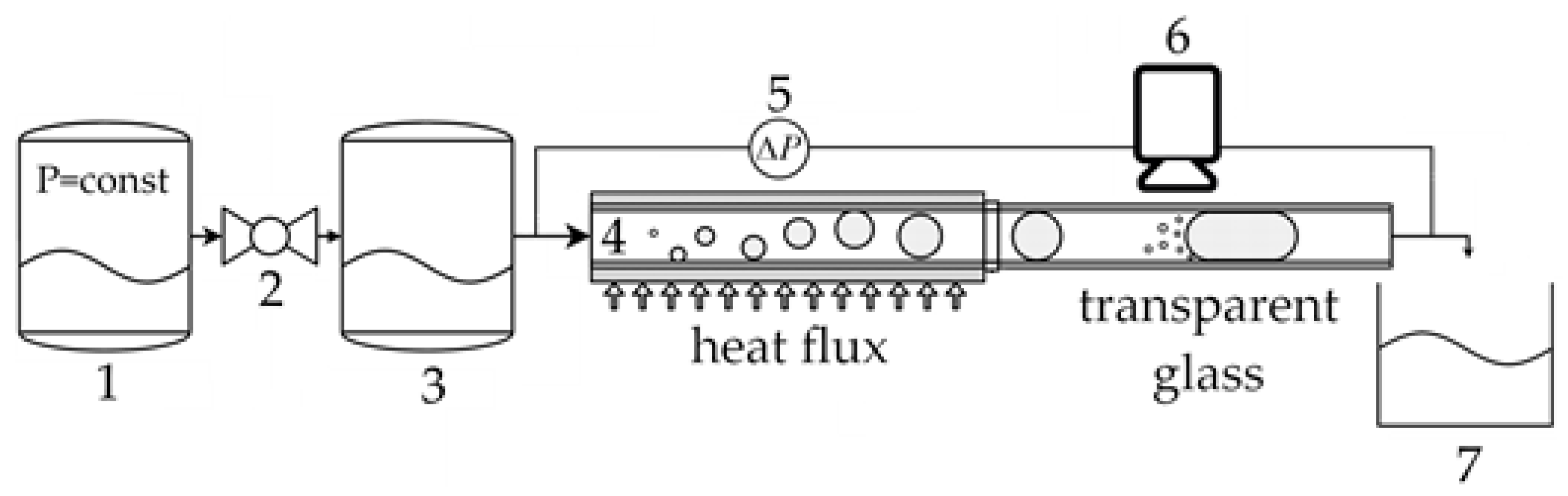
2.1. Experimental Setup

The schematic diagram of the boiling system is shown in Figure 1. A detailed description of the experimental setup is described in [22]. Working fluid (distilled water) was pushed out from the supply tank (1—Figure 1) floated through the surge tank (3—Figure 1) to the heated section. The constant overpressure was maintained in the supply tank, which was 50 kPa. The ball valve (2—Figure 1) was used to regulate the liquid flow rate. The heated section (4—Figure 1) was made of a single round brass pipe with an inner diameter of 1 mm and an outer diameter of 2 mm. The heat was supplied to the pipe at a length of 100 mm. The outlet of the brass pipe was connected to the glass tube to allow the two-phase flow observation and recording. The pressure difference (5—Figure 1) between the inlet of the brass pipe and the outlet of the glass pipe is measured. The outlet pressure was atmospheric pressure.

The Phantom v1610 high-speed camera (6—Figure 1) was used to record the flow patterns inside the minichannel at a frame rate equal to 1000 fps. During the experiment, high-amplitude density wave oscillations (DWO) superimposed on the long-period pressure drop oscillations (PDO) were observed over a short period. Pressure drop and videos were recorded for a whole PDO cycle occurring for constant mass flow rate G and input heat flux P. The pressure drop oscillations during a single PDO cycle shown in Figure 2 (acquired at 1000 Hz) were used for analysis. In a single PDO cycle, the following flow patterns were observed: liquid flow, bubble flow, confident bubble flow, slug flow, elongated slug flow, churn flow, and wavy annular flow.

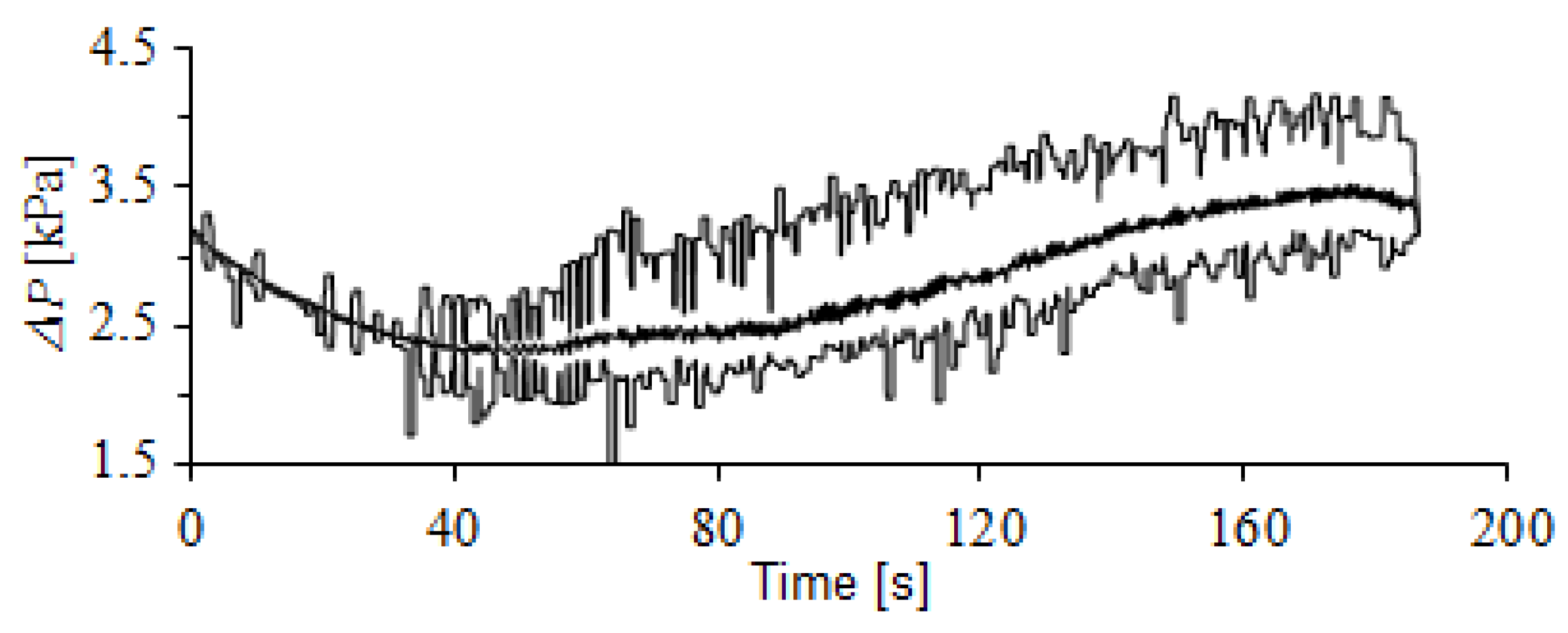
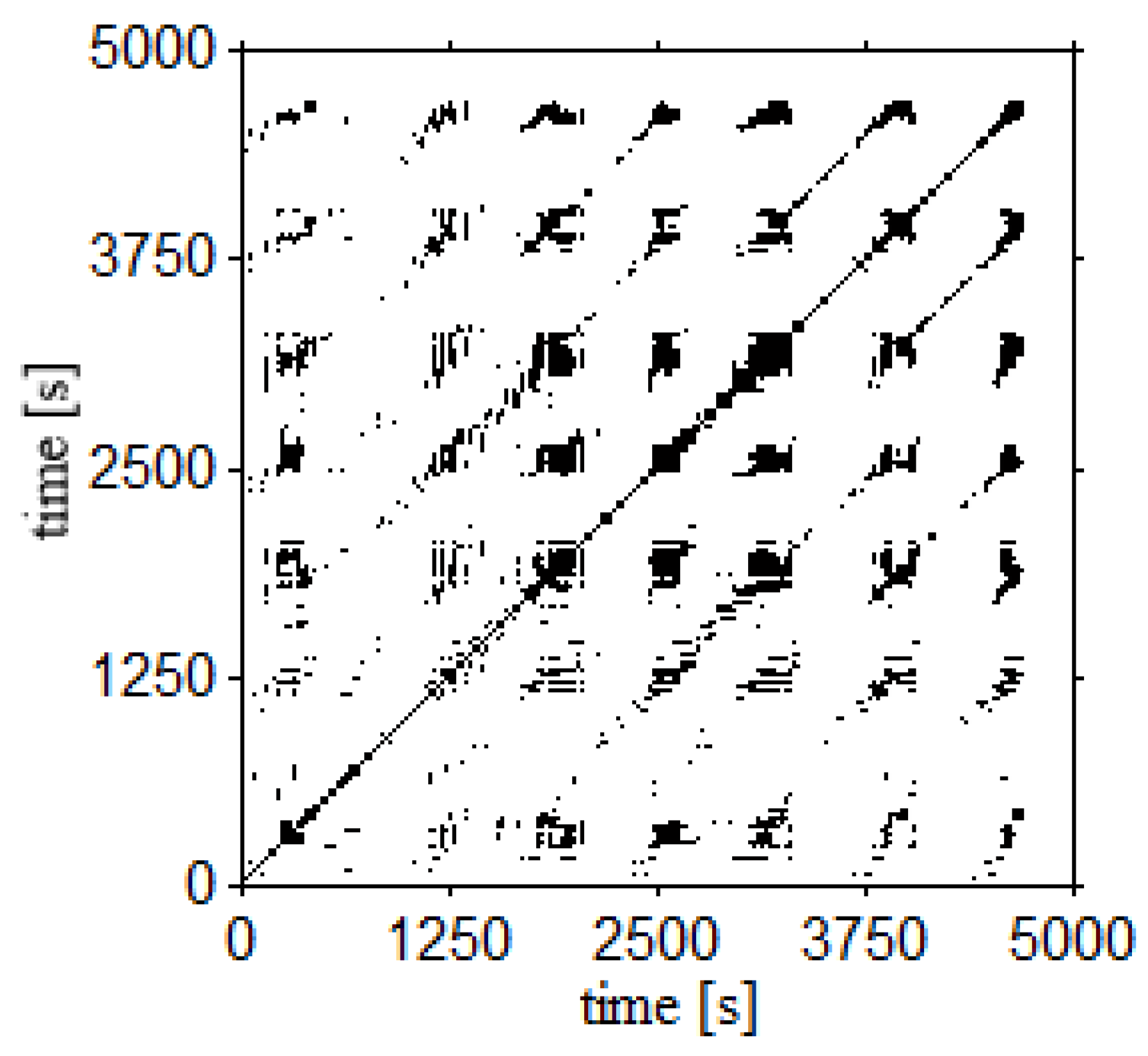
2.2. Recurrence Quantification Analysis

In order to detect changes in the dynamics of pressure drop oscillations, a recurrence window analysis was used. This method is based on a quantitative analysis of recurrence plots (RP) [23]. Eckmann et al. suggested a two-dimensional representation of the recurrences of a dynamical system according to the formula [24]:

$$R_{i,j}=\theta \left({\epsilon }_i-\Vert x_i-x_j\Vert \right),x_i\in R^m,i,j=1\dots N$$

(1)

where N is the number of considered states x, ε is a threshold distance, || || is a norm in m–dimensional space, θ is the Heaviside function, and R is a set of real numbers.

In order to compute an RP, appropriate parameters for attractor reconstruction must be estimated [25]. In this paper, the appropriate time delay τ was estimated as a τ for which the mutual information [26] vs. time delay reaches its first minimum. The embedding dimension m was obtained by the algorithm of a fraction of false nearest neighbors. For pressure fluctuations in the period of time between 101–106 s (Figure 2), the first minimum was reached for τ equal to 100 samples (0.1 s). The false nearest neighbor algorithm estimated m as equal being to 4. The results of the estimation of τ and m are shown in Figure 3.

The important parameter of the RP is the threshold ε. If the value of ε is too small, the RP would have a small number of recurrence points. On the other hand, if ε was too big, RP becomes black [23]. Several methods for selecting ε have been recommended in the literature [28,29,30,31]. In this paper, it was assumed that the value of ε was determined by the size of the reconstructed attractor in the m-dimensional phase space and was 10% of the maximum attractor diameter. The example of RP for pressure fluctuations recorded in the period of time between 101–106 s is shown in Figure 4.

The visible points’ arrangement on the RP characterizes the properties of the dynamic system [23]. In order to achieve their quantitative determining, Zbilut and Webber [30] proposed a method called Recurrence Quantification Analysis (RQA). In this paper, the four RQA coefficients are used to describe the characteristic states occurring in the RP (single points, diagonal line, vertical line, horizontal line). The following RQA coefficients, the values of which change significantly in a single PDO cycle, are considered:

The determinism, DET, is a percentage measure of recurrence points that belong to diagonal lines on RP. Determinism is defined as follows [23]:

$$DET=\frac{{\displaystyle {\sum }_{l=l_{\min }}^{N}lP\left(l\right)}}{{\displaystyle {\sum }_{l=l}^{N}lP\left(l\right)}}$$

(2)

where P(l) defines the distribution of diagonal line lengths l, and N is the length of the time series.

Diagonal lines in RP are created by the parallel segments of attractor trajectories. Such parallel segments occur when the system under consideration returns to similar states after a certain time period. The lengths of the diagonal lines are determined by the duration of processes that repetitively appear. In case of pressure drop fluctuations, such similar states appear when in a minichannel similar flow patterns occur. We can conclude that the DET coefficient is a measure of the intensity of repetitively appearing similar flow patterns.

The average length of the vertical lines, L, is described by the following relation [23]:

$$L=\frac{{\displaystyle {\sum }_{l=l_{\min }}^{N}lP\left(l\right)}}{{\displaystyle {\sum }_{l=l_{\min }}^{N}P\left(l\right)}}$$

(3)

Vertical lines in RP are created by segments of trajectory in which the system states do not change or change very slowly. The duration of these states can be measured by the length of vertical lines, but the average length of vertical lines characterizes the average duration of these processes in the considered system. The vertical distance between vertical lines is a measure of time that is necessary for the repetitive appearance of slowly changed states. In the case of pressure drop fluctuations, the pressure drop changed slowly when the existing in minichannel flow pattern does not rapidly change in time. Therefore, we can conclude that the average length of the vertical lines measures the duration of the appearance of a stable (not rapidly changing in time) two-phase flow pattern. The average time period between such not rapidly changing in time two-phase flow patterns is measured by the recurrence time of the second type. The dynamics of the changes of the the time periods between such not rapidly changing in time two-phase flow patterns are described by recurrence period density entropy.

The recurrence time of the second type, T², calculated the average vertical distances between the white and black pixels in the columns in the RP [32]. T² is defined as:

$$T_j^2=\left|\left\{i,j:{\overrightarrow{x}}_i,{\overrightarrow{x}}_j\in R_i,{\overrightarrow{x}}_{j-1}\in R_i\right\}\right|$$

(4)

The recurrence period density entropy, RPDE, described the complexity of a signal and determined the periodicity of a signal [33]. The periodic system has an RPDE with a value close to 0, whereas a chaotic system has an RPDE a close to 1 [34]. The RPDE can be computed as follows:

$$RPDE=-{\left(\ln T_{\max }\right)}^{-1}{\displaystyle {\sum }_{t=1}^{T_{\max }}P\left(t\right)\ln P\left(t\right)}$$

(5)

where T_max and P(t) are the largest recurrence value and the recurrence period density function, respectively.

These coefficients were considered because they can detect the difference between two-phase flow patterns.

For long time series such as pressure drop oscillations, usually, the windowed RQA is applied. In windowed RQA, the set of recurrence plots is being created for subsequent parts of the signal and then each RP is quantified by RQA coefficients. The moving window for windowed RQA contained 5000 samples (5 s) and the window shift was equal to 1000 samples (1 s). In a single PDO cycle, the entire procedure the windowed RQA was repeated 181 times. The values of the RQA coefficients have been calculated using the CRP toolbox for Matlab^® [27].

RQA analyzes the behavior of dynamic systems associated with the recurrence occurrence. It seems that it is the most effective analysis tool when the analyzed signal contains a periodic component that is chaotically disturbed. The RQA method becomes less effective when the analyzed signal is similar to the noise. In the case of pressure fluctuation analysis, pressure changes are caused by the increase and decrease in the bubbles in the minichannel, when the sampling frequency is high enough, then the pressure fluctuations do not change abruptly (as in the case of noise). Such signal behavior allows us to use the RQA.

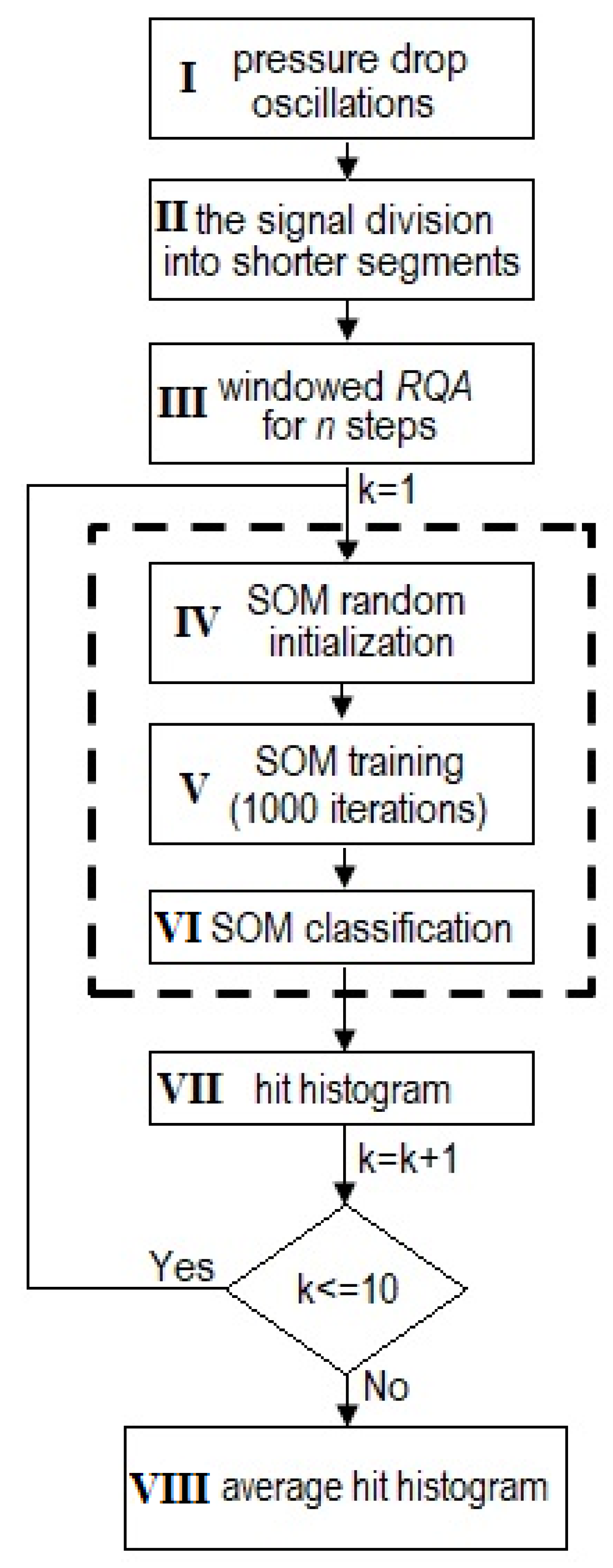
2.3. Self-Organizing Map

The Kohonen network [35] is an example of an unattended network. It has a special property of effectively creating a spatially organized internal representation of various input data features and providing topology-preserving mapping from a high dimensional space into what is usually a two-dimensional space. The idea of a self-organizing map (SOM) appeared in the 1950s and was proposed by Finnish computer scientist Teuvo Kohonen. In the classic Kohonen algorithm, each small element (or neuron) gets many inputs and generates only one output signal. The individual input connections have an assigned weight. When a neuron receives an input pattern, it usually calculates the weighted sum of inputs. In principle, it is useful to consider the values of different weights as components of the weight vector and individual input signals as components of the input vector. As a result of the windowed RQA, 4 input points for each window of pressure drop oscillation were obtained. The input vector describes the following relationship:

$$X={[{DET}_n,\frac{1}{L_n},T_n^2,\frac{1}{{RPDE}_n}]}^{\mathrm{T}}$$

(6)

where n is the row number, which corresponds to the duration of the pressure drop signal.

These time series are shown in Figure 5. In Figure 5b,c, we presented graphs on a logarithmic scale to indicate a change in the dynamics of the T² and RPDE coefficients.

In the SOM algorithm, the weight vector is as follows [36]:

$$W={\left[w_{j,DET},w_{j,1/L},w_{j,T^2},w_{j,1/RPDE}\right]}^{\mathrm{T}}$$

(7)

where j is the number of neurons in the network. In our analysis, j is from 1 to 36.

Therefore, this algorithm is expressed in the following way [19]:

$$Y=W\cdot X={\displaystyle {\sum }_{i=1}^{i=n}{w}_i\cdot x_i}$$

(8)

where X is the input vector, W is the weight vector, the dimension of which is 36 × 4, and Y is the output vector.

During the subsequent iterations, neurons compete for the privilege of learning. The best neuron is the winner of the competition. The winning neuron generates an output signal, while others generate 0. The winning neuron and its nearest neighbors are the only neurons that can learn to present the pattern or can adjust their weights [37,38].

Kohonen’s learning rule can be expressed as follows [19]:

$$W_{new}=W_{old}+\lambda \left(X-W_{old}\right)$$

(9)

where λ is the learning constant; its default value is 1.

The structure of the Kohonen’s self-organizing neural network consists of two layers. The first layer is the input layer. In our case, this is RQA vectors and the second one is the output layer–2D matrix (6 × 6), which represents neurons. Thus, each of the RQA results (180) was assigned to 1 of 36 neurons arranged in matrix (6 × 6). Such a 2D map is called the hit histogram and visualizes the density of points on the SOM by counting how many input vectors are mapped onto each SOM node. Neurons of similar weight locate themselves close to one another, while dissimilar neurons are far from each other [19,37].

In our algorithm, the network training was performed 10 times using some RQA results. In Figure 6, the procedure of SOM combined with RQA for pressure drop oscillation is presented. The analysis using SOM was conducted in Matlab software using the Neural Network Clustering App [39]. The self-organizing process involves four basic elements: initialization, competition, cooperation, and adaptation. The procedure has been summarized in eight steps:

• Loading the pressure drop oscillations;
• The division of the signal (185,000 samples) into segments of 5000 samples;
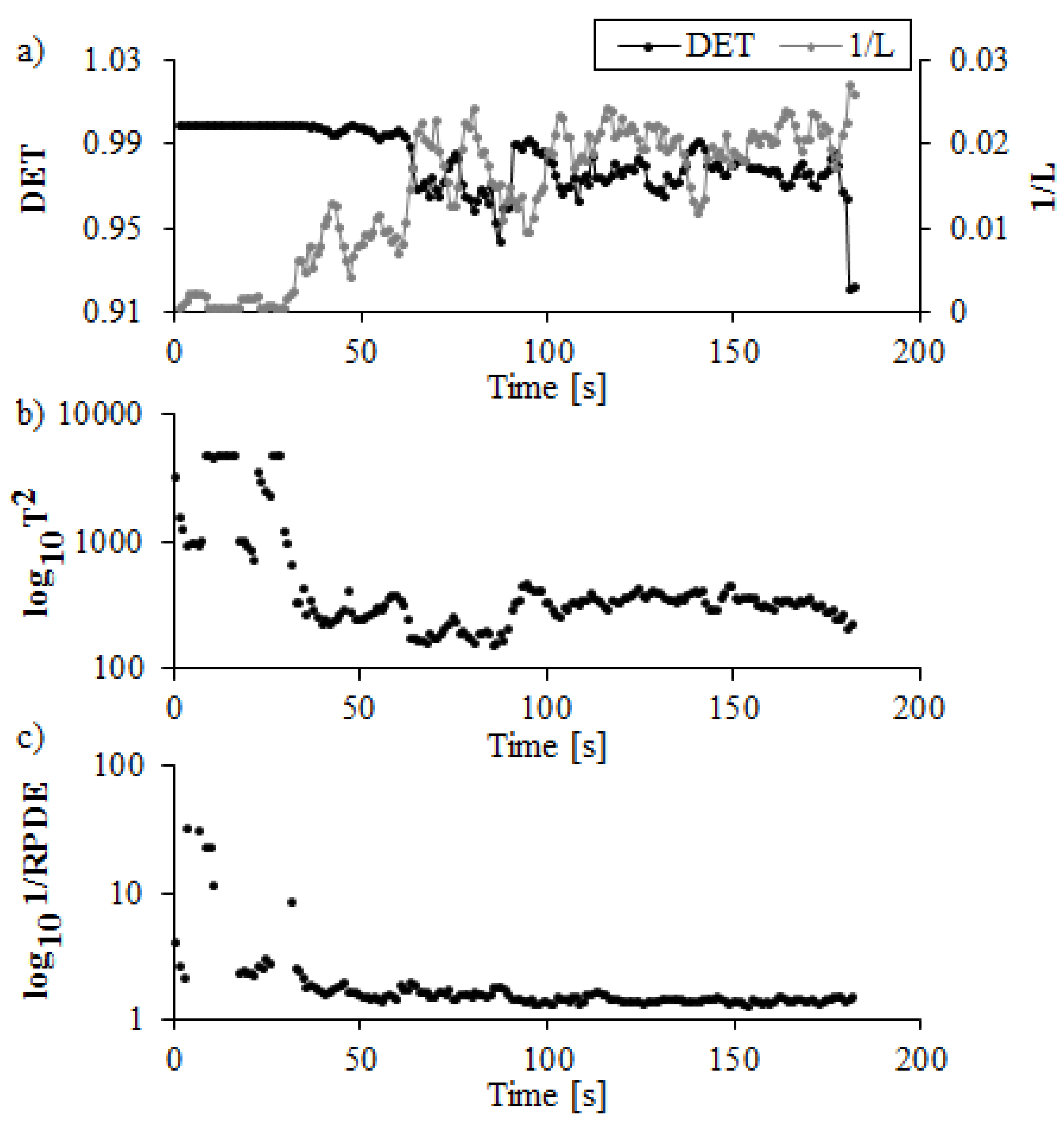
• Conducting the windowed RQA analysis for each segment. As the results of the analysis, the matrix containing the RQA coefficients is being created (DET, 1/L, T² and 1/RPDE).
• SOM random initialization;
• SOM training using 1000 iterations;
• Comparison of each test vector with prototypes of the map (SOM classification);
• Obtaining the results of SOM analysis—the hit histogram is created;
• After receiving 10 results of the SOM analysis, the average hit histogram is constructed.

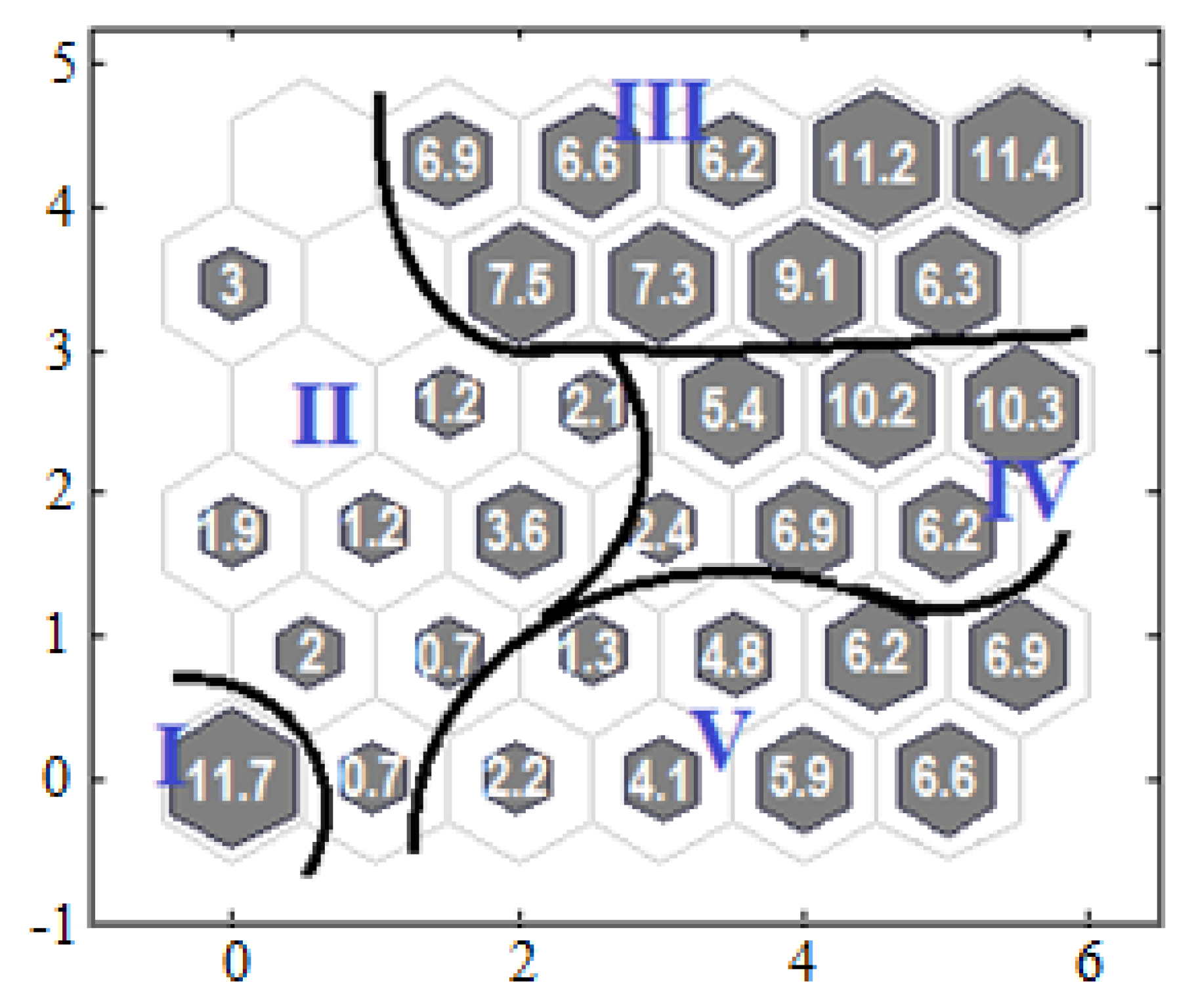
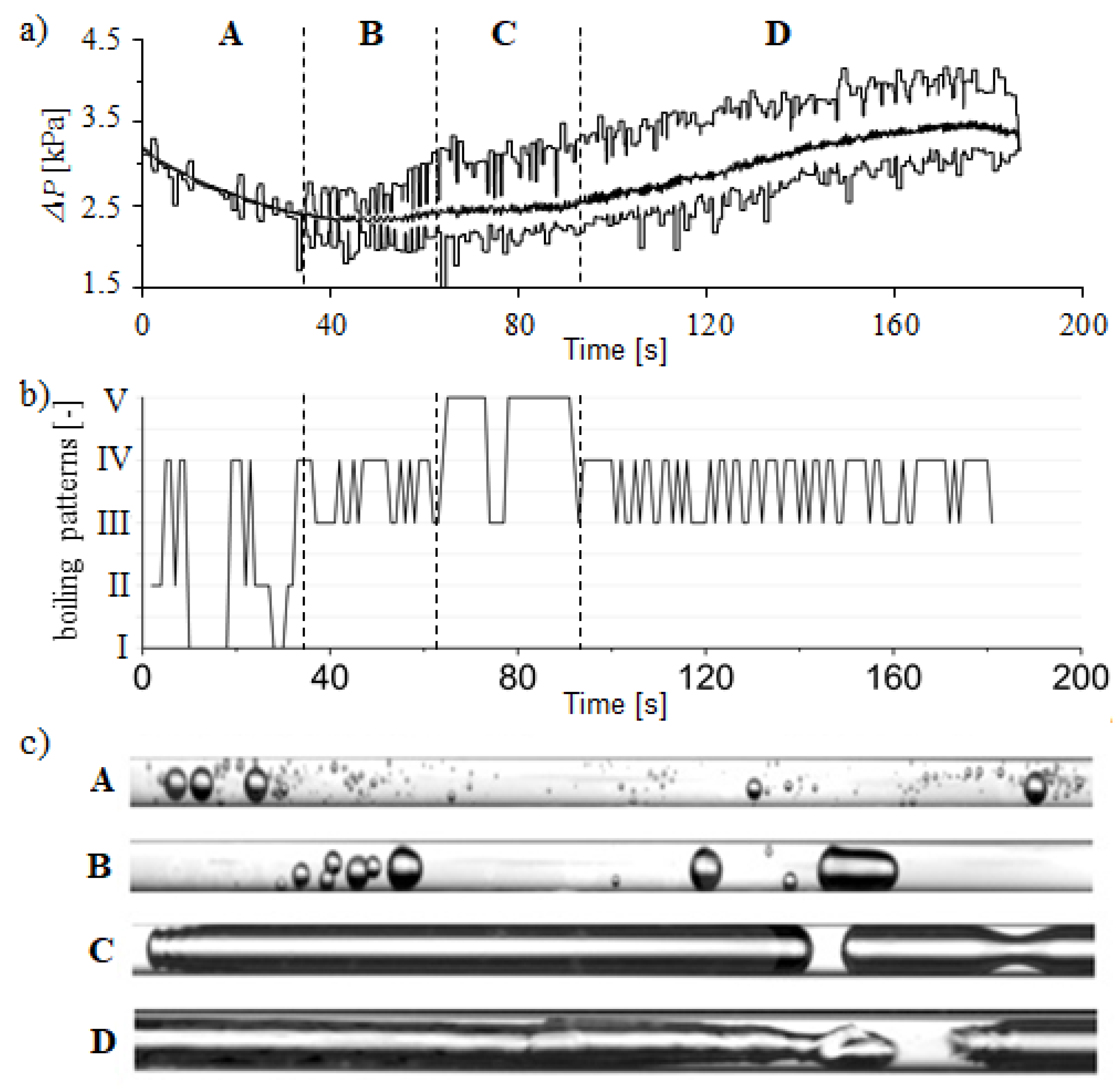
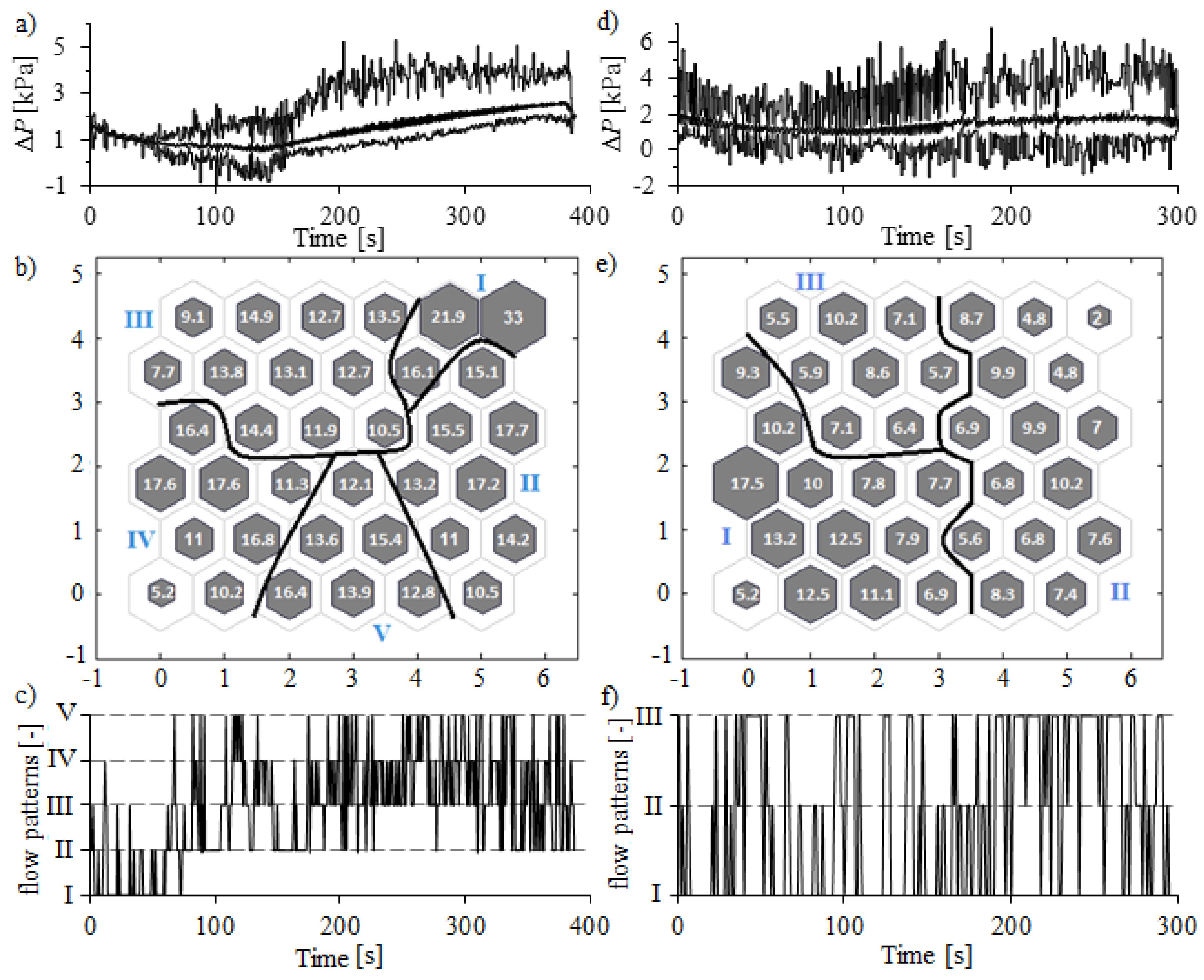
3. Results and Discussion

In Figure 7, the average hit histogram obtained from 10 results of SOM is presented. The points of the hit histogram were located according to the similarity of each output layer weight. Neurons of similar weight locate themselves close to one another, while dissimilar neurons are far from each other. In such a way the SOM algorithm created the 2D map identifying the differences between system dynamics (dynamics of pressure drop oscillations).

The hit histogram was divided into five areas that were matched to the five two-phase flow patterns identified during a single PDO cycle. The following two-phase flow patterns were identified (Figure 7): I—liquid flow; II—liquid flow with small vapor bubbles; III—confined bubble flow; IV—wavy annular flow; and V—vapor slug flow.

The history of building the hit histogram allows us to identify which part of the pressure drop time series is assigned to each part of the hit histogram. The result is shown in Figure 8b and was compared with the pressure drop time series (Figure 8a). On the y-axis in Figure 8b, specific flow patterns were determined, where I is liquid flow, II is bubble flow, III is long slug flow, IV is confined bubble flow, and V is slug flow. The character of the oscillations between the different flow patterns (Figure 8b) allows us to distinguish four different boiling regimes during a single PDO cycle.

We defined the following boiling regimes: A—liquid flow, bubbles flow and confined bubble flow, B—long slug flow and confined bubble flow, C—long slug flow and slug flow, and D—long slug flow and confined bubble flow. Examples of flow observed in such defined boiling regimes are shown in Figure 8c.

In boiling regime A, the boiling starts when the channel is filled with water. Due to heat being supplied to the minichannel, the small bubbles start to appear in the glass channel. Next, the confined bubbles appear. It causes the pressure drop increases that are accompanied by a water flow rate increase. Finally, the higher pressure at the inlet of the minichannel causes the removal of the confined bubbles and pressure drop decreases. In boiling regime B, the oscillations start when the channel is filled by the confined bubbles. Next, the long slugs appear in the glass pipe. In the condenser section, the long slug starts to shrink and the confined bubble flow appears in the minichannel again. In boiling regime C, the oscillations between the long slug flow and the slug flow appear in the glass channel. In boiling regime D, oscillations appear between the long slugs’ flow and the bubble flow in a short period of time.

The accuracy of the postulated approach is determined by the length of the moving window in windowed RQA. We set the moving window length on 5000 samples (5 s), which means that all phenomena during less than 5 s are not identified, while processes that are longer than 5 s are identified. The accuracy of two-phase flow pattern identification using SOM analysis depends on the number of data and the size of the hit histogram map. Because of a limited number of data, it is difficult to determine the accuracy of the SOM analysis.

The method proposed in this paper was also used to a preliminary analysis of pressure drop fluctuations in a single minichannel (diameter of 1 mm) obtained at different water flow rates and heating electrical power. Figure 9 shows the results of the analysis made at G = 61.65 kg/m²s and P = 75.6 W (Figure 9a–c) and at G = 38.8 kg/m²s and P = 55.8 W (Figure 9d–f).

In the case presented in Figure 9b, the hit histogram has five local maximums; therefore, it can be divided into five areas. Comparing Figure 9c with Figure 9a and the recorded video enables us to suppose that the following two-phase flow patterns were distinguished: I—liquid flow, II—liquid flow with small vapor bubbles, III—confined bubble flow, IV—wavy annular flow, and V—vapor slug flow.

In the case presented in Figure 9e the hit histogram has three local maximums; therefore, it can be divided into three areas. Comparing Figure 9f with Figure 9d and the recorded video enables us to suppose that the following two-phase flow patterns were distinguished: I—bubble flow, II—slug flow, and III—wavy annular flow.

The obtained results show that the proposed method (the combination of RQA and SOM) can be used to analyze changes in two-phase flow patterns in a non-stationary boiling. However, it seems that the use of more complex algorithms of neural networks and their learning process can lead to the automation of the process of identifying boiling regimes in minichannel heat exchangers.

4. Conclusions

In this paper, a self-organizing map combined with the recurrence quantification analysis was used to identify flow boiling patterns in a circular horizontal minichannel with a diameter of 1 mm and determine the flow boiling regimes during a single pressure-drop oscillations cycle.

In the self-organizing map, neurons of similar weight locate themselves close to one another, while dissimilar neurons are far from each other. Therefore, the 2D self-organizing map identifying the differences between system dynamics was created. The input data for the self-organizing map was the results of the quantitative analysis of recurrence plots created from pressure drop oscillations.

The self-organizing map allows us to distinguish five types of two-phase flow patterns, such as bubble flow, confined bubble flow, wavy annular flow, liquid flow, and slug flow. The flow pattern identification was confirmed by images obtained using a high-speed camera.

The self-organizing map successfully classified four boiling regimes during a single cycle of the long-period pressure drop oscillations. We can conclude that this technique is promising as an objective classifier of boiling flow patterns.

The combination of the RQA and the neural network (SOM) proposed in this paper shows that the adopted method of pressure fluctuation analysis allows the identification of various flow patterns in non-stationary boiling in minichannels. At the current stage of the research, the method of selecting the correct RQA coefficients has not been solved. Although, the obtained results suggest that the application of more complex neural network algorithms will allow for the automation of boiling regime identification by analyzing all RQA coefficients.