Abstract
Accurate measurement of pressure drop in energy sectors especially oil and gas exploration is a challenging and crucial parameter for optimization of the extraction process. Many empirical and analytical solutions have been developed to anticipate pressure loss for non-Newtonian fluids in concentric and eccentric pipes. Numerous attempts have been made to extend these models to forecast pressure loss in the annulus. However, there remains a void in the experimental and theoretical studies to establish a model capable of estimating it with higher accuracy and lower computation. Rheology of fluid and geometry of system cumulatively dominate the pressure gradient in an annulus. In the present research, the prediction for Herschel–Bulkley fluids is analyzed by Bayesian Neural Network (BNN), random forest (RF), artificial neural network (ANN), and support vector machines (SVM) for pressure loss in the concentric and eccentric annulus. This study emphasizes on the performance evaluation of given algorithms and their pitfalls in predicting accurate pressure drop. The predictions of BNN and RF exhibit the least mean absolute error of 3.2% and 2.57%, respectively, and both can generalize the pressure loss calculation. The impact of each input parameter affecting the pressure drop is quantified using the RF algorithm.
1. Introduction
Non-Newtonian fluids have been used extensively in drilling oil and gas wells. The accurate simulation of such complex fluid models aid in energy conservation and efficient operation management. During drilling operation drilling fluid or mud is circulated through drill string and annular space and carries out drilled cutting from wellbore which results in significant pressure loss. Hershel and Bulkley [1] proposed a three-parameter model which is considered to be a near optimum model for rheological behavior of Non-Newtonian fluids, and it has been known to replace Bingham and power-law models in recent years [2,3,4,5,6,7,8,9].
Wellbore hydraulic modeling is a key component for a successful drilling operation as it not only enhances the rate of penetration (ROP) but minimizes the risk of potential problems encountered during drilling operations such as stuck pipe, kicks, loss circulation, and other various activities leading to non-productive time (NPT). Calculation of pressure drop in a wellbore is a critical parameter in planning and improving the efficiency of a drilling operation. The pressure drop in a pipe system is widely affected by the flow regime, frictional forces by inner walls of pipe and fitting, changes in elevation, the dimension of pipes and rheological properties of the fluid being transported. As the drilling mud is pumped from the mud tank to the well bore, it endures pressure loss while in circulation due to numerous pipe connections and frequent elevation changes. The estimation of flowing pressure gradient in an annulus for well control or drilling operation optimization is very crucial for accurate calculation of pressure drop in the annulus.
American Petroleum Institute (API) RP 13D recommends Herschel–Bulkley model for drilling fluids to calculate the frictional pressure drop in drill pipe and annulus. Different studies [2,3,4,5] have been carried out that utilized this model for eccentric and concentric annulus geometry. Most of the literature do not account for wide range of eccentricity of annuli and the proposed solutions are either iterative or involve assumptions based on laboratory experiment or theoretical studies. The aim of the current research is to develop an intuitive methodology based on collinearity of the features in the dataset containing the Herschel–Bulkley fluid model parameters and geometric constraints to predict pressure drop. To the authors’ knowledge, such investigation is not been studied in the existing literature describing the novelty of the present research. This study evaluates the performance of machine learning for the non-Newtonian flow under fully developed laminar flow. This emphasis of this work is to demonstrate that machine learning algorithms can be a proficient alternative to approximated physics-based solutions. A wide range of pipe diameters, eccentricity, yield stress, fluid index, and fluid composition have been considered in this study. This study implies that RF algorithm can model such nonlinear fluid in high as well as low pressure regime. A comprehensive investigation is performed on the effectiveness of different data-driven algorithms such as Support Vector Machine (SVM), artificial neural network (ANN), and random forest (RF) in comparison to a deep neural network like the Bayesian Neural Network (BNN).
2. Related Work
Numerous theoretical and experimental studies have been reported in the literature on the non-Newtonian fluids for the concentric and eccentric annulus, but the study on the transient and the turbulent flows are limited. Laminar flow in the concentric annulus for power-law and Bingham fluids were studied by Fredrickson et al. [10] with an analytical approach, while Hanks et al. [11] and Buchtelova et al. [12] developed a non-analytical solution for Herschel–Bulkley fluids concluding some errors in the former approach. The correlations developed by Heywood and Cheng [13] predicted the head loss for turbulent flow in pipes within range of ±50% for Herschel–Bulkley fluids. The solution of the flow for yield power law in the concentric annulus was given by Gucuyener and Mehmetoglu [14]. A model proposed by Reed and Pilehvari [15] covered the laminar, transitional, and turbulent flow in the concentric annulus for Herschel–Bulkley fluids and introduced new effective diameter concept. The solution of laminar flow for non-Newtonian fluid in eccentric annulus was evaluated by Haciislamoglu [16], and later Haciislamoglu and Langlinais [17] developed a correlation for power-law fluids in eccentric annuli. This correlation was applied by Kelessidis et al. [18] to determine the pressure drop in eccentric annulus for non-Newtonian fluids.
Ahmed [19] used the generalized hydraulic equation developed for fluids in arbitrary shaped ducts. In his study, the investigations of Kozicki [20], Luo and Peden [21], and Haciislamoglu and Langlinais [17] were used to determine the frictional pressure loss in eccentric annulus for flow under laminar conditions. To predict the pressure loss in the annulus, Computational Fluid Dynamic (CFD) was applied by Karimi et al. [22] and Titus et al. [23] to address the flow of Herschel–Bulkley fluid in eccentric annuli. A comprehensive solution for Herschel–Bulkley fluids for laminar flow in concentric annulus was presented by Kelessidis et al. [24] which was extended to transitional and turbulent flows by Founargiotakis et al. [25]. Sorgun and Ozbayoglu [26] used the Eulerian–Eulerian CFD model to evaluate the velocity profile and determine frictional pressure loss in non-Newtonian fluids for both eccentric and concentric annulus. Theoretical and experimental investigations conducted by Ahmed et al. [27] on (Yield Power Law) YPL fluids in eccentric and concentric annulus with pipe rotation to estimate the overall pressure loss. In another study by Ogugbue and Shah [28], different flow regimes were investigated for YPL fluids to investigate the flow properties in eccentric and concentric annuli for drag-reducing polymers. Mokhtari et al. [29] studied the impact on both velocity profiles and pressure loss across annulus by eccentricity. Vajargah and Van Oort et al. [30] concluded that laminar flow is comparatively affected more by eccentricity in comparison to turbulent flow. Erge et al. [31] suggested that while circulating, YPL fluids eccentricity has a dominant effect on annular pressure loss.
Artificial intelligence in the past decade has played an important role in complex optimization problems [32,33] especially in the oil and gas industry to enhance the understanding of the non-homogeneous subsurface conditions with application of algorithms, such as Case Based Reasoning (CBR), Artificial Neural Network (ANN), Support Vector Machine (SVM), and fuzzy logics. Osman and Aggour [34] and Jeirani and Mohebbi [35] used ANN with backpropagation to determine the density of the drilling mud and mud cake permeability, while Siruvuri et al. [36], Miri et al. [37] and Murillo et al. [38] used it for prediction of the stuck pipe while drilling. Apart from these mentioned cases ANN have been applied to a variety of conditions such as, Ahmed et al. [39] predicted ROP with higher accuracy using ANN and Elkanty [40] used ANN to predict drilling fluid rheological properties in real-time. Ozbayoglu et al. [41] analyzed cutting bed height in high angle and horizontal wells using ANN trained with feed-forward with back propagation (BPNN). Rooki [42,43] used General Regression Neural Network (GRNN) and BPNN for predicting pressure drop using the Herschel–Bulkley fluid model. Rooki and Rakhshkhorshid [44] used Radial Basis Neural Network (RBFN) for determining the hole cleaning condition during foam drilling. The fuzzy logics were used for mud density estimation by Ahmadi et al. [45]. Yunhu et al. [46] used it for identifying the loss circulation zone while Chhantyal et al. [47,48] predicted mud density and mud outflow. Skalle et al. [49] used CBR by creating 50 case-based information of North Sea to solve problem of lost. Al-Azani et al. [50] used SVM for predicting cutting concentration in directional wells. Sameni and Chamkalani [51] used SVM to evaluate the performance of drilling in shaly formations with the help of coupled simulated annealing (CSA). Ahmed et al. [39] used SVM to predict ROP with higher performance margin than achieved by theoretical equations. ANN and SVM were used by Kankar et al. [52] for fault diagnosis of ball bearing. Guo et al. [53] and Wen et al. [54] used deep convolutional neural network for diagnosing fault. Castano et al. [55] used machine learning for object detection using virtual on-chip lidar sensor.
In recent years, these data mining algorithms have been used in many aspects of drilling industry. The success of an algorithm depends on the problem, its variables, bounds, and other complexities like pattern within data. However, the effectiveness of an algorithm to make it a solution for a given problem has no guarantee that it may outperform a random search [56].
3. Methodology
3.1. Herschel–Bulkley Rheological Model
Rheology is the study of the flow of fluids or materials that accounts for the behavior of non-Newtonian fluids. Bingham plastic [57] and the power law [58,59] are two-parameter models that were initially used in several studies to describe non-Newtonian characteristics of fluids. Hershel and Bulkley [1] suggested a three-parameter model, also known as Yield Power Law (YPL), and later more complex models up to 5 parameters have also been suggested [3]. However, these high dimensional rheological models are uncommon due to the complexity in evaluating the flow parameters such as velocity profile, Reynolds number, pressure drop, and the hydraulic parameters. These parameters could only be determined by numerical simulations [24]. To maintain the simplicity and calculation accuracy, Herschel–Bulkley model is widely used in industry. The literature reveals that it better fits the two-parameter models [2, 3] which describes the drilling fluids rheology precisely [18,19,20,21,22,23,24]. The model is defined in Equation (1).
where shear stress is represented by τ,
Yield stress by τy, fluid consistency by ĸ, n is fluid behavior index and γ denotes shear rate. The pressure loss for the concentric annulus is calculated by Equation (2).
where, Do is outer diameter of annulus (m), Di is inner tube’s diameter of annulus (m), ρ is density of fluid (kg/m3), τw is shear stress of wall (Pa), ƒ is the friction factor (dimensionless). Determination of the friction factor (ƒ) for different flow regimes requires an iterative trial and error method.
The non-Newtonian fluids represented by Herschel–Bulkley model pose few challenges while performing numerical simulations because the flow around the centre is characterized as plug region and near the wall as non-plug flow. There are certain parametric conditions imposed under which the above-mentioned model can approximate the behaviour of such fluids, such as K > 0, > 0 and 0 < n < . Due to such restrictions, the complexity of the derived governing equations increases making it highly non-linear in nature and requires strenuous effort to solve it. Many analytical and experimental work conducted in the past have been outlined in aforementioned literature that clearly illustrate the difficulty associated with approximating the behaviour of such nonlinear three parameter fluid model.
3.2. Data Mining Algorithms
In the current study, three different architecture of machine learning models are investigated, such as Support Vector Machine which maps the m dimensional space data with a linear or nonlinear function. Artificial Neural Network is also considered as black box as it depends on backpropagation of randomly initialized weights to approximate solution for the targeted output. Random Forest is an ensemble machine learning technique capable of performing regression using multiple decision trees with a statistical technique called bagging. The detailed working of the algorithms used in this study is given in Appendix A. The algorithms are implemented in Python 3.7 using Scikit-Learn, Tensorflow and the results can be easily reproduced using the framework and software library.
3.3. Description of Experimental Data
Ahmed et al. [19] conducted detailed experiments for fully developed laminar flow and measured the corresponding pressure drop in concentric and eccentric annulus for fluids with various concentration of Xanthan Gum (XCD) and Polyanionic Cellulose (PAC). The data from their study was utilized in current investigation (details of the fluid - Appendix B). The uncertainty in the data and its reliability for scientific analysis is crucial for algorithmic realization of a physical process, and numerous methods were proposed recently [60,61,62] which deal with analyzing the unreliability of the data. In the presented study water test were conducted to evaluate and verify the reliability of instrumentation and data acquisition system, followed by Yield Power Law (YPL) fluids after establishing strong confidence on measurement. Zero readings of differential pressure and flow rate was verified by Ahmed [19] to minimize the uncertainty in the experimental setup. However, the exact values of uncertainty and inconsistency in data is not reported in the reference [19]. The flow rate was maintained until the steady-state condition was achieved. The data acquisition system recorded measurements at the rate of 4 Hz (four data points per second) for one to two-minute duration. The dimensions of the testing facility used in the prediction is tabulated in Table 1. The input parameters used to predict the pressure drop are outlined in Table 2, while the temperature is maintained from the range of 27.8–45 °C and the pressure from 144.37–1332 kPa. Table 3 shows the range of the data used in this study, where Di/Do is the inner and the outer cylinder diameter ratio, e is the eccentricity, n is the flow behavior index, flow consistency index is given by K, τy is shear stress, Q is the fluid flow rate, ΔP is measured pressure drop. Fluids of varying concentrations of XCD and PAC (Appendix B) are circulated through different di/do ratio and eccentricity. The properties of all the fluids used in the study were measured with pipe viscometer. Total of 903 data points are collected, where 70% of them are used for training the algorithm and 30% for testing the proposed models.

Table 1.
Dimension of the annular sections used in the study.

Table 2.
Input parameters for the proposed data mining algorithms.

Table 3.
Range of experimental data.
3.4. Performance Metrics
The data collected from the flow loop experiment has a variety of different dimensional units and ranges. It is evident from Table 2 and Table 3 that parameters such as e is unitless and ranging from 0 to 1, whereas, pressure loss is in the range of 0.196 to 381.23 kPa. In order to bring out a common scale to analyze the features in the data without distorting or losing the values, we have transformed the data in the range of [0, 1] using a transformation function, given in Equations (3) and (4).
where is the dimensional data while is the scaled transformation of using Equation (3) and Equation (4), was used as input for subsequent algorithms. Three performance metrics, namely Mean Absolute Error (MAE), Coefficient of Determination (R2), and Root Mean Squared Error (RMSE) are used to measure the effectiveness of the applied predictive algorithm. RMSE quantifies the disagreement between the predicted and observed data points that can be determined from Equation (5). MAE is indication of the relative divergence of the measured and the predicted values are computed from Equation (6).
The coefficient of determination can be calculated using Equation (7). It is a statistical measure of the regression prediction and approximation with the real data point, where 1 indicates the regression prediction perfectly fits the data.
where ŷi represents the predicted values, number of observations is represented by n, yi is the given data point and Ӯi is the mean of the given values. The optimal condition for a predictive algorithm is when the RMSE = 0 and R2 = 1, the lower the RMSE and MAE score the better the quality of the result.
Four algorithms are used in this study to predict pressure drop in concentric and eccentric annulus, i.e., SVM, ANN, BNN, and RF.
4. Result and Discussion
The algorithms are evaluated based on the previously described metrics of RMSE, MAE, and R2. The predicted and the actual values are compared for train and test datasets. In a base case scenario, the predicted and the experimental values should yield a 45° slope line that can be illustrated as best fit curve to visually inspect the deviation.
4.1. Prediction and Validation
4.1.1. Predictions via Support Vector Machine (SVM)
The parameters tuned for SVM are soft margin constant (C), kernel parameter, width of Gaussian kernel (gamma), and degree of polynomial fit. Hyperparameter C is typically a regularization parameter for trade-off between the errors of training data. Kernel is iteratively selected to be radial bias function as it gives higher accuracy in this case compared to other functions. Gamma is defined as the extent of influence by a single training example and is used for non-linear hyper planes and the degree is a parameter basically to define the polynomial fit of a hyper plane. The pressure loss for laminar flow in concentric and eccentric annular annulus is predicted using SVM. The predicted values for the training and the test data are plotted in Figure 1 with observed pressure loss in the experimental setup. The RMSE of 21.92 kPa and MAE of 17.92% is calculated for train data set with R2 = 0.925, while for test data RMSE is 22 kPa, MAE is 18.34% with R2 = 0.83. Figure 1 illustrates that majority of the deviation from the 45° best fit curve lies below 50 kPa data points. The deviation is observed to be slightly increasing towards higher pressure scale.
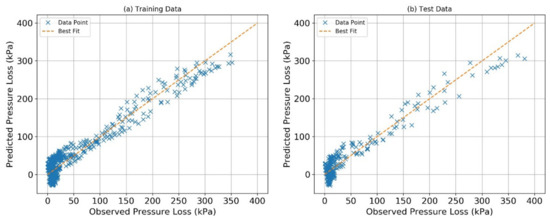
Figure 1.
Support Vector Machine (SVM) predicted pressure plotted with observed pressure loss: (a) training dataset and (b) test dataset.
4.1.2. Predictions via Artificial Neural Network (ANN)
ANN is manually tuned at initial stages to yield lower error rate compared to SVM. The number of layers is 2 and the number of neurons in each layer is 3. The activation function for input and hidden layer is ReLU and Linear for output layer. The dropout ratio is 0.15 and the number of iterations is 1000. Figure 2 illustrates a comparison of the predicted and observed pressure loss from the experimental setup. The RMSE and MAE are found to be 17.8 kPa and 10.7%, respectively, with R2 = 0.915 for training data. Similarly, the obtained values for the test data are 21.36 kPa for RMSE and 12.34% for MAE with R2 = 0.904. The prediction for the test and train data is good below 50 kPa as the values are clustered around the best fit curve, but a drift from the best fit towards the upper region can be observed. Different precautionary measures are taken to avoid overfitting, such as monitoring the RMSE score, early stopping criteria, and dropout regularization. The proposed ANN is shallow in structure, therefore, changes in number of neuros in each layer, number of layers, and the activation functions are also iteratively selected. The lowest RMSE score of unseen test data may leads to generalizing better results.
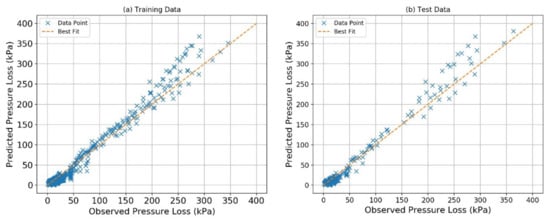
Figure 2.
Artificial neural network (ANN) predicted pressure plotted with observed pressure loss: (a) training dataset and (b) test dataset.
4.1.3. Predictions via Bayesian Neural Network (BNN)
The BNN inhibits similar architecture of ANN but instils a difference with the setting up of the hyperparameters selection criteria that yields lowest error on testing and training sets with help of Sequential Model Based Optimization (SMBO). This study utilizes SMBO to avoid over fitting and optimize number of neurons in hidden layer, number of hidden layers, learning rate, dropout rate, and suitable activation function with least RMSE in the suggested solution space. In Figure 3, a comparative study of neurons in each hidden layer and different number of hidden layers is plotted. The black dots represent the samples taken from the defined solution space and the red star represents the point with least error among the selected sample points. In this case, the optimum number of neurons in each layer is 35 and number of hidden layers is 16. Figure 4 illustrates a comparative analysis of number of neurons and learning rate. The number of neurons is determined in Figure 3, whereas, the corresponding learning rate and dropout ratio are found to be 0.0067 and 0.30, respectively. Figure 5 shows the sample count of the different activation functions. The acquisition function in SMBO algorithm shifts towards the sample space with approximates the surrogate function with the true objective function. In this study, a large number of solution samples are taken from Rectified Linear Unit (ReLU) activation function in comparison with Sigmoid and Tanh, and it concludes that the ReLU function is the most suitable for this case study. Figure 6 compares the pressure loss prediction for the training and the test data. RMSE and MAE for BNN are found to be 5.3 kPa and 2.85% with R2 = 0.99 for train data, while test data shows RMSE and MAE of 8.38 kPa and 3.7% with R2 = 0.989. The prediction for train and test data is in good correlation with best fit curve. The data points form a closed cloud for train data and deviate from best fit after 250 kPa in case of test data.
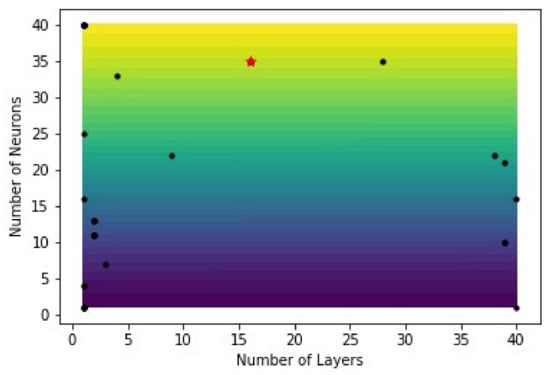
Figure 3.
Optimized Bayesian Neural Network (BNN) number of neurons in each layer plotted with number of layers.
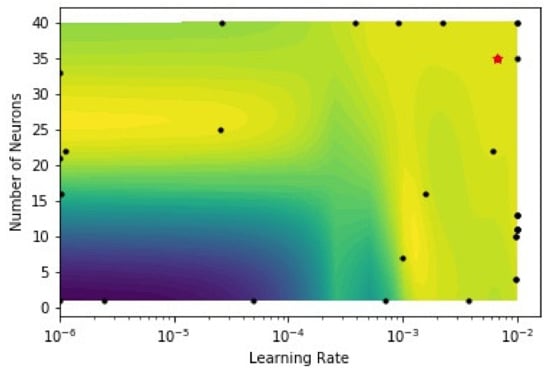
Figure 4.
Optimized BNN learning rate plotted with number of neurons in each layer.
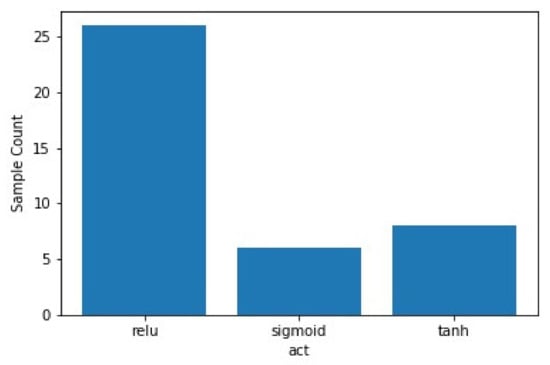
Figure 5.
Sample count from the different sample of the proposed solution space.
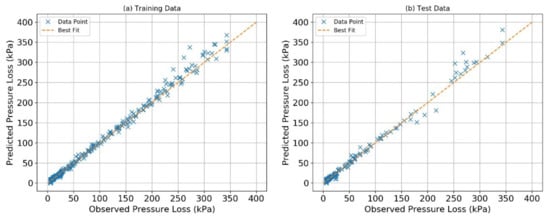
Figure 6.
BNN predicted pressure plotted with observed pressure loss: (a) training dataset and (b) test dataset.
4.1.4. Predictions via Random Forest (RF)
The hyperparameters tuned for this algorithm are the number of estimators (to initiate the total number of decision trees) and the evaluation criteria (to measure the error difference between the predicted and observed values). The plots for the train and test data are shown in Figure 7 for predicted vs. observed pressure loss. The calculated RMSE and MAE for train data is 4.7 kPa and 1.74% with R2 = 0.99, whereas, for test data RMSE and MAE is 9.09 kPa and 3.4% with R2 = 0.986. The prediction for train data is observed to be excellent due to cloud formation around the best fit line till 200 kPa. A slight distortion is observed along the best fit line for the test dataset. The data points lie in close approximation to the best fit line and drifts further much after 200 kPa.
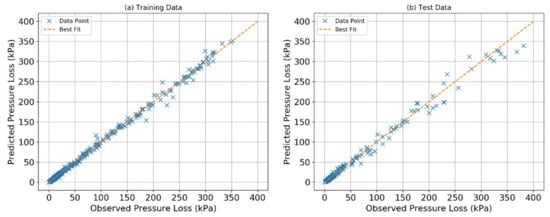
Figure 7.
Random Forest predicted pressure plotted with observed pressure loss: (a) training dataset and (b) test dataset.
4.2. Algorithm’s Performance Evaluation
The performance of the proposed algorithms is summarized in Table 4 based on the metrics, such as RMSE, MAE, and R2 for the training and test dataset. RMSE is plotted in Figure 8 for different algorithms. It is observed that RF and BNN performance on test and train data is very similar and lowest. Both methods surpass the RMSE score for ANN followed by SVM. MAE score is plotted in Figure 9 with different algorithms. It is found that the performance of the BNN and RF is similar and lowest in comparison to ANN and SVM, while RF maintains a marginal accuracy than BNN. The R2 plot is also analyzed (shown in Figure 10) with different algorithms and it is found that the test and train datasets are very concise and clear. The accuracy of RF and BNN are close to 1, whereas, it is near 0.9 for both ANN and SVM.

Table 4.
Summary of metrics to evaluate performance of ANN, BNN, SVM, and random forest (RF).
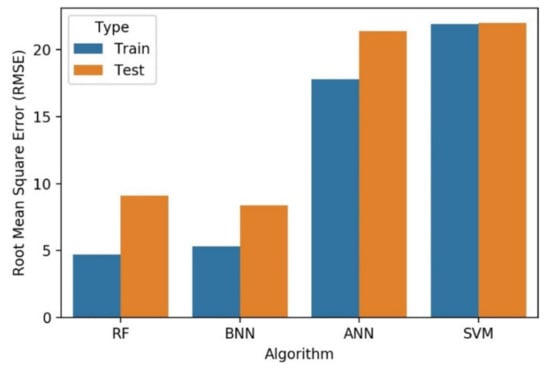
Figure 8.
Analysis of root mean square error.
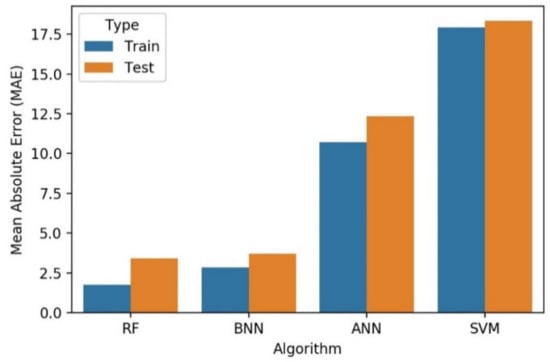
Figure 9.
Analysis of mean absolute error.
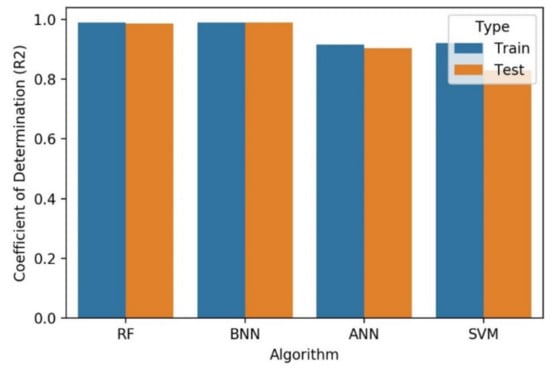
Figure 10.
Analysis of coefficient of determination (R2).
The average RMSE for SVM train and test dataset is 21.96 kPa. However, ANN, RF, and BNN exhibit 19.58, 6.895, and 6.84 kPa, respectively. The average MAE is also lowest for RF at 2.57% followed by BNN at 3.275% and for ANN and SVM it is estimated to be 11.52% and 18.13%, respectively. The average R2 for RF and BNN is 0.988 and 0.989, while ANN and SVM exhibits 0.9 and 0.875, respectively. The performance of RF and BNN are optimum and can accurately determine the pressure drop of Herschel–Bulkley fluids in eccentric and concentric annulus with higher accuracy compared to ANN and SVM. In Figure 11 and Figure 12, the error distribution for train and test datasets are plotted for Bayesian neural network and random forest. The black outline in Figure 11 and Figure 12 denotes the theoretical normal distribution while the red color represents the distribution of the residual error of the test and train dataset respectively. The error distribution for Bayesian neural network is uniformly distributed around mean of −1.25 with standard deviation of 6.7 for train dataset, while same for test dataset is −0.9 with standard deviation of 5.18. The error distribution for random forest train dataset lie around the mean value of −0.21 with standard deviation of 4.4 and the same for test dataset mean is 0.877 with standard deviation of 8.98.
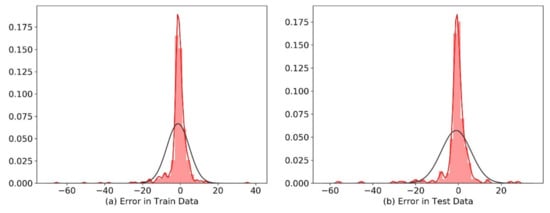
Figure 11.
Distribution of error for train and test dataset, Bayesian Neural Network. Black outline denotes the theoretical normal distribution and the red color represents the distribution of the residual error.
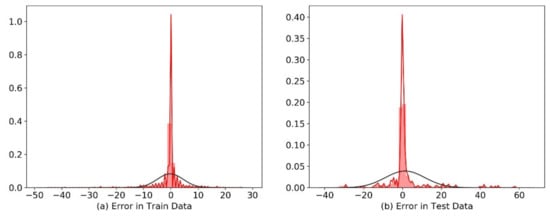
Figure 12.
Distribution of error for train and test dataset, Random Forest. Black outline denotes the theoretical normal distribution and the red color represents the distribution of the residual error.
The pressure loss predicted with RF and BNN algorithm is plotted in Figure 13, Figure 14, Figure 15 and Figure 16. The data sets are divided into two regimes i.e., low-pressure loss (less than 50 kPa) and high-pressure loss (greater than 50 kPa) for a better understanding of predictive algorithms. By analyzing the performance of RF and BNN in high and low regime, it can be concluded that RF performance under low pressure regime is better than BNN. It is observed that BNN may not generalize the fluid behavior at low flow rates and low pressure drop (Figure 14 and Figure 16). The overall performance of both the algorithms is similar at high pressure regime and it can be concluded that the predicted values lie well within the range of the observed data ranges. The observed and predicted dataset in the former analysis is the split train and test data (Section 3.3). The dataset for train was used as measured data points while the test dataset was used as predicted data points. Ahmed [19] proposed a theoretical model based on the experimental results. A comparison is performed in Figure 17 and Figure 18 exhibiting pressure drop predictions from this study and Ahmed [19] for a selected range of annulus diameter (0.020828 m) and fluid XCD5 (Appendix B). The BNN shows a slight resemblance to the derived results of Ahmed [19], while the RF predicted data points lies around the vicinity of the theoretical results, hence, concluding the better performance of the later method.
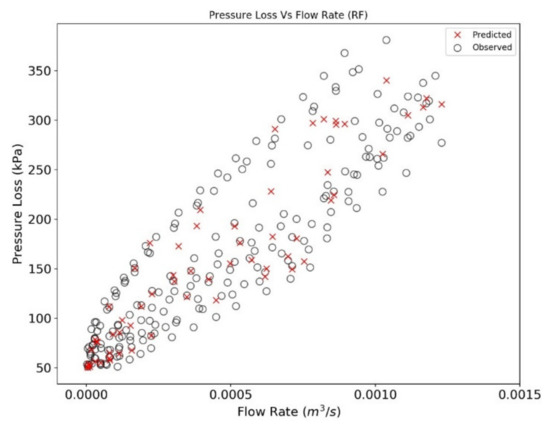
Figure 13.
Observed and predicted pressure loss is plotted with flow rate for RF algorithm for high pressure regime.
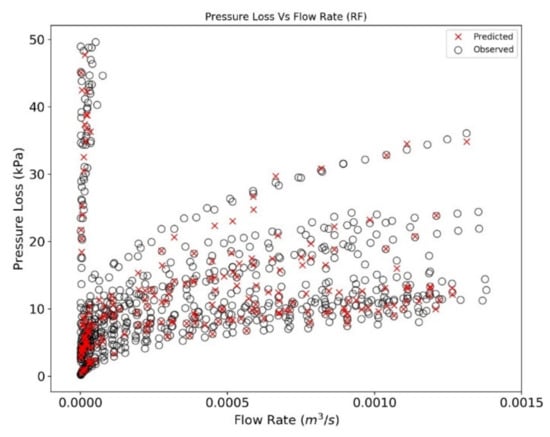
Figure 14.
Observed and predicted pressure loss is plotted with flow rate for RF algorithm for low pressure regime.
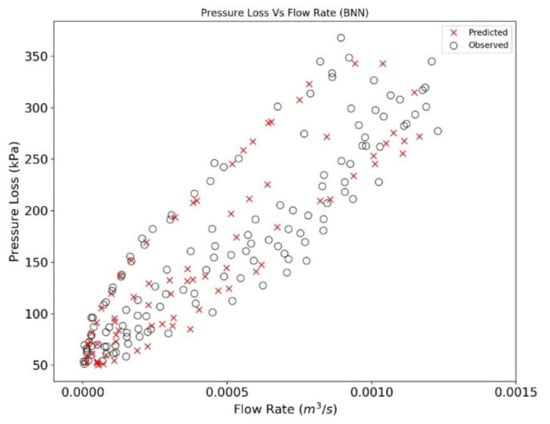
Figure 15.
Observed and predicted pressure loss is plotted with flow rate for BNN algorithm for high pressure regime.
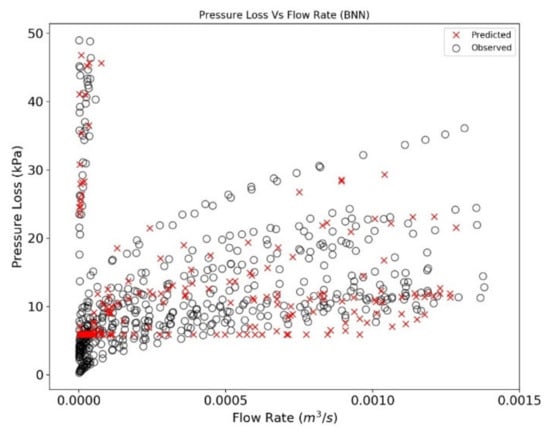
Figure 16.
Observed and predicted pressure loss is plotted with flow rate for BNN algorithm for low pressure regime.
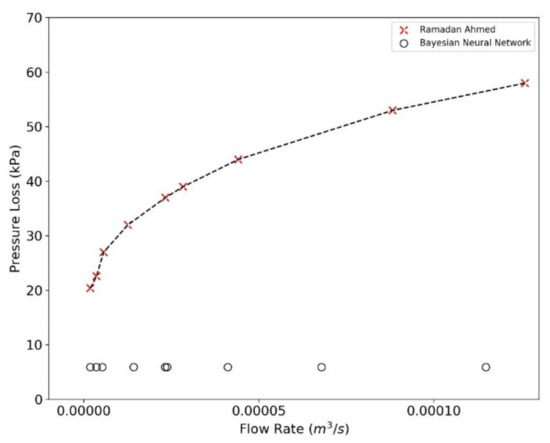
Figure 17.
Comparative analysis of the theoretical solution by Ahmed et al. [19] and the BNN.
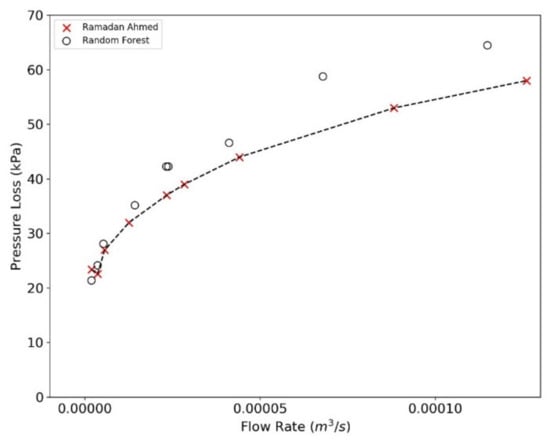
Figure 18.
Comparative analysis of the theoretical solution by Ahmed et al. [19] and the Random Forest.
RF is an ensemble model, where multiple decision trees are created based on randomly sampled datasets to approximate and lower the error. The model also quantifies the contribution of each input parameter towards predicting output. Subsequently, this property can be used to determine the importance of each input parameter to predict the desired output. The percentage-wise bar plot is shown in Figure 19 for each input parameter that have effect on the predicted output values. The diameter ratio (Di/Do) is the highest dominating parameter with contribution of approximately 58% out of the six-input followed by flow rate m3/s i.e., 37%. The diameter ratio and flow rate account for 95% dominance in predicting the pressure loss, while the Herschel–Bulkley fluid parameters has low accountability of remaining 5% where the consistency Index (K) has a share of 3.5% while flow index and shear stress have less than 1% contribution and eccentricity has negligible effect of the pressure loss.
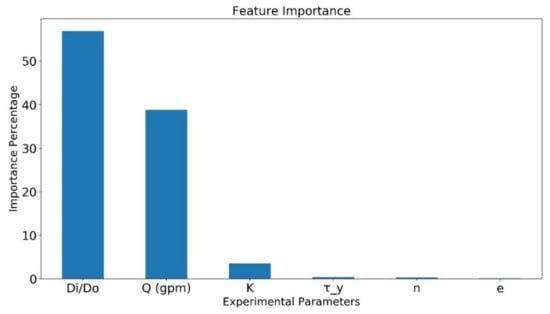
Figure 19.
Feature importance of input parameters based on RF algorithm.
5. Conclusions
This study comprises an analysis of four different algorithms (SVM, ANN, BNN, and RF) to predict the pressure drop in Herschel–Bulkley fluids flowing through eccentric and concentric horizontal annuli. There are six different input parameters such as Di/Do, e, n, K, τy, Q, and one output for prediction pressure loss (ΔP). RMSE, MAE, and R2 are used to evaluate the performance of the proposed algorithms. SVM’s overall performance is found to be the lowest with an RMSE of 21.96 kPa, MAE of 18.13%, and R2 of 0.875. The performance of ANN is slightly better than SVM with an RMSE of 19.58 kPa, MAE of 11.52%, and R2 of 0.90. Alternatively, BNN is used which employs the basic architecture of ANN but additionally considers SMBO to optimize and determine optimum number of hidden layers, number of neurons, learning rate, dropout ratio, and best activation function for the hidden layer. The RMSE, MAE, and R2 for train data are 5.3 kPa, 2.85%, and 0.99, whereas, and test data exhibit 8.38 kPa, 3.7%, and 0.989, respectively. The results clearly indicate that BNN performance is very good on training and test dataset and the model can predict ΔP with very high accuracy. In comparison to BNN, RF reports an RMSE of 4.7 and 9.09 kPa, MAE of 1.74% and 3.4%, and R2 of 0.99 and 0.986 for train and test dataset. The performance of BNN and RF are almost similar, and both can generalize the pressure loss calculation in eccentric and concentric annulus for Herschel–Bulkley fluids, but the performance of RF is better than BNN at low flow rate. The comparison of RF predictions with the theoretical result shows much better agreement than BNN. However, feature analysis concludes that eccentricity (e) has no impact on ΔP prediction. Herschel–Bulkley fluid parameters, such as flow behavior index (n), consistency index (K), and shear stress (τy) have less than 5% effect on ΔP prediction, while diameter ratio (Di/Do) and flow rate (Q) accounts for more than 95% on ΔP.
Author Contributions
Conceptualization, A.K. and S.R.; Methodology, A.K., S.R., S.U.I., and P.V.; Software, A.K.; Validation, A.K.; Formal Analysis, A.K.; Investigation, A.K., S.R., S.U.I., and P.V.; Resources, A.K. and S.R.; Data Curation, A.K.; Writing- Original Draft Preparation, A.K.; Writing- Review and Editing, S.R., S.U.I., and T.G.; Visualization, A.K. and S.R.; Supervision, S.R., P.V., and T.G.; Project Administration, A.K., S.U.I., and T.G.; Funding Acquisition, S.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded by YUTP, grant number 0153AA-E87.
Acknowledgments
This work is supported by Petroleum Engineering Department and Institute of Hydrocarbon Recovery at Universiti Teknologi PETRONAS, Malaysia.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Appendix A.1. Artificial Neural Network
Artificial neural network (ANN) is designed to mimic the working ways of the biological brain. One of the concepts widely recognized regarding ANN is its capability to map and approximate complex functions relationships and the natural propensity to utilize massively distributed processing capacity to store experimental knowledge and makes its use. The common structure of ANN consists of some basic components, namely input layer, weights (connection strength), output layer, and activation function (for hidden and output layer). Each input neurons are multiplied with adjustable weights and summed up with extra value known as bias which is then fed through a nonlinear activation function iteratively to predict results as shown in Figure A1. The transfer function can be given as (ƒ) = WX + b and the output of the network can be calculated by Equation (A1a).
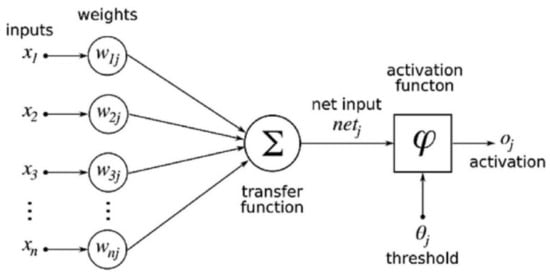
Figure A1.
Single artificial neuron schema [63].
Sigmoid = ϕ z = 11 + e − z
There are several combinations to train a neural network on a given data set and many possible numbers of hyperparameters such as number of neurons in a hidden layer, number of hidden layers, activation function, learning rate, etc., hence, determining the optimal network configuration is a challenging task. In the present work, back propagation algorithm was used to lower the error between the predicted and actual datasets, and the network is optimized for hyperparameters manually.
Appendix A.2. Bayesian Neural Network
The Bayesian neural network (BNN) has the same architecture as of the ANN (described in Appendix A.1), but additionally it uses Sequential Model Based Optimization (SMBO) to determine the hyperparameters of an ANN such as learning rate, number of neurons, etc. A detailed flowchart of SMBO is shown in Figure A2. The machine learning algorithms are generally termed as black box algorithms and optimizing their hyperparameters for performance enhancement could be termed as black art which requires extensive experience or brute force search of solution space. The evaluation for optimum selection of hyperparameters for a function ƒ(x) is computationally extensive. Therefore, it is important to minimize the number of samples drawn. Bayesian optimization incorporates prior belief about ƒ(x) and updates the prior with samples drawn from ƒ(x) to get posterior that better approximates it. This method had been used previously to tune the hyperparameters of Markov Chain Monte Carlo (MCMC) by Mahendran et al., [64], and Hutter et al. [65] used it to develop strategies for configuring the satisfiability of a mixed integer programing solver using random forest. Application of Sequential Model Based Optimization (SMBO) has been established by Snoek el al. [66] for optimizing hyperparameters for SVM and convolution neural networks. SMBO method iterates between fitting a surrogate model to approximate the objective function ƒ(x) and an acquisition function that directs the sampling to the area where an improvement over the current sample observation. In this study, SMBO has been used to optimize the hyperparameters of ANN such as number of neurons, number of hidden layers, drop out ratio and learning rate for predicting the pressure loss.
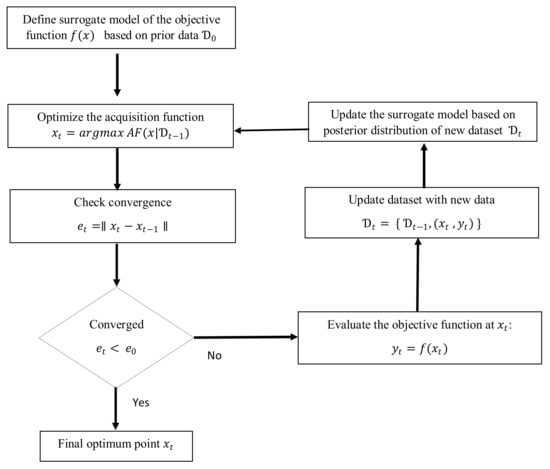
Figure A2.
Flowchart for sequential based model optimization.
The acquisition function in this study is Expected Improvement (EI), given in Equation (A2a).
where ƒ(x+) is the value of the best sample so far and x+ is the location of that sample and the expected improvement for Gaussian model can be defined using Equation (A2b) and Equation (A2c).
where σ(x) and μ(x) are standard deviation and mean of the posterior prediction at x, respectively, Φ and ϕ are the Cumulative Distribution Function and Probability Distribution Function of the standard normal distribution and ξ is the constant of exploration during optimization and the recommended default value is 0.01. An objective function is shown in Figure A3 represented by yellow dashed line and a Gaussian based surrogate function which approximates the objective function (shown in blue) and the samples are the outcome of the expected improvement for sample selection (marked in black).
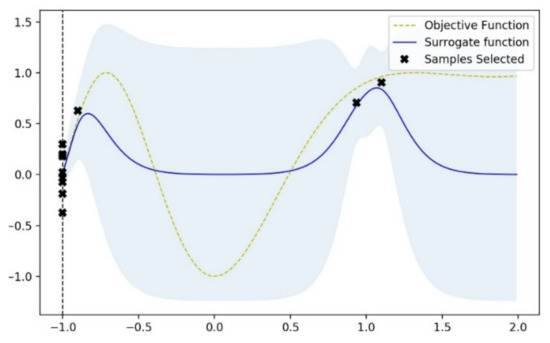
Figure A3.
Plot representing an objective function, Gaussian based surrogate function and expected improvement-based samples selected for optimization of surrogate function to match the true objective function.
Appendix A.3. Support Vector Machine
Support Vector Machine (SVM) is known for supervised learning model used for regression and classification problems. SVM employ nonlinear mapping method to transfer input into high dimensional feature space. This hypothesis of optimal hyperplane separation is the most effective mathematical approach for prediction because it is derived from minimizing structural risk theory. The working principle of SVM is shown in Figure A4.
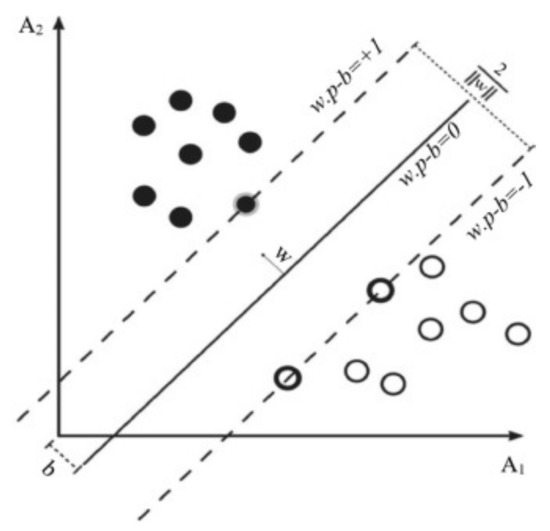
Figure A4.
Hyperplane classification for the training dataset with weight (w) and bias (b) [63].
Consider x separable training datasets in the range of {x1, x2, x3, ……, xn}, where each x is a dimensional vector and a hyperplane H was applied to separate them using Equation (A3a).
Here, hyperplane separator bias value is b, and w is the weight vector perpendicular to the hyperplane. In this present context of a linearly separable case, there are two classes, namely, H+ and H-, which are called support vectors and they separate the data into two planes, given in Equation (A3b) and Equation (A3c).
The distance between these hyperplanes is a margin with no data points, so the distance between them is 2/||w|| and to achieve an optimal margin hyperplane ||w|| should be minimized which means maximize the width.
Appendix A.4. Random Forest
Random Forest (RF) can be used for regression or classification. It is an ensemble of different regression trees and is used for nonlinear multiple regression. Each leaf contains a distribution for the continuous output variables. Random forest builds multiple decision trees and merges them together to get a more accurate and stable prediction. For each estimator, it selects a random subsample of features. It can be used to rank the importance of variables in a regression or classification problem naturally. Figure A5 exemplifies a decision tree based on flow rate and then dividing up further into leaf.
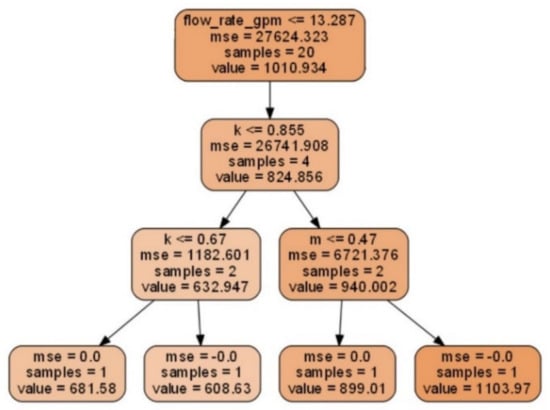
Figure A5.
Single leaf node of tree-based model in random forest with various decision nodes.
Appendix B

Table A1.
Details of the fluid.
Table A1.
Details of the fluid.
| Fluid and Annuli | n | ||
|---|---|---|---|
| XCD1 (Annulus #3) | 4.3 | 1.29 | 0.38 |
| XCD2 (Annulus #3) | 11.3 | 1.85 | 0.35 |
| XCD3 (Annulus #3) | 14.4 | 1.56 | 0.39 |
| XCD4 (Annulus #3) | 5.1 | 1.26 | 0.36 |
| XCD-PAC1 (Annulus #3) | 7.5 | 1.07 | 0.47 |
| XCD-PAC2 (Annulus #3) | 4.8 | 4.49 | 0.35 |
| XCD-PAC3 (Annulus #1,2,4) | 0 | 0.99 | 0.48 |
| XCD5 (Annulus #1,2,4) | 6.5 | 0.64 | 0.48 |
| XCD6 (Annulus #1,2,4) | 12.6 | 1.77 | 0.38 |
| XCD7 (Annulus #1,2,4) | 6.4 | 0.81 | 0.45 |
| XCD8 (Annulus #1,2,4) | 4.9 | 0.7 | 0.45 |
| XCD-PAC4 (Annulus #1,2,4) | 1.9 | 4.28 | 0.36 |
| XCD-PAC5 (Annulus #1,2,4) | 3.5 | 3.27 | 0.39 |
| XCD-PAC6 (Annulus #1,2,4) | 0 | 1.12 | 0.49 |
| XCD9 (Annulus #1,2,4) | 8.1 | 0.9 | 0.45 |
| XCD-PAC7 (Annulus #1,2,4) | 0 | 1.4 | 0.46 |
| XCD10 (Annulus #1,2,4) | 9 | 1.01 | 0.48 |
| XCD-PAC8 (Annulus# 1,2,4) | 3.8 | 2.98 | 0.4 |
References
- Herschel, W.H.; Bulkley, R. Konsistenzmessungen von Gummi-Benzollösungen. Kolloid Z. 1926, 39, 291–300. [Google Scholar] [CrossRef]
- Hemphill, T.; Campos, W.R.; Pilehvari, A.A. Yield-Power Law Model more Accurately Predicts Mud Rheology. Oil and Gas Journal 1993, 19, 34. [Google Scholar]
- Technology Equations Determine Flow States for Yield-Pseudoplastic Drilling Fluids.|Oil & Gas Journal. Available online: https://www.ogj.com/home/article/17234529/technology-equations-determine-flow-states-for-yieldpseudoplastic-drilling-fluids (accessed on 9 March 2020).
- Rheologic and Hydraulic Parameter Integration Improves Drilling Operations.|Oil & Gas Journal. Available online: https://www.ogj.com/home/article/17230023/rheologic-and-hydraulic-parameter-integration-improves-drilling-operations (accessed on 9 March 2020).
- Maglione, R.; Robotti, G.; Romagnoli, R. In-situ rheological characterization of drilling mud. SPE J. 2000, 5, 377–386. [Google Scholar] [CrossRef]
- Bailey, W.J.; Peden, J.M. A generalized and consistent pressure drop and flow regime transition model for drilling hydraulics. In SPE Drilling and Completion; Soc Pet Eng (SPE): Englewood, CO, USA, 2000; Volume 15, pp. 44–56. [Google Scholar]
- Becker, T.E.; Morgan, R.G.; Chin, W.C.; Griffith, J.E. Improved rheology model and hydraulics analysis for tomorrow’s Wellbore Fluid Applications. In Proceedings of the SPE Production and Operations Symposium, Oklahoma City, OK, USA, 23–26 March 2003. [Google Scholar]
- Kelessidis, V.C.; Tsamantaki, C.; Dalamarinis, P. Effect of pH and electrolyte on the rheology of aqueous Wyoming bentonite dispersions. Appl. Clay Sci. 2007, 38, 86–96. [Google Scholar] [CrossRef]
- AADE-05-NTCE-27 Comparing a Basic Set of Drilling Fluid Pressure-Loss Relationships to Flow-Loop and Field Data. Available online: https://www.aade.org/application/files/1915/7304/0408/AADE-05-NTCE-27_Zamora.pdf (accessed on 9 March 2020).
- Fredrickson, A.; Bird, R.B. Non-newtonian flow in annuli. Ind. Eng. Chem. 1958, 50, 347–352. [Google Scholar] [CrossRef]
- Hanks, R.W. The axial laminar flow of yield-pseudoplastic fluids in a concentric annulus. Ind. Eng. Chem. Process Des. Dev. 1979, 18, 488–493. [Google Scholar] [CrossRef]
- Buchtelová, M. Comments on “The Axial Laminar Flow of Yield-Pseudoplastic Fluids in a Concentric Annulus. ” Ind. Eng. Chem. Res. 1988, 27, 1557–1558. [Google Scholar] [CrossRef]
- Heywood, N.I.; Cheng, D.C.H. Comparison of methods for predicting head loss in turbulent pipe flow of non-newtonian fluids. Meas. Control 1984, 6, 33–45. [Google Scholar] [CrossRef]
- Gücüyener, I.H.; Mehmetoǧlu, T. Characterization of flow regime in concentric annuli and pipes for yield-pseudoplastic fluids. J. Pet. Sci. Eng. 1996, 16, 45–60. [Google Scholar] [CrossRef]
- Reed, T.D.; Pilehvari, A.A. A new model for laminar, transitional, and turbulent flow of drilling muds. In Proceedings of the SPE Production Operations Symposium, Oklahoma City, Oklahoma, 21–23 March 1993. [Google Scholar]
- Non-Newtonian Fluid Flow in Eccentric Annuli and Its Application to Petroleum Engineering Problems. Available online: https://digitalcommons.lsu.edu/cgi/viewcontent.cgi?referer=&httpsredir=1&article=5847&context=gradschool_disstheses (accessed on 9 March 2020).
- Haciislamoglu, M.; Langlinais, J. Non-newtonian flow in eccentric annuli. J. Energy Resour. Technol. Trans. ASME 1990, 112, 163–169. [Google Scholar] [CrossRef]
- Kelessidis, V.C.; Dalamarinis, P.; Maglione, R. Experimental study and predictions of pressure losses of fluids modeled as Herschel-Bulkley in concentric and eccentric annuli in laminar, transitional and turbulent flows. J. Pet. Sci. Eng. 2011, 77, 305–312. [Google Scholar] [CrossRef]
- Ahmed, R. Experimental Study and Modeling of Yield Power-Law Fluid Flow in Pipes and Annuli. Available online: https://edx.netl.doe.gov/dataset/experimental-study-and-modeling-of-yield-power-law-fluid-flow-in-pipes-and-annuli/resource_download/131420e2-5b16-4e4b-9ceb-74b73f9393b1 (accessed on 9 March 2020).
- Kozicki, W.; Chou, C.H.; Tiu, C. Non-newtonian flow in ducts of arbitrary cross-sectional shape. Chem. Eng. Sci. 1966, 21, 665–679. [Google Scholar] [CrossRef]
- Luo, Y.; Peden, M. Flow of Non·Newtonian Fluids Through Eccentric Annuli; Society of Petroleum Engineers: Englewood, CO, USA, 1990. [Google Scholar]
- Vajargah, A.K.; Fard, F.N.; Parsi, M.; Hoxha, B.B. Investigating the impact of the “tool joint effect” on equivalent circulating density in deep-water wells. In Proceedings of the Society of Petroleum Engineers—SPE Deepwater Drilling and Completions Conference, Galveston, TX, USA, 10–11 September 2014; pp. 341–352. [Google Scholar]
- CFD Method for Predicting Annular Pressure Losses and Cuttings Concentration in Eccentric Horizontal Wells. Available online: https://www.hindawi.com/journals/jpe/2014/486423/ (accessed on 9 March 2020).
- Kelessidis, V.C.; Maglione, R.; Tsamantaki, C.; Aspirtakis, Y. Optimal determination of rheological parameters for Herschel-Bulkley drilling fluids and impact on pressure drop, velocity profiles and penetration rates during drilling. J. Pet. Sci. Eng. 2006, 53, 203–224. [Google Scholar] [CrossRef]
- Founargiotakis, K.; Kelessidis, V.C.; Maglione, R. Laminar, transitional and turbulent flow of Herschel-Bulkley fluids in concentric annulus. Can. J. Chem. Eng. 2008, 86, 676–683. [Google Scholar] [CrossRef]
- Sorgun, M.; Ozbayoglu, M.E.; Aydin, I. Modeling and experimental study of newtonian fluid flow in annulus. J. Energy Resour. Technol. Trans. ASME 2010, 132. [Google Scholar] [CrossRef]
- Ahmed, R.M.; Miska, S.; Miska, W. Friction pressure loss determination of yield power law fluid in eccentric annular laminar flow. In Proceedings of the Wiertnictwo Nafta Gaz, Krakow, Poland, 23 January 2006; Volume 23, pp. 47–53. [Google Scholar]
- Ogugbue, C.C.; Shah, S.N. Friction pressure correlations for oilfield polymeric solutions in eccentric annulus. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering—OMAE, Honolulu, HI, USA, 31 May–5 June 2009; Volume 7, pp. 583–592. [Google Scholar]
- Mokhtari, M.; Ermila, M.; Tutuncu, A.N. Accurate Bottomhole Pressure for Fracture Gradient Prediction and Drilling Fluid Pressure Program—Part I; American Rock Mechanics Association: Woodland Terrance, VA, USA, 2012. [Google Scholar]
- Karimi Vajargah, A.; Van Oort, E. Determination of drilling fluid rheology under downhole conditions by using real-time distributed pressure data. J. Nat. Gas Sci. Eng. 2015, 24, 400–411. [Google Scholar] [CrossRef]
- Erge, O.; Karimi Vajargah, A.; Ozbayoglu, M.E.; Van Oort, E. Frictional pressure loss of drilling fluids in a fully eccentric annulus. J. Nat. Gas Sci. Eng. 2015, 26, 1119–1129. [Google Scholar] [CrossRef]
- A Novel Hybrid Bat Algorithm with Harmony Search for Global Numerical Optimization. Available online: https://www.hindawi.com/journals/jam/2013/696491/ (accessed on 9 March 2020).
- La Fe-Perdomo, I.; Beruvides, G.; Quiza, R.; Haber, R.; Rivas, M. Automatic selection of optimal parameters based on simple soft-computing methods: A case study of micromilling processes. IEEE Trans. Ind. Inform. 2019, 15, 800–811. [Google Scholar] [CrossRef]
- Osman, E.A.; Aggour, M.A. Determination of drilling mud density change with pressure and temperature made simple and accurate by ANN. In Proceedings of the Middle East Oil Show, Bahrain, 9–12 June 2003. Society of Petroleum Engineers. [Google Scholar]
- Jeirani, Z.; Mohebbi, A. Artificial neural networks approach for estimating filtration properties of drilling fluids. J. Jpn. Pet. Inst. 2006, 49, 65–70. [Google Scholar] [CrossRef]
- Siruvuri, C.; Nagarakanti, S.; Samuel, R. Stuck pipe prediction and avoidance: A convolutional neural network approach. In Proceedings of the IADC/SPE Drilling Conference, Miami, FL, USA, 21–23 February 2006. Society of Petroleum Engineers. [Google Scholar]
- Miri, R.; Sampaio, J.H.B.; Afshar, M.; Lourenco, A. Development of artificial neural networks to predict differential pipe sticking in iranian offshore oil fields. In Proceedings of the International Oil Conference and Exhibition in Mexico, Cancun, Mexico, 31 August–2 September 2006. Society of Petroleum Engineers. [Google Scholar]
- Murillo, A.; Neuman, J.; Samuel, R. Pipe sticking prediction and avoidance using adaptive fuzzy logic and neural network modeling. In Proceedings of the SPE Production and Operations Symposium, Oklahoma City, Oklahoma, 4–8 April 2009; Society of Petroleum Engineers. pp. 244–258. [Google Scholar]
- Abdulmalek Ahmed, S.; Elkatatny, S.; Abdulraheem, A.; Mahmoud, M.; Ali, A.Z. Prediction of rate of penetration of deep and tight formation using support vector machine. In Proceedings of the Society of Petroleum Engineers—SPE Kingdom of Saudi Arabia Annual Technical Symposium and Exhibition 2018, SATS 2018, Dammam, Saudi Arabia, 23–26 April 2018. Society of Petroleum Engineers. [Google Scholar]
- Elkatatny, S. Real-time prediction of rheological parameters of KCl water-based drilling fluid using artificial neural networks. Arab. J. Sci. Eng. 2017, 42, 1655–1665. [Google Scholar] [CrossRef]
- Ozbayoglu, E.M.; Miska, S.Z.; Reed, T.; Takach, N. Analysis of Bed Height in Horizontal and Highly-Inclined Wellbores by Using Artificial Neuraletworks; Society of Petroleum Engineers (SPE): Englewood, CO, USA, 2002. [Google Scholar]
- Rooki, R. Estimation of pressure loss of herschel–bulkley drilling fluids during horizontal annulus using artificial neural network. J. Dispers. Sci. Technol. 2015, 36, 161–169. [Google Scholar] [CrossRef]
- Rooki, R. Application of general regression neural network (GRNN) for indirect measuring pressure loss of Herschel-Bulkley drilling fluids in oil drilling. Meas. J. Int. Meas. Confed. 2016, 85, 184–191. [Google Scholar] [CrossRef]
- Rooki, R.; Rakhshkhorshid, M. Cuttings transport modeling in underbalanced oil drilling operation using radial basis neural network. Egypt. J. Pet. 2017, 26, 541–546. [Google Scholar] [CrossRef]
- Ahmadi, M.A.; Shadizadeh, S.R.; Shah, K.; Bahadori, A. An accurate model to predict drilling fluid density at wellbore conditions. Egypt. J. Pet. 2018, 27, 1–10. [Google Scholar] [CrossRef]
- Lu, Y.; Chen, M.; Jin, Y.; Hou, B.; Jia, L.; Hui, H. Identification of leak zone pre-drilling based on fuzzy control. In Proceedings of the PEAM 2011—Proceedings: 2011 IEEE Power Engineering and Automation Conference, Wuhan, China, 8–9 September 2011; Volume 3, pp. 353–356. [Google Scholar]
- Chhantyal, K.; Viumdal, H.; Mylvaganam, S. Ultrasonic level scanning for monitoring mass flow of complex fluids in open channels—A novel sensor fusion approach using AI techniques. In Proceedings of the Proceedings of IEEE Sensors, Glasgow, UK, 29 October–1 November 2017; pp. 1–3. [Google Scholar]
- Chhantyal, K.; Viumdal, H.; Mylvaganam, S. Soft sensing of non-newtonian fluid flow in open venturi channel using an array of ultrasonic level sensors—AI models and their validations. Sensors (Switzerland) 2017, 17, 2458. [Google Scholar] [CrossRef]
- Skalle, P.; Sveen, J.; Aamodt, A. Improved efficiency of oil well drilling through case based reasoning. In Proceedings of the Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2000; Volume 1886 LNAI, pp. 712–722. [Google Scholar]
- Al-Azani, K.; Elkatatny, S.; Abdulraheem, A.; Mahmoud, M.; Ali, A. Prediction of cutting concentration in horizontal and deviated wells using support vector machine. In Proceedings of the Society of Petroleum Engineers—SPE Kingdom of Saudi Arabia Annual Technical Symposium and Exhibition 2018, SATS 2018, Dammam, Saudi Arabia, 23–26 April 2018. Society of Petroleum Engineers. [Google Scholar]
- Sameni, A.; Chamkalani, A. The application of least square support vector machine as a mathematical algorithm for diagnosing drilling effectivity in shaly formations. J. Pet. Sci. Technol. 2018, 8, 3–15. [Google Scholar]
- Kankar, P.K.; Sharma, S.C.; Harsha, S.P. Fault diagnosis of ball bearings using machine learning methods. Expert Syst. Appl. 2011, 38, 1876–1886. [Google Scholar] [CrossRef]
- Guo, X.; Chen, L.; Shen, C. Hierarchical adaptive deep convolution neural network and its application to bearing fault diagnosis. Meas. J. Int. Meas. Confed. 2016, 93, 490–502. [Google Scholar] [CrossRef]
- Wen, L.; Li, X.; Gao, L.; Zhang, Y. A new convolutional neural network-based data-driven fault diagnosis method. IEEE Trans. Ind. Electron. 2018, 65, 5990–5998. [Google Scholar] [CrossRef]
- Castaño, F.; Beruvides, G.; Haber, R.E.; Artuñedo, A. Obstacle recognition based on machine learning for on-chip LiDAR sensors in a cyber-physical system. Sensors 2017, 17, 2109. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Bingham, E.C. Fluidity and Plasticity, 2nd ed.; McGraw-Hill: New York, NY, USA, 1922. [Google Scholar]
- Govier, G.W.; George, W.; Aziz, K. The Flow of Complex Mixtures in Pipes, 2nd ed.; Society of Petroleum Engineers: Richardson, TX, USA, 2008; ISBN 9781555631390. [Google Scholar]
- Bourgoyne, A.T. Applied Drilling Engineering; Society of Petroleum Engineers: Englewood, CO, USA, 1986; ISBN 9781555630010. [Google Scholar]
- Castaño, F.; Strzełczak, S.; Villalonga, A.; Haber, R.E.; Kossakowska, J. Sensor reliability in cyber-physical systems using internet-of-things data: A review and case study. Remote Sens. 2019, 11, 2252. [Google Scholar] [CrossRef]
- Ding, Y.; Xiao, X.; Huang, X.; Sun, J. System identification and a model-based control strategy of motor driven system with high order flexible manipulator. Ind. Robot 2019, 46, 672–681. [Google Scholar] [CrossRef]
- Matía, F.; Jiménez, V.; Alvarado, B.P.; Haber, R. The fuzzy Kalman filter: Improving its implementation by reformulating uncertainty representation. Fuzzy Sets Syst. 2019. [Google Scholar] [CrossRef]
- Abbas, A.K.; Al-haideri, N.A.; Bashikh, A.A. Implementing artificial neural networks and support vector machines to predict lost circulation. Egypt. J. Pet. 2019, 28, 339–347. [Google Scholar] [CrossRef]
- Adaptive MCMC with Bayesian Optimization. 2010. Available online: http://proceedings.mlr.press/v22/mahendran12/mahendran12.pdf (accessed on 9 March 2020).
- Hutter, F.; Hoos, H.H.; Leyton-Brown, K. Sequential model-based optimization for general algorithm configuration. In Proceedings of the Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2011; Volume 6683 LNCS, pp. 507–523. [Google Scholar]
- Practical Bayesian Optimization of Machine Learning Algorithms. Available online: https://papers.nips.cc/paper/4522-practical-bayesian-optimization-of-machine-learning-algorithms.pdf (accessed on 9 March 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).