Improved Active Disturbance Rejection-Based Decentralized Control for MIMO Nonlinear Systems: Comparison with The Decoupled Control Scheme
Abstract
1. Introduction
1.1. Active Disturbance Rejection Control
1.2. Related Works
1.3. Paper Contribution
1.4. Paper Organization
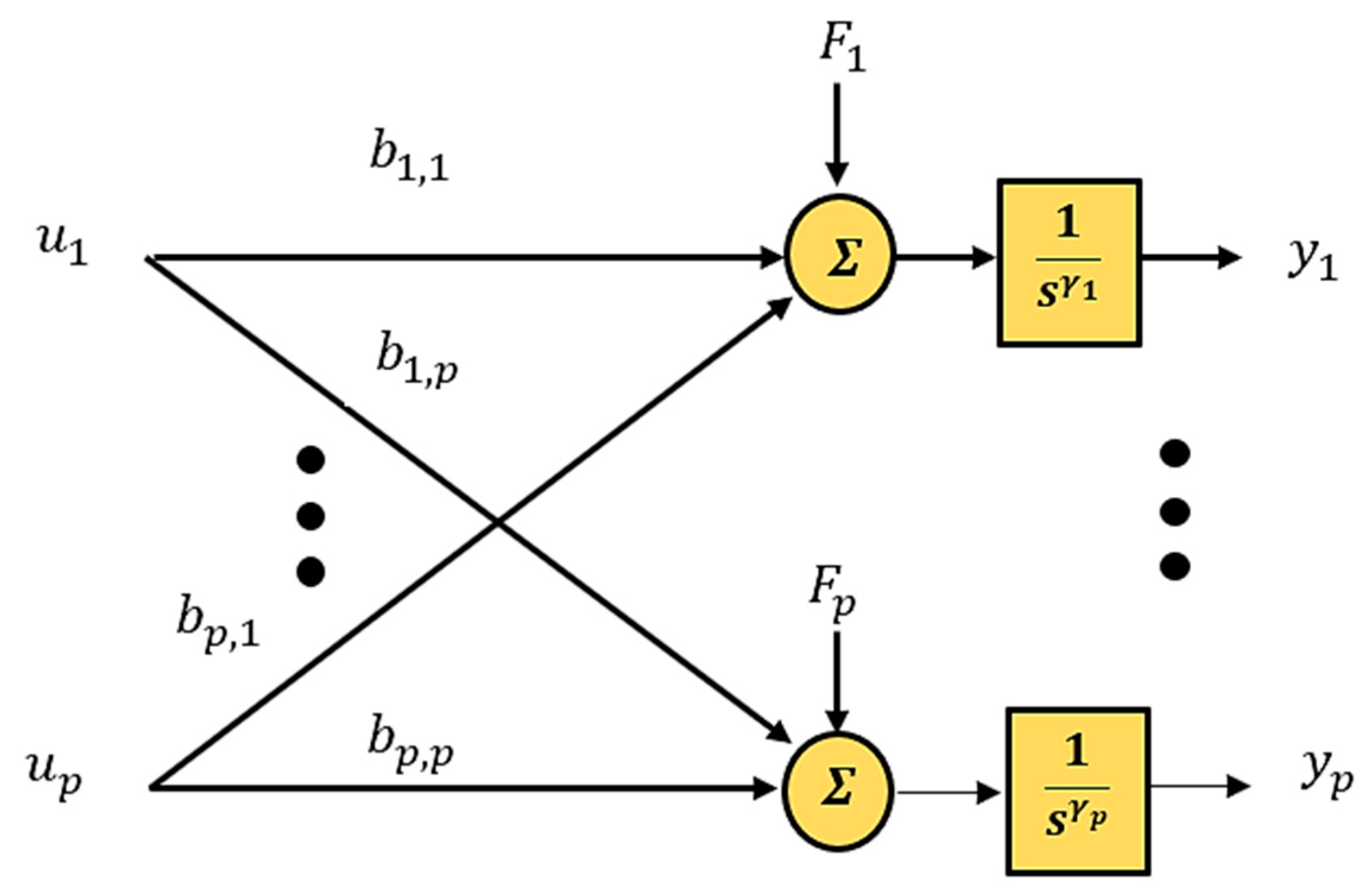
2. Problem Statement
- Disassociation of the state couplings.
- Disassociation of the input couplings.
- Rejects the effect of the generalized disturbance, , on the outputs.
- Maintaining an acceptable performance during both transient and steady-state responses.
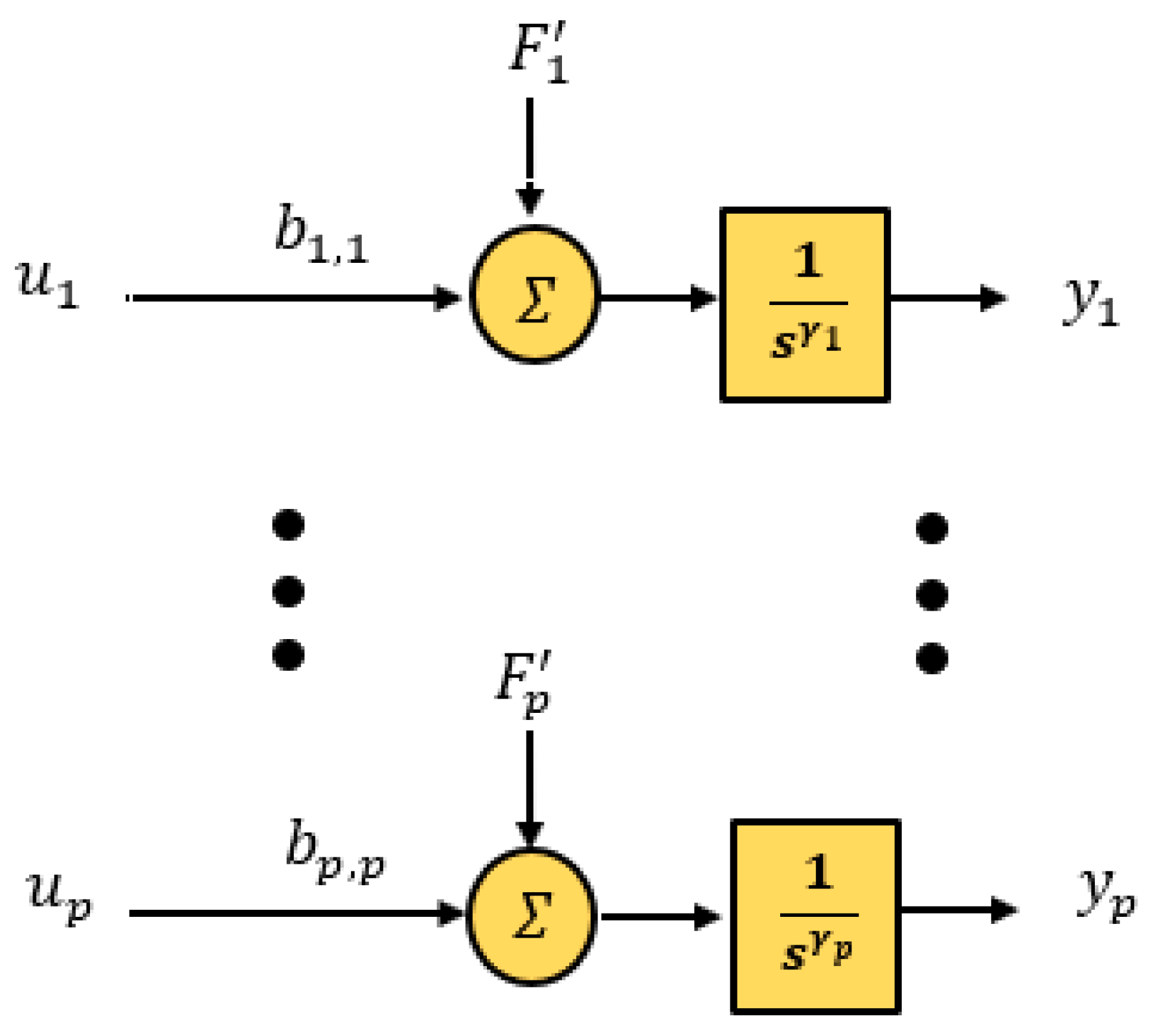
3. Decoupled Control [23]
4. Main Results
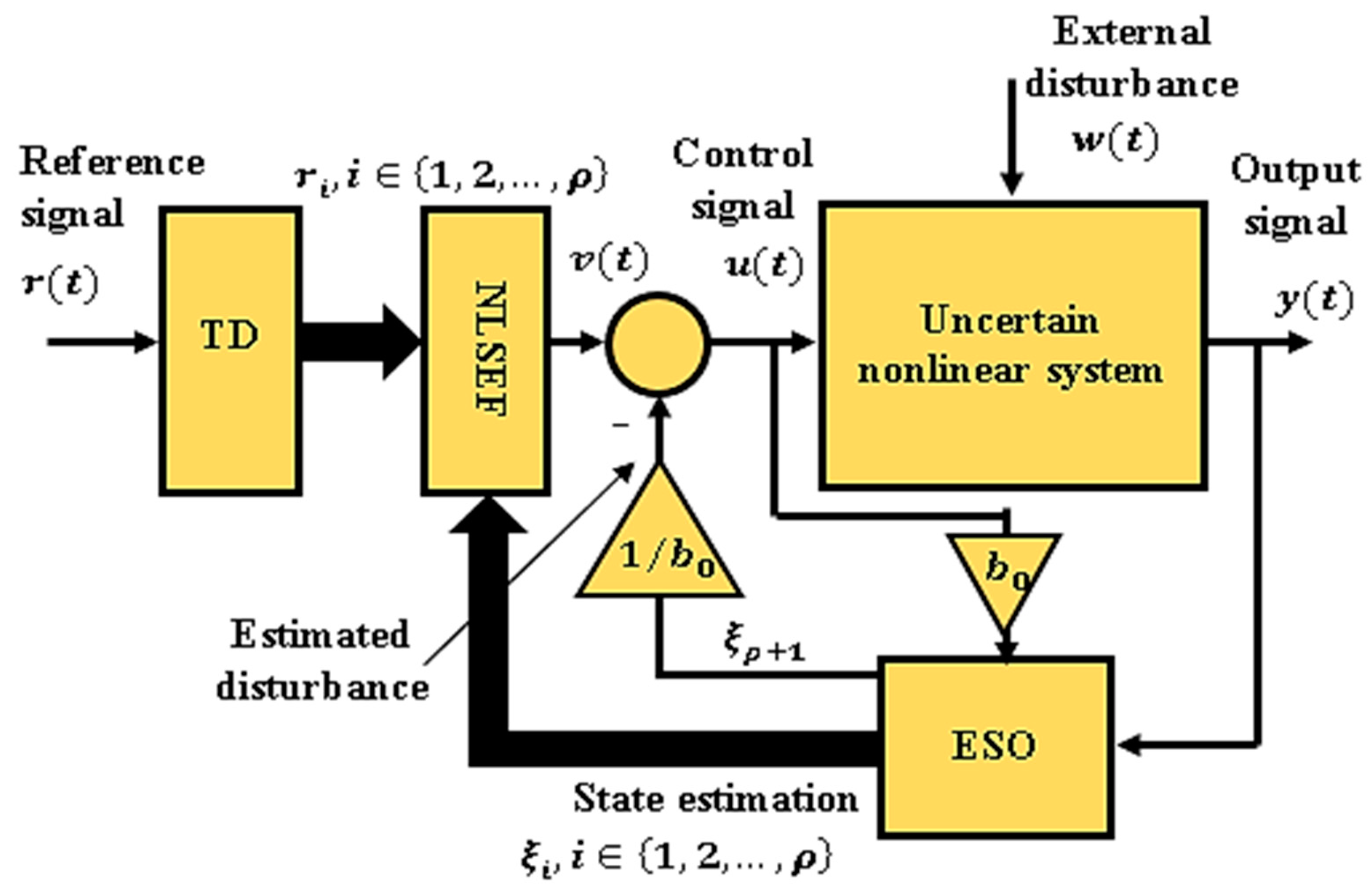
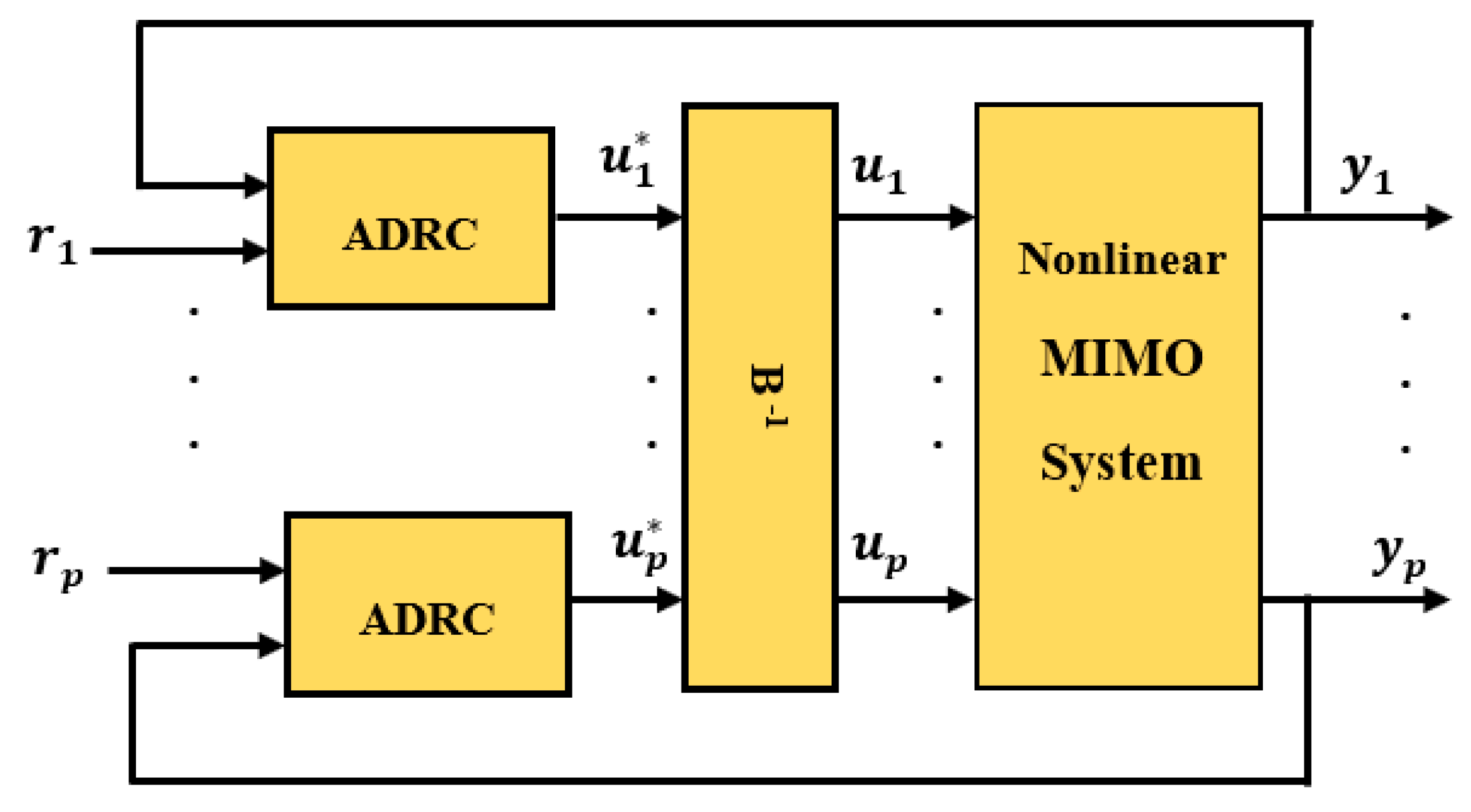
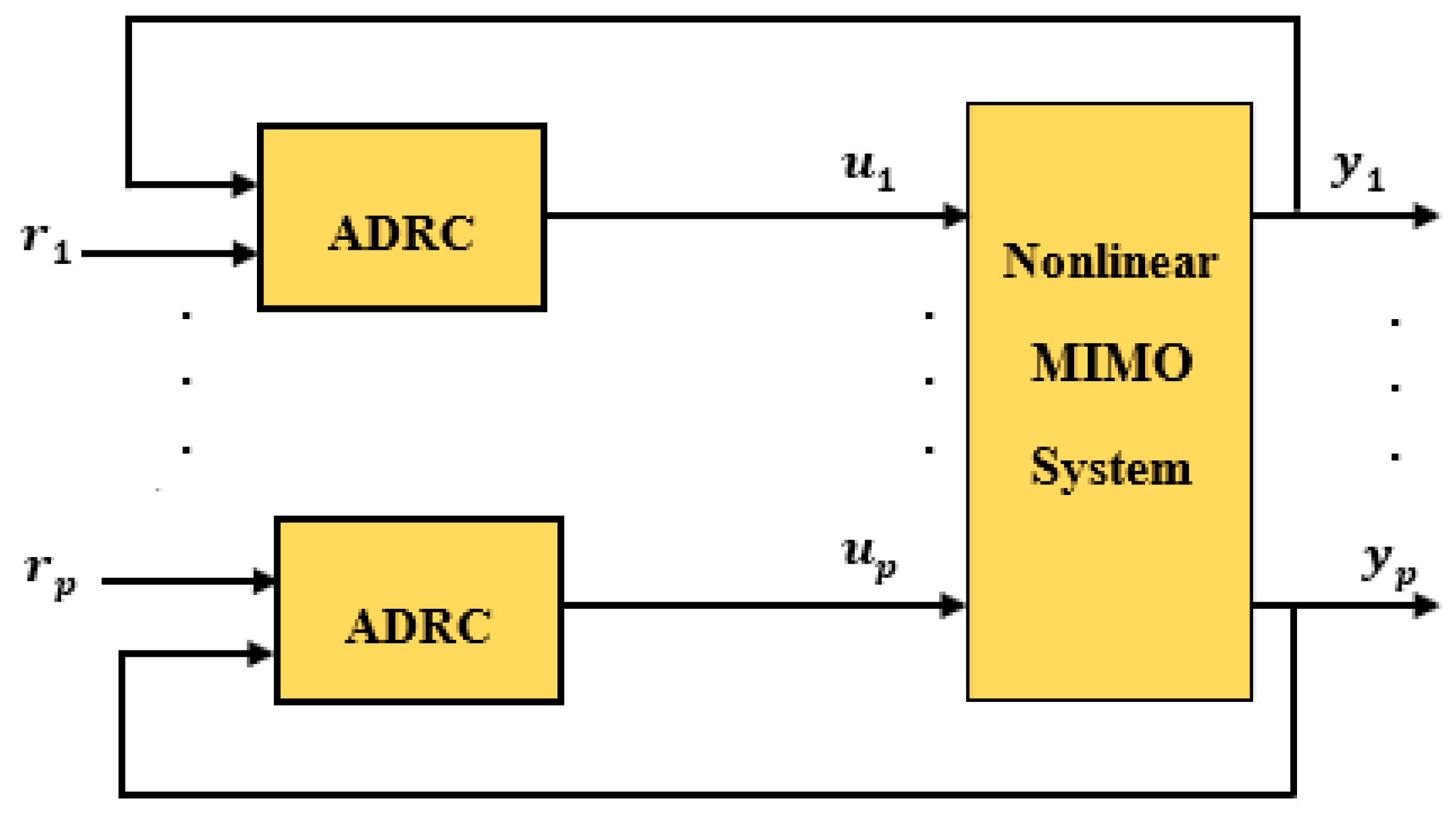
4.1. The Proposed Decentralized Scheme Based on ADRC
4.2. The Improved ADRC (IADRC)
4.3. Closed-Loop Stability Analysis
5. Numerical Simulations
- Conventional TD, described by Reference [62]:where , is an application-dependent design parameter and it is set accordingly to speed up or slow down the transient profile.
- fal-based control law, given as:where is the tracking error and are design parameters.
- The LESO, given as follows [62]:where the vectors and are the observed model states, are the estimated generalized disturbance, and , is the bandwidth of the NHOESO of the i-th subsystem.
- Conventional TD is given by Equation (43).
- fal-based control law given by Equation (44).
- A novel NHOESO, proposed as:where the vectors and are the observed model states, are the estimated generalized disturbances, , are design parameters, and is the bandwidth of the NHOESO of the i-th subsystem. The nonlinear function is designed as in Reference [63]:withwhere are positive design parameters and is the estimation error.
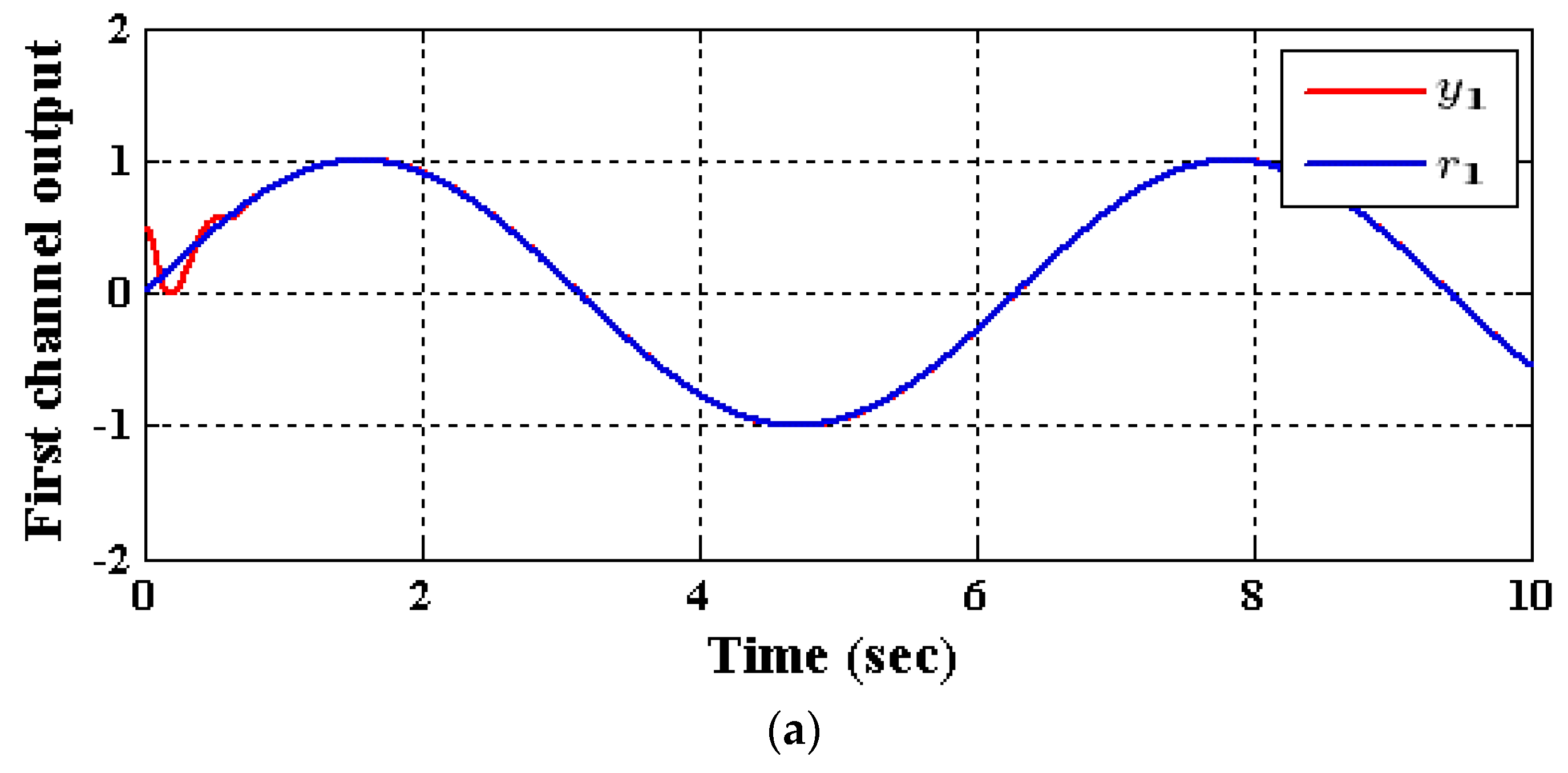
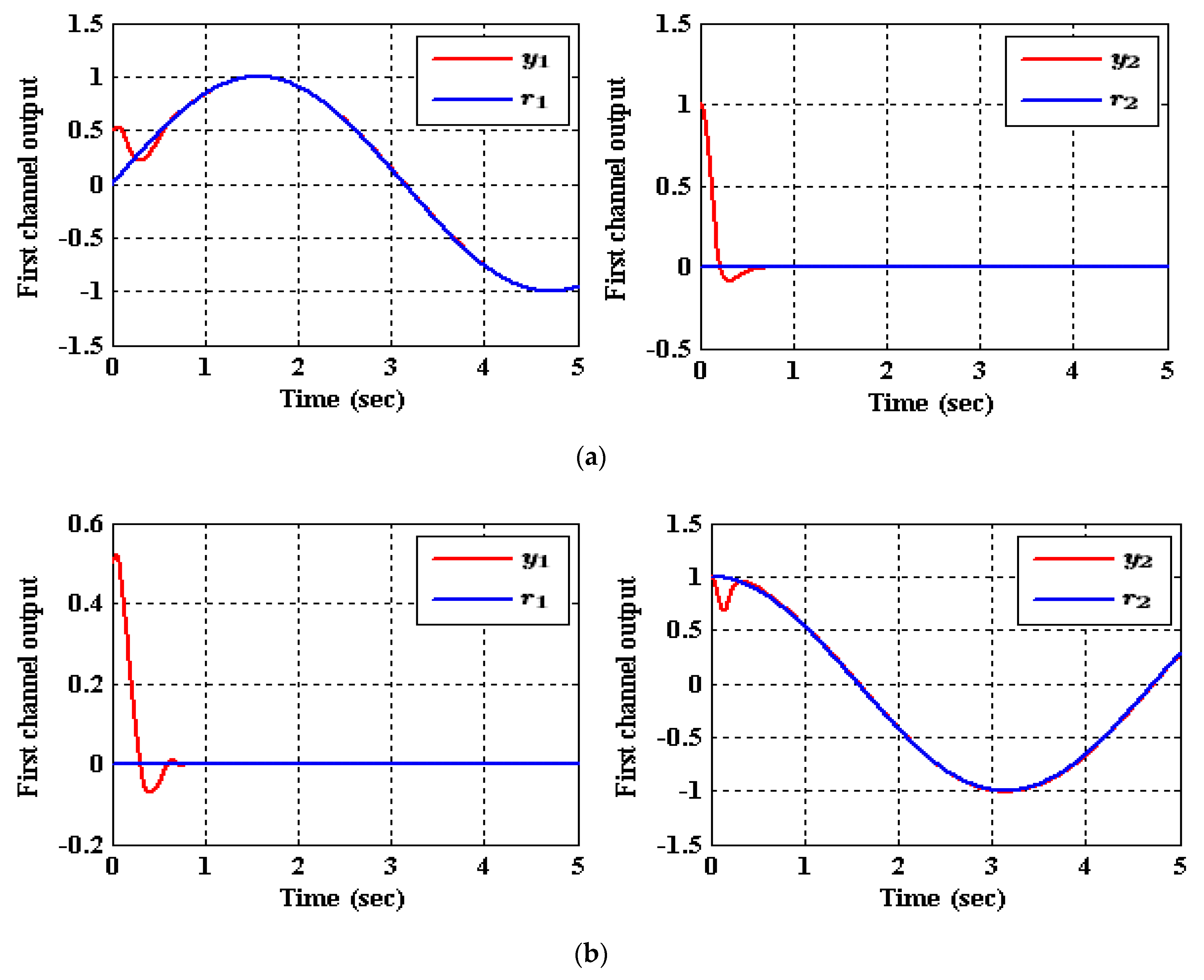
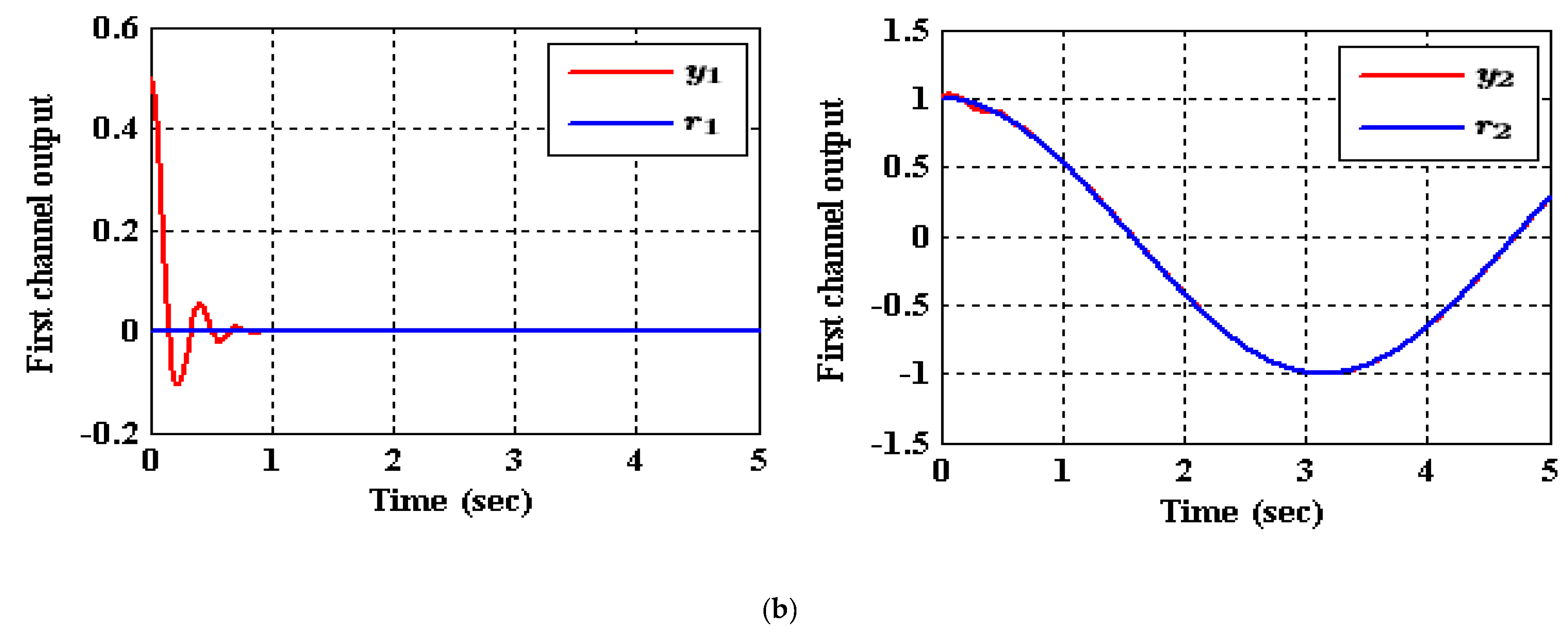
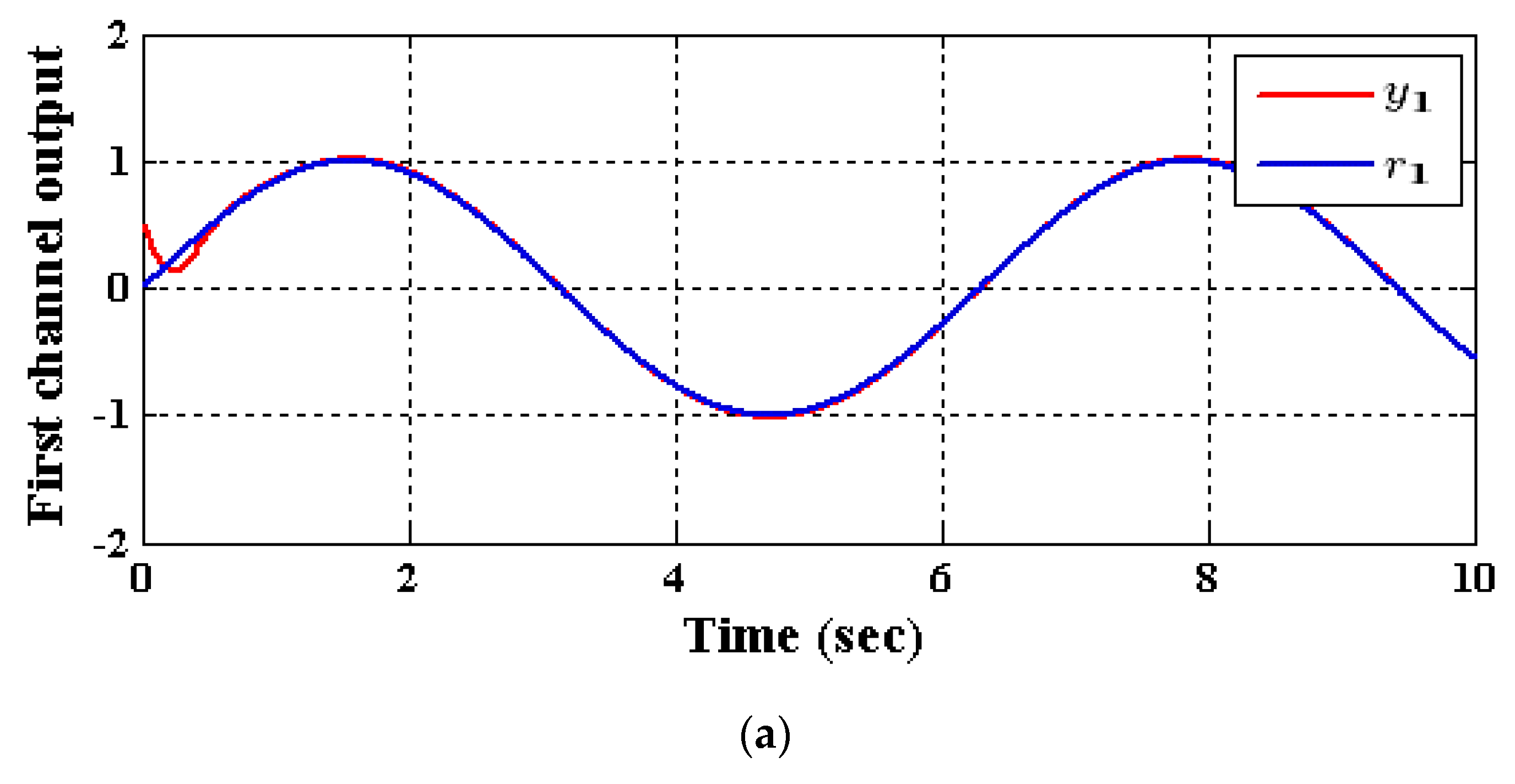
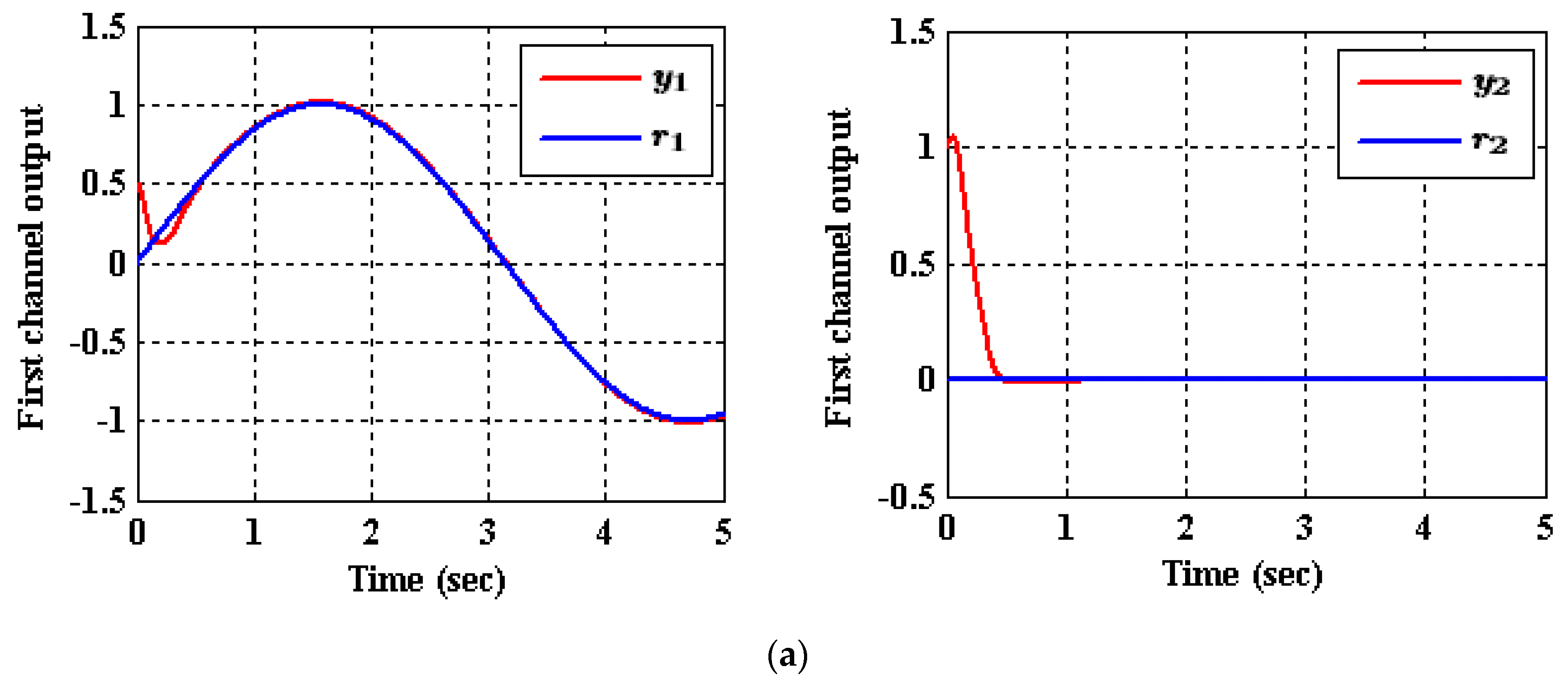
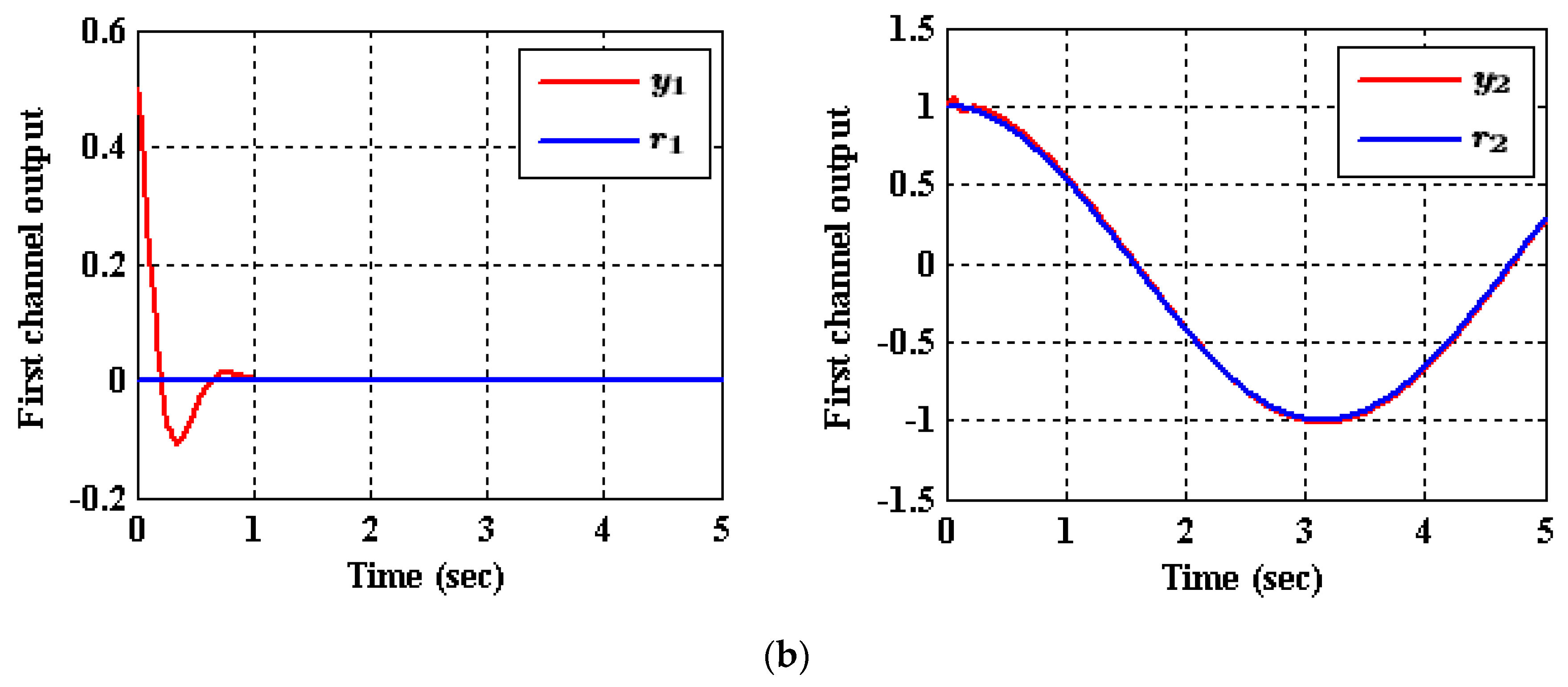
5.1. Results of the Decoupled ADRC Control Scheme [23]
- Case (1): Output Tracking
- Case (2): Input and State Decoupling
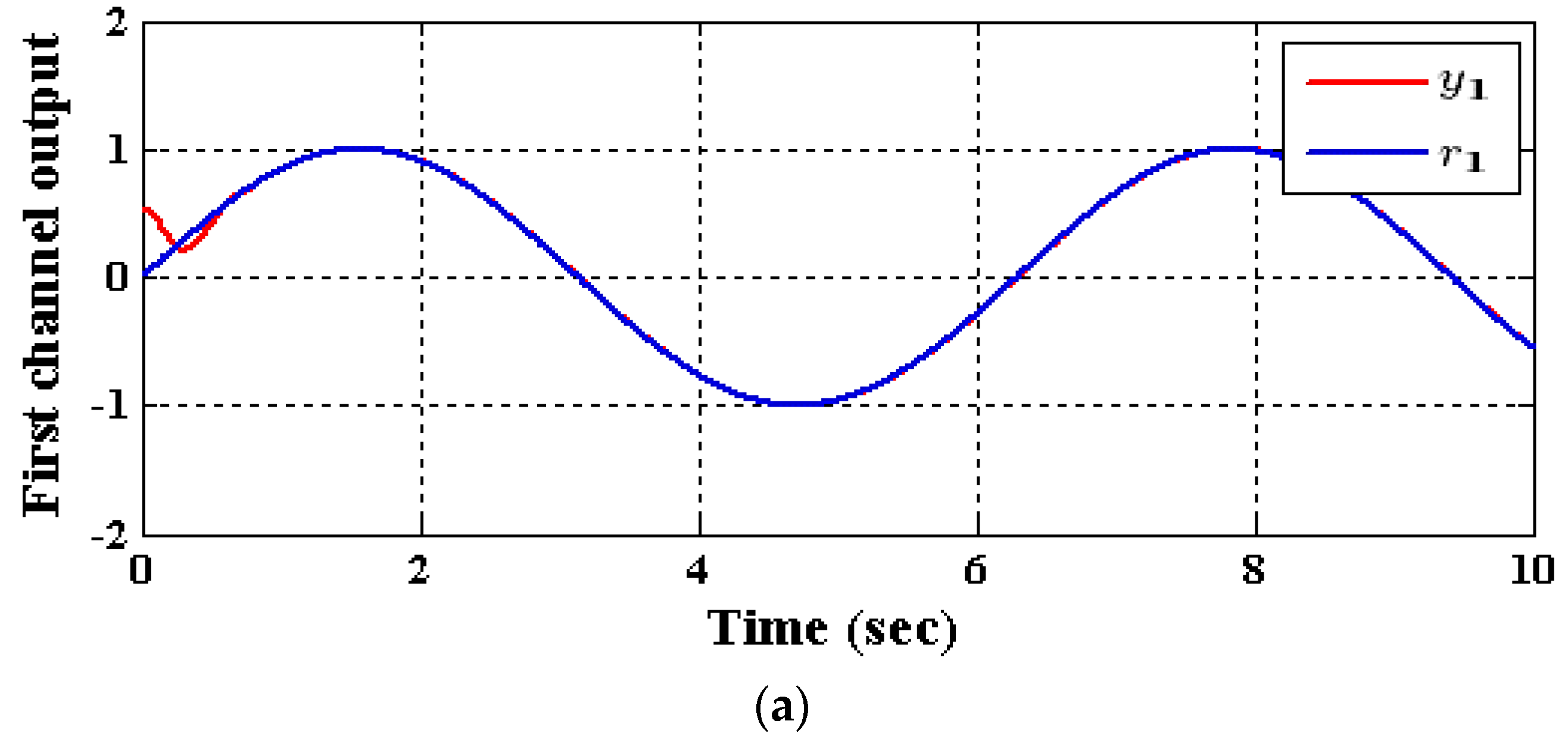
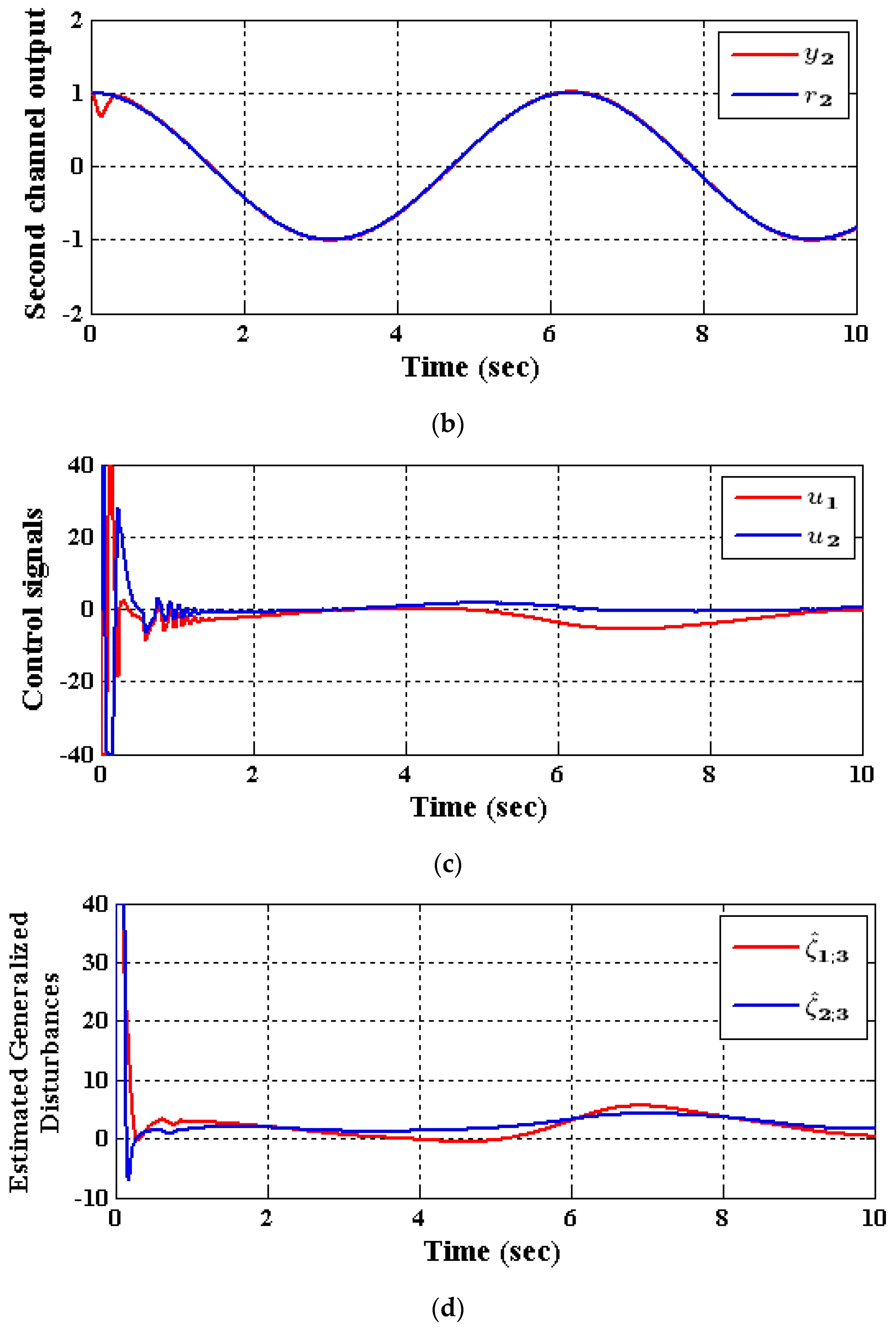
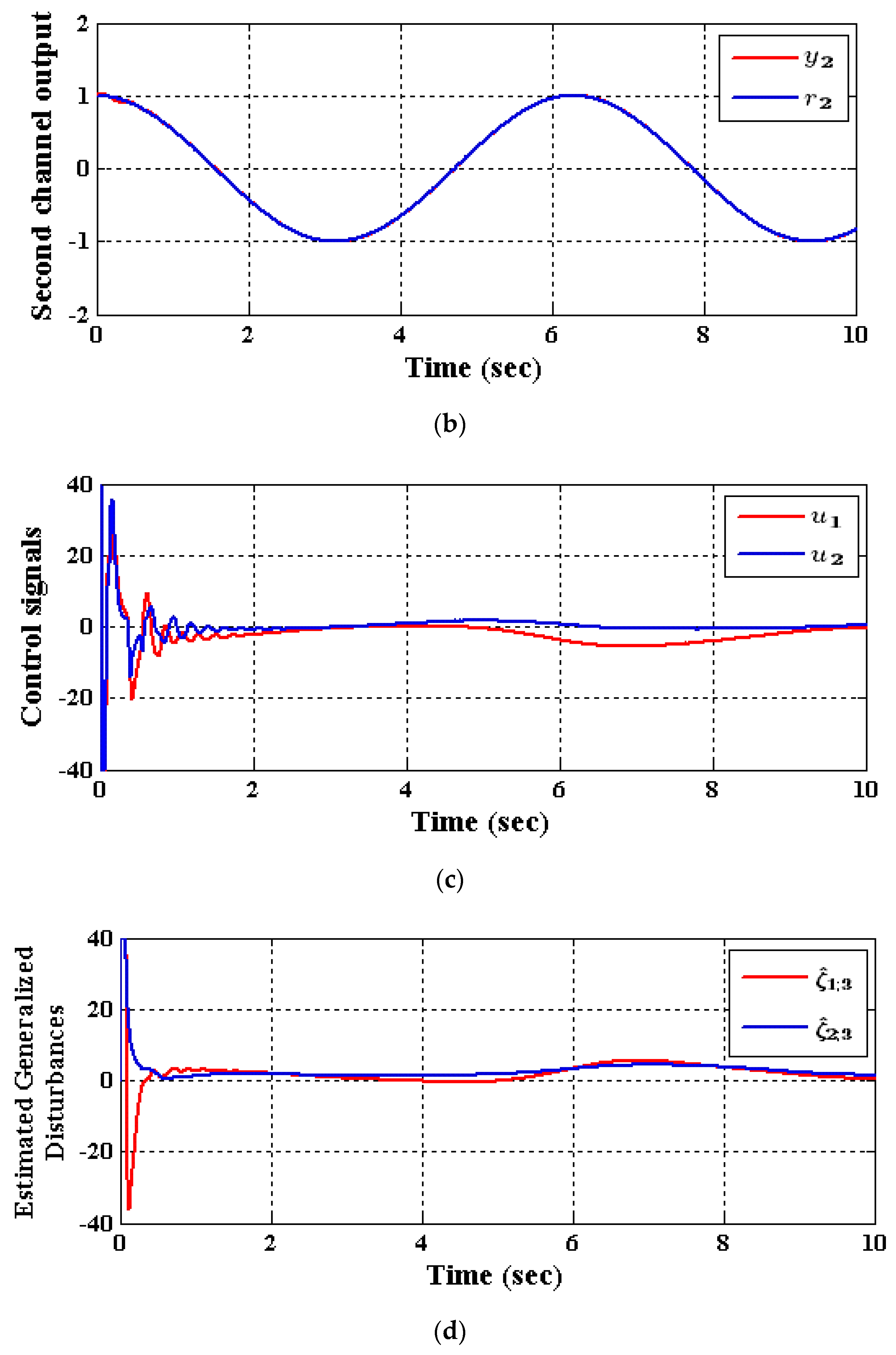
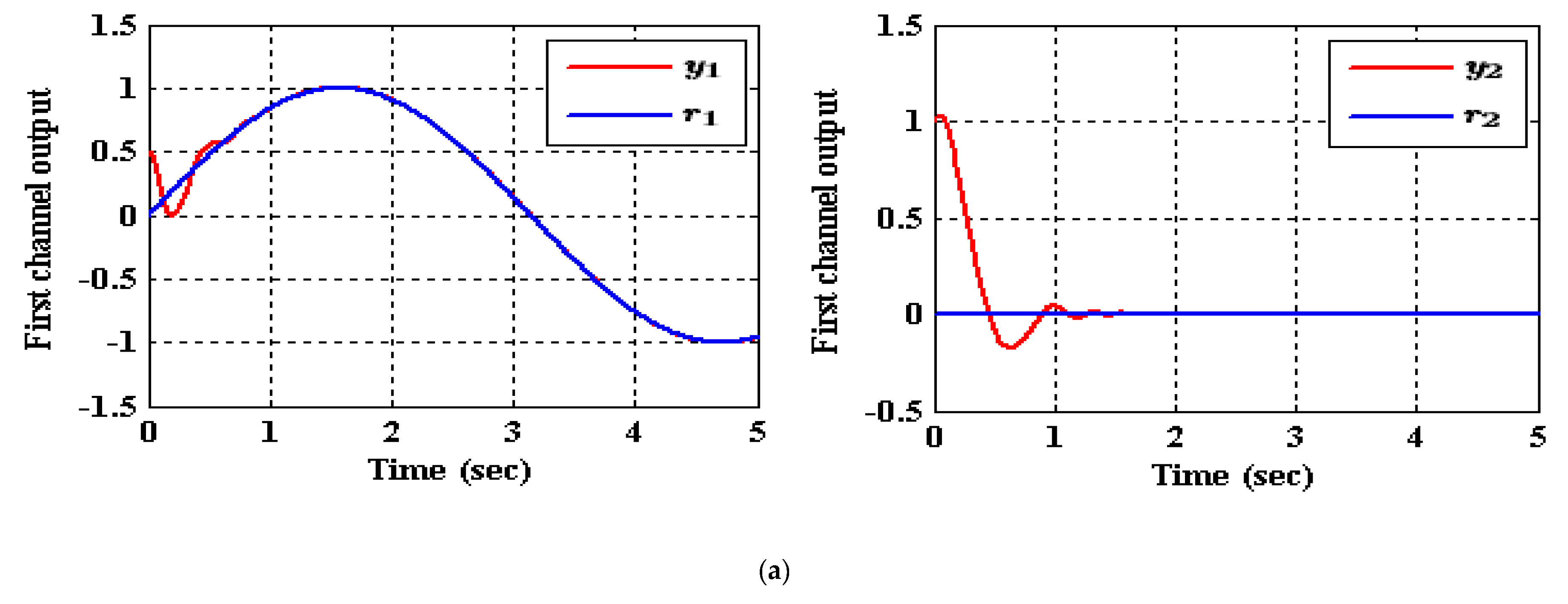
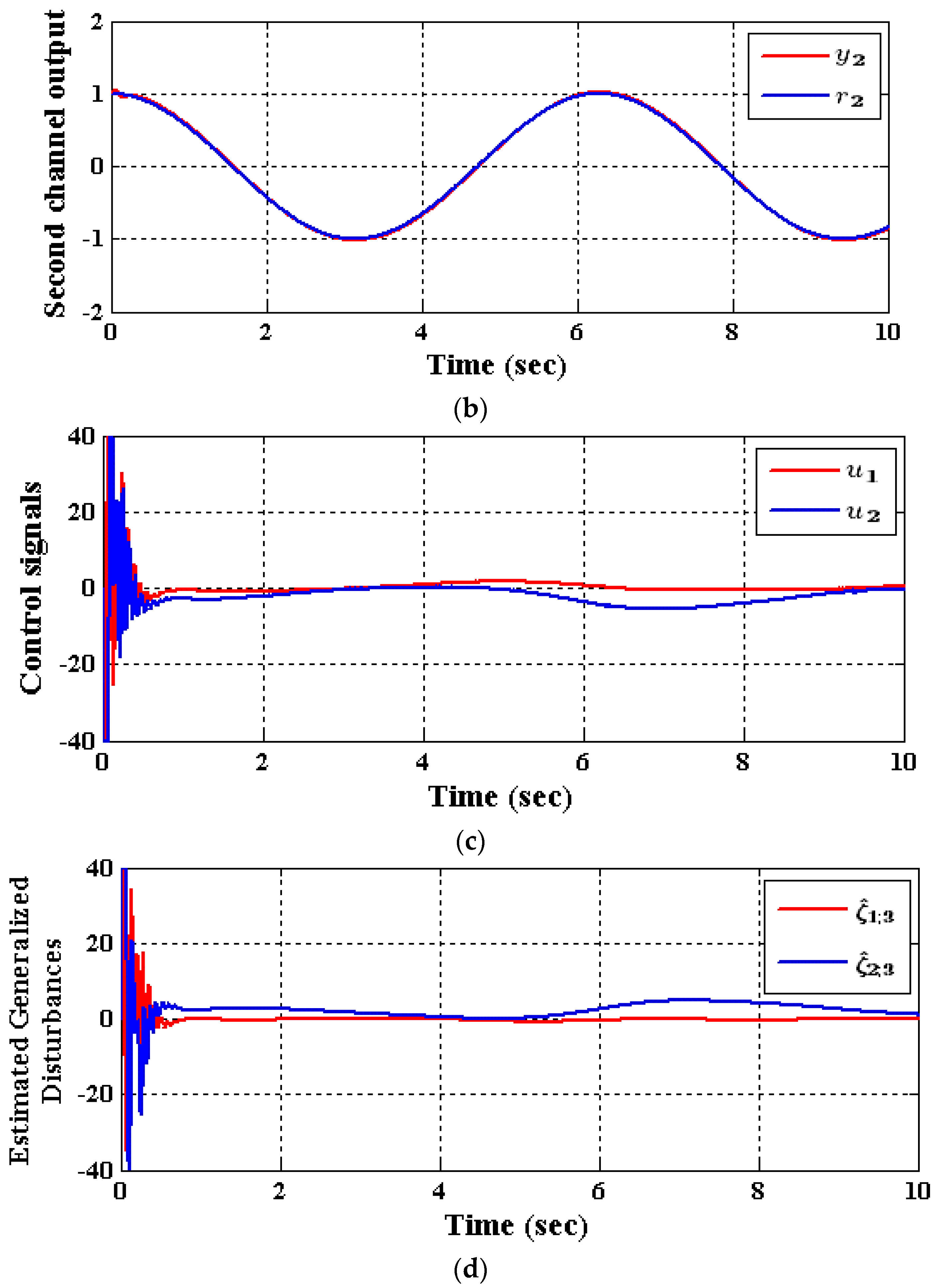
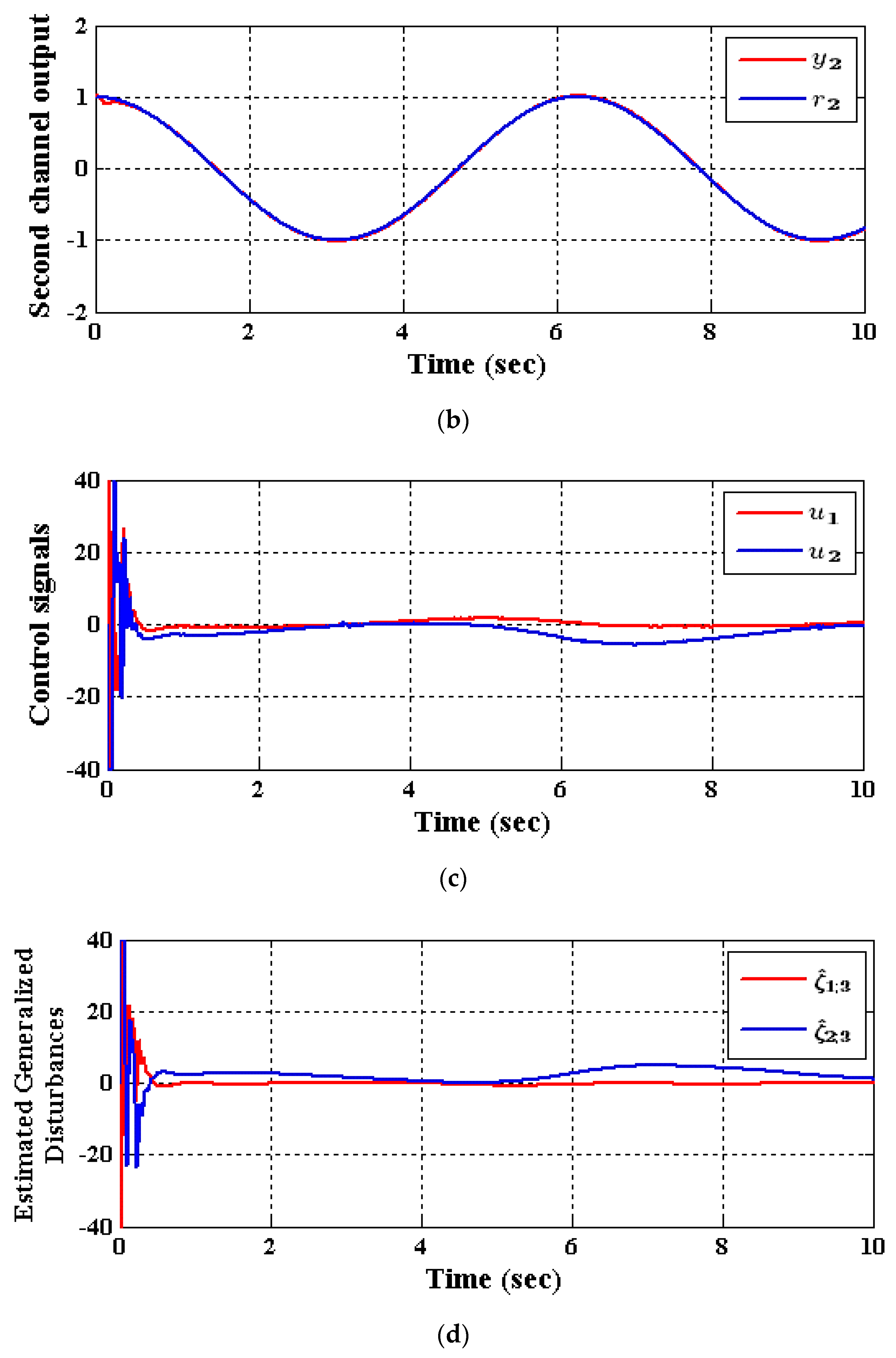
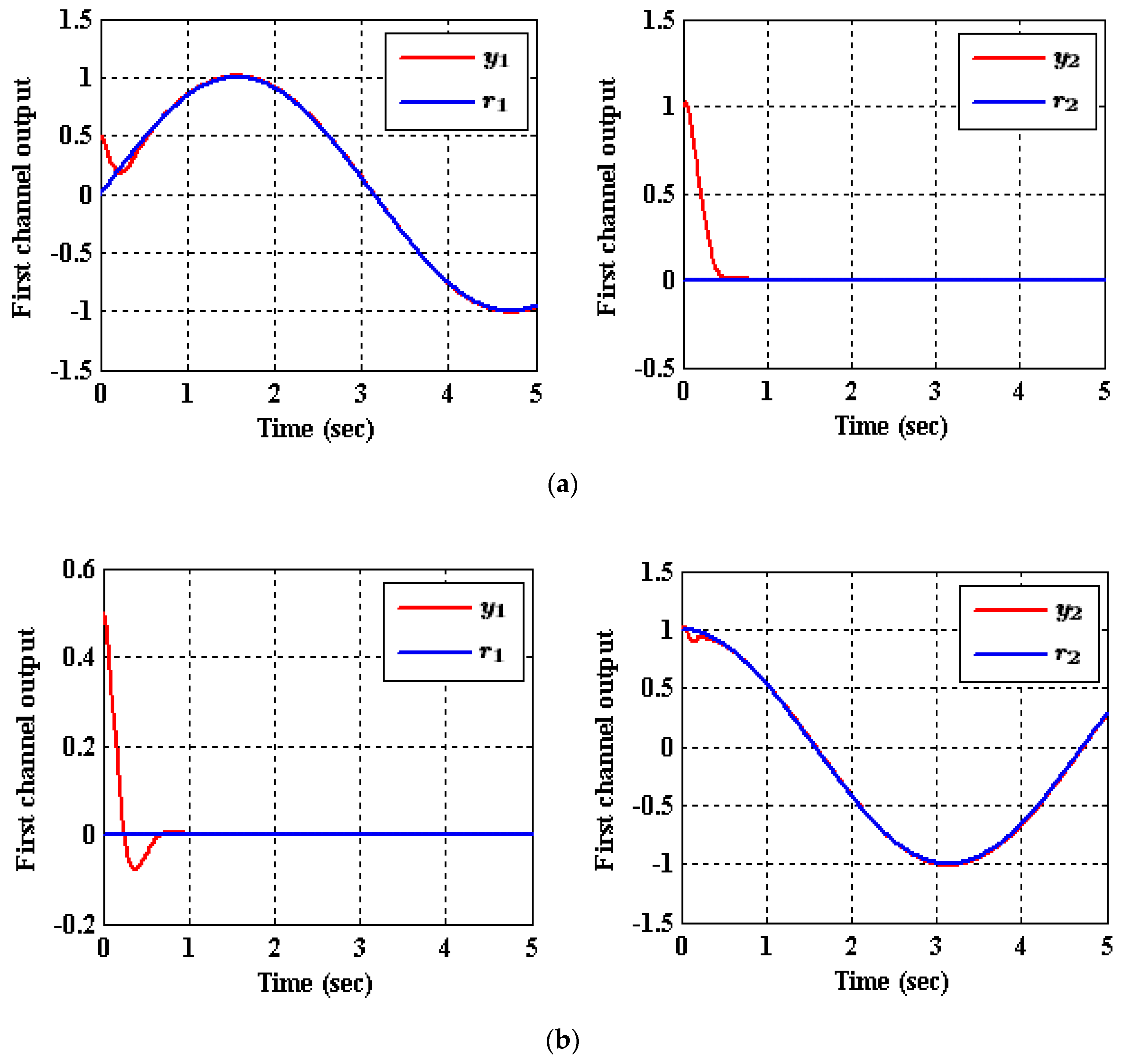
5.2. Results of the Decentralized ADRC Control Scheme
- Case (1): Output tracking
- Case (2): Input and State Decoupling
5.3. Comparison between the Proposed Decentralized Scheme and the Decoupled Control [23]
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Han, J. A Class of Extended State Observers for Uncertain Systems. Control Decis. 1995, 10, 85–88. [Google Scholar]
- Gao, Z. Scaling and bandwidth-parameterization based controller tuning. In Proceedings of the American Control Conference, Denver, CO, USA, 4–6 June 2003; pp. 4989–4996. [Google Scholar] [CrossRef]
- Humaidi, A.J.; Ibraheem, I.K. Speed Control of Permanent Magnet DC Motor with Friction and Measurement Noise Using Novel Nonlinear Extended State Observer-Based Anti-Disturbance Control. Energies 2019, 12, 1651. [Google Scholar] [CrossRef]
- Ibraheem, I.K.; Abdul-Adheem, W.R. A Novel Second-Order Nonlinear Differentiator with Application to Active Disturbance Rejection Control. In Proceedings of the 1st International Scientific Conference of Engineering Sciences—3rd Scientific Conference of Engineering Science (ISCES), Diyalah, Iraq, 10–11 January 2018; pp. 68–73. [Google Scholar] [CrossRef]
- Ibraheem, I.K.; Abdul-Adheem, W.R. An Improved Active Disturbance Rejection Control for a Differential Drive Mobile Robot with Mismatched Disturbances and Uncertainties. arXiv 2018, arXiv:1805.12170. [Google Scholar]
- Chen, Z.; Wang, Y.; Sun, M.; Sun, Q. Convergence and stability analysis of active disturbance rejection control for first-order nonlinear dynamic systems. Trans. Inst. Meas. Control 2019, 41, 2064–2076. [Google Scholar] [CrossRef]
- Cheng, Y.; Chen, Z.; Sun, M.; Sun, Q. Cascade Active Disturbance Rejection Control of a High-Purity Distillation Column with Measurement Noise. Ind. Eng. Chem. Res. 2018, 57, 4623–4631. [Google Scholar] [CrossRef]
- Hou, Y.; Gao, Z.; Jiang, F.; Boulter, B.T. Active Disturbance Rejection Control for Web Tension Regulation. In Proceedings of the 40th IEEE Conference on Decision and Control, Orlando, FL, USA, 4–7 December 2001; pp. 4974–4979. [Google Scholar] [CrossRef]
- Su, Y.X.; Zheng, C.H.; Sun, D.; Duan, B.Y. A simple nonlinear velocity estimator for high-performance motion control. IEEE Trans. Ind. Electron. 2005, 52, 1161–1169. [Google Scholar] [CrossRef]
- Sun, B.; Gao, Z. A DSP-Based Active Disturbance Rejection Control Design for a 1-kW H-Bridge DC-DC Power Converter. IEEE Trans. Ind. Electron. 2005, 52, 1271–1277. [Google Scholar] [CrossRef]
- Zheng, Q.; Chen, Z.; Gao, Z. A Dynamic Decoupling Control Approach and Its Applications to Chemical Processes. In Proceedings of the American Control Conference, New York, NY, USA, 11–13 July 2007; pp. 5176–5181. [Google Scholar] [CrossRef]
- Zheng, Q.; Dong, L.; Gao, Z. Control and rotation rate estimation of vibrational MEMS gyroscopes. In Proceedings of the International Conference on Control Applications, Singapore, 1–3 October 2007; pp. 118–123. [Google Scholar] [CrossRef]
- Goforth, F.J.; Gao, Z. An Active Disturbance Rejection Control Solution for Hysteresis Compensation. In Proceedings of the American Control Conference, Seattle, WA, USA, 11–13 June 2008; pp. 2202–2208. [Google Scholar] [CrossRef]
- Yan, B.; Tian, Z.; Shi, S.; Weng, Z. Fault diagnosis for a class of nonlinear systems via ESO. ISA Trans. 2008, 47, 386–394. [Google Scholar] [CrossRef]
- Wu, D.; Chen, K. Design and analysis of precision active disturbance rejection control for noncircular turning process. IEEE Trans. Ind. Electron. 2009, 56, 2746–2753. [Google Scholar] [CrossRef]
- Li, S.; Yang, X.; Yang, D. Active disturbance rejection control for high pointing accuracy and rotation speed. Automatica 2009, 45, 1854–1860. [Google Scholar] [CrossRef]
- Sira-Ramirez, H.; Lopez-Uribe, C.; Velasco-Villa, M. Linear observer-based active disturbance rejection control of the omnidirectional mobile robot. Asian J. Control 2013, 15, 51–63. [Google Scholar] [CrossRef]
- Leonard, F.; Martini, A.; Abba, G. Robust nonlinear controls of model-scale helicopters under lateral and vertical wind gusts. IEEE Trans. Control Syst. Technol. 2012, 20, 154–163. [Google Scholar] [CrossRef]
- Madoński, R.; Kordasz, M.; Sauer, P. Application of a disturbance-rejection controller for robotic-enhanced limb rehabilitation trainings. ISA Trans. 2014, 53, 899–908. [Google Scholar] [CrossRef] [PubMed]
- Texas Instruments. Technical Reference Manual for TMS320F28069M, TMS320F28068M InstaSPIN-MOTION Software; Texas Instruments: Dallas, TX, USA, 2014; pp. 1–57. [Google Scholar]
- Zheng, Q.; Gao, Z. On Practical Applications of Active Disturbance Rejection Control. In Proceedings of the 29th Chinese Control Conference, Beijing, China, 29–31 July 2010; pp. 6095–6100. [Google Scholar]
- Yi, H.; Wenchao, X.U.E.; Gao, Z.; Sira-ramirez, H.; Dan, W.; Mingwei, S. Active Disturbance Rejection Control: Methodology, Practice and Analysis. In Proceedings of the 33rd Chinese Control Conference, Nanjing, China, 28–30 July 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Abdul-adheem, W.R.; Ibraheem, I.K. Decoupled control scheme for output tracking of a general industrial nonlinear MIMO system using improved active disturbance rejection scheme. Alex. Eng. J. 2019, 58, 1145–1156. [Google Scholar] [CrossRef]
- Elmali, H.; Olgac, N. Robust output tracking control of nonlinear MIMO systems via sliding mode technique. Automatica 1992, 28, 145–151. [Google Scholar] [CrossRef]
- Costa, R.R.; Hsu, L.; Imai, A.K.; Kokotovic, P. Lyapunov-based adaptive control of MIMO systems. Automatica 2003, 39, 1251–1257. [Google Scholar] [CrossRef]
- Liu, X.; Jutan, A.; Rohani, S. Almost disturbance decoupling of MIMO nonlinear systems and application to chemical processes. Automatica 2004, 40, 465–471. [Google Scholar] [CrossRef]
- Bagni, G.; Basso, M.; Genesio, R.; Tesi, A. Synthesis of MIMO controllers for extending the stability range of periodic solutions in forced nonlinear systems. Automatica 2005, 41, 645–654. [Google Scholar] [CrossRef]
- Mizumoto, I.; Chen, T.; Ohdaira, S.; Kumon, M.; Iwai, Z. Adaptive output feedback control of general MIMO systems using multirate sampling and its application to a cart—Crane system. Automatica 2007, 43, 2077–2085. [Google Scholar] [CrossRef]
- Gündes, A.N.; Mete, A.N.; Palazoglu, A. Reliable decentralized PID controller synthesis for two-channel MIMO processes. Automatica 2009, 45, 353–363. [Google Scholar] [CrossRef]
- Chen, M.; Ge, S.S.; Ren, B. Adaptive tracking control of uncertain MIMO nonlinear systems with input constraints. Automatica 2011, 47, 452–465. [Google Scholar] [CrossRef]
- Chiu, C.S. Derivative and integral terminal sliding mode control for a class of MIMO nonlinear systems. Automatica 2012, 48, 316–326. [Google Scholar] [CrossRef]
- Lu, L.; Yao, B. Online constrained optimization based adaptive robust control of a class of MIMO nonlinear systems with matched uncertainties and input/state constraints. Automatica 2014, 50, 864–873. [Google Scholar] [CrossRef]
- Hashemi, M.; Ghaisari, J.; Askari, J. Adaptive control for a class of MIMO nonlinear time delay systems against time varying actuator failures. ISA Trans. 2015, 57, 23–42. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Yu, X.; Zhang, T.; Cao, Z.; Yang, Y.; Yi, Y. Sliding mode control of MIMO Markovian jump systems. Automatica 2016, 68, 286–293. [Google Scholar] [CrossRef]
- Pandey, V.K.; Kar, I.; Mahanta, C. Controller design for a class of nonlinear MIMO coupled system using multiple models and second level adaptation. ISA Trans. 2017, 69, 256–272. [Google Scholar] [CrossRef]
- Wang, L.; Isidori, A.; Liu, Z.; Su, H. Robust output regulation for invertible nonlinear MIMO systems. Automatica 2017, 82, 278–286. [Google Scholar] [CrossRef]
- Feng, Y.; Zhou, M.; Zheng, X.; Han, F.; Yu, X. Full-order terminal sliding-mode control of MIMO systems with unmatched uncertainties. J. Frankl. Inst. 2018, 355, 653–674. [Google Scholar] [CrossRef]
- Zhao, K.; Song, Y.; Zhang, Z. Tracking control of MIMO nonlinear systems under full state constraints: A Single-parameter adaptation approach free from feasibility conditions. Automatica 2019, 107, 52–60. [Google Scholar] [CrossRef]
- Li, J.; Du, J. Adaptive disturbance cancellation for a class of MIMO nonlinear Euler–Lagrange systems under input saturation. ISA Trans. 2020, 96, 14–23. [Google Scholar] [CrossRef]
- Chen, M.; Mei, R.; Jiang, B. Sliding mode control for a class of uncertain MIMO nonlinear systems with application to near-space vehicles. Math. Probl. Eng. 2013, 2013, 180589. [Google Scholar] [CrossRef]
- Chen, M.; Shi, P.; Lim, C.C. Robust Constrained Control for MIMO Nonlinear Systems Based on Disturbance Observer. IEEE Trans. Automat. Contr. 2015, 60, 3281–3286. [Google Scholar] [CrossRef]
- Floquet, T.; Spurgeon, S.K.; Edwards, C. An output feedback sliding mode control strategy for MIMO systems of arbitrary relative degree. Int. J. Robust Nonlinear Control 2011, 21, 119–133. [Google Scholar] [CrossRef]
- Polyakov, A.; Efimov, D.; Perruquetti, W. Sliding Mode Control Design for MIMO Systems: Implicit Lyapunov Function Approach. In Proceedings of the 2014 European Control Conference (ECC), Strasbourg, France, 24–27 June 2014; pp. 2612–2617. [Google Scholar] [CrossRef]
- Ibraheem, I.K. Anti-Disturbance Compensator Design for Unmanned Aerial Vehicle. J. Eng. 2020, 26, 86–103. [Google Scholar] [CrossRef][Green Version]
- Khalil, H.K. Extended High-Gain Observers as Disturbance Estimators. SICE J. Control. Meas. Syst. Integr. 2017, 10, 125–134. [Google Scholar] [CrossRef]
- Tong Shaocheng, T.; Bin, C.; Yongfu, W. Fuzzy adaptive output feedback control for MIMO nonlinear systems. Fuzzy Sets Syst. 2005, 156, 285–299. [Google Scholar] [CrossRef]
- Kim, E.; Lee, S. Output feedback tracking control of MIMO systems using a fuzzy disturbance observer and its application to the speed control of a PM synchronous motor. IEEE Trans. Fuzzy Syst. 2005, 13, 725–741. [Google Scholar]
- Zhang, T.P.; Yang, Y.I. Adaptive Fuzzy Control for a Class of MIMO Nonlinear Systems with Unknown Dead-zones. Acta Autom. Sin. 2007, 33, 96–99. [Google Scholar] [CrossRef]
- Chen, C.H.; Lin, C.M.; Chen, T.Y. Intelligent adaptive control for MIMO uncertain nonlinear systems. Expert Syst. Appl. 2008, 35, 865–877. [Google Scholar] [CrossRef]
- Yousef, H.; Hamdy, M.; El-Madbouly, E.; Eteim, D. Adaptive fuzzy decentralized control for interconnected MIMO nonlinear subsystems. Automatica 2009, 45, 456–462. [Google Scholar] [CrossRef]
- Liu, Y.J.; Tong, S.C.; Li, T.S. Observer-based adaptive fuzzy tracking control for a class of uncertain nonlinear MIMO systems. Fuzzy Sets Syst. 2011, 164, 25–44. [Google Scholar] [CrossRef]
- Li, T.; Li, R.; Wang, D. Adaptive neural control of nonlinear MIMO systems with unknown time delays. Neurocomputing 2012, 78, 83–88. [Google Scholar] [CrossRef]
- Li, C.; Wang, W. Fuzzy almost disturbance decoupling for MIMO nonlinear uncertain systems based on high-gain observer. Neurocomputing 2013, 111, 104–114. [Google Scholar] [CrossRef]
- Zhen, H.T.; Qi, X.H.; Li, J.; Tian, Q.M. Neural network L1 Adaptive control of MIMO systems with nonlinear uncertainty. Sci. World J. 2014, 2014, 1–8. [Google Scholar] [CrossRef]
- Rong, H.J.; Wei, J.T.; Bai, J.M.; Zhao, G.S.; Liang, Y.Q. Adaptive neural control for a class of MIMO nonlinear systems with extreme learning machine. Neurocomputing 2015, 149, 405–414. [Google Scholar] [CrossRef]
- Yan, P.; Liu, D.; Wang, D.; Ma, H. Data-driven controller design for general MIMO nonlinear systems via virtual reference feedback tuning and neural networks. Neurocomputing 2016, 171, 815–825. [Google Scholar] [CrossRef]
- Shi, W. Observer-based adaptive fuzzy prescribed performance control for feedback linearizable MIMO nonlinear systems with unknown control direction. Neurocomputing 2019, 368, 99–113. [Google Scholar] [CrossRef]
- Huo, X.; Ma, L.; Zhao, X.; Zong, G. Event-triggered adaptive fuzzy output feedback control of MIMO switched nonlinear systems with average dwell time. Appl. Math. Comput. 2020, 365, 124665. [Google Scholar] [CrossRef]
- Wang, L.Y.; Zhang, J.F. Fundamental Limitations and Differences of Robust and Adaptive Control. In Proceedings of the 2001 American Control Conference, Arlington, VA, USA, 25–27 June 2001; pp. 4802–4807. [Google Scholar]
- Hespanha, J.P.; Liberzon, D.; Morse, A.S. Overcoming the limitations of adaptive control by means of logic-based switching. Syst. Control Lett. 2003, 49, 49–65. [Google Scholar] [CrossRef]
- Mandoski, R. On Active Disturbance Rejection in Robotic Motion Control. Ph.D. Thesis, University of Poznan, Poznań, Poland, 2016. [Google Scholar] [CrossRef]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Abdul-adheem, W.R.; Ibraheem, I.K. Improved Sliding Mode Nonlinear Extended State Observer based Active Disturbance Rejection Control for Uncertain Systems with Unknown Total Disturbance. Int. J. Adv. Comput. Sci. Appl. 2016, 7, 80–93. [Google Scholar] [CrossRef]

| Unit | First Channel Parameters | Second Channel Parameters | ||
|---|---|---|---|---|
| Parameter | Value | Parameter | Value | |
| TD | 92.2713 | 88.4424 | ||
| LESO | 68.3308 | 53.1690 | ||
| fal-based control law | 0.0010 | 0.14456 | ||
| 0.2834 | 0.73456 | |||
| 0.1629 | 0.02730 | |||
| 0.7946 | 0.93745 | |||
| 12.8015 | 18.3095 | |||
| 11.2999 | 19.52670 | |||
| 40 | 40 | |||
| Unit | First Channel Parameters | Second Channel Parameters | ||
|---|---|---|---|---|
| Parameter | Value | Parameter | Value | |
| TD | 192.7715 | 148.9279 | ||
| NHOESO | 135.6086 | 22.8802 | ||
| 2.31423 | 3.3264 | |||
| 4.5361 | 4.66885 | |||
| 2.0465 | 1.48218 | |||
| 0.1658 | 0.04076 | |||
| 0.9000 | 0.9000 | |||
| 0.9000 | 0.9000 | |||
| 0.1000 | 0.1000 | |||
| 0.0100 | 0.0100 | |||
| fal-based control law | 0.0341 | 0.0082 | ||
| 0.6008 | 0.8162 | |||
| 0.0207 | 0.0120 | |||
| 0.3372 | 0.7222 | |||
| 18.3186 | 6.84822 | |||
| 8.9993 | 6.5260 | |||
| 40 | 40 | |||
| Performance Index | CADRC | IADRC | %Reduction |
|---|---|---|---|
| ITAE1 | 0.1628 | 0.1210 | 25.7% |
| ITAE2 | 0.3536 | 0.0937 | 73.5% |
| ISU1 | 314.1064 | 308.4248 | 1.8% |
| ISU2 | 296.8865 | 225.7019 | 24% |
| Unit | First Channel Parameters | Second Channel Parameters | ||
|---|---|---|---|---|
| Parameter | Value | Parameter | Value | |
| TD | 92.2713 | 88.4423 | ||
| LESO | 68.3308 | 53.1690 | ||
| 1.0000 | −1.0000 | |||
| fal-based Control law | 0.0010 | 0.1445 | ||
| 0.2834 | 0.7346 | |||
| 0.1629 | 0.0273 | |||
| 0.7946 | 0.9375 | |||
| 12.8015 | 18.3095 | |||
| 11.2999 | 19.5267 | |||
| 40 | 40 | |||
| Unit | First Channel | Second Channel | ||
|---|---|---|---|---|
| Parameter | Value | Parameter | Value | |
| TD | 155.2564 | 107.6494 | ||
| NHOESO | 94.9942 | 123.7601 | ||
| 1.0000 | −1.0000 | |||
| 1.7315 | 3.6546 | |||
| 5.0845 | 3.8128 | |||
| 1.5151 | 2.0353 | |||
| 1.1444 × 10−6 | 1.1230 × 10−6 | |||
| 0.8028 | 0.5043 | |||
| 0.9300 | 0.6982 | |||
| 0.2381 | 0.8338 | |||
| 0.6221 | 0.9534 | |||
| fal-based Control law | 0.1250 | 0.2510 | ||
| 0.4163 | 0.4531 | |||
| 0.2750 | 0.3312 | |||
| 0.7658 | 0.2783 | |||
| 25.6305 | 30.3227 | |||
| 10.6899 | 20.2694 | |||
| 40 | 40 | |||
| Performance Index | CADRC | IADRC | %Reduction |
|---|---|---|---|
| ITAE1 | 0.3890 | 0.3081 | 20.8% |
| ITAE2 | 0.6434 | 0.4600 | 28.5% |
| ISU1 | 181.5489 | 123.6903 | 31.9% |
| ISU2 | 302.3266 | 265.2197 | 12.3% |
| CARDC | IADRC | ||||
|---|---|---|---|---|---|
| Decoupled | Decentralized | %Reduction | Decoupled | Decentralized | %Reduction |
| 610.9921 | 483.8755 | 20.8 | 534.1267 | 388.91 | 27.18 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdul-Adheem, W.R.; Ibraheem, I.K.; Azar, A.T.; Humaidi, A.J. Improved Active Disturbance Rejection-Based Decentralized Control for MIMO Nonlinear Systems: Comparison with The Decoupled Control Scheme. Appl. Sci. 2020, 10, 2515. https://doi.org/10.3390/app10072515
Abdul-Adheem WR, Ibraheem IK, Azar AT, Humaidi AJ. Improved Active Disturbance Rejection-Based Decentralized Control for MIMO Nonlinear Systems: Comparison with The Decoupled Control Scheme. Applied Sciences. 2020; 10(7):2515. https://doi.org/10.3390/app10072515
Chicago/Turabian StyleAbdul-Adheem, Wameedh Riyadh, Ibraheem Kasim Ibraheem, Ahmad Taher Azar, and Amjad J. Humaidi. 2020. "Improved Active Disturbance Rejection-Based Decentralized Control for MIMO Nonlinear Systems: Comparison with The Decoupled Control Scheme" Applied Sciences 10, no. 7: 2515. https://doi.org/10.3390/app10072515
APA StyleAbdul-Adheem, W. R., Ibraheem, I. K., Azar, A. T., & Humaidi, A. J. (2020). Improved Active Disturbance Rejection-Based Decentralized Control for MIMO Nonlinear Systems: Comparison with The Decoupled Control Scheme. Applied Sciences, 10(7), 2515. https://doi.org/10.3390/app10072515






