2.1. System
Let us consider a single ion of mass
m moving in a dilute gas of neutral atoms of the same species. Throughout this work we will focus on the case of Rb atoms which are experimentally most relevant, but our result can also be applied to other cases. The ion motion is assumed to be unconstrained, meaning that the characteristic length scale of the ion trap (if present at all) is larger than the ion–atom interaction range as well as the typical interparticle distance. Such a situation can be realized, e.g., by utilizing optical ion traps or by ionization of an ultracold atom directly from the gas. Once produced, the ion will undergo collisions with the surrounding atoms. The ion–atom interaction at long range is governed by the
term (leading induction coefficient in the multipole expansion) [
1], with
. Here,
q is the ionic charge,
the atomic polarizability, and
r denotes the ion–atom distance. One can define the length scale
and energy scale
associated with this potential as
with
denoting the reduced mass of the ion–atom system.
In addition to two-body elastic collisions and charge transfer processes which determine the ion mobility [
22], three-body recombination is expected to occur, leading to association of molecular ions [
2]. The classical three-body cross section for this process has been obtained in reference [
15] and is described with a universal formula
. Although little is known about the product state distribution after the recombination process, experiments and theory developed for neutral Rb atoms interacting via van-der-Waals forces have led to the conclusion that the resulting molecules are mostly weakly bound [
3]. Here, rather than in the recombination, we are interested in the dynamics of the molecular ion after it has been produced. Note that it is also technically possible to associate molecular ions using a Raman process without relying on three-body recombination, which should give access to better control over the initial state [
23]. Atom–atom–ion three-body recombination has been observed in references [
2,
24] for trapped Rb
and Ba
ions immersed in a Rb gas prepared at typical densities of ≈
. For the trapped ions, the typical collision energies are in the few to tens of mK regime, set by the trap-induced ion micromotion. For these conditions, recombination timescales on the order of a second have been observed. Note that for higher atomic densities typical of a Bose–Einstein condensate (≈
), the recombination time can be expected to reach even the microsecond timescale, highlighting the much larger cross section for ion–neutral-neutral recombination as compared to the recombination of three neutral atoms.
The homonuclear molecular ion does not posses a dipole moment, and thus its long-range interaction with the surrounding atoms is also described by the
potential. The complete interaction potential surface consists of interactions among three particles, the ion (labeled as 1 in the equation below) and two atoms (labeled 2 and 3)
where
and
are the ion–atom potentials and
describes the van-der-Waals interaction between neutral atoms. For Rb, we have
with
being the Bohr radius, while the characteristic van-der-Waals length for Rb is only about
. The characteristic energy
in the case of Rb is
Hz, or equivalently
nK [
1].
Elastic collisions between a molecular ion and an atom do not fundamentally differ from atomic ion–neutral atom collisions, which have been widely studied already [
1,
25]. At collision energies
E high enough to involve multiple partial waves, the elastic and reactive collision cross sections can be well approximated by quasiclassical formulas derived in the framework of the Langevin capture model, yielding
and
, respectively. In the case of an initially highly excited molecular ion, a natural question to ask is how exactly will its internal state relax as a result of collisions with the buffer gas. Here the three-body nature of the problem becomes relevant. As we are only interested in processes in which the molecular ion remains bound (the collision energy is not sufficient to dissociate it), the problem can be recast as two-body scattering, but with multiple possible states after the collision, as described in the next section.
2.2. Inelastic Scattering
Let us now briefly recall the foundations of reactive scattering theory [
26]. First let us introduce the Jacobi coordinates and denote the relative position vector between the center of mass of the molecule and the atom by
, and the internal coordinates of the molecular ion as
. The center of mass motion of the particles is not relevant. At large distances where the interaction can be neglected, the molecular ion can be described by its rovibrational states
, where
v and
j label the vibrational and rotational quantum number of the molecule, respectively. It is now convenient to move to the body-fixed frame of the molecule [
27,
28,
29], introducing the quantum numbers
for the total angular momentum and its projection which are both conserved. The relative orbital angular momentum
ℓ fulfills the relation
. The rest of the basis states forming the basis for close-coupled equations can be labelled as
, where
and
are the spherical angles describing the orientation of the molecule-atom pair and the molecule itself in the space-fixed frame.
We note that the three-body potential landscape is only weakly anisotropic due to the lack of a dipole moment of the molecule and the short range of the van-der-Waals interaction. This validates the use of the coupled-states approximation [
12,
30,
31], which states that the angular momentum projection
on the molecular axis is conserved and that in general intermultiplet couplings are negligible so that one can decouple the molecular and orbital angular momenta.
We can now calculate the potential matrix in the channel states basis simply by integrating the full three-body potential (
2) over the molecular states. The rovibrational molecular state with quantum numbers
has the corresponding binding energy denoted further as
. After decoupling the angular momenta, one obtains
with the matrix element
containing the interaction between the free atom and the molecule as the interaction term within the molecule has been incorporated in the molecular energies. Here the integration over the polar angle gives a constant factor of
. Furthermore,
is the reduced mass of the atom–molecular ion pair and the orbital angular momentum (which is now also a good quantum number)
Furthermore,
denote spherical harmonics and
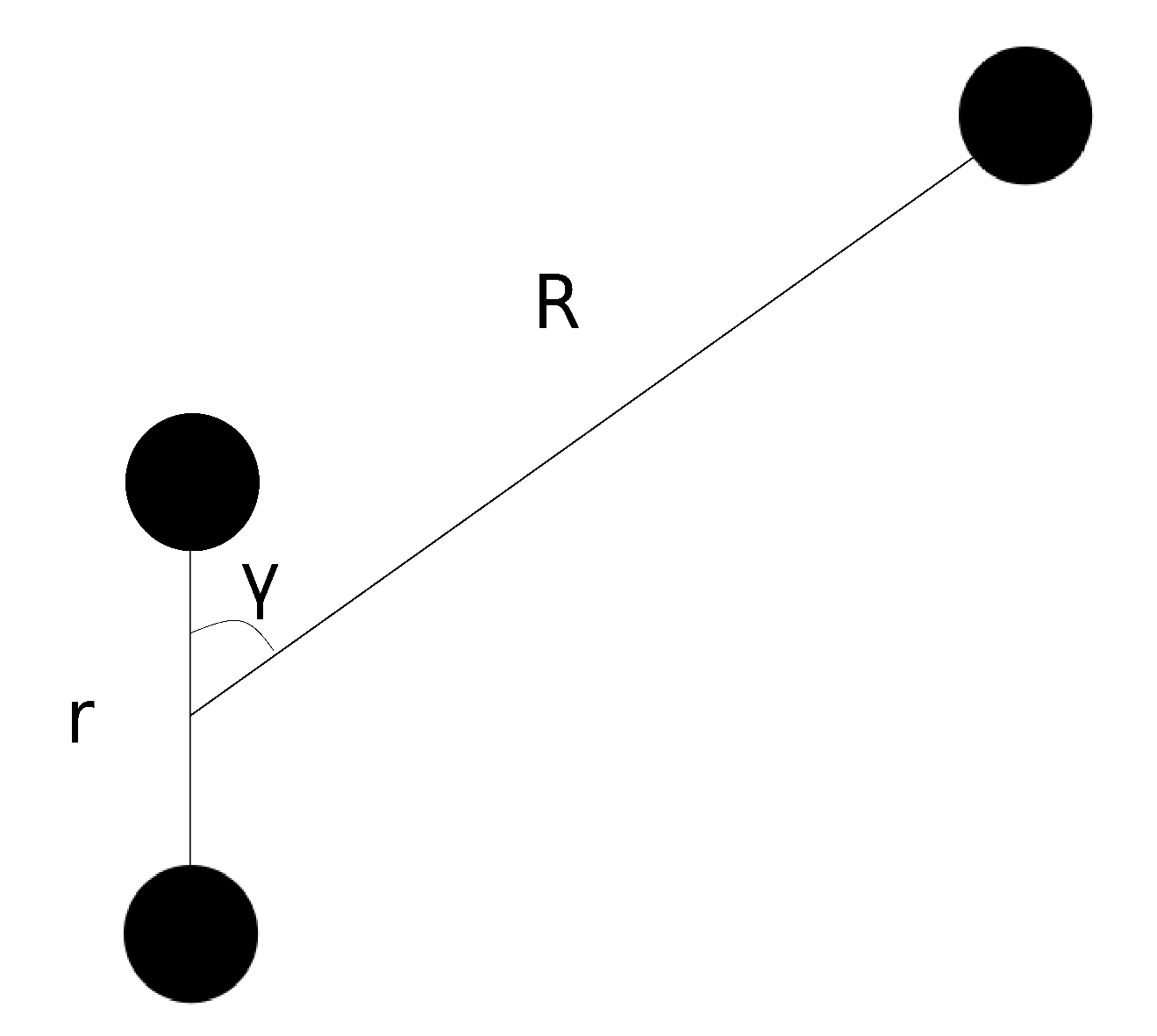
is the Jacobi angle (see
Figure 1).
The nondiagonal terms of the potential matrix provide the coupling between the channels responsible for vibrationally inelastic collisions. Equation (
3) provides the potential matrix for the multichannel scattering problem
with the matrix
containing the radial wavefunctions. Assuming the channels are open (as is the case if we start from the weakly bound state which has higher energy than all the others), at large distances the solution takes the canonical form
where matrices
,
are diagonal and consist of spherical Bessel functions, e.g.,
with
being the asymptotic channel wavenumber. The amplitude matrix
can be linked to the reactance matrix
by
. Finally, the scattering matrix
which contains full information about the scattering is given by the formula
The inelastic collision rate constant is given by the nondiagonal elements of the S matrix and reads
2.3. Effective Potentials
With the basic formalism at hand, we now proceed to the analysis of the particular case of the molecular ion scattering with a neutral atom. The first step needed to derive the potential matrix (
3) is to calculate the two-body rovibrational wavefunctions of the molecular ion alone and their binding energies. State of the art ab initio methods can be used to calculate the interaction potential of Rb
in the electronic ground state with a finite precision of the order of
[
32]. While this kind of accuracy is sufficient for spectroscopic data such as the vibrational spacing of the lower levels, it is unfortunately not enough to predict the binding energies of the weakly bound Rb
states. This is in part due to the large reduced mass of the system. For this reason we are allowed to choose a simple model potential to work with and obtain the knowledge about the general features of the ion–molecule systems. We have tested several model potentials such as the Lennard-Jones type interaction of the form
with the cutoff
, the flat-bottom regularization
for various potential depths, as well as used the analytical solutions of the polarization potential [
33], and found no fundamental difference in the behavior of the resulting effective potentials. In what follows, we will use
and
of the atom–ion system as the units of length and energy, so that asymptotically the two-body ion–atom potentials approach
.
One might expect that the effective atom–molecule potentials given by Equation (
4) will follow the
power law, but with a possibly varying coupling coefficient. This can be understood assuming the deeply bound states are pointlike compared to the range of the interparticle potential, and the contribution to the integral (
4) comes only from
r∼0. The next term which can be extracted perturbatively and takes into account the spatial structure of the molecule can be obtained by expanding the angle-averaged atom–molecule potential
at large distances
R in power series, which gives
with
denoting the characteristic distance corresponding to the van-der-Waals interaction
, which is typically an order of magnitude smaller than
[
34]. Thus, there is a contribution to the coupling matrix element proportional to
. This term should be relevant for weakly bound states whose spatial extent cannot be neglected, both for the diagonal and nondiagonal matrix elements. This intuitively explains why the potential curves are largely independent of the exact form of the two-body potentials, as the short-range corrections only set in at distances smaller than
.
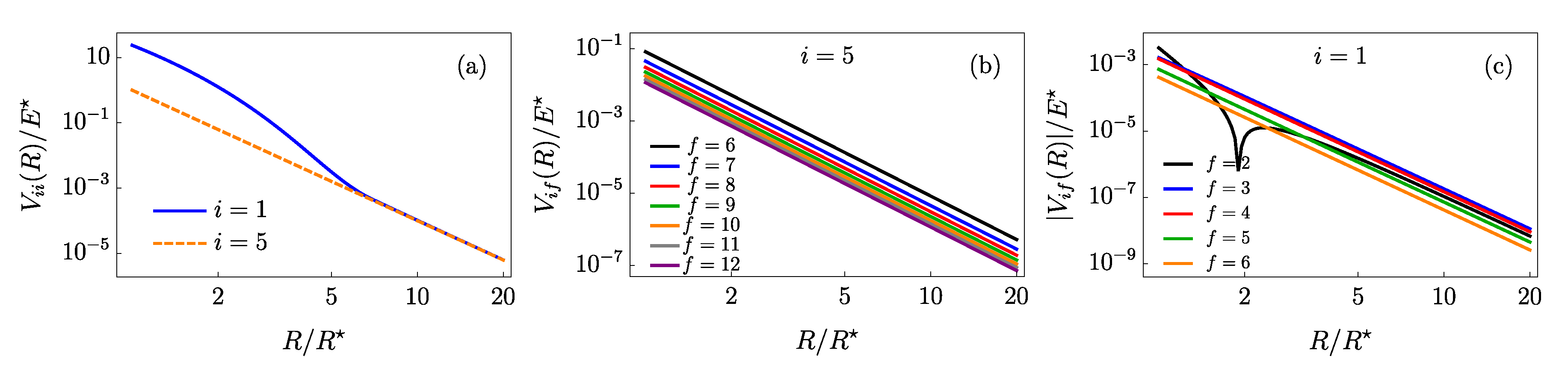
Two of the diagonal matrix elements of Equation (
4) are presented in the first panel of
Figure 2. As expected, they decay according to the
power law at long range with the fitted
coefficient equal to the original one. For the most weakly bound state, which in our case extends to around
and has the binding energy of only ≈
, the van-der-Waals term is also clearly visible. However, as this only provides a short-range correction we can conclude that the elastic scattering is just governed by the polarization potential with some unknown scattering length which depends on the short-range details.
Two exemplary cases of the coupling potential curves are shown in the middle and the right panel of
Figure 2. As expected, the couplings between deeply bound levels (middle panel) always follow the effective power-law potential with
dependence. However, for the most weakly bound state (right panel) the coupling to the state right below it has a different form as we again observe the impact of the
term at
. In addition, the potential changes its sign, leading to a dip on the logarithmic scale that has a finite depth due to the data points resolution. The effective
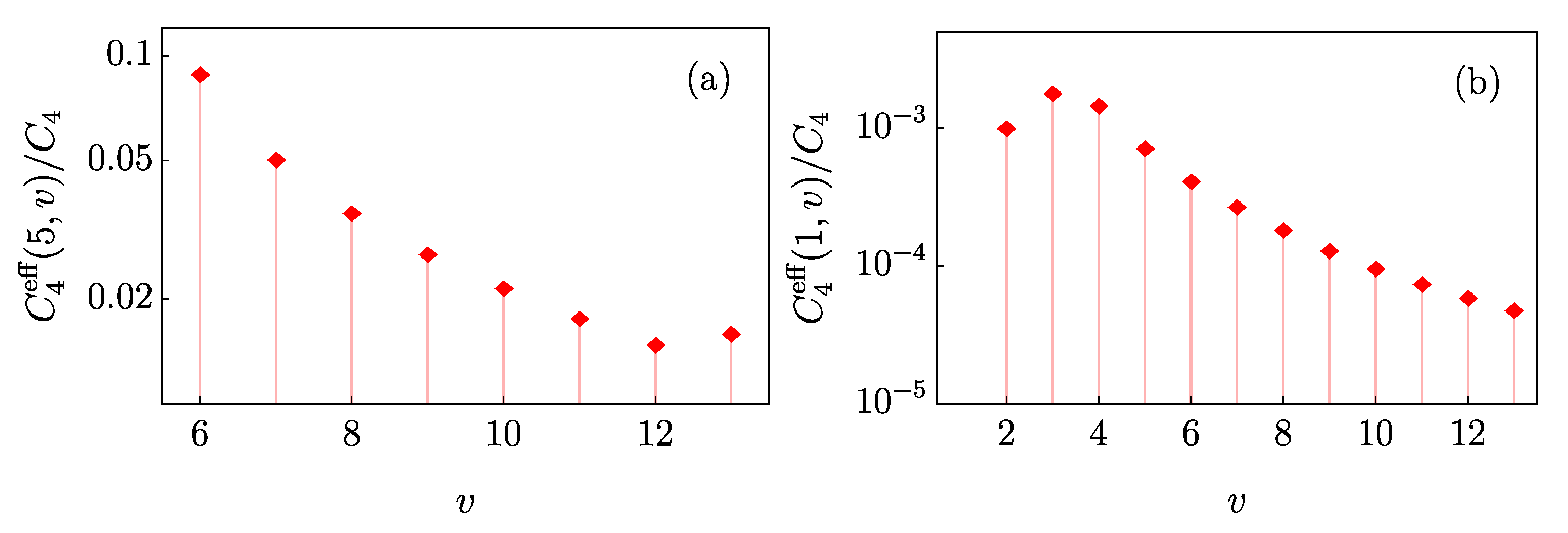
coupling coefficients generally decrease for states lying further from each other, as summarized in
Figure 3.
The calculations shown here have been performed for the ground rotational state of the molecular ion. We have checked that the excited rotational states show the same asymptotic behavior leading to ∼
dependence of the couplings. As we are dealing with the case of homonuclear ions, the rotationally inelastic collisions are suppressed. This is due to the small anisotropy of the potential surface in the absence of the charge-dipole term, which would be present for a heteronuclear molecular ion giving a contribution
[
29]. In our case the leading terms in the potential that couple different rotational levels behave like
, being relevant only in higher order.
Finally, let us mention that for vibrational relaxation the impact of the atom–atom interaction in the potential landscape is negligible due to the length scale separation between the van-der-Waals and polarization potential. The van-der-Waals forces set in only at distances at which the particles would already form a collision complex, which is beyond the scope of the current analysis.
2.4. Distorted Wave Born Approximation
Having calculated the effective interaction potential, we now turn to the analysis of the scattering. At this point, an issue concerning the short-range effects arises. Namely, if the reactants form a collision complex, the short-range three-body physics becomes relevant and impacts the recombination process. Ergodic dynamics of the complex would lead to statistical distribution of the product states. The effective potential (
3) is written in the rovibrational state basis and thus does not capture dynamics of the three-body complex. Furthermore, as demonstrated above, the coupling between different vibrational states of the molecular ion arising in the collision has rather long-range nature. It is then warranted to focus on the close-coupled system described by Equation (
3), disregarding the possibility of the complex formation. A possible minimal extension of the current results would be to impose (partially) absorbing boundary conditions at short range in order to mimick the long-lived complex creation and treat the part of the flux reaching the inner region statistically [
12,
35].
Rather than solving the scattering problem set by Equation (
3) in full, as we are anyway working with an approximate model potential, we will now proceed by employing the distorted wave Born approximation (DWBA) to estimate the inelastic collision rates. DWBA is a method based on perturbation theory [
26,
36], which utilizes the knowledge of the scattering solution to the elastic part of the problem and has been widely used to describe atom–molecule inelastic collisions [
11,
37,
38]. This is particularly suitable for our problem since the diagonal potentials are analytically solvable [
33].
Within the DWBA, the off-diagonal elements of the
matrix in Equation (
8) are given by
where the
functions denote the energy normalized scattering solution for the diagonal potential in channel
i (in our case given solely by the
term) and
is the coupling matrix element between the initial and the final state given by Equation (
4). The elastic scattering within the DWBA is not affected by the nondiagonal terms in the potential and can be described analytically by energy- and angular momentum-dependent phase shifts
. Then the scattering matrix and all observable quantities can be calculated from Equation (
8). Note that the matrix elements need to be calculated for all partial waves involved in the collision.
Interestingly, assuming that the coupling between the channels behaves as
, the matrix element (
11) can be calculated analytically assuming the channel wavefunctions are given by spherical Bessel functions and for angular momenta of the two states fulfilling
. This provides the threshold law for the K-matrix element
. In particular, for
one obtains
where
is the hypergeometric function. In the limit of a far-from-threshold exit channel (large energy difference between the states compared to the initial kinetic energy) this quantity scales as
. In practice, we are anyway imposing a short-range cutoff to the interaction and use the full scattering solutions of the polarization potential which oscillate quickly at small distances giving no contribution there.
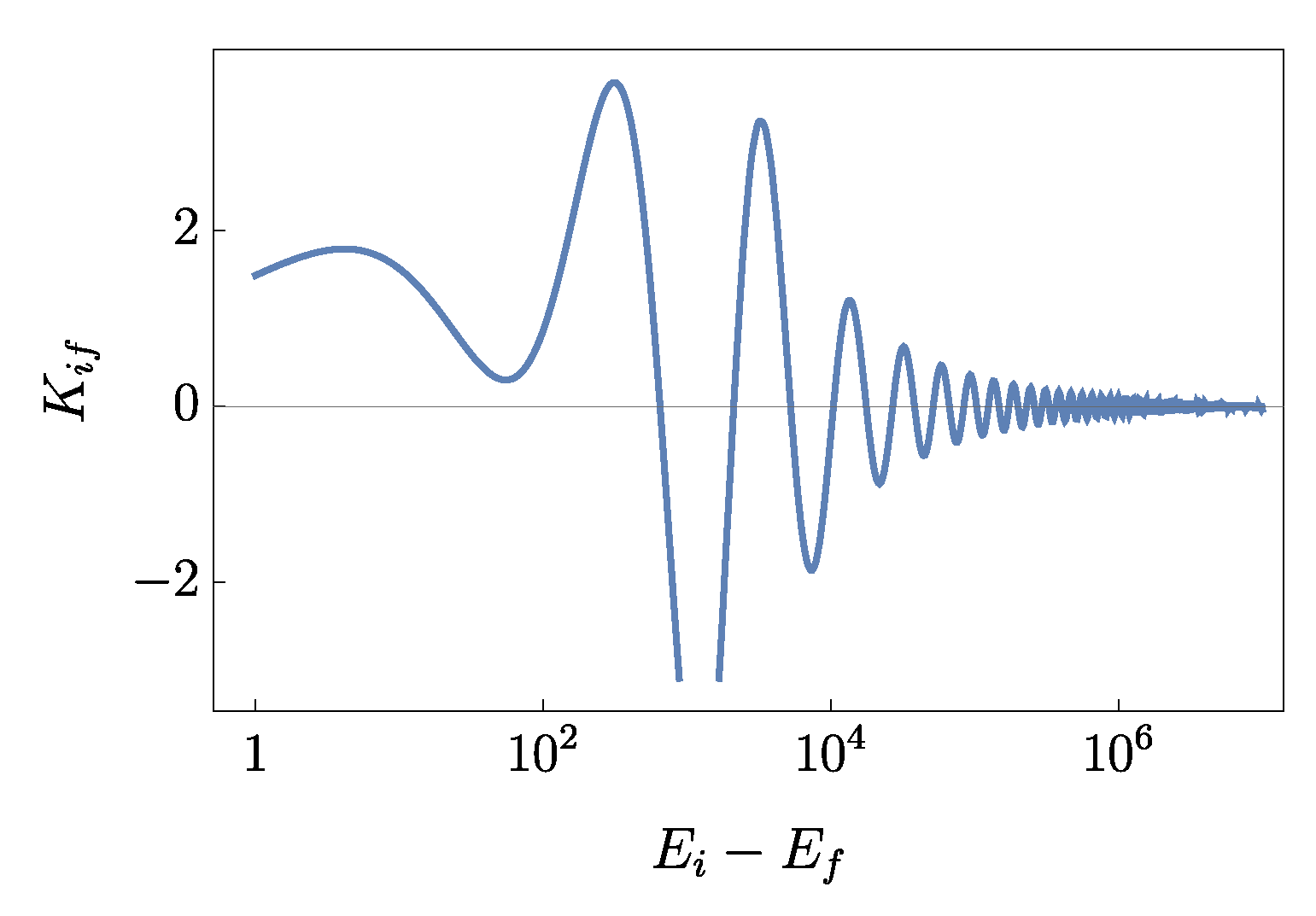
In
Figure 4, we show the dependence of the inelastic K-matrix element (assuming a dimensionless
potential) on the energy difference between the two channels for the initial state with kinetic energy of
and scattering length equal to
. The rapid decrease in magnitude and fast oscillations result from the properties of the outgoing state. At relatively low energy difference between the states (roughly below
) one could in principle expect visible resonant effects provided that the reactants can be prepared in a single quantum state (although when the calculated matrix elements are large, DWBA cannot be trusted any more). However, the polarization potential anyway does not support a dense enough bound-state spectrum and apart from the coupling between the two most weakly bound levels one cannot expect any resonant enhancement. Moreover, in experiment the results would be further blurred by thermal averaging. More specifically, in order to calculate the rate constant at finite temperature one needs to take a convolution according to
.
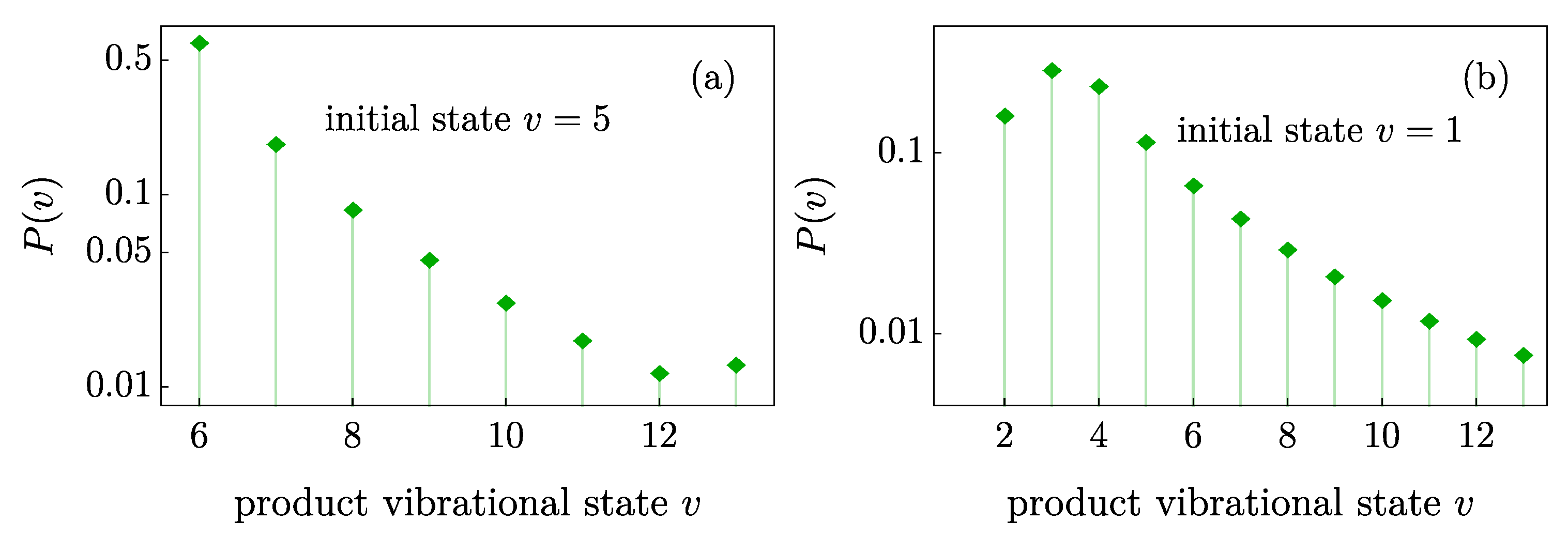
Along with the coupling coefficients calculated above, the DWBA allows for a simple estimate of the product distribution. As an example, we focus again on the initial vibrational state
and
counting from the dissociation threshold. The obtained distribution is shown in
Figure 5. The result of the collision is affected by the magnitude of the effective coupling coefficients as well as the difference in energy between the channels. We have averaged the results over the rapid oscillations of the Bessel functions involved in the integral (
11). We find that in both cases the distribution of reaction products is rather broad and favors the nearby states, in agreement with the classical trajectory calculations [
16]. Due to the large number of available product states, the total inelastic collision cross section follows the universal Langevin prediction
. We have checked that as long as the collision energy
(≈
K for Rb) the product distribution does not change significantly.