Electromagnetic Scattering from Surfaces with Curved Wedges Using the Method of Auxiliary Sources (MAS)

1. Introduction

Computational Electromagnetics techniques have traditionally been utilized in the mathematical modeling of problems related to radiation and the propagation of electromagnetic waves. Standard applications involve antennas, diffraction, scattering, waveguides, propagation in complex environments, etc., while boundary surfaces are typically either perfectly conducting or dielectric. Recently, important technological advances have been based on the electromagnetic properties of Near-Zero Index (NZI) materials [1,2], plasmonics [3], metasurfaces [4], graphene [5], nanoparticles [6], etc.

Analytical and asymptotic methods were originally the only mathematical tool to perform relevant calculations, naturally being restricted to canonical geometries. However, computers demonstrated explosive progress over the last few decades, thus rendering numerical techniques indispensable in extracting approximate results of controllable accuracy for arbitrary geometries. In general terms, numerical techniques discretize either integral [7,8] or differential equations [9,10] involved in the mathematical simulation of physical problems. A variant of differential equation techniques is based on the construction of equivalent circuit or transmission line models [11,12,13]. Each group of the aforementioned techniques is characterized by advantages and disadvantages, and therefore their suitability and efficiency depend on the particular configuration. For example, in scattering problems, where the Radar Cross Section (RCS) of a target must be calculated, differential equation methods should ideally discretize the entire space all the way to infinity, which is obviously impossible. Mesh truncation is a complicated task that needs to be resolved in order to obtain accurate results. On the contrary, integral equation methods are usually more complicated in terms of calculations, and the computational cost may be exceedingly high due to dense matrices involved in the resulting linear system of equations. However, field behavior at infinity is automatically incorporated into the Green’s function, and therefore modeling the entire space is easily tractable. Integral equation solutions and their procedure optimization is an important research topic, which recently triggered some especially unconventional approaches [14].

The method of auxiliary sources (MAS) [15] is an integral equation technique that has successfully been used in computational physics, including a wide range of electromagnetic radiation and scattering applications [16]. MAS is superficially similar to the point matching version of the method of moments (MoM) [7]; however, the auxiliary current sources are located at a distance from, and not right on the surface boundaries. Moreover, the MAS basis functions set, used in the field expansions, has been proven to be complete [17], which is not always easy to prove in MoM, therefore the method is mathematically rigorous. Finally, unlike MoM, MAS is free of singularity complications, it does not require any time-consuming numerical integrations and is much easier to implement algorithmically. A quantitative assessment of MAS performance is given in [18], where a detailed comparison is carried out between the computational costs of MAS and MoM. It is demonstrated that for the same discretization density, MAS is always more efficient than MoM, but even if a higher number of unknowns is required for MAS, the latter is still less computationally intensive than MoM under certain conditions.

Although MAS has been invoked in several problems with various configurations and material properties, further research is necessary to determine the optimal source location for arbitrary geometry layouts. Particular difficulties arise when the outer boundary of the scatterer contains wedges, i.e., when the analytical expression of the boundary curve is not differentiable. In that case, the solution accuracy deteriorates because the boundary condition close to the wedge tip is hard to satisfy sufficiently well. To apply MAS to such configurations, a set of auxiliary sources (ASs) is positioned on a fictitious surface, which is generally conformal to the physical boundary, except in the vicinity of the tips. In the areas surrounding the wedges, the ASs are densely packed, simultaneously approaching the tips, to account for the edge effects, as suggested in [19]. Similar strategies were employed in the case of a scattering problem associated with coated perfectly electric conducting (PEC) surfaces including wedges [20], where the surface was modeled via the standard impedance boundary condition (SIBC) [21].

While this deformation of the auxiliary surface has proven efficient for straight wedges, especially when the latter form right angles, no evidence is known from the literature about its applicability to arbitrarily shaped wedges. The aim of this paper is to investigate whether MAS accuracy improves through this deformation, when the wedge is shaped as an intersection of circular arcs with non-coincident centers. Moreover, as an improvement over the heuristic approaches in [19,20], explicit algorithms should be developed for the definition of the deformed auxiliary surface. The scatterer is thus defined as an infinite cylinder, either conducting or dielectric, with an eye-shaped cross-section. The auxiliary surface is generally retained as conformal to the scatterer’s boundary, except in the neighborhood of the wedge tips, where various deformation schemes are employed and accuracy comparisons are drawn.

The format of this paper, which is an extension of [22], including additional data on perfectly conducting case, lossless, and lossy dielectrics, is as follows: Section 2 briefly presents the mathematical formulation of MAS for 2D scatterers, illuminated by a transverse magnetic (TM) polarized plane wave. Furthermore, in Section 3 various algorithms are proposed for the deformation of the auxiliary surfaces close to the wedge tips. Section 4 includes a variety of data for the eye-shaped scatterer and checks the satisfaction of the boundary condition. Finally, the method is summarized and discussed, whereas useful conclusions are drawn.

A $+j\omega t$ time variation convention is assumed and suppressed throughout the paper.

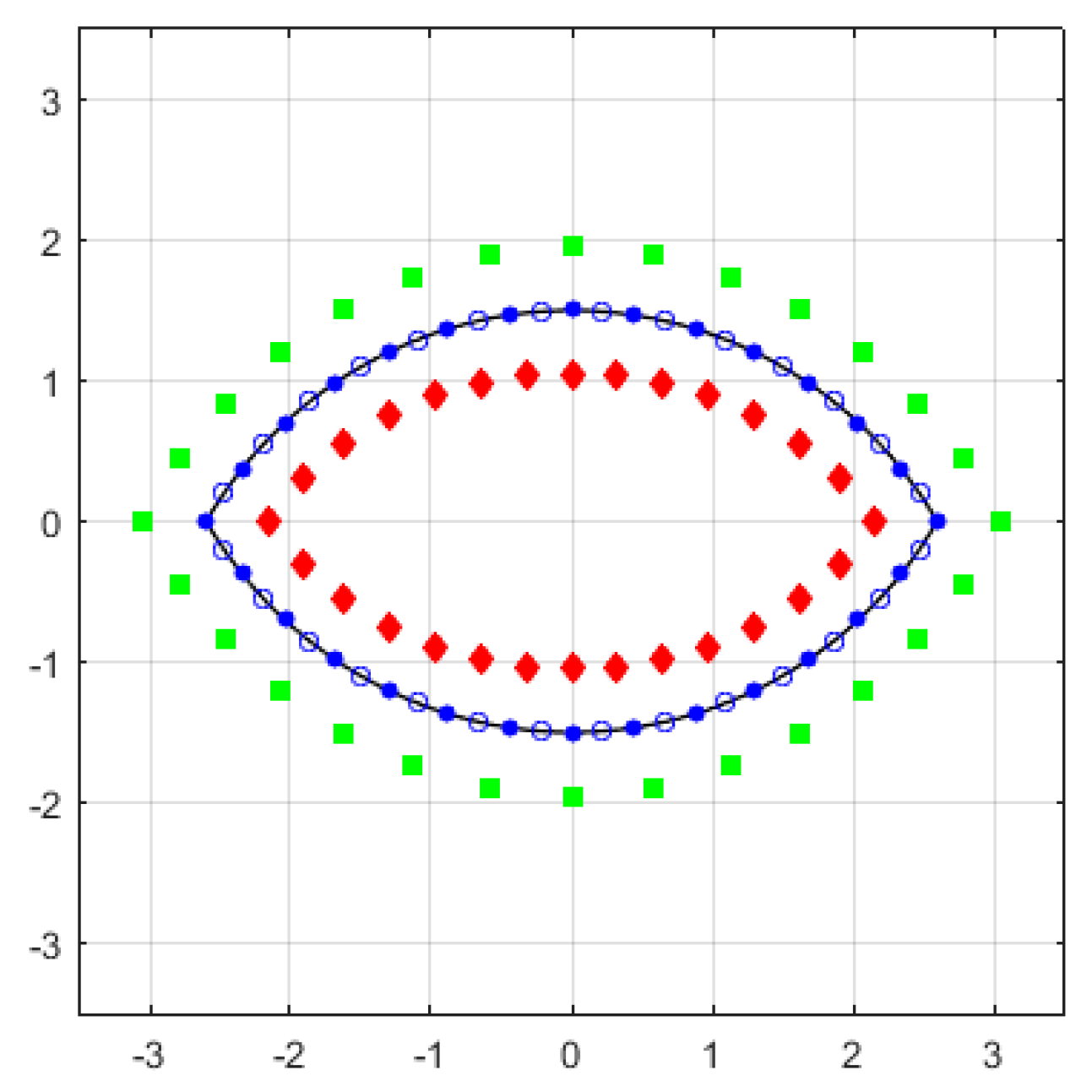
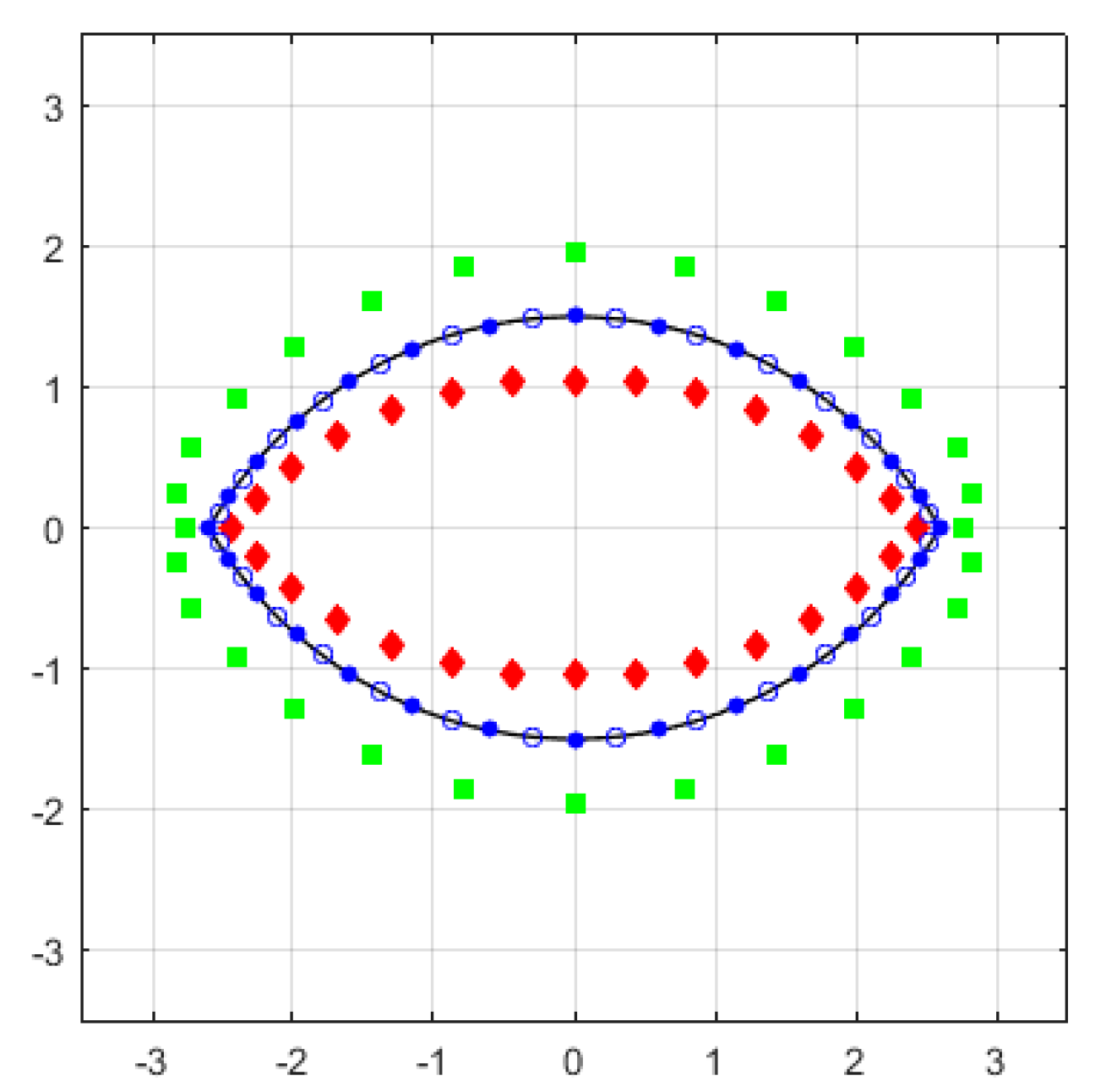
2. MAS for Eye-Shaped Scatterers

We assume an infinitely long cylinder with a cross section that resembles an eye (Figure 1). We investigate two separate cases: perfect electric conductor (PEC) or linear- homogeneous-isotropic dielectric. The geometry of the scatterer, depicted by a solid line, comprises two circular arcs with identical radii equal to $\rho$, but with different centers. In particular, the Cartesian coordinates of the upper arc are given by (1):

$$x_u=\rho \cos \phi , y_u=\rho \sin \phi -d,$$

(1)

whereas those of the lower arc are given by (2):

$$x_l=\rho \cos \phi , y_l=\rho \sin \phi +d,$$

(2)

where $\phi$ is the azimuth angle and $\pm d$ is the vertical displacement of each arc center, taken equal to the arc apothem (see Figure 2). Obviously, $\phi$ does not span the entire $\left[0,2\pi \right)$ interval, but it is limited by the arc width itself, which is given by (3):

$${\phi }_{arc}=2\arccos \frac{d}{\rho }.$$

(3)

The scatterer is illuminated by a TM plane wave impinging from an azimuth angle equal to ${\phi }_{inc}$. Therefore, the incident electric field ${\mathit{E}}_{inc}$ is given by (4):

$${\mathit{E}}_{inc}\left(x,y\right)=E_0\exp \left\{j{k}_0\left(x\cos {\phi }_{inc}+y\sin {\phi }_{inc}\right)\right\}\widehat{\mathit{z}},$$

(4)

where $E_0$ is the amplitude of the incident electric field, $k_0$ is the free space wavenumber, and a hat denotes a unit vector along the corresponding direction. The incident magnetic field ${\mathit{H}}_{inc}$ is given by (5):

$${\mathit{H}}_{inc}\left(x,y\right)=-\frac{E_0}{{\zeta }_0}\left(\sin {\phi }_{inc}\widehat{\mathit{x}}-\cos {\phi }_{inc}\widehat{\mathit{y}}\right)\exp \left\{j{k}_0\left(x\cos {\phi }_{inc}+y\sin {\phi }_{inc}\right)\right\},$$

(5)

where ${\zeta }_0$ is the free space intrinsic impedance. To solve the scattering problem via MAS, two sets of ASs are generally defined, each one of multitude $N$, as shown in Figure 1. In the PEC case, only the inner set is used; the outer set is necessary only in the dielectric configuration. In standard MAS formulation, both inner and outer auxiliary surfaces are conformal to the scatterer boundary. The electric field due to the $n$th inner AS, located at point ${\mathit{r}}_n$ and radiating in the outer space, is as follows:

$$E_{sn}\left(\mathit{r}\right)=\widehat{\mathit{z}}{E}_n{H}_0^{\left(2\right)}\left(k_0\left|\mathit{r}-{\mathit{r}}_n\right|\right),$$

(6)

where $E_n$ is the corresponding unknown weight, $\left(n=1,2,\dots , N\right)$, and $H_0^{\left(2\right)}$ is the Hankel function of the zero order and second kind (2D Green’s function). The corresponding magnetic field of the $n$th auxiliary source is obviously proportional to the curl of (6), given explicitly in [20]. Similar expressions hold for the outer ASs, radiating in the inner space of the dielectric scatterer, except for $k_0$ and ${\zeta }_0$, which have to be replaced by $k$ and $\zeta ,$ respectively, corresponding to the scatterer’s dielectric properties. The total scattered $E$ field is expressed as the superposition of the fields in (6) and the $H$ field accordingly. By applying the boundary conditions for both fields at the $N$ collocation points (CPs) $\left(x_m,y_m\right)$ $\left(m=1,2,\dots , N\right)$ of the scattering boundary (blue solid dots in Figure 1), we cast a linear system of equations as in (7):

$$\left[\mathit{Z}\right]\left\{\mathit{I}\right\}=\left\{\mathit{V}\right\},$$

(7)

where $\left\{\mathit{I}\right\}$ is the column vector of the unknown weights $E_n$. In the PEC case, $\left[\mathit{Z}\right]$ is a square matrix of size $N\times N$ with elements determined by the interaction between ASs and CPs, and $\left\{\mathit{V}\right\}$ is the column vector of the incident $E$ fields calculated at the CPs. In the dielectric case, the $\left[\mathit{Z}\right]$ interaction matrix is of size $2N\times 2N$ and $\left\{\mathit{V}\right\}$ is the column vector of both the incident $E$ and $H$ fields calculated at the CPs.

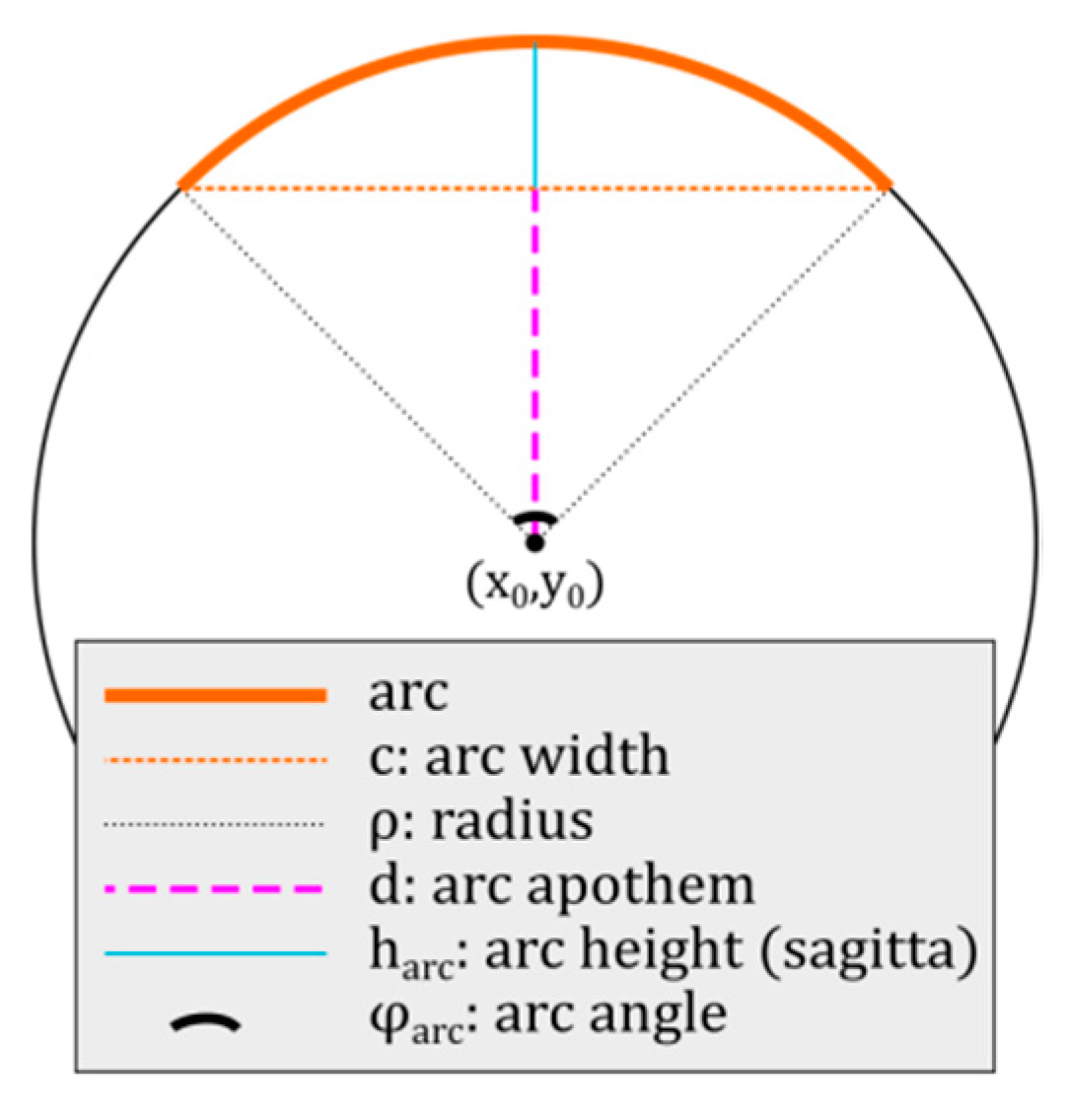
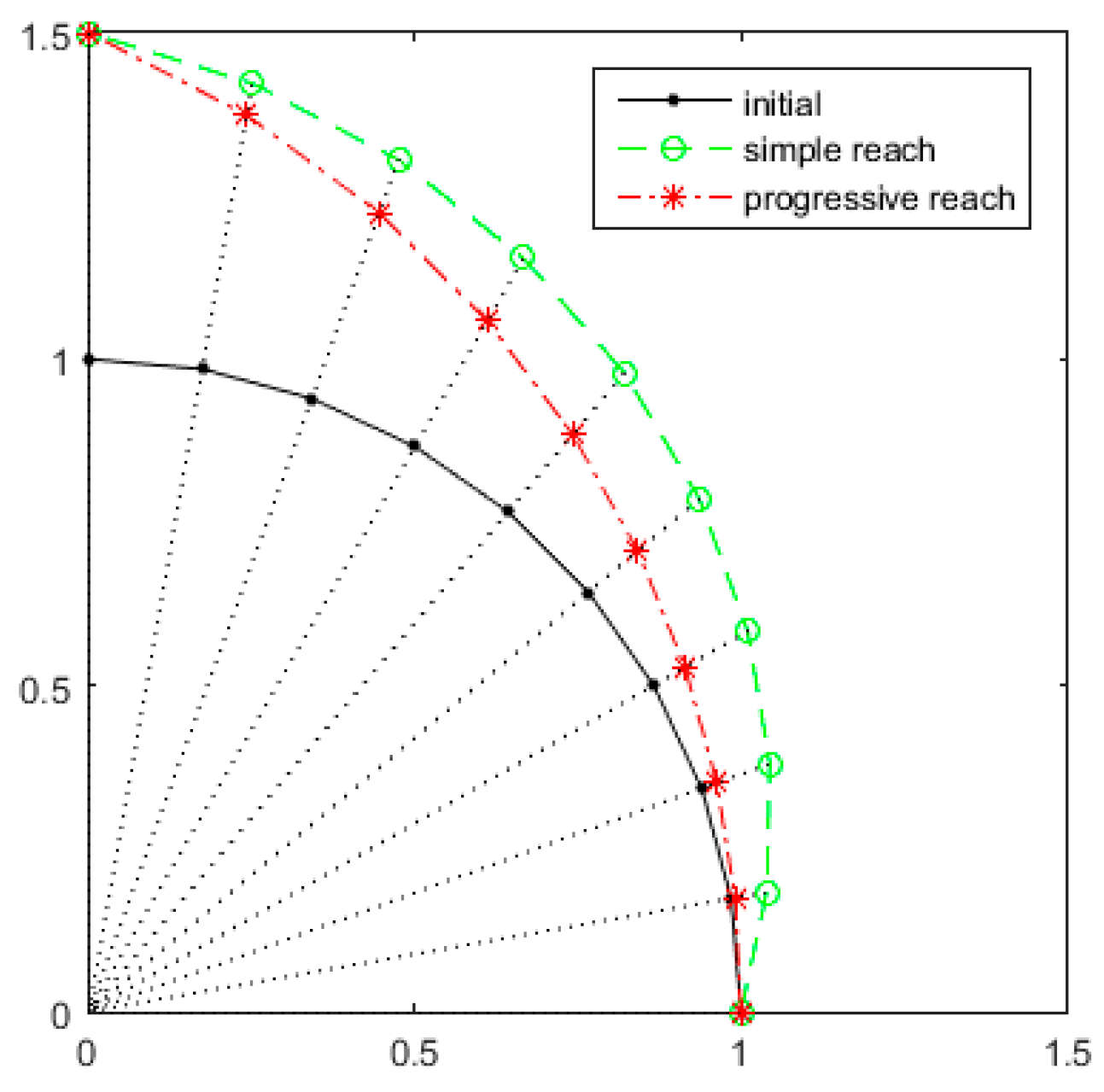
3. Improvement of the Auxiliary Surface Layout

As mentioned in [19,20], MAS becomes less accurate when the auxiliary surfaces are conformal to boundaries encompassing wedges. In particular, satisfaction of the boundary condition at midpoints (MPs) (see Figure 1) close to the tips is no longer sufficiently good. To overcome this complication, the auxiliary surface, defined by radius ${\rho }_{aux}$ and using expressions analogous to (1-3), may be deformed so that ASs not only approach the tips closely, but become denser in the tip neighborhood as well. ASs may approach CPs following several patterns. In this work, two basic patterns were tested. Let $M$ be the number of ASs to be moved. Let ${\rho }_m$ be the polar radius of the $m$th AS ($m=1, 2, \dots , M$), and let $g$ be the maximum polar radius difference between the $m$th AS and the $m$th CP. Finally, let $s$ be the proximity factor, defined in $\left[0,1\right]$, so that $0$ corresponds to no approach and $1$ corresponds to the maximum approach (resulting in coincident ASs and CPs). Then, the schemes proposed for the auxiliary surface deformation are defined in (8) as follows:

$${\rho }_m^{\prime }={\rho }_m+gs{\left(\frac{m}{M}\right)}^{\nu },$$

(8)

where $\nu =1$ for simple and $\nu =2$ for progressive reach. The deformation effect is graphically described in Figure 3.

Furthermore, in a way similar to [20], ASs and CPs, accordingly, should become denser close to the wedge tip. Again, there is no unique way to accomplish this. In this work, the scheme implemented multiplies the polar angle ${\phi }_m$ of the $m$th AS location by a factor $D_m$, $0<D_{start}\le D_m\le 1$, where $D_{start}$ is user-defined. For example, in the first quadrant of the ‘eye’, $D_m$ is defined as being close to $0$ for ASs near the wedge tip, and close to $1$ for ASs close to the vertical axis. For progressive densification, the scheme proposed is: ${\phi }_m^{\prime }={\phi }_m{D}_m^2$. Moreover, additional ASs may be superimposed to the already existing ones close to the tips if necessary. The combined effect of the tip approach and densification is depicted in Figure 4.

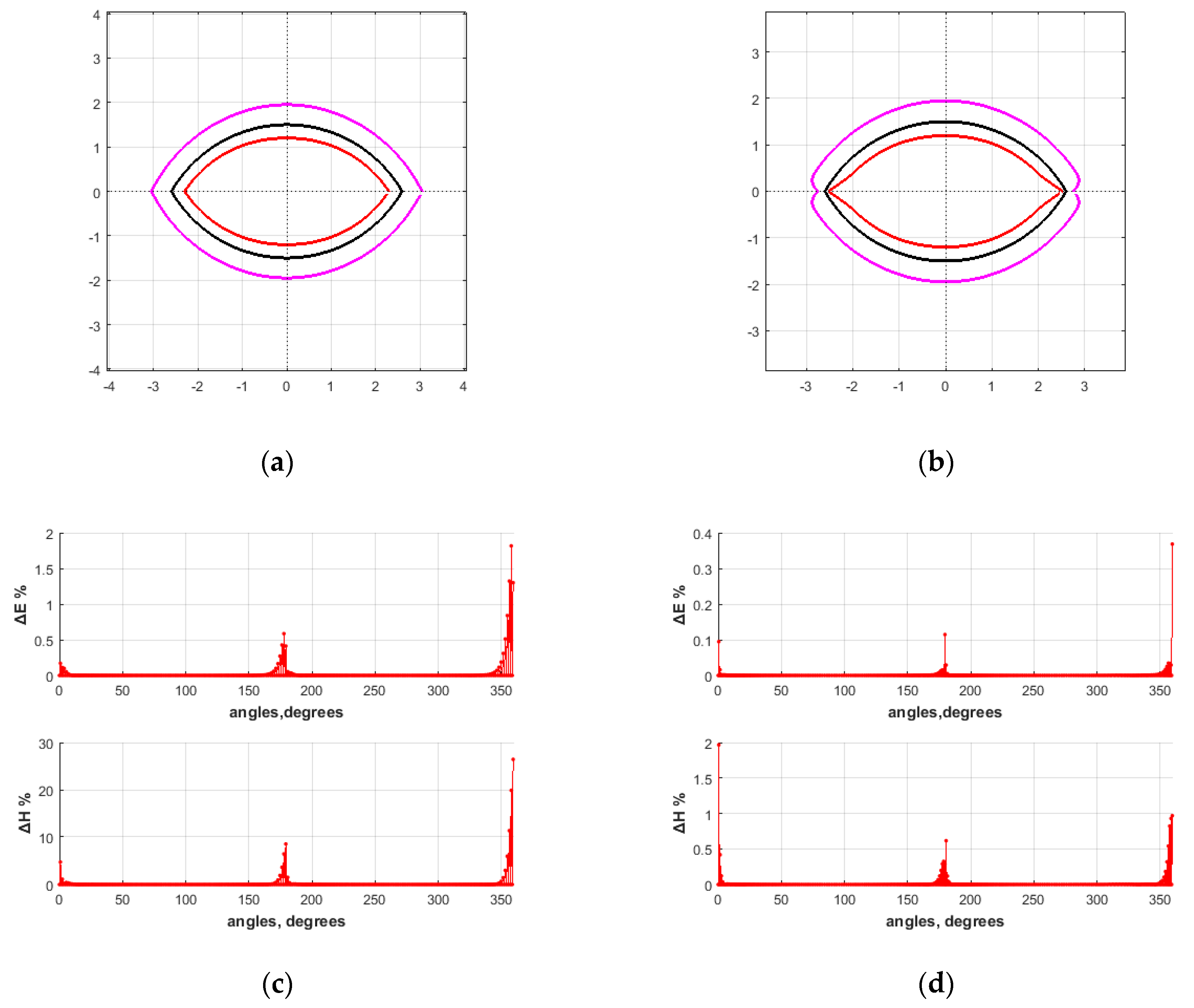
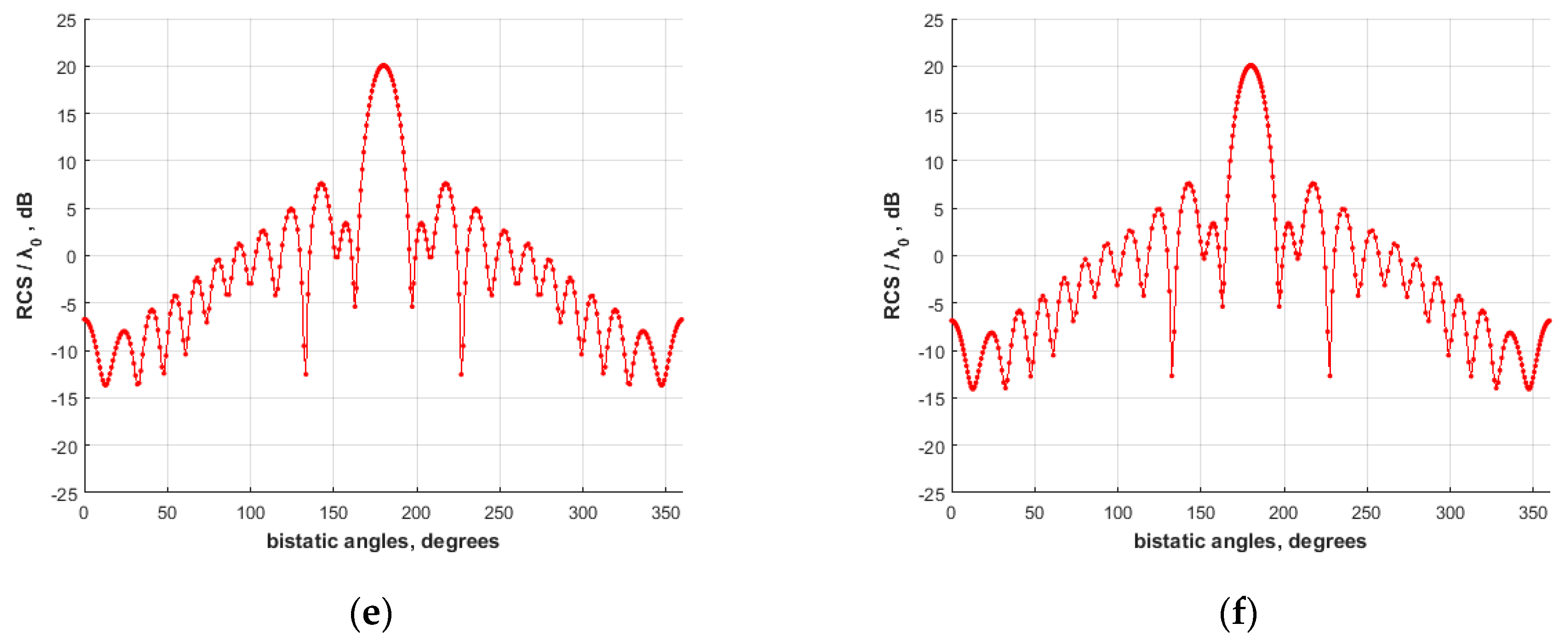
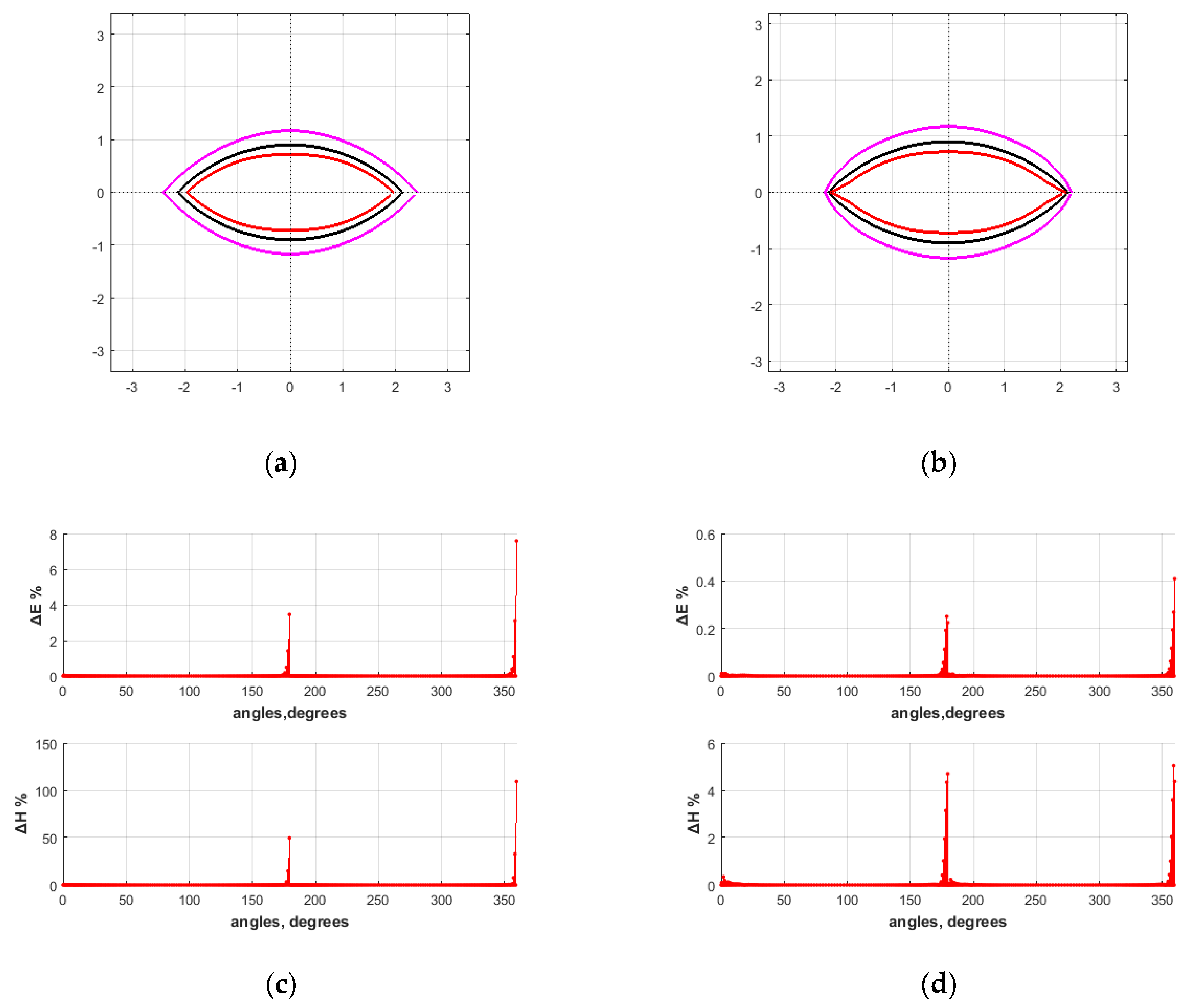
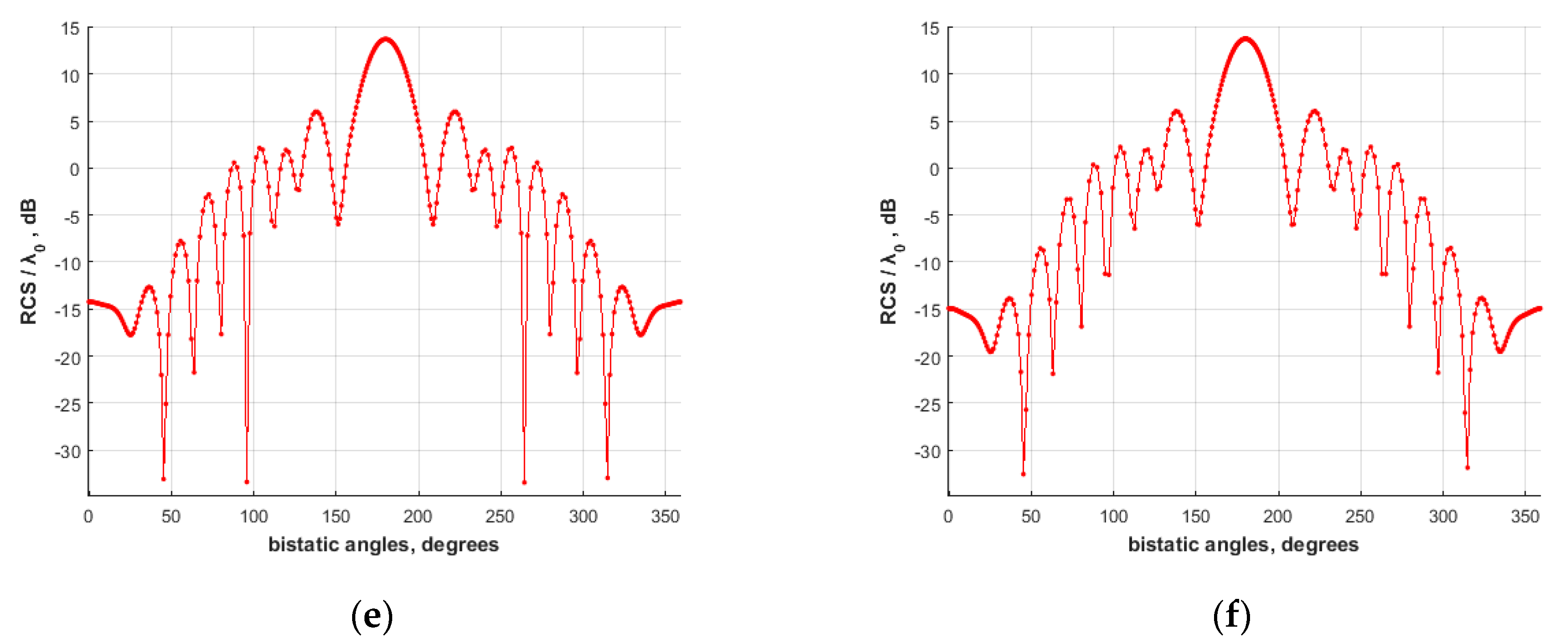
4. Results

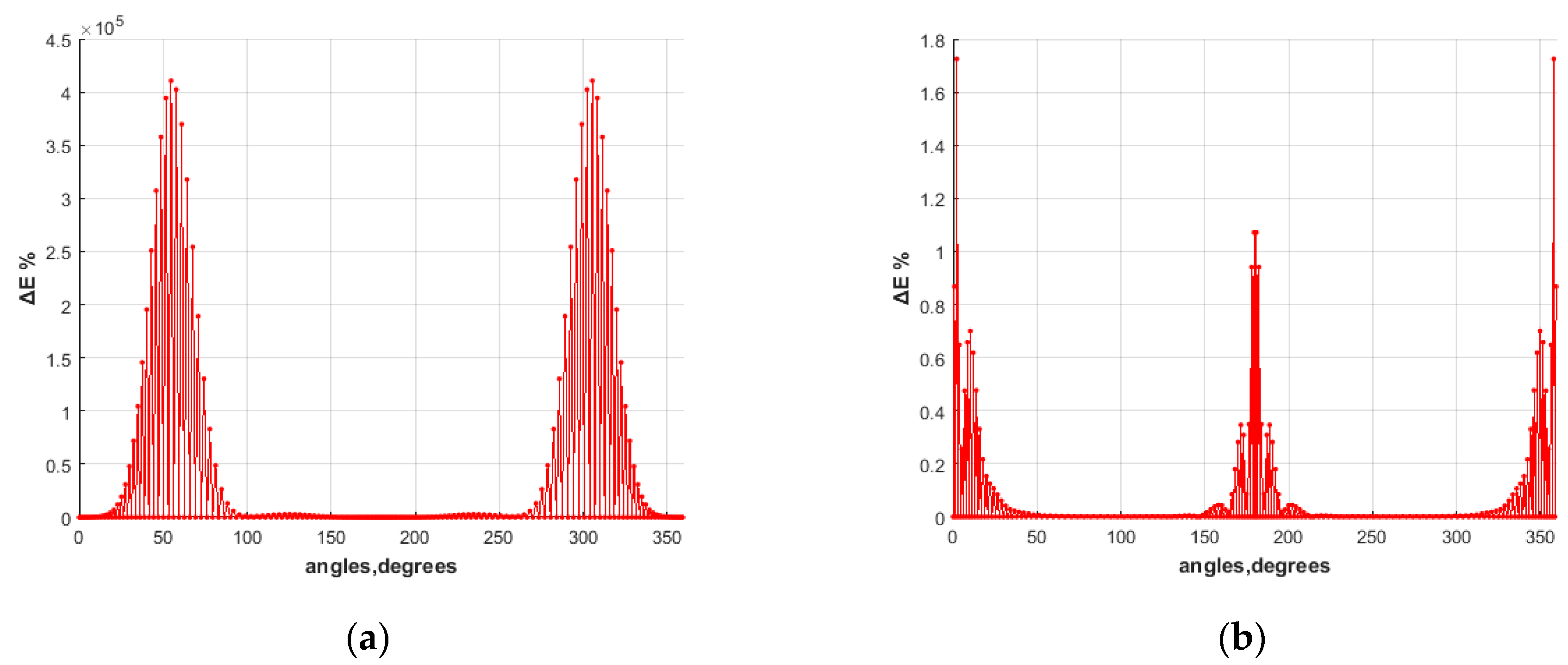
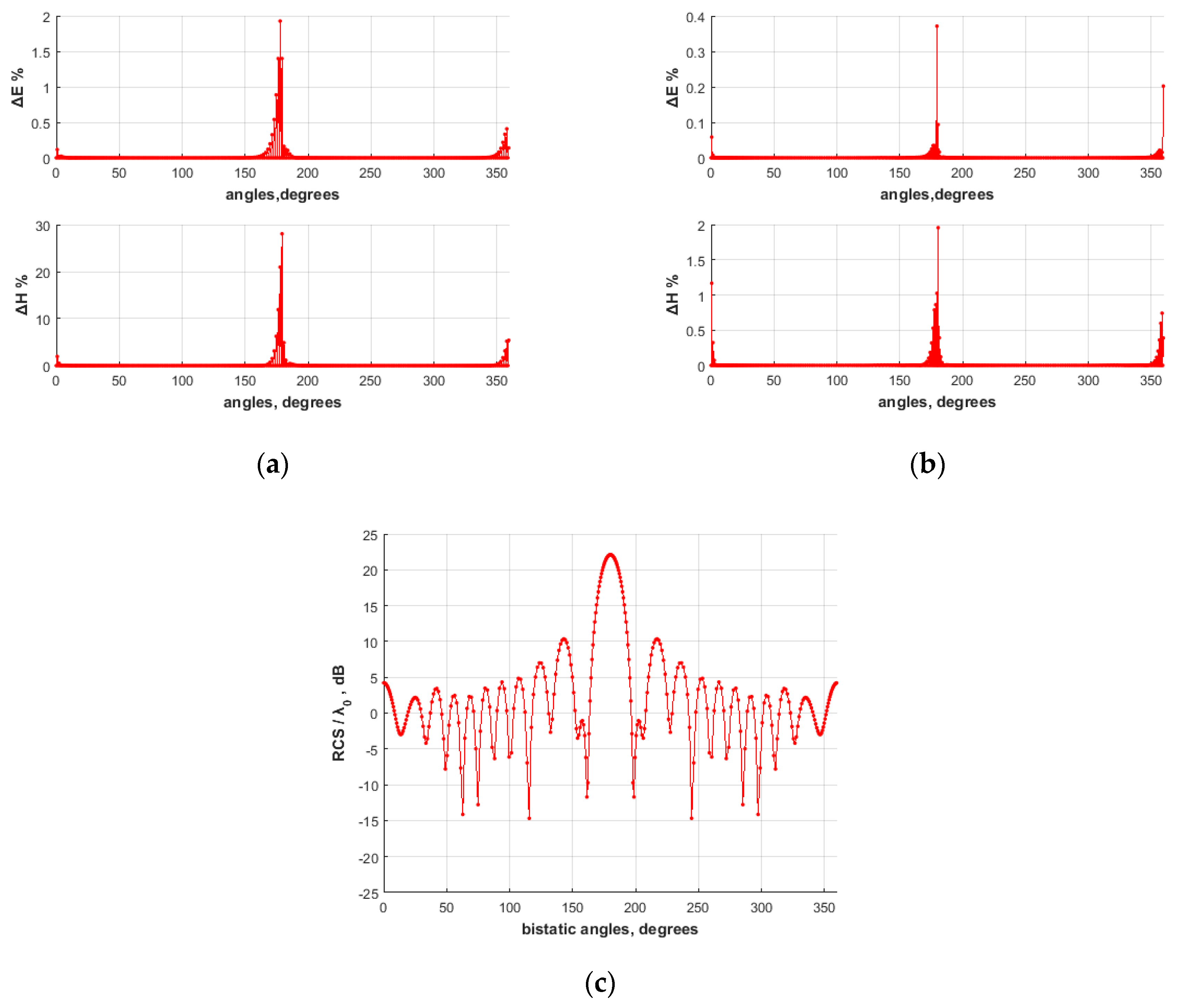
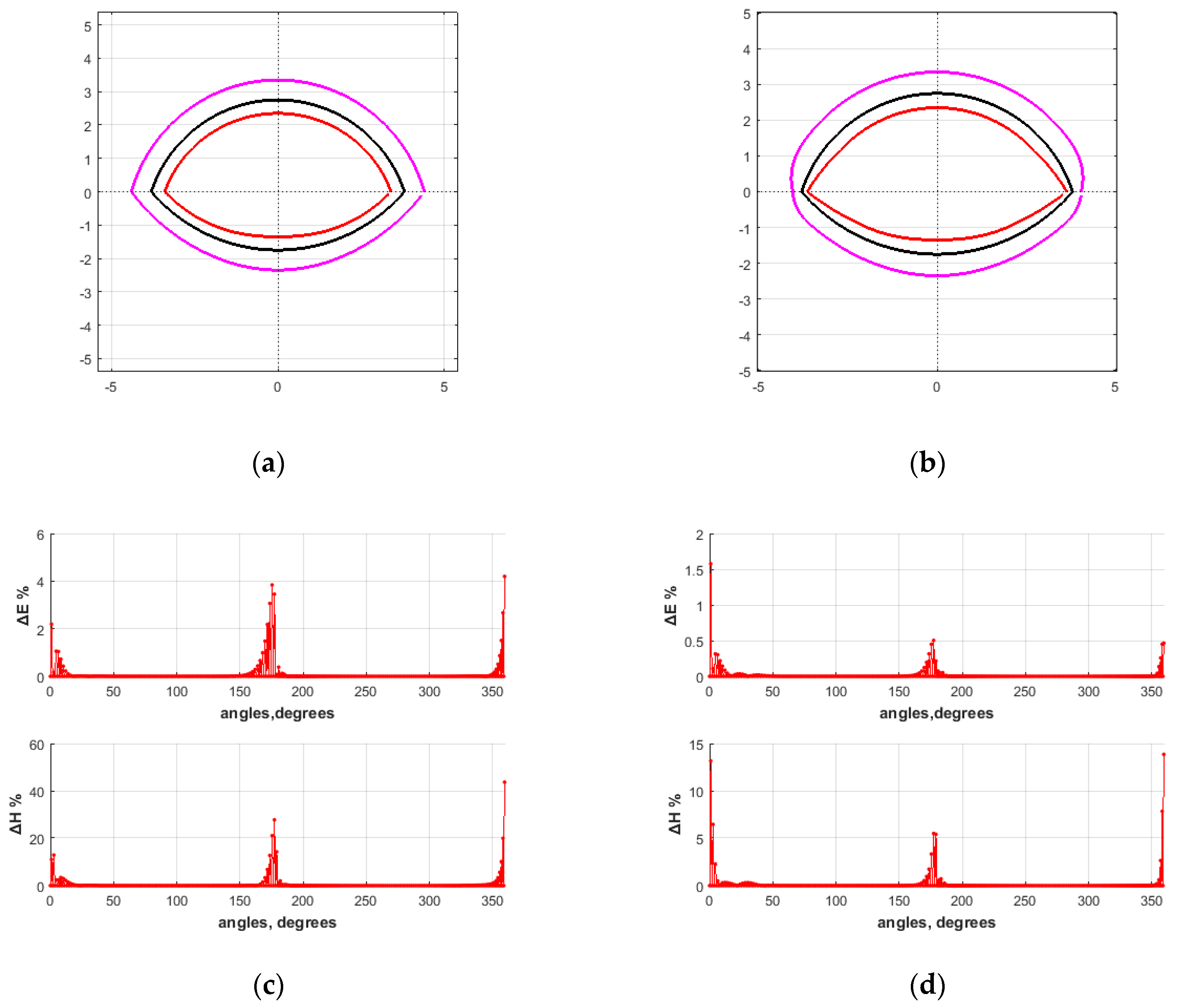
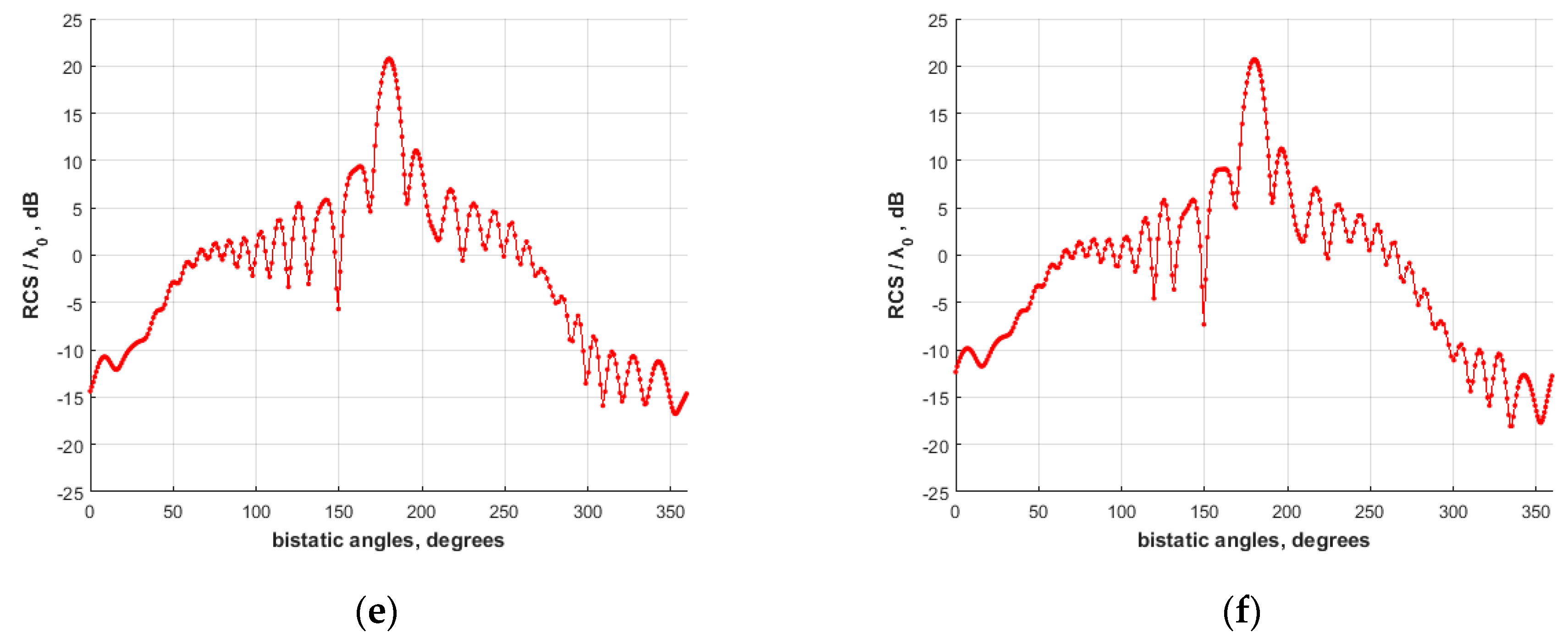
4.1. PEC Scatterer

To test the efficiency of the method, a PEC scatterer is initially defined by radius $\rho =3\lambda$, arc displacement $d=0.5\rho =1.5\lambda$, incidence angle ${\phi }_{inc}=0$, auxiliary surface radius ${\rho }_{aux}=\rho -0.075\lambda$, and originally $136$ CPs and therefore 136 inner ASs. The solution to the problem without any deformation yields the results of Figure 5a, which depicts the quantified error in the generic boundary condition (BC) of the $E$ field along the boundary stretch, i.e.,:

$$\Delta {{\rm E}}_{bc}=\frac{\left|\widehat{\mathit{n}}\times \left({\mathit{E}}_{in}-{\mathit{E}}_{out}\right)\right|}{{\left|{\mathit{E}}_{inc}\right|}_{max}},$$

(9)

where in (9) $\widehat{\mathit{n}}$ is the normal unit vector on the boundary, pointing outwards, and ${\mathit{E}}_{in}, {\mathit{E}}_{out}$ are the electric fields just inside and just outside the scatterer, respectively, the former obviously vanishing for the PEC case.

To improve the satisfaction of the BC, the deformation scheme proposed above was implemented. After several trials, the following parameters were finally invoked: All ASs were displaced as well as densified and the proximity factor was set equal to $s=0.88$, whereas $D_{start}=0.9$. No extra ASs were added since their presence proved to achieve only incremental improvement. The results are displayed in Figure 5b, which shows that the overall $E$ field error at MPs was substantially reduced.

It is worth noting that the proper placement of the auxiliary surface is of great importance in order to avoid caustics exclusion by the auxiliary surface or any potential resonance effects, as presented in [23]. To illustrate the possibly detrimental influence on the BC error, specifically, in this case, keeping the multitude of CPs consistent (and thus the multitude of ASs consistent) but moving the auxiliary surface further away from the scattering boundary (${\rho }_{aux}=\rho -0.15\lambda$) produced the results in Figure 6a,b, before and after applying the deformation scheme, respectively. Severe complications are revealed in Figure 6a, while it may be deduced from Figure 6b that utilizing an improved auxiliary surface layout, compared to a conformal one, may be much less prone to accuracy degradation, presumably because caustics are still retained within the auxiliary surface.

4.2. Lossless dielectric scatterer

Next, a lossless dielectric scatterer was considered, with radius $\rho =3\lambda$, arc displacement $d=0.5\rho =1.5\lambda$, relative permittivity ${\epsilon }_r=2.56$, incidence angle ${\phi }_{inc}=0$, inner and outer auxiliary surface radius ${\rho }_{aux in}=\rho -0.3\lambda$ and ${\rho }_{aux out}=\rho +0.45\lambda$, and, originally, $160$ CPs (hence $160$ inner and $160$ outer ASs). Like in the PEC case, the efficiency of MAS was initially tested using a conformal auxiliary surface and the extracted results of the BC error are presented in Figure 7a, where the upper subplot depicts the quantified error for the $E$ field ($\Delta {\rm E} \%$) and the lower one for the $H$ field ($\Delta H \%$), both being relatively significant near the wedge tips.

Afterwards, the improvement of the BC was examined by employing the aforementioned deformation scheme with the following parameters, obtained through multiple trials: the portion of ASs to be displaced was $1/5$ for the inner and $1/8$ for the outer ones, with a proximity factor of $s=0.75$ and $s=0.65,$ respectively, while all of them were densified with $D_{start}=0.80$. The addition of extra ASs offered no further refinement and was skipped once more. Figure 7b depicts the considerably decreased quantified BC error, and the corresponding radar cross section (RCS) is displayed in Figure 7c.

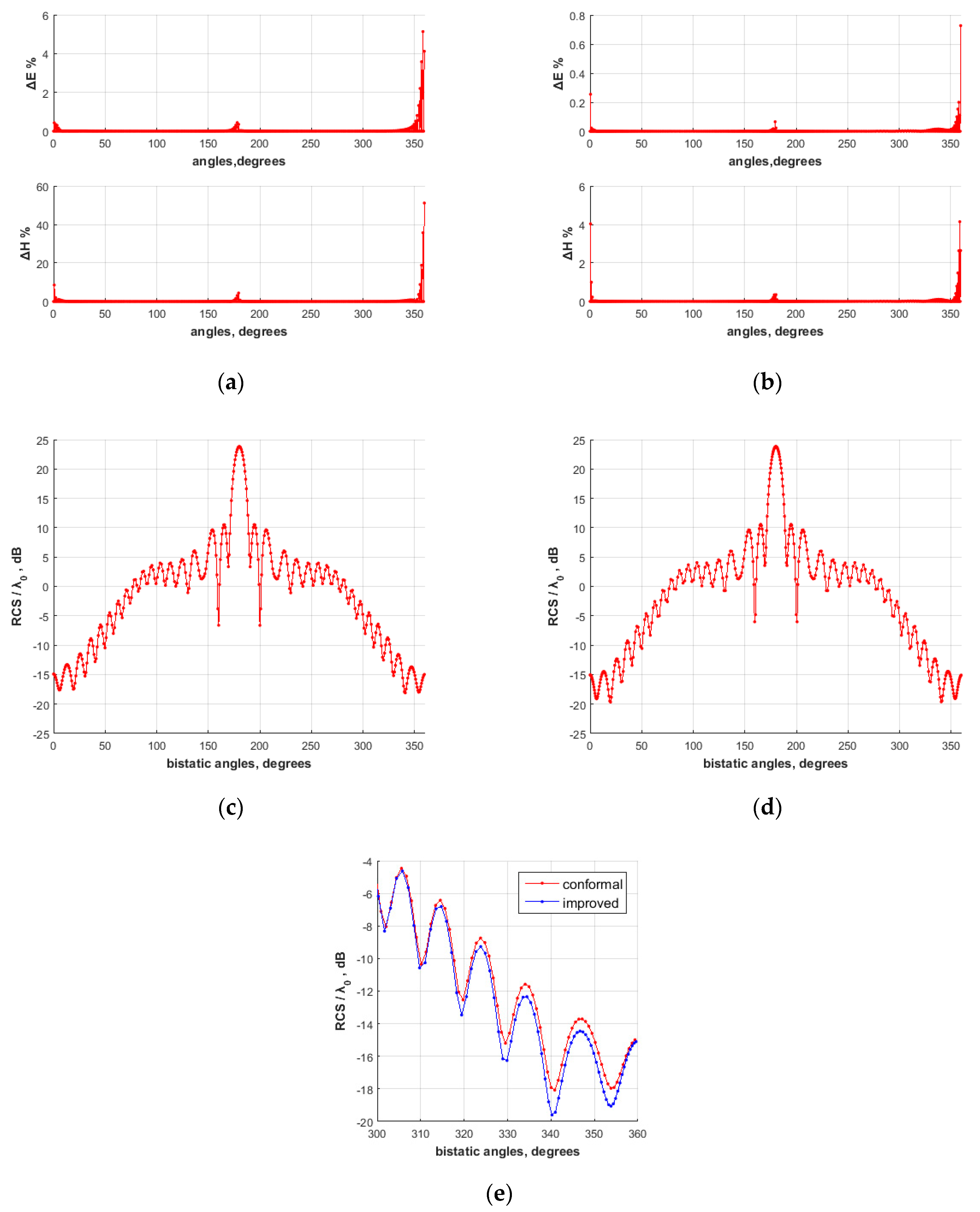
4.3. Lossy Dielectric Scatterer

Finally, a lossy dielectric scatterer of radius $\rho =5\lambda$, arc displacement $d=0.5\rho =2.5\lambda$, relative permittivity ${\epsilon }_r=2.56-0.102 j$, incidence angle ${\phi }_{inc}=0$, inner and outer auxiliary surface radius ${\rho }_{aux in}=\rho -0.5\lambda$ and ${\rho }_{aux out}=\rho +0.75\lambda$, and originally $180$ CPs (hence $180$ inner and $180$ outer ASs) was analyzed. Similar BC tests were conducted for conformal auxiliary surface, once again resulting in a relatively sizable BC error in the neighborhood of the wedge tips (Figure 8a).

The deformation scheme proposed above was also implemented in order to enhance the satisfaction of the boundary condition. The parameters found to produce the lowest BC error, shown in Figure 8b, are as follows: $1/5$ of the inner ASs and $1/8$ of the outer ones were displaced, with a proximity factor set equal to $s=0.75$ and $s=0.65,$ respectively, whereas all of them were included in the densification with $D_{start}=0.80$. Adding extra ASs did not prove to be beneficial and, therefore, was not employed. The maximum $E$ field error at MPs was reduced from $5.13\ast {10}^{-2}$ to $7.27\ast {10}^{-3}$ and the maximum $H$ field error from $5.11\ast {10}^{-1}$ to $4.14\ast {10}^{-2}$.

The computed RCSs, using conformal and deformed auxiliary surface layouts, are depicted in Figure 8c,d, respectively. Although not visually discernible in these plots due to their wide dynamic range, comparing their values at angles close to the scatterer’s wedges exhibits an observable improvement, e.g., from 300° to 360° in Figure 8e, in the azimuthal direction where $\Delta {\rm E}$ and $\Delta H$ obtain their greatest values.

It is worth mentioning that placing ASs too close to the wedge tip is not advisable. Indeed, an AS right on the wedge tip causes severe ill-conditioning of the linear system matrix, whereas proximity factor $\mathrm{s}=0.99$ for both inner and outer ASs lead to inadequate error reduction, namely $3.16\ast {10}^{-2}$ for the $E$ field and $4.43\ast {10}^{-1}$ for the $H$ field.

Furthermore, the symmetry of the geometry should be accompanied by symmetry in the ASs/CPs. As a counterexample, the same lossy dielectric scatterer was experimentally analyzed via unequal CP densities in the two arcs, namely 45 for the upper and 90 for the lower one, leading to excessively high errors and completely wrong RCS plots, as demonstrated in Figure 9.

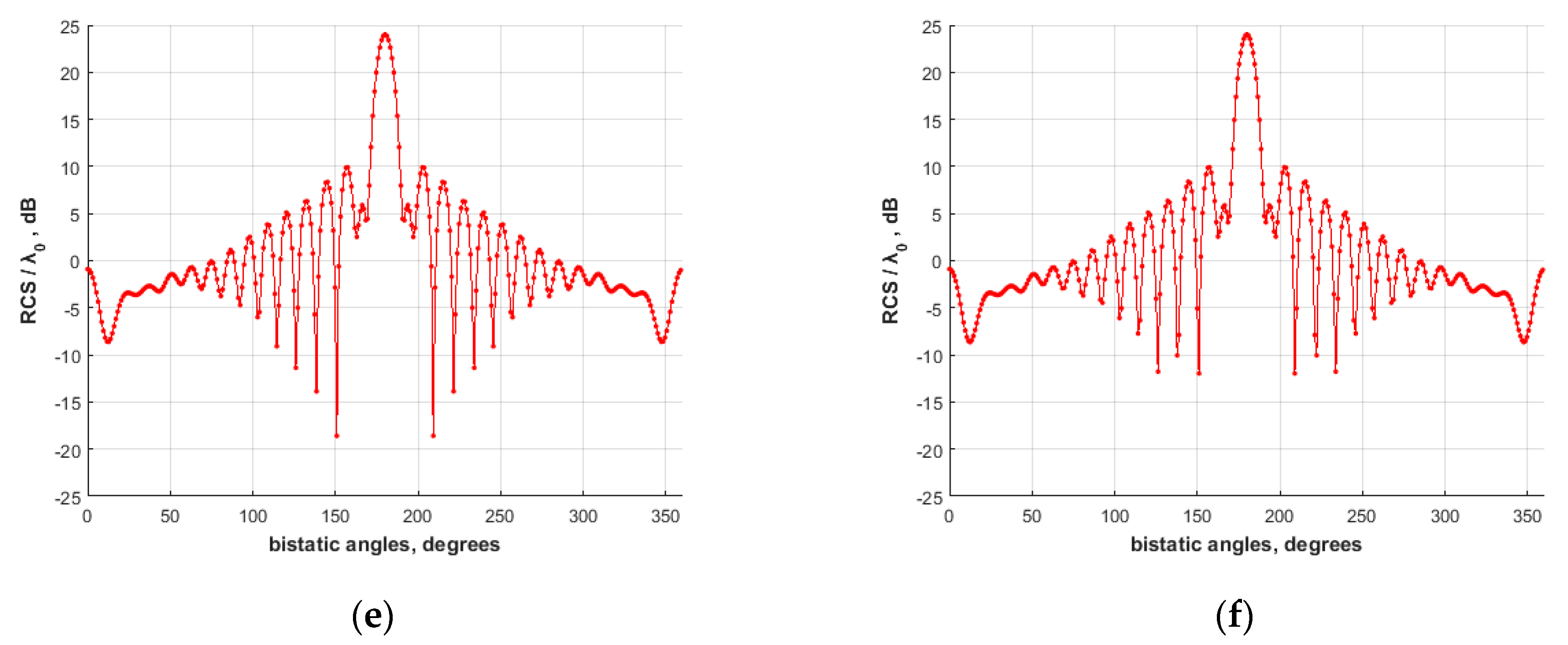
4.4. Investigation of the Solution Behavior for Various Geometry Modifications

To check the robustness of the method described above, several modifications of the geometry were carried out and the respective results were extracted. In all cases below, lossy dielectric material with relative permittivity ${\epsilon }_r=2.56-0.102 j$ is considered, whereas the incidence angle is always ${\phi }_{inc}=0$ with an arc radius of $\rho =3\lambda$.

First, a scatterer that deviates only slightly from a circle was studied, i.e., a layout with small arc displacement $d=0.1\rho =0.3\lambda$, followed by a scatterer with a moderate deviation from a circle, i.e., a layout with mediocre arc displacement $d=0.5\rho =1.5\lambda$, and, finally, a scatterer with a significant distortion with respect to a circle, which, therefore, encompasses sharp wedges, i.e., a layout with large arc displacement $d=0.7\rho =2.1\lambda$. All three geometries and their computed results are depicted in Figure 10, Figure 11 and Figure 12, respectively, while their MAS parameters and the quantified error in the generic boundary condition of the electromagnetic field are presented in

Table 1. Geometry definition, method of auxiliary sources (MAS) parameters, and computed BC error of the electromagnetic field.

Arc displacement d	$0.1\rho =0.3\lambda$	$0.5\rho =1.5\lambda$	$0.7\rho =2.1\lambda$
number of points (ASs, CPs)	160	160	156
displaced inner ASs fraction	1/2	1/5	1/6
displaced outer ASs fraction	1/2	1/8	1/2
inner proximity factor s	0.55	0.75	0.74
outer proximity factor s	0.15	0.65	0.8
densification factor $D_{start}$	0.94	0.8	0.8
maximum $\Delta {{\rm E}}_{bc}$ 1, conformal	$1.89\ast {10}^{-3}$	$1.81\ast {10}^{-2}$	$7.58\ast {10}^{-2}$
maximum $\Delta {{\rm E}}_{bc}$ 1, improved	$5.06\ast {10}^{-4}$	$3.68\ast {10}^{-3}$	$4.09\ast {10}^{-3}$
maximum $\Delta H_{bc}$ 1, conformal	$3.31\ast {10}^{-2}$	$2.64\ast {10}^{-1}$	1.09
maximum $\Delta H_{bc}$ 1, improved	$2.16\ast {10}^{-2}$	$1.96\ast {10}^{-2}$	$5.04\ast {10}^{-2}$

¹ Boundary condition error at midpoints (MPs).

.

As a verification of the broad applicability of the technique, an asymmetric scatterer was also analyzed. Namely, two unequal circular arcs were connected, forming a “sorrowful” eye. The geometry parameters were chosen as follows: radius $\rho =4\lambda$ and arc displacement $d=0.5\rho =2\lambda$ for the upper arc, radius $\rho =5\lambda$ and arc displacement $d=0.5\rho =2.5\lambda$ for the lower arc, originally $160$ CPs (hence $160$ inner and $160$ outer ASs), $1/2.5$ of the inner ASs and $1/4$ of the outer ones were displaced, with proximity factor set equal to $s=0.6$ and $s=0.6,$ respectively. No densification was implemented and no extra ASs were added. The maximum $E$ field error at MPs was reduced from $4.19\ast {10}^{-2}$ to $1.57\ast {10}^{-2}$ and the maximum $H$ field error from $4.36\ast {10}^{-1}$ to $1.38\ast {10}^{-1}$. The results are depicted in Figure 13.

Judging from the outcome of the aforementioned tests, the method proposed herein is very robust, producing reliable results for blunt, acute, or non-symmetric wedges.

5. Discussion

The applicability range of the approach presented above may span various aspects of computational electromagnetics. MAS has already been used in the literature to simulate practical problems, such as scattering by a raindrop [24], although that particular geometry is smooth, without wedges. Wedge treatment, as discussed in this paper, enhances MAS accuracy for applications such as jet engine inlet modeling [25,26,27], where interior blades contain sharp edges, or even further military aircraft scattering simulation, such a stealth design. Moreover, additional possible applications may include automotive modeling, for example, the functionality of a telecommunications antenna in the presence of the vehicle surface. Furthermore, the algorithm may be used in the design of absorbers and cloaking materials [28,29,30], or generally wave manipulation [31] when the geometry layout contains wedges.

Although the numerical results presented were very good, they are limited to wedges formed by intersecting circular arcs only. It is anticipated that analogous techniques would be equally efficient in more general cases (i.e., arbitrarily shaped curved wedges); however, this is yet to be proven in future research. Likewise, other issues to be investigated include TE (Transverse Electric) incidence, the three-dimensional counterpart of this problem, unconventional materials, as well as a robust methodology to choose the optimal deformation parameters.

Furthermore, by studying various geometries, proposing schemes for wedge treatment and obtaining solutions by choosing alternative configurations for the incident wave, material properties, etc., an extensive data set can be acquired. The latter, a combination of input variables and their respective exported results may be used as training data for building a mathematical model via Machine Learning algorithms. Machine Learning, the usage of computational methods in order to produce/”learn” information directly from data without relying on explicit instructions, improves its accuracy and performance proportionally to the amount of available training data. A larger data set is, therefore, required to find hidden patterns or intrinsic properties that can be utilized in the procedure of determining the optimal settings for the scattering problem and, hopefully, automating it.

6. Conclusions

The method of auxiliary sources (MAS) was applied to scattering from a PEC or dielectric cylinder whose geometry contains curved wedges, formed by intersections of circular arcs. The BC error in the vicinity of the wedge tips is significant for standard, conformal auxiliary surfaces due to field singularities. To overcome such a complication, the deformation of the auxiliary sources was proposed. When close to the tips, both inner and outer (when applicable) ASs approached the CPs, and their distribution was also forced to become denser. The BC error was shown to decrease significantly for both the $E$ and the $H$ fields, resulting in more accurate RCS results.