Abstract
Machine learning (ML) algorithmic developments and improvements in Earth and planetary science are expected to bring enormous benefits for areas such as geospatial database construction, automated geological feature reconstruction, and surface dating. In this study, we aim to develop a deep learning (DL) approach to reconstruct the subsurface discontinuities in the subsurface environment of Mars employing the echoes of the Shallow Subsurface Radar (SHARAD), a sounding radar equipped on the Mars Reconnaissance Orbiter (MRO). Although SHARAD has produced highly valuable information about the Martian subsurface, the interpretation of the radar echo of SHARAD is a challenging task considering the vast stocks of datasets and the noisy signal. Therefore, we introduced a 3D subsurface mapping strategy consisting of radar echo pre-processors and a DL algorithm to automatically detect subsurface discontinuities. The developed components the of DL algorithm were synthesized into a subsurface mapping scheme and applied over a few target areas such as mid-latitude lobate debris aprons (LDAs), polar deposits and shallow icy bodies around the Phoenix landing site. The outcomes of the subsurface discontinuity detection scheme were rigorously validated by computing several quality metrics such as accuracy, recall, Jaccard index, etc. In the context of undergoing development and its output, we expect to automatically trace the shapes of Martian subsurface icy structures with further improvements in the DL algorithm.
1. Introduction
Conventional computer algorithms in the geoscience field have been applied mainly for spatial data processing such as stereo analysis of topography, multispectral/hyperspectral analysis, and other remote sensing data compiling. These days, novel approaches combined with contemporary machine learning algorithms are changing the trend of computational geoscience. This is because several ground and remote sensors are producing gigantic geoscientific datasets, which cannot be managed effectively by manual interpretation in terms of precision and speed. The active dynamics of the terrestrial surface provide an optimal ground, where a massive data collection scheme and machine leaning play a significant role. In [1,2], a digital terrain model (DTM) of a wide area with very high resolution was constructed using an advanced stereo machine vision algorithm on the Advanced Land Observing Satellite (ALOS) Panchromatic Remote-Sensing Instrument for stereo mapping (PRISM) and WorldView satellite data respectively.
These trends, such as rapid interepretation of remote sensing data and its automated processing, combined with machine learning, are not limited to only the terrestrial surface. The continuing success of planetary missions for the last few decades has naturally resulted in an enormous number of planetary surface datasets. For instance, the Venus Magellan Mission in 1990 generated more surface image datasets than the total datasets of all previous planetary missions [3]. The 21st century’s planetary missions, such as the Mars Reconnaissance Orbiter (MRO) High-Resolution Imaging Science Experiment (HiRISE) observe with higher spatial resolution than the highest resolution commercial satellite sensors available in Earth’s orbit. [4]. Moreover, coverage of the planetary mission sensor often includes the entire planet’s or satellite’s surface. With the advancement in powerful analytical approaches such as stereo topographic construction [5], the research communities would be benefited enormously by tracing the shape of and changes in the planetary surface. This enables the introduction of more sophisticated study tools such as virtual reality [6,7], numerical modeling [8,9], and surface dating [10,11].
The recent developments in planetary surface research are moving towards the employment of high-end machine learning algorithms for many applications, such as the study of surface chronology based on automated crater counting [12], the classification of geomorphic features [13,14], and the detection of surface changes [15,16].
The clues on planetary geological evolution can be traced by deep and shallow subsurface data, which are extracted either by gravitational measurement [17,18] or shallow surface electromagnetic scanning of orbital ground penetration radar (GPR) [19,20], as well as surface image analysis. Although the information achieved by subsurface sensing of the planetary mission is highly valuable, it should be noted that the interpretation of orbital GPR equipped in a planetary mission is usually more complicated compared to that of the surface imaging. Data collection in track-wise scanning and an absence of reference information for the subsurface strata of planets are some of the highly challenging technical issues. Moreover, the noise level caused by the interactions between the high energy particles in the planetary ionosphere and the long-wavelength of GPR signal [21] brings a significant difficulty in manual interpretation even for experts.
In that context, we aim to develop a machine learning approach for the proper interpretation of in-orbital planetary GPR and reconstruction of shallow subsurface structures in solid planets. We expect that the success of this effort will result in a highly valuable interpretation tool for future planetary missions as well as contemporary GPR sensors (for instance, SHARAD, in Martian orbit, which provides the target data in this study). The current state-of-the-art algorithm [22] uses thresholding on the product of original and co-registered radargram for clutter detection; however, deep learning has not been attempted previously in studies involving discontinuity detection on the Martian subsurface. The DL/ML algorithm for detection of cavities and other objects in the subsurface environment of Earth has been discussed in [23,24].
In terms of paleoclimatic conditions that, crucially, control the existence of a habitable environment, the subsurface strata of Martian topography have been of interest to the scientific community to indicate valuable clues representative of the geological history of Mars. The idea that the footprints of paleoclimatic factors such as precipitation, glaciation, and permafrost can be found in the underground layers of Mars promoted the development of GPR in Martian orbit and led to the deployment of Mars Advanced Radar for Subsurface and Ionosphere Sounding (MARSIS) [19] onboard Mars Express and SHARAD onboard MRO [20], employing a very long electromagnetic wave, which enables the subsurface observation of Mars with significant penetration depth. However, as stated, the interpretation of orbital GPR data, especially over Mars, brought several difficulties. The noise components, such as ionospheric interferences and signal delay, are the primary issues, and must be considered a priority [21,25]. The conversion of time-domain reflectance from subsurface strata into high-dimensional (2D/3D) mapping products requires some assumptions regarding the dielectric permittivity of the underlying materials [26,27]. However, the primary barrier in Martian subsurface research, employing MARSIS and SHARAD, is the methodology to effectively trace the discontinuities from subsurface signals.
Thus, in this study, we focused on the development of an automated algorithm for subsurface discontinuity detection using DL. The detected discontinuities were later utilized for subsurface reconstruction. Considering the high signal-to-noise ratio of SHARAD, we actively employed a deep-learning approach: specifically, a convolutional neural network along with add-on processors for noise reduction, registration between clutter simulation and radargram, and feature extraction.
The constructed algorithms were tested on Martian geomorphic features such as Lobate Debris Apron (LDA), Polar Layered Deposits, and mid-latitude potential ice layers beneath the Phoenix landing site, as described in Section 2. The technical details of the algorithms are stated in Section 3. The result and validation outcomes employing error metrics are presented in Section 4 and Section 5, along with relevant discussion.
2. Background
2.1. Target Area
The first target area to test the discontinuity detection is LDA, which is regarded as an evidence of potential glacial processes [28] or ice debris transport in the ancient Martian environment [29]. It can be characterized as an alluvial-fan-like mass of debris, whose thickness varies between tens to hundreds of meters, that flowed from the mountain slope covered by a glacier or periglacial landforms roughly some million years ago [30]. Despite ongoing arguments regarding the formation mechanism of LDA [28,29,30,31], its geomorphic origin is still unclear. Therefore, the subsurface investigation of LDA employing SHARAD data is expected to provide useful clues for LDA structures. It is worth noting that LDAs are mostly distributed along with the dichotomy of the southern hemisphere and northern lowlands [32]. Therefore, the hypothesis that such highland features were presumably involved with glacial and periglacial processes has gained attention. Thus, the scenario established on this clear evidence is that climate change induced the melting of the glaciers, which allowed sediment flow down through the steep sides of LDAs and produced their fan-shaped features (see Figure 1c,d).
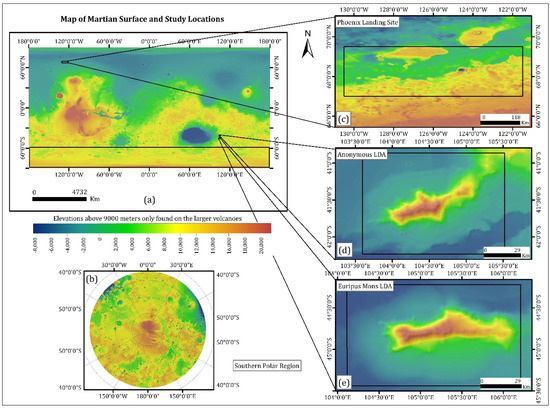
Figure 1.
(a) The map of Martian surface and location of target areas using Mars Orbiter Laser Altimeter (MOLA) digital elevation model (DEM), (b) Southern polar region of Mars (between latitude 55° S and 90° S), (c) Phoenix landing site, (d) Anonymous LDA and (e) Euripus Mons LDA. The same colormap has been used in all maps throughout the paper.
In this study, two sites, i.e., Euripus Mons LDA & an anonymous LDA ( ) close to Euripus Mons, were chosen as the target for SHARAD subsurface feature detection. Based on previous studies, high ice content has already been identified [28] in those target areas. It has also been proposed that at least some of them might be composed of pure ice and, protected from sublimation by a thin debris cover. Recent modeling practices, assuming glacial deformation, have helped to reconstruct some of the inherent structural properties [33]. Moreover, similar modeling studies employing High Resolution Stereo Camera (HRSC) DEM and non-linear flow calculations have shown a potential involvement of dirty ice [34]. Considering the undergoing arguments over these target areas, the identification of subsurface structures by a deep-learning approach may imply essential clues about the origin of LDA and its deposits. Therefore, we choose two LDAs as our first target area to deploy the developed algorithms.
Possibly, the Martian deposits in the southern polar zone represent the most interesting history of the evolution of Mars as a solid planet. Several researchers have proposed that the multiple layers of the southern Martian pole represent a sequence of episodic climate changes [35,36]. Therefore, the Martian south polar layered deposits (SPLD) presumably have involvements with the other footprints of episodic environmental changes, as shown in the potential coastal line of the northern hemisphere [37,38], layered fluvial deposition [39,40] and a recently claimed underground lake [41]. The investigation of the subsurface structure of SPLD was proposed as a prime target of SHARAD and MARSIS campaigns, which revealed expected multiple subsurface layering as described in [42]. However, a high density of discontinuity points in SPLD induced severe difficulties in correctly inferring the detailed structures and locations of subsurface layers. Therefore, we choose a part of the SPLD structure as a test area for the constructed algorithm (Figure 1c). The most challenging target area for the application of the developed algorithms is the Phoenix landing site (Figure 1d), where weak discontinuity caused by potential icy bodies are expected. There have been assumptions that the layer of permafrost is extended to the mid-latitude region of Mars [43], which were later confirmed from the excavation during the Phoenix mission [44]. However, such ice layers close to the surface were not the target of SHARAD and MARSIS. Although SHARAD data analysis on the Phoenix landing site identified the discontinuity (which may be an extension of the ice layer very close to the surface), the discontinuity signals are very weak. Due to this difficulty, the application to SHARAD data over the Phoenix landing site should be tested to prove the robustness of developed algorithms.
2.2. SHARAD Data Products
2.2.1. Introduction to SHARAD Sensors
MARSIS, equipped in Mars Express [19], is the first spaceborne ground penetration RADAR (GPR) to map the upper portions of the crust of a solid planet or satellite with an extremely low-frequency electromagnetic wave. Although the demand to investigate the subsurface liquid and solid water in the footprint of Martian geological evaluation has been actively proposed [45], the observation priority of MARSIS was given on the Martian polar deposits, as they may play a crucial role in atmospheric circulation and evolution [46,47]. In contrast, the SHARAD instrument of the Mars Reconnaissance Orbiter, which was developed through collaboration with the Italian Space Agency and the Jet Propulsion Laboratory, was launched in 2005 and characterized by better vertical resolution but lower penetration capability. Due to such system specifications, the complex substructures of the Martian crust, such as polar deposits, pedestal craters [48], and LDA [28], have been successfully observed employing SHARAD. To understand the system characteristics and operational concepts of SHARAD, see Table 1 and Figure 2, respectively. Since this study aims to extract detailed information on subsurface layering utilizing ML algorithms, SHARAD became the prime data source rather than MARSIS. The potential application to MARSIS data with developed ML algorithms will be explored in a future study.

Table 1.
System characteristics of the SHARAD instrument onboard the MRO satellite.
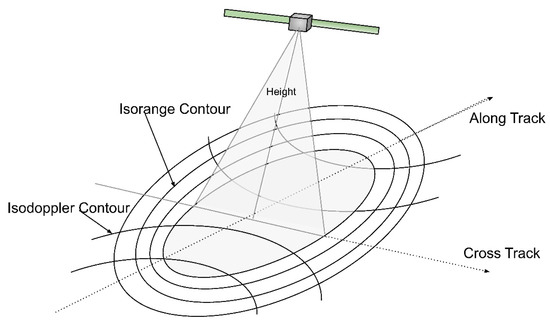
Figure 2.
Operational concept of SHARAD. Ground resolution is determined from the range-to-surface distance in cross-track way and the Doppler shift of the returned signal along the track.
2.2.2. Introduction to SHARAD Data Products
SHARAD tracks on our target areas are identified (see Table 2) using the interfaces established on Planetary Data System (PDS, https://ode.rsl.wustl.edu/mars/indexproductsearch.aspx). The SHARAD tracks are footprints of the signals collected by the sensor. They consist of varying along-track lengths. The data obtained from the PDS comprises of a radargram image file, which is a real-valued image of the radar backscatter power, with the vertical and horizontal axis representing the time delay and along-track samples, respectively. The along-track samples have a spacing of 128 pixels per degree (nearly 460 m) and are associated with latitude–longitude pairs, spacecraft position, planetary radius, and other information contained in a geometry file. The round-trip delay samples in the vertical axis are uniform at 0.0375 microseconds per pixel. The coordinate system is planetocentric with longitude positive toward the east [49]. On-board pre-summing is usually performed with typical pre-summing factors like 4 or 8, to control data volume transmission to Earth [50]. The degree of pre-summing affects only the Doppler frequency bandwidth (in Hz) of the Doppler spectrum. Doppler processing narrows the along-track resolution by filtering out signals that return to the sensor with more than a specified Doppler shift. Echoes from areas perpendicular to the flight path at this band of Doppler components are characterized only by round-trip delay, so reflections from features far from the ground track can appear as apparent subsurface returns and are depicted as clutters [51].

Table 2.
The extent of regions and the SHARAD tracks from respective areas considered for the discontinuity detection using our model for training and testing.
Since the data processing algorithm is not feasible to implement into in-house S/W, the CO-SHARPS [52] processing boutique is employed for radar signal processing. We describe the CO-SHARPS processing parameters in Section 3.1.
3. Processing Method
The complete process, covering radargram preprocessing, discontinuity detection and validation in addition to subsequent analysis is shown in Figure 3. The flowchart can be summarized as follows:
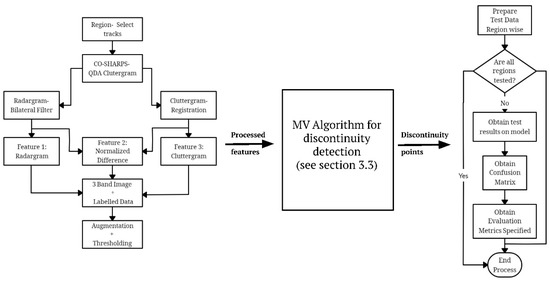
Figure 3.
Flow chart of employed algorithms (see Section 3.3 for the details of ML algorithms).
- The SHARAD tracks for the target regions are identified by inspecting track locations/coverage.
- The processed and raw radargrams are obtained using the CO-SHARPS processing boutique.
- A bilateral filtering method is applied to the radargram to reduce the backscatter noise.
- The clutter-gram is co-registered with raw radargram using a Fourier-based phase correlation process.
- The labelled data is prepared by manually detecting discontinuities in the radargram.
- New features such as Euclidean norm, entropy, etc. are prepared for training the CNN model.
- The model is validated using various quality metrics. The discontinuity points are accumulated and processed into a subsurface discontinuity plane reconstruction algorithm.
A detailed description of the methodology is provided in following sub-sections.
3.1. Pre-Processing
After identifying the product IDs of tracks over proposed target areas, the CO-SHARPS processing boutique was employed for the purpose of clutter simulation. The clutter simulator available in the CO-SHARPS boutique is based on the JPL (Jet Propulsion Laboratory, Caltech) focussed processor and comprises products called QDA clutter-grams [53].
The processing parameters of the CO-SHARPS boutique are decided as follows. The QDA products have a fixed aperture (frames) of 4096. The pre-sum value, which varies the bandwidth or frame interval, is set as 16. A Hann window is selected to reduce sidelobes in the azimuth compression. The QDA products in this study are simulated using MOLA DEM with the ellipsoid as the equipotential reference surface, i.e., aeroid. The multi-look bandwidth is fixed to 15 Hz for the QDA products. The simulator also offers the depth-corrected radargram if a dielectric constant is specified during QDA processing. It is worth noting that the dielectric constant in the clutter simulator is assumed to be uniform over the entire subsurface for simplified processing (, in this study). The dielectric constant varies in both latitudinal and longitudinal direction according to the subsurface material properties and is an area of ongoing research [26,27]. However, a dielectric constant value of 3.15 has been used as a suitable approximation in past studies of the Euripus Mons region [54,55].
It is optional to adopt either the depth-converted radargram or the time-domain radargram. The process of depth conversion results in under-sampling of the signals and, hence, would lead to loss of useful information, potentially indicative of desired clutter. In this study, the time-domain radargram is utilized as it does not suppress the original signal. The selection of dielectric constant does not affect the DL algorithm in this study, as the model has been trained on time-domain radargram, and the depth conversion has been employed only for 3D-subsurface reconstruction.
Noise-reduction techniques are introduced to reduce the backscatter or background speckles in radargram images. It supports the identification of discontinuities in the data as the signal-to-noise ratio in the original radargram is not adequate. Several filtering methods such as log-Gabor filtering, block-matching, and wavelet shrinkage denoising, etc. [56] were applied for suppressing the backscatter noise. Finally, bilateral filtering was employed (refer Figure 4) as it provides a balanced outcome between the preservation of the original signals and the noise levels.
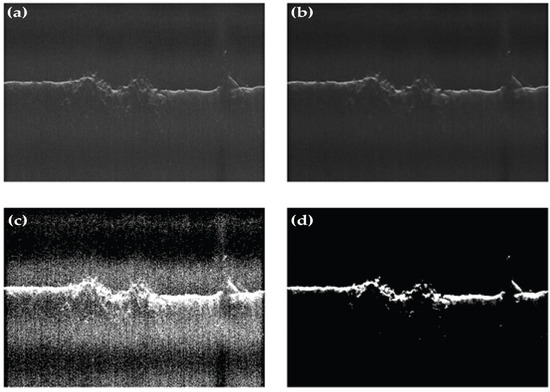
Figure 4.
A noise filtering result in magnified radargram over Euripus Mons. Original radargram (a) and noise-filtered radargram after bilateral filtering (b). Results of background removal from original image (c) and background removal from bilateral filtered image (d).
3.2. Feature Space Construction
The clutter-simulated radargram is co-registered with the original radargram to remove vertical and horizontal offsets. Due to the nature of radargram signals, translation, rotation, and scale-invariant image registration are essential. Therefore, we employed a fast Fourier transform (FFT)-based registration method, which utilizes frequency domain analysis to find matching signals [57]. The performance of the FFT-based registration method is demonstrated in Figure 5.

Figure 5.
Original overlap between the radargram and clutter-gram (horizontal and vertical offset present) (a), overlap after registration of clutter-gram with radargram (b).
The labelled discontinuity is prepared manually for approximately twenty tracks from different regions for the training components of the machine learning algorithm (see Figure 6) The characteristics of “subsurface discontinuity” do not vary significantly for different regions, as per our experiences. Therefore, our deep learning model does not employ regionally selected training vectors. The construction of relevant feature spaces is highly essential for the performance of the ML algorithm. Several features are generated and tested with approaches such as normalized difference, mean, Gabor filter and image entropy, etc. Finally, a three-channel feature space is constructed using the radargram, registered clutter-gram, and the normalized difference of the radargram and clutter-gram (refer to Figure 6). In order to enhance the robustness of the model and increase the number of training samples, an additional training data set was created using varied orientation and affine transforms on the original dataset. The augmentation was performed by rotating the images through a range of −5 to +5 degrees, mirror/left-right flip, resampling and image zooming. The overall training dataset consisted of 2160 images of size 256 × 256.
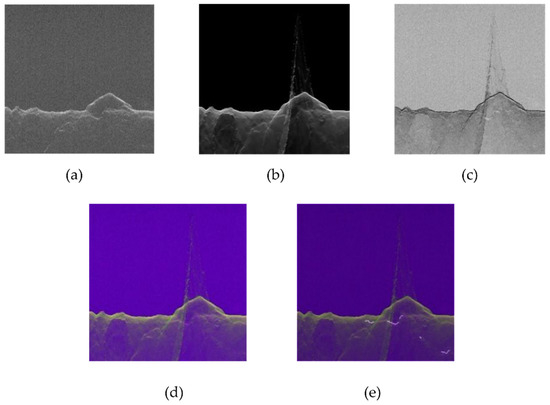
Figure 6.
(a) Original radargram; (b) clutter-gram (registered), (c) normalized difference, (d) 3-Band composite image for training (generated from images (a–c,e) labelled discontinuity superimposed on training image.
3.3. Machine Vision Algorithm
The convolutional neural network has been used for training of the model. The trained network can be divided into two parts (i.e., the down-sampling or contracting path and the up-sampling or expanding path) [58]. The architecture of the CNN model used in this research can be represented by Figure 7.
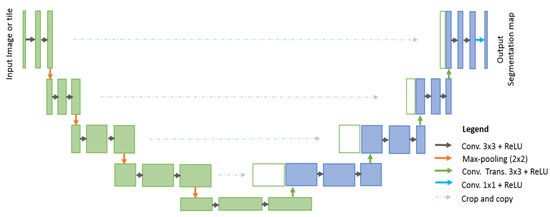
Figure 7.
CNN architecture uses convolutional encoding and decoding units. It takes an image as an input and produces the segmentation as an output.
The down-sampling or contracting path is composed of blocks, which are comprised of 3 × 3 Convolution layer and a 2 × 2 Max Pooling layer with an activation function at each layer [50]. The input layer is normalized by adjusting and scaling the activations or batch normalization. The batch normalization improves the speed, performance, and stability of neural networks [59]. The trained deep learning model in this research draws its strength from making normalization a part of the model architecture and performing the normalization for each training mini batch. The network uses max-pooling layers, which reduce the height and width information while keeping the number of channels of the input matrix constant. These layers are intended to increase the resolution of the output. Pooling layers can work with different methods, including maximum, average, or median layers. The contracting path captures the context of the input image in order to perform segmentation. This coarse contextual information is transferred to the expanding path using skip connections. The expanding path is composed of the block with 3 × 3 convolution layers, deconvolution layers and a concatenation operation on the cropped feature map from the contracting path. The purpose of expanding the path is to enable precise localization. The workflow for training and testing the image dataset is shown in Figure 8.
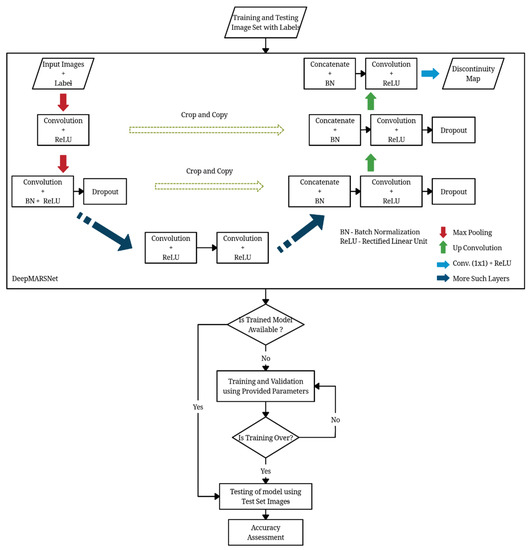
Figure 8.
Flowchart showing CNN Model training and testing Procedure.
3.4. Evaluation Metric
Several evaluation metrics such as accuracy, precision, F-score, etc. have been used to evaluate the performance of the model. The accuracy depicts the ratio of the correctly classified samples to the total number of samples. Precision helps to evaluate how well the model classifies the relevant class with respect to the total number of predicted instances of that class. A similar metric called “specificity” is also used.
Recall (also known as sensitivity) denotes the fraction of correctly predicted relevant instances (class y = 1) in the actual number of relevant instances. This gives us a measure of how accurately the model predicts with respect to the actual instances of that class.
These two terms, i.e., precision and recall, give a good estimate of the model. The ideal value for both is close to 1. To combine and evaluate these together, we use the metric F-score or F-measure. A high F-score is an indication of a good model.
The area under curve (AUC) of the receiver operating characteristics (ROC) curve is a statistical value that denotes the ability of a classifier to perform as its discrimination threshold (probability) is varied. An ideal AUC value is close to 1.
The Jaccard Index or IoU (Intersection over Union) is a metric is used to measure the similarities or overlap between predicted and actual sample sets A and B, respectively. It is defined as the cardinality or size of the intersection divided by the size of the union of the two sets. A value close to 1 is considered to be ideal, i.e., when both the sets are equal.
4. Results and Discussion
The training was performed on the tracks over Euripus Mons, which also contained the portion beyond the geographic extent of Euripus mons. Several new tracks, with almost no similarity to the other tracks in the region, were processed for testing. The results obtained are shown in Figure 9. Table 3 and Table 4 show the confusion matrix and performance metrics over the respective target areas. The testing performed on the Euripus Mons tracks illustrate the best overall results as expected. It is important to note that a substantial proportion of the total labelled discontinuities belonged to the Euripus Mons region when compared to the Anonymous LDA and Polar region (refer to columns 1 and 3 of Table 3). The testing on the Anonymous LDA region also yielded fair results considering the true class size ratio. The model was able to predict 22 of the total 81 discontinuity pixels in the area. A few tracks in the polar region were also processed for testing. It can be inferred from Table 3 that there was no true class in the actual data for this region. However, the model predicted a small number of false positives. Despite the vast size of the Polar region, not many tracks which cover the Euripus Mons region also pass through it (refer Table 2).
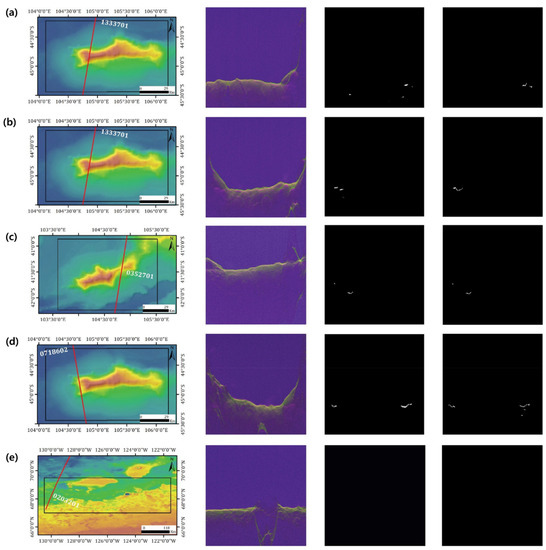
Figure 9.
SHARAD tracks in Euripus Mons (a–d) and Phoenix landing site (e). Target locations (1st column), testing images (2nd column), results of the model (3rd column) and manually labelled data (4th column) are presented.

Table 3.
The distribution of test data, and confusion matrices for each region.

Table 4.
The metrics and statistics for each region.
The model, when tested on tracks from the Phoenix landing site, did not predict any pixel as discontinuity even though there were 67 manually detected true class pixels. While preparing the labelled dataset for this region, some tracks were omitted, as there was no/very little discontinuity in the region. Since the Phoenix landing site does not contain significant topographical variation, the discontinuities are not considerable. The test results were not very accurate, as expected in this region, indicating that geographically more distributed labelled data is required for training, to enhance the robustness of the model. However, it is important to note that the manually detected labelled data had only 1 of 3000 pixels as discontinuity pixels.
Moreover, the Phoenix landing site lies in the northern lowland of Mars, and the training dataset belongs to the southern hemisphere, which has a different geological origin. Due to significant variation in the subsurface strata of Euripus Mons, a southern hemispheric highland, and the Phoenix landing site, a primary northern lowland of Mars, the training may not be spatially robust. To overcome this problem, and improve the model accuracy, more training data must be prepared covering a wide array of the geographical locations of Mars. The model was trained for 20 epochs with a batch size of 16, making it approximately 135 iterations. The epoch refers to a complete cycle of training, i.e., one forward pass and one backward pass of all the training samples. The training and validation loss as well as accuracy plotted at each epoch are shown in Figure 10. The training loss is initially high and decreases monotonically in subsequent epochs, demonstrating that the model did not present a bias (or no-skill) and was trained adequately. The accuracy increases with the number of epochs. Although some undulations occur in training accuracy, however, they may be attributed to a random sampling of training data in each epoch.
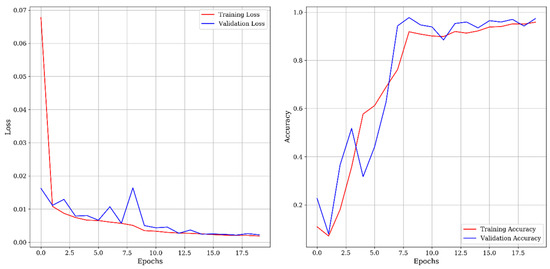
Figure 10.
Epochs vs. loss for training and validation (left); epochs vs. accuracy for training and validation (right).
It is essential to assess the outcomes of the model in the geological context, as well as in terms of quantitative metrics for further scientific applications. The efforts towards geological applications were accomplished using discontinuity plane reconstruction, together with contextual interpretation.
After collecting all discontinuity points from the sublayers, the points were clustered using the Balanced iterative reducing and clustering using hierarchies (BIRCH) algorithm [60] into a few initial groups according to their spatial distributions. Kriging was applied to extract interpolated sublayer planes and the Euclidian distances between discontinuity points and interpolated planes. The best fit underground sublayers were extracted using an iterative procedure to attain an optimal number of clusters and distances. In this research, manual intervention was required to accomplish this task; however, the development of an automated/semi-automated routine is under development. The above procedure to reconstruct the underlying discontinuity planes revealed the gridded subsurface structures of Euripus Mons and anonymous LDAs, as shown in Figure 11. We discovered three clear discontinuity sublayers underneath the Euripus Mons LDA, represented by the yellow, green, and blue face.
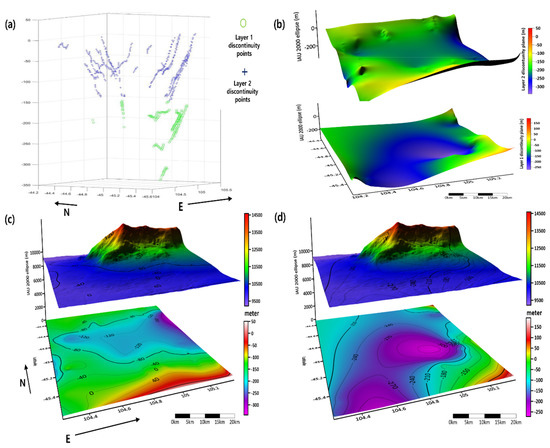
Figure 11.
Euripus Mons LDA subsurface mapping result. (a) The distribution of discontinuity points with classified layer numbers, (b) 3D perspective view of two discontinuity planes gridded by kriging; (c) the structure of layer 1 overlaid on Euripus Mons DEM; (d) the structure of layer 2 overlaid on Euripus Mons DEM. Note that the discontinuity planes were rotated for the best view.
We also identified two discontinuity layers under anonymous LDA, as shown in Figure 11, and ascertained different morphologies in northern and southern aprons. We propose that such different morphologies of the two subsurface layers imply a certain temporal/contextual disconnection between paleoclimate events and progressive developments during intermediate periods, perhaps involving sublimation. This is a significant clue towards identifying the morphological evolution of LDAs. We did not observe three discontinuity layers, which follow the shape of surface topography, as claimed in a previous study [61]. This may be due to sparsity in the reconstructed discontinuity points. Moreover, the integration of several studies [25,26] for the estimation of dielectric constants will be considered for future discontinuity layer reconstruction algorithms. The depth of discontinuity layers will be adjusted to precisely depict subsurface structures using varying dielectric constants.
Finally, the assessment of our automated discontinuity detection approach guarantees sufficient accuracy to replace manual detection, given that proper training and pre-processing are preceded. Moreover, the reconstructed discontinuity planes over LDAs and the automated MV algorithms on SHARAD signals can provide meaningful geological information. The latter implies the potential of our method to mine significant clues regarding Martian evolution.
5. Conclusions and Future Work
Although the data analysis of orbital radars such as MARSIS and SHARAD are producing many compelling clues about Martian surface and climate evolution, their interpretation still depends on 1D profiling of signals, which are created manually by experienced interpreters. This manual profiling has reduced the potential for synthesized use of SHARAD and MARSIS data sets with other spatial information to extract scientific clues about the Martian surface and subsurface. Therefore, we have developed an automated 3D subsurface mapping procedure that enables us to automatically define surface discontinuity and reconstruct subsurface layers from SHARAD signals using ML/DL. We have applied the established scheme over several target areas such as LDAs in the Euripus Mons region, high altitude potential permafrost, and polar deposit. The developed method automatically identified several discontinuity layers with adequate accuracy. The detected discontinuity points were utilized to reconstruct subsurface discontinuity planes.
In comparison to the precedent studies aimed at bringing partially automated improvement for the analysis of SHARAD and MARSIS data sets such as point detection, auto registration, filtering, and reconstruction, our method depicts further potential to be developed as a comprehensive SHARAD and MARSIS procedure with improved accuracy. We are planning to improve the established algorithms as follows.
- (a)
- Employment of HRSC & Context Camera (CTX) stereo DTMs for better clutter simulation.
- (b)
- Automated subsurface layer clustering based on more robust approaches, such as support vector machine (SVM) algorithms.
- (c)
- ML algorithm improvement, by preparing more labelled data from spatially varied regions to increase the robustness of the model.
We will publish these improvements in the public domain after the fully stabilized components are integrated with the MARSIS/SHARAD signal processor. However, for robust training, SHARAD tracks and discontinuity labels from several other areas will be required based on user feedback for the published software. The case will not be limited only to Mars, and may also apply to future planetary subsurface radars such as Radar for Europa Assessment and Sounding: Ocean to Near-surface (REASON) [62].
Author Contributions
V.G. was charged of major data processing and writing. S.K.G. developed ML algorithms and wrote corresponding text. J.K. designed the overall strategy and structured the draft. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors appreciate a number of professional supports and technical advices from CO-SHARPS administrators. S.K.G. and V.G. thank Dericks P. Shukla, IIT Mandi for kindly providing computational facilities and financial support to V.G.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Tadono, T.; Ishida, H.; Oda, F.; Naito, S.; Minakawa, K.; Iwamoto, H. Precise Global DEM Generation by ALOS PRISM. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, II-4, 71–76. [Google Scholar] [CrossRef]
- Jawak, S.D.; Luis, A.J. Applications of WorldView-2 satellite data for Extraction of Polar Spatial Information and DEM of Larsemann Hills, East Antarctica. In Proceedings of the International Conference on Fuzzy Systems and Neural Computing, Hong Kong, China, 20–21 February 2011. [Google Scholar]
- Saunders, R.S.; Pettengill, G.H.; Arvidson, R.E.; Sjogren, W.L.; Johnson, W.T.K.; Pieri, L. The Magellan Venus Radar Mapping Mission. J. Geophys. Res. 1990, 95, 8339–8355. [Google Scholar] [CrossRef]
- Zurek, R.W.; Smrekar, S.E. An overview of the Mars Reconnaissance Orbiter (MRO) science mission. J. Geophys. Res. E Planets 2007, 112, E5. [Google Scholar] [CrossRef]
- Heipke, C.; Oberst, J.; Albertz, J.; Attwenger, M.; Dorninger, P.; Dorrer, E.; Ewe, M.; Gehrke, S.; Gwinner, K.; Hirschmüller, H.; et al. Evaluating planetary digital terrain models-The HRSC DTM test. Planet. Space Sci. 2007, 55, 2173–2191. [Google Scholar] [CrossRef]
- Höllerer, T.; Feiner, S.; Terauchi, T.; Rashid, G.; Hallaway, D. Exploring MARS: Developing indoor and outdoor user interfaces to a mobile augmented reality system. Comput. Graph. 1999, 23, 779–785. [Google Scholar] [CrossRef]
- Kim, J.R.; Lin, S.Y.; Hong, J.W.; Kim, Y.H.; Park, C.K. Implementation of Martian virtual reality environment using very high-resolution stereo topographic data. Comput. Geosci. 2012, 44, 184–195. [Google Scholar] [CrossRef]
- McIntyre, N.; Warner, N.H.; Gupta, S.; Kim, J.R.; Muller, J.P. Hydraulic modeling of a distributary channel of Athabasca Valles, Mars, using a high-resolution digital terrain model. J. Geophys. Res. E Planets 2012, 117, E3. [Google Scholar] [CrossRef]
- Kim, J.R.; Schumann, G.; Neal, J.C.; Lin, S.Y. Megaflood analysis through channel networks of the Athabasca Valles, Mars based on multi-resolution stereo DTMs and 2D hydrodynamic modeling. Planet. Space Sci. 2014, 99, 55–69. [Google Scholar] [CrossRef]
- Michael, G.G.; Neukum, G. Planetary surface dating from crater size-frequency distribution measurements: Partial resurfacing events and statistical age uncertainty. Earth Planet. Sci. Lett. 2010, 294, 223–229. [Google Scholar] [CrossRef]
- Robbins, S.J.; Hynek, B.M. The secondary crater population of Mars. Earth Planet. Sci. Lett. 2014, 400, 66–76. [Google Scholar] [CrossRef]
- Jung, R.K.; Muller, J.P.; Van Gasselt, S.; Morley, J.G.; Neukum, G. Automated crater detection, a new tool for Mars cartography and chronology. Photogramm. Eng. Remote Sens. 2005, 71, 1205–1217. [Google Scholar]
- Palafox, L.F.; Hamilton, C.W.; Scheidt, S.P.; Alvarez, A.M. Automated detection of geological landforms on Mars using Convolutional Neural Networks. Comput. Geosci. 2017, 101, 48–56. [Google Scholar] [CrossRef] [PubMed]
- Buscombe, D.; Ritchie, A.C. Landscape classification with deep neural networks. Geoscience 2018, 8, 244. [Google Scholar] [CrossRef]
- Castano, A.; Fukunaga, A.; Biesiadecki, J.; Neakrase, L.; Whelley, P.; Greeley, R.; Lemmon, M.; Castano, R.; Chien, S. Automatic detection of dust devils and clouds on Mars. Mach. Vis. Appl. 2008, 19, 467–482. [Google Scholar] [CrossRef]
- Gor, V.; Castano, R.; Manduchi, R.; Anderson, R.C.; Mjolsness, E. Autonomous rock detection for mars terrain. In Proceedings of the AIAA Space 2001 Conference and Exposition, Williamsburg, VA, USA, 23–26 July 2001. [Google Scholar]
- Williams, J.G.; Konopliv, A.S.; Boggs, D.H.; Park, R.S.; Yuan, D.N.; Lemoine, F.G.; Goossens, S.; Mazarico, E.; Nimmo, F.; Weber, R.C.; et al. Lunar interior properties from the GRAIL mission. J. Geophys. Res. Planets 2014, 119, 1546–1578. [Google Scholar] [CrossRef]
- Park, R.S.; Konopliv, A.S.; Bills, B.G.; Rambaux, N.; Castillo-Rogez, J.C.; Raymond, C.A.; Vaughan, A.T.; Ermakov, A.I.; Zuber, M.T.; Fu, R.R.; et al. A partially differentiated interior for (1) Ceres deduced from its gravity field and shape. Nature 2016, 537, 515–517. [Google Scholar] [CrossRef]
- Orosei, R.; Jordan, R.L.; Morgan, D.D.; Cartacci, M.; Cicchetti, A.; Duru, F.; Gurnett, D.A.; Heggy, E.; Kirchner, D.L.; Noschese, R.; et al. Mars Advanced Radar for Subsurface and Ionospheric Sounding (MARSIS) after nine years of operation: A summary. Planet. Space Sci. 2015, 112, 98–114. [Google Scholar] [CrossRef]
- Seu, R.; Phillips, R.J.; Biccari, D.; Orosei, R.; Masdea, A.; Picardi, G.; Safaeinili, A.; Campbell, B.A.; Plaut, J.J.; Marinangeli, L.; et al. SHARAD sounding radar on the Mars Reconnaissance Orbiter. J. Geophys. Res. E Planets 2007, 112, E5. [Google Scholar] [CrossRef]
- Campbell, B.A.; Putzig, N.E.; Foss, F.J.; Phillips, R.J. SHARAD signal attenuation and delay offsets due to the Martian ionosphere. IEEE Geosci. Remote Sens. Lett. 2013, 11, 632–635. [Google Scholar] [CrossRef]
- Ferro, A.; Pascal, A.; Bruzzone, L. A novel technique for the automatic detection of surface clutter returns in radar sounder data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3037–3055. [Google Scholar] [CrossRef]
- Kang, M.S.; Kim, N.; Lee, J.J.; An, Y.K. Deep learning-based automated underground cavity detection using three-dimensional ground penetrating radar. Struct. Heal. Monit. 2020, 19, 173–185. [Google Scholar] [CrossRef]
- Travassos, X.L.; Avila, S.L.; Ida, N. Artificial Neural Networks and Machine Learning techniques applied to Ground Penetrating Radar: A review. Appl. Comput. Inform. 2018. [CrossRef]
- Campbell, B.A.; Watters, T.R. Phase compensation of MARSIS subsurface sounding data and estimation of ionospheric properties: New insights from SHARAD results. J. Geophys. Res. Planets 2016, 121, 180–193. [Google Scholar] [CrossRef]
- Alberti, G.; Castaldo, L.; Orosei, R.; Frigeri, A.; Cirillo, G. Permittivity estimation over Mars by using SHARAD data: The Cerberus Palus area. J. Geophys. Res. E Planets 2012, 117, E9. [Google Scholar] [CrossRef]
- Castaldo, L.; Mège, D.; Gurgurewicz, J.; Orosei, R.; Alberti, G. Global permittivity mapping of the Martian surface from SHARAD. Earth Planet. Sci. Lett. 2017, 462, 55–65. [Google Scholar] [CrossRef]
- Holt, J.W.; Safaeinili, A.; Plaut, J.J.; Head, J.W.; Phillips, R.J.; Seu, R.; Kempf, S.D.; Choudhary, P.; Young, D.A.; Putzig, N.E.; et al. Radar sounding evidence for buried glaciers in the southern mid-latitudes of Mars. Science 2008, 322, 1235–1238. [Google Scholar] [CrossRef]
- Hauber, E.; van Gasselt, S.; Chapman, M.G.; Neukum, G. Geomorphic evidence for former lobate debris aprons at low latitudes on Mars: Indicators of the Martian paleoclimate. J. Geophys. Res. E Planets 2008, 113, E2. [Google Scholar] [CrossRef]
- van Gasselt, S.; Kim, J.; Baik, H.S. Euripus Mons-Landform Evolution and Climate Constraints in Promethei Terra. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 17–22 April 2016. [Google Scholar]
- Plaut, J.J.; Safaeinili, A.; Holt, J.W.; Phillips, R.J.; Head, J.W.; Seu, R.; Putzig, N.E.; Frigeri, A. Radar evidence for ice in lobate debris aprons in the mid-northern latitudes of Mars. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- van Gasselt, S.; Hauber, E.; Neukum, G. Cold-climate modification of Martian landscapes: A case study of a spatulate debris landform in the Hellas Montes Region, Mars. J. Geophys. Res. E Planets 2007, 112, E9. [Google Scholar] [CrossRef]
- Karlsson, N.B.; Schmidt, L.S.; Hvidberg, C.S. Volume of Martian midlatitude glaciers from radar observations and ice flow modeling. Geophys. Res. Lett. 2015, 42, 2627–2633. [Google Scholar] [CrossRef]
- Schmidt, L.S.; Hvidberg, C.S.; Kim, J.R.; Karlsson, N.B. Non-linear flow modelling of a Martian Lobate Debris Apron. J. Glaciol. 2019, 65, 889–899. [Google Scholar] [CrossRef]
- Cutts, J.A.; Lewis, B.H. Models of climate cycles recorded in Martian polar layered deposits. Icarus 1982, 50, 216–244. [Google Scholar] [CrossRef]
- Hvidberg, C.S.; Fishbaugh, K.E.; Winstrup, M.; Svensson, A.; Byrne, S.; Herkenhoff, K.E. Reading the climate record of the martian polar layered deposits. Icarus 2012, 221, 405–419. [Google Scholar] [CrossRef]
- Fairén, A.G.; Dohm, J.M.; Baker, V.R.; de Pablo, M.A.; Ruiz, J.; Ferris, J.C.; Anderson, R.C. Episodic flood inundations of the northern plains of Mars. Icarus 2003, 165, 53–67. [Google Scholar] [CrossRef]
- Perron, J.T.; Mitrovica, J.X.; Manga, M.; Matsuyama, I.; Richards, M.A. Evidence for an ancient martian ocean in the topography of deformed shorelines. Nature 2007, 447, 840–843. [Google Scholar] [CrossRef]
- Pondrelli, M.; Rossi, A.P.; Marinangeli, L.; Hauber, E.; Gwinner, K.; Baliva, A.; Di Lorenzo, S. Evolution and depositional environments of the Eberswalde fan delta, Mars. Icarus 2008, 197, 429–451. [Google Scholar] [CrossRef]
- Levrard, B.; Forget, F.; Montmessin, F.; Laskar, J. Recent ice-rich deposits formed at high latitudes on Mars by sublimation of unstable equatorial ice during low obliquity. Nature 2004, 431, 1072–1075. [Google Scholar] [CrossRef]
- Orosei, R.; Lauro, S.E.; Pettinelli, E.; Cicchetti, A.; Coradini, M.; Cosciotti, B.; Di Paolo, F.; Flamini, E.; Mattei, E.; Pajola, M.; et al. Radar evidence of subglacial liquid water on Mars. Science 2018, 361, 490–493. [Google Scholar] [CrossRef]
- Plaut, J.J.; Picardi, G.; Safaeinili, A.; Ivanov, A.B.; Milkovich, S.M.; Cicchetti, A.; Kofman, W.; Mouginot, J.; Farrell, W.M.; Phillips, R.J.; et al. Subsurface radar sounding of the south polar layered deposits of Mars. Science 2007, 316, 92–95. [Google Scholar] [CrossRef]
- Putzig, N.E.; Phillips, R.J.; Campbell, B.A.; Mellon, M.T.; Holt, J.W.; Brothers, T.C. SHARAD soundings and surface roughness at past, present, and proposed landing sites on Mars: Reflections at Phoenix may be attributable to deep ground ice. J. Geophys. Res. E Planets 2014, 119, 1936–1949. [Google Scholar] [CrossRef]
- Cull, S.; Arvidson, R.E.; Mellon, M.T.; Skemer, P.; Shaw, A.; Morris, R.V. Compositions of subsurface ices at the mars phoenix landing site. Geophys. Res. Lett. 2010, 37, 24. [Google Scholar] [CrossRef]
- Carr, M.H. Water on Mars; Oxford University Press: New York, NY, USA, 1987; ISBN 9780195099386. [Google Scholar]
- Picardi, G.; Plaut, J.J.; Biccari, D.; Bombaci, O.; Calabrese, D.; Cartacci, M.; Cicchetti, A.; Clifford, S.M.; Edenhofer, P.; Farrell, W.M.; et al. Planetary science: Radar soundings of the subsurface of Mars. Science 2005, 310, 1925–1928. [Google Scholar] [CrossRef] [PubMed]
- Zuber, M.T.; Phillips, R.J.; Andrews-Hanna, J.C.; Asmar, S.W.; Konopliv, A.S.; Lemoine, F.G.; Plaut, J.J.; Smith, D.E.; Smrekar, S.E. Density of mars’ south polar layered deposits. Science 2007, 317, 1718–1719. [Google Scholar] [CrossRef] [PubMed]
- Nunes, D.C.; Smrekar, S.E.; Fisher, B.; Plaut, J.J.; Holt, J.W.; Head, J.W.; Kadish, S.J.; Phillips, R.J. Shallow Radar (SHARAD), pedestal craters, and the lost Martian layers: Initial assessments. J. Geophys. Res. E Planets 2011, 116, E04006. [Google Scholar] [CrossRef]
- Campbell, B.; Phillips, R. Mars Reconnaissance Orbiter Shallow Radar Radargram Data, MRO-M-SHARAD-5-RADARGRAM-V1.0; NASA: Washington, DC, USA, 2014. [Google Scholar]
- Campbell, B. U.S. Shallow Radar (SHARAD) Data Product Description for the Planetary Data System; Smithsonian Institute: Washington, DC, USA, 2014; Available online: https://pds-geosciences.wustl.edu/mro/mro-m-sharad-5-radargram-v1/mrosh_2001/document/rgram_processing.pdf (accessed on 2 January 2020).
- Holt, J.W.; Kempf, S.D.; Young, D.A. Clutter and Cross-Track Slopes: Interpreting Airborne and Orbital Radar-Sounding Data in Glacial Environments; University of Texas at Austin: Austin, TA, USA, 2013; Available online: https://www.cresis.ku.edu/sites/default/files/NewsEvents/Meetings/Presentations/Holt.pdf (accessed on 2 January 2020).
- Putzig, N.E.; Phillips, R.J.; Campbell, B.A.; Plaut, J.J.; Holt, J.W.; Bernardini, F.; Egan, A.F.; Smith, I.B. Custom SHARAD processing via the CO-SHARPS Processing Boutique. In Proceedings of the 47th Lunar and Planetary Science Conference, The Woodlands, TA, USA, 21–25 March 2016; p. 3010. Available online: https://www.hou.usra.edu/meetings/lpsc2016/pdf/3010.pdf (accessed on 2 January 2020).
- Putzig, N.E. CPB: The CO-SHARPS Processing Boutique. In Proceedings of the SHARAD/MARSIS Data Users’ Workshop; Southwest Research Institute: San Antonio, TA, USA, 2014. Available online: https://pds-geosciences.wustl.edu/workshops/SHARAD_MARSIS_Mar14/Putzig_CO-SHARPS-Processing-Boutique.pdf (accessed on 2 January 2020).
- Parsons, R.; Holt, J. Constraints on the formation and properties of a Martian lobate debris apron: Insights from high-resolution topography, SHARAD radar data, and a numerical ice flow model. J. Geophys. Res. E Planets 2016, 121, 432–453. [Google Scholar] [CrossRef]
- Whitten, J.L.; Campbell, B.A.; Morgan, G.A. A subsurface depocenter in the South Polar Layered Deposits of Mars. Geophys. Res. Lett. 2017, 44, 8188–8195. [Google Scholar] [CrossRef]
- Xiong, S.; Muller, J.P. Automated reconstruction of subsurface interfaces in Promethei Lingula near the Martian south pole by using SHARAD data. Planet. Space Sci. 2019, 166, 59–69. [Google Scholar] [CrossRef]
- Srinivasa Reddy, B.; Chatterji, B.N. An FFT-based technique for translation, rotation, and scale-invariant image registration. IEEE Trans. Image Process. 1996, 5, 1266–1271. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2015; Volume 9351, pp. 234–241. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the 32nd International Conference on Machine Learning (ICML 2015), Lille, France, 6–11 July 2015; Volume 1, pp. 448–456. [Google Scholar]
- Zhang, T.; Ramakrishnan, R.; Livny, M. BIRCH: An Efficient Data Clustering Method for Very Large Databases. SIGMOD Rec. (ACM Spec. Interes. Gr. Manag. Data) 1996, 25, 103–114. [Google Scholar]
- Baik, H.; Kim, J. The development of 3D sub-surface mapping scheme and its application to Martian lobate debris aprons. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences-ISPRS Archives. Int. Soc. Photogramm. Remote Sens. 2017, 42, 1–5. [Google Scholar]
- Schroeder, D.M.; Romero-Wolf, A.; Carrer, L.; Grima, C.; Campbell, B.A.; Kofman, W.; Bruzzone, L.; Blankenship, D.D. Assessing the potential for passive radio sounding of Europa and Ganymede with RIME and REASON. Planet. Space Sci. 2016, 134, 52–60. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).