A Simple Analytical Solution for the Designing of the Birdcage RF Coil Used in NMR Imaging Applications
Abstract
1. Introduction
2. Analytical Solution for Birdcage RF Coil
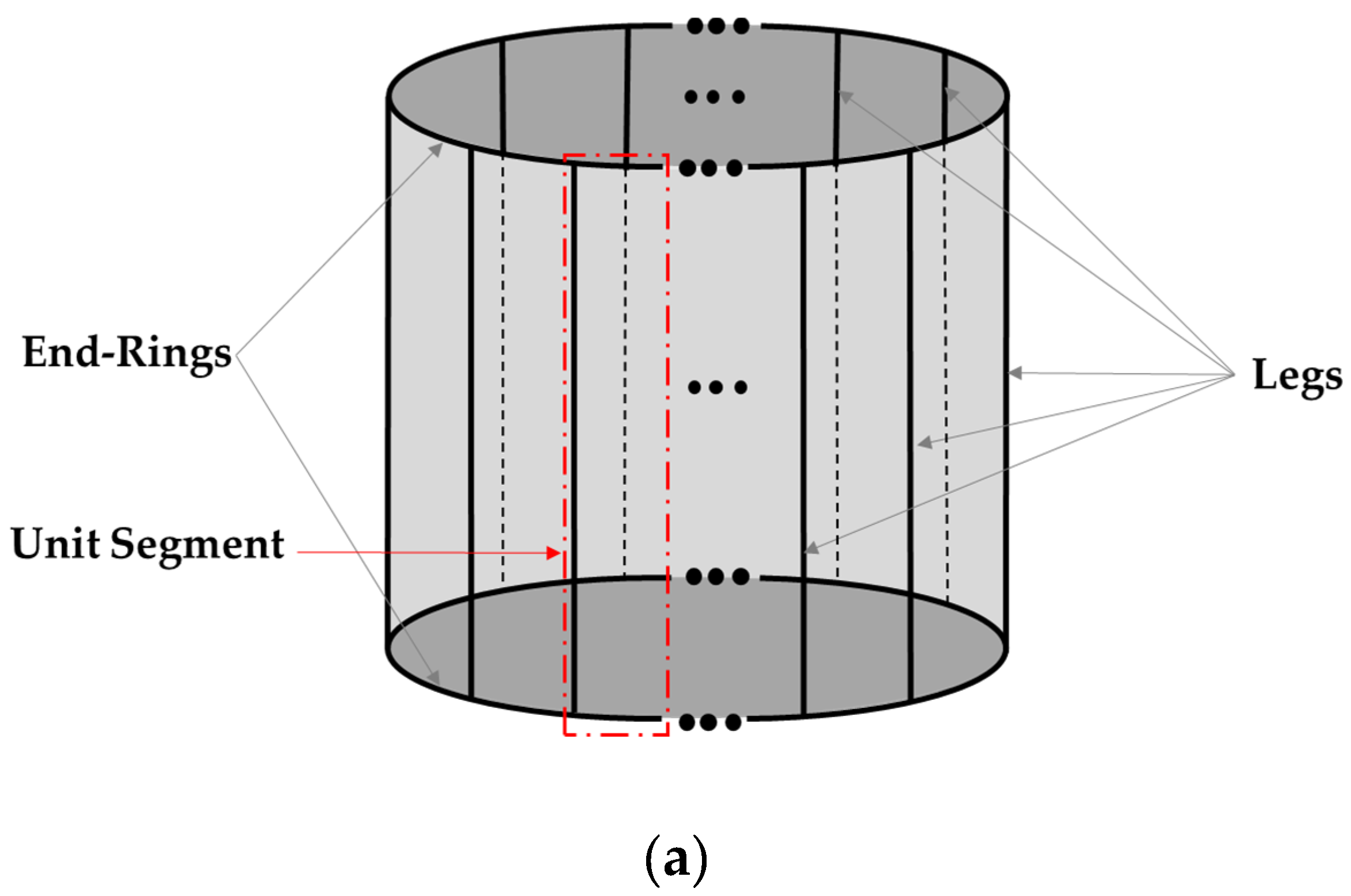
2.1. Configuration of the Birdcage RF Coil
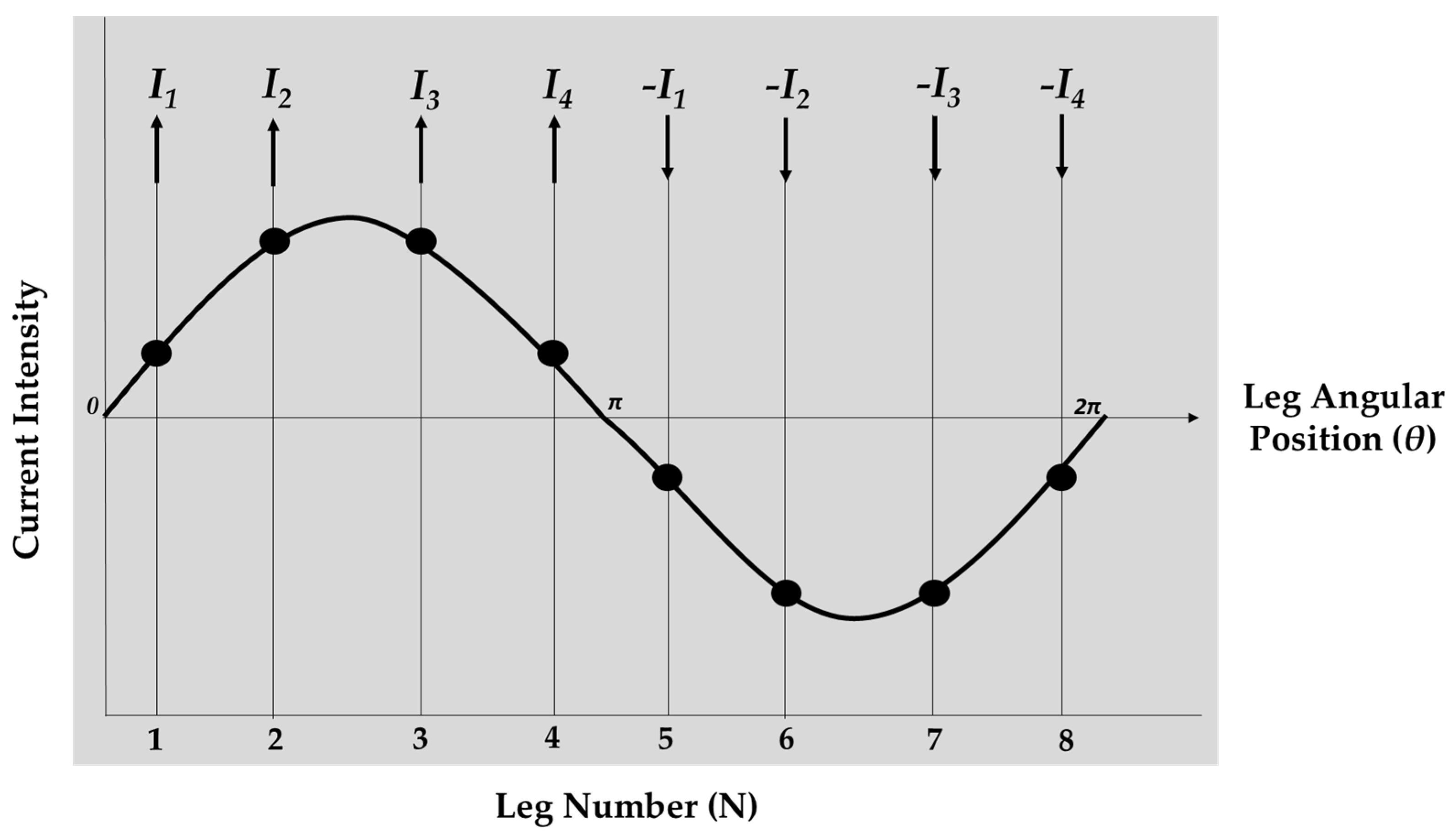
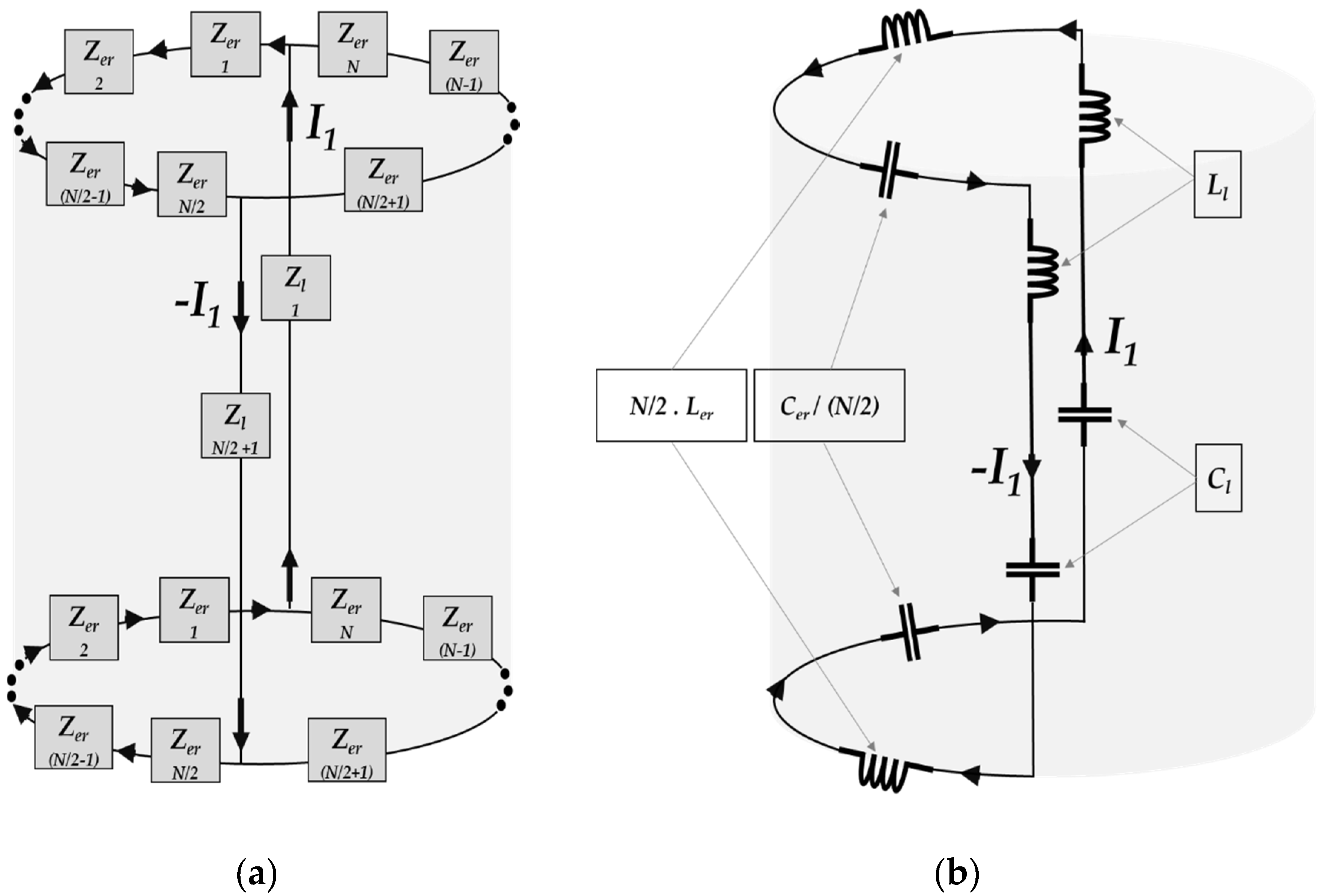
2.2. Dominant Resonance Path
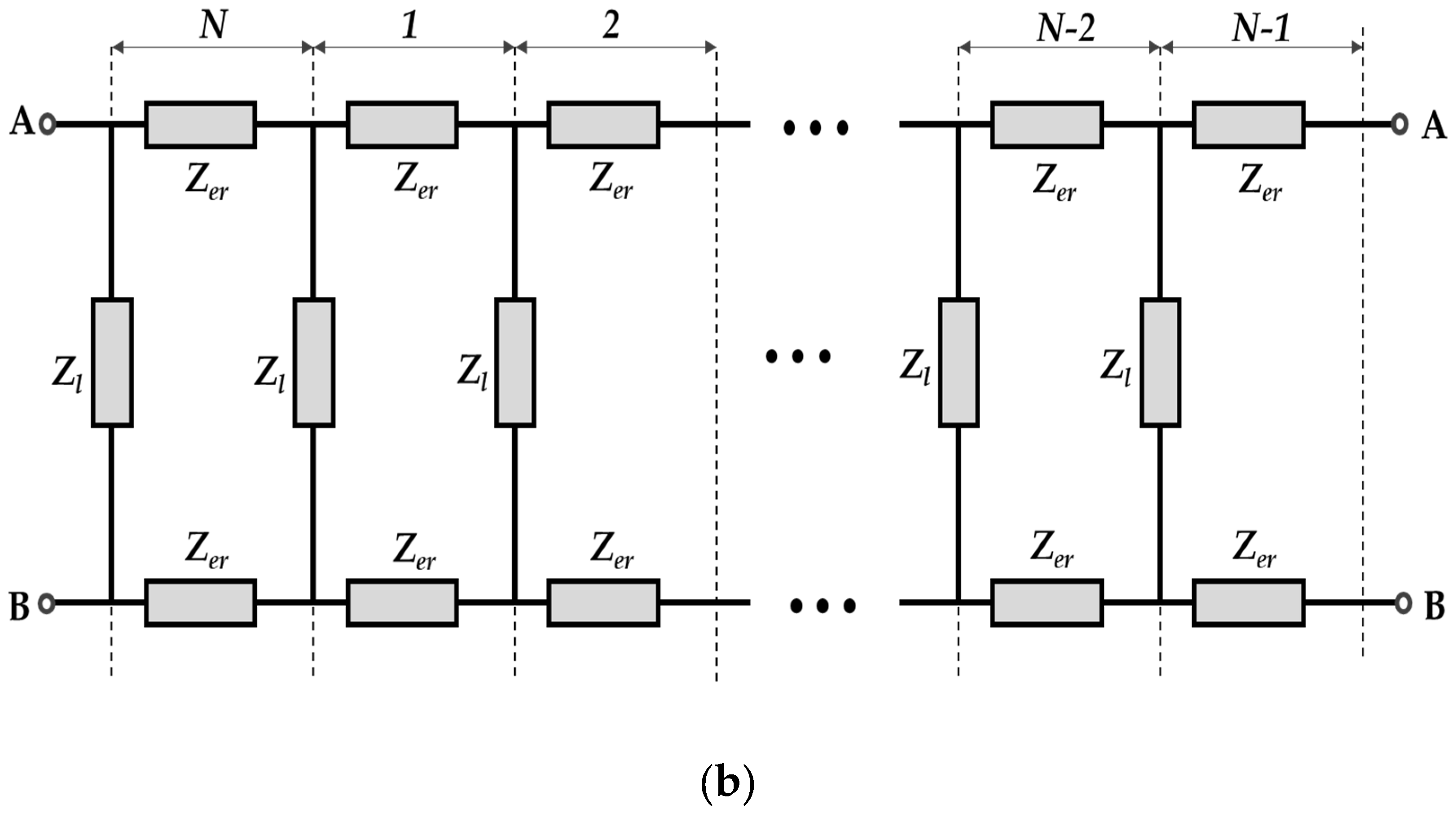
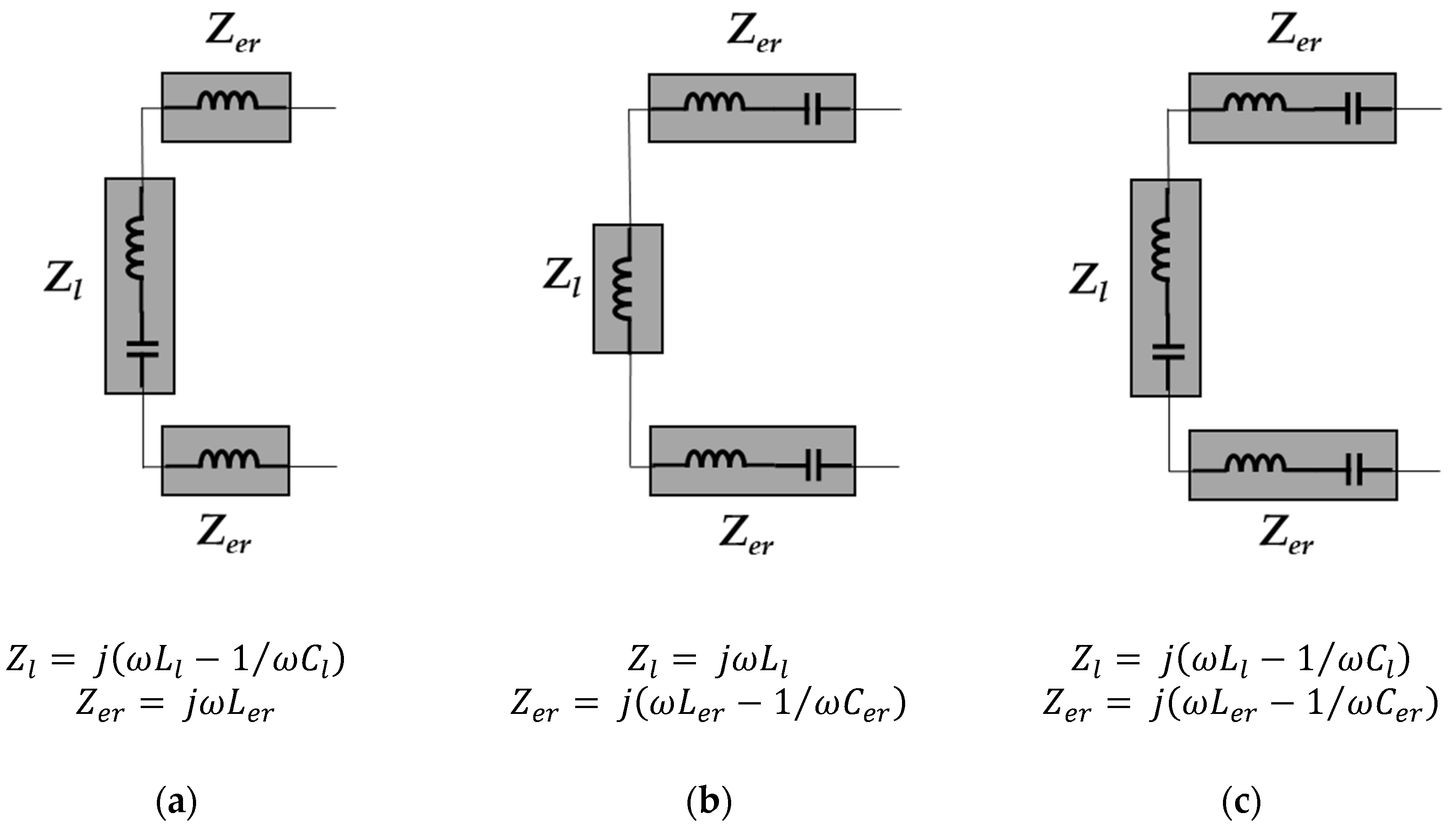
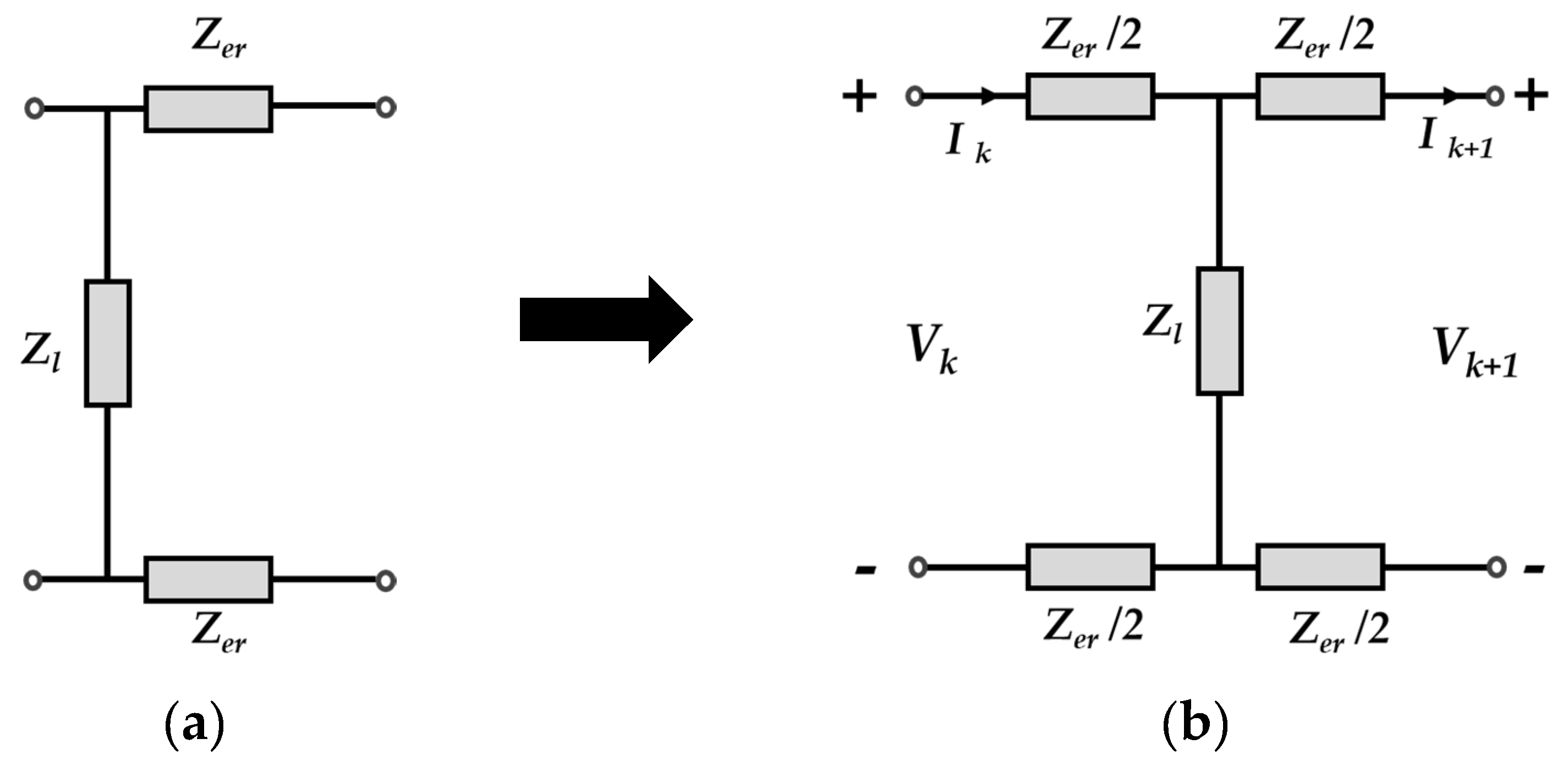
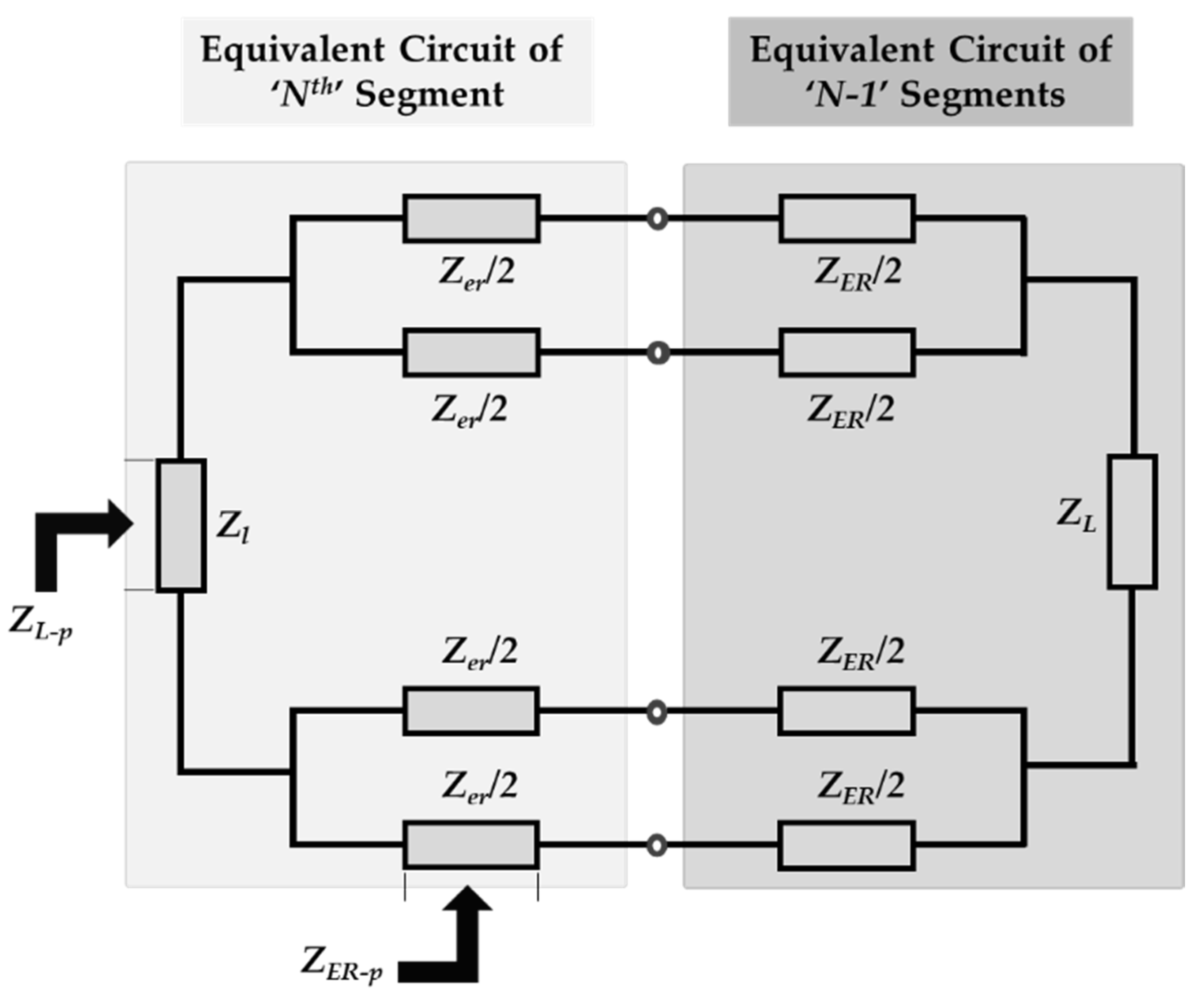
2.3. Equivalent Circuit Analysis
3. Design and Analysis of the Birdcage RF Coil
3.1. Design Based on Analytical Solution
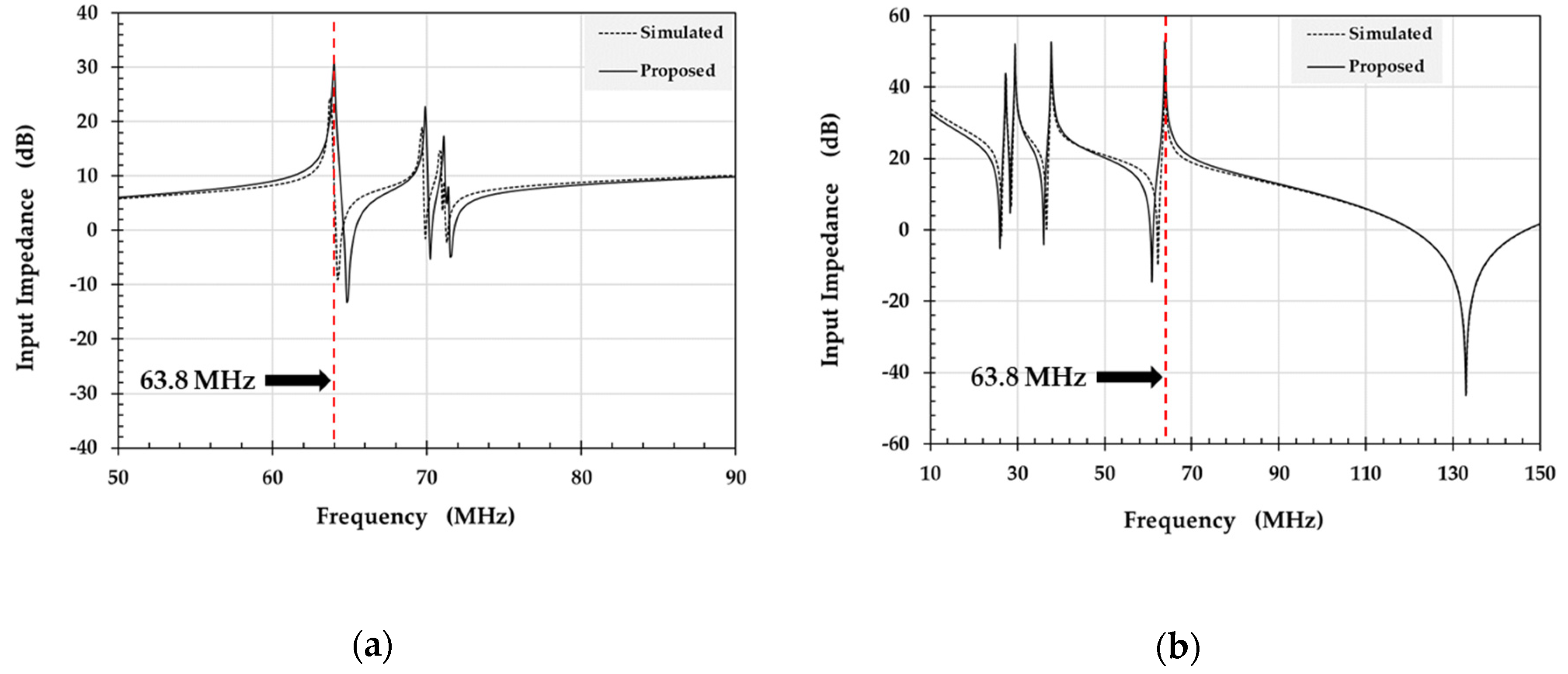
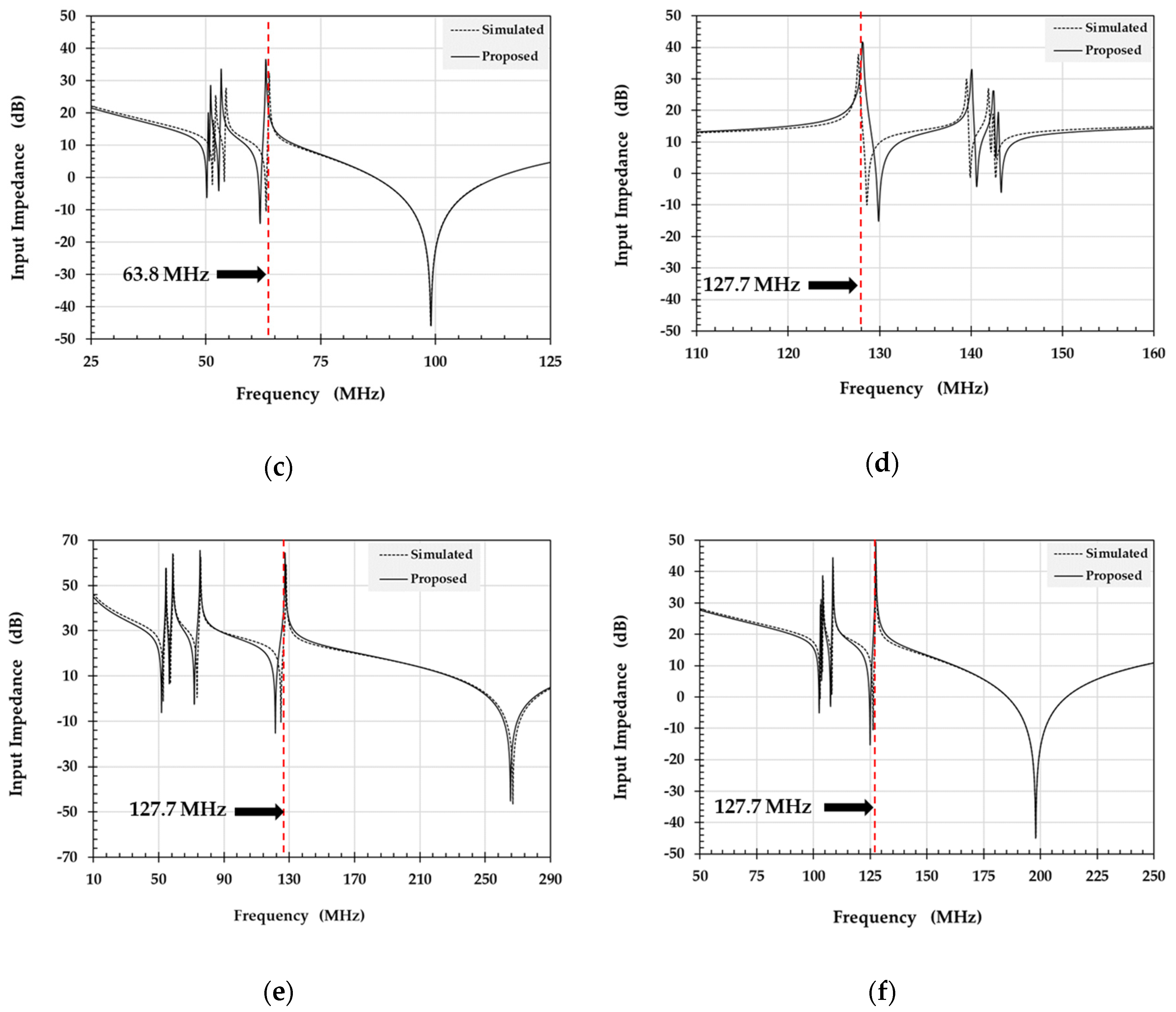
3.2. Resonance Frequency
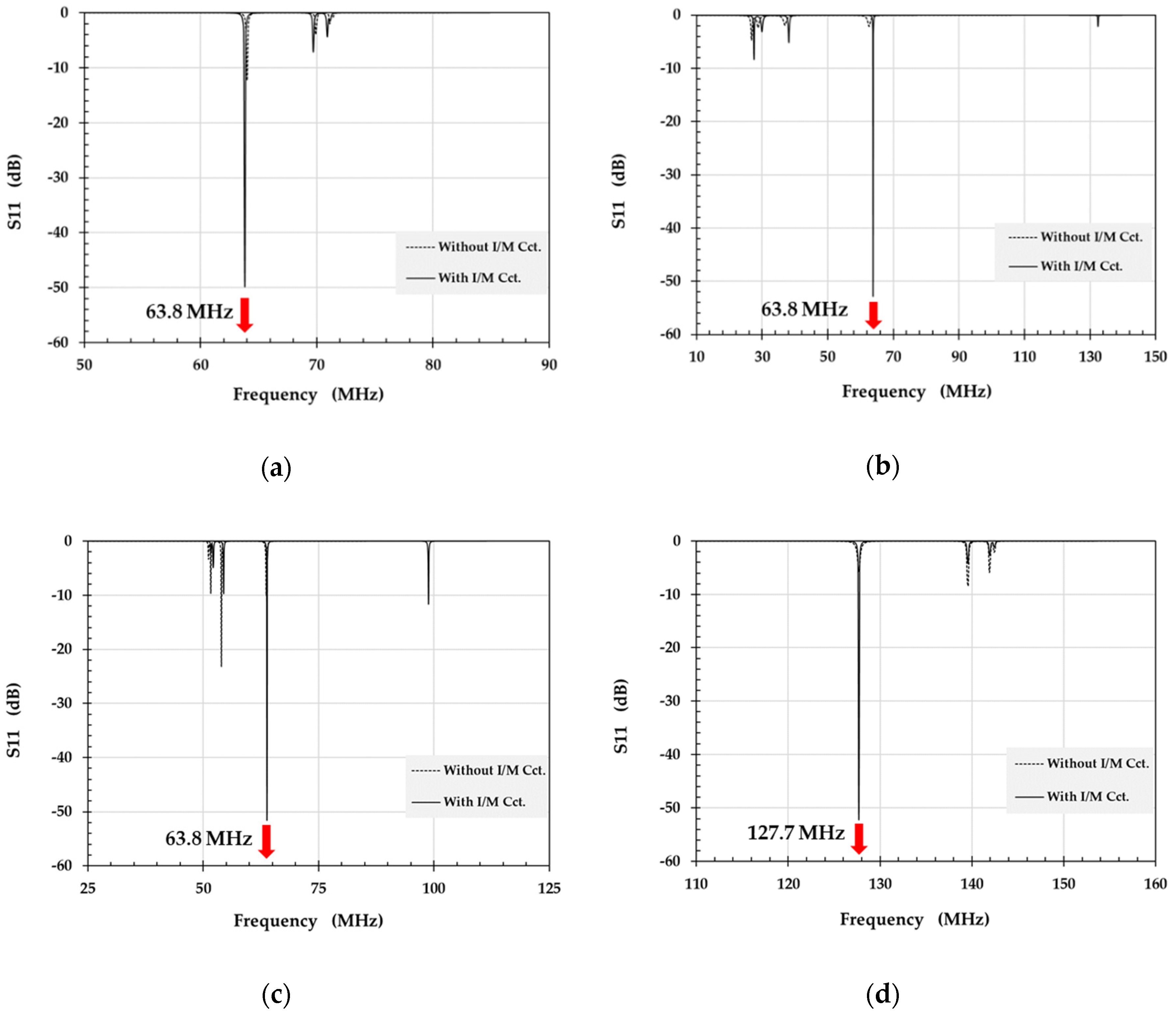
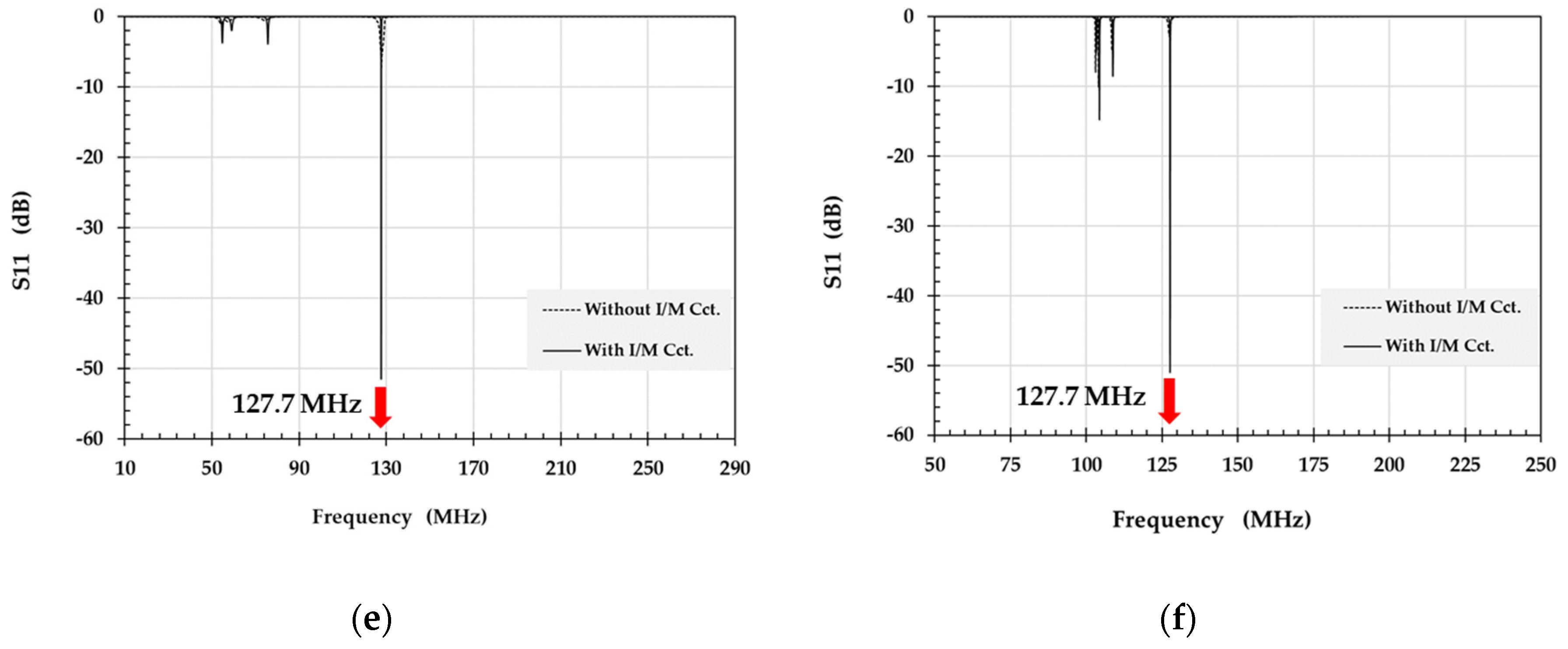
3.3. Impedance Matching
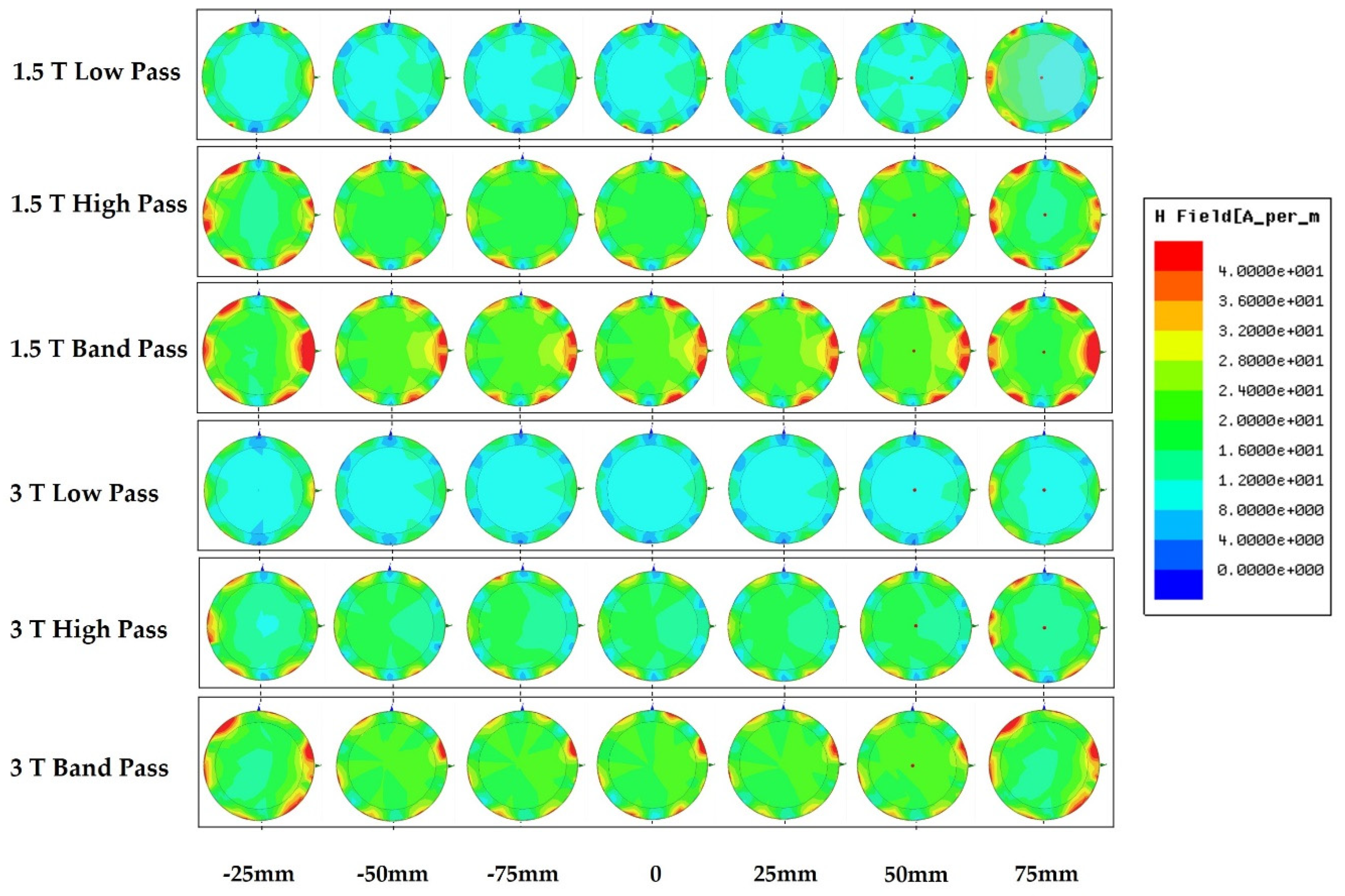
3.4. Magnetic Field Homogeneity
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mansfield, P. Imaging by nuclear magnetic resonance. J. Phys. E Sci. Instrum. 1988, 21, 18. [Google Scholar] [CrossRef]
- Mallard, J.; Hutchison, J.M.; Edelstein, W.; Ling, R.; Foster, M. Imaging by nuclear magnetic resonance and its bio-medical implications. J. Biomed. Eng. 1979, 1, 153–160. [Google Scholar] [CrossRef]
- Blow, N. How to get ahead in imaging. Nature 2009, 458, 925–928. [Google Scholar] [CrossRef] [PubMed]
- Haase, A.; Odoj, F.; Kienlin, M.V.; Warnking, J.; Fidler, F.; Weisser, A.; Nittka, M.; Rommel, E.; Lanz, T.; Kalusche, B.; et al. NMR probeheads for in vivo applications. Concepts Magn. Reson. 2000, 12, 361–388. [Google Scholar] [CrossRef]
- Gruettrt, G.; Weisdorf, S.A.; Rajanayagan, V.; Terpsta, M.; Merkle, H.; Truwit, C.L.; Garwood, M.; Nyberg, S.L.; Uğurbil, K. Resolution improvements in in vivo 1H NMR spectra with increased magnetic field strength. J. Magn. Reson. 1998, 135, 260–264. [Google Scholar] [CrossRef]
- Hayes, C.E. The development of the birdcage resonator: A historical perspective. NMR Biomed. 2009, 22, 908–918. [Google Scholar] [CrossRef]
- Ahmad, S.F.; Kim, H.D. FPCB-based birdcage-type receiving coil sensor for small animal 1H 1.5T magnetic resonance imaging system. J. Sens. Sci. Technol. 2017, 26, 245–250. [Google Scholar]
- Yeung, D.; Hutchison, J.M.S.; Lurie, D.J. An efficient birdcage resonator at 2.5 MHz using a novel multilayer self-capacitance construction technique. MAGMA 1995, 3, 163–168. [Google Scholar] [CrossRef]
- Ahmad, S.F.; Kim, Y.C.; Choi, I.C.; Kim, H.D. Birdcage type NMR receiver coil sensor with integrated detuning circuit for 3T MRI system. In Proceedings of the IEEE SENSORS 2015, Busan, Korea, 1–4 November 2015; IEEE: Piscataway, NJ, USA, 2015; p. 2038. [Google Scholar]
- Solis, S.E.; Cuellar, G.; Wang, R.R.; Tomasi, D.; Rodriguez, A.O. Transceiver 4-leg birdcage for high field MRI: Knee imaging. Rev. Mex. Fis. 2008, 54, 215–221. [Google Scholar]
- Pimmel, P.; Briguet, A. A Hybrid Bird Cage Resonator for Sodium Observation at 4.7 T. Magn. Reason. Med. 1992, 24, 158–162. [Google Scholar] [CrossRef]
- Wang, C.; Li, Y.; Wu, B.; Xu, D.; Nelson, S.J.; Vigneron, D.B.; Zhang, X. A practical multinuclear transceiver volume coil for in-vivo MRI/MRS at 7T. Magn. Reason. Imaging 2012, 30, 78–84. [Google Scholar] [CrossRef]
- Bernard, J.D.; Shizhe, L.; Christopher, M.C.; Gerald, D.W.; Michael, B.S. A birdcage coil tuned by RF shielding for applications at 9.4T. J. Magn. Reason. 1998, 131, 32–38. [Google Scholar]
- Hayes, C.E.; Edelstein, W.A.; Schenk, J.F.; Muller, O.M.; Eash, M. An efficient, highly homogeneous radiofrequency coil for whole-body NMR imaging at 1.5 T. J. Magn. Reason. 1985, 63, 622–628. [Google Scholar] [CrossRef]
- Leifer, M.C. Resonant modes of birdcage coil. J. Magn. Reason. 1997, 124, 51–60. [Google Scholar] [CrossRef]
- Tropp, J. The Theory of the bird-cage resonator. J. Magn. Reason. 1989, 82, 51–62. [Google Scholar] [CrossRef]
- Tropp, J. The Theory of an arbitrarily perturbed bird-cage resonator and a simple method for restoring it to full symmetry. J. Magn. Reason. 1991, 95, 235–243. [Google Scholar] [CrossRef]
- Pascone, R.J.; Garcia, B.J.; Ftizgerald, T.M.; Vullo, T.; Zipagan, R.; Cahill, P.T. Generalized electrical analysis of low-pass and high-pass birdcage resonators. Magn. Reason. Imaging 1991, 9, 395–408. [Google Scholar] [CrossRef]
- Giovannetti, G.; Landini, L.; Santarelli, F.M.; Positano, V. A fast and accurate simulator for the design of birdcage coils in MRI. Magn. Reson. Mater. Phys. Biol. Med. 2002, 15, 36–44. [Google Scholar] [CrossRef] [PubMed]
- Novikov, A. Advanced theory of driven birdcage resonator with losses for biomedical magnetic resonance imaging and spectroscopy. Magn. Reason. Imaging 2011, 29, 260–271. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Ahmad, S.F.; Kim, Y.C.; Choi, I.C.; Choi, S.W.; Kim, T.G.; Ahn, C.M.; Kim, H.D. Fast and efficient birdcage coil design process for high field MRI system by combining equivalent circuit model and 3D electromagnetic simulation. In Proceedings of the 2017 Asia Modelling Symposium (AMS), Kota Kinabalu, Malaysia, 4–6 December 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 188–194. [Google Scholar]
- Kim, H.D. Analysis of the bird-cage receiver coil for MRI system employing a equivalent circuit model based on transmission matrix. J. Korea Multimed. Soc. 2017, 20, 1024–1029. [Google Scholar]
- Jianming, J. Analysis and design of RF coils. In Electromagnetic Analysis and Design in Magnetic Resonance Imaging, 1st ed.; CRC Press: Boca Raton, FL, USA, 1999; pp. 57–164. [Google Scholar]
- Mispelter, J.; Lupu, M. Homogeneous resonators for magnetic resonance: A review. C. R. Chim. 2008, 11, 340–355. [Google Scholar] [CrossRef]
- Chin, C.L.; Collins, C.M.; Li, S.; Dardzinski, B.J.; Smith, M.B. BirdcageBuilder: Design of specified-geometry birdcage coils with desired current pattern and resonant frequency. Concepts Magn. Reson. 2002, 15, 156–163. [Google Scholar] [CrossRef] [PubMed]
- ANSYS Electronics Desktop. Available online: http://www.ansys.com/products/electronics/ansys-electronics-desktop (accessed on 20 December 2019).
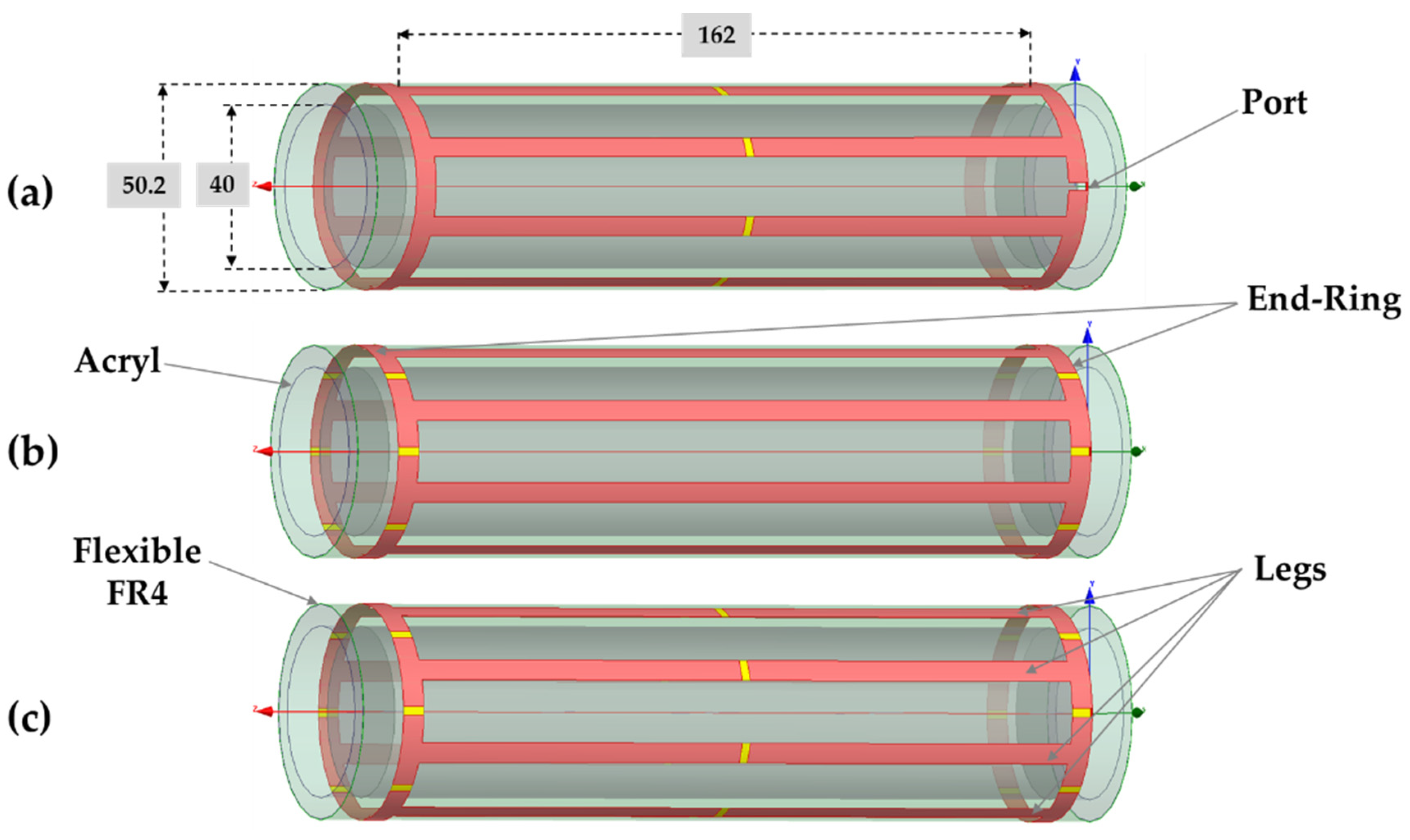
| Parameters | Leg | End-Ring |
|---|---|---|
| Length (l) | 162 mm | 19.8 mm |
| Width (w) | 5 mm | 5 mm |
| Calculated Inductance (Lcal) | 151.4 nH | 10.2 nH |
| Effective Inductance (Leff) | 147.5 nH | 12.9 nH |
| Method | Low Pass | High Pass | Band Pass (Cer = 200) | ||||
|---|---|---|---|---|---|---|---|
| Cl | %Error | Cer | Error | Cl | Error | ||
| Proposed | C cal | 32.4 | −0.034 | 129.7 | −0.107 | 92.2 | −0.052 |
| C eff | 31.3 | −0.023 | 125.3 | −0.063 | 84 | 0.03 | |
| Conventional | C cal | 33.4 | −0.044 | 114 | 0.05 | 77.8 | 0.092 |
| C eff | 32.4 | −0.034 | 111 | 0.08 | 72.7 | 0.143 | |
| 2D Simulation | C cal | 33.5 | −0.045 | 111 | 0.075 | 73 | 0.161 |
| C eff | 32.5 | −0.035 | 108 | 0.11 | 72.4 | 0.146 | |
| 3D Simulation | C 3D | 29.4 | −0.004 | 120 | −0.01 | 88 | −0.01 |
| Measured | C mes | 29 | 119 | 87 | |||
| Method | Low Pass | High Pass | Band Pass (Cer = 50) | ||||
|---|---|---|---|---|---|---|---|
| Cl | %Error | Cer | Error | Cl | Error | ||
| Proposed | C cal | 8.1 | −0.01 | 32.4 | −0.034 | 22.9 | −0.023 |
| C eff | 7.8 | −0.007 | 31.3 | −0.023 | 20.9 | −0.003 | |
| Conventional | C cal | 8.35 | −0.0125 | 28.5 | 0.005 | 19.4 | 0.012 |
| C eff | 8.11 | −0.0101 | 27.7 | 0.013 | 18.2 | 0.024 | |
| 2D Simulation | C cal | 8.35 | −0.0125 | 27.7 | 0.013 | 18.8 | 0.018 |
| C eff | 8.12 | −0.0102 | 26 | 0.03 | 17.8 | 0.028 | |
| 3D Simulation | C 3D | 7 | 0.001 | 29.5 | −0.005 | 20.5 | 0.001 |
| Measured | C mes | 7.1 | 29 | 20.6 | |||
| MRI System | Coil Configuration | ZER_p (Ohm) | Cm (pF) | Lm (nH) |
|---|---|---|---|---|
| 1.5 T | Low Pass | 34.42 − j10.86 | 33.7 | 85.6 |
| High Pass | 439.88 − j37.44 | 15.3 | 350 | |
| Band Pass | 68.65 − j29.33 | 10.8 | 98.2 | |
| 3.0 T | Low Pass | 131.74 − j54.57 | 8.3 | 90 |
| High Pass | 13.23 + j137.45 | 13.5 | 333 | |
| Band Pass | 82.20 + j130.45 | 16.3 | 136.3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, Y.C.; Kim, H.D.; Yun, B.-J.; Ahmad, S.F. A Simple Analytical Solution for the Designing of the Birdcage RF Coil Used in NMR Imaging Applications. Appl. Sci. 2020, 10, 2242. https://doi.org/10.3390/app10072242
Kim YC, Kim HD, Yun B-J, Ahmad SF. A Simple Analytical Solution for the Designing of the Birdcage RF Coil Used in NMR Imaging Applications. Applied Sciences. 2020; 10(7):2242. https://doi.org/10.3390/app10072242
Chicago/Turabian StyleKim, Young Cheol, Hyun Deok Kim, Byoung-Ju Yun, and Sheikh Faisal Ahmad. 2020. "A Simple Analytical Solution for the Designing of the Birdcage RF Coil Used in NMR Imaging Applications" Applied Sciences 10, no. 7: 2242. https://doi.org/10.3390/app10072242
APA StyleKim, Y. C., Kim, H. D., Yun, B.-J., & Ahmad, S. F. (2020). A Simple Analytical Solution for the Designing of the Birdcage RF Coil Used in NMR Imaging Applications. Applied Sciences, 10(7), 2242. https://doi.org/10.3390/app10072242





