Featured Application
Motion Prediction, Target Intent Inference, Urban Intersection, Automated Driving.
Abstract
Research shows that urban intersections are a hotspot for traffic accidents which cause major human injuries. Predicting turning, passing, and stop maneuvers against surrounding vehicles is considered to be fundamental for advanced driver assistance systems (ADAS), or automated driving systems in urban intersections. In order to estimate the target intent in such situations, an interacting multiple model (IMM)-based intersection-target-intent estimation algorithm is proposed. A driver model is developed to represent the driver’s maneuvering on the intersection using an IMM-based target intent classification algorithm. The performance of the intersection-target-intent estimation algorithm is examined through simulation studies. It is demonstrated that the intention of a target vehicle is successfully predicted based on observations at an individual intersection by proposed algorithms.
1. Introduction
Advanced driving assistance system (ADAS) and autonomous driving system (AD) are expected to be at the center of future transportation systems as well as highly enhance traffic safety. To successfully bring autonomous vehicles (AVs) into our lives, they must be capable of managing complex urban environments, including various participants and complex traffic infrastructure. Among them, intersections are one of the most dangerous urban traffic infrastructures. It is reported that 21.5% of fatalities and even 40% of all accidents in the United States occur at intersections [1]. Although recent commercialized vehicles are equipped with ADAS functions, human drivers still need to focus on complex driving situations such as urban intersections. To deal with this, the predict-and-plan approach is typically applied; during the ‘predict’ step, the ego vehicle integrates numerous signals from sources such as sensors or traffic infrastructure and predicts future actions of several agents in the vicinity. In the planning step, the ego vehicle generates maneuvers based on the trajectory from the predict step. Therefore, the predict step is essential in the entire decision-making process, so several researchers have tried to develop methods to predict the intention of other traffic agents which not only have behavior patterns but also inherent uncertainty.
Recently, most of cars that have been newly released have a certain level of ADAS built into the vehicle. For instance, in the most recently released GV80, Hyundai Motors group provides general ADAS functions such as forward collision-avoidance assist (FCA) and lane keeping assist (LKA) by default. The FCA offers a more diverse range of recognition options, including when a vehicle passes through an intersection or is laterally approaching. It also provides Highway Driving Assist II (HDAII), which includes machine-learning-based adaptive cruise control (ACC), automatic lane change assist when operating direction indicator lamps, and near-field vehicle recognition technology [2]. Hyundai Motors Group also announced that they have a plan to mass-produce highway driving pilots (HDPs) in the near future, which enables the vehicle to drive on its own, even if the driver leaves the steering wheel when driving on highways [3]. Practically, it is equivalent to SAE (Society of Automotive Engineer) Level 3, which is often compared to Tesla’s Navigate on Autopilot (NOA). Tesla’s autopilot is capable of steering, acceleration, and deceleration of the vehicle. In addition, the most recently updated feature, NOA, based on autopilot, enables the vehicle to change lanes and overtake other cars using map data [4]. As such, the vehicles on the market with most advanced ADAS are assessed to be within the SAE Level 2–3. Now, most of the conventional carmakers and vehicle technology providers are testing AD vehicles that are equivalent to SAE Level 4 within a certain area, and they have claimed that these verified AD vehicles can be used as shuttles and taxis, for example, ‘Waymo One’ of Waymo [5], Google’s subsidiary, ‘Robotaxi’ of Tesla [6], and ‘Pilot Project’ by Mercedes Benz, and Bosch [7]. This trend of technological advancement once again confirms that the vehicle’s responsibilities are increasing, and the perception and control technology must ensure a certain level.
As stated above, since obtaining effective vehicle behavior analysis is critical for urban autonomous driving, tracking and calculating of the expected trajectory must be conducted. To better estimate the trajectory of vehicle movement, the performance of the state of estimation algorithms is one of the most significant factors. Thus, various approaches that have been theorized in literature have been tested, such as dynamic Bayesian networks (DBN), hidden Markov models (HMM), support vector machines (SVM), interacting multiple model (IMM), and vehicle-to-vehicle (V2V) communication [8,9,10,11,12]. Traditional learning methods like DBN and HMM are frequently used since they are simple, fast, and do not require lots of data to become trained [13]. For instance, S. Lefèvre et al. uses DBN, combining probabilistically uncertain observations on the vehicle’s behavior and local characteristic information to estimate driver maneuvers [14]. In addition, Streubel et al. proposed a prediction framework based on HMM using a database of real driving data such as speed, acceleration, and yaw rate [15]. As a discriminative approach, SVM is used as a learning framework for binary classification. Aoude et al. present a comparison and validation of performances of SVM, HMM, and other traditional approaches consisting of TTI-, RDP-, and SDR-based algorithms [16]. In recent years, along with the advancement of information and communication technologies, V2V communication is often applied to the prediction protocol. Aoki et al. introduce a decentralized intersection protocol for mixed traffic environments where all automated vehicles use V2V communications [17]. Since this information-driven control research area is active, not only V2V but also vehicle-to-infrastructure (V2I), vehicle-to-pedestrian (V2P), technologies are arousing interest.
As stated above, the IMM algorithm is a method used to determine the expected target trajectory in selecting among filter models derived from the behavior of targets. To select the best hypothesis, the IMM consists of four main steps: interaction, filtering, update, and combination. At the interaction step, the initial values of each model for the filtering step are calculated by receiving signals from sensors. These initial values are transferred to the filtering step. In the filtering step, each model independently conducts the calculation and deduces the state prediction. Typically, a Kalman filter (KF) is applied at this step. Then, the probabilities of models are updated at the update step, and by combining the probabilities and sending them to the interaction step again at the combination step, one cycle of the IMM is finished.
Since the IMM was introduced in the late 1980s, it is generally known and has been implemented on a wide range of conditions. Tsunashima et al. used IMM to estimate vehicle state differing road friction [18]. Rubin et al. illustrate that the noble IMM estimator works accurately with the external disturbances and inputs of steering [19]. As the IMM is verified in plenty of conditions, the IMM algorithms are also often modified. Wang et al. presents an adaptive IMM which utilizes the models for an adaptive turn rate in order to track a target for maneuvering [20]. In addition, the IMMs are classified depending on how they use multi-model fusion criteria as scalar weight IMM (SIMM), diagonal-matrix-weight interacting multiple model, and matrix weight interacting multiple model [21,22]. These new approaches weigh differently when mixing beginning model values with states and corresponding covariances at each step of the IMM algorithm. Fu et al. also introduced H∞ filtering into the distributed interacting multiple model (DIMM) algorithm instead of KF, for target tracking of maneuvering during which the measurement noise is statistically unknown [23]. Park et al. propose a new algorithm suitable for multi-object tracking using multi-data fusion by applying centralized KF to a typical IMM. Since it is reasonable and easily adaptable, the IMM is applied in a variety of fields which require tracking of the maneuvering target. The IMM filter is often applied in aircraft tracking problems, such as in the study by Li et al. [24]. Tong et al. used IMM for 3D human motion tracking [25]. For application to autonomous vehicles, an IMM filter that integrates market commercial GPS and vehicle local sensors is implemented to develop a vehicle localization algorithm [26]. Since the IMM algorithm is incorporated in both the kinematic and dynamic model of the vehicle, the positioning performance is improved demonstrating high accuracy under the various driving conditions.
Thanks to the advantages described above, we propose an intersection-target-intent estimation algorithm based on IMM [27].
In this research, we focus on the target intent estimation algorithm at urban intersections, and the paper is structured as follows. The next section demonstrates use of the intersection driver behavior model to represent the intent of the driver’s maneuvering at the intersection. In Section 3, an IMM-based target intent classification algorithm is demonstrated by reflecting continuity of driver behavior while improving the accuracy of state prediction. The target intent estimation algorithm for urban intersections is verified via simulation studies in Section 4. Finally, conclusions are provided in Section 5.
2. Intersection Driver Behavior Model
The target road is set to be an intersection of two-way streets. Under these circumstances, if the target approaches the intersection using the leftmost lane from the south, there are eight possible maneuvers recognized, as shown in Figure 1. The possible trajectory is depicted as a red line, the entrance as a red cross, and the exit as a blue circle. Note that there are 64 possible maneuvers if we consider each case of possible entrance. To describe all of these behaviors, the behavior of the target vehicle is represented by path-tracking, with slowing down before turning left, right, or making a U-turn. In order to illustrate these motions, two vectors (state and input vector) are established as shown below:
where and are the x- and y-axis of each frame, respectively; illustrates the relative position; depicts the relative yaw angle; is the velocity; is the yaw rate; is the notation of the acceleration. The input vector is calculated by the driver model as follows:
where is the driver model and is a reference path of the target vehicle when it intends to go the m-th exit.
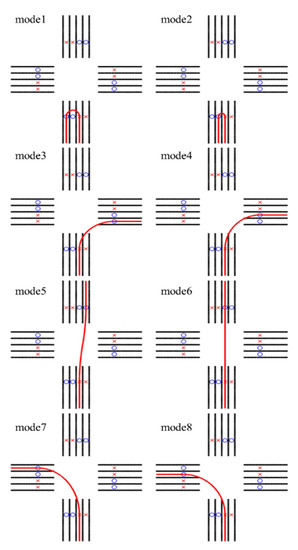
Figure 1.
Eight modes of possible behavior of the target approaching the intersection by using the leftmost lane from the south.
3. IMM/EKF-Based Intersection-Target-Intent Estimation
By receiving the validated measurement for every single target, extended Kalman filters (EKFs) are implemented as the local filter which matches every single mode. This is incorporated using the interacting multiple model (IMM) approach to retain the best estimate of the state vectors and the best matching modes. The algorithm for estimation of intersection target intent is described below. It is noted that the time index is to be omitted unless otherwise needed for clear explanations.
(1). Interaction ():
With the weights of , the specifically depicts , and the related covariance , which are used to calculate the mixed condition for an initial condition which is used for a filter matched to the state of mode . It should be noted that if the implemented modes contain different dimensions of state vectors, the lower dimension state of an augmentation with zeros observed may cause a bias toward zero for components of the larger state vector. According to [21], to avoid the issue of ‘biasing’, a simple procedure is suggested, combined with a proper augmentation of the smaller state’s covariance, and it yields unbiased and consistent mixing.
Mode probability with Predictions:
Mixing probability:
Mixed condition:
(2). EKF Approach:
Every single pair of the values has weights of , , and it is used to input to an EKF approach which is matched to the state of mode .
Time update:
Filter gain:
Innovation:
Measurement update:
(3). Mode Probability Update:
From the innovations of , the EKFs are updated.
Likelihood function:
Mode probability:
(4). Combination Step:
This is just for output purposes, and and are calculated with the
Combined condition:
4. Simulation Results
The developed IMM-based intersection-target-intent estimation algorithm is implemented and verified via simulation studies. The test scenario is a left turn situation of the target vehicle. To check the generality of the algorithm, the target is set to approach the intersection from the east using the most left lane. The initial speed and the set speed are 50 kph which is too high for a stable and safe turn. The velocity profile in the case of the left turn is illustrated in Figure 2. As briefly shown in the figure, a proposed driver model slows down the car approaching the intersection and performs a stable left turn at low speed even though the set speed is 50 kph.
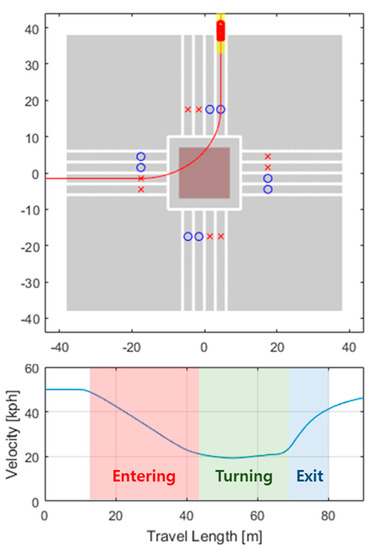
Figure 2.
Case example of slowing down driver model before left turn.
Figure 3 demonstrates the mode probability adaptation results along the axis of travel length. We can see that the updated result is very similar to the real mode. From 20–40 m, which describes a period of the approaching target vehicle at the intersection with deceleration, it can be observed that the probability of mode 5 has the highest rank, which means the left turn to exit #5. The observed result is that we cannot tell which exit the target vehicle will head to during that period if we only measure pose and heading. Since two vectors (state and input vector) were established in Section 2, this allows prediction of the motion of the target with accuracy and reliability. From this result, the proposed approach delivers good results from the viewpoint of classification performance and the target vehicle’s behavior predictions.
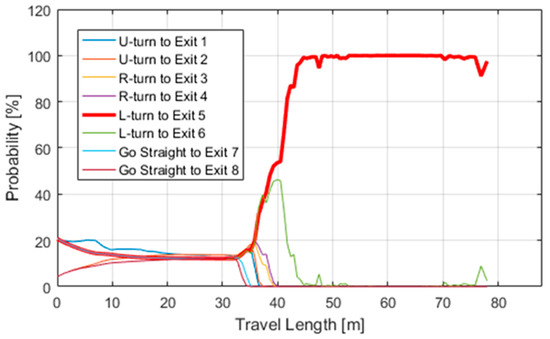
Figure 3.
Mode probability update results for left turning case.
5. Discussion & Conclusions
We propose a simple and real-time approach to estimate a target vehicle’s intent at urban intersections. It is based on a driver model for representing the real driver’s intersection maneuvering and use of an IMM to classify the target intent. It is demonstrated that the proposed method allows us to achieve good classification performance via simulation study.
This paper focused on the implementation of the proposed algorithm and a real road test. By applying the proposed algorithm to an emergency driver support system, or an automated driving technology, it is expected that intersection safety can be significantly improved.
Since the IMM approach using extended Kalman filters (EKFs) for multi-target state estimation of intelligent vehicle has already been verified by Figure 4, and in the work of Suh et al. [28], the proposed algorithm will be improved in the urban intersection, which is a more complex driving situation using the perception of a multi-target vehicle. Furthermore, it is expected to be equipped as a generalized perception module for various applications of advanced driver assistance systems (ADAS) which use the lane change assistance system, intersection driving assistance system, steering assist system, side-crash prevention system, and autonomous emergency braking system. Using our proposed algorithm, it is possible to make generic assessments as well as an overall assessment of collision risks with multi-target vehicles in complex urban intersections.
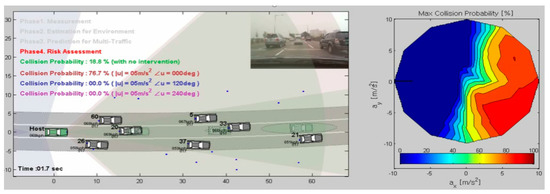
Figure 4.
Multi-target state estimation test results for complex urban road.
Considering a mixed traffic situation, which would include many other cars and more lanes with different types of intersection shapes in urban roads, a deep learning approach should be taken into account in future research.
The deep-learning approach is also useful to streamline the method stated in this paper to some degree of complex urban road. Since urban traffic is quite complicated and hard to predict, the algorithm needs to be improved using both a rule-based and deep-learning approach. The rule-based EKF approach, as previously demonstrated in this paper, is still beneficial to guarantee the safety of a vehicle in any driving situation.
Author Contributions
Conceptualization, D.S., M.P. and S.Y.; Methodology, D.S., K.-m.P. and S.Y.; Software, D.S. and K.-m.P.; Validation, D.S.; Formal Analysis, D.S.; Investigation, D.S. and K.-m.P.; Resources, M.P. and S.Y.; Data Curation, K.-m.P.; Writing—Original Draft Preparation, D.S and S.Y.; Writing—Review and Editing, K.-m.P. and M.P.; Visualization, K.-m.P.; Supervision, M.P.; Project Administration, D.S.; Funding Acquisition, M.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by a grant (code 20PQOW-B152473-02) from R&D Program funded by Ministry of Land, Infrastructure and Transport of Korean government, by the Road Traffic Authority grant funded by the Korea government (KNPA) (No. POLICE-L-00001-02-101, Development of control system and AI driving capability test for autonomous driving), and by the Sookmyung Women’s University Research Grants (1-1903-2022).
Acknowledgments
This research was supported by a grant (code 20PQOW-B152473-02) from R&D Program funded by Ministry of Land, Infrastructure and Transport of Korean government, by the Road Traffic Authority grant funded by the Korea government (KNPA) (No. POLICE-L-00001-02-101, Development of control system and AI driving capability test for autonomous driving), and by the Sookmyung Women’s University Research Grants (1-1903-2022).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Choi, E.-H. Crash Factors in Intersection-Related Crashes: An On-Scene Perspective; National Highway Traffic Safety Administration: Washington, DC, USA, 2010.
- Genesis GV80 More Specifics Revealed. Available online: https://www.autoblog.com/2020/01/29/genesis-gv80-more-details/ (accessed on 10 March 2020).
- Szymkowski, S. 2021 Genesis GV80 Offers Sharp Looks, Great Value to Beat Competition. Available online: https://www.cnet.com/roadshow/news/2021-genesis-gv80-price-msrp-features/ (accessed on 9 March 2020).
- Autopilot. Available online: https://www.tesla.com/autopilot (accessed on 9 March 2020).
- Waymo One. Available online: https://waymo.com/waymo-one/ (accessed on 9 March 2020).
- Tesla Plans to Launch a Robotaxi Network in 2020; TechCrunch: Bay Area, CA, USA, 2020.
- Daimler and Bosch: Start of the San José Pilot Project for Automated Ride-Hailing Service | Daimler > Innovation > Product Innovation > Autonomous Driving. Available online: https://www.daimler.com/innovation/case/autonomous/pilot-city-san-jose.html (accessed on 9 March 2020).
- Shin, D.; Kim, B.; Yi, K.; Carvalho, A.; Borrelli, F. Human-centered risk assessment of an automated vehicle using vehicular wireless communication. IEEE Trans. Intell. Transp. Syst. 2018, 20, 667–681. [Google Scholar] [CrossRef]
- Shin, D.; Kim, B.; Yi, K. Probabilistic threat assessment of vehicle states using wireless communications for application to integrated risk management system. In Proceedings of the FAST-Zero’15: 3rd International Symposium on Future Active Safety Technology toward Zero Traffic Accidents, Gothenburg, Sweden, 9–11 September 2015. [Google Scholar]
- Shin, D.; Park, K.; Park, M. Effects of vehicular communication on risk assessment in automated driving vehicles. Appl. Sci. 2018, 8, 2632. [Google Scholar] [CrossRef]
- Shin, D.; Yi, K. Compensation of wireless communication delay for integrated risk management of automated vehicle. In Proceedings of the 2015 IEEE Intelligent Vehicles Symposium (IV), Seoul, Korea, 29 June–1 July 2015; pp. 1355–1360. [Google Scholar]
- Shin, D.; Kim, B.; Seo, J.; Yi, K. Effects of wireless communication on integrated risk management based automated vehicle. In Proceedings of the 2015 IEEE 18th International Conference on Intelligent Transportation Systems, Gran Canaria, Spain, 15–18 September 2015; pp. 1767–1772. [Google Scholar]
- Shirazi, M.S.; Morris, B. Observing behaviors at intersections: A review of recent studies & developments. In Proceedings of the 2015 IEEE Intelligent Vehicles Symposium (IV), Seoul, Korea, 29 June–1 July 2015; pp. 1258–1263. [Google Scholar]
- Lefèvre, S.; Laugier, C.; Ibañez-Guzmán, J. Exploiting map information for driver intention estimation at road intersections. In Proceedings of the 2011 IEEE Intelligent Vehicles Symposium (IV), Baden-Baden, Germany, 5–9 June 2011; pp. 583–588. [Google Scholar]
- Streubel, T.; Hoffmann, K.H. Prediction of driver intended path at intersections. In Proceedings of the 2014 IEEE Intelligent Vehicles Symposium, Dearborn, MI, USA, 8–11 June 2014; pp. 134–139. [Google Scholar]
- Aoude, G.S.; Desaraju, V.R.; Stephens, L.H.; How, J.P. Driver behavior classification at intersections and validation on large naturalistic data set. IEEE Trans. Intell. Transp. Syst. 2012, 13, 724–736. [Google Scholar] [CrossRef]
- Aoki, S.; Rajkumar, R. V2V-based synchronous intersection protocols for mixed traffic of human-driven and self-driving vehicles. In Proceedings of the 2019 IEEE 25th International Conference on Embedded and Real-Time Computing Systems and Applications (RTCSA), Hangzhou, China, 18–21 August 2019; pp. 1–11. [Google Scholar]
- Tsunashima, H.; Murakami, M.; Miyataa, J. Vehicle and road state estimation using interacting multiple model approach. Veh. Syst. Dyn. 2006, 44, 750–758. [Google Scholar] [CrossRef]
- Rubin, D.; Gutman, P.-O.; Oshman, Y.; Jodorkovsky, M. State and disturbance estimation for a road vehicle via IMM filtering. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 2403–2408. [Google Scholar]
- Wang, X.; Han, C.; Zhang, H. An imm-uf algorithm for tracking highly maneuvering target. In Proceedings of the 2010 IEEE International Conference on Mechatronics and Automation, Xi’an, China, 4–7 August 2010; pp. 1862–1867. [Google Scholar]
- Fu, X.; Jia, Y.; Du, J.; Yu, F. New interacting multiple model algorithms for the tracking of the manoeuvring target. IET Control Theory Appl. 2010, 4, 2184–2194. [Google Scholar] [CrossRef]
- Fu, X.; Jia, Y.; Du, J.; Yuan, S. A novel interacting multiple model algorithm based on multi-sensor optimal information fusion rule. In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 1201–1206. [Google Scholar]
- Fu, X.; Shang, Y.; Yuan, H. Improved diagonal interacting multiple model algorithm for manoeuvering target tracking based on H ∞ filter. IET Control Theory Appl. 2015, 9, 1887–1892. [Google Scholar] [CrossRef]
- Pitre, R.R.; Jilkov, V.P.; Li, X.R. A comparative study of multiple-model algorithms for maneuvering target tracking. In Signal Processing, Sensor Fusion, and Target Recognition XIV; International Society for Optics and Photonics: San Diego, CA, USA, 2005; Volume 5809, pp. 549–560. [Google Scholar]
- Tong, M.; Bian, H. 3D human motion tracking by using interactive multiple models. J. Shanghai Jiaotong Univ. (Sci.) 2011, 16, 420–428. [Google Scholar] [CrossRef]
- Jo, K.; Chu, K.; Sunwoo, M. Interacting multiple model filter-based sensor fusion of GPS with in-vehicle sensors for real-time vehicle positioning. IEEE Trans. Intell. Transp. Syst. 2011, 13, 329–343. [Google Scholar] [CrossRef]
- Yuan, T.; Bar-Shalom, Y.; Willett, P.; Mozeson, E.; Pollak, S.; Hardiman, D. A multiple IMM estimation approach with unbiased mixing for thrusting projectiles. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 3250–3267. [Google Scholar] [CrossRef]
- Suh, J.; Kim, B.; Yi, K. Stochastic predictive control based motion planning for lane change decision using a vehicle traffic simulator. In Proceedings of the 2016 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Busan, Korea, 1–4 June 2016; pp. 900–907. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).