Abstract
To overcome the problems of slow convergence speed, premature convergence leading to local optimization and parameter constraints when solving high-dimensional multi-modal optimization problems, an adaptive dynamic disturbance strategy for differential evolution algorithm (ADDSDE) is proposed. Firstly, this entails using the chaos mapping strategy to initialize the population to increase population diversity, and secondly, a new weighted mutation operator is designed to weigh and combinemutation strategies of the standard differential evolution (DE). The scaling factor and crossover probability are adaptively adjusted to dynamically balance the global search ability and local exploration ability. Finally, a Gauss perturbation operator is introduced to generate a random disturbance variation, and to accelerate premature individuals to jump out of local optimization. The algorithm runs independently on five benchmark functions 20 times, and the results show that the ADDSDE algorithm has better global optimization search ability, faster convergence speed and higher accuracy and stability compared with other optimization algorithms, which provide assistance insolving high-dimensionaland complex problems in engineering and information science.
1. Introduction
The differential evolution (DE) algorithm was proposed by Storn and Price in 1995 [1,2]. It was originally used to solve the Chebyshev polynomial problem, and is a bionic optimization algorithm based on swarm evolution. DE’s unique population memory capability gives the algorithm a strong global search capability and robust performance. As a highly efficient parallel search algorithm with few controlled parameters, the DE algorithm has been widely used in neuron networks [3,4], power systems [5,6], vehicle routing problems [7,8,9,10,11] and many other fields [12,13,14,15,16,17,18,19,20]. Like other intelligent algorithms, however, the DE algorithm also has disadvantages such as precocity, strong parameter dependence and difficulty in obtaining global optimum values for high-dimensional complex objective functions [21,22,23,24,25,26,27]. Therefore, researchers proposed a number of improvement strategies for DE’s existing shortcomings. First, to improve the existing parameters—Chiou et al. [28] proposed a variable scaling factor differential evolution algorithm, which does not require mutation selection. The type of operation, compared to the random scaling factor, has a large improvement in performance. Secondly, adding new operations was suggested—Wang et al. [29] proposed a generalized inverse differential evolution algorithm, which introduces generalized opposition-based learning based on reverse learning techniques; this prevents the algorithm from falling into a local optimum to a certain extent. Third, multiple groups—Ali et al. [30] divided the population into independent subgroups, with each having different mutation and updating strategies, and introduced a multi-population DE to solve large-scale global optimization problems. Finally, the fourth suggestion was the hybrid algorithm—Trivedi et al. [31] proposed a hybrid evolutionary model based on genetic algorithms and differential evolution. The binary variables evolved based on the genetic algorithm and the continuous variables evolved based on the DE algorithm, which was used to solve a nonlinear, high-dimensional, highconstrained and mixed-integeroptimization problem.
These classical improved algorithms improve the optimization performance of the DE algorithm to a certain extent, but for some high-dimensional and complex problems, there are still disadvantages of falling into the local optimum. Experiments show that the most critical operation in the DE algorithm is differential variation, and the core of differential variation is the composition of differential vectors. Most of the existing improved algorithms adopt adaptive adjustment parameters or randomly choose a mutation strategy. Although the random strategy improves the global search ability of the algorithm and population diversity, the evolutionary direction of the population is more difficult to control, which may cause the population to deviate from the direction of the optimal value search, and an excessive number of iterations will also lead to a decrease in the convergence rate of the algorithm.
In order to balance the global optimum and the local optimum, an adaptive dynamic disturbance strategy differential evolution algorithm is proposed in this paper. On the basis of the adaptive adjustment of policy level control parameters, it is added a dimensional variation disturbance strategy. Through the theoretical analysis of algorithm factors and performance testing of standard test functions, the results show that when the adaptive dynamic disturbance strategy for differential evolution (ADDSDE) algorithm is used to solve complex optimization problems such as high-dimensions and multi-peaks, the global optimal solution can be obtained with a minimum number of iterations, and the algorithm has strong robustness.
2. Standard Differential Evolution Algorithms
The differential evolution (DE) algorithm is a group heuristic optimization algorithm based on real coding. Its basic idea is to dynamically search the global optimal value through information sharing between groups and the unique memory of each individual. The main operations include mutation, crossover and selection. According to the loop iterations of mutation, crossover and selection operations, the population continuously evolves towards the optimal value. The specific definition is as follows:
Each population in the DE algorithm consists of individuals, and is expressed as: , where is the number of populations; each individual corresponds to the solution of the problem to be solved, expressed as: , where is the dimension of solution, is the -th component of the -th evolving individual in the -th generation of the population.
2.1. Initialization
The DE algorithm initializes the population according to the principle of randomness, and sets the optimization interval for variables as . The initialization operation is defined as follows
where is a random number uniformly distributed in the interval [0,1].
2.2. Mutation Operation
In each generation of evolution, the DE algorithm generates variant individuals for each individual in the population, based on the mutation operation. Currently, there are multiple versions of the variants, which are expressed as , and among them, is the type of the mutation operator, which is generally valued as rand and best: rand means randomly selecting an individual from the population as the mutation base, and best represents selecting the optimal individual from the population as the mutation base; while represents the number of differential terms, which is generally an integer. Common mutation operation schemes are as follows:
:
:
:
:
Among these, and , is the number of populations, is the optimal individual of the -th generation and is the scaling factor.
2.3. Crossover Operation
In order to increase the diversity of the population, the DE algorithm cross-processes the original individual with the generated variant individual according to the crossover probability , thereby generating a new variant individual . Common crossovers have two crosses, defined as follows:
Among these: is the random number that is uniformly distributed in the interval [0,1], is the crossover probability and is the random integer in the interval .
2.4. Selection Operation
In order to determine which individual evolved to adopt the greedy choice method for the next-generation DE algorithm—that is, to compare the fitness function values of the mutant individual with the original individual —the individual with higher fitness value is selected to enter the next generation. The definition is as follows:
Among these: is the fitness function or objective function.
3. An adaptive Dynamic Disturbance Strategy for Differential Evolution Algorithm
The core idea of an improved differential evolution (DE) algorithm is to generate variation disturbance according to vector difference, ensure the diversity of the population, balance global search and local development ability, avoid precocity of population, accelerate the rate of population convergence and improve the convergence accuracy. So, the adaptive dynamic disturbance strategy for differential evolution (ADDSDE) algorithm mainly improves the algorithm from four aspects of population initialization, parameter adaptation, mutation strategy and disturbance strategy, and comprehensively improves the global optimization search ability and convergence speed of the algorithm. Firstly, the chaos mapping theory is used to initialize the population. The standard DE algorithm is a random initialization population. Although it is beneficial to the diversity of population, it is difficult to guarantee that the quality of the population individual and the efficiency of the algorithm is reduced. Second, an adaptive adjustment mechanism for scaling factor F and crossover probability CR is adopted to improve the convergence speed and stability of the algorithm. Third, the mutation strategies and are dynamically weighted, and balance the global search and local search. Finally, the Gauss perturbation strategy is introduced to accelerate individuals to jump out of the local optimum and improve the global search ability.
3.1. Population Initialization of Chaotic Maps
The initial population of the standard DE algorithm is randomly generated. The initial population may gather in a certain area that deviates from the optimal value, thereby reducing the efficiency of the algorithm. Chaos is a stochastic phenomenon generated by a deterministic nonlinear dynamical system. It has the characteristics of equilibrium instability and mutation. It can go through all states within a certain range without repetition—that is, the randomness, regularity and ergodicity of chaos. The most commonly used chaotic model is a one-dimensional Logistic nonlinear mapping [32], and its optimization formula is:
In this formula, is the control parameter whose value is a normal number, and = 0, 1, 2 … is the number of iterations. When the value of is determined, given the initial value , the population sequence is obtained after several iterations. According to experience, when = 4, the system presents full chaos phenomenon, and there is no stable solution.
Randomly generate a D-dimensional vector , obtain chaotic vectors , according to Equation (8), and substitute the components of vectors into , , and , respectively. At this point, the initial population after chaos is obtained, the objective function value of the initial population is calculated, and the optimal N vectors are selected as the initial solution.
3.2. Adaptive Adjustment Strategies for Zoom Factor and Crossover Probability
In the DE algorithm, the control parameters that have a great influence on the optimization performance of the algorithm are the zoom factor and the crossover probability . The zoom factor affects the search range of the algorithm. The larger the value of , the higher the diversity of the population and the better the global search ability, but the convergence speed of the algorithm will be reduced accordingly; and the smaller the value of , the better the retention of good individuals, and the faster the convergence speed of the algorithm, but it is easy to fall into the local optimum—cross-probability determines the search direction of the algorithm. The smaller the value of , the better the global search ability of the algorithm. Otherwise, it will help improve the local development ability.
The control of the parameters needs different adjustments in different periods. Therefore, two relatively simple parameter adaptive strategies are proposed:
Among them, is the maximum value of the zoom factor and is the minimum value of the zoom factor. This article takes 0.9, = 0.2, is the -th generation and is the maximum number of iterations [33].
This takes 0.9, 0.2.
3.3. Weighted Dynamic Mutation Strategy
The core idea of the DE algorithm lies in how to balance global exploration capabilities and local development capabilities. The standard DE algorithm uses the mutation strategy of Equation (2). Individuals that are mutated are randomly selected individuals in the current population. This increases the diversity of the mutated individuals and improves the overall exploration ability, but the randomness largely influences the direction of evolution, which may lead to the evolution of the population deviating from the optimal value, as well as a reduction in the convergence speed of the algorithm. Equation (3) makes use of the optimal individual as the base of variation, which ensures the optimization direction of evolution, improves the local development capability and accelerates the convergence speed of the algorithm. But the optimal individuals are too single, which greatly reduces the diversity of the population, and makes the algorithm easy to fall into local optimum. In order to better balance the algorithm’s global exploration and local development capabilities, we improved Equation (3) and weightily combined it with Equation (2) to propose a new weighted dynamic mutation strategy:
Among them, , and , while is the random number evenly distributed in the interval [0,1] and is the optimal solution of the g-th generation population.
From Equation (12), we can see that the weighted operator is a monotonically decreasing function. After weighted combination, the early stage of mutation operation focuses on the overall exploration, and the later stage focuses on local development, making the algorithm better balanced in global exploration and local development, which is not only conducive to the diversity of the population, but also increases the convergence speed of the algorithm. The improvement of Equation (3) mainly considers the singleness of the population optimal solution. Using a random selection of the optimal solution and performing a difference with any individual of the population can increase the diversity of the population, and can randomly adjust the evolutionary direction of the population, making the population evolve towards the optimal direction.
3.4. Disturbance Mutation Strategy
Evolutionary algorithms are prone to fall into premature phenomenon in the late iterations. For the DE algorithm, at the later stage of the iteration, the differences between population individuals are gradually narrowed, and the diversity of populations is drastically reduced, thus forming the “aggregation” phenomenon. If at this time populations findthe global optimal solution, it has no impact on the algorithm; if it the local optimal solution is found, it is not conducive to the further exploration of the population, and cann’t find the global optimal solution. To describe this state, the following precocious definition is given:
Definition 1 variance of population fitness is shown as follows:
Among these, is the current individual fitness value, is the average fitness value of the individual and is the number of populations. From the equation, we can see that the smaller the value of , the more the population gathers together easily. Otherwise, it is in a stage of random search.
Definition 2 population precocious cardinality, if and
Then we can say that the individual is premature at the g-th generation.
Among these, is the optimal value for the g-th generation, is the variance threshold value and is precision value. This algorithm setting = 1 × 10−6, = 1 × 10−6.
If there is a precocious phenomenon in the g-th generation, a new mutation operation is carried out on individuals, and the mutation strategy is as follows:
Among these, the weighting coefficient is the same as Equation (8), and are a random number of interval [1,N]. N is the number of populations, and is a random number in interval [1,D]. is the optimum of the i-th population, while is the random variable submitted to .
From Equation (15), we can see that the new mutation strategy comprises two parts: the part is weighted by random and optimal individuals, and use the information of the optimal individual to guide other individuals to evolve in the direction of optimization; while the part uses Gaussian perturbation vector differences to randomly generate perturbation mutates in order to accelerate individuals to jump out of the local optimum and improve the overall search ability.
3.5. Algorithm for Implementation Process
- Step 1
- Initialize each parameter. The number of populations , the dimension of the solution , the maximum evolutionary generation , the upper and lower bounds of the individual variables , , the maximum and minimum of the scaling factor , , the maximum and minimum of the mutation probability , , the precocious cycle , the precision value and the variance threshold value .
- Step 2
- Initialize the population. The chaotic mapping strategy was used to generate NP initial populations, and the fitness values of the individuals were calculated and ranked in order of magnitude. From the NP populations, the top N fitness values were selected as the initial population of the algorithm.
- Step 3
- Calculate , , according to Equations (9), (10) and (12).
- Step 4
- Mutation operation. Calculate variant individuals according to Equation (11).
- Step 5
- Crossover operation. Find a new variant individual. according to Equation (6).
- Step 6
- Selection operation. The next generation is obtained from Equation (7).
- Step 7
- Update the local and global optimal values.
- Step 8
- Check whether the population is precocious or not; if it isprecocious, the mutation operation will be carried out again.If and , for to , Calculate new individuals according to Equations (15) and (16), and update the optimal value.
- Step 9
- Repeat Steps 4–8 for N times.
- Step 10
- If g does not reach the maximum number of iterations , then go to Step 3, otherwise output , .
4. Simulation Experiment and Algorithm Performance Analysis
4.1. Test Function and Comparison of Algorithms
To verify the feasibility, effectiveness and overall optimization of the algorithm, this algorithm was compared with the standard differential evolution (DE) algorithm, the well-known SADE algorithm [34] and the CAPSO algorithm [35]. All the algorithms went through 30 independent tests on five benchmark functions with different characteristics to compare the performance of each algorithm in terms of convergence speed, the accuracy of the optimal solution and their robustness. Among them, is the simple unimodal function, is the non-convex and ill-conditioned unimodal function and is the multi-peak function. There are approximately 10 n local minimum points in the interval of variables. is the multi-peak function, and there are a large number of local minimum points. is the non-convex and ill-conditioned multi-modal function. The test function description is shown in Table 1.

Table 1.
Test Functions.
4.2. Analysis of Results
This experiment was programmed using Matlab. It was run 20 times independently on a HP PC with Intel(R) Core(TM) i5-2450M CPU, 2.50 GHz RAM 4.00 GB. The algorithm parameters were set as follows: The adaptive dynamic disturbance strategy for differential evolution (ADDSDE) algorithm, population number = 50, = 0.9, = 0.2, = 0.9, = 0.2, = 15, = 1 × 10−6, the parameter settings of the comparison algorithm DE, SADE and CAPSO are the same as the original. Consider the cases when variable dimension D = 30 and D = 50. The number of iterations is appropriately changed according to the complexity of each test function. The optimal value, average optimal value and standard deviation of each algorithm are shown in Table 2 and Table 3, and the convergence curve of each algorithm is shown in Figure 1.

Table 2.
30-dimensional function optimization results.

Table 3.
50-dimensional function optimization results.
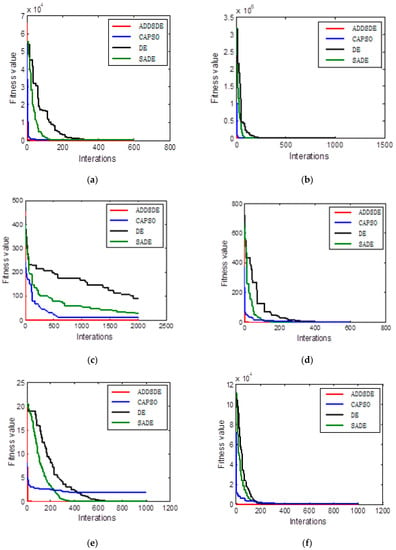
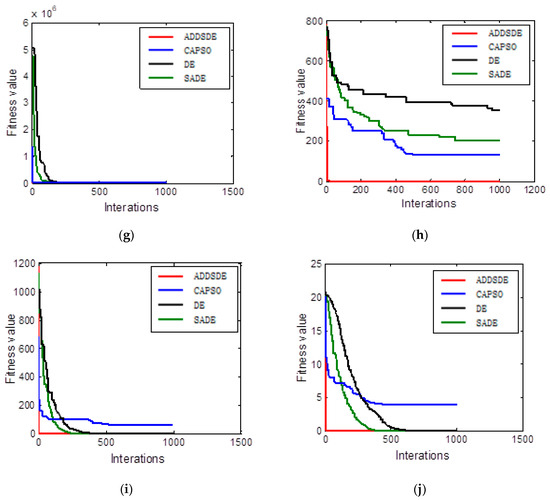
Figure 1.
Convergence curve of each algorithm: (a) Function f1 = Sphere when D = 30; (b) Function f2 = Rosenbrock when D = 30; (c) Function f3 = Rastrigin when D = 30; (d) Function f4 = Griewank when D = 30; (e) Function f5 = Ackley when D = 30; (f) Function f1 = Sphere when D = 50; (g) Function f2 = Rosenbrock when D = 50; (h) Function f3 = Rastrigin when D = 50; (i) Function f4 = Griewank when D = 50; and (j) Function f5 = Ackley when D = 50.
As can be seen from Table 2 and Table 3, the optimization result of the ADDSDE algorithm is significantly higher than that of the other three algorithms. For the five standard test functions selected, the ADDSDE algorithm can obtain the optimal value 0, except f5 = Ackley function. The convergence accuracy is optimal. The standard deviation shows that the ADDSDE algorithm is very stable. For ill-conditioned high-dimensional complex functions, other algorithms cannot get the theoretical optimal value, some algorithms are far from the theoretical optimal value, and the stability of the algorithm is not satisfactory. From Table 2 and Table 3, it can be seen that with the increase of the dimension of the solution, the evolutionary abilities of other algorithms also decrease accordingly with different degrees.
Analyzing the convergence curve of each algorithm in Figure 1, we know that the convergence curve of ADDSDE converges to the optimal solution almost at the speed of vertical descent. Additionally, its optimization ability is strong, and the convergence accuracy is high. Even for high-dimensional solutions, it can be quickly fixed to the optimal position. Due to the complexity of the function and the high dimension of the problem, the other comparison algorithms are easily trapped in the local optimumand the convergence speed is also slow.
5. Conclusions
For the solution of high-dimensional complex optimization problems, many improved DE algorithms still have many deficiencies in solution accuracy, speed, and so on. For this reason, this paper uses the advantages of the standard differential evolution (DE) mutation strategy to improve and combine mutation strategies based on chaotic mapping theory. The control parameters are adaptively weighted, and Gaussian perturbation strategies are adopted in the later iterations to prevent prematureness and jumping out of local optima, thus constituting an adaptive dynamic disturbance strategy differential evolution algorithm (ADDSDE). In order to verify the feasibility, effectiveness and optimization of the algorithm, five standard tests were selected for performance testing and compared with the DE algorithm, the SADE algorithm and the CAPSO algorithm. Finally, the simulation results show that when the algorithm is applied to high-dimensional and complex optimization problems, it can still quickly converge to the theoretical optimal value. It has a strong ability of global exploration and jumping out of the local optimal. Besides, the algorithm is stable and has a certain reference value and promotion value, which provide assistance in solving high-dimensionaland complex problems in engineering and information science.
Author Contributions
T.W. designed the main idea, the chaotic mapping strategy and the adaptive adjustment strategies of the manuscript. K.W. designed the weighted dynamic mutation Strategy and disturbance mutation strategy of the manuscript. T.D. implemented the algorithm and analyzed the experimental results. X.C. revised the manuscript and perfected the language of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was fundedby the National Social Science Foundation of China (No. 15CGL001).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Storn, R.; Price, K. Differential evolution a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Price, K.; Storn, R.M.; Lampinen, J.A. Differential Evolution: A Practical Approach to Global Optimization; Natural Computing Series; Springer: New York, NY, USA, 2005. [Google Scholar]
- Bas, E. The Training Of Multiplicative Neuron Model Based Artificial Neural Networks With Differential Evolution Algorithm For Forecasting. J. Artif. Intell. Soft Comput. Res. 2016, 6, 5–11. [Google Scholar] [CrossRef]
- Bao, J.; Chen, Y.; Yu, J.S. A regeneratable dynamic differential evolution algorithm for neural networks with integer weights. Front. Inf. Technol. Electron. Eng. 2010, 11, 939–947. [Google Scholar] [CrossRef]
- Lakshminarasimman, L.; Subramanian, S. A modified hybrid differential evolution for short-term scheduling of hydrothermal power systems with cascaded reservoirs. Energy Convers. Manag. 2008, 49, 2513–2521. [Google Scholar] [CrossRef]
- Xu, Y.; Dong, Z.Y.; Luo, F.; Zhang, R.; Wong, K.P. Parallel-differential evolution approach for optimal event-driven load shedding against voltage collapse in power systems. IET Gener. Transm. Distrib. 2013, 8, 651–660. [Google Scholar] [CrossRef]
- Berhan, E.; Krömer, P.; Kitaw, D.; Abraham, A.; Snavel, V. Solving Stochastic Vehicle Routing Problem with Real Simultaneous Pickup and Delivery Using Differential Evolution. In Innovations in Bio-inspired Computing and Applications, Proceedings of the 4th International Conference on Innovations in Bio-Inspired Computing and Applications, IBICA 2013, Ostrava, Czech Republic, 22–24 August 2013; Springer: Berlin/Heidelberg, Germany, 2014; Volume 237, pp. 187–200. [Google Scholar]
- Teoh, B.E.; Ponnambalam, S.G.; Kanagaraj, G. Differential evolution algorithm with local search for capacitated vehicle routing problem. Int. J. Bio Inspired Comput. 2015, 7, 321–342. [Google Scholar] [CrossRef]
- Pu, E.; Wang, F.; Yang, Z.; Wang, J.; Li, Z.; Huang, X. Hybrid Differential Evolution Optimization for the Vehicle Routing Problem with Time Windows and Driver-Specific Times. Wirel. Pers. Commun. 2017, 95, 1–13. [Google Scholar] [CrossRef]
- Lai, M.Y.; Cao, E.B. An improved differential evolution algorithm for vehicle routing problem with simultaneous pickups and deliveries and time windows. Eng. Appl. Artif. Intell. 2010, 23, 188–195. [Google Scholar]
- Al-Turjman, F.; Deebak, B.D.; Mostarda, L. Energy Aware Resource Allocation in Multi-Hop Multimedia Routing via the Smart Edge Device. IEEE Access 2019, 7, 151203–151214. [Google Scholar] [CrossRef]
- Jazebi, S.; Hosseinian, S.H.; Vahidi, B. DSTATCOM allocation in distribution networks considering reconfiguration using differential evolution algorithm. Energy Convers. Manag. 2011, 52, 2777–2783. [Google Scholar] [CrossRef]
- Wu, K.J.; Li, W.Q.; Wang, D.C. Bifurcation of modified HR neural model under direct current. J. Ambient Intell. Humaniz. Comput. 2019. [Google Scholar] [CrossRef]
- Kotb, Y.; Ridhawi, I.A.; Aloqaily, M.; Baker, T.; Jararweh, Y.; Tawfik, H. Cloud-Based Multi-Agent Cooperation for IoT Devices Using Workflow-Nets. J. Grid Comput. 2019, 17, 625–650. [Google Scholar] [CrossRef]
- Reddy, S.S. Optimal power flow using hybrid differential evolution and harmony search algorithm. Int. J. Mach. Learn. Cybern. 2018, 10, 1–15. [Google Scholar] [CrossRef]
- Sangaiah, A.K.; Medhane, D.V.; Han, T.; Hossain, M.S.; Muhammad, G. Enforcing Position-Based Confidentiality with Machine Learning Paradigm Through Mobile Edge Computing in Real-Time Industrial Informatics. IEEE Trans. Ind. Inform. 2019, 15, 4189–4196. [Google Scholar] [CrossRef]
- Sangaiah, A.K.; Samuel, O.W.; Li, X.; Abdel-Basset, M.; Wang, H. Towards an efficient risk assessment in software projects–Fuzzy reinforcement paradigm. Comput. Electr. Eng. 2017. [Google Scholar] [CrossRef]
- Qiu, T.; Wang, H.; Li, K.; Ning, H.; Sangaiah, A.K.; Chen, B. SIGMM: A Novel Machine Learning Algorithm for Spammer Identification in Industrial Mobile Cloud Computing. IEEE Trans. Ind. Inform. 2019, 15, 2349–2359. [Google Scholar] [CrossRef]
- Jamdagni, A.; Tan, Z.Y.; He, X.J.; Nanda, P.; Liu, R.P. RePIDS: A Multi Tier Real-time Payload-Based Intrusion Detection System. Comput. Netw. 2013, 57, 811–824. [Google Scholar] [CrossRef]
- Autili, M.; Mostarda, L.; Navarra, A.; Tivoli, M. Synthesis of decentralized and concurrent adaptors for correctly assembling distributed component-based systems. J. Syst. Softw. 2008, 81, 2210–2236. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, Y.; Li, S.; Tan, Z.; Zhao, X.; Zhou, J. FIMPA: A Fixed Identity Mapping Prediction Algorithm in Edge Computing Environment. IEEE Access 2020, 8, 17356–17365. [Google Scholar] [CrossRef]
- Ambusaidi, M.A.; He, X.; Nanda, P.; Tan, Z. Building an Intrusion Detection System Using a Filter-Based Feature Selection Algorithm. IEEE Trans. Comput. 2016, 65, 2986–2998. [Google Scholar] [CrossRef]
- Aljeaid, D.; Ma, X.; Langensiepen, C. Biometric identity-based cryptography for e-Government environment. In Proceedings of the Science & Information Conference, London, UK, 27–29 August 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 581–588. [Google Scholar]
- Ramirez, R.C.; Vien, Q.T.; Trestian, R.; Mostarda, L.; Shah, P. Multi-path Routing for Mission Critical Applications in Software-Defined Networks. In Proceedings of the International Conference on Industrial Networks and Intelligent Systems, Da Nang, Vietnam, 27–28 August 2018; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Brest, J.; Greiner, S.; Boskovic, B.; Mernik, M.; Zumer, V. Self-Adapting Control Parameters in Differential Evolution: A Comparative Study on Numerical Benchmark Problems. IEEE Trans. Evol. Comput. 2006, 10, 646–657. [Google Scholar] [CrossRef]
- Wainwright, M.J. Structured Regularizers for High-Dimensional Problems: Statistical and Computational Issues. Annu. Rev. Stat. Its Appl. 2014, 1, 233–253. [Google Scholar] [CrossRef]
- Sun, G.; Peng, J.; Zhao, R. Differential evolution with individual-dependent and dynamic parameter adjustment. Soft Comput. 2017, 22, 1–27. [Google Scholar] [CrossRef]
- Chiou, J.P.; Chang, C.F.; Su, C.T. Variable scaling hybrid differential evolution for solving network reconfiguration of distribution systems. IEEE Trans. Power Syst. 2005, 20, 668–674. [Google Scholar] [CrossRef]
- Wang, H.; Wu, Z.; Rahnamayan, S. Enhanced opposition-based differential evolution for solving high-dimensional continuous optimization problems. Soft Comput. 2011, 15, 2127–2140. [Google Scholar] [CrossRef]
- Ali, M.Z.; Awad, N.H.; Suganthan, P.N. Multi-population differential evolution with balanced ensemble of mutation strategies for large-scale global optimization. Appl. Soft Comput. 2015, 33, 304–327. [Google Scholar] [CrossRef]
- Trivedi, A.; Srinivasan, D.; Biswas, S.; Reindl, T. A genetic algorithm—Differential evolution based hybrid framework: Case study on unit commitment scheduling problem. Inf. Sci. 2016, 354, 275–300. [Google Scholar] [CrossRef]
- Ou, C.M. Design of block ciphers by simple chaotic functions. Comput. Intell. Mag. IEEE 2008, 3, 54–59. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, Y. Operating Point Optimization of Auxiliary Power Unit Using Adaptive Multi-Objective Differential Evolution Algorithm. IEEE Trans. Ind. Electron. 2016, 64, 115–124. [Google Scholar] [CrossRef]
- Qin, A.K.; Huang, V.L.; Suganthan, P.N. Differential Evolution Algorithm with Strategy Adaptation for Global Numerical Optimization. IEEE Trans. Evol. Comput. 2009, 13, 398–417. [Google Scholar] [CrossRef]
- Ying, W.; Zhou, J.; Lu, Y.; Qin, H.; Wang, Y. Chaotic self-adaptive particle swarm optimization algorithm for dynamic economic dispatch problem with valve-point effects. Energy Convers. Manag. 2011, 38, 14231–14237. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).