Abstract
We implement externally excited ZnO Mie resonators in a framework of a generalized Hubbard Hamiltonian to investigate the lifetimes of excitons and exciton-polaritons out of thermodynamical equilibrium. Our results are derived by a Floquet-Keldysh-Green’s formalism with Dynamical Mean Field Theory (DMFT) and a second order iterative perturbation theory solver (IPT). We find that the Fano resonance which originates from coupling of the continuum of electronic density of states to the semiconductor Mie resonator yields polaritons with lifetimes between ps and ps. These results are compared to ZnO polariton lasers and to ZnO random lasers. We interpret the peaks of the exciton-polariton lifetimes in our results as a sign of gain narrowing which may lead to stable polariton lasing modes in the single excited ZnO Mie resonator. This form of gain may lead to polariton random lasing in an ensemble of ZnO Mie resonators in the non-equilibrium.
Keywords:
Mie resonance; Fano resonance; Floquet modes; Stark effect; exciton; polariton; semiconductors; nano-structures; lasers; dynamical mean field theory; complex media; non-equilibrium PACS:
42.55.-f lasers; 71.10.-w theories and models of many-electron systems; 42.50.Hz strong-field excitation of optical transitions in quantum systems; multi-photon processes; dynamic Stark shift; 74.40+ Fluctuations; 03.75.Lm Tunneling, Josephson effect, Bose-Einstein condensates in periodic potentials, solitons, vortices, and topological excitations; 72.20.Ht high-field and nonlinear effects; 71.36.+c polaritons; 71.35.-y excitons and related phenomena; 42.55.Px semiconductor lasers, laser diodes; 89.75.-k complex systems
1. Introduction
Semiconductor micro-cavities operating in the strong coupling regime are optical resonators in which the eigenmodes are no longer purely excitonic or photonic, but a mixed light matter state is occurring. This evolution has finally led to polariton lasing [1,2,3,4,5,6,7,8,9]. Random lasing [10] has been claimed to be fundamentally incompatible with polaritons. From recent research developments however it turns out that it is not yet clear whether random lasers are either pure photon lasers or pure polariton lasers, or whether they even have both characteristics at the same time [11]. Thresholds like in conventional lasers may be observed [12,13]. We show in this article that for excitations of the quantum many-body system of ZnO nano-resonators by experimentally feasible threshold intensities of the optical pump found in random laser experiments we derive theoretically well confined peaks in terms of gain narrowing in the spectrum of the lifetime for the cavity polariton in the non-equilibrium. These peaks give evidence that such a sample may undergo a transition towards exciton-polariton lasing rather than a transition to exciton-photon lasing, at least a coexistence of both regimes may occur. ZnO is known for excellent light-matter coupling characteristics [7,14,15,16,17,18,19,20,21,22,23,24,25,26,27]; it is predestined for this study. It has been experimentally derived that ZnO can be considered as a Mott insulator under certain conditions [16,18]. A feature of ZnO nano-structures is a transition from the non-centrosymmetric wurtzite structure to the centrosymmetric rocksalt configuration with a variation of temperature and pressure, see Figure 1. When the system is externally pumped, Figure 1c, lasing may occur eventually. The propagating light intensity in the random laser may experience Mie resonances as a whispering gallery resonance of light at the inner surface of the individual nano-structure. In a complex medium, which pumped ZnO in the non-equilibrium certainly is, the resonant Mie mode forms a light matter bound state in the form of a Fano resonance. It leads to quantum many body physics and the renormalization of the bands under excitations. We consider (i) the semiconductor material as it is subjected to the strong external AC field of the optical pump in the sense of a topological excitation [14,15]. We model the coupling of the classical laser, eV, to the quantum many body system as well as higher-order photon absorption processes, eV etc., by means of the Floquet matrix [28,29,30,31]. The band structure and the lifetimes of light-matter coupled states are derived by the Dynamical Mean Field Theory (DMFT) [32,33,34,35] in the sense of a generalized Hubbard-Hamiltonian out-of thermodynamical equilibrium. The Hubbard Hamiltonion includes strictly local interactions between electrons with opposite spins. It is predestined to describe the exciton dynamics of excited matter in a physical time range where additional impurity scattering is not expected. Bulk ZnO develops under excitation in the near band gap region an exciton dynamics. In the second step of this work (ii) we additionally consider photons which populate the Mie resonance of the individual nano-resonator and we study the formation of polaritons. The spectral features are compared to experimental emission spectra of ZnO random lasers and polariton lasers and we find a very good agreement in either case.
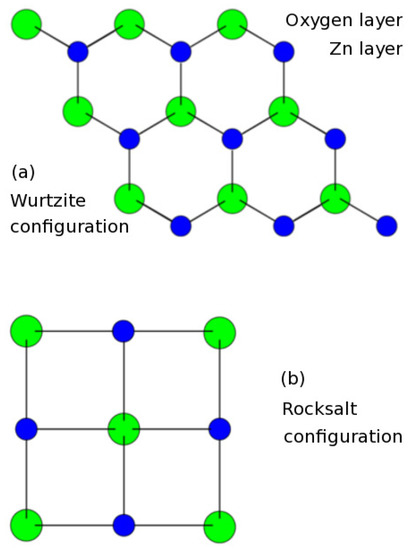
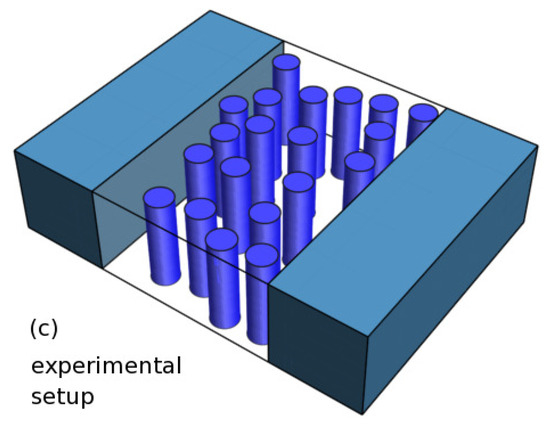
Figure 1.
ZnO structure (ab-plane). (a) non-centrosymmetric, hexagonal, wurtzite configuration; (b) centrosymmetric, cubic, rocksalt configuration (Rochelle salt) [22,25,26]. The rocksalt configuration is distinguished by a tunable gap from eV up to eV, a gap value of eV is typical for the monocrystal rocksalt configuration without oxygen vacancies [23,24]. As such the rocksalt configuration could be suited for higher harmonics generation under non-equilibrium topological excitation [14,15,36]; (c) Typical setup of a solid state random laser: Densely packed disordered ZnO nano-resonators are embedded in a waveguide. The sample is externally pumped in (111) direction. Mie resonances [37] occur at the inner cylinder jacket and they couple to the density of bulk states in the sense of a Fano resonance. We consider in this article the exciton and exciton polariton dynamics of the single scatterer as the building block of the solid state random laser or the polariton random laser. Laser gain is attributed to the accumulation of excited states at a certain level along with a significantly increased life-time of the excited state, i.e., a stable laser in stationary state. In the random laser each scatterer of a well defined area or volume as part of an ensemble of several scatterers is going to lase. The investigation of the complex Mie-resonance in the non-equilibrium as the origin of pronounced laser levels for polariton lasing is on target. The formation of the polariton as a quasiparticle is characterized by the coupling strength of the bulk electronic procedures and the cavity resonance which is on the order of the band width or one order below and thus it is in the polariton range [38]. The waveguide principally plays only a subordinate role; it does not serve as the dominating conventional laser resonator cavity.
2. Theory
2.1. Hubbard Model for Excitons and Exciton-Polaritons
The interacting Hamiltonian for the complex driven semiconductor resonator can be written as follows
The electrons are described as a tight binding model, see Figure 2, where the splitting into valence and conduction band symmetrically to the Fermi level is included by means of the Coulomb interaction U, see Figure 2b. The ZnO gap assumes the value of eV [16,17]. The first term in the Hamiltonian denotes the local onsite potential. The term is devoted to the onsite Coulomb interaction U between electrons with opposite spins. The third term is due to the hopping processes with the amplitude t between nearest neighbor sites. The classical external pumping is described in terms of the time dependent field with the laser frequency , and respectively. In the term is noted the renormalization of the hopping processes due to interaction with the pump field. The electronic dipole operator is given with strength . The photonic cavity mode with the resonance frequency is coupled to the electron system as with a coupling strength g in units of the standard hopping t. The single band effective Hubbard model has been proven to be perfectly suited for the description of the movement of hole-bound electrons, excitons, as a quasiparticle through the lattice of metal ions [39,40,41], which is a lattice of Zn ions here. For the solution of the Hamiltonian for driven bulk matter (i) as well as for the bulk-cavity coupled system (ii) including the fifth and the sixth term of Equation (1), the explicit time dependence of the external field has to be accounted for as well as the dynamics of the system. It yields Green’s functions which depend on two separate time arguments. The double Fourier transform from time to frequency coordinates leads to two separate frequencies which are chosen as relative and center-of-mass frequency [30,31,34,35] and we can thus expand the underlying physical procedures into Floquet modes, the graphical explanation is found in Figure 2a,
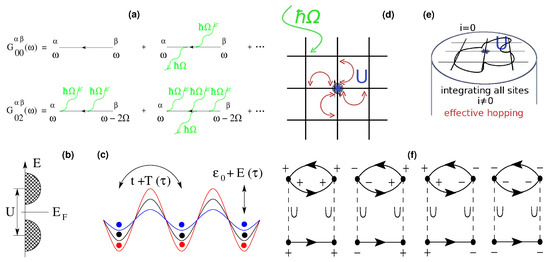
Figure 2.
Theoretical setup (a) Floquet expansion of the Green’s function G into higher harmonics of . (b) Hubbard model of the electronic system. The gap between bands is defined by the Coulomb interaction U symmetrically to the Fermi Energy . (c) Tight binding system of the crystal lattice. The hopping parameter t is renormalized by external time dependent excitations . are renormalizations of the local potential alone; (d) non-equilibrium DMFT. Pump photons enhance electronic hopping which is mapped on the single site on the background of the surrounding identical lattice sites, the bath. (e) integration over all sites yields an effective self-consistent theory including non-equilibrium effects. The electronic system is coupled to Mie resonances; (f) diagrammatic contributions of the second order IPT.
In Equation (2) label the Floquet modes and label the branch of the Keldysh contour (±) where the respective time argument resides. Floquet modes in time-space an analogue to Bloch modes in real space. The physical meaning of the expansion into Floquet modes is however noteworthy, since it is the quantized absorption and emission of energy out of and into the classical external driving field.
In case of uncorrelated electrons, , an analytical solution for the Green’s function is found by solving the Hamiltonian. The retarded component of is
represents the externally induced dispersion which is to be distinguished from the lattice dispersion . are the cylindrical Bessel functions of integer order, and characterize the external driving laser. The physical Green’s function for the optically excited band electron (LB) is derived
2.2. Dynamical Mean-Field Theory for Electromagnetically Driven Semiconductors in d = 3 Dimensions
The Hamiltonian for the correlated system, , Equation (1), is solved numerically with a single-site Dynamical Mean Field Theory (DMFT) [33,34,35] and an iterated perturbation theory solver (IPT), see Figure 2f. The laser-band-electron Green’s function , Equation (4), is characterized by the wave vector k, describing the periodicity of the lattice, the electronic energy and the external driving frequency as contained in the Floquet indices . The DMFT self-consistency relation assumes the form of a dimensional matrix equation in regular Keldysh space and in becomes dimensional in Floquet space. The IPT is generalized to Keldysh-Floquet form as well. The resulting numerical algorithm proves to be efficient and stable for all values of U.
The coupling under the assumption of the Coulomb gauge , that is in Fourier space , generates the factor that cancels the term in the renormalized cylindrical Bessel function; for details see Equation (7) of Ref. [34]. By checking the Floquet sum we find that considering the first ten ( ) Floquet modes is sufficient within the numerical accuracy of the DMFT [14,15]. A cut-off after a smaller number would lead to a drift in the total energy of the system and thus it would hurt conservation laws.
While the quasienergy spectra of excitons and the Franz-Keldysh effect in the non-equilibrium have been broadly investigated in d = 2 dimensions for semiconductors in the THz regime, especially for GaAs [42,43,44]; only recently the first numerical studies of the excitonic quasienergy spectra under topological excitations in the optical regime have been performed for ZnO with DMFT in d = 3 dimensions [14,15]. Whereas DMFT has been so far preferentially used for typical Mott insulators [45] like NiO [46,47], this DMFT study [14,15] is remarkable, since ZnO as a wide-gapped transition metal oxide from the group IIb in the table of the elements which may be considered to behave as a Mott insulator at zero temperature [16,18], especially in driven nano-structures this is the case. ZnO is broadly investigated for random lasing in disordered ensembles of nano-pillars and nano-grains, i.e., Mie spheres, and a restriction to two-dimensional electronic processes is no necessary condition in these ensembles [10]. Two-dimensionality is a priori also not necessary for the considering the formation of polaritons [1].
3. Results
For driven ZnO bulk we display in Figure 3a the local density of excitonic states (LDOS) for 10.0 MW/cm pump power and the varying external laser frequency . The systems parameters are found in the caption of Figure 3. A multitude of Floquet bands arises due to the AC Stark effect and sub-gaps are formed whereas the original gap closes. These results are computed for a cubic lattice structure and their physical interpretation besides the formation of exciton-quasiparticles is the generation of bands of even higher harmonics due to the symmetry of the system. For the fixed value of eV, Figure 3b, we find an increasing LDOS for excitons in the ZnO gap region. The solid black line indicates the undriven bandstructure with a half band width of eV. In the valence and the conduction band sub gaps towards the near-gap band edges at eV and eV are formed, while at the inner band edges a step-like decrease is found. A smooth mid-gap feature is building up with increasing pump strength. In the results for the inverse lifetime, , of excitons , Figure 3c, which characterizes the dynamics of the excitons we find a sharp peak at the Fermi edge, i.e., small lifetimes of excitons as we expected it. is increasing in the gap near the equilibrium band edges. We find an increasing LDOS for excitons with the increase of the external excitation strength. The lifetimes of the near-edge states are therefore progressively decreased. A plateauing of exciton lifetimes is observed in the band gap otherwise, whereas deep in the band at e.g., eV we find for increasing external pump intensity a crossover of the corresponding excitonic lifetimes. Here exhibits a local maximum around a pump intensity of MW/cm which then transforms with further increasing pump strength into a local minimum (orange dash-dotted line) and eventually reaches lifetimes almost as high as in the un-driven equilibrium system (black solid line). For the cavity coupled system, Figure 3d, we find a qualitatively different behavior. It should be noted first that the presence of the cavity also for the weakly coupled case in the non-equilibrium always has an influence on the full spectrum of the LDOS. This is necessarily the case for energy and particle conservation. The semiconductor pillars with a full diameter of nm are chosen with a geometrical Mie resonance as a single whispering gallery mode on the inner jacket of the resonator. The coat thickness may vary with the fineness of the ZnO material. As such it may determine the Q-factor of the single Mie resonator in principle [48]; however, in the non-equilibrium regime and in the corresponding physical time range microscopic interactions in the sense of impurity scattering in the selvedge have no fundamental influence. The Mie resonance of eV corresponds to the wavelength nm [37]; effectively this whispering gallery is populated in the resonance by photons. Thus, the classical picture of the Mie resonance [49] of a sole geometric resonance of otherwise passive matter is replaced here by the Fano resonance [50] of the single mode with the continuum of excitons which is embedded in a Floquet matrix [28,29,30,31]. The Floquet matrix, see Figure 2a, represents mathematically the physics of high amplitude excitations and higher harmonics [36] under the presumption of energy conservation. We display the exciton-polariton lifetimes for at zero temperature and at half filling. The coupling strength as such is characteristic for the formation of polaritons [38]. The results are derived for an external optical pump intensity of 2.4 MW/cm which on the other side is a typical pump strength for solid state random lasers [51,52,53,54]. We find a sharp dip in the lifetimes of polaritonic states at the Fermi energy. In agreement with the results for the bulk we also find the characteristic features around the Fermi edge. The dip of at eV for the driving intensity of 2.4 MW/cm for bulk persists in the full cavity coupled system, Figure 3d. The magnitude of the exciton-polariton lifetimes in the marked features of gap states is ps (for eV and eV), ps (for eV), and ps (for eV). The peak of the exciton-polariton lifetimes in the original band at eV is derived as ps. The peaks in the results for the polaritonic lifetime (black arrows in Figure 3d) are all emerging quite far off from the cavity’s resonance at eV which is a proof of the dynamic Fano coupling in the driven non-equilibrium system. The peaks can be interpreted as a splitting into several polariton branches which for the given parameters of random lasers may define the laser spectrum of a random polariton laser consisting of ZnO Mie resonators. The result for the optical DC-conductivity as the materials characteristics in the non-equilibrium is displayed for in the inset of Figure 3d in the THz region and the same parameters otherwise. assumes a finite value. The pronounced minima in are another signature of gain and gain narrowing in the full polaritonic spectrum. Our results of lifetimes of excitons and exciton-polaritons are corroborated by the experimental findings of laser spectra in several setups of ZnO Mie resonators as well as in ZnO random lasers [20,21,51,52,53,54,55], where, in either experiment, stable lasing modes at 3.13 eV have been found. In either system the spectral result is attributed to the coupling of the excited electronic subsystem of ZnO bulk to the resonator mode of the single scatterer. Refs. [20,21,55] interpret their findings as exciton-polaritons.
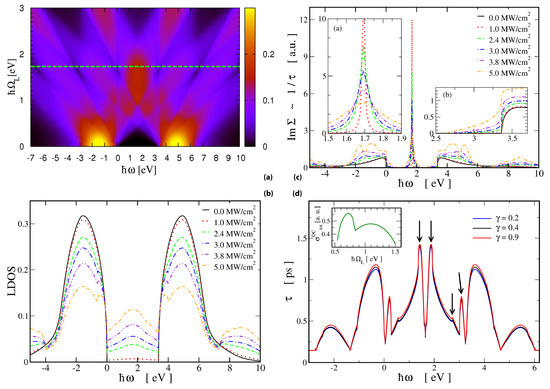
Figure 3.
(a) LDOS of bulk ZnO for varying excitation laser frequency . The electronic gap in equilibrium is eV, the microscopic dipole moment equals cm, the lattice constant is . The excitation strength is 10.0 MW/cm . A multitude of Floquet bands and sub-gaps emerge due to the AC Stark effect; (b) excitonic LDOS for the driving frequency if eV, with increasing intensity, 0 to 5.0 MW/cm . Spectral weight is shifted into the Floquet bands which cross in the gap region. Mid-gap states emerge; (c) inverse excitonic lifetime , , for parameters as in (b); (inset a) the peak centered at eV indicates small lifetimes and a fast decay of mid-gap states (red line); (inset b) the excitonic lifetime near the band edges is reduced but finite. With increasing pump intensity the near band-edge lifetime decreases but in comparison to the value in the band it is increased; (d) lifetimes of exciton-polaritons in ZnO nano-pillars. Parameters are: pump wavelength nm (1.75 eV), cavity resonance at nm, (2.45 eV, passive refractive index ) pump intensity 2.4 MW/cm . Sharp features at eV and eV, ( nm) show gain narrowing. The increase of the coupling strength of bulk matter and cavity yields rather small effects. (inset) The optical conductivity for exciton-polaritons, , in the THz regime in the non-equilibrium is finite.
4. Conclusions
We presented in this article results for the local density of states and the lifetimes of excitons and of exciton-polaritons in excited ZnO Mie resonators in the non-equilibrium. The sharp spectral features of the polaritonic lifetimes are in clear qualitative and quantitative contrast to the results for the exciton lifetimes. Furthermore they are in qualitative and in quantitative agreement with experimental results of ZnO polariton lasers on the one hand and on the other hand they also agree with results for the spectrum and the life times of solid state random lasers. We conclude that a random polariton laser can be built as an application of ZnO Mie resonators in the non-equilibrium.
Author Contributions
All authors contributed equally to this work. All authors wrote and reviewed the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no funding.
Acknowledgments
The authors thank H. Cao, P. Guyot-Sionnest, H. Kalt, A.-P. Jauho, M. Richard, J.K. Freericks and G. Kotliar for fruitful discussions.
Conflicts of Interest
The authors declare no conflict of interests.
References
- Yamamoto, Y. Half-matter, half-light amplifier. Nature 2000, 405, 629–630. [Google Scholar] [CrossRef]
- Imamoglu, A.; Ram, R.J.; Pau, S.; Yamamoto, Y. Nonequilibrium condensates and lasers without inversion: Exciton-polariton lasers. Phys. Rev. A 1996, 53, 4250–4253. [Google Scholar] [CrossRef] [PubMed]
- Zamfirescu, M.; Kavokin, A.; Gil, B.; Malpuech, G.; Kaliteevski, M. ZnO as a material mostly adapted for the realization of room-temperature polariton lasers. Phys. Rev. B 2002, 65, 161205(R). [Google Scholar] [CrossRef]
- Deng, H.; Weihs, G.; Santori, C.; Bloch, J.; Yamamoto, Y. Condensation of semiconductor microcavity exciton polaritons. Science 2002, 298, 199–202. [Google Scholar] [CrossRef]
- Kasprzak, J.; Richard, M.; Kundermann, S.; Baas, A.; Jeambrun, P.; Keeling, J.M.; Marchetti, F.M.; Szymanska, M.H.; Andre, R.; Staehli, J.L.; et al. Bose-Einstein condensation of exciton polaritons. Nature 2006, 443, 409–414. [Google Scholar] [CrossRef] [PubMed]
- Schneider, C.; Rahimi-Iman, A.; Kim, Y.N.; Fischer, J.; Savenko, I.G.; Amthor, M.; Lermer, M.; Wolf, A.; Worschech, L.; Kulakovskii, V.D.; et al. An electrically pumped polariton laser. Nature 2013, 497, 348–352. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Orosz, L.; Kamoun, O.; Bouchoule, S.; Brimont, C.; Disseix, P.; Guillet, T.; Lafosse, X.; Leroux, M.; Leymarie, J.; et al. Fabrication and characterization of a room-temperature ZnO polariton laser. Appl. Phys. Lett. 2013, 102, 191118. [Google Scholar] [CrossRef]
- Guillet, T.; Mexis, M.; Levrat, J.; Rossbach, G.; Brimont, C.; Bretagnon, T.; Gil, B.; Butte, R.; Grandjean, N.; Orosz, L.; et al. Polariton lasing in a hybrid bulk ZnO microcavity. Appl. Phys. Lett. 2011, 99, 161104. [Google Scholar] [CrossRef]
- Bajoni, D. Polariton lasers. Hybrid light-matter lasers without inversion. J. Phys. D Appl. Phys. 2012, 45, 313001. [Google Scholar] [CrossRef]
- Cao, H.; Zhao, Y.G.; Ho, S.T.; Seelig, E.W.; Wang, Q.H.; Chang, R.P.H. Random Laser Action in Semiconductor Powder. Phys. Rev. Lett. 1999, 82, 11–2278. [Google Scholar] [CrossRef]
- Niyuki, R.; Fujiwara, H.; Nakamura, T.; Ishikawa, Y.; Koshizaki, N.; Tsuji, T.; Sasaki, K. Double threshold behavior in a resonance-controlled ZnO random laser. APL Photonics 2017, 2, 036101. [Google Scholar] [CrossRef]
- Lu, T.-C.; Lai, Y.-Y.; Lan, Y.-P.; Huang, S.-W.; Chen, J.-R.; Wu, Y.-C.; Hsieh, W.-F.; Deng, H. Room temperature polariton lasing vs. photon lasing in a ZnO-based hybrid microcavity. Opt. Express 2012, 20, 5530. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Zhang, B.; Wang, Z.; Fischer, J.; Brodbeck, S.; Kamp, M.; Schneider, C.; Höfling, S.; Deng, H. Coherent Polariton Laser. Phys. Rev. X 2016, 6, 011026. [Google Scholar] [CrossRef]
- Lubatsch, A.; Frank, R. Evolution of Floquet Topological Quantum States in Driven Semiconductors. Eur. Phys. J. B 2019, 92, 215. [Google Scholar] [CrossRef]
- Lubatsch, A.; Frank, R. Behavior of Floquet Topological Quantum States in Optically Driven Semiconductors. Symmetry 2019, 11, 1246. [Google Scholar] [CrossRef]
- Chang, P.-C.; Lu, J.G. Temperature dependent conduction and UV induced metal-to-insulator transition in ZnO nanowires. Appl. Phys. Lett. 2008, 92, 212113. [Google Scholar] [CrossRef]
- Aghamalyan, N.R.; Aslanyan, T.A.; Vardanyan, E.S.; Kafadaryan, Y.A.; Hovsepyan, R.K.; Petrosyan, S.I.; Poghosyan, A.R. Metal-insulator electronic phase transitions in wide-gap ZnO semiconductors. J. Contemp. Phys. 2012, 47, 275–281. [Google Scholar] [CrossRef]
- Chang, P.-C.; Chien, C.-J.; Stichtenoth, D.; Ronning, C.; Lu, J.G. Finite size effect in ZnO nanowires. Appl. Phys. Lett. 2007, 90, 113101. [Google Scholar] [CrossRef]
- Shimada, R.; Xie, J.; Avrutin, V.; Özgür, Ü.; Morkovic, H. Cavity polaritons in ZnO-based hybrid microcavities. Appl. Phys. Lett. 2008, 92, 011127. [Google Scholar] [CrossRef]
- Dai, J.; Xu, C.X.; Sun, X.W.; Zhang, X.H. Exciton-polariton microphotoluminescence and lasing from ZnO whispering-gallery mode microcavities. Appl. Phys. Lett. 2011, 98, 161110. [Google Scholar] [CrossRef]
- Duan, Q.; Xu, D.; Liu, W.; Lu, J.; Zhang, L.; Wang, J.; Wang, Y.; Gu, J.; Hu, T.; Xie, W.; et al. Polariton lasing of quasi-whispering gallery modes in a ZnO microwire. Appl. Phys. Lett. 2012, 103, 022103. [Google Scholar] [CrossRef]
- Razavi-Khosroshahi, H.; Edalati, K.; Wu, J.; Nakashima, Y.; Arita, M.; Ikoma, Y.; Sadakiyo, M.; Inagaki, Y.; Staykov, A.; Yamauchi, M.; et al. High-pressure zinc oxide phase as visible-light-active photocatalyst with narrow band gap. J. Mater. Chem. A 2017, 5, 20298–20303. [Google Scholar] [CrossRef]
- Huang, F.; Lin, Z.; Lin, W.; Zhang, J.; Ding, K.; Wang, Y.; Zheng, Q.; Zhan, Z.; Yan, F.; Chen, D.; et al. Research progress in ZnO singlecrystal: Growth, scientific understanding, and device applications. Chin. Sci. Bull. 2014, 59, 1235. [Google Scholar] [CrossRef]
- Park, W.I.; Jun, Y.H.; Jung, S.W.; Yi, G.-C. Excitonic emissions observed in ZnO single crystal nanorods. Appl. Phys. Lett. 2003, 82, 964–966. [Google Scholar] [CrossRef]
- Fritsch, D.; Schmidt, H.; Grundmann, M. Pseudopotential band structures of rocksalt MgO, ZnO, and Mg1-xZnxO. Appl. Phys. Lett. 2006, 88, 134104. [Google Scholar] [CrossRef]
- Dixit, H.; Saniz, R.; Lamoen, D.; Partoens, B. The quasiparticle band structure of zincblende and rocksalt ZnO. J. Phys. Condens. Matter 2010, 22, 125505. [Google Scholar] [CrossRef]
- Koster, R.S.; Changming, M.F.; Dijkstra, M.; van Blaaderen, A.; van Huis, M.A. Stabilization of Rock Salt ZnO Nanocrystals by Low-Energy Surfaces and Mg Additions: A First-Principles Study. J. Phys. Chem. C 2015, 119, 5648–5656. [Google Scholar] [CrossRef]
- Floquet, G. Sur les équations différentielles linéaires à coefficients périodiques. Ann. l’ Ecole Norm. Sup. 1883, 12, 47–88. [Google Scholar] [CrossRef]
- Grifoni, M.; Hänggi, P. Driven quantum tunneling. Phys. Rep. 1998, 304, 229–354. [Google Scholar] [CrossRef]
- Frank, R. Coherent control of Floquet-mode dressed plasmon polaritons. Phys. Rev. B 2012, 85, 195463. [Google Scholar] [CrossRef]
- Frank, R. Non-equilibrium polaritonics - Nonlinear effects and optical switching. Ann. Phys. 2013, 525, 66–73. [Google Scholar] [CrossRef]
- Georges, A.; Kotliar, G.; Krauth, W.; Rozenberg, M.J. Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions. Rev. Mod. Phys. 1996, 68, 13. [Google Scholar] [CrossRef]
- Lubatsch, A.; Kroha, J. Optically driven Mott-Hubbard systems out of thermodynamical equilibrium. Ann. Phys. 2009, 18, 863–867. [Google Scholar] [CrossRef]
- Frank, R. Quantum criticality and population trapping of fermions by non-equilibrium lattice modulations. New J. Phys. 2013, 15, 123030. [Google Scholar] [CrossRef]
- Frank, R. Population trapping and inversion in ultracold Fermi gases by excitation of the optical lattice-Non-equilibrium Floquet - Keldysh description. Appl. Phys. B 2013, 113, 41–47. [Google Scholar] [CrossRef][Green Version]
- Faisal, F.H.M.; Kaminski, J.Z. Floquet-Bloch theory of high-harmonic generation in periodic structures. Phys. Rev. A 1997, 56, 748. [Google Scholar] [CrossRef]
- Lubatsch, A.; Frank, R. Self-consistent quantum field theory for the characterization of complex random media by short laser pulses. Phys. Rev. Res. 2020, in press. [Google Scholar]
- Forn-Diaz, P.; Lamata, L.; Rico, E.; Kono, J.; Solano, E. Ultrastrong coupling regimes of light-matter interaction. Rev. Mod. Phys. 2019, 91, 025005-1. [Google Scholar] [CrossRef]
- Zhang, F.C.; Rice, T.M. Effective Hamiltonian for the superconducting Cu oxides. Phys. Rev. B 1998, 37, 3759. [Google Scholar] [CrossRef]
- Jarell, M.; Freericks, J.K.; Pruschke, T. Optical conductivity of the infinite-dimensional Hubbard model. Phys. Rev. B 1995, 51, 11704. [Google Scholar] [CrossRef]
- Eder, R.; van den Brink, J.; Sawatzky, G.A. Intersite Coulomb interaction and Heisenberg exchange. Phys. Rev. B 1996, 54, 732(R). [Google Scholar] [CrossRef] [PubMed]
- Jauho, A.-P.; Johnsen, K. Dynamical Franz-Keldysh Effect. Phys. Rev. Lett. 1996, 76, 4576–4579. [Google Scholar] [CrossRef] [PubMed]
- Nordstrom, K.B.; Johnsen, K.; Allen, S.J.; Jauho, A.-P.; Birnir, B.; Kono, J.; Noda, T.; Akiyama, H.; Sakaki, H. Excitonic Dynamical Franz-Keldysh Effect. Phys. Rev. Lett. 1998, 81, 457–460. [Google Scholar] [CrossRef]
- Johnsen, K.; Jauho, A.-P. Quasienergy Spectroscopy of Excitons. Phys. Rev. Lett. 1999, 83, 1207–1210. [Google Scholar] [CrossRef]
- Savrasov, S.Y.; Kotliar, G. Linear Response Calculations of Lattice Dynamics in Strongly Correlated Systems. Phys. Rev. Lett. 2003, 90, 056401-1. [Google Scholar] [CrossRef] [PubMed]
- Fiebig, M.; Fröhlich, D.; Lottermoser, T.; Pavlov, V.V.; Pisarev, R.V.; Weber, H.-J. Second Harmonic Generation in the Centrosymmetric Antiferromagnet NiO. Phys. Rev. Lett. 2001, 87, 137202-1. [Google Scholar] [CrossRef]
- Castell, M.R.; Wincott, P.L.; Condon, N.G.; Muggelberg, C.; Thornton, G.; Dudarev, S.L.; Sutton, A.P.; Briggs, G.A.D. Atomic-resolution STM of a system with strongly correlated electrons:NiO(001) surface structure and defect sites. Phys. Rev. B 1997, 55, 7859. [Google Scholar] [CrossRef]
- Gibbs, H.M.; Khitrova, G.; Koch, S.W. Exciton–polariton light–semiconductor coupling effects. Nat. Photonics 2011, 5, 275–282. [Google Scholar] [CrossRef]
- Mie, G. Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen. Ann Phys. (Berl.) 1908, 4, 377–445. [Google Scholar] [CrossRef]
- Fano, U. Effects of Configuration Interaction on Intensities and Phase Shifts. Phys. Rev. A 1961, 124, 1866. [Google Scholar] [CrossRef]
- Lubatsch, A.; Frank, R. A Self-Consistent Quantum Field Theory for Random Lasing. Appl. Sci. 2019, 9, 2477. [Google Scholar] [CrossRef]
- Kalt, H.; Fallert, J.; Dietz, R.J.B.; Sartor, J.; Schneider, D.; Klingshirn, C. Random lasing in nanocrystalline ZnO powders. Phys. Status Solidi B 2010, 247, 1448–1452. [Google Scholar] [CrossRef]
- Lubatsch, A.; Frank, R. Coherent transport and symmetry breaking - laser dynamics of constrained granular matter. New J. Phys. 2014, 16, 083043. [Google Scholar] [CrossRef]
- Lubatsch, A.; Frank, R. Tuning the Quantum Efficiency of Random Lasers - Intrinsic Stokes-Shift and Gain. Sci. Rep. 2015, 5, 17000. [Google Scholar] [CrossRef]
- Lai, Y.-Y.; Chou, Y.-H.; Lan, Y.-P.; Lu, T.-C.; Wang, S.-C.; Yamamoto, Y. Crossover from polariton lasing to exciton lasing in a strongly couples ZnO microcavity. Sci. Rep. 2015, 6, 20581. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).