Identification Method of Geometric Deviations for Multi-Tasking Machine Tools Considering the Squareness of Translational Axes
Abstract
:1. Introduction
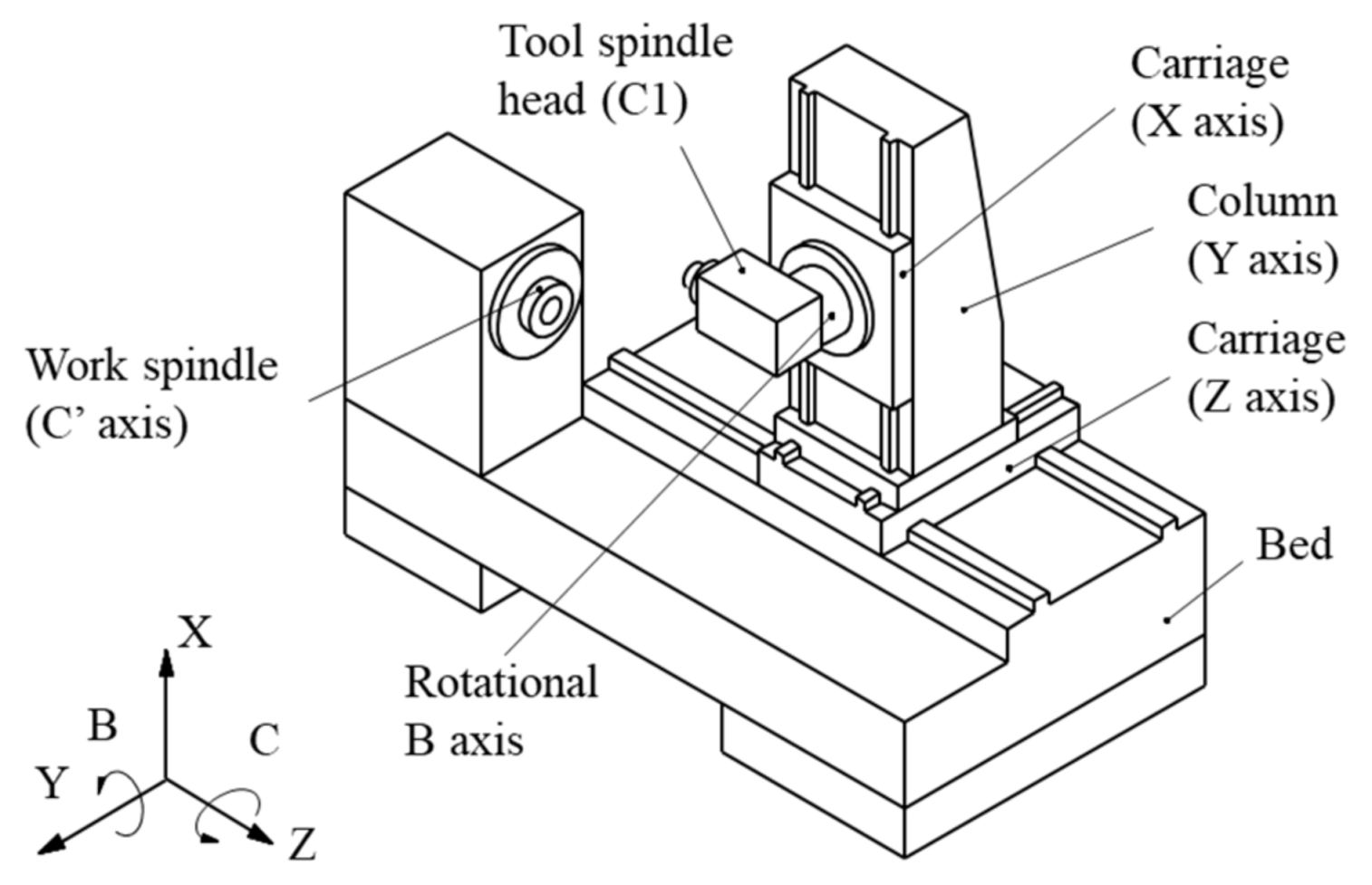
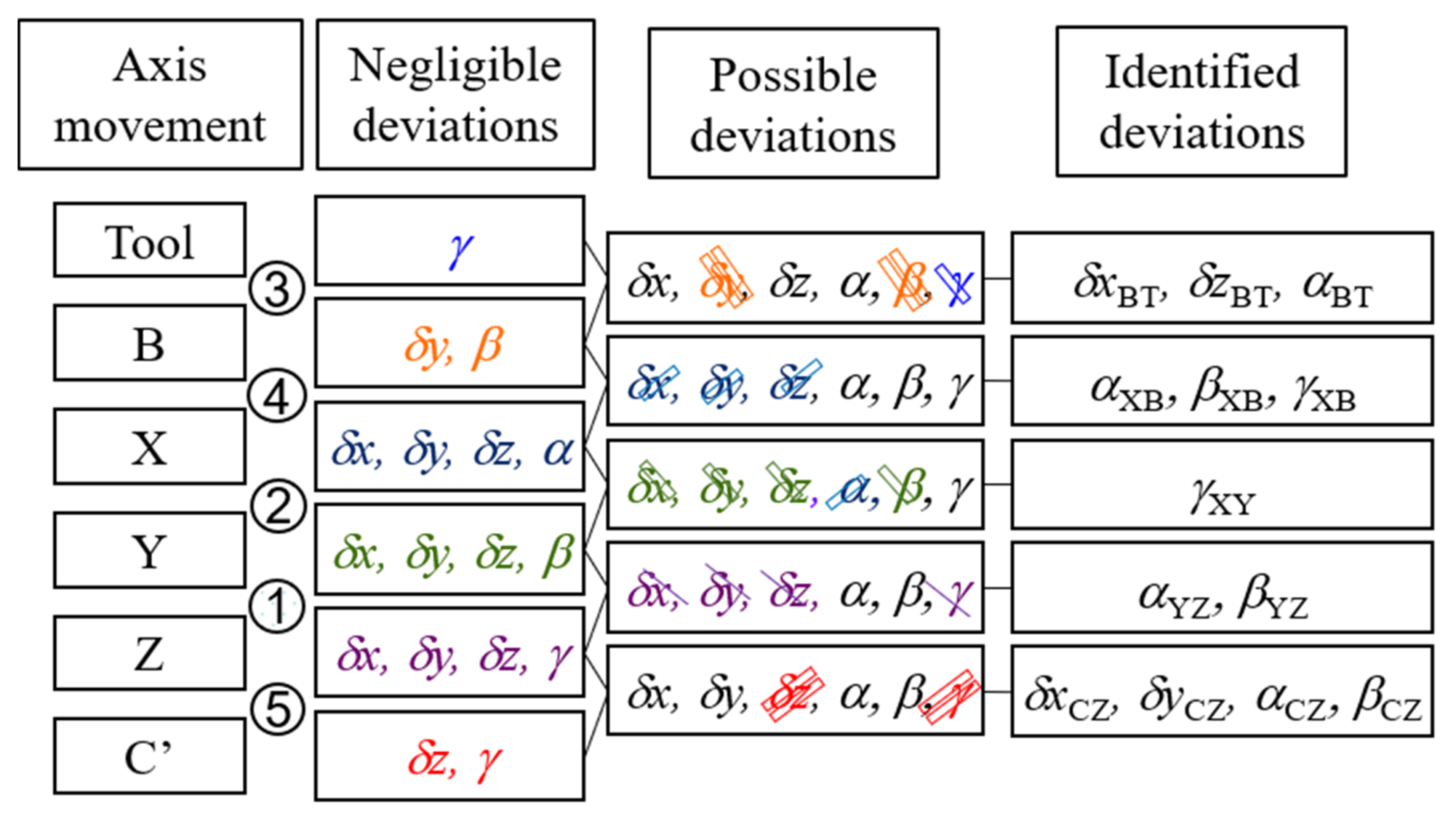
2. Coordinate System and Geometric Deviations of Multi-Tasking Machine Tools
3. Simultaneous Three-Axis Control Movements and Mathematical Model
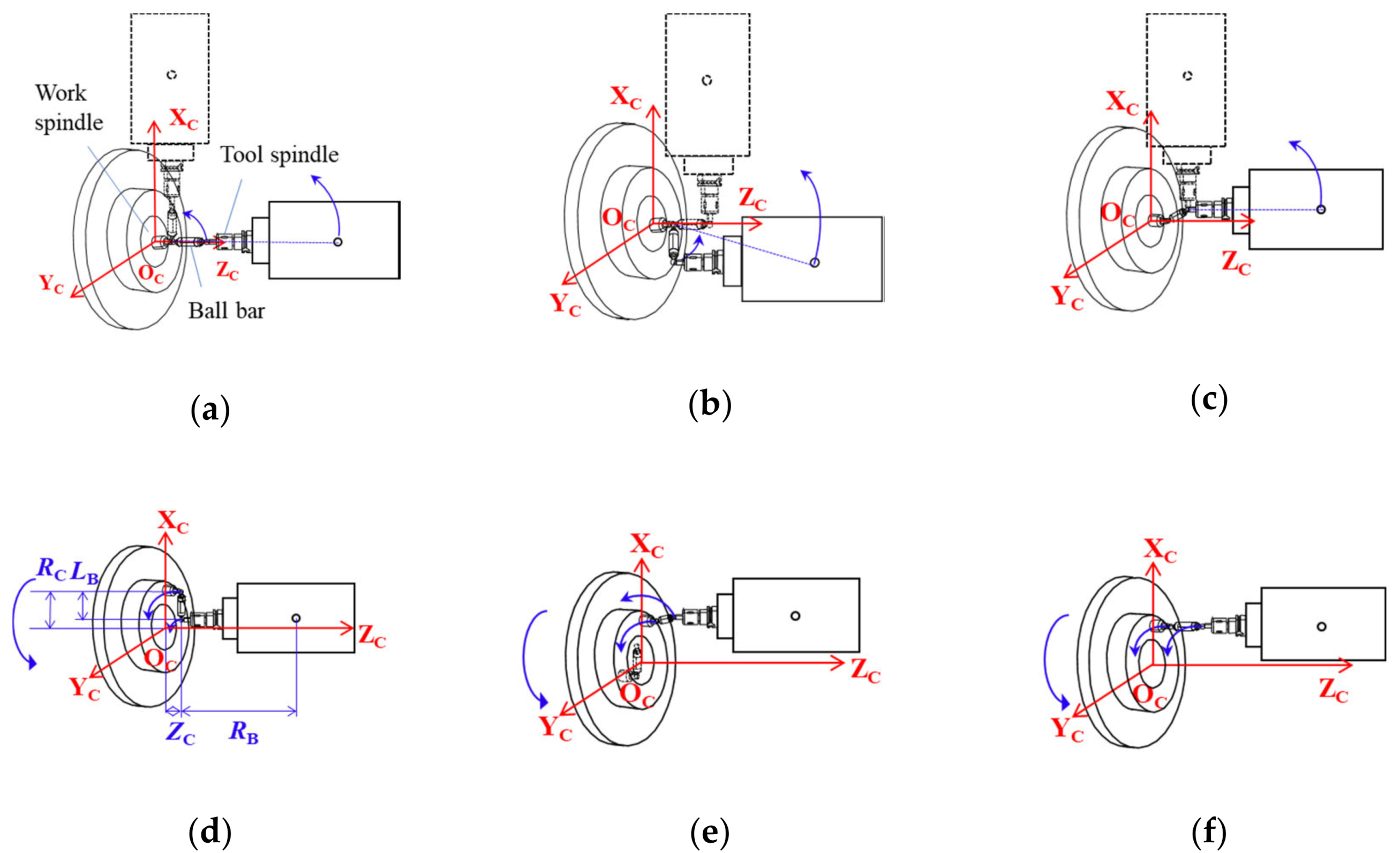
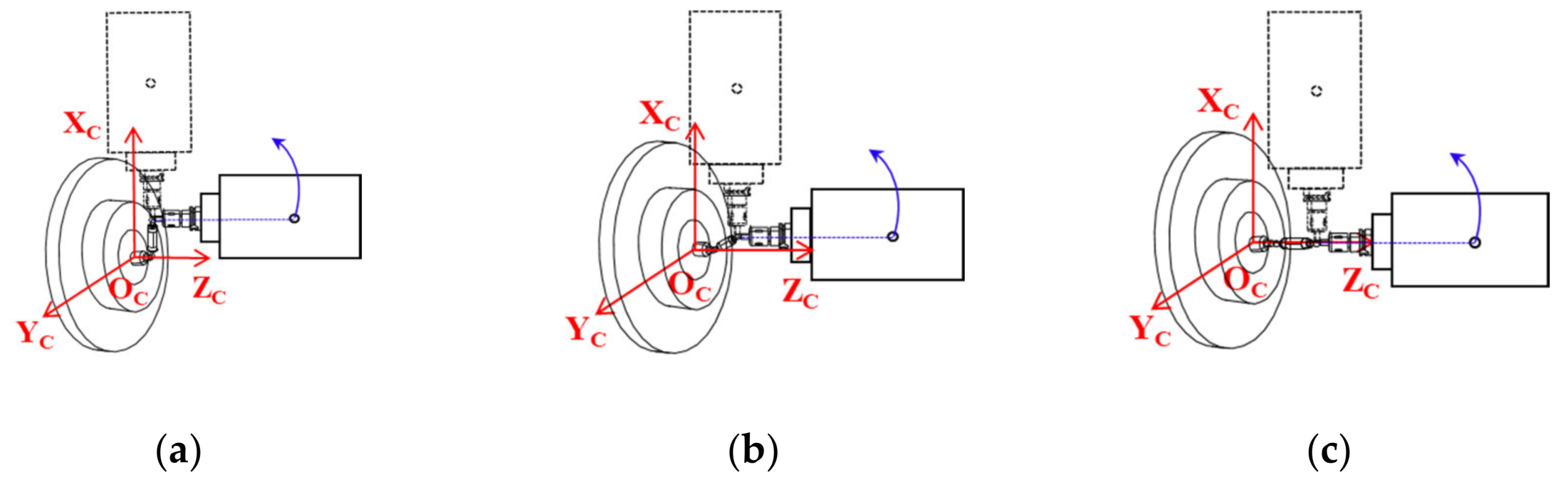
3.1. Simultaneous Three-Axis Control Movements
3.2. Mathematical Model
3.2.1. Determination of Center Coordinate T of the T-Side Ball Viewed from the Machine Coordinate System
3.2.2. Determination of Center Coordinate W of the W-Side Ball Viewed from the Machine Coordinate System
3.2.3. Determination of the Initial Position of Center Coordinate of the W-Side Ball
3.2.4. Calculation of the Difference ∆L between Reference Length and Measured Length of Ball Bar
4. Simulation
- The position of trajectory center is changed; for example, the effect of δxBT on eccentricity in case of the B axis radial measurement.
- The size of trajectory radius is changed; for example, the effect of δzBT on eccentricity in case of the B axis radial measurement.
- The shape of trajectory is changed; for example, the effect of βYZ on eccentricity in case of the B axis radial measurement.
4.1. Influence of Mounting Errors of Ball Bar on Circular Trajectories
4.2. Influence of Squareness of Translational Axes
5. Identification Procedures and Validity
5.1. Mathematical Expressions between Eccentricities and Geometric Deviations
5.2. Formulae Considering Squareness of Translational Axes to Calculate Geometric Deviations
5.3. Measurement to Identify Geometric Deviations
5.4. Validity of the Proposed Identification Method
6. Conclusions
- (1)
- The identification method for 12 geometric deviations, in which two squareness deviations of translational axes αYZ and βYZ are included, is proposed.
- (2)
- From the simulation results, it is confirmed that in order to eliminate the influence of the mounting errors of the W-side ball on the eccentricities of the circular trajectories, measurements for the B axis should be performed in Cartesian coordinate system and those for the C axis should be performed in cylindrical coordinate system.
- (3)
- Considering the squareness of translational axes, six measurements by means of the ball bar are necessary to identify twelve geometric deviations.
- (4)
- The results of numerical experiments agree well with the given intentional deviations. Therefore, the influence of the analysis accuracy of the formulae on the identification could be considered to be negligible.
Author Contributions
Funding
Conflicts of Interest
References
- Álvarez, Á.; Calleja, A.; Ortega, N.; De Lacalle, L. Five-Axis Milling of Large Spiral Bevel Gears: Toolpath Definition, Finishing, and Shape Errors. Metals 2018, 8, 353. [Google Scholar] [CrossRef] [Green Version]
- Calleja, A.; Bo, P.; González, H.; Bartoň, M.; De Lacalle, L.N.L. Highly accurate 5-axis flank CNC machining with conical tools. Int. J. Adv. Manuf. Technol. 2018, 97, 1605–1615. [Google Scholar] [CrossRef] [Green Version]
- Bo, P.; Bartoň, M.; Plakhotnik, D.; Pottmann, H. Towards efficient 5-axis flank CNC machining of free-form surfaces via fitting envelopes of surfaces of revolution. Comput. Aided Des. 2016, 79, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Calleja, A.; Gonzalez Barrio, H.; Polvorosa Teijeiro, R.; De Lacalle Marcaide, L.N.L. MÁQUINAS MULTITAREA: EVOLUCIÓN, RECURSOS, PROCESOS Y PROGRAMACIÓN. DYNAII 2017, 92, 637–642. [Google Scholar] [CrossRef] [Green Version]
- Gomez-Acedo, E.; Olarra, A.; Orive, J.; De Lacalle, L.N.L. Methodology for the design of a thermal distortion compensation for large machine tools based in state-space representation with Kalman filter. Int. J. Mach. Tools Manuf. 2013, 75, 100–108. [Google Scholar] [CrossRef]
- Pelayo, G.U.; Olvera, D.; De Lacalle, L.N.L.; Beranoagirre, A.; Elías-Zúñiga, A.; De Lacalle, L.N.L. Prediction Methods and Experimental Techniques for Chatter Avoidance in Turning Systems: A Review. Appl. Sci. 2019, 9, 4718. [Google Scholar]
- Olvera, D.; De Lacalle, L.N.L.; Compeán, F.I.; Fz-Valdivielso, A.; Lamikiz, A.; Campa, F.J. Analysis of the tool tip radial stiffness of turn-milling centers. Int. J. Adv. Manuf. Technol. 2012, 60, 883–891. [Google Scholar] [CrossRef]
- Zargarbashi, S.H.H.; Mayer, J.R.R. Assessment of machine tool trunnion axis motion error, using magnetic double ball bar. Int. J. Mach. Tools Manuf. 2006, 46, 1823–1834. [Google Scholar] [CrossRef]
- Lei, W.T.; Paung, I.M.; Yu, C.-C. Total ballbar dynamic tests for five-axis CNC machine tools. Int. J. Mach. Tools Manuf. 2009, 49, 488–499. [Google Scholar] [CrossRef]
- Lei, W.T.; Sung, M.P.; Liu, W.L.; Chuang, Y.C. Double ballbar test for the rotary axes of five-axis CNC machine tools. Int. J. Mach. Tools Manuf. 2007, 47, 273–285. [Google Scholar] [CrossRef]
- Tsutsumi, M.; Saito, A. Identification and compensation of systematic deviations particular to 5-axis machining centers. Int. J. Mach. Tools Manuf. 2003, 43, 771–780. [Google Scholar] [CrossRef]
- Tsutsumi, M.; Saito, A. Identification of angular and positional deviations inherent to 5-axis machining centers with a tilting-rotary table by simultaneous four-axis control movements. Int. J. Mach. Tools Manuf. 2004, 44, 1333–1342. [Google Scholar] [CrossRef]
- Tsutsumi, M.; Tone, S.; Kato, N.; Sato, R. Enhancement of geometric accuracy of five-axis machining centers based on identification and compensation of geometric deviations. Int. J. Mach. Tools Manuf. 2013, 68, 11–20. [Google Scholar] [CrossRef]
- Tsutsumi, M.; Miyama, N.; Tone, S.; Saito, A.; Cui, C.; Dasssanayake, K.M. Correction of Squareness of Translational Axes for Identification of Geometric Deviations Inherent to Five-Axis Machining Centres with a Tilting-Rotary Table. Trans. Jpn. Soc. Mech. Eng. Ser. C 2013, 79, 759–774. [Google Scholar] [CrossRef]
- Lee, K.-I.; Yang, S.-H. Measurement and verification of position-independent geometric errors of a five-axis machine tool using a double ball-bar. Int. J. Mach. Tools Manuf. 2013, 70, 45–52. [Google Scholar] [CrossRef]
- Xiang, S.; Deng, M.; Li, H.; Du, Z.; Yang, J. Volumetric error compensation model for five-axis machine tools considering effects of rotation tool center point. Int. J. Adv. Manuf. Technol. 2019, 102, 4371–4382. [Google Scholar] [CrossRef]
- Yang, J.; Ding, H. A new position independent geometric errors identification model of five-axis serial machine tools based on differential motion matrices. Int. J. Mach. Tools Manuf. 2016, 104, 68–77. [Google Scholar] [CrossRef]
- Chen, J.; Lin, S.; He, B. Geometric error measurement and identification for rotary table of multi-axis machine tool using double ballbar. Int. J. Mach. Tools Manuf. 2014, 77, 47–55. [Google Scholar] [CrossRef]
- Dassanayake, K.M.M.; Tsutsumi, M.; Saito, A. A strategy for identifying static deviations in universal spindle head type multi-axis machining centers. Int. J. Mach. Tools Manuf. 2006, 46, 1097–1106. [Google Scholar] [CrossRef]
- Li, J.; Mei, B.; Shuai, C.; Liu, X.; Liu, D. A volumetric positioning error compensation method for five-axis machine tools. Int. J. Adv. Manuf. Technol. 2019, 103, 3979–3989. [Google Scholar] [CrossRef]
- Li, J.; Xie, F.; Liu, X.-J.; Dong, Z.; Song, Z.; Li, W. A geometric error identification method for the swiveling axes of five-axis machine tools by static R-test. Int. J. Adv. Manuf. Technol. 2017, 89, 3393–3405. [Google Scholar] [CrossRef]
- Ibaraki, S.; Sawada, M.; Matsubara, A.; Matsushita, T. Machining tests to identify kinematic errors on five-axis machine tools. Precis. Eng. 2010, 34, 387–398. [Google Scholar] [CrossRef] [Green Version]
- Uddin, M.S.; Ibaraki, S.; Matsubara, A.; Matsushita, T. Prediction and compensation of machining geometric errors of five-axis machining centers with kinematic errors. Precis. Eng. 2009, 33, 194–201. [Google Scholar] [CrossRef] [Green Version]
- Ibaraki, S.; Yoshida, I. A Five-Axis Machining Error Simulator for Rotary-Axis Geometric Errors Using Commercial Machining Simulation Software. Int. J. Autom. Technol. 2017, 11, 179–187. [Google Scholar] [CrossRef]
- Ibaraki, S.; Nagai, Y.; Otsubo, H.; Sakai, Y.; Morimoto, S.; Miyazaki, Y. R-Test Analysis Software for Error Calibration of Five-Axis Machine Tools—Application to a Five-Axis Machine Tool with Two Rotary Axes on the Tool Side. Int. J. Autom. Technol. 2015, 9, 387–395. [Google Scholar] [CrossRef]
- Hong, C.; Ibaraki, S. Observation of Thermal Influence on Error Motions of Rotary Axes on a Five-Axis Machine Tool by Static R-Test. Int. J. Autom. Technol. 2012, 6, 196–204. [Google Scholar] [CrossRef]
- Hong, C.; Ibaraki, S.; Oyama, C. Graphical presentation of error motions of rotary axes on a five-axis machine tool by static R-test with separating the influence of squareness errors of linear axes. Int. J. Mach. Tools Manuf. 2012, 59, 24–33. [Google Scholar] [CrossRef]
- Ibaraki, S.; Oyama, C.; Otsubo, H. Construction of an error map of rotary axes on a five-axis machining center by static R-test. Int. J. Mach. Tools Manuf. 2011, 51, 190–200. [Google Scholar] [CrossRef] [Green Version]
- Ibaraki, S.; Ota, Y. Error Calibration for Five-Axis Machine Tools by On-the-Machine Measurement Using a Touch-Trigger Probe. Int. J. Autom. Technol. 2014, 8, 20–27. [Google Scholar] [CrossRef]
- Mayer, J.R.R. Five-axis machine tool calibration by probing a scale enriched reconfigurable uncalibrated master balls artefact. CIRP Ann. 2012, 61, 515–518. [Google Scholar] [CrossRef]
- Iñigo, B.; Ibabe, A.; Aguirre, G.; Urreta, H.; De Lacalle, L.N.L. Analysis of Laser Tracker-Based Volumetric Error Mapping Strategies for Large Machine Tools. Metals 2019, 9, 757. [Google Scholar] [CrossRef] [Green Version]
- Díaz-Tena, E.; Ugalde, U.; López de Lacalle, L.N.; De La Iglesia, A.; Calleja, A.; Campa, F.J. Propagation of assembly errors in multitasking machines by the homogenous matrix method. Int. J. Adv. Manuf. Technol. 2013, 68, 149–164. [Google Scholar] [CrossRef]
- Portman, V.; Inasaki, I.; Sakakura, M.; Iwatate, M. Form-Shaping Systems of Machine Tools: Theory and Applications. CIRP Ann. 1998, 47, 329–332. [Google Scholar] [CrossRef]

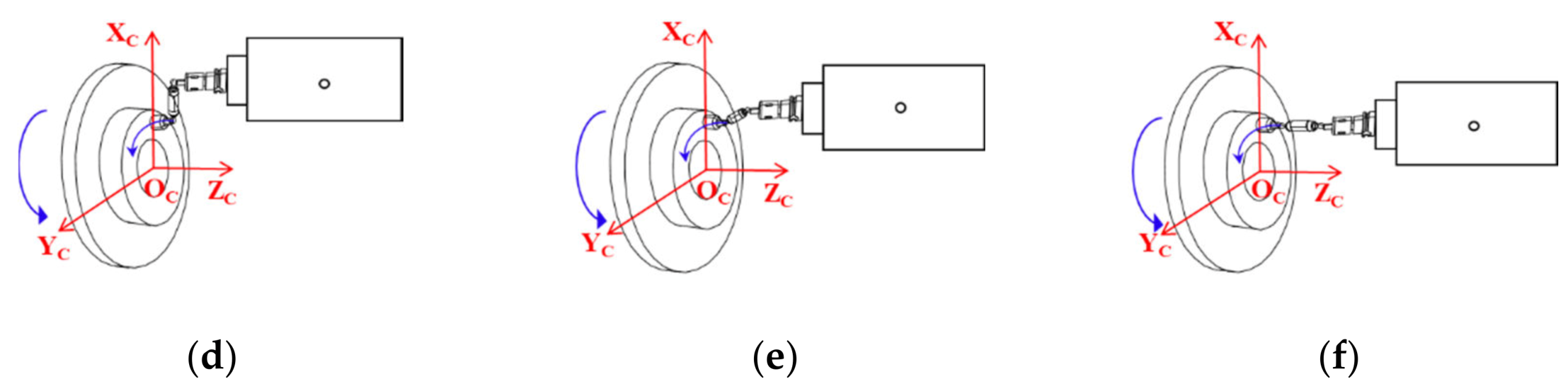
| Symbol | Description |
|---|---|
| δxBT | X-direction offset of tool spindle axis of rotation with respect to B axis origin |
| δzBT | Z-direction offset of tool spindle axis of rotation with respect to B axis origin |
| αBT | Squareness error of B axis with respect to tool spindle axis of rotation about X axis |
| αXB | Squareness error of B axis of rotation with respect to Z axis motion |
| βXB | Initial angular position error of B axis of rotation with respect to X (Z) axis motion |
| γXB | Squareness error of B axis of rotation with respect to X axis motion |
| γXY | Squareness error between X axis motion and Y axis motion |
| αYZ | Squareness error between Y axis motion and Z axis motion |
| βYZ | Squareness error between Z axis motion and X axis motion |
| δxCZ | X-direction offset of C axis origin with respect to machine coordinate origin |
| δyCZ | Y-direction offset of C axis origin with respect to machine coordinate origin |
| αCZ | Parallelism error of C axis of rotation with respect to Z axis about X axis |
| βCZ | Parallelism error of C axis of rotation with respect to Z axis about Y axis |
| Cylindrical | B Axis | C Axis | ||||
|---|---|---|---|---|---|---|
| Radial | Tangential | Axial | Radial | Tangential | Axial | |
| Command X | (LB + RB) sin φ | RBT sin (φ + tan−1LB/RB) a | RB sin φ | (RC − LB) cos θ | RCT cos (θ + tan−1LB/RC) b | RC cos θ |
| Command Y | 0 | 0 | LB | (RC − LB) sin θ | RCT sin (θ + tan−1LB/RC) b | RC sin θ |
| Command Z | ZC + (LB + RB) cos φ | ZC + RBT cos (φ + tan−1LB/RB) a | ZC + RB cos φ | ZC + RB | ZC + RB | ZC + LB + RB |
| Command B | φ | φ | φ | 0 | 0 | 0 |
| Command C | 0 | 0 | 0 | θ | θ | θ |
| Cartesian | X-direction | Y-direction | Z-direction | X-direction | Y-direction | Z-direction |
| Command X | LB + RB sin φ | RB sin φ | RB sin φ | LB + RC cos θ | RC cos θ | RC cos θ |
| Command Y | 0 | LB | 0 | RC sin θ | LB + RC sin θ | RC sin θ |
| Command Z | ZC + RB cos φ | ZC + RB cos φ | LB + ZC + RB cos φ | ZC + RB | ZC + RB | LB + ZC + RB |
| Command B | φ | φ | φ | 0 | 0 | 0 |
| Command C | 0 | 0 | 0 | θ | θ | θ |
| B axis Radial |  |  |  | 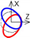 | |||||||||
| B axis Tangential | 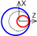 | 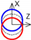 | 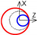 |  | |||||||||
| B axis Axial | 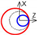 |  |  | ||||||||||
| B axis X-direction |  | 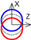 |  | 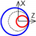 | |||||||||
| B axis Y-direction | 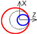 | 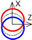 |  | ||||||||||
| B axis Z-direction | 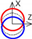 | 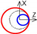 | 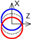 | ||||||||||
| C axis Radial | 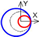 | 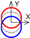 | 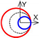 |  | 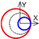 | 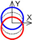 |  |  |  | 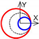 | 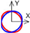 | ||
| C axis Tangential |  |  | 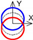 | 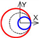 | 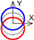 | 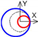 |  | 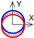 |  |  |  | ||
| C axis Axial |  |  | 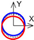 | 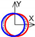 | |||||||||
| C axis X-direction |  | 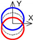 | 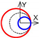 | 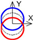 | 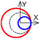 | 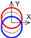 |  | 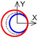 | 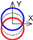 | 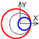 | |||
| C axis Y-direction | 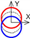 | 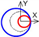 | 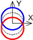 |  |  | 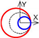 | 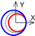 | 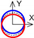 |  | 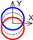 | 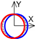 | ||
| C axis Z-direction |  | 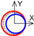 |  | 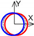 |
 : +20 µm, +0.005°,
: +20 µm, +0.005°,  : −20 µm, −0.005°, Blank: No influence.
: −20 µm, −0.005°, Blank: No influence.| Cylindrical coordinate system | B axis Radial |  |  |  |  | ||
| B axis Tangential |  |  |  |  | |||
| B axis Axial |  | ||||||
| Cartesian coordinate system | B axis X-direction |  |  |  | |||
| B axis Y-direction |  | ||||||
| B axis Z-direction |  |  |  | ||||
| Cylindrical coordinate system | C axis Radial |  |  | 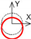 | |||
| C axis Tangential | 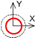 | 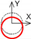 | 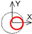 | ||||
| C axis Axial |  | ||||||
| Cartesian coordinate system | C axis X-direction |  |  |  |  | ||
| C axis Y-direction |  |  |  |  | |||
| C axis Z-direction |  |
| ex | ey | ez | |
|---|---|---|---|
| B: X-direction | δzBT | — | δxBT − RBβXB − RBβYZ |
| B: Y-direction | −RBγXB | — | RBαXB + RBαYZ |
| B: Z-direction | RBβXB − δxBT | δzBT | |
| C: Radial | −δxBT + RBβXB + δxCZ + ZCβCZ + RBβYZ | −RBαXB − RBαBT + δyCZ − ZCαCZ − RBαYZ | — |
| C: Tangential | RBαXB + RBαBT − δyCZ + ZCαCZ + RBαYZ | −δxBT + RBβXB + δxCZ + ZCβCZ + RBβYZ | |
| C: Axial | RCβCZ − RCβYZ | RCαYZ − RCαCZ | — |
| Direction | B Axis (μm) | C Axis (μm) | ||||
|---|---|---|---|---|---|---|
| X a | Y a | Axial a | Radial a | Radial b | Radial c | |
| ex | 16.63 | −11.24 | 0.29 | 25.73 | 26.89 | 28.97 |
| ey | - | - | 0.05 | −19.59 | −20 | −23.26 |
| ez | −4.02 | 10.05 | - | - | - | - |
| Initial Values | Identified Values | Difference | |
|---|---|---|---|
| δxBT (µm) | 11.00 | 10.96 | −0.04 |
| δzBT (µm) | 17.00 | 16.63 | −0.37 |
| αBT (″) | 7.63 | 7.69 | 0.06 |
| αXB (″) | 3.51 | 3.44 | −0.07 |
| βXB (″) | 3.92 | 3.80 | −0.12 |
| γXB (″) | 6.39 | 6.44 | 0.05 |
| αYZ (″) | 2.27 | 2.32 | 0.05 |
| βYZ (″) | 4.74 | 4.79 | 0.05 |
| δxCZ (µm) | 13.00 | 13.01 | 0.01 |
| δyCZ (µm) | 7.00 | 6.96 | −0.04 |
| αCZ (″) | 2.06 | 2.11 | 0.05 |
| βCZ (″) | 5.98 | 5.98 | 0.00 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, Y.; Nishizawa, K.; Kato, N.; Tsutsumi, M.; Nakamoto, K. Identification Method of Geometric Deviations for Multi-Tasking Machine Tools Considering the Squareness of Translational Axes. Appl. Sci. 2020, 10, 1811. https://doi.org/10.3390/app10051811
Yao Y, Nishizawa K, Kato N, Tsutsumi M, Nakamoto K. Identification Method of Geometric Deviations for Multi-Tasking Machine Tools Considering the Squareness of Translational Axes. Applied Sciences. 2020; 10(5):1811. https://doi.org/10.3390/app10051811
Chicago/Turabian StyleYao, Yan, Keisuke Nishizawa, Noriyuki Kato, Masaomi Tsutsumi, and Keiichi Nakamoto. 2020. "Identification Method of Geometric Deviations for Multi-Tasking Machine Tools Considering the Squareness of Translational Axes" Applied Sciences 10, no. 5: 1811. https://doi.org/10.3390/app10051811
APA StyleYao, Y., Nishizawa, K., Kato, N., Tsutsumi, M., & Nakamoto, K. (2020). Identification Method of Geometric Deviations for Multi-Tasking Machine Tools Considering the Squareness of Translational Axes. Applied Sciences, 10(5), 1811. https://doi.org/10.3390/app10051811




