1. Introduction
The steel industry is an industry with a lot of development potential due the fact that its products have multiple uses. Since the financial crisis in 2008, world steel production has increased significantly, both in emerging and nonemerging countries, so research in the steel industry turns out to be a very beneficial action for the social and economic ambit [
1].
Steel is considered the most important material or resource for various industries: Steel industry, metallurgical industry, automobile industry, aerospace industry, arms industry, construction industry, among other industries.
Peru has large iron deposits, raw material for the production of all types of steel, according to information provided by the Ministry of Energy and Mines. Therefore, Peru has a lot of potential in relation to the manufacture of steel, because this country has natural reserves of coal, coke, and limestone (CO3Ca), which are used to make steel [
2].
The most modern steel factories have slab reheating furnaces composed of three zones: The reheating zone, the heating zone, and the soaking zone, that are separated with partial walls, which effectively block radiation transfer and hinder convective transfer [
1]. These zones have the function of heating the slabs in the furnace to a desired temperature ranging from 1000 to 1250 °C.
In the slab reheating furnaces the uniform heating of the slab takes place and subsequently hot rolled in successive passes obtaining a defined structure. The process of laminating the slabs depends largely on the temperature in the slab reheating furnace [
3].
A poor temperature obtained in the slab reheating furnaces could cause serious damage to the surface of the rolling rollers that make up the rolling mill stands, generating substantial material damage and a significant increase in the costs of maintenance and production for prolonged stops of the productive process [
4].
The slab reheating process is a complex physical and chemical process, which involves combustion, thermal radiation, bulk flow of gases, heat input from the burners, heat exchange among furnace walls, flames, skids, and steel slabs [
5]. Consequently, a considerable research in mathematical modeling of this process, based on the physical properties and the first principles, has been performed in the last decades, see, e.g., [
5,
6,
7,
8,
9,
10,
11].
Usually, the derived mathematical models of the slab reheating process are represented by a set of partial nonlinear differential equations [
6]. Therefore, the use of these models in the design of effective controllers is very difficult.
Currently, the temperature control in most of the slab reheating furnaces is carried out through the use of conventional proportional integral/proportional integral derivative (PI/PID) controllers [
12,
13]. Therefore, these furnaces are characterized by high fuel consumption (oil and/or gas), and generate high pollution through the emission of toxic gases that pollute the environment [
14].
The dynamics of the slab reheating furnaces are characterized by nonlinear behaviors and temperature variations within the furnace. These dynamic characteristics incorporate them in the category of industrial processes with complex dynamic behaviors [
1].
It is well known that conventional controllers (PI/PID) do not achieve effective control of industrial processes characterized by having complex dynamic behaviors [
15,
16,
17], which generates serious production problems such as damage to the furnace refractory, deformation of mechanical equipment, deformation of the slabs, among other problems.
These problems support the development of advanced control strategies, as well as structural control systems that optimize the production process, increasing the quality of the final product, reducing environmental pollution and damage of mechanical equipment, and increasing the quality of the steel products [
18,
19,
20].
Robust H
2 control is an effective control technique that has greatly contributed to practical industry applications minimizing the effect of disturbances [
21,
22,
23]. The robust H
2 control is based on minimizing the quadratic norm of the transfer function between the input disturbance signal and the plant output signal or H
2 norm [
24,
25,
26].
The purpose of this paper is to design, for the first time, a robust H2 state feedback controller (H2-SFC) for the effective temperature control in the heating zone of a steel slab reheating furnace.
The robust H2-SFC controller uses a mathematical model of the industrial process to be controlled to calculate an optimal sequence of actions that are projected to design the dynamics of the system through state feedback based on the minimization of the quadratic norm of the transfer function between the input disturbance signal and the plant output signal.
Among the most outstanding features of the robust H
2-SFC controller is the possibility of taking advantage of the representation in states space of the transfer function taking advantage of the continuous feedback of the information on the states and the output of the system in order to stabilize the said function minimizing its H
2 norm [
26].
An important advantage of this type of advanced controller is the possibility of incorporating a significant performance measure that guarantees the stability and performance of the system allowing efficient design criteria under the influence of external disturbances [
26]. An optimal sequence of controller actions that are calculated taking into account the system behavior and uncertainties from the design stage is estimated, this introduces two important improvements: Good performance and greater robustness. The controller sequence converges complying with the restriction of the H
2 norm.
Unlike a PI/PID controller, the robust H
2-SFC controller has a greater tolerance or insensitivity to changes or disturbances that may occur in the operation conditions of the industrial process [
26].
This paper presents the following contributions: (1) A mathematical model that characterized the dynamic behavior of the heating zone of a steel slab reheating furnace based on the available field data and system identification procedures is obtained. (2) For the first time, a robust H2 state feedback controller (H2-SFC) for the effective temperature control in the heating zone of a steel slab reheating furnace is designed.
This paper is organized as follows. In
Section 2, a mathematical model of the heating furnace zone under study is obtained using systems identification techniques. In
Section 3, the design of the robust H
2-SFC controller is developed.
Section 4 shows the discussions of the obtained results. Finally,
Section 5 gives some conclusions.
2. Identification of the Dynamic Behavior of the Steel Slab Reheating Furnace
The steel slab reheating furnace under study belongs to the Aceros Arequipa Corporation, which is the most important steel bar producing company in the country.
One of the fundamental stages of the corrugated bar production process is the slab reheating process, in which the slabs are heated in order to adopt ductility properties for the customer rolling process [
27].
The stage of slab heating is one of the most important processes in the manufacture of corrugated iron. Therefore, the control of the heating zone temperature in the slab reheating furnaces is key. This is due to the fact that a high temperature can generate an excessive increase of the grains (crystallites) producing cracks in the slabs, and a low temperature can produce the decrease of the flexibility of the steel increasing the resistance to deformation and causing damage to the equipment during the rolling process [
28,
29].
The slab reheating furnace under study is composed of an automation system for control of the heating zone temperature which consists of a feedback mechanism widely used in the industry. Since the slabs must reach a certain uniform temperature, if the necessary operational measures are not taken to control the temperature of the zones that make up the furnace, serious damage to the mechanics of the system can be generated [
30].
The controllers used for the control of the heating temperature in this slab reheating furnaces are the well-known PI/PID controller, which does not ensure the effective control of industrial processes characterized by a difficult dynamic behavior [
31,
32,
33].
For the design of effective industrial controllers, mathematical models that characterize the dynamic behavior of the processes under study are required, see, e.g., [
34,
35]. However, in the case of slab reheating furnaces, it is very complicated to obtain this kind of model using mass and energy balance equations (first principles) [
1].
Currently, system identification is a powerful tool for obtaining mathematical models of the complex dynamical processes using real-time data of their observed variables, such as input variables and output variables [
36,
37].
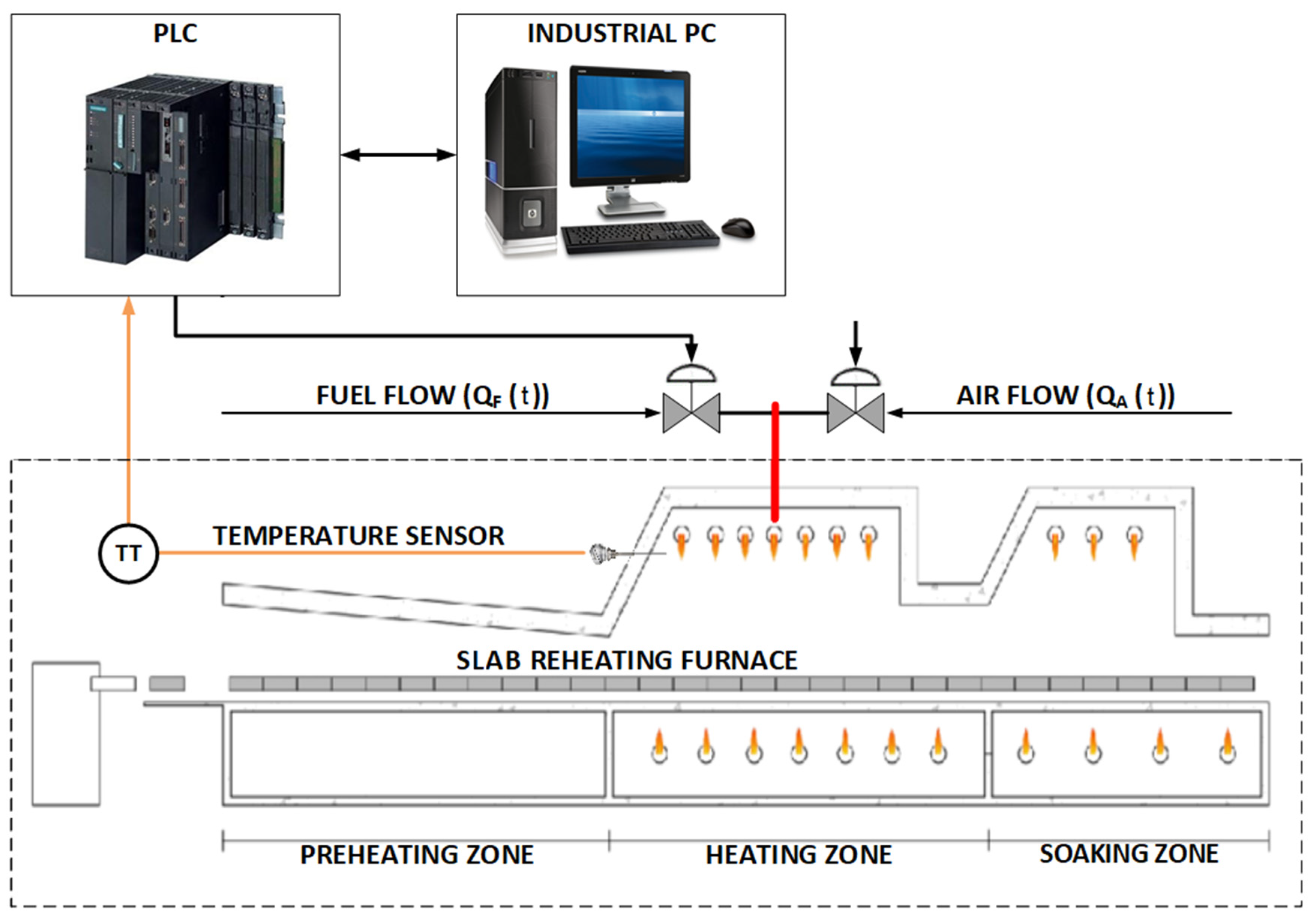
The slab reheating furnace under study is provided with a heating zone temperature sensor, air flow, and fuel flow sensors, as well as two proportional valves for the control of the critical variables. Additionally, this furnace has a SCADA supervision system (WinCC) for monitoring the entire production process, which favors the work of collecting and storing input and output data [
38,
39,
40,
41].
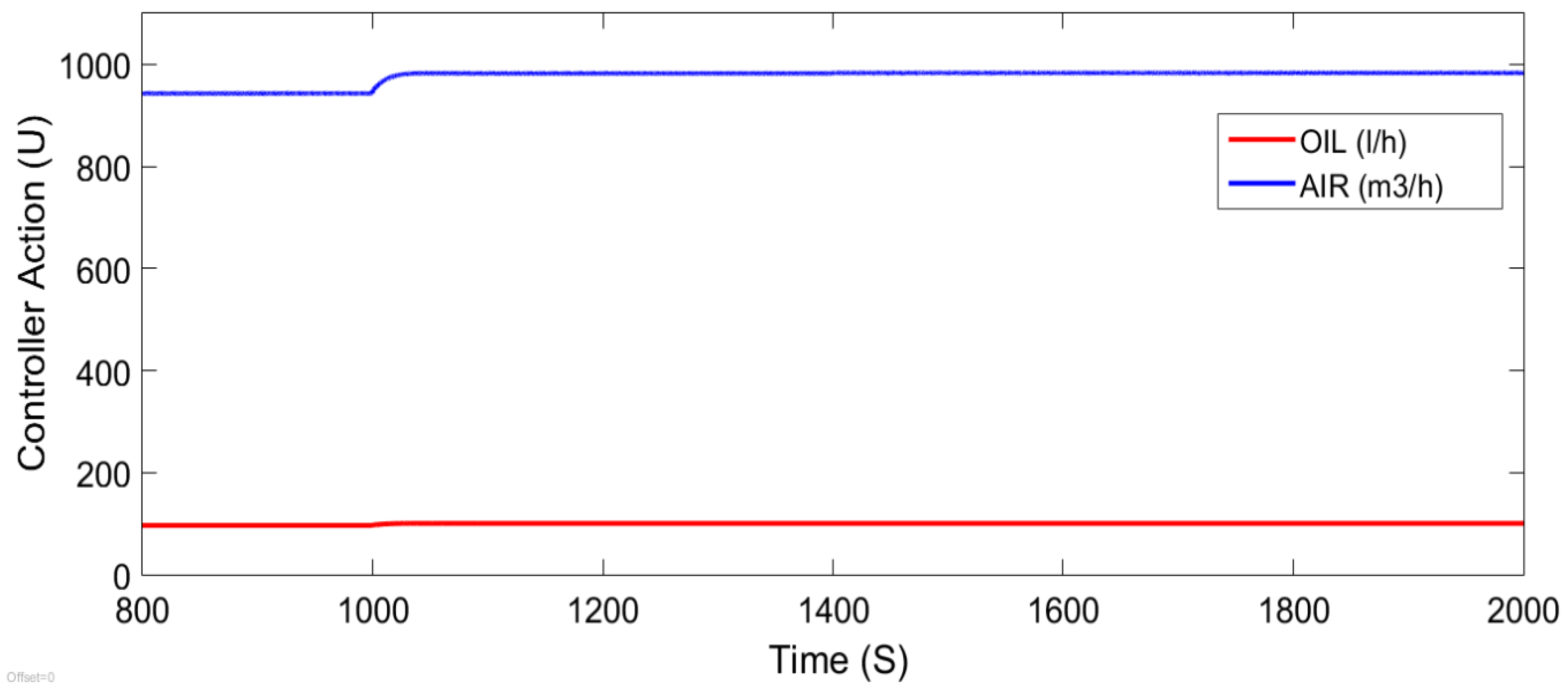
For the development of the systems identification experiments, the variation of the fuel flow that feed the furnace burner were considered as input variable (manipulated) , and as output variable the heating zone temperature variation inside the slab reheating furnace .
In addition, this process is influenced by different disturbances among which are the variation in the number of slabs that enter the reheating furnace, the calorific power of the fuel, the air temperature, etc.
Figure 1 shows a diagram of the experimental arrangement for the collection of output/input data in operating conditions of the slab reheating furnace under study. For the development of this experiment the following instruments were used: An industrial PC, a programmable logic controller (PLC), and a temperature sensor.
To obtain the mathematical model that describes the nominal dynamic behavior of the heating zone temperature, an experiment with a step signal was initially developed, with the purpose of calculating a first estimate of the order and parameters of the model of the said process.
The fuel flow valve was excited in order to obtain a variation of the heating zone temperature in the slab reheating furnace. To achieve this, the valve was manipulated, generating an increase of 60.9% to 65.8%, which is within the range of nominal operating variations of the fuel flow in the heating zone of the slab reheating furnace under study.
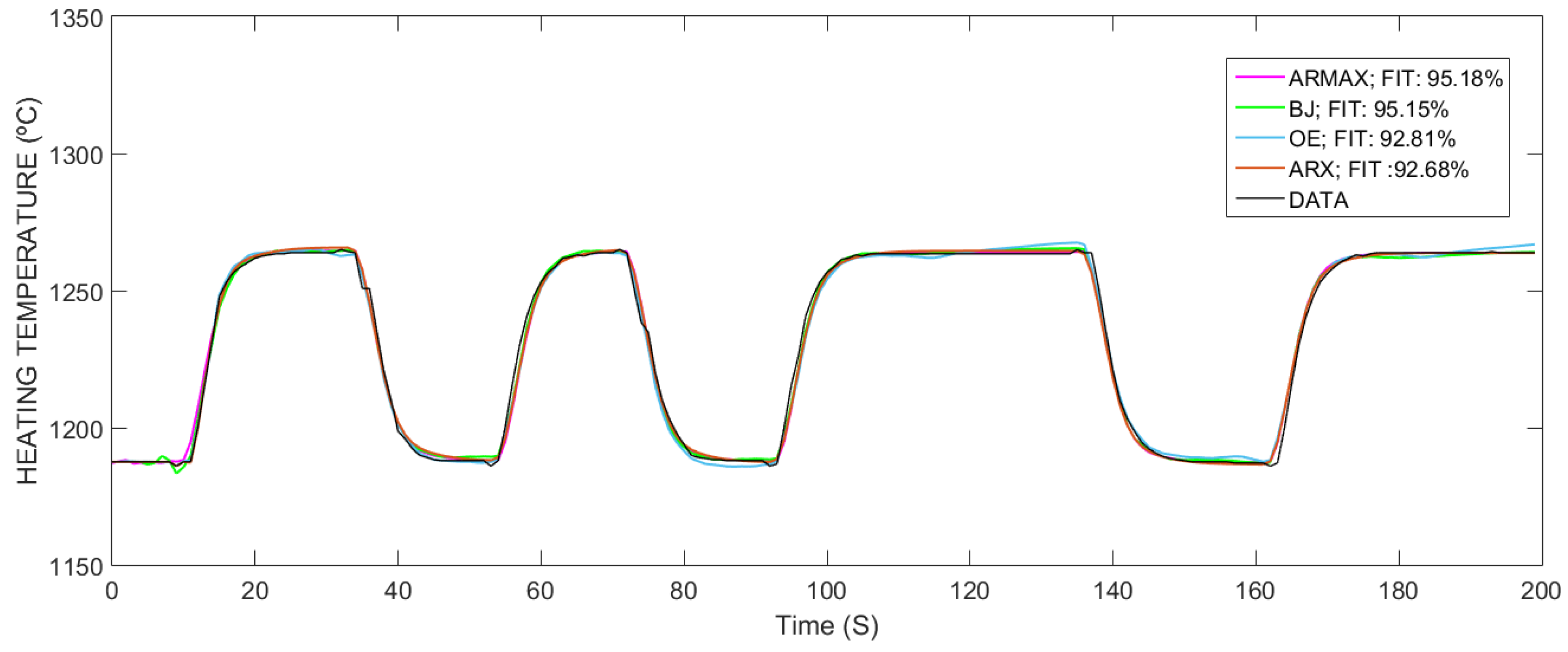
A second experiment with a pseudorandom binary sequence (PRBS) was performed. The data were sampled with a sampling period of 1 s. The experiment lasted 200 s and from the results obtained a model with ARMAX structure was chosen, because the best results were obtained with this structure. The results of the output/input data collection experiment with a PRBS signal are shown in
Figure 2.
Different discrete model structures (ARMAX, BJ, OE, and ARX) were evaluated and parameter estimation was performed using the error prediction method. For the validation of the model, a comparison was made between the results of the model obtained and the results of the measured plant as shown in
Table 1.
As result of this experiment, a fourth order and nondelayed model with an ARMAX structure was obtained which describes the nominal dynamic behavior of the furnace heating zone under study with an adjustment index (FIT) of 95.18%, which demonstrates the validity of the model reached. This ARMAX model is represented by the following Equation [
36]:
where:
and
is the white noise of zero mean.
The resulting model is of fourth order and without time delay with ARMAX structure (with the parameters estimated under normal operating conditions of the furnace heating zone), and it is represented by the following discrete time equations:
Figure 3 shows the validation results of the nominal mathematical models obtained from the industrial process under study, which show a high degree of adequacy (FIT). Therefore, it was obtained that the model with ARMAX structure, fourth order and without time delay was the one that presented the best FIT (95.18%), and therefore it was the model selected for the design purposes of the H
2-SFC.
3. Design of a H2-SFC Controller
The objective of this paper is to design a robust H2-SFC controller that generates a better behavior than a conventional PI/PID controller against the effect of complex dynamic behavior influenced by external disturbances. For this reason, this work raises the design of a robust H2-SFC controller.
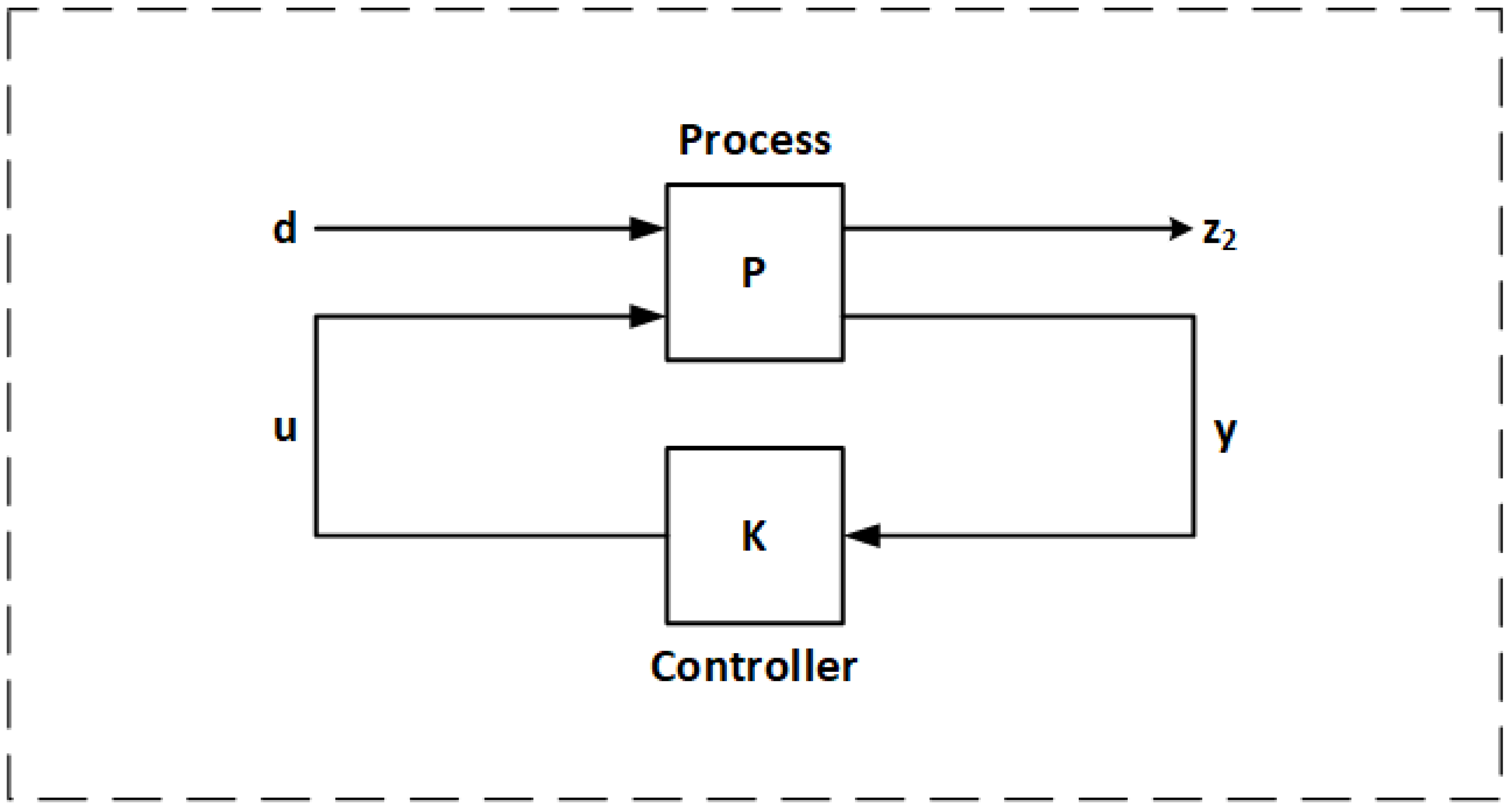
Figure 4 shows the block diagram of a control system with robust H
2 controller, conformed by the controller
K, the linear dynamic process
P, the output of the system y, the control signal u, the output signal z, and the disturbance of input d with which we have
and
. The realization of
P is equal to
.
This controller is characterized by using a state space model to obtain the sequence of control signals
u(
k). The model of states spaces is found through Equation (6), thus we have:
where:
The following assumptions were made:
- (i)
is stabilizable and is detectable.
- (ii)
and have full rank.
- (iii)
has full rank.
- (iv)
has full rank.
Assumption (i) guarantees the stabilizability by the output feedback. Assumption (ii) guarantees that the optimal H2 controller is linear and invariant in time and dimensional finite (nonsingular case). Assumptions (iii) and (iv) guarantee the solvability of algebraic Riccati equations. For and . The assumption is made to simplify algebra. With the assumption becomes strictly proper.
The problem H
2 is to find a stabilizer controller K that minimizes the
norm of the states and the action of the controller given the realization of the state space [
42,
43,
44]. The tracking gain
F allows the system output to reach the
R reference by solving the nonzero reference tracking problem of the system being the error
. Here, it should be fulfilled:
After inserting Equation (8) into the dynamic system, Equation (7) turns out:
We determine the matrices
K and
F as follows:
For the design of the robust H
2-SFC controller, it is necessary to consider the model of the plant under study in Equation (5) for which we assume that the new input
. The transfer matrix from
to
is as follows:
The problem H
2 is to find
K such that
is Hurwitz and
for the minimum value of
that meets the following linear matrix inequality, with
X and
Q being symmetric matrices [
41]:
where:
Furthermore, by adjustment by trial and error it was determined that and . The gains of the PI/PID controller are and .
The open loop poles of the system are: 0.2716 + 0.6732i, 0.2716 − 0.6732i, 0.9964 + 0.0000i, and 0.8883 + 0.0000i.
The closed loop poles of the system are: −1.0333 + 0.0000i, −0.8685 + 0.0000i, −0.3146 + 0.6850i, and −0.3146 − 0.6850i.
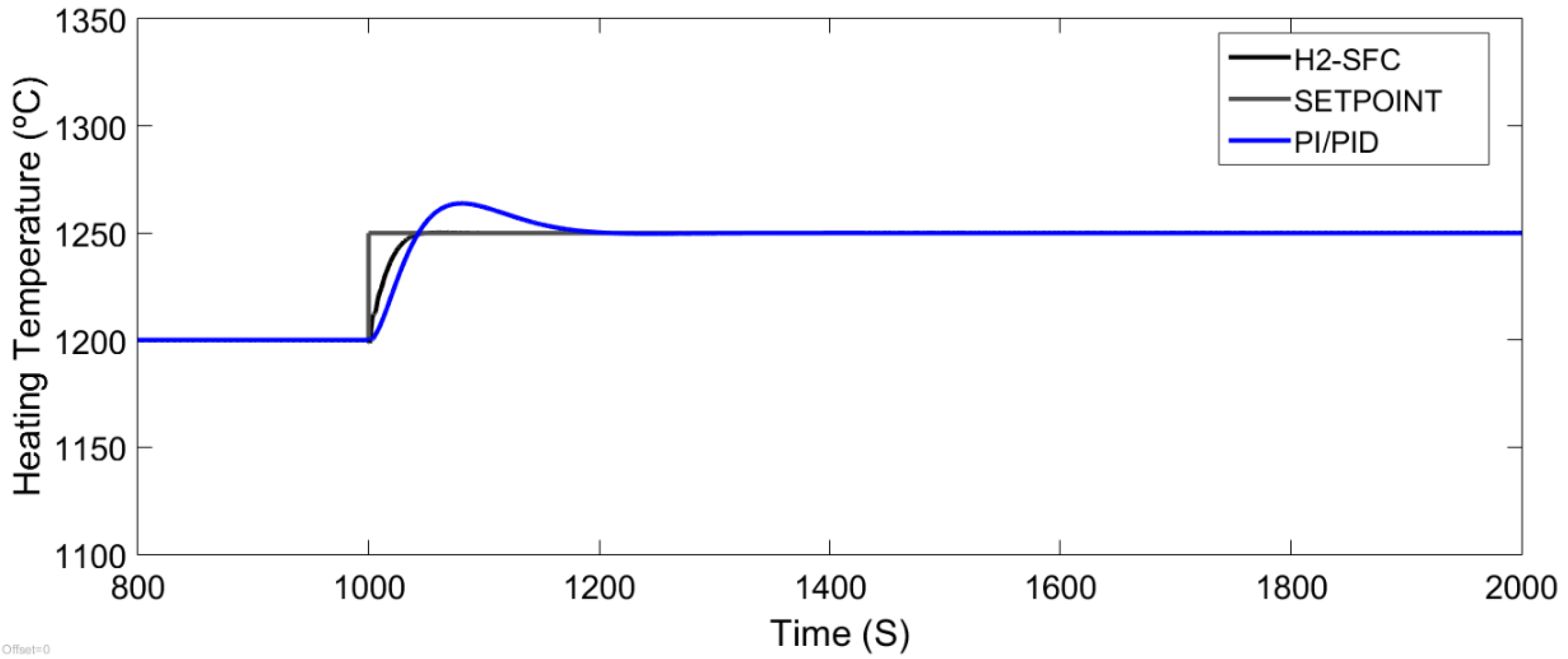
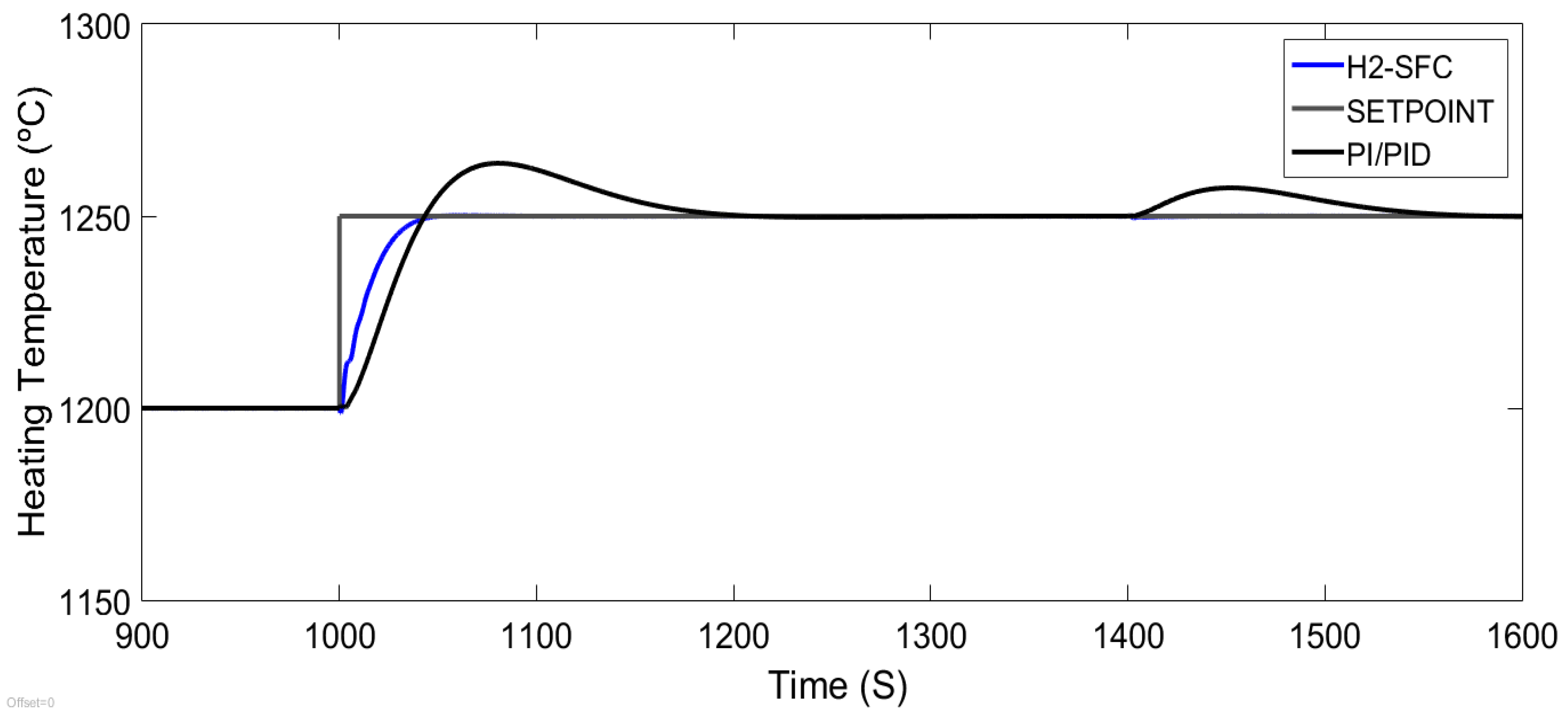
The transient response characteristics of the closed loop control system of the PID controller are: Delay time: 40 s, rise time: 44 s, peak time: 80 s, overshoot: 22%, and settling time: 200 s.
The transient response characteristics of the closed loop control system of the H2-SFC controller are: Delay time: 8 s, rise time: 40 s, peak time: 40 s, overshoot: 0%, and settling time: 40 s.
The block diagram of the heating zone temperature control system of the slab reheating furnace under study is shown in
Figure 5.
4. Analysis and Discussion of Results
In order to verify the effectiveness of the designed H2-SFC controller, some simulations of the control system of the furnace heating zone temperature under study using the equivalent model in discrete time (6) were carried out for the conventional PI/PID controller, (which was designed in the frequency domain using the second Ziegler-Nichols method). Moreover, using the equivalent state space model (7) for the controller H2-SFC, both were designed under similar time response conditions.
By varying the reference signal, the capacity of the PI/PID and H
2-SFC controllers were tested. The results of the control system responses with both controllers are shown in
Figure 6. The time response with the H
2-SFC controller does not present overshoot and is much faster with respect to the response of the conventional PI/PID controller. In
Figure 7 the controller efforts are shown when the reference presents step characteristics.
To assess the robustness of the PI/PID and H
2-SFC controllers, these were tested in the presence of internal and external disturbances in the feedback loop.
Figure 8 shows the results of the time responses of the control systems with both controllers in the presence of an external step disturbance d(k) of 1 L/h at the fuel flow inlet that feeds the burner that causes an increase in heating temperature from 1250 to 1260 °C. It can be seen that the H
2-SFC controller is more robust than the PI/PID controller by completely rejecting this negative effect almost immediately while the PI/PID controller rejects it in a period of 150 s.
Figure 9 shows the time responses of the control systems with both controllers in the presence of an internal disturbance that causes a dynamic variation of the process in a variation range of +/− 25% of the system gain. It can be seen that the H
2-SFC controller is more robust than the PI/PID controller by completely rejecting this negative effect almost immediately while the PI/PID controller rejects it in a considerable period of time.
As the first performance index, the integral of the mean square error (integral square error (ISE)) was used for the time response of the system.
Table 2 presents the performance index obtained for the PI/PID and H
2-SFC controllers.
As the second performance index, the integral of the absolute error (integral absolute error (IAE)) was used for the time responses of the system.
Table 3 presents the performance index obtained for the PI/PID and H
2-SFC controllers.
As can be seen, the H2-SFC controller has a lower ISE value and a lower IAE value, which means it has a lower position error, reaching the desired temperature conditions faster with respect to the PI/PID controller. This implies that the H2-SFC controller has greater robustness and better performance indexes.
From the point of view of classical control, the robustness of a control loop is evaluated through the phase margin (Фm) and gain margin (Am) indicators [
45,
46].
Figure 10 shows the Bode diagram of the system with PI/PID controller under the influence of the external disturbance
d(
k) with phase margin (Фm) equal to 50° and with gain margin (Am) equal to 27.4 dB.
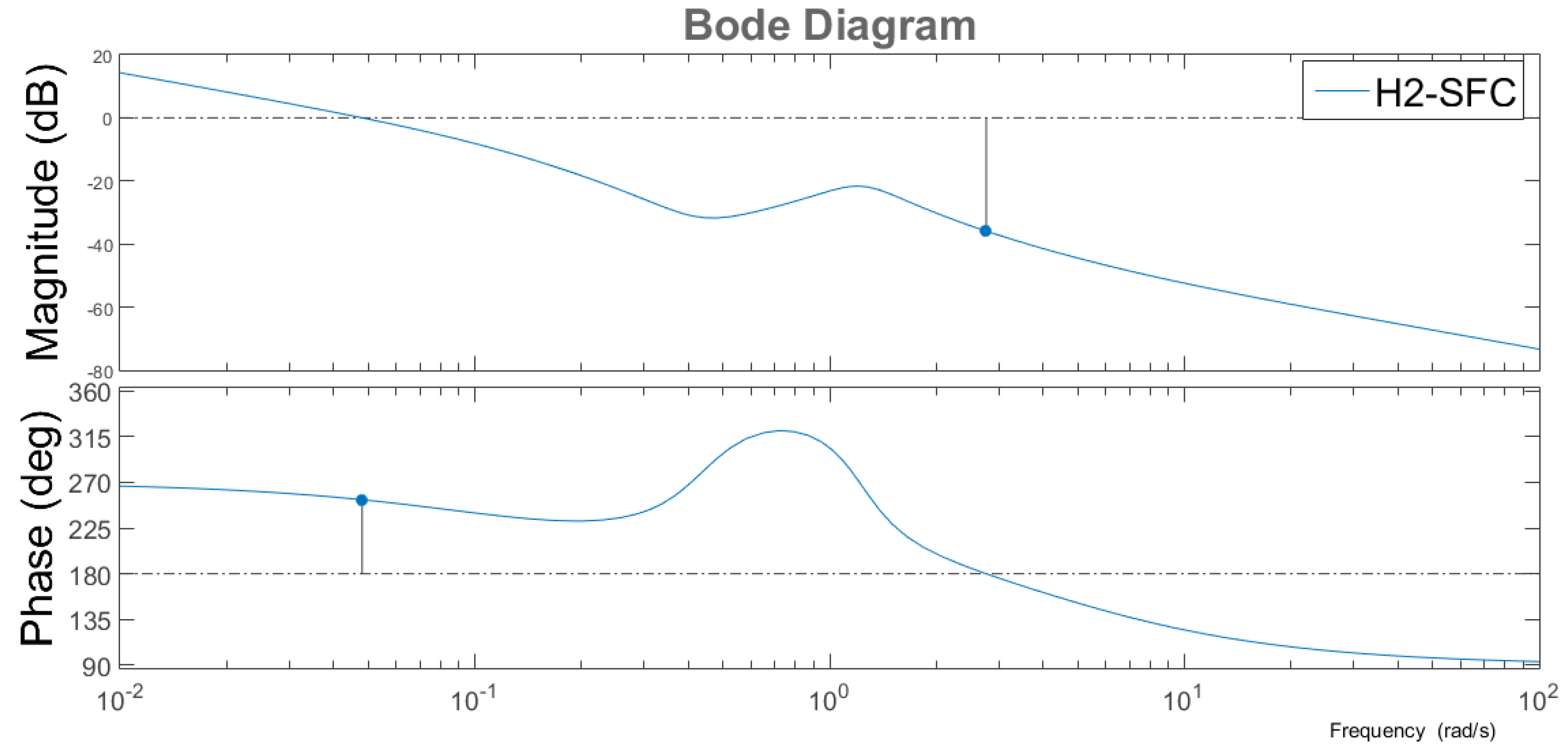
Figure 11 shows the Bode diagram of the system with H
2-SFC controller under the influence of the external disturbance
d(
k) with phase margin (Фm) equal to 72.8° and with gain margin (Am) equal to 35.9 dB.
Once again, the results obtained show that the best performance is obtained with the H2-SFC controller due the fact that it shows a greater phase margin and a greater gain margin under the influence of the external step disturbance d(k) of 1 L/h at the fuel flow inlet that feeds the burner.
Therefore, the H2-SFC controller makes it possible to obtain a significant increase in the effective control of the heating zone temperature of the slab reheating furnace under study, which implies producing better quality steel with a reduction in mechanical equipment deterioration, and with a decrease in the emission of toxic gases to the environment.
5. Conclusions
Based on the application of system identification procedure, a mathematical model that describes the dynamic behavior of the heating zone temperature in a slab reheating furnace was obtained. The model attained is fourth order and without time delay.
The design of an H2-SFC controller for the effective control of the heating temperature of the slab reheating furnace under study was carried out. The results of the control system designed with conventional PI/PID controllers vs. H2-SFC controller showed that the second one has a better performance guaranteeing a faster response.
It is important to highlight that in this work one of the few experiences related to the design and evaluation of a conventional PI/PID controller vs. a robust H2-SFC controller for the effective control of the heating zone temperature in a slab reheating furnace is presented. To obtain better results on the effectiveness of the designed controller, it is necessary to implement the said controller in the heating zone of the slab reheating furnace under study and develop experiments with respect to its operation in real time.
The next step of our investigations consists in the implementation of the designed controller in the industrial steel slab reheating furnace under study.
The benefits obtained of the effective heating zone temperature control in a slab reheating furnace are directly related to an immediate increase in the quality of the corrugated bars, as well as a significant improvement in the combustion process. Reducing fuel consumption by improving the stoichiometric ratio of air and fuel, by minimizing losses from unburned fuels, and avoiding the depletion of nonrenewable fossil fuels consumed unnecessarily during the combustion process. Reducing the environmental impact by decreasing the emission and pollution of the atmosphere with toxic gases that harm man, flora, and fauna. By reducing the emission of substances that cause the so-called greenhouse effect contributing negatively to the elevation of the temperature of our planet.