Nonlinear Aeroelastic in-Plane Behavior of Suspension Bridges under Steady Wind Flow

Abstract

The nonlinear aeroelastic behavior of suspension bridges, undergoing dynamical in-plain instability (galloping), is analyzed. A nonlinear continuous model of bridge is formulated, made of a visco-elastic beam and a parabolic cable, connected each other by axially rigid suspenders, continuously distributed. The structure is loaded by a uniform wind flow which acts normally to the bridge plane. Both external and internal damping are accounted for the structure, according to the Kelvin-Voigt rheological model. The nonlinear aeroelastic effects are evaluated via the quasi-static theory, while structural nonlinearities are not taken into account. First, the free dynamics of the undamped bridge are addressed, and the natural modes determined. Then, the nonlinear equations ruling the dynamics of the aeroelastic system, close to the bifurcation point, are tackled by the Multiple Scale Method. This is directly applied to the partial differential equations, and provides the finite-dimensional bifurcation equations. From these latter, the limit-cycle amplitude and its stability are evaluated as function of the mean wind velocity. A case study of suspension bridge is analyzed.

1. Introduction

Suspension bridges are long, slender and flexible structures which are very sensitive to dynamic actions induced by wind, which potentially cause a variety of instability phenomena. The importance of wind-resistant design for these structures has been highly recognized and has led to many research works and investigations on bridge aerodynamics. Some historical views of long-span bridge aerodynamics are presented in [1,2].

The first studies were addressed on the dynamic of suspended cables, pertinent to suspension bridges but without the inclusion of the stiffening girder, see Irvine and Caughey [3] and Irvine [4]. Since the 1980s, starting with Hagerdon and Schafer [5] and Luongo et al. [6,7], there has been a large number of studies on the free and forced nonlinear vibrations of suspended cables (see the review of Rega, in [8,9]). In particular, some papers investigated wind-induced aeroelastic instabilities, as [10,11,12].

After the Tacoma Narrows Bridge failure in 1940, major efforts were made to understand the dynamic of suspension bridge, including the effects of the stiffening girder. Bleich [13] modeled the stiffening girder as a flexural beam attached to the elastic cables by inextensible hangers. Additional contributions to the continuum model were made by Pugsley [14]. Abdel-Ghaffar [15] extended the approach to include coupled vertical–torsional vibrations and the effects of cross-sectional distortion. Hayashikawa and Watanabe [16] and Kim et al. [17] enriched the linearized continuum model including the effects of shear deformation and rotary inertia of the stiffening girder, by concluding that these effects are relatively small and only affect the higher modes of vibration. More recently, in [18] the classical continuum model for the free linear vertical vibrations of a suspension bridge is re-examined.

Remarkable attention has been addressed to the aeroelastic behavior of long-span bridges, and especially to the aeroelastic instability, as galloping (1 d.o.f) or flutter (2 d.o.f.), which may cause catastrophic effects, like in the famous Tacoma Narrows bridge. The modern era of bridge aeroelasticity was launched by Farquharson [19]. Bleich [20], for the first time, analyzed the bridge flutter behavior by exploiting the Theodorsen theory of thin airfoils, with the potential flow assumption. During the same period, empirical formulas were proposed, based on the bridge structural properties only, to directly obtain the critical flutter wind velocity without involving any consideration of the flow field (e.g., [21]). Scanlan and his colleagues [22] introduced a semiempirical linearized analysis, referred to as “unsteady theory”, based on the so-called “flutter derivatives”, which is nowadays still popular among researchers. In [23], advances in aeroelastic analyses of suspension bridges are described, with focus on the numerical simulations carried out for a long-span suspension bridge, using finite difference and discrete vortex methods. More recently, many linear and nonlinear aeroelastic analyses for cable-supported bridges were developed, e.g., [24,25,26,27,28]. In [24], a nonlinear aerodynamic force model and associated time domain analysis is performed to predict the aeroelastic response of bridges under turbulent winds. In [25], a numerical method for full-bridge aeroelasticity is presented, based on unsteady cross-sectional wind loads and on the finite-element modeling of the structure. In [26], a fully nonlinear model of suspension bridge is proposed to describe overall three-dimensional motions. Torsional-divergence and flutter are studied by numerical methods, able to tackle the coupled nonlinear partial-differential equations of motion. In [27], after a review of the existing linear and nonlinear analyses, two advanced nonlinear models are introduced to study the aeroelastic effects under smooth/turbulent wind conditions: (a) artificial neural network and, (b) Volterra series-based models. In [28], the limit-cycle oscillations exhibited by long-span suspension bridges in post-flutter condition are investigated. The governing aeroelastic partial differential equations are solved by the Faedo-Galerkin method.

Most of the studies about the aerodynamic instability of the bridge were devoted to flutter phenomena, according to which the aeroelastic instability involves two coalescent modes, one torsional, the other flexural. This is the case of bridges with low torsional stiffness, for which the natural torsional and flexural frequencies are close each other, prone to coalesce under aerodynamic excitation. On the contrary, bridges with high torsional stiffness (e.g., box-girder bridges) have the fundamental torsional frequency much larger than the flexural one, so that the aerodynamic instability exclusively occurs in the flexural mode (galloping instability). This class of bridges also attracted some interest, justified by the fact that, after the Tacoma collapse, many existing bridges were torsionally stiffened and the new bridges were designed with stiffer trusses (e.g., the Verrazzano bridge in New York, Tago bridge in Lisbon or the Japanese bridge Akashi Kaikyo). Many works in literature dealt with the galloping instability separately in the beam (see, e.g., [29,30,31,32,33]) and in the cable (see, e.g., [34,35,36,37]). With reference to the class of bridges with high torsional stiffness, the interest was addressed mainly to the galloping control (see, e.g., [38,39,40]).

In this paper, the interest is focused on galloping of suspension bridges. Differently from the current research trend, according to which fine discretized models are used to analyze particular bridges, here the aeroelastic behavior is investigated via a continuous model, in order to study families of bridges, and to identify the key dimensionless parameters which govern the mechanical behavior. The main innovative aspect, therefore, relies in directly attacking the continuous problem by perturbation methods (similarly to what done by the same authors in [41]), which leads to approximate formulae, suitable for preliminary design. A simple continuous model of suspension bridge, subjected to steady wind flow, is proposed to analyze the aeroelastic in-plain instability (galloping). Linear visco-elastic beam and cable are considered, coupled by vertical suspenders, modeled as axially rigid links uniformly distributed. Both external and internal damping are accounted, both for the beam and cable, according to the Kelvin-Voigt rheological model. A steady and uniform wind flow is applied exclusively to the beam. The aeroelastic effects of the wind are evaluated via the classical quasi-static theory (a discussion about strengths and weaknesses of the method is reported in [42]). First, the linear free dynamic of the undamped model is studied; then, the nonlinear bifurcation problem is tackled by the Multiple Scale Method (MSM) which naturally reduces the infinite-dimensional system to the proper finite-dimensional Center Manifold. From the bifurcation equation, the limit cycles and their stability are evaluated as function of the mean wind velocity. The asymptotic results are validated via numerical time-integration of ordinary differential equations derived by in-space finite differences. A case study of suspension bridge is analyzed.

The paper is organized as follows. In Section 2, a continuous visco-elastic model of standard single-span suspension bridge under uniformly distributed steady wind flow, is formulated. In Section 3, the free dynamic of the undamped problem is addressed. In Section 4 the Multiple Scale Method is directly applied to the partial differential equations, to get the bifurcation equation governing the motion close to a Hopf bifurcation. In Section 5, a finite-dimensional model is formulated. In Section 6, the numerical outcomes are presented. Finally, in Section 7 the main findings of the work are summarized. An Appendix A, containing details about damping parameter identification, closes the paper.

2. Continuous Model

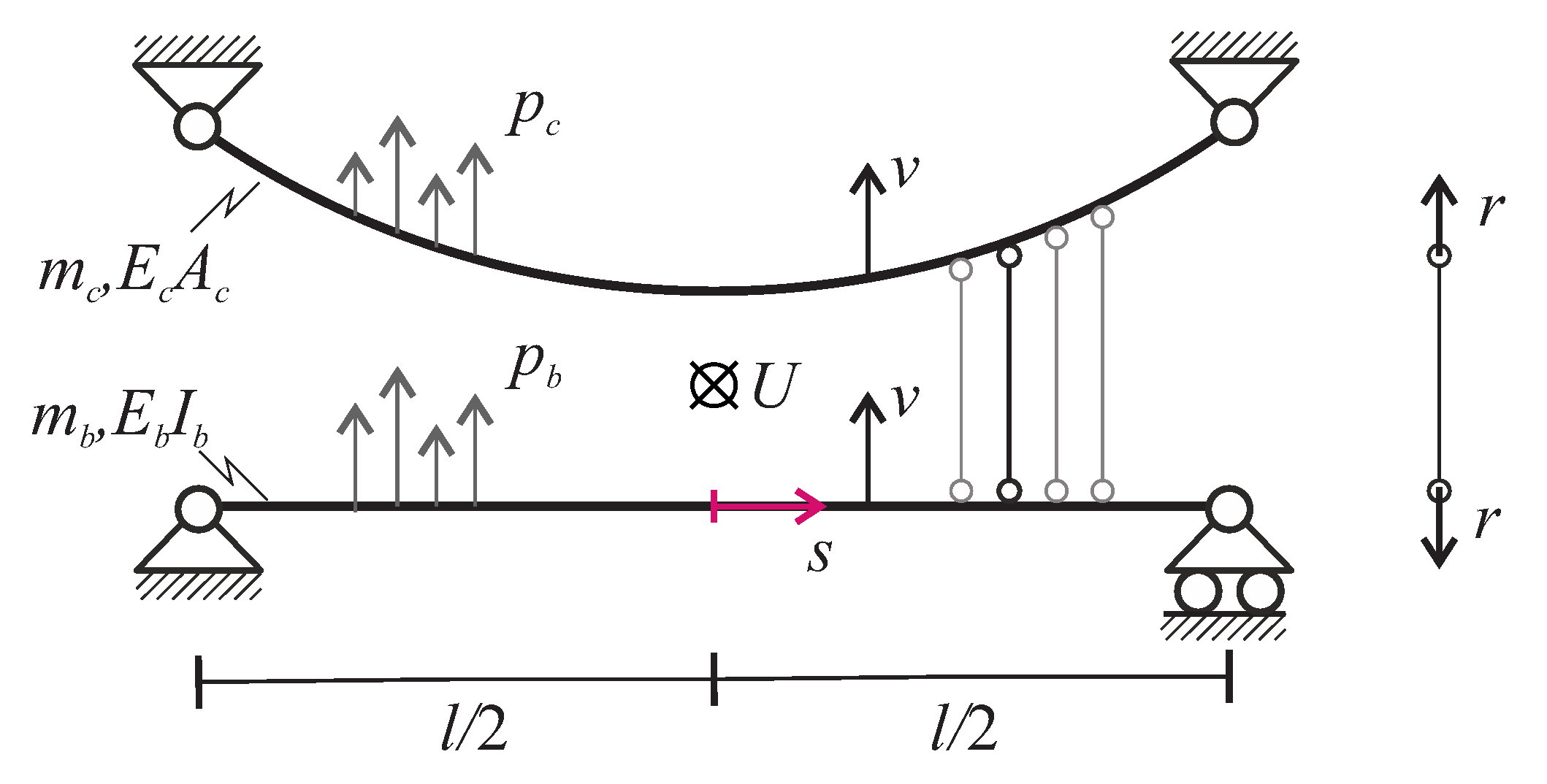
A standard single-span suspension bridge is considered, consisting of a main cable, a stiffening girder, equispaced hangers (or suspenders) and two supporting towers (Figure 1).

The main cable, modeled as uniform, elastic and perfectly flexible (no bending stiffness) is connected to the tip of towers, taken to be infinitely rigid. The girder is modeled as an Euler-Bernoulli beam, simply supported at both ends. The structure is subjected to a steady and uniform wind flow of velocity U. The dynamics of the structure are studied in the vertical plane, while the out-of-plane motions are ignored.

The main cable is modeled according the Irvine’s theory [3], holding for sag-to-span ratios up to about 1:10. The cable assumes a parabolic profile under the initial dead load, and experiences vibrations in which the tangent component is statically condensed. Beam and cable are coupled by vertical hangers, here assumed to be massless, inextensible and continuously distributed along the span of the bridge (curtain of hangers) which apply equal and opposite distributed reactive forces $r(s,t)$ to the two substructures.

2.1. Equations of Motion

Kinematics of the beam are assumed to be linear; nonlinearities are accounted for in the description of the aerodynamic forces only. The current configuration, both of the beam and of the cable, is described by the common transverse displacement field $v\left(s,t\right)$, with $s\in \left(-l/2,l/2\right)$ an abscissa along the beam axis and t the time. The equations ruling the in-plane motion, obtained eliminating the reactive forces $r(s,t)$ between the cable and the beam equations, are:

$$\begin{array}{c}{E}_b{I}_b{v}^{⁗}-T_0{v}^{″}+E_c{A}_c{\displaystyle \frac{k^2}{l}}{\displaystyle \underset{-l/2}{\overset{l/2}{\int }}}vds+\left(m_b+m_c\right)\ddot{v}-\left(p_b+p_c\right)=0\hfill \\ \begin{array}{cc}v\left(-l/2,t\right)=0,\hfill & E_b{I}_b{v}^{″}\left(-l/2,t\right)=0\hfill \\ v\left(l/2,t\right)=0,\hfill & E_b{I}_b{v}^{″}\left(l/2,t\right)=0\hfill \end{array}\hfill \end{array}$$

(1)

where $E_b{I}_b$ is the flexural stiffness of the beam, $E_c{A}_c$ is the axial stiffness of the cable, and $m_b$ and $m_c$ are the beam and cable linear mass density, respectively (and therefore the total bridge linear mass density is $m:=m_b+m_c$). Here $T_0$ is the prestress of the cable, assumed constant on s, and $k=mg/T_0$, with g the acceleration gravity, is the prestress curvature, also assumed to be constant. The integral term accounts for the increment of tension, which depends on the time only.

In Equation (1), the non-inertial contribution of the external loads are decomposed in the damping and aerodynamic parts, as:

$$p_{\alpha }:=p_{\alpha }^d+p_{\alpha }^a$$

(2)

where the subscripts $\alpha =b,c$ refer respectively the beam and cable.

The Equation (1) is a generalization of the motion equations provided for the first time by Bleich et al. in [13], and recently re-examined in [18]. They include damping and aerodynamic loads, not present in the original formulation.

2.2. Damping Forces

A damping continuous model, accounting for both external damping (due to firm air-structure interaction) and internal damping (due to material dissipation), is used. This approach is different from that usually followed in literature, in which an ‘overall’ damping is attributed to the modes of the discrete system on experimental (or of literature) ground.

The contribution of the internal damping is related to two different physical mechanisms (see [37]): (a) elongation of the longitudinal fibers, both in cable and in beam, and (b) internal friction of the prestressed fibers of the cable. By adopting the Kelvin-Voigt model for mechanism (a), the elastic modulus $E_{\alpha }$$\left(\alpha =b,c\right)$ must be replaced by $E_{\alpha }\left(1+{\eta }_{\alpha }{\partial }_t\right),$ with ${\eta }_{\alpha }$ an internal viscous damping coefficient, having physical dimensions of a time. By adopting the same rule for mechanisms (b), the pretension $T_0$ must be replaced by $T_0\left(1+{\eta }_c{\partial }_t\right)$. In symbols:

$$\begin{array}{c}{E}_{\alpha }\to E_{\alpha }\left(1+{\eta }_{\alpha }{\partial }_t\right)\hfill \\ T_0\to T_0\left(1+{\eta }_c{\partial }_t\right)\hfill \end{array}$$

(3)

Accordingly, the time-differential damping operator is proportional to the elasto-geometric stiffness operator. Such a type of damping is usually referred as proportional, or Raleigh model, in the context of the finite-dimensional systems.

The external damping is modeled by forces proportional to velocities, as:

$$p_{\alpha }^d=-c_{e\alpha }\dot{v}\alpha =b,c$$

(4)

in which $c_{eb}$ and $c_{ec}$ are beam and cable external damping coefficients, from which $c_e:=c_{eb}+c_{ec}$ is the coefficient of total external damping.

Note that the damping model introduced here is able to distinguish the beam and cable contributions. The four damping parameters can be calibrated to reproduce modal damping of as many modes.

2.3. Aerodynamic Forces

The aerodynamic part of the load is caused by the wind, which blows orthogonally to the plane of bridge, with a steady velocity U. It triggers forces on the beam and on the cable, acting both in-plane and out-of-plane of the structure. Due to the higher out-of-plane stiffness of the beam and to the smaller dimensions of the cable (which, being of circular shape, is exclusively subjected to drag forces), only in-plane forces acting on the beam are taken into account.

The quasi-static theory (see [29]) is used here to express such forces. The choice is corroborated by the discussion carried out in [28], where it is stated that: (a) the use of a nonlinear quasi-steady theory is justified in the range of low reduced frequencies, in which long-span bridges are expected to fall; and, (b) the previsions of the quasi-steady model are conservative, a few percent lower than those of a fully unsteady model. In particular, it is known that (see e.g., [43,44]), the quasi-steady assumption is valid only if the main frequency of periodic components of fluid forces, associated with vortex-shedding, is well above the dominant structural frequency, i.e., $n_s>>n_0$, where $n_0$ is the natural frequency of the crosswind vibration mode of the structure and $n_s=S_{t}U/b$, with $S_t$ the Struhal number and b the deck width. The occurrence of the frequency condition will be verified in the numerical application. When the inequality is not satisfied, it is needed to resort to a non-steady theory. However, while this latter is well codified in the linear range, few studies concern nonlinear dynamics (e.g., [44,45,46]).

In the framework of the quasi-steady theory, the forces depend on the structural velocity $\dot{v}$ only (not on the frequency of the oscillations), as result of the aeroelastic interaction. By expressing them in series of powers of the ${\displaystyle \frac{\dot{v}}{U}}$ ratio, by assuming the cross-section is symmetric with respect the horizontal axis, and truncating the series to the fifth order, they read:

$$\begin{array}{cc}\hfill p_b^a& =-{\displaystyle \frac{1}{2}}{\varrho }_{a}D{U}^2\left[A_1\left({\displaystyle \frac{\dot{v}}{U}}\right)+A_3{\left({\displaystyle \frac{\dot{v}}{U}}\right)}^3+A_5{\left({\displaystyle \frac{\dot{v}}{U}}\right)}^5\right]\hfill \\ \hfill & =-\left(b_{1}U\dot{v}+b_3\frac{1}{U}{\dot{v}}^3+b_5\frac{1}{U^3}{\dot{v}}^5\right)\hfill \end{array}$$

(5)

Here, ${\varrho }_a$ is the air mass density, $A_i$ are dimensionless aerodynamic coefficients (depending on the shape of the cylinder cross-section), D is a transverse characteristic length, and $b_i:={\displaystyle \frac{1}{2}}{\varrho }_{a}D{A}_i$ ( $i=1,3,5$) are dimensional coefficients, introduced to simplify the notation.

2.4. Dimensionless Equation of Motion

By introducing the following non-dimensional quantities:

$$\tilde{v}=\frac{v}{l},\tilde{s}=\frac{s}{l},\tilde{t}=t\Omega ,\Omega :=\frac{1}{l}\sqrt{\frac{T_0}{m}}$$

(6)

and parameters:

$${\varrho }^2:=\frac{E_b{I}_b}{l^2{T}_0},{\Lambda }^2:={\left(kl\right)}^2\frac{E_c{A}_c}{T_0},{\tilde{\eta }}_{\alpha }={\eta }_{\alpha }\Omega ,{\tilde{c}}_{e\alpha }=c_{e\alpha }\frac{\Omega l^2}{T_0},{\tilde{b}}_i=b_i\frac{{\Omega }^2{l}^3}{T_0},u=\frac{U}{\Omega l}$$

(7)

the equations of motion are recast in non-dimensional form:

$$\begin{array}{c}{\varrho }^2\left(1+{\eta }_b{\partial }_t\right)v^{⁗}-\left(1+{\eta }_c{\partial }_t\right)v^{″}+{\Lambda }^2\left(1+{\eta }_c{\partial }_t\right){\displaystyle \underset{-1/2}{\overset{1/2}{\int }}}vds+\ddot{v}+\left(c_e+b_{1}u\right)\dot{v}+b_3{\displaystyle \frac{1}{u}}{\dot{v}}^3+b_5{\displaystyle \frac{1}{u^3}}{\dot{v}}^5=0\hfill \\ \begin{array}{cc}v\left(-1/2,t\right)=0,\hfill & {\varrho }^2\left(1+{\eta }_b{\partial }_t\right)v^{″}\left(-1/2,t\right)=0\hfill \\ v\left(1/2,t\right)=0,\hfill & {\varrho }^2\left(1+{\eta }_b{\partial }_t\right)v^{″}\left(1/2,t\right)=0\hfill \end{array}\hfill \end{array}$$

(8)

In Equation (8), prime and dot denote differentiation with respect to non-dimensional space and time, respectively, and the tilde is dropped for convenience. It is noticed that nonlinearities are only due to aerodynamics.

The dimensionless parameter ${\Lambda }^2$ is the well-known Irvine-Caughey parameter [3], accounting for geometric and mechanical properties of the cable. The dimensionless parameter ${\rho }^2$ (also used in [13,47,48] and others), describes the beam-to-cable stiffness ratio. For long bridges, it tends to zero, so that such bridges behave as a cable with an appended mass. However, still in this case, the ${\rho }^2$ parameter causes the occurrence of boundary layers close to the constraints and the point-loads, where the flexural behavior cannot be neglected. In this paper, attention will be devoted to bridges of medium length, in which the role of the beam is not negligible, as it will be discussed soon. A parametric study about the influence of both parameters on the free dynamic of the bridge is carried out in [18].

3. Linear Undamped Oscillations

First, the free dynamics of the undamped problem are addressed to evaluate the natural frequencies and modes. Although this problem has already been solved in literature (see, e.g., [13,18]), it is shortly resumed here for completeness.

The relevant equations of motion are:

$$\begin{array}{c}{\varrho }^2{v}^{⁗}-v^{″}+{\Lambda }^2{\displaystyle \underset{-1/2}{\overset{1/2}{\int }}}vds+\ddot{v}=0\hfill \\ \begin{array}{cc}v\left(-1/2,t\right)=0,\hfill & {\varrho }^2{v}^{″}\left(-1/2,t\right)=0\hfill \\ v\left(1/2,t\right)=0,\hfill & {\varrho }^2{v}^{″}\left(1/2,t\right)=0\hfill \end{array}\hfill \end{array}$$

(9)

By separating the variables as $v\left(s,t\right)=\varphi \left(s\right)e^{i\omega t}$, a space eigenvalue problem follows:

$$\begin{array}{c}{\varrho }^2{\varphi }^{⁗}-{\varphi }^{″}-{\omega }^2\varphi =-{\Lambda }^2{\displaystyle \underset{-\frac{1}{2}}{\overset{\frac{1}{2}}{\int }}}\varphi ds\hfill \\ \begin{array}{cc}\varphi \left(-1/2\right)=0,\hfill & {\varrho }^2{\varphi }^{″}\left(-1/2\right)=0\hfill \\ \varphi \left(1/2\right)=0,\hfill & {\varrho }^2{\varphi }^{″}\left(1/2\right)=0\hfill \end{array}\hfill \end{array}$$

(10)

whose eigensolutions $\left({\omega }_n,{\varphi }_n\right)$, $n=1,2,\dots$, are the natural frequencies and modes, respectively. Due to the symmetry of the structure with respect $s=0$, the modes are of anti-symmetric and symmetric types.

3.1. Anti-Symmetric Modes

In the anti-symmetric modes, the integral term in the equations disappears (no change of tension occurs), so that the system behaves as a string, stiffned by an in-parallel beam. Accordingly:

$${\varphi }_n\left(s\right)=sin\left(2n\pi s\right)n=1,2,\dots$$

(11)

and

$$\begin{array}{c}{\omega }_n=2\pi \sqrt{4{\pi }^2{n}^4{\rho }^2+n^2}\hfill \end{array}$$

(12)

are the nth anti-symmetric eigenpair. It is independent of ${\Lambda }^2$, i.e., of the elasto-geometric properties of the cable, but depends on the parameter ${\rho }^2$, i.e., on the stiffness ratio. It is worth noticing that the frequency of the first mode ($n=1$) nearly doubles with respect to that of the string $({\omega }_n=2\pi )$ when ${\rho }^2=0.075$. It is concluded that the stiffening effect of the girder is significant when ${\rho }^2=O\left({10}^{-2}\right)$.

3.2. Symmetric Mode

The nth symmetric natural mode is found to be:

$${\varphi }_n\left(s\right)=\frac{1}{B_N}\left(B_{1}cos\left({\beta }_{1}s\right)+B_{2}cosh\left({\beta }_{2}s\right)+B_0\right)n=1,2,\dots$$

(13)

where the following definitions hold for the coefficient $B_i$:

$$\begin{array}{c}{B}_1:={\displaystyle \frac{{\beta }_2}{{\beta }_1}cosh\left(\frac{{\beta }_2}{2}\right)}\hfill \\ B_2:={\displaystyle \frac{{\beta }_1}{{\beta }_2}cos\left(\frac{{\beta }_1}{2}\right)}\hfill \\ B_0:={\displaystyle -\frac{2{\Lambda }^2}{{\beta }_1{\beta }_2\left({\Lambda }^2-{\omega }_n^2\right)}\left({\beta }_2{B}_{1}sin\left(\frac{{\beta }_1}{2}\right)+{\beta }_1{B}_{2}sinh\left(\frac{{\beta }_2}{2}\right)\right)}\hfill \end{array}$$

(14)

and $B_N:=B_0+B_1+B_2$ is a normalization factor, such that ${\varphi }_n\left(0\right)=1$. In Equation (13), ${\beta }_1$, ${\beta }_2$ are frequency-dependent wave-numbers, defined as follows:

$$\begin{array}{c}{\beta }_1={\displaystyle \sqrt{\frac{-1+\sqrt{1+4{\varrho }^2{\omega }_n^2}}{2{\varrho }^2}}}\\ {\beta }_2=\sqrt{{\displaystyle \frac{1+\sqrt{1+4{\varrho }^2{\omega }_n^2}}{2{\varrho }^2}}}\end{array}$$

(15)

The unknown squared frequency ${\omega }_n^2$ is found as a root of the transcendent characteristic equation:

$$\frac{{\beta }_1{\beta }_2\left({\beta }_1^2+{\beta }_2^2\right)\left({\Lambda }^2-{\omega }_n^2\right)}{2{\Lambda }^2}={{\beta }_1}^{3}tanh\left(\frac{{\beta }_2}{2}\right)+{{\beta }_2}^{3}tan\left(\frac{{\beta }_1}{2}\right)$$

(16)

Therefore, an explicit expression for the natural frequency of the symmetric modes cannot be provided.

4. Aeroelastic Stability Analysis

To investigate the behavior of the structure in the nonlinear field and close to the dynamic bifurcation, a nonlinear analysis is carried out. To solve the nonlinear problem, Equation (8), the asymptotic Multiple Scale Method (MSM) is used, by directly attacking the partial differential equations of motion. The method consists in expanding the dependent variables in a formal series of a small perturbation parameter $ϵ$ (to be reabsorbed at the end of the procedure), as well as introducing independent time scales. Substitution of these expansions in the nonlinear equations and separation of terms of different orders, lead to linear differential equations to be solved in sequence. Here, the MSM is used as reduction method, as an alternative to the Center Manifold Method ([49,50]). It provides a bifurcation equation ruling the dynamic on a center manifold of finite dimension (two-dimensional in the case of simple Hopf bifurcation).

4.1. Bifurcation Equation

According to the MSM, a small dimensionless parameter $ϵ$ is introduced by a suitable ordering of variables and parameters. First, the displacement is rescaled as $v\left(s,t\right)\to ϵv\left(s,t\right)$, so that $ϵ$ is of the order of the amplitude of motion. Then, damping and aerodynamic coefficients are rescaled as: ${\eta }_b\to ϵ{\eta }_b$, ${\eta }_c\to ϵ{\eta }_c$, $c_e\to ϵc_e$, $b_1\to ϵb_1$, $b_3\to {ϵ}^{-1}{b}_3$, $b_5\to {ϵ}^{-3}{b}_5$, i.e., nonlinear coefficients are taken much larger than the linear ones (as suggested by the numerical application illustrated ahead), in order linear and nonlinear aerodynamic forces appear at the same level in the perturbation scheme. Moreover, independent time-scales $t_0:=t$, $t_1:=ϵt$, ..., are introduced, so that $v\left(s,t;ϵ\right)=v\left(s,t_0\left(t\right),t_1\left(t\right),\dots ;ϵ\right)$. Hence, by exploiting the chain rule, the following formal expansions for the time differential operators hold:

$$\begin{array}{c}{\partial }_t={\partial }_0+ϵ{\partial }_1+\dots \hfill \\ {\partial }_t^2={\left({\partial }_0+ϵ{\partial }_1+\dots \right)}^2\hfill \end{array}$$

(17)

in which ${\partial }_j:=\partial /\partial t_j$, $j=0,1,\dots$. Finally, the independent variable is expanded in series of $ϵ$ as:

$$v\left(s,t;ϵ\right)=v_0\left(s,t_0,t_1,\dots \right)+ϵv_1\left(s,t_0,t_1,\dots \right)+\dots$$

(18)

By introducing rescaling and expansions in the equations of motion, and collecting the coefficients of the different powers of $ϵ$, the following perturbation equations are derived.

Order ${ϵ}^0$:

$$\begin{array}{c}{\varrho }^2{v}_0^{⁗}-v_0^{″}+{\Lambda }^2{\displaystyle \underset{-1/2}{\overset{1/2}{\int }}}{v}_{0}ds+{\partial }_0^2{v}_0=0\hfill \\ \begin{array}{cc}{v}_0\left(-1/2,t_0,t_1,\dots \right)=0,\hfill & {\varrho }^2{v}_0^{″}\left(-1/2,t_0,t_1,\dots \right)=0\hfill \\ v_0\left(1/2,t_0,t_1,\dots \right)=0,\hfill & {\varrho }^2{v}_0^{″}\left(1/2,t_0,t_1,\dots \right)=0\hfill \end{array}\hfill \end{array}$$

(19)

Order $ϵ$:

$$\begin{gathered} \begin{array}{ll}{\varrho }^2{v}_1^{⁗}-v_1^{″}+{\Lambda }^2{\displaystyle \underset{-1/2}{\overset{1/2}{\int }}}{v}_{1}ds+{\partial }_0^2{v}_1=& -{\varrho }^2{\eta }_b{\partial }_0{v}_0^{⁗}+{\eta }_c{\partial }_0{v}_0^{″}-{\Lambda }^2{\eta }_c{\partial }_0{\displaystyle \underset{-1/2}{\overset{1/2}{\int }}}{v}_{0}ds-2{\partial }_0{\partial }_1{v}_0+\\ & -\left(c_e+b_{1}u\right){\partial }_0{v}_0-b_3{\displaystyle \frac{1}{u}}{\left({\partial }_0{v}_0\right)}^3-b_5{\displaystyle \frac{1}{u^3}}{\left({\partial }_0{v}_0\right)}^5\end{array} \\ \begin{array}{ll}{v}_1\left(-1/2,t_0,t_1,\dots \right)=0,& {\varrho }^2{v}_1^{″}\left(-1/2,t_0,t_1,\dots \right)=-{\varrho }^2{\eta }_b{\partial }_0{v}_0^{″}\left(-1/2,t_0,t_1,\dots \right)\\ v_1\left(1/2,t_0,t_1,\dots \right)=0,& {\varrho }^2{v}_1^{″}\left(1/2,t_0,t_1,\dots \right)=-{\varrho }^2{\eta }_b{\partial }_0{v}_0^{″}\left(1/2,t_0,t_1,\dots \right)\end{array} \end{gathered}$$

(20)

The generating problem, Equation (19), admits the monomodal solution:

$$v_0\left(s,t\right)=A\left(t_1\right)\varphi \left(s\right)e^{i\omega t_0}+\mathrm{c}.\mathrm{c}.$$

(21)

in which $A\left(t_1\right)$ is an unknown complex modulating function, c.c. stands for complex conjugate terms, and $\left(\omega ,\varphi \left(s\right)\right)$ is a real eigenpair of the undamped and unloaded model, determined in Section 3.

When the $ϵ$-order problem, Equation (20), is considered, damping and aerodynamics terms appear on the right hand side of the equation, to be evaluated via Equation (21). Here, the internal damping ${\eta }_b$ would trigger point-moments at the boundaries, equal to $-{\varrho }^2{\eta }_b{\partial }_0{v}_0^{″}\left(\pm 1/2\right)$; however, this last contribution is zero, because of the lower-order conditions ${\varrho }^2{v}_0^{″}\left(\pm 1/2\right)=0$. Equation (20) therefore read:

$$\begin{array}{c}{\varrho }^2{v}_1^{⁗}-v_1^{″}+{\Lambda }^2{\displaystyle \underset{-\frac{1}{2}}{\overset{\frac{1}{2}}{\int }}}{v}_{1}ds+{\partial }_0^2{v}_1=q\left(s,t_1\right)e^{i\omega t_0}+\mathrm{NRT}+\mathrm{c}.\mathrm{c}.\hfill \\ \begin{array}{cc}{v}_1\left(-1/2,t_0,t_1,\dots \right)=0,\hfill & {\varrho }^2{v}_1^{″}\left(-1/2,t_0,t_1,\dots \right)=0\hfill \\ v_1\left(1/2,t_0,t_1,\dots \right)=0,\hfill & {\varrho }^2{v}_1^{″}\left(1/2,t_0,t_1,\dots \right)=0\hfill \end{array}\hfill \end{array}$$

(22)

where NRT stands for Non Resonant Terms, and

$$\begin{array}{cc}q\left(s,t_1\right):=& -i\omega \left[2{\partial }_{1}A\left(t_1\right)\varphi \left(s\right)+\left(b_{1}u\varphi \left(s\right)+c_e\varphi \left(s\right)+{\rho }^2{\eta }_b{\varphi }^{⁗}\left(s\right)+{\Lambda }^2{\eta }_c{\int }_{-\frac{1}{2}}^{\frac{1}{2}}\varphi \left(s\right)ds\right.\right.\hfill \\ & \left.\left.-{\eta }_c{\varphi }^{″}\left(s\right)\right)A\left(t_1\right)+{\displaystyle \frac{3b_3{\omega }^2\varphi {\left(s\right)}^3}{u}}A{\left(t_1\right)}^2\overline{A}\left(t_1\right)+{\displaystyle \frac{10b_5{\omega }^4\varphi {\left(s\right)}^5}{u^3}}A{\left(t_1\right)}^3\overline{A}{\left(t_1\right)}^2\right]\hfill \end{array}$$

(23)

Since the operator is singular (i.e., it admits a nontrivial homogeneous solution), the non-homogeneous problem cannot be solved for a generic know term. Therefore, a compatibility (or solvability) condition, known as Fredholm alternative, has to be enforced on it. This condition requires the $\omega$-frequency forcing terms are orthogonal to the kernel of the self-adjoint operator, i.e.,

$${\displaystyle \underset{-\frac{1}{2}}{\overset{\frac{1}{2}}{\int }}}\varphi \left(s\right)q\left(s,t_1\right)=0$$

(24)

A detailed discussion on solvability conditions is provided in [51,52], in the framework of perturbation methods.

From Equation (24), an ordinary differential equation on the $t_1-$scale is obtained for the amplitude. By coming back to the true time t via backward rescaling, the equation assumes the well-known normal form for the Hopf bifurcation, i.e.,

$$\dot{A}=\left(d_0+u{d}_1\right)A+\frac{d_3}{u}{A}^2\overline{A}+\frac{d_5}{u^3}{A}^3{\overline{A}}^2$$

(25)

where the real quantities $d_i$ are defined as follows:

$$\begin{array}{c}{d}_0:={\displaystyle \frac{{\int }_{-\frac{1}{2}}^{\frac{1}{2}}\left(-c_e\varphi {\left(s\right)}^2-{\eta }_b{\rho }^2\varphi \left(s\right){\varphi }^{⁗}\left(s\right)-{\eta }_c{\Lambda }^2\varphi \left(s\right){\int }_{-\frac{1}{2}}^{\frac{1}{2}}\varphi \left(s\right)ds+{\eta }_c\varphi \left(s\right){\varphi }^{″}\left(s\right)\right)ds}{2{\int }_{-\frac{1}{2}}^{\frac{1}{2}}\varphi {\left(s\right)}^{2}ds}}\hfill \\ d_1:=-{\displaystyle \frac{b_1}{2}}\hfill \\ d_3:=-\frac{{\displaystyle 3b_3{\omega }^2{\int }_{-\frac{1}{2}}^{\frac{1}{2}}}{\displaystyle \varphi {\left(s\right)}^{4}ds}}{{\displaystyle 2{\int }_{-\frac{1}{2}}^{\frac{1}{2}}}{\displaystyle \varphi {\left(s\right)}^{2}ds}}\hfill \\ d_5:=-\frac{{\displaystyle 5b_5{\omega }^4{\int }_{-\frac{1}{2}}^{\frac{1}{2}}\varphi {\left(s\right)}^{6}ds}}{{\displaystyle {\int }_{-\frac{1}{2}}^{\frac{1}{2}}\varphi {\left(s\right)}^{2}ds}}\hfill \end{array}$$

(26)

Finally, by letting $A\left(t\right)={\displaystyle \frac{1}{2}a\left(t\right)}{e}^{i\phi \left(t\right)}$, and separating real and imaginary parts in Equation (25), the real form of the bifurcation equation is derived:

$$\begin{array}{c}\dot{a}={\displaystyle \left(d_0+u{d}_1\right)a+\frac{1}{4}\frac{d_3}{u}{a}^3+\frac{1}{16}\frac{d_5}{u^3}{a}^5}\hfill \\ a\dot{\phi }=0\hfill \end{array}$$

(27)

Equation (27)-b supplies $\phi =\mathrm{const}$, since structural nonlinearities, that would be responsible for phase modulations, have been ignored. The steady solutions $a=\mathrm{const}$ of Equation (27)-a are periodic solutions for the original system; the $T-$periodic solutions $a\left(t+T\right)=a\left(t\right)$ are quasi-periodic solutions for the original system. Due to the normalization adopted for the natural modes, the real amplitude a describes: (a) the maximum modulus of the displacement in the anti-symmetric modes, and, (b) the displacement at $s=0$ in the symmetric modes.

4.2. Linear Stability Analysis and Critical Wind Velocity

The dynamic of the bridge, close to the rest position, is ruled by the linear part of Equation (25), which admits the solution $a\left(t\right)=a\left(0\right)e^{\lambda t}$, where $\lambda :=d_0+u{d}_1$. The position is asymptotically stable if $\lambda <0$ and unstable if $\lambda >0.$ The condition of incipient instability occurs for $\lambda =0$, that is for the wind velocity getting its critical (galloping velocity) value:

$$u_c:=-{\displaystyle \frac{d_0}{d_1}}$$

(28)

at which a Hopf bifurcation occurs. Since, from Equation (26), $d_0<0$ (dissipative damping), bifurcation occurs only if $d_1>0$ (self-exciting aerodynamics, entailing $A_1<0$). Once the wind direction has been fixed, this last condition occurs only for some cross-section shape (just said, aerodynamically unstable).

The critical wind velocity depends on the mode at which the bridge is oscillating, each velocity being associated to each mode. The lowest critical velocity is associated with the lowest mode (at which the internal damping is minimum), which can be either symmetric (Equation (13)) or anti-symmetric (Equation (11)). For this latter, an explicit formula can be derived, namely:

$$u_c=-\frac{c_e+16{\pi }^4{\eta }_b{\rho }^2+4{\pi }^2{\eta }_c}{b_1}$$

(29)

The beneficial influence of the flexural stiffness should be noticed, since the critical wind velocity increases with ${\rho }^2$. This is due to the fact that the internal damping is proportional to the stiffness, according to the Kelvin-Voigt model adopted.

4.3. Limit-Cycle Analysis

Steady non-trivial solutions of the bifurcation Equation (27)-a describe periodic oscillations occurring on limit-cycles. By letting $\dot{a}=0$ and solving the biquadratic algebraic equation, two explicit solutions are found (to within an unessential sign):

$$a_{\pm }=u\sqrt{-{\displaystyle \frac{2}{d_5}\left(d_3\pm \sqrt{▵\left(u\right)}\right)}}$$

(30)

where:

$$▵\left(u\right):=d_3^2-\frac{4d_5\left(d_{1}u+d_0\right)}{u}$$

(31)

They describe two velocity-dependent branches (denoted by the ± index) of the bifurcation diagram $a_{\pm }=a_{\pm }\left(u\right)$. Depending on u, two, one o zero nontrivial real solutions exist. In order to discuss the number of solutions, here the interesting case in which $A_3<0$ and $A_5>0$ is considered, which entails $d_3>0$ and $d_5<0$. This case is typical, for example, of rectangular cross-sections with a 2:1 aspect ratio (see [29,31]), according which the qualitative galloping response is plotted in Figure 2.

Preliminary, it is observed that $d_{1}u+d_0$ is negative in the subcritical $u<u_c$ range and positive in the supercritical $u>u_c$ range. Then, the sign of the discriminant is discussed. Let:

$$u^{*}:={\displaystyle \frac{4d_5{d}_0}{d_3^2-4d_5{d}_1}}\equiv u_c\frac{1}{1-\frac{d_3^2}{4d_1{d}_5}}$$

(32)

be the value of velocity at which the discriminant vanishes, i.e. $▵\left(u^{*}\right)=0$. Since $u^{*}<u_c$, it follows that:

• when $u<u^{*}$, it is $▵\left(u\right)<0$, so that no real solutions $a_{\pm }$ exist;
• when $u^{*}<u<u_c$, it is $▵\left(u\right)>0$; however, due $d_{1}u+d_0<0$, it is $\sqrt{▵\left(u\right)}<d_3$, so that both the $a_{+}$ and $a_{-}$ roots are real;
• when $u>u_c$, in addition to $▵\left(u\right)>0$, it is also $d_{1}u+d_0>0$; consequently, $\sqrt{▵\left(u\right)}>d_3$, which entails that only $a_{+}$ is real.

The two branches coalesce at $u=u^{*}$, at which $a_{+}=a_{-}=u^{*}\sqrt{{\displaystyle -\frac{2}{d_5}{d}_3}}$ and a turning point manifests itself.

4.4. Stability Analysis

To detect stability of the periodic solutions, the 1-dimensional dynamical system described by Equation (27)-a is perturbed, by letting $a\to a_{\pm }+\delta a$, where $\delta a$ is a small deviation from the steady solution solution $a_{\pm }$. By linearizing in the perturbation, the following variational equation is obtained:

$$\delta \dot{a}=\left(d_0+d_{1}u+\frac{3d_3}{4u}{a}_{\pm }^2+\frac{5d_5}{16u^3}{a}_{\pm }^4\right)\delta a$$

(33)

which decides about stability of $a_{\pm }$. From this, by using Equation (30), the following conclusions are derived:

• the lower non-trivial solution $a_{-}$ is unstable in its domain of existence $u^{*}<u<u_c$;
• the upper non-trivial solution $a_{+}$ is stable in its domain of existence $u>u^{*}$.

By summarizing (Figure 2), a subcritical Hopf bifurcation occurs at $u=u_c$. Here, the trivial solution loses stability, and a family of unstable limit cycles of amplitude $a_{-}\left(u\right)$ bifurcates, whose existence is limited to a portion of the subcritical range. Indeed, at $u=u^{*}$, a turning point modifies unstable to stable cycles, which extend their existence to the supercritical range. As a consequence, if the wind velocity is quasi-statically increased from below through $u_c,$ the rest position loses stability and the system jumps from zero to a finite value $a_{+}\left(u_c\right)$. A reverse jump occurs at $u^{*}$ when the wind velocity is decreased from above. An hysteresis can occur for wind velocity periodically changed. Such a behaviour is related to the opposite signs of the aerodynamic coefficients, $b_3$ and $b_5$, causing a change of the qualitative behaviour of the system, namely: (i) at small amplitudes the cubic terms in the motion Equation (8) prevails over the quintic term; (ii) at higher amplitudes, the opposite occurs. This phenomenon is known in literature as “hard loss of stability”, and observed in several different problems (see, e.g., [53], where the effects of the nonlinear damping on the post-critical behavior of the Ziegler’s column are discussed).

5. Finite-Dimensional Model

Aimed to validate asymptotic results, a finite-dimensional model of bridge for galloping analysis is formulated. The finite-difference method is applied to transform the partial integro-differential Equation (8) into a set of ordinary differential equations, to be numerically integrated for given initial conditions.

The space domain (changed in $\left[0,1\right]$ for simplicity) is divided in $N>2$ equispaced subintervals of amplitude $\Delta =1/N$. The following notation is adopted:

$$\begin{array}{cccc}\hfill s_j& :=j\Delta ,\hfill & \hfill j& =-1,\dots ,N+1,\hfill \\ \hfill v_j& :=v\left(s_j,t\right),\hfill & \hfill j& =-1,\dots ,N+1.\hfill \end{array}$$

(34)

in which two external nodes, $j=-1,N+1$, have been introduced.

The space derivatives are expressed via the central finite differences:

$$\begin{array}{cc}\hfill f^{⁗}& =\frac{f_{j-2}-4f_{j-1}+6f_j-4f_{j+1}+f_{j+2}}{{\Delta }^4}\hfill \\ \hfill f^{″}& =\frac{f_{j+1}-2f_j+f_{j-1}}{{\Delta }^2}\hfill \end{array}$$

(35)

and the integral term via the trapezoidal rule:

$$\underset{0}{\overset{1}{\int }}f\mathrm{d}x=\Delta {\displaystyle \sum _{j=1}^{N-1}}{f}_j$$

(36)

in which the boundary conditions $f_0,f_N=0$ have been accounted for. The field equation in (8), accordingly, becomes:

$$\begin{array}{l}{\displaystyle {\ddot{v}}_j+{\varrho }^2\frac{v_{j-2}-4v_{j-1}+6v_j-4v_{j+1}+v_{j+2}}{{\Delta }^4}+{\varrho }^2{\eta }_b\frac{{\dot{v}}_{j-2}-4{\dot{v}}_{j-1}+6{\dot{v}}_j-4{\dot{v}}_{j+1}+{\dot{v}}_{j+2}}{{\Delta }^4}+}\\ {\displaystyle -\frac{v_{j+1}-2v_j+v_{j-1}}{{\Delta }^2}-\frac{{\dot{v}}_{j+1}-2{\dot{v}}_j+{\dot{v}}_{j-1}}{{\Delta }^2}{\eta }_c}+{\Lambda }^2\Delta {\displaystyle \sum _{j=1}^{N-1}}{v}_j+{\Lambda }^2{\eta }_c\Delta {\displaystyle \sum _{j=1}^{N-1}}{\dot{v}}_j+\\ +\left(c_e+b_{1}u\right){\dot{v}}_j+b_3{\displaystyle \frac{1}{u}}{\dot{v}}_j^3+b_5{\displaystyle \frac{1}{u^3}}{\dot{v}}_j^5=0j=1,\dots ,N-1\end{array}$$

(37)

and the boundary equations read:

$${\displaystyle \begin{array}{c}{v}_0=0\hfill \\ {\varrho }^2{\displaystyle \frac{v_1-2v_0+v_{-1}}{{\Delta }^2}+\frac{{\dot{v}}_1-2{\dot{v}}_0+{\dot{v}}_{-1}}{{\Delta }^2}{\eta }_b}{\varrho }^2=0\hfill \\ v_N=0\hfill \\ {\varrho }^2{\displaystyle \frac{v_{N+1}-2v_N+v_{N-1}}{{\Delta }^2}+\frac{{\dot{v}}_{N+1}-2{\dot{v}}_N+{\dot{v}}_{N-1}}{{\Delta }^2}{\eta }_b}{\varrho }^2=0\hfill \end{array}}$$

(38)

Equations (37) and (38) are a set of $N+3$ (ordinary and algebraic) equations for the $N+3$ unknown nodal displacements $v_j\left(t\right)$, $j=-1,\dots ,N+1$.

6. Numerical Results

The behavior of the long-span suspension bridges is often well-described by the cable only. Here, however, the focus is addressed to cases in which the beam significantly influences the overall mechanics, as it happens when the dimensionless parameter ${\rho }^2$ is of order ${10}^{-2}$, (see, e.g., [13,18,48]). Therefore, a case study is considered: (a) the geometrical and mechanical characteristics are $l=195$ m, $E_b{I}_b=2.4\times {10}^9$ Nm${}^2$, $E_c{A}_c=4.75\times {10}^9$ N, $m_b=917.86$ kg/m and $m_c=177.6$ kg/m; (b) the prestress is evaluated as $T_0=mg{l}^2/8d$, where $d=19.5$ m is the cable sag; (c) the damping ratio is taken as ${\xi }_A=1.5\%$ in the antisymmetric mode, and ${\xi }_S=1.3\%$ in the symmetric mode (corresponding to ${\eta }_b=0.0044$ s, $c_{eb}=55.88$ Ns/m${}^2$, ${\eta }_c=0.00022$ s, and $c_{ec}=6.29$ Ns/m${}^2$, whose calibration is shown in Appendix A). A rectangular boxed cross-section of dimension $2\times 1$ m (and so with an aspect ratio 2:1) is assumed for the beam. The aerodynamic dimensionless coefficients in Equation (5) are drawn from literature (obtained by wind tunnel tests in [30]), namely $A_1=-3.47$, $A_3=-490.25$, $A_5=44744.21$. The air mass density is ${\varrho }_a=1.25$ kg/m${}^3$.

This example is representative of a class of bridges, whose nondimensional parameters are: ${\rho }^2=0.023997$, ${\Lambda }^2=1161.79$, $b_1=-0.386264$, $b_3=-54.5443$, $b_5=4978.17$, ${\eta }_b=0.0011$, ${\eta }_c=0.000056$, $c_e=0.223$. All numerical values assumed by the parameters are consistent with the ordering performed in the perturbation analysis.

6.1. Linear Stability Analysis

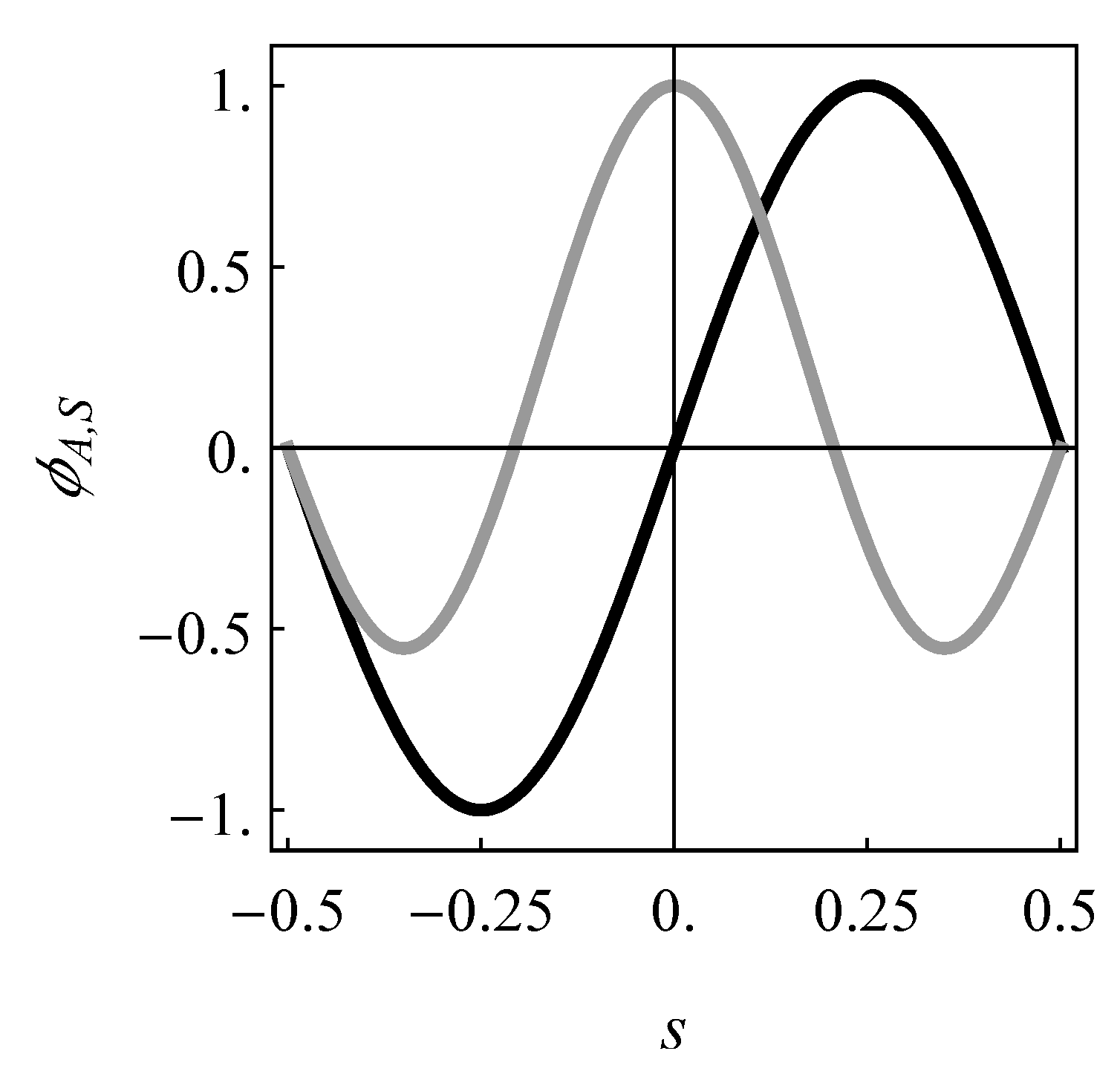
The modal properties of the undamped model were first analyzed. The first natural mode was found to be anti-symmetric (defined by Equation (11) for $n=1$) and the corresponding natural frequency is $\omega =2.12$ rad/s. The second natural mode was found to be symmetric (defined by Equation (13) for $n=1$) and the natural frequency is $\omega =3.91$ rad/s (see Figure 3).

The critical conditions corresponding to the antisymmetric and symmetric modes are shown in

Table 1. Critical frequency and wind velocity in the antisymmetric and symmetric critical modes.

Mode	${\tilde{\mathit{\omega }}}_{\mathit{c}}$	${\mathit{u}}_{\mathit{c}}$	${\mathit{\omega }}_{\mathit{c}}$	${\mathit{U}}_{\mathit{c}}$
			[rad/s]	[m/s]
A	$8.77$	$0.7$	$2.12$	$34.13$
S	$15.61$	$1.05$	$3.91$	$51.3$

. It is observed that the bridge galloped in its first antisymmetric natural mode, in corresponding of which the critical wind velocity assumed the minimum value $U_c=34.13$ m/s.

Since the critical velocities corresponding to the antisymmetric and symmetric modes were sufficiently far from each other, nonlinear interactions between modes, leading to multimodal galloping, were excluded.

It was observed that the quasi-steady theory was valid in the case study considered. Indeed, the natural frequency of the first crosswind vibration mode was $n_0={\omega }_c/2\pi =0.33$ Hz, while the vortex-shedding frequency was $n_s=1.02$ Hz at the critical galloping velocity $U_c=34.13$ m/s, according to a Struhal number $S_t=0.06$ (as indicated by [54] for a rectangular cross-section with a 2:1 aspect ratio) and a deck width of 2 m. Note that the quasi-steady theory worked mainly due to the narrow width of the cross section.

6.2. Galloping Response

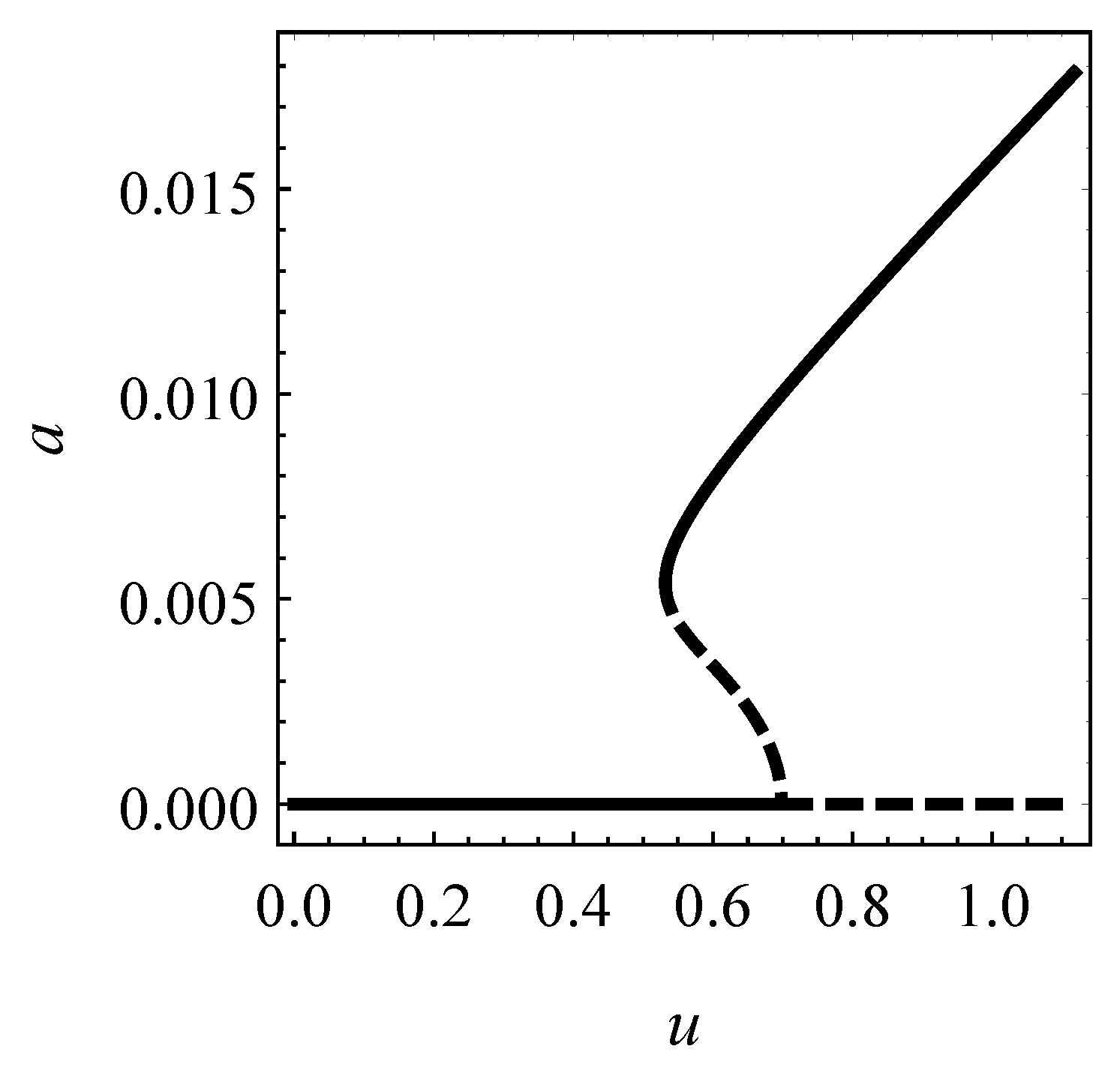
The postcritical behavior relevant to the case study is described by the bifurcation diagram in Figure 4. There, the (dimensionless) steady amplitude a of the anti-symmetric mode, experienced by the bridge on the limit-cycle, is plotted $vs$ the (dimensionless) wind velocity u. It is seen that, the hard loss of stability caused amplitudes of about $1\%$ of the length (i.e., of the order of 2 m), as far the critical wind velocity was passed.

Such a bad mechanical behavior is due to the unfavorable shape of the cross-section ([23,30]).

6.3. Validation by Finite-Dimensional Model

The asymptotic solution was validated against numerical results, relevant to the discretized version (Equations (37) and (38)) of the nonlinear continuous model (Equation (8)). The space interval was divided in $N=128$ subintervals, and numerical integration carried out, via commercial routines, for given initial conditions. Regardless of these latter, after a transient had been exhausted, the motion stabilized either on a limit cycle or comes back to the trivial state. In order to compare the transient motion $v_j\left(t\right)$ to that predicted by the MSM via the amplitude $a\left(t\right)$, an initial deflection shape coincident with the first natural mode of the undamped bridge was chosen.

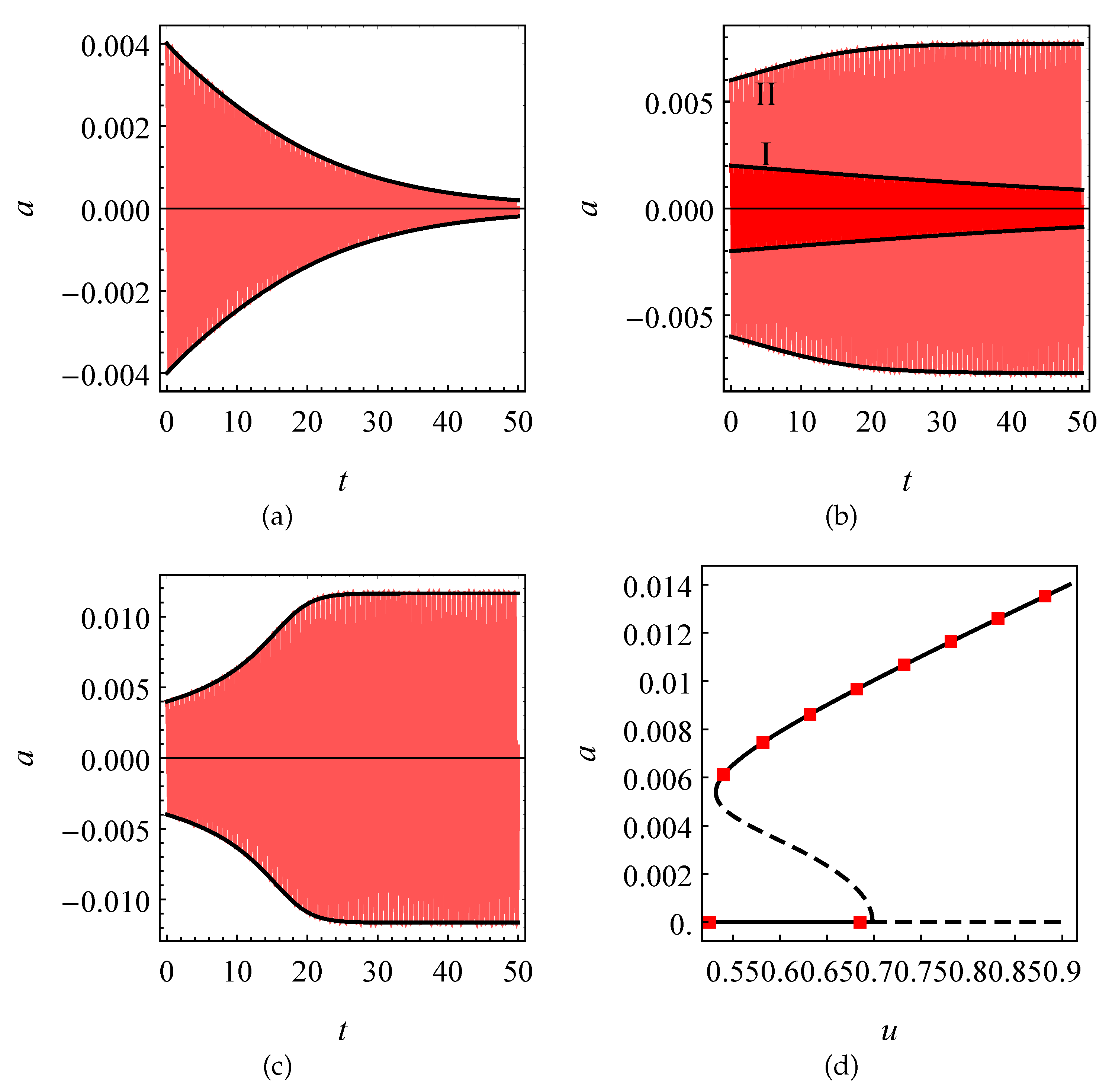
Four typical time-histories are shown in Figure 5 for different wind velocities. It was observed that: (a) when $u<u^{*}$ (Figure 5a) the motion stabilized on the trivial solution $a=0$; (b) when $u^{*}<u<u_c$ (Figure 5b) the motion stabilized either: (I) on the trivial solution $a=0$, if the initial condition was sufficiently small, or (II) on a limit cycle of amplitude $a\ne 0$, if the initial condition was sufficiently large; (c) when $u>u_c$ (Figure 5c) the motion stabilized on a limit cycle of amplitude $a\ne 0$. All the time-histories were compared with the numerical integration of the bifurcation Equation (27). It was seen that this latter captured at the best extent the exact (numerical) solution.

To compare the numerical to the asymptotic limit-cycles, the numerical amplitudes were extracted by the recorded time-histories for different wind velocities, and bullets superimposed to the asymptotic bifurcation diagram (see Figure 5d), showing an excellent accordance. Note the power of the perturbation methods in providing accurate predictive formulae (as for the galloping velocity, Equation (29) and for the amplitudes of the limit-cycles, Equation (30)).

7. Conclusions

The nonlinear aeroelastic behavior of suspension bridges, undergoing dynamic in-plain instability (galloping), has been analyzed. A nonlinear continuous model of bridge has been formulated, made of a visco-elastic beam and a parabolic cable, connected each other by axially rigid suspenders, uniformly distributed. A damping continuous model, accounting for both external damping and internal damping (according to the Kelvin-Voigt rheological model), has been used. The structure is loaded by a uniform wind flow, acting normally to its plane. The nonlinear aeroelastic effects have been evaluated via the quasi-static theory, while structural nonlinearities have been ignored. The nonlinear equations ruling the dynamics of the aeroelastic system have been tackled by the Multiple Scale Method, directly applied to the partial differential equations, to get bifurcation equations for the Hopf bifurcation. The limit-cycle amplitude and its stability have been evaluated as functions of the mean wind velocity. The analytical solutions have been validated against numerical integration of the finite-difference discretized equations.

Numerical results have been obtained for a case study of suspension bridge, whose beam has a rectangular boxed cross-section, with an aspect ratio 2:1. It has been found that the bridge gallops in its first antisymmetric natural mode (having natural frequency $\omega =2.12$ rad/s). An explicit formula has been derived for the critical wind velocity, assuming the value $U_c=34.13$ m/s. The validity of the quasi-steady theory, when related to the vortex-induced vibration phenomenon, has been checked. The postcritical behavior has been investigated, and the bifurcation diagram provided. The well-known (and dangerous) phenomenon of “hard loss of stability” has been found to occur, according which, as far the critical wind velocity is passed, the motion amplitude reaches values equal to $1\%$ of the bridge length (i.e., of the order of 2 m). Such a bad mechanical behavior is due to the unfavorable shape of the cross-section. All the asymptotic results, relevant to the transient as well to the steady motions, have been fully validated by the numerical analysis. This work is susceptible of farther insights, namely, (a) analysis of the influence of the flexibility of the pylons on the bridge dynamics; (b) study of the interaction between vortex-induced vibrations and galloping; (c) validation of the results by wind tunnel tests. Concerning item (a), elasticity of supports could cause (in principle, and to be investigated in the filed of the real bridges) an inversion between the now dominant antisymmetric and the first symmetric mode, as discussed in [6]. Such an inversion could also trigger (d) nonlinear interaction between the two modes. Concerning item (b) and (c), study of literature, as described in [55] could be exploited.