Effects of Barriers on Fault Rupture Process and Strong Ground Motion Based on Various Friction Laws
Abstract
Featured Application
Abstract
1. Introduction
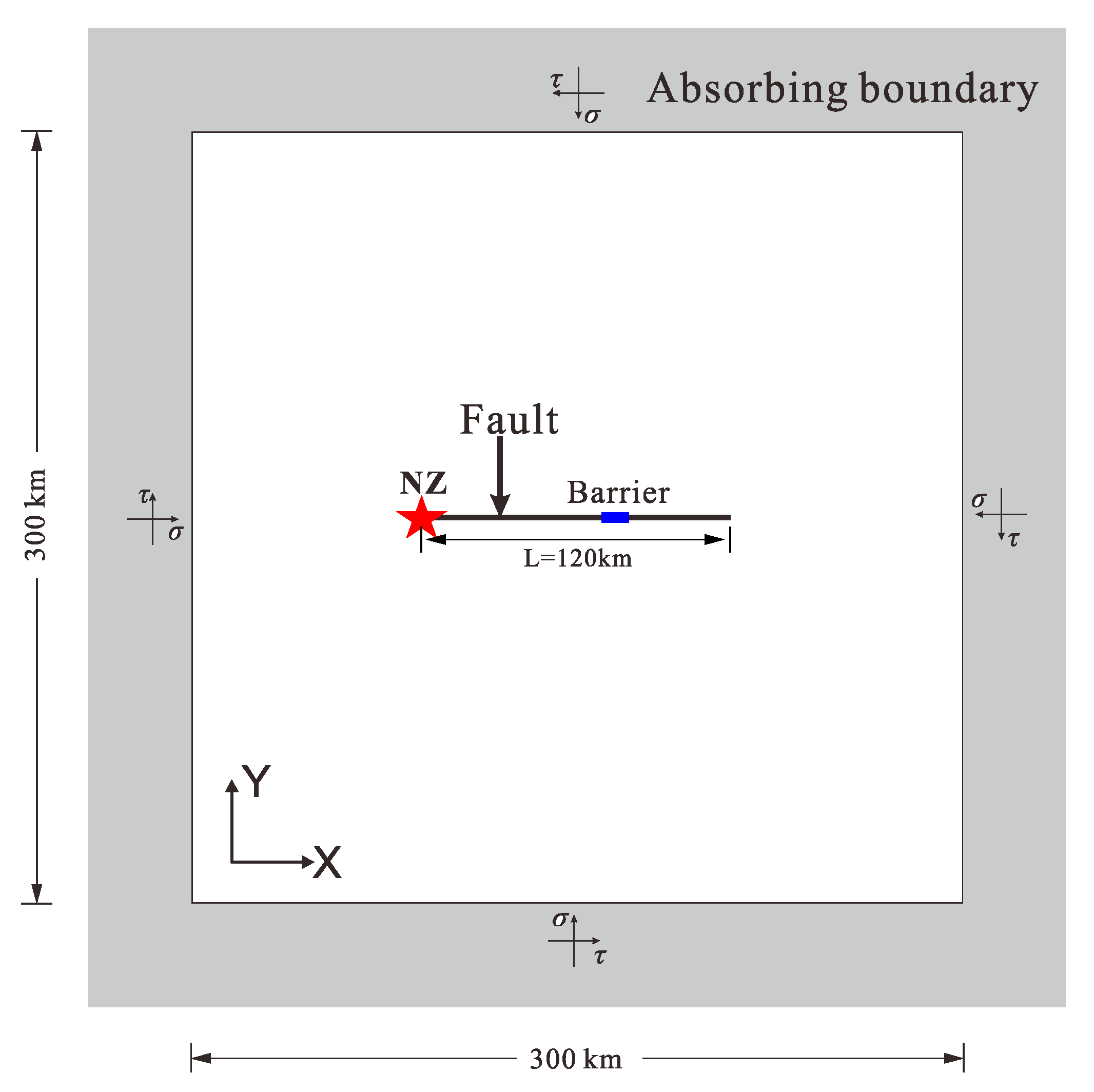
2. Models and Methods
2.1. Models
2.2. Finite Element Formulation
2.3. Friction Laws
3. Results
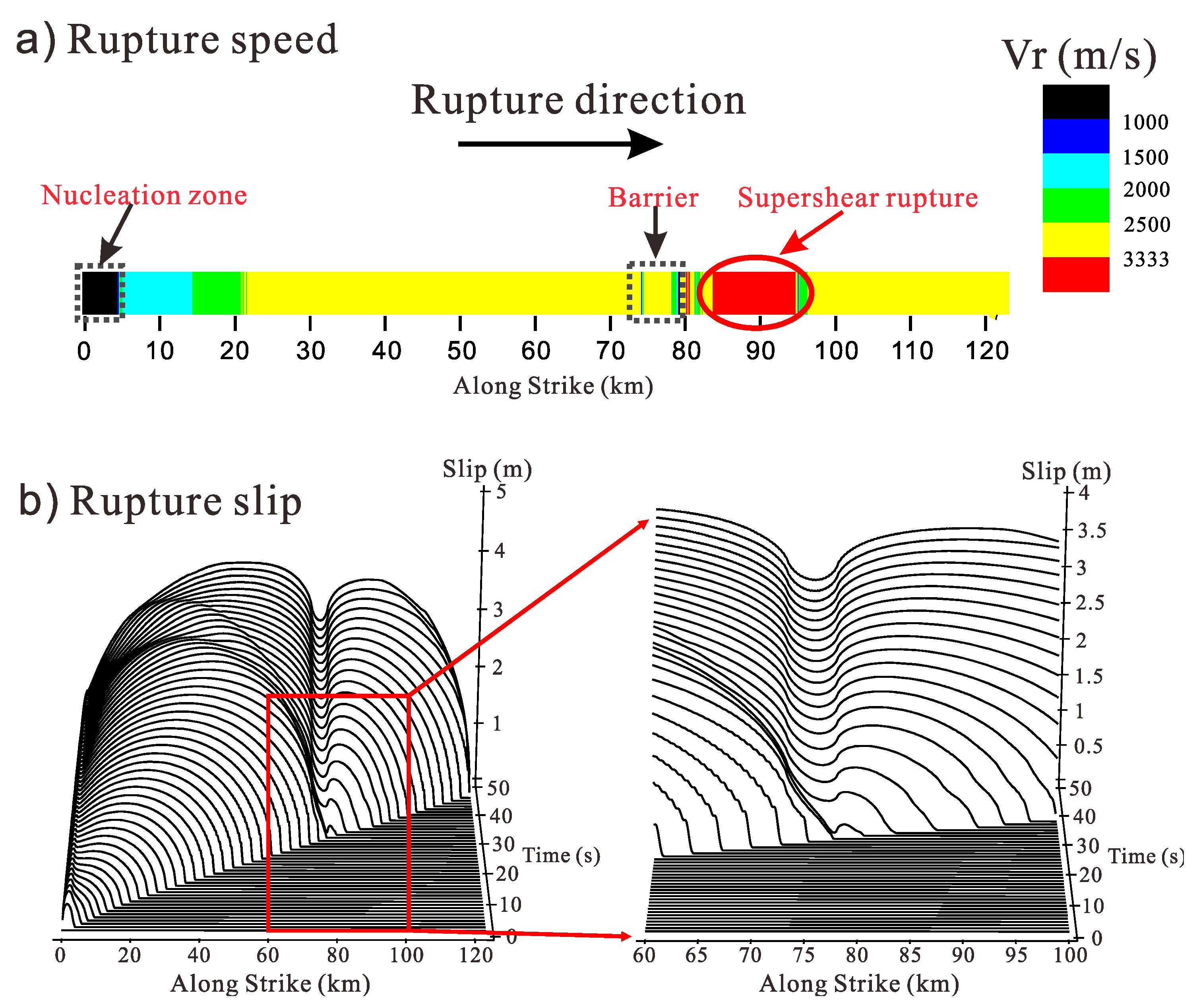
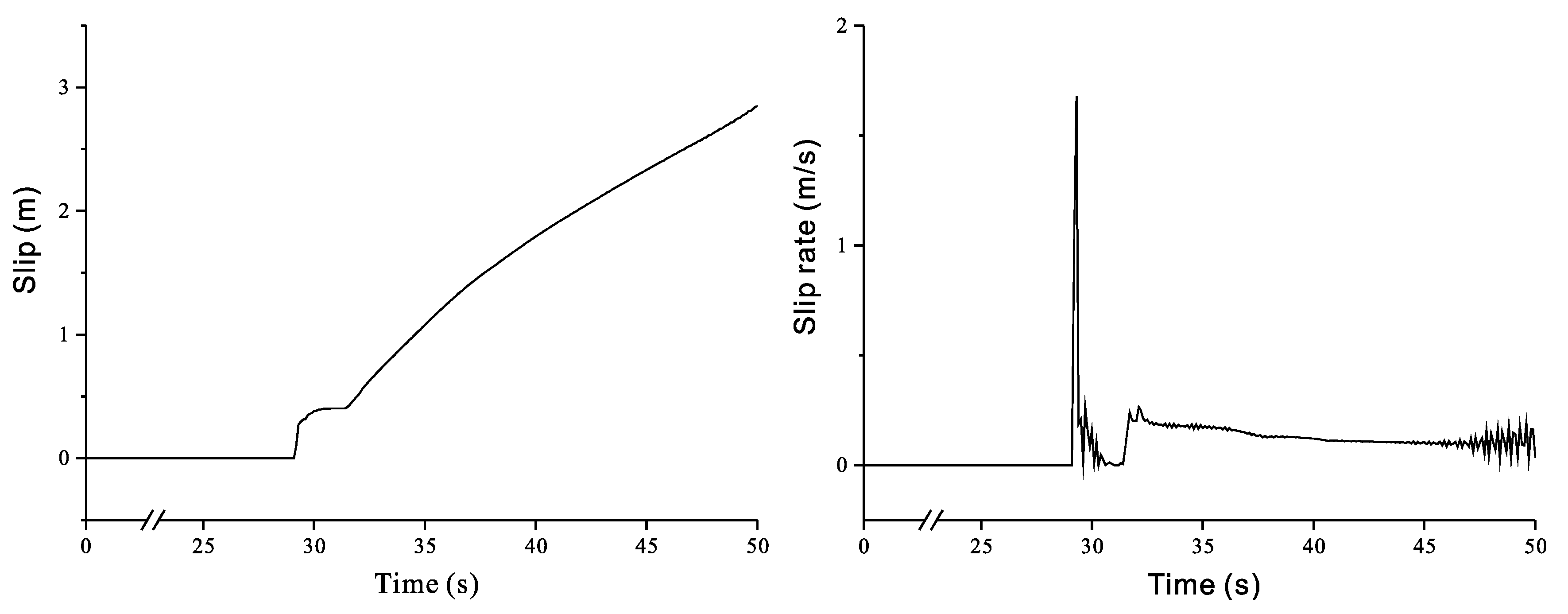
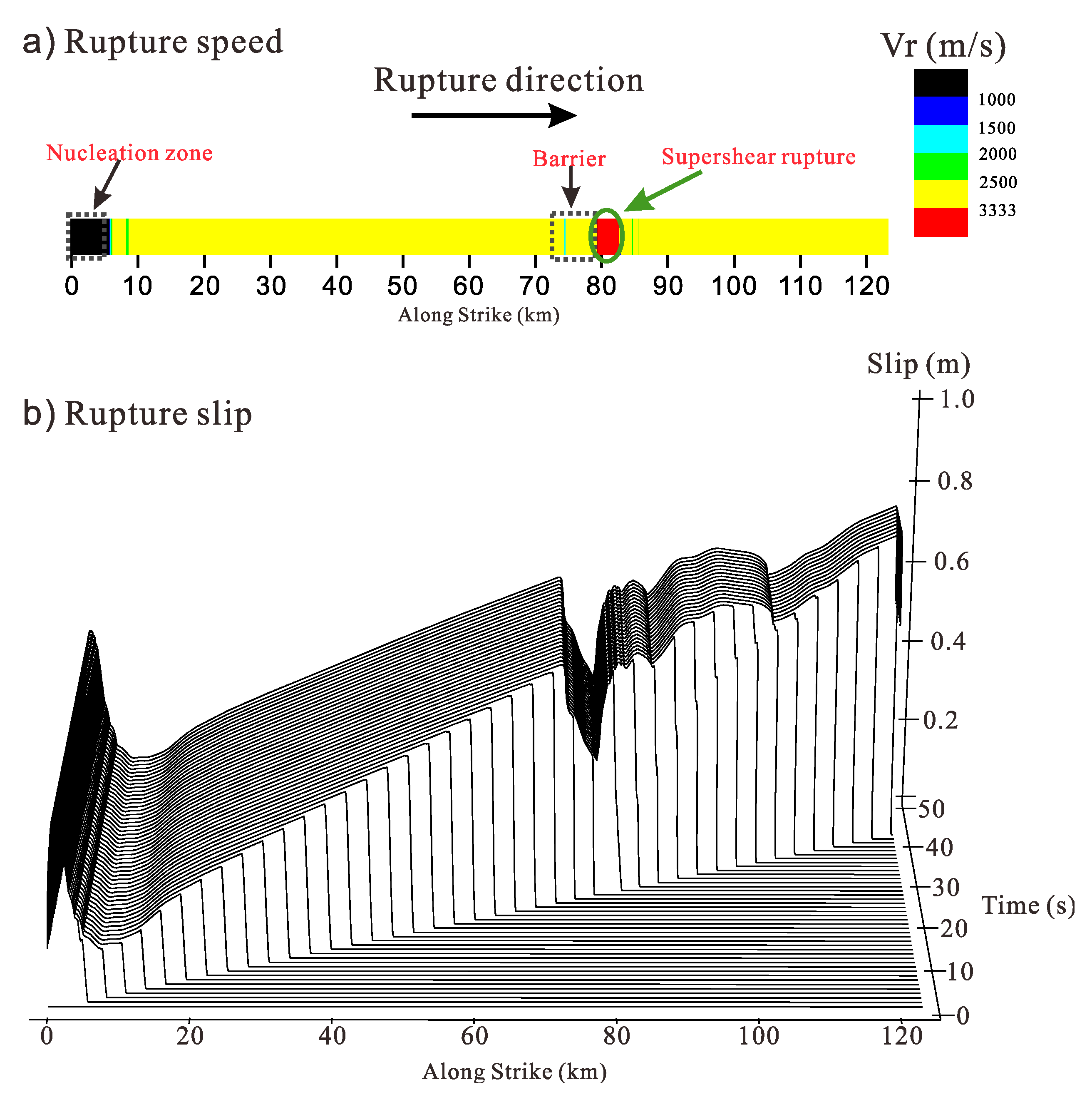
3.1. Comparing the Effect of Barrier with Various Friction Laws
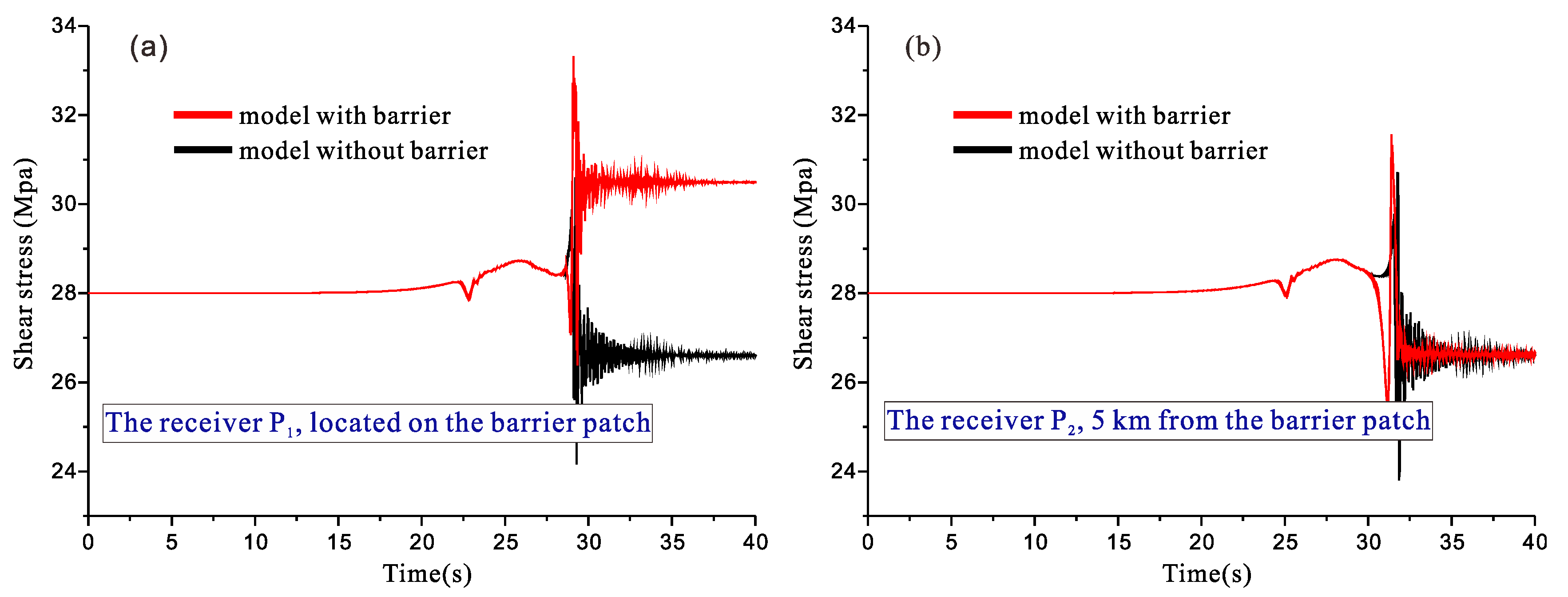
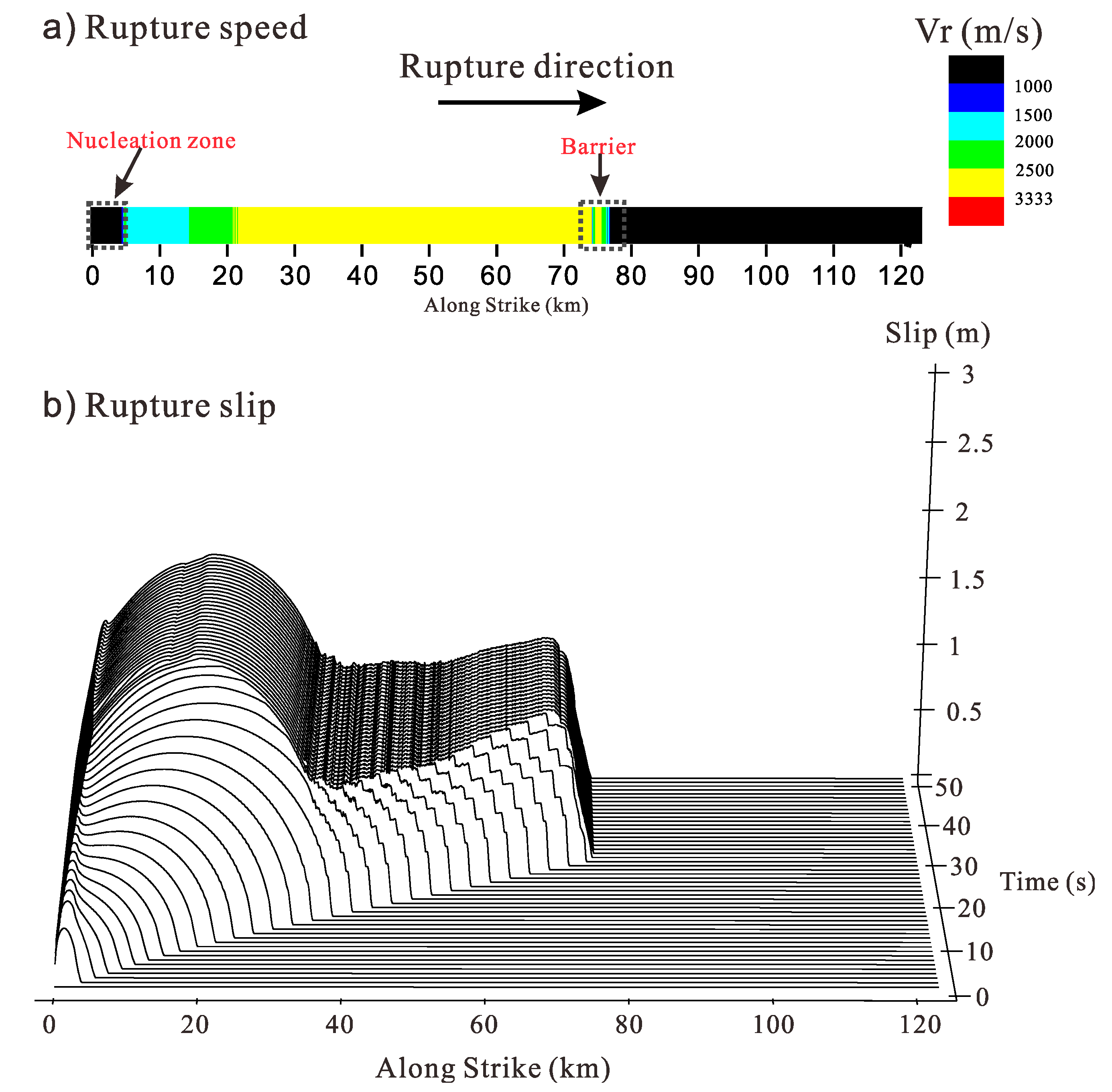
3.1.1. Barrier with Classical Slip-Weakening Friction Law
3.1.2. Barrier with Rate-State Friction Law
3.1.3. Barrier with Modified Slip-Weakening Friction Law
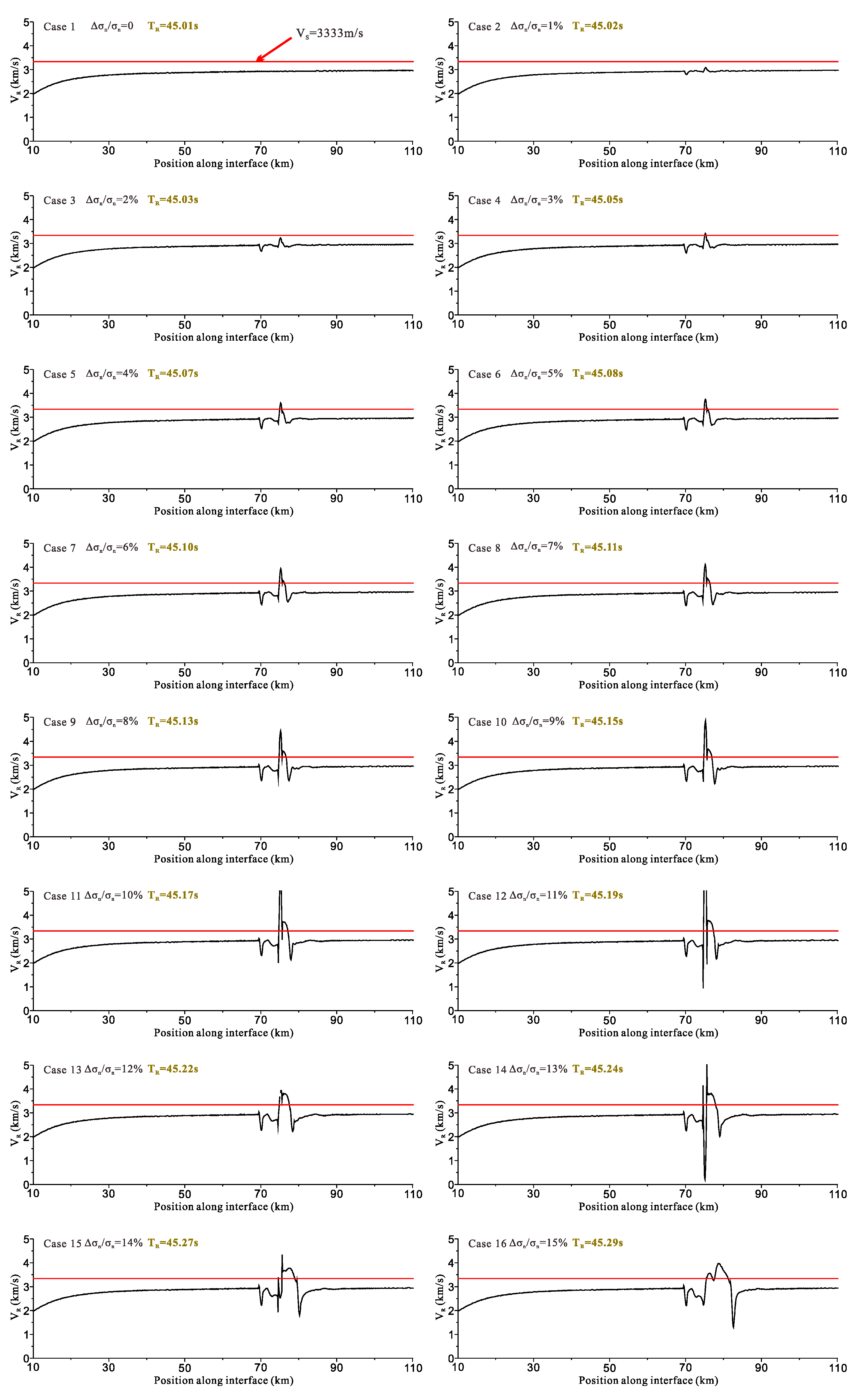
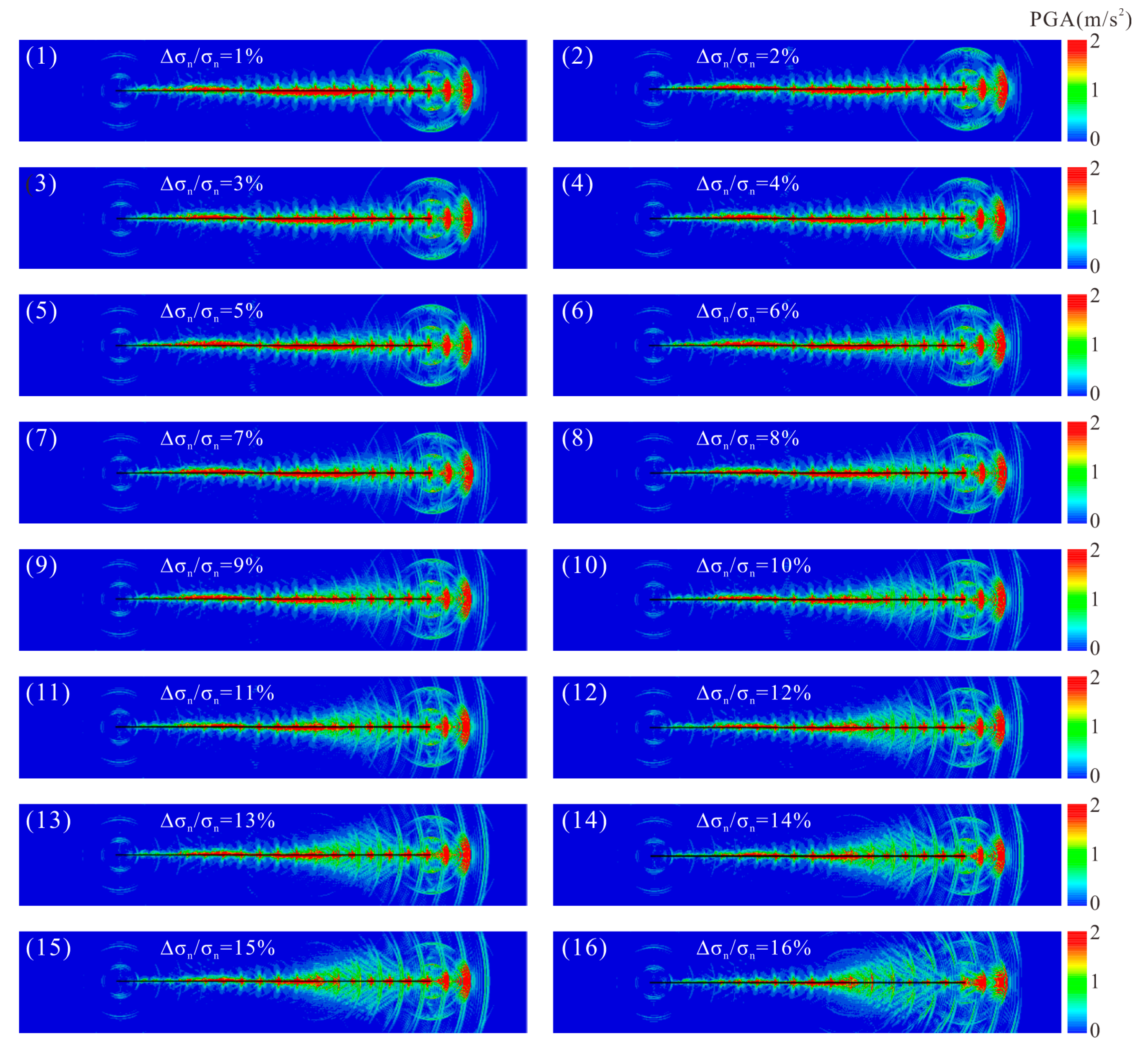
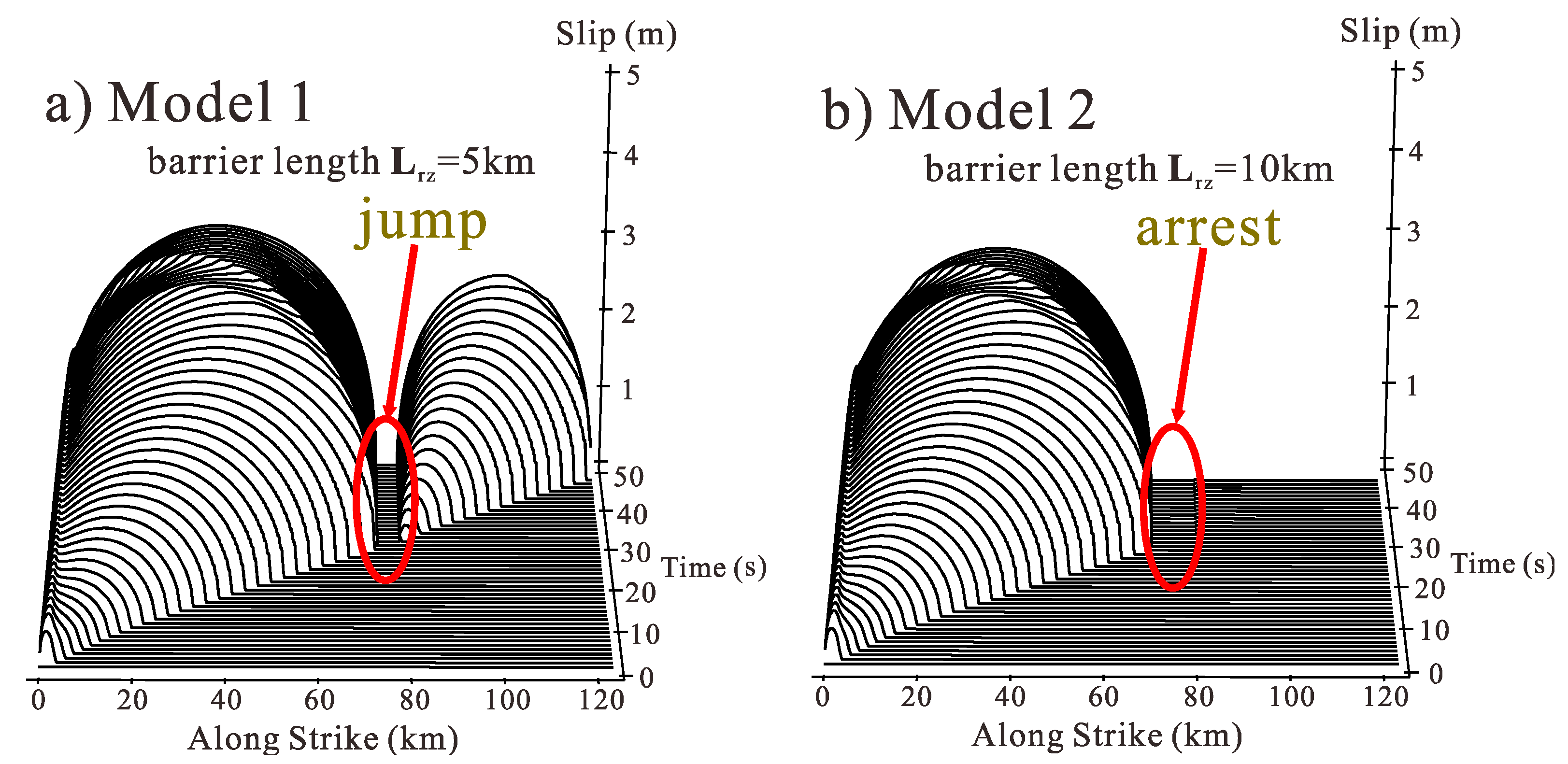
3.2. Effect of the Barrier Strength on the Fault Rupture Process
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Archuleta, R. A faulting model for the 1979 Imperial Valley earthquake. J. Geophys. Res. Atmos. 1984, 89, 4559–4586. [Google Scholar] [CrossRef]
- Bouchon, M.; Bouin, M.P.; Karabulut, H.; Toksöz, M.N.; Dietrich, M.; Rosakis, A.J. How fast is rupture during an earthquake? New insights from the 1999 Turkey earthquakes. Geophys. Res. Lett. 2001, 28, 2723–2726. [Google Scholar] [CrossRef]
- Bouchon, M.; Vallée, M. Observation of long supershear rupture during the magnitude 8.1 Kunlunshan earthquake. Science 2003, 301, 824–826. [Google Scholar] [CrossRef]
- Dunham, E.; Archuleta, R. Evidence for a Supershear Transient during the 2002 Denali Fault Earthquake. Bull. Seismol. Soc. Am. 2004, 94, S256–S268. [Google Scholar] [CrossRef]
- Yue, H.; Lay, T.; Freymueller, J.T.; Ding, K.; Rivera, L.; Rupppert, N.A.; Keper, K.D. Supershear rupture of the 5 January 2013 Craig, Alaska (Mw 7.5) earthquake. J. Geophys. Res. 2013, 118, 5903–5919. [Google Scholar] [CrossRef]
- Burridge, R. Admissible Speeds for Plane-Strain Self-Similar Shear Cracks with Friction but Lacking Cohesion. Geophys. J. Int. 1973, 35, 439–455. [Google Scholar] [CrossRef]
- Burridge, R.; Conn, G.; Freund, L. The stability of a rapid mode II shear crack with finite cohesive traction. J. Geophys. Res. Atmos. 1979, 84, 2210–2222. [Google Scholar] [CrossRef]
- Fukuyama, E.; Madariaga, R. Dynamic Propagation and Interaction of a Rupture Front on a Planar Fault. Pure Appl. Geophys. 2000, 157, 1959–1979. [Google Scholar] [CrossRef]
- Fukuyama, E.; Olsen, K. A Condition for Super-shear Rupture Propagation in a Heterogeneous Stress Field. Pure Appl. Geophys. 2002, 159, 2047–2056. [Google Scholar] [CrossRef]
- Andrews, D. Rupture velocity of plane strain shear cracks. J. Geophys. Res. 1976, 81, 5679–5687. [Google Scholar] [CrossRef]
- Andrews, D. Dynamic plane-strain shear rupture with a slip-weakening friction law calculated by a boundary integral method. Bull. Seismol. Soc. Am. 1985, 75, 1–21. [Google Scholar]
- Das, S.; Aki, K. A numerical study of two-dimensional spontaneous rupture propagation. Geophys. J. R. Astron. Soc. 1977, 50, 643–668. [Google Scholar] [CrossRef]
- Dunham, E.; Favreau, P.; Carlson, J. A Supershear Transit. Mech. Cracks. Sci. 2003, 299, 1557–1559. [Google Scholar]
- Dunham, E. The Dynamics and Near-Source Ground Motion of Supershear Earthquakes; University of California: Santa Barbara, CA, USA, 2005. [Google Scholar]
- Dunham, E.; Bhat, H. Attenuation of radiated ground motion and stresses from three-dimensional supershear ruptures. J. Geophys. Res. 2008, 113, B08319. [Google Scholar] [CrossRef]
- Madariaga, R.; Olsen, K.; Archuleta, R. Modeling dynamic rupture in a 3D earthquake fault model. Bull. Seismol. Soc. Am. 1998, 88, 1182–1197. [Google Scholar]
- Okubo, P. Dynamic rupture modeling with laboratory-derived constitutive relations. J. Geophys. Res. 1989, 94, 12321–12335. [Google Scholar] [CrossRef]
- Passelègue, F.X.; Schubnel, A.; Nielsen, S.; Bhat, H.S.; Madariaga, R. From sub-Rayleigh to supershear ruptures during stick-slip experiments on crustal rocks. Science 2013, 340, 1208–1211. [Google Scholar] [CrossRef]
- Rosakis, A. Intersonic shear cracks and fault ruptures. Adv. Phys. 2002, 51, 1189–1257. [Google Scholar] [CrossRef]
- Rosakis, A.J.; Samudrala, O.; Singh, R.P.; Shukla, A. Intersonic crack propagation in bimaterial systems. J. Mech. Phys. Solids 1998, 46, 1789–1814. [Google Scholar] [CrossRef]
- Rosakis, A.; Samudrala, O.; Coker, D. Cracks faster than the shear wave speed. Science 1999, 284, 1337. [Google Scholar] [CrossRef]
- Rosakis, A.; Samudrala, O.; Coker, D. Intersonic shear crack growth along weak planes. Mater. Res. Innov. 2000, 3, 236–243. [Google Scholar] [CrossRef]
- Samudrala, O. Subsonic and intersonic crack growth along weak planes and bimaterial interfaces. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2001. [Google Scholar]
- Samudrala, O.; Huang, Y.; Rosakis, A. Subsonic and intersonic shear rupture of weak planes with a velocity weakening cohesive zone. J. Geophys. Res. 2002, 107, ESE 7-1–ESE 7-32. [Google Scholar] [CrossRef]
- Xia, K.; Rosakis, A.; Kanamori, H. Laboratory Earthquakes: The Sub-Rayleigh-to-Supershear Rupture Transition. Science 2004, 303, 1859. [Google Scholar] [CrossRef] [PubMed]
- Xia, K.; Rosakis, A.; Kanamori, H. Supershear and subrayleigh-intersonic transition observed in laboratory earthquake experiments. Exp. Tech. 2005, 29, 63–66. [Google Scholar] [CrossRef]
- Xia, K.; Rosakis, A.J.; Kanamori, H.; Rice, J.R. Laboratory earthquakes along inhomogeneous faults: Directionality and supershear. Science 2005, 308, 681–684. [Google Scholar] [PubMed]
- Aki, K. Characterization of barriers on an earthquake fault. J. Geophys. Res. 1979, 84, 6140–6148. [Google Scholar] [CrossRef]
- Das, S.; Aki, K. Fault plane with barriers: A versatile earthquake model. J. Geophys. Res. 1977, 82, 5658–5670. [Google Scholar] [CrossRef]
- Weng, H.; Huang, J.; Yang, H. Barrier-induced supershear ruptures on a slip-weakening fault. Geophys. Res. Lett. 2015, 42, 4824–4832. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, Z.; Chen, X. The effects of barriers on supershear rupture. Geophys. Res. Lett. 2018, 43, 7478–7485. [Google Scholar] [CrossRef]
- Olsen, K.B.; Madariaga, R.; Archuleta, R.J. Three-Dimensional Dynamic Simulation of the 1992 Landers Earthquake. Science 1997, 278, 834–838. [Google Scholar] [CrossRef]
- Liu, Y.; Lapusta, N. Transition of mode II cracks from sub-Rayleigh to intersonic speeds in the presence of favorable heterogeneity. J. Mech. Phys. Solids 2008, 56, 25–50. [Google Scholar] [CrossRef]
- Bizzarri, A. On the deterministic description of earthquakes. Rev. Geophys. 2011, 49, RG3002. [Google Scholar] [CrossRef]
- Lu, X.; Lapusta, N.; Rosakis, A. Pulse-like and crack-like dynamic shear ruptures on frictional interfaces: Experimental evidence, numerical modeling, and implications. Int. J. Fract. 2010, 163, 27–39. [Google Scholar] [CrossRef]
- Wang, X. Finite Method; Tsinghua University Press: Beijing, China, 2003. (In Chinese) [Google Scholar]
- Templeton, E.; Rice, J. Off-fault plasticity and earthquake rupture dynamics: 1. Dry materials or neglect of fluid pressure changes. J. Geophys. Res. 2008, 113, B09306. [Google Scholar] [CrossRef]
- Viesca, R.; Templeton, E.; Rice, J. Off-fault plasticity and earthquake rupture dynamics: 2. Effects of fluid saturation. J. Geophys. Res. 2008, 113, B09307. [Google Scholar] [CrossRef]
- Hibbitt, H.; Karlsson, B.; Sorensen, P. ABAQUS Theory Manual, Version 6.3; Hibbitt Karlsson & Sorensen Inc.: Pawtucket, RI, USA, 2006. [Google Scholar]
- Harris, R.A.; Barall, M.; Archuleta, R.; Dunham, E.; Aagaard, B.; Ampuero, J.P.; Bhat, H.; Cruz-Atienza, V.; Dalguer, L.; Dawson, P.; et al. The SCEC/USGS dynamic earthquake rupture code verification exercise. Seismol. Res. Lett. 2009, 80, 119–126. [Google Scholar] [CrossRef]
- Ida, Y. Cohesive force across the tip of a longitudinal-shear crack and Griffith’s specific surface energy. J. Geophys. Res. 1972, 77, 3796–3805. [Google Scholar] [CrossRef]
- Palmer, A.; Rice, J. The growth of slip surfaces in the progressive failure of over-consolidated clay. Proc. R. Soc. Lond. A 1973, 332, 527–548. [Google Scholar]
- Olsen-Kettle, L.M.; Weatherley, D.; Saez, E.; Gross, L.; Mühlhaus, H.B.; Xing, H.L. Analysis of slip-weakening frictional laws with static restrengthening and their implications on the scaling, asymmetry, and mode of dynamic rupture on homogeneous and bimaterial interfaces. J. Geophys. Res. 2008, 113, B08307. [Google Scholar]
- Yuan, J.; Zhu, S. FEM simulation of the dynamic processes of fault spontaneous rupture. Chin. J. Geophys. 2014, 57, 138–156. (In Chinese) [Google Scholar]
- Ampuero, J.; Ben-Zion, Y. Cracks, pulses and macroscopic asymmetry of dynamic rupture on a bimaterial interface with velocity-weakening friction. Geophys. J. Int. 2008, 173, 674–692. [Google Scholar] [CrossRef]
- Finzi, Y.; Langer, S. Predicting rupture arrests, rupture jumps and cascading earthquakes. J. Geophys. Res. 2012, 117, B12303. [Google Scholar] [CrossRef]
- Langer, S.; Olsen-Kettle, L.; Weatherley, D. Identification of supershear transition mechanisms due to material contrast at bimaterial faults. Geophys. J. Int. 2012, 190, 1169–1180. [Google Scholar] [CrossRef]
- Ma, S.; Beroza, G. Rupture dynamics on a bimaterial interface for dipping faults. Bull. Seismol. Soc. Am. 2008, 98, 1642–1658. [Google Scholar] [CrossRef]
- Rubin, A.; Ampuero, J. Aftershock asymmetry on a bimaterial interface. J. Geophys. Res. 2007, 112, B05307. [Google Scholar] [CrossRef]
- Yuan, J.; Zhu, S. Distributions of strong ground motion due to dynamic ruptures across a bimaterial fault: Implications for seismic hazard analyses. J. Asian Earth Sci. 2016, 131, 81–94. [Google Scholar] [CrossRef]
- Yuan, Y. Impact of intensity and loss assessment following the great Wenchuan Earthquake. Earthq. Eng. Eng. Vib. 2008, 7, 247–254. [Google Scholar] [CrossRef]
| Description | Parameter | Value |
|---|---|---|
| Shear wave speed | Vs (m/s) | 3333 |
| Dilatational wave speed | Vp (m/s) | 5774 |
| Initial normal stress | σ0 (MPa) | 50 |
| Initial shear stress | τ0 (MPa) | 28 |
| Density | ρ (kg/m3) | 2700 |
| Poisson’s ratio | v | 0.25 |
| Shear stress within nucleation zone | τnucl (MPa) | 31.7 |
| Barrier strength | Δσn/σn | 1%~16% |
| Nucleation size | Lnz (km) | 3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, J.; Wang, J.; Zhu, S. Effects of Barriers on Fault Rupture Process and Strong Ground Motion Based on Various Friction Laws. Appl. Sci. 2020, 10, 1687. https://doi.org/10.3390/app10051687
Yuan J, Wang J, Zhu S. Effects of Barriers on Fault Rupture Process and Strong Ground Motion Based on Various Friction Laws. Applied Sciences. 2020; 10(5):1687. https://doi.org/10.3390/app10051687
Chicago/Turabian StyleYuan, Jie, Jinting Wang, and Shoubiao Zhu. 2020. "Effects of Barriers on Fault Rupture Process and Strong Ground Motion Based on Various Friction Laws" Applied Sciences 10, no. 5: 1687. https://doi.org/10.3390/app10051687
APA StyleYuan, J., Wang, J., & Zhu, S. (2020). Effects of Barriers on Fault Rupture Process and Strong Ground Motion Based on Various Friction Laws. Applied Sciences, 10(5), 1687. https://doi.org/10.3390/app10051687






