Influence of Vertical Fastener Stiffness on Rail Sound Power Characteristics: Numerical Study and Field Measurement
Abstract
1. Introduction
2. Model and Method
2.1. Model and Method for the Rail Mobility/Receptance
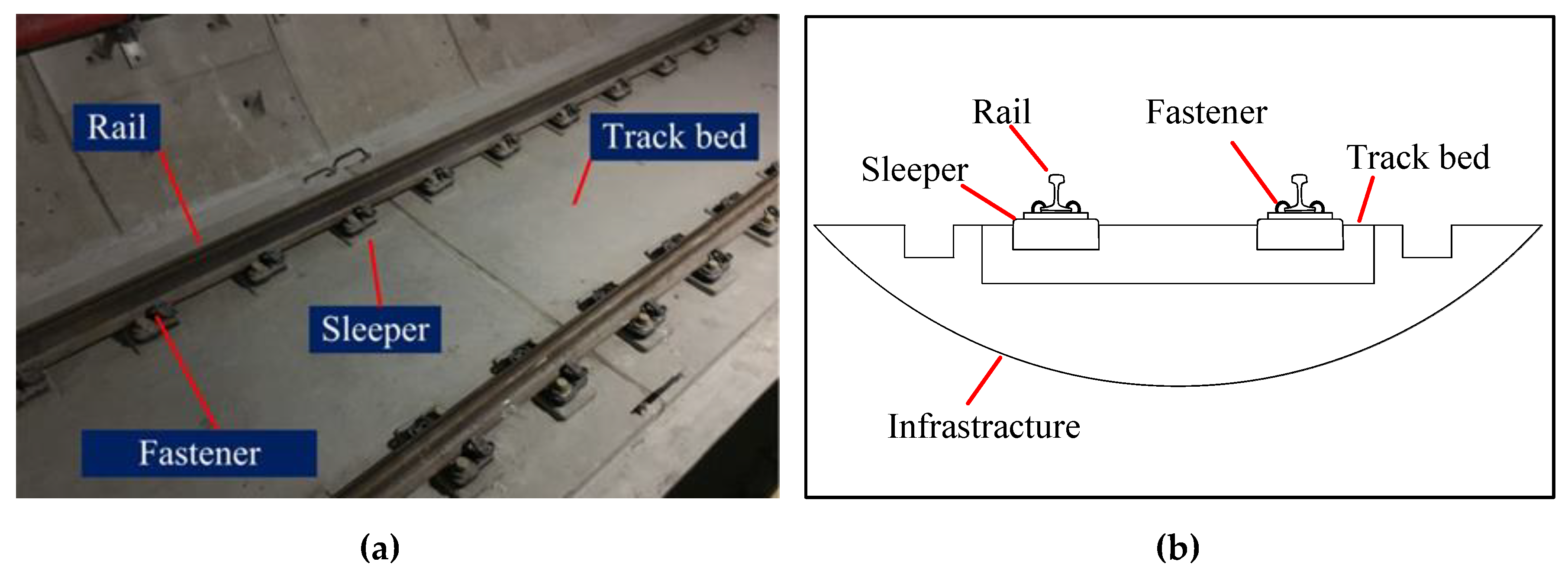
2.1.1. Monolithic Track Bed Structure
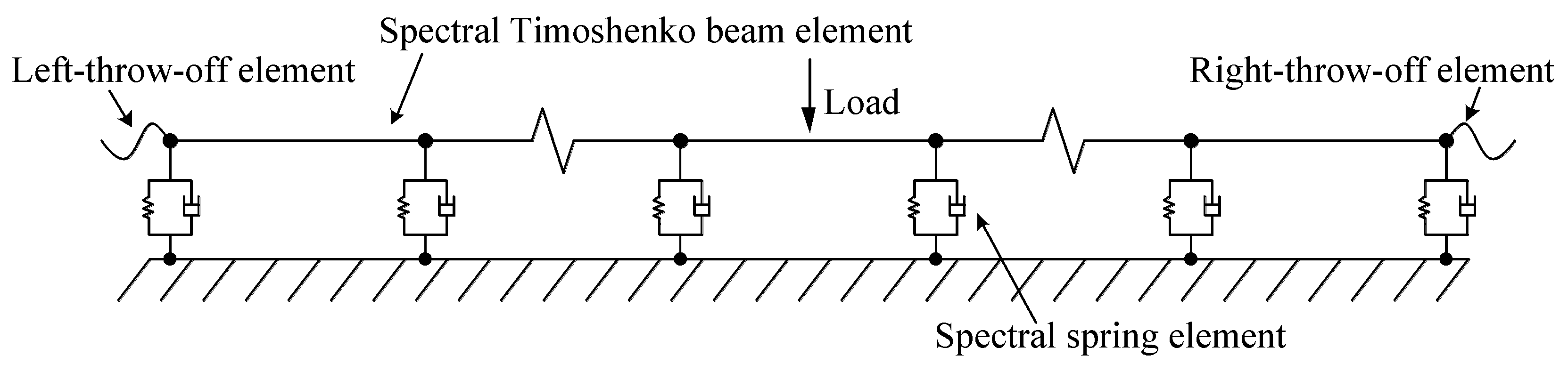
2.1.2. Timoshenko-Beam Track Model
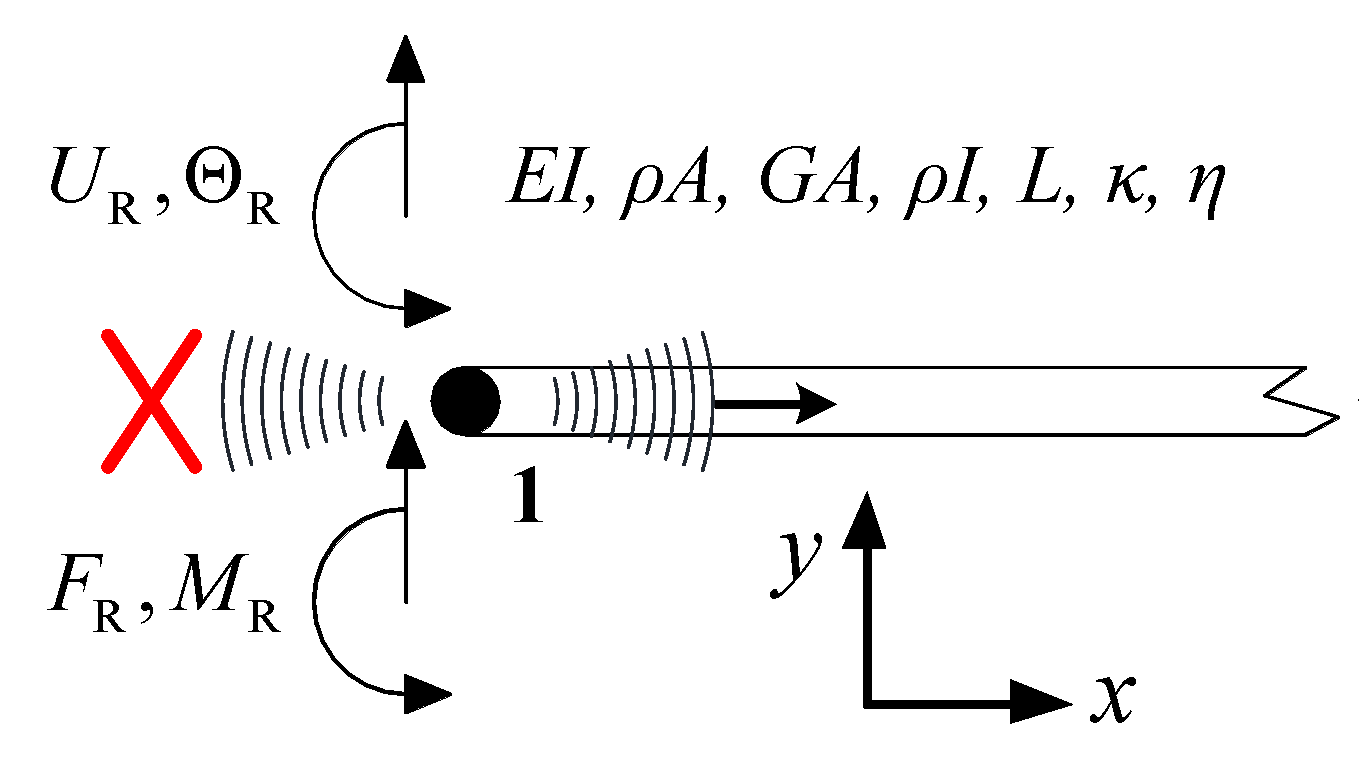
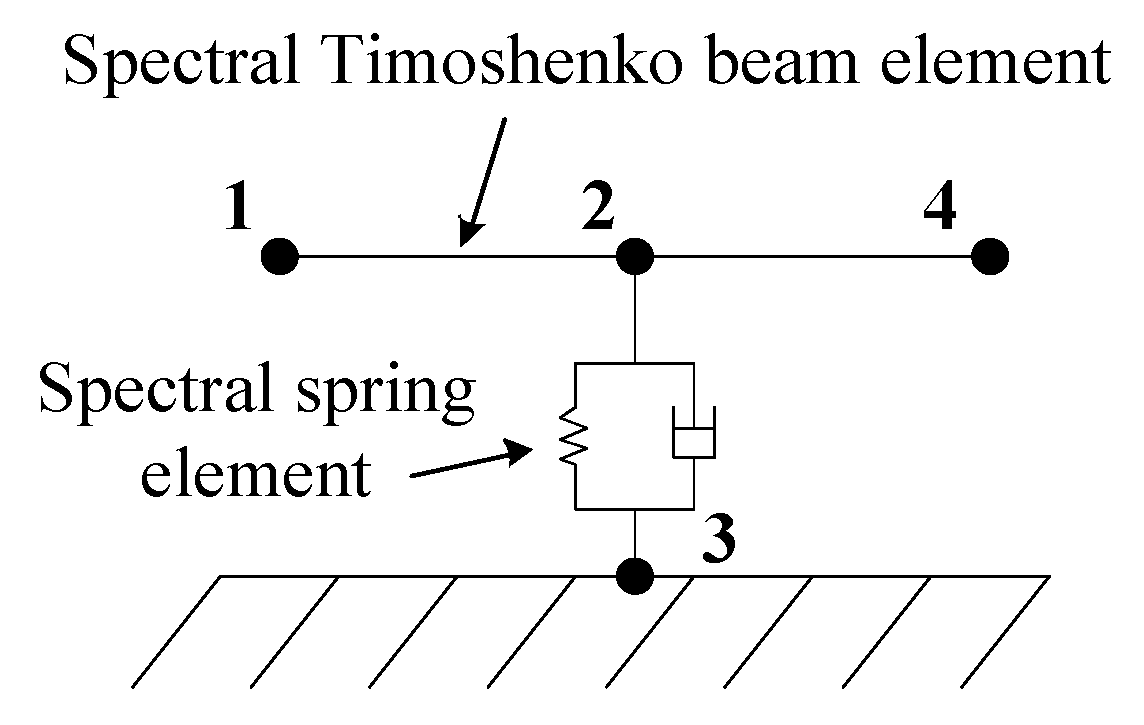
2.1.3. Spectral Element Method
2.2. Model and Method for the Decay Rate
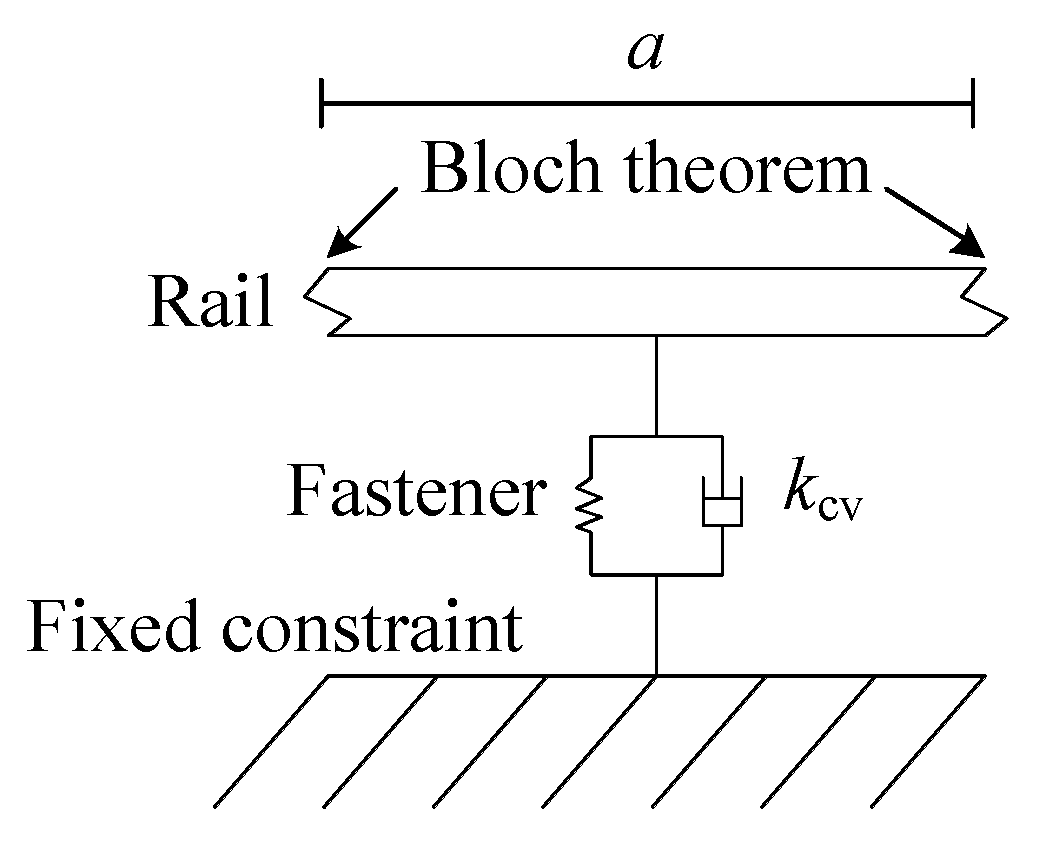
2.2.1. Periodic Track Model
2.2.2. Spectral Transfer Matrix Method
2.3. Calculation of Rail Sound Power Level
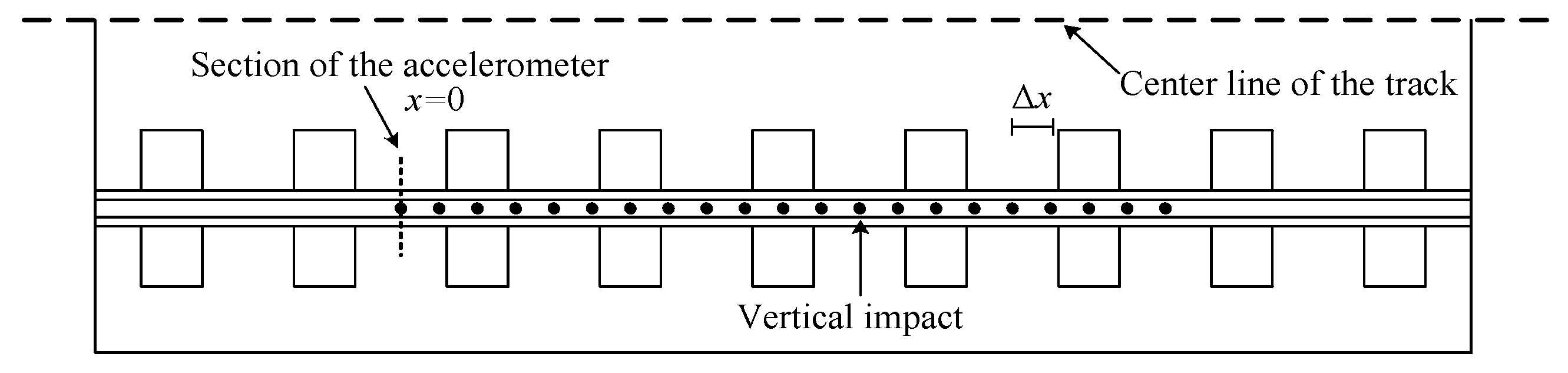
3. Field Measurement
3.1. Rail Accelerance
3.2. Decay Rate
4. Results
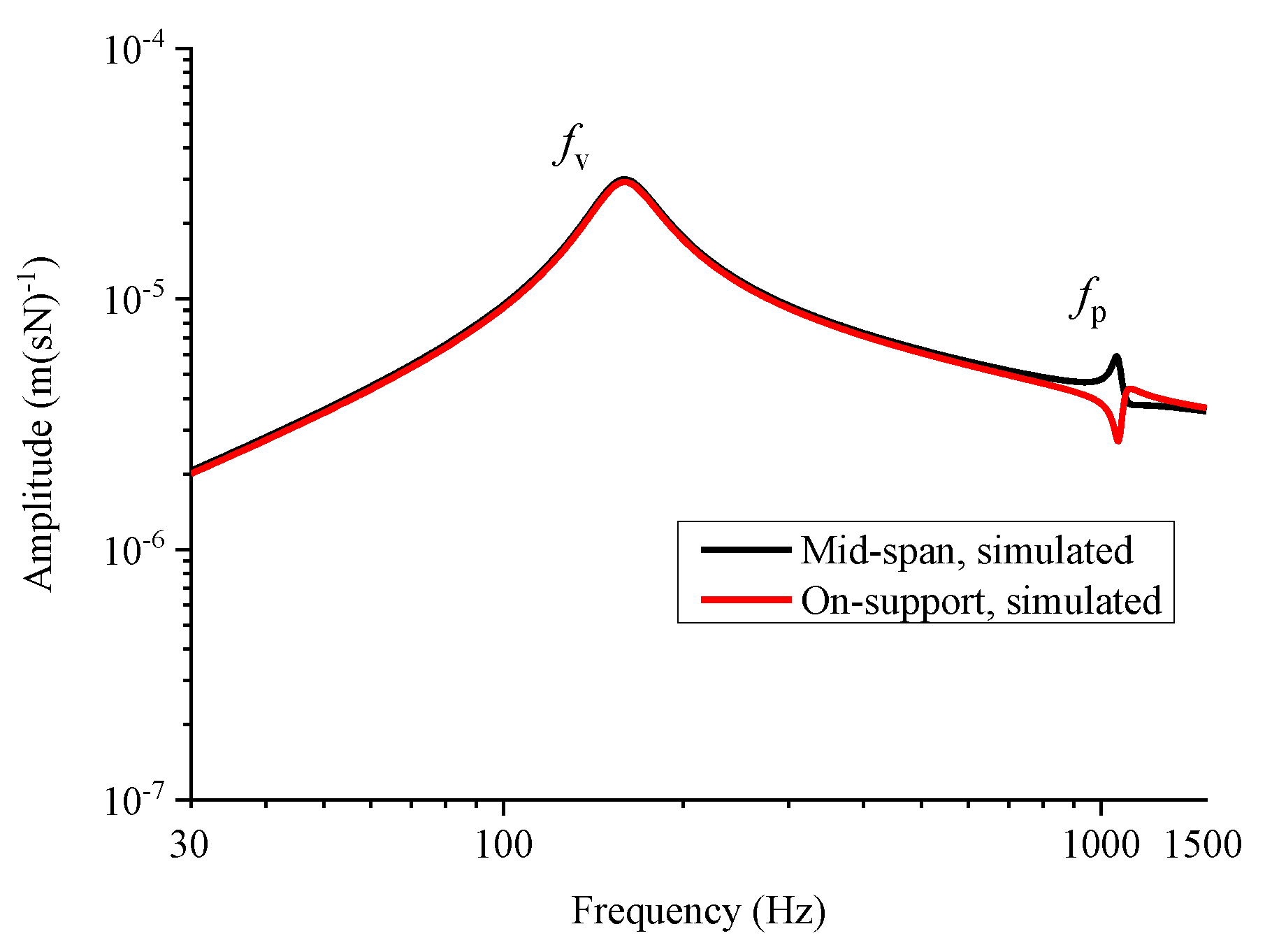
4.1. Rail Accelerance and Mobility
4.2. Decay Rate
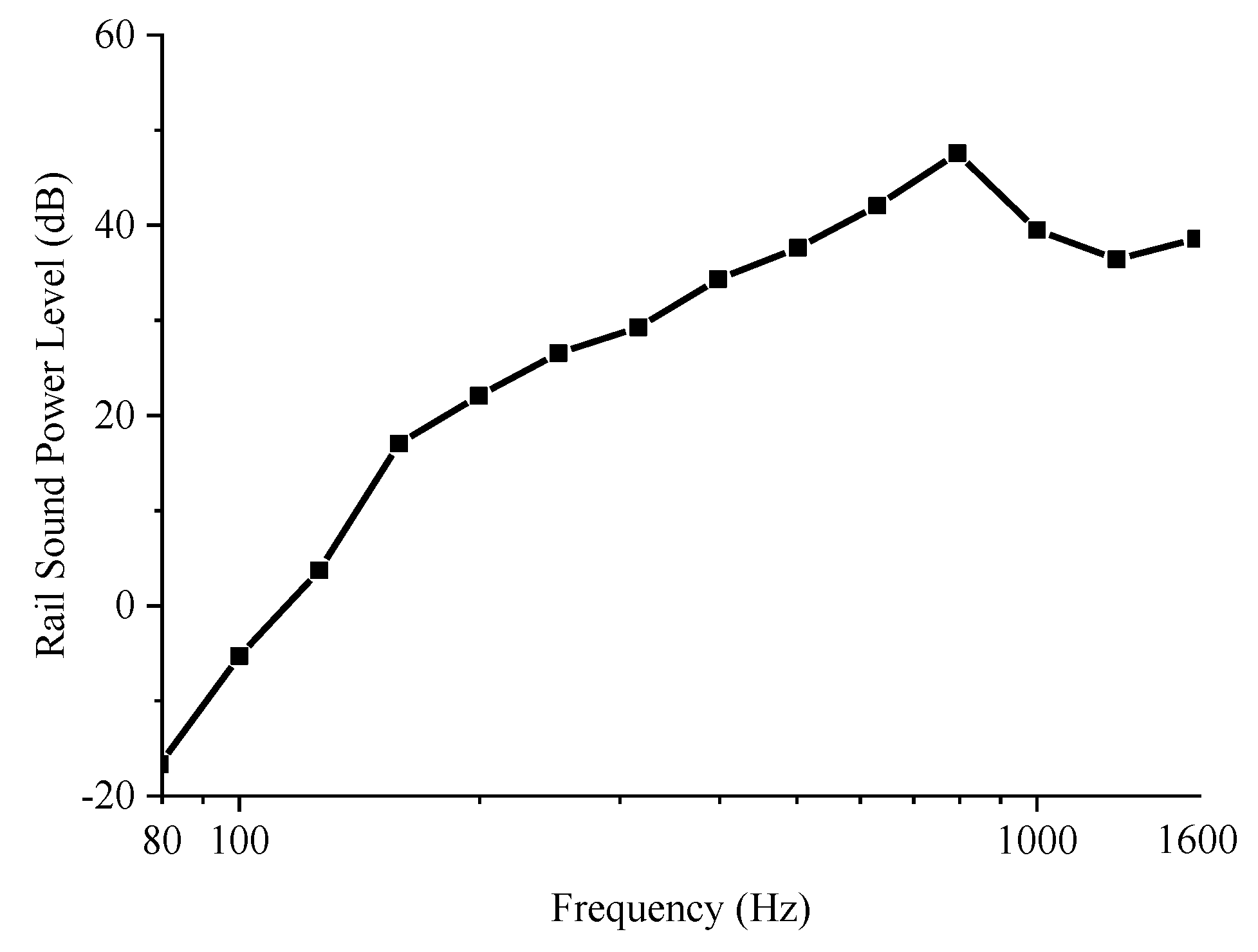
4.3. Rail Sound Power Level
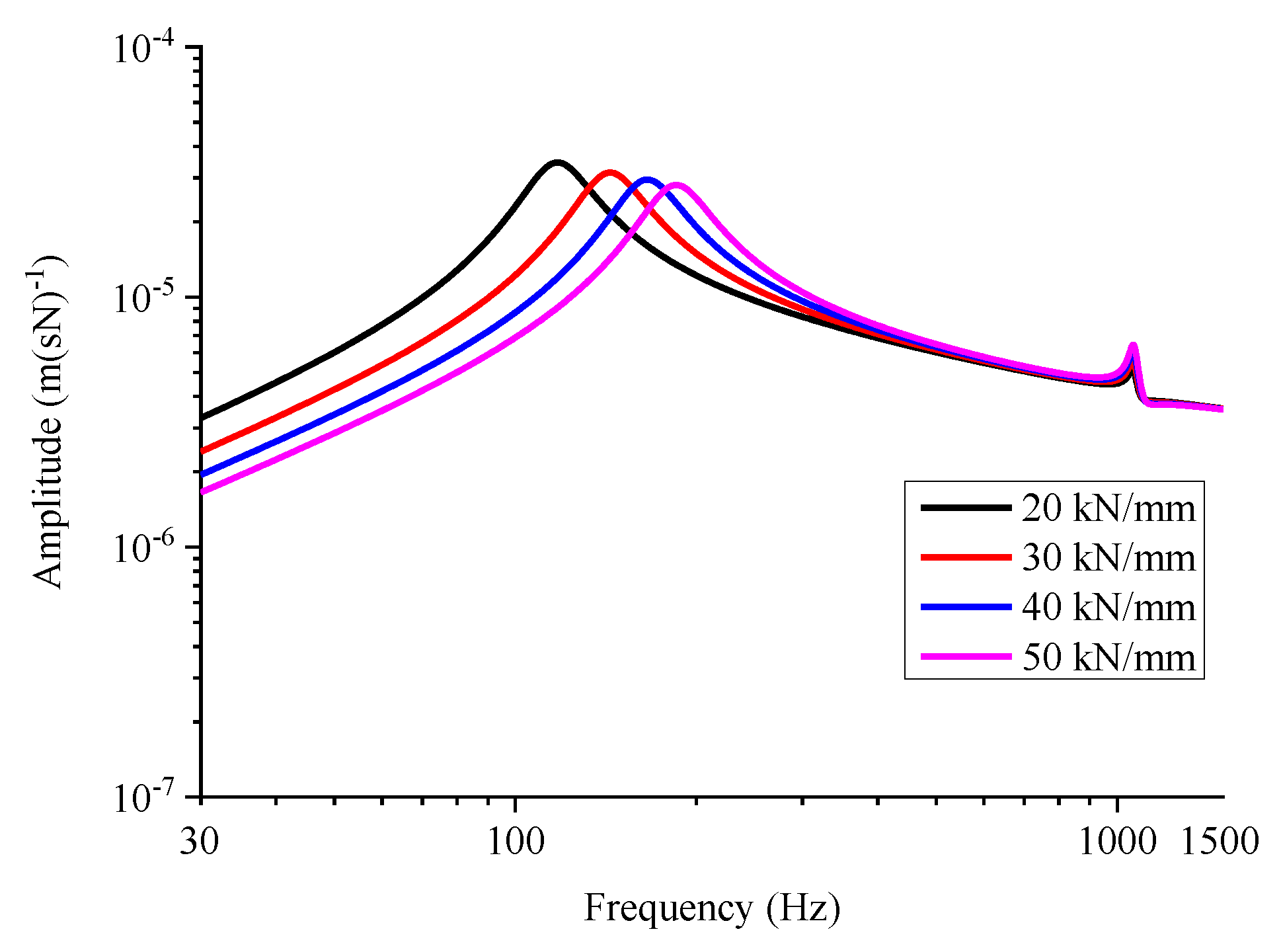
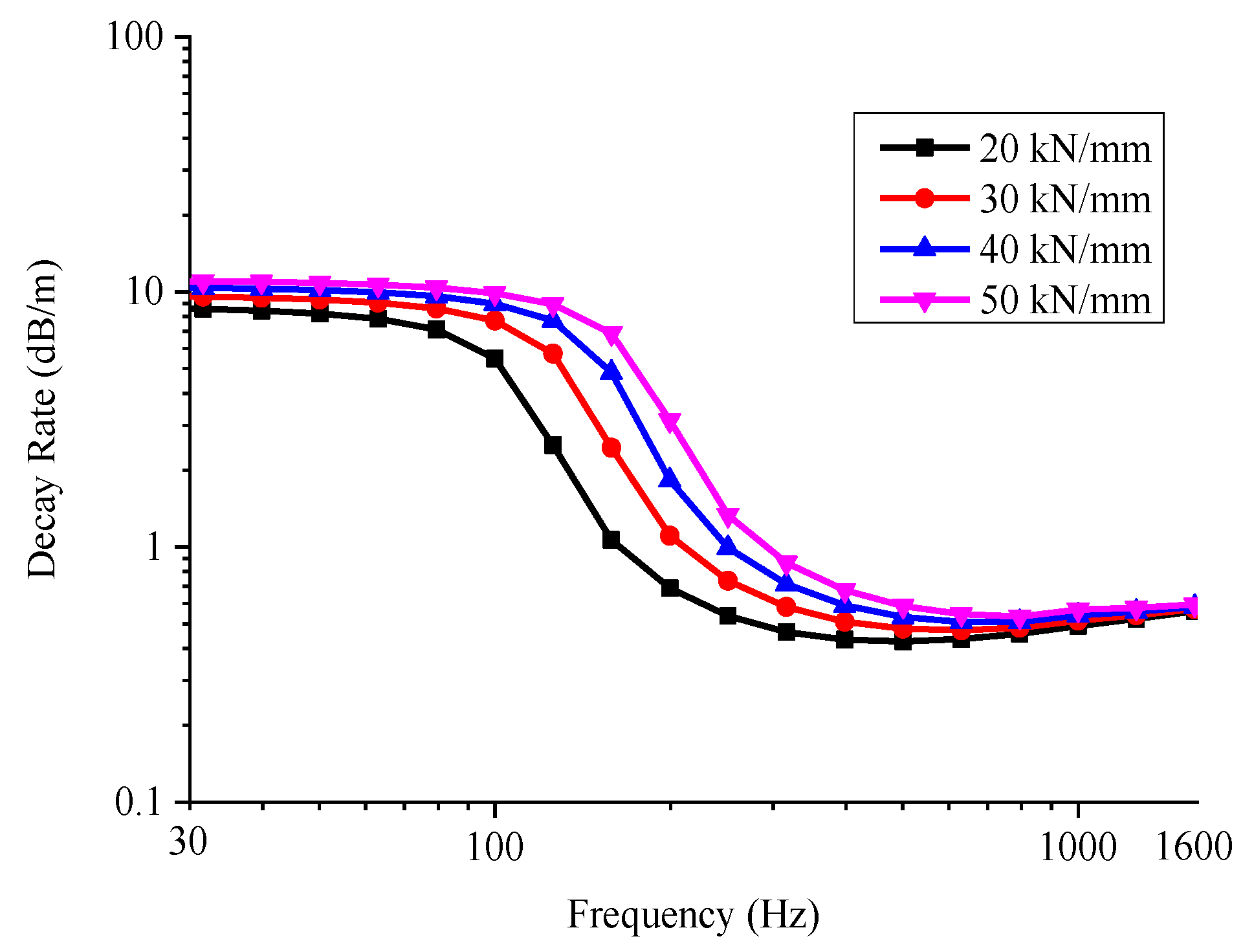
5. Influence of the Vertical Fastener Stiffness
5.1. Influence on the Rail Mobility Amplitude
5.2. Influence on the Decay Rate
5.3. Influence on the Rail Sound Power Level
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gupta, S.; Degrande, G.; Lombaert, G. Experimental validation of a numerical model for subway induced vibrations. J. Sound Vib. 2009, 321, 786–812. [Google Scholar] [CrossRef]
- Thompson, D.J. Railway Noise and Vibration: Mechanisms, Modelling and Means of Control; Elsevier Limited: Oxford, UK, 2008; pp. 195–196. [Google Scholar]
- Knothe, K.; Wu, Y. Receptance behaviour of railway track and subgrade. Arch. Appl. Mech. 1998, 68, 457–470. [Google Scholar] [CrossRef]
- Kaewunruen, S.; Remennikov, A.M. Field trials for dynamic characteristics of railway track and its components using impact excitation technique. NDT E Int. 2007, 40, 510–519. [Google Scholar] [CrossRef]
- Oregui, M.; Li, Z.; Dollevoet, R. An investigation into the vertical dynamics of tracks with monoblock sleepers with a 3D finite-element model. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2016, 230, 891–908. [Google Scholar] [CrossRef]
- Arlaud, E.; D’Aguiar, S.C.; Balmes, E. Receptance of railway tracks at low frequency: Numerical and experimental approaches. Transp. Geotech. 2016, 9, 1–16. [Google Scholar] [CrossRef]
- Jones, C.J.C.; Thompson, D.J.; Diehl, R.J. The use of decay rates to analyse the performance of railway track in rolling noise generation. J. Sound Vib. 2006, 293, 485–495. [Google Scholar] [CrossRef]
- Squicciarini, G.; Toward, M.G.R.; Thompson, D.J. Experimental procedures for testing the performance of rail dampers. J. Sound Vib. 2015, 359, 21–39. [Google Scholar] [CrossRef]
- Betgen, B.; Squicciarini, G.; Thompson, D.J. On the prediction of rail cross mobility and track decay rates using Finite Element Models. In Proceedings of the 10th European Congress and Exposition on Noise Control Engineering, Maastricht, The Netherlands, 31 May–3 June 2015. [Google Scholar]
- Li, W.; Dwight, R.A.; Zhang, T. On the study of vibration of a supported railway rail using the semi-analytical finite element method. J. Sound Vib. 2015, 345, 121–145. [Google Scholar] [CrossRef]
- Vincent, N.; Bouvet, P.; Thompson, D.J.; Gautier, P.E. Theoretical optimization of track components to reduce rolling noise. J. Sound Vib. 1996, 193, 161–171. [Google Scholar] [CrossRef]
- Zhang, X.; Squicciarini, G.; Thompson, D.J. Sound radiation of a railway rail in close proximity to the ground. J. Sound Vib. 2016, 362, 111–124. [Google Scholar] [CrossRef]
- Lee, U.; Kim, D.; Park, I. Dynamic modeling and analysis of the PZT-bonded composite Timoshenko beams: Spectral element method. J. Sound Vib. 2013, 332, 1585–1609. [Google Scholar] [CrossRef]
- Igawa, H.; Komatsu, K.; Yamaguchi, I.; Kasai, T. Wave Propagation Analysis of Frame Structures Using the Spectral Element Method. J. Sound Vib. 2004, 277, 1071–1081. [Google Scholar] [CrossRef]
- Lee, U. Spectral Element Method in Structural Dynamics; John Wiley and Sons: New York, NY, USA, 2009; pp. 365–369. [Google Scholar]
- Sheng, X.; Zhao, C.; Wang, P.; Liu, D. Study on Transmission Characteristics of Vertical Rail Vibrations in Ballast Track. Math. Probl. Eng. 2017, 2017, 5872419. [Google Scholar] [CrossRef]
- Wei, K.; Wang, P.; Yang, F.; Xiao, J. The effect of the frequency-dependent stiffness of rail pad on the environment vibrations induced by subway train running in tunnel. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2016, 230, 697–708. [Google Scholar] [CrossRef]
- Thompson, D.J. Wheel-rail Noise Generation, Part III: Rail Vibration. J. Sound Vib. 1993, 161, 421–446. [Google Scholar] [CrossRef]
- Bulgakov, E.N.; Sadreev, A.F.; Maksimov, D.N. Light trapping above the light cone in one-dimensional arrays of dielectric spheres. Appl. Sci. 2017, 7, 147. [Google Scholar] [CrossRef]
- Ryue, J.; Thompson, D.J.; White, P.R.; Thompson, D.R. Decay rates of propagating waves in railway tracks at high frequencies. J. Sound Vib. 2009, 320, 955–976. [Google Scholar] [CrossRef]
- Thompson, D.J.; Vincent, N. Track Dynamic Behaviour at High Frequencies. Part 1: Theoretical Models and Laboratory Measurements. Veh. Syst. Dyn. 1995, 24, 86–99. [Google Scholar] [CrossRef]
- Man, A.P.D. A Survey of Dynamic Railway Track Properties and Their Quality. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2002. [Google Scholar]
- CEN. EN 15461:2008+A1:2010, Railway Applications—Noise Emission—Characterization of the Dynamic Properties of Track Selections for Pass by Noise Measurements; Management Center: Brussels, Belgium, 2010. [Google Scholar]
- Thompson, D.J. Experimental analysis of wave propagation in railway tracks. J. Sound Vib. 1997, 203, 867–888. [Google Scholar] [CrossRef]
- Ewins, D.J. Modal Testing: Theory and Practice; Research studies Press: Letchworth, UK, 1984. [Google Scholar]






| Track component | Parameter | Symbol | Value |
|---|---|---|---|
| CHN60 rail | Elastic modulus (GPa) | E | 210 |
| Cross-section area (m2) | A | 7.745 × 10−3 | |
| Mass density (kg/m3) | ρ | 7850 | |
| Shear correction factor | κ | 0.5329 | |
| Area moment of inertia (m4) | I | 3.217 × 10−5 | |
| Damping loss factor | ηr | 0.05 | |
| Shear elastic modulus (GPa) | G | 80.77 | |
| Fastener | Vertical stiffness (kN/mm) | kv | 37 |
| Damping loss factor | ηf | 0.25 | |
| Spacing (m) | a | 0.625 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheng, X.; Zhang, Y.; Liu, X. Influence of Vertical Fastener Stiffness on Rail Sound Power Characteristics: Numerical Study and Field Measurement. Appl. Sci. 2020, 10, 1682. https://doi.org/10.3390/app10051682
Sheng X, Zhang Y, Liu X. Influence of Vertical Fastener Stiffness on Rail Sound Power Characteristics: Numerical Study and Field Measurement. Applied Sciences. 2020; 10(5):1682. https://doi.org/10.3390/app10051682
Chicago/Turabian StyleSheng, Xi, Ying Zhang, and Xiaozhou Liu. 2020. "Influence of Vertical Fastener Stiffness on Rail Sound Power Characteristics: Numerical Study and Field Measurement" Applied Sciences 10, no. 5: 1682. https://doi.org/10.3390/app10051682
APA StyleSheng, X., Zhang, Y., & Liu, X. (2020). Influence of Vertical Fastener Stiffness on Rail Sound Power Characteristics: Numerical Study and Field Measurement. Applied Sciences, 10(5), 1682. https://doi.org/10.3390/app10051682





