Comparison of Selected Parameters of a Planetary Gearbox with Involute and Convex–Concave Teeth Flank Profiles
Abstract
1. Introduction
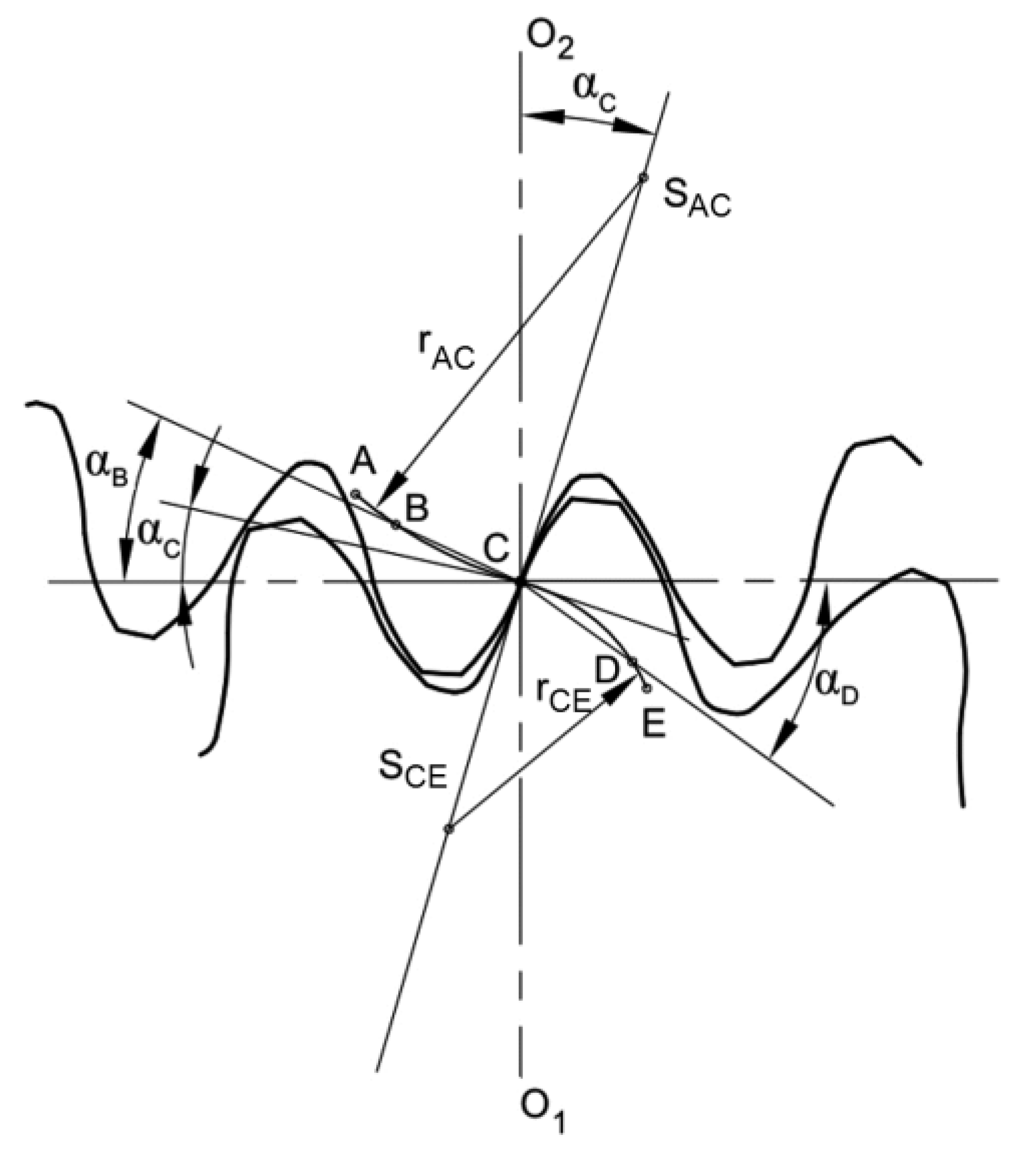
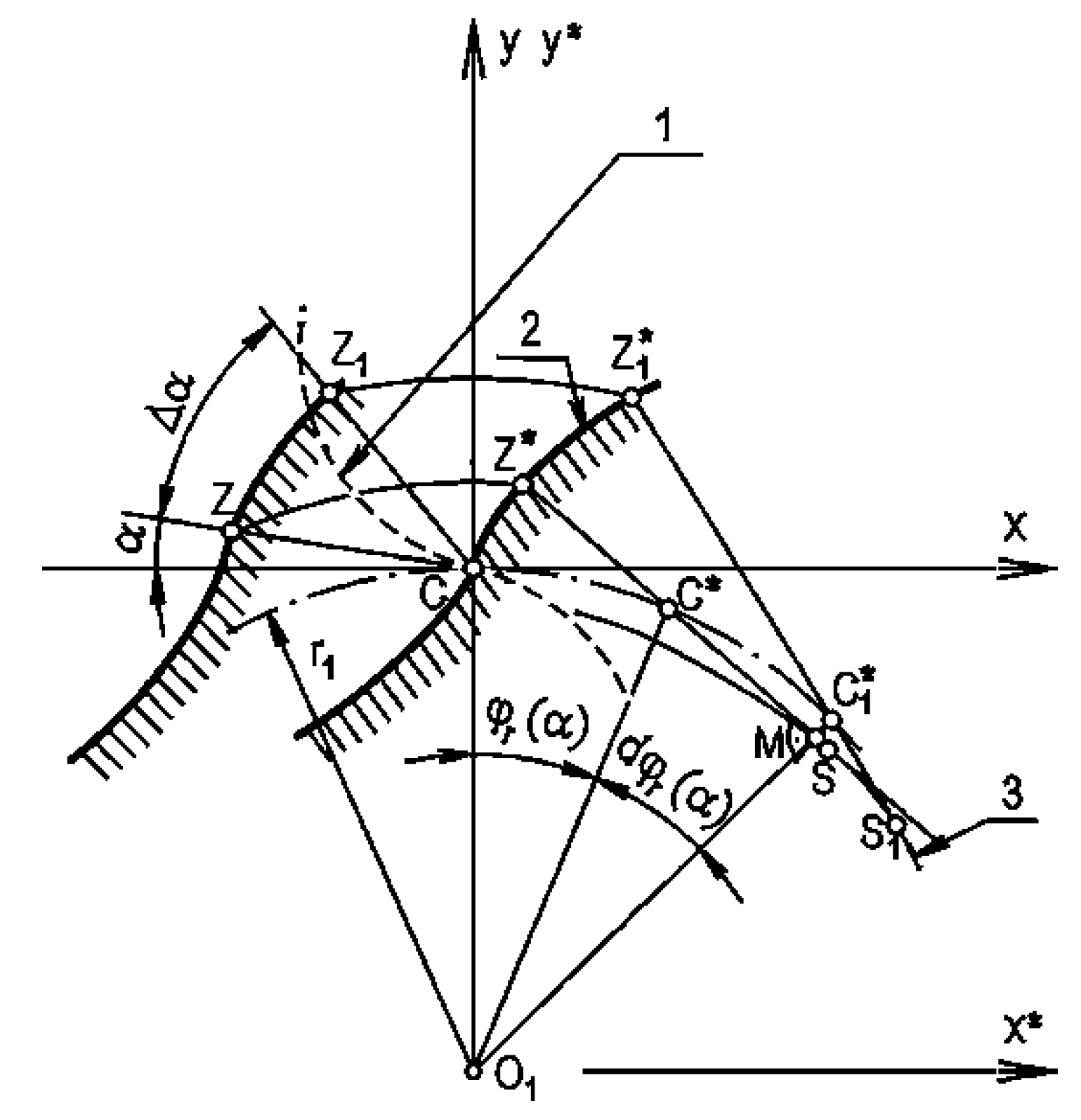
2. Geometry of the Teeth Flanks
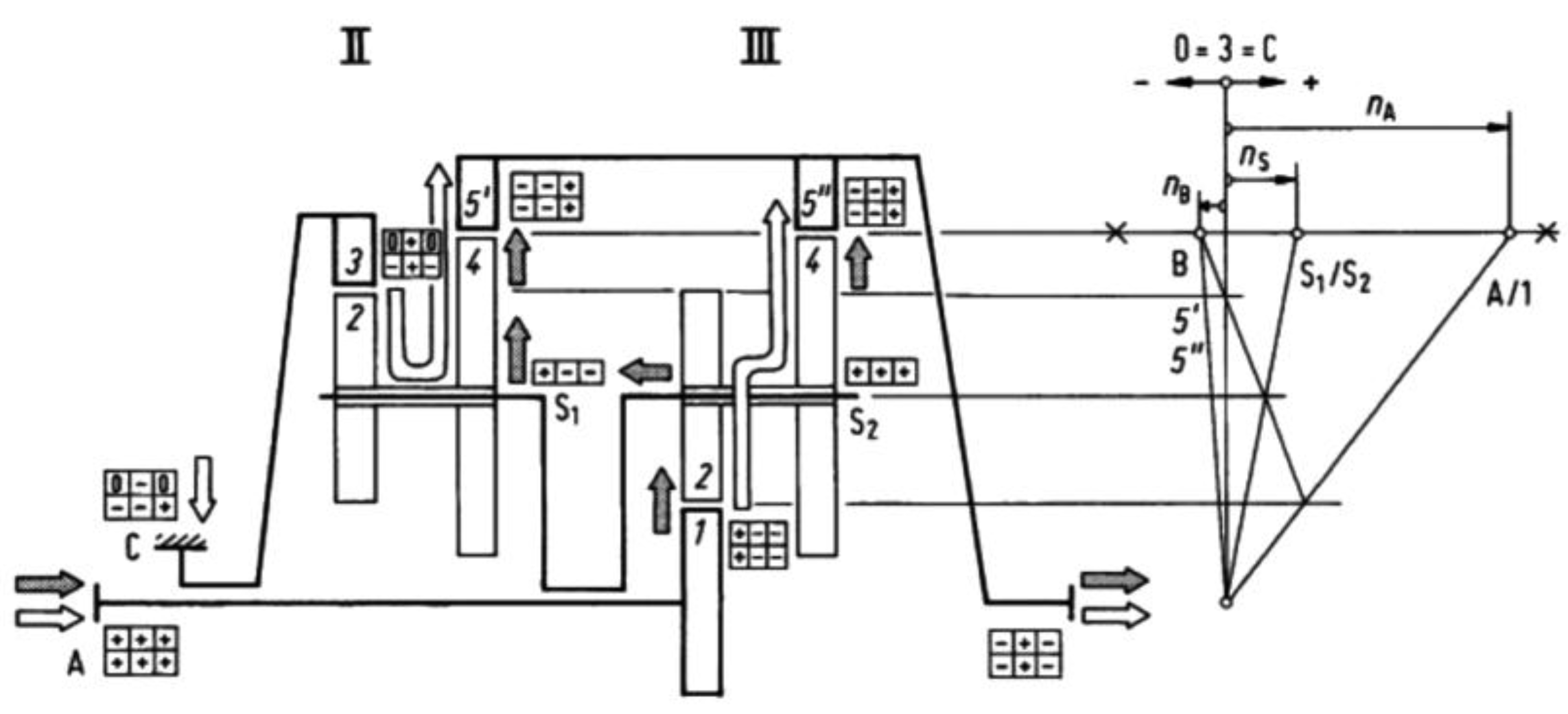
3. Reduced Planetary Gearbox Parameters
4. Calculation of Planetary Gearbox Gear Pairs Parameters
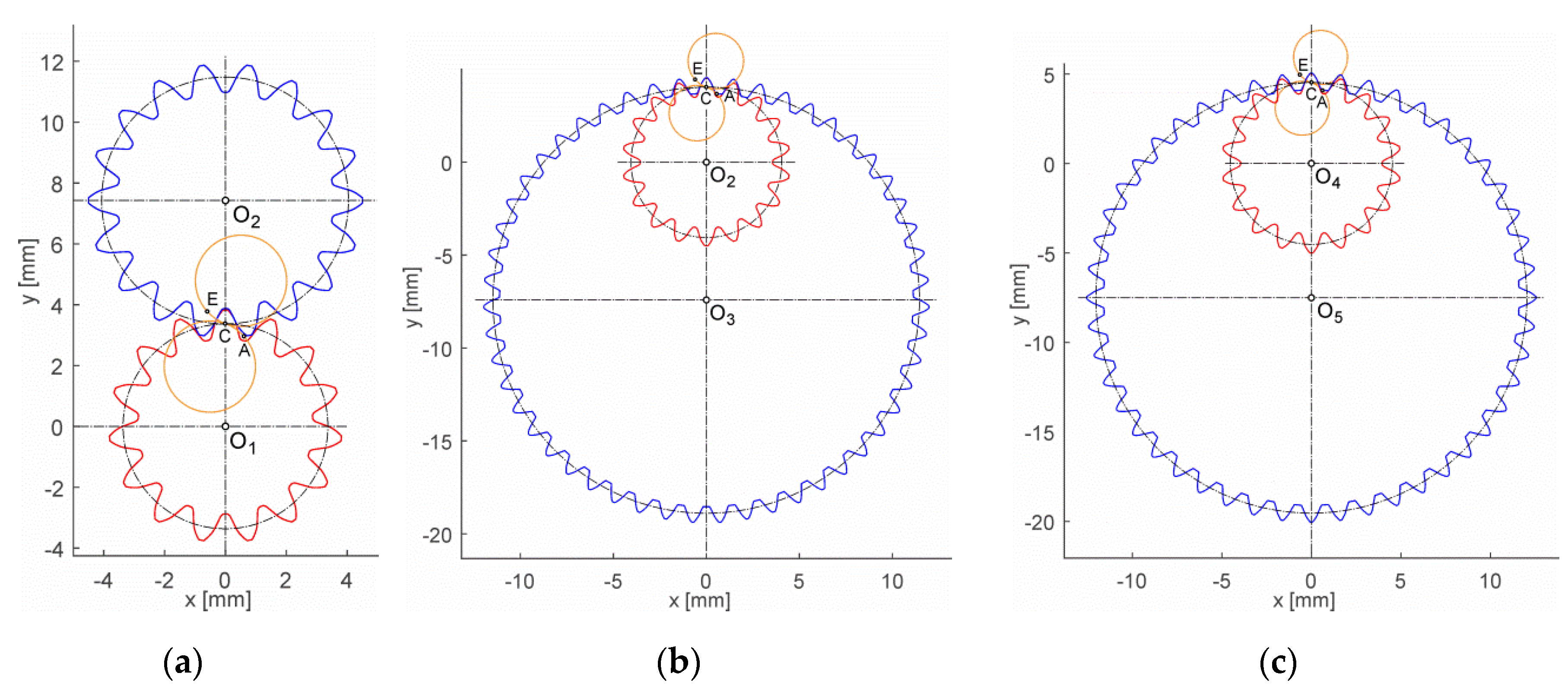
4.1. Geometry
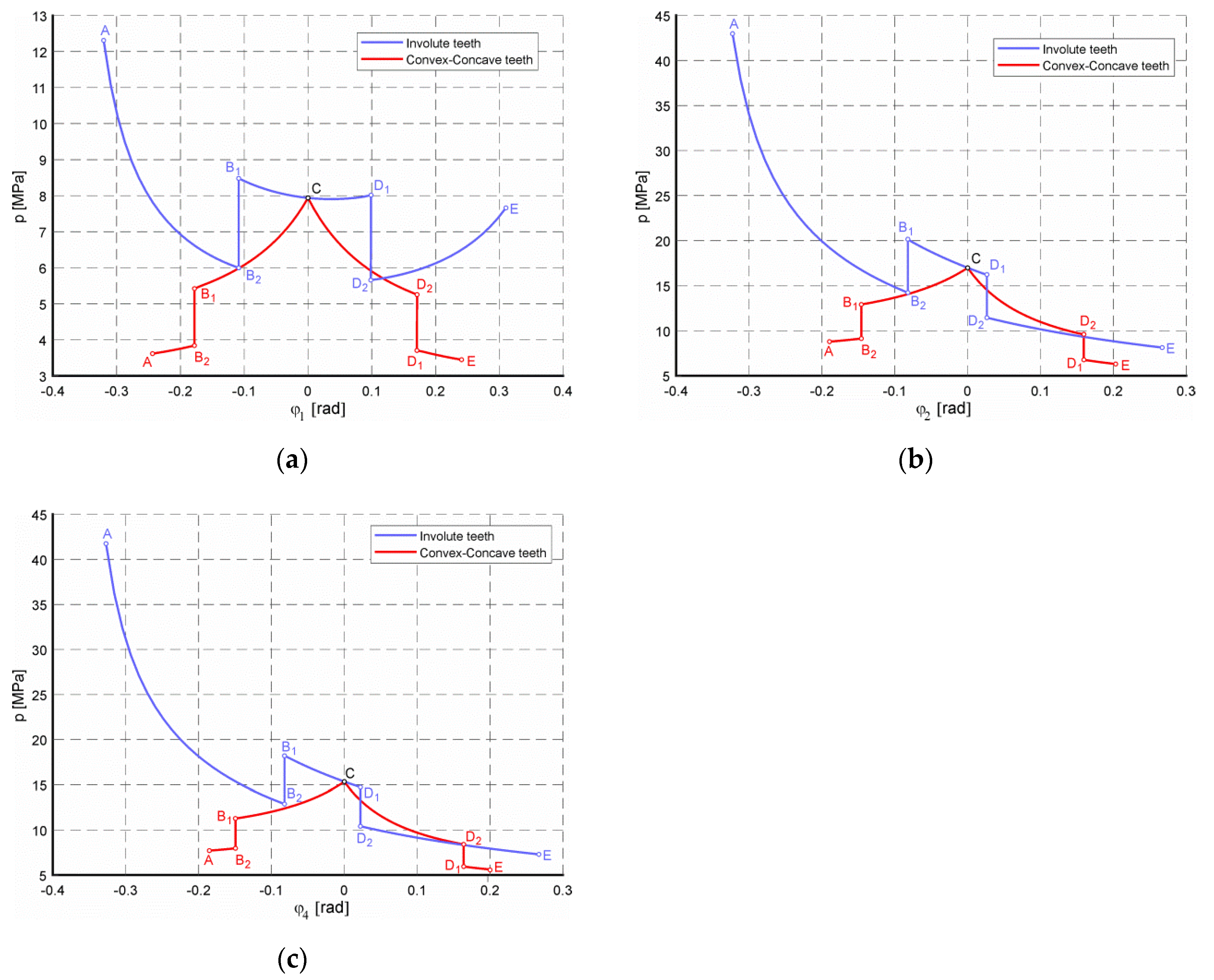
4.2. Contact Pressures
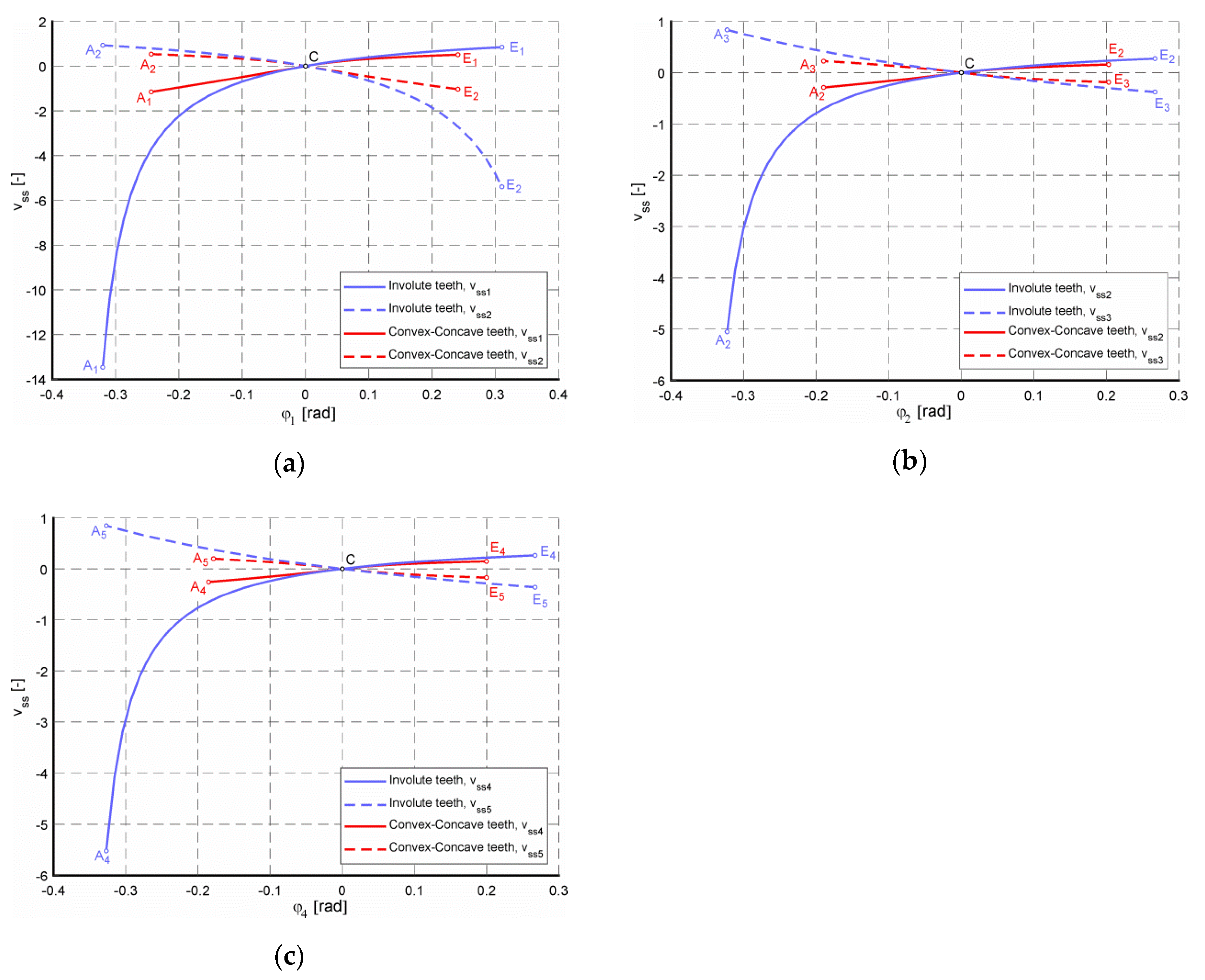
4.3. Specific Sliding Ratios
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kim, G.H.; Lee, J.W.; Seo, T.I. Durability Characteristics Analysis of Plastic Worm Wheel with Glass Fiber Reinforced Polyamide. Materials 2013, 6, 1873–1890. [Google Scholar] [CrossRef]
- Hlebanja, G.; Kulovec, S.; Hlebanja, J.; Duhovnik, J. On endurance of the S-shaped plastic gears. Int. Conf. Power Transm. 2016, 79–86. [Google Scholar]
- Gola, A. Reliability analysis of reconfigurable manufacturing system structures using computer simulation methods. Eksploat. I Niezawodn. Maint. Reliab. 2019, 21, 90–102. [Google Scholar] [CrossRef]
- Chen, Z.; Shao, Y. Dynamic simulation of planetary gear with tooth root crack in ring gear. Eng. Fail. Anal. 2013, 31, 8–18. [Google Scholar] [CrossRef]
- Li, X.; Elasha, F.; Shanbr, S.; Mba, D. Remaining Useful Life Prediction of Rolling Element Bearings Using Supervised Machine Learning. Energies 2019, 12, 2705. [Google Scholar] [CrossRef]
- Kia, S.H.; Henao, H.; Capolino, G.A. Gear tooth surface damage fault detection using induction machine stator current space vector analysis. IEEE Trans. Ind. Electron. 2015, 62, 1866–1878. [Google Scholar] [CrossRef]
- Sun, W.; Yao, B.; Zeng, N.; Chen, B.; He, Y.; Cao, X.; He, W. An Intelligent Gear Fault Diagnosis Methodology Using a Complex Wavelet Enhanced Convolutional Neural Network. Materials 2017, 10, 790. [Google Scholar] [CrossRef]
- Ruqiang, Y.; Yuning, Q.; Zhoudi, H.; Gao, R.X. Rolling bearing defect severity evaluation using recurrence plot entropy. In Proceedings of the 2011 IEEE International Instrumentation and Measurement Technology Conference, Binjiang, China, 10–12 May 2011. [Google Scholar] [CrossRef]
- Jedliński, Ł.; Jonak, J. A disassembly-free method for evaluation of spiral bevel gear assembly. Mech. Syst. Signal Process. 2017, 88, 399–412. [Google Scholar] [CrossRef]
- Sawalhi, N.; Randall, R.B. Gear parameter identification in a wind turbine gearbox using vibration signals. Mech. Syst. Signal Process. 2014, 42, 368–376. [Google Scholar] [CrossRef]
- Karioja, K.; Lahdelma, S.; Litak, G.; Ambrożkiewicz, B. Extracting periodically repeating shocks in a gearbox from simultaneously occurring random vibration. In Proceedings of the 15th International Conference on Condition Monitoring and Machinery Failure Prevention Technologies, CM/MFPT 2018, Nottingham, UK, 10–12 September 2018; pp. 456–464. [Google Scholar]
- Soualhi, A.; Medjaher, K.; Zerhouni, N. Bearing health monitoring based on Hilbert-Huang transform, support vector machine and regression. IEEE Trans. Instrum. Meas. 2015, 64, 52–62. [Google Scholar] [CrossRef]
- Marichal, G.N.; Del Castillo, M.L.; López, J.; Padrón, I.; Artés, M. An Artificial Intelligence Approach for Gears Diagnostics in AUVs. Sensors 2016, 16, 529. [Google Scholar] [CrossRef]
- Ambrożkiewicz, B.; Meier, N.; Guo, Y.; Litak, G.; Georgiadis, A. Recurrence-based diagnostics of rotary systems. IOP Conf. Ser. 2019, 710, 012014. [Google Scholar] [CrossRef]
- Syta, A.; Jonak, J.; Jedliński, Ł.; Litak, G. Failure diagnosis of a gear box by recurrences. J. Vib. Acoust. 2012, 134, 41006. [Google Scholar] [CrossRef]
- Hadryś, D.; Bąkowski, H.; Stanik, Z.; Kubik, A. Analysis of shaft wear in turbocharges of automotive vehicles. Transp. Prob. 2019, 14, 85–95. [Google Scholar] [CrossRef]
- Bąkowski, H. Wear mechanism of spheroidal cast iron piston ring-aluminum matrix composite cylinder liner contact. Arch. Metall. Mater. 2018, 63, 481–490. [Google Scholar]
- Longwic, A.; Nieoczym, A.; Kordos, P. Evaluation of the combustion process in a spark-ignition engine based on the unrepeatability of the maximum pressure. IOP Conf. Ser. Mater. Sci. Eng. 2018, 421, 1–9. [Google Scholar] [CrossRef]
- Makareviciene, V.; Matijosius, J.; Pukalskas, S.; Vegneris, R.; Kazanceva, I.; Kazancev, K. The exploitation and environmental characteristics of diesel fuel containing rapeseed butyl esters. Transport 2013, 28, 158–165. [Google Scholar] [CrossRef]
- Balytskyi, A.; Abramek, K.F.; Stoeck, T.; Osipowicz, T. Diagnostic of degradation of the lock seal ring by the loss of combustion engine working gases. Mater. Sci. 2014, 50, 156–169. [Google Scholar] [CrossRef]
- Ignaciuk, P.; Gil, L. Damages to injectors in diesel engines. Adv. Sci. Technol. Res. J. 2014, 8, 58–61. [Google Scholar]
- Osipowicz, T.; Abramek, K.F.; Matuszak, Z.; Jaśkiewicz, M.; Ludwinek, K.; Poliak, M. The analysis of technical condition common rail fuel system components. In Proceedings of the 11th International Scientific and Technical Conference on Automotive Safety, Casta Papiernicka, Slovakia, 18–20 April 2018. [Google Scholar] [CrossRef]
- Szpica, D. Investigating fuel dosage non-repeatability of low-pressure gas-phase injectors. Flow Meas. Instrum. 2018, 59, 147–156. [Google Scholar] [CrossRef]
- Glos, J.; Sejkorova, M. Tribo-diagnostics as an indicator and input for the optimization of vehicles preventive maintenance. In Proceedings of the 11th International Conference on Intelligent Technologies in Logistics and Mechatronics Systems (ITELMS’2016), Panevezys, Lithuania, 28–29 April 2016; pp. 83–89. [Google Scholar]
- Sejkorova, M.; Hurtova, I. Engine oil analysis-effective instrument to evaluate reliability of tractor engines. In Proceedings of the 18th International Scientific Conference Engineering for Rural Development, Jelgava, Latvia, 22–24 May 2019; pp. 971–976. [Google Scholar]
- Stoeck, T.; Abramek, K.F. Application of the polynomial interpolation method for determining performance characteristics of a diesel engine. Metrol. Meas. Syst. 2014, 21, 157–168. [Google Scholar] [CrossRef]
- Tucki, K.; Mruk, R.; Orynycz, O.; Gola, A. The effects of pressure and temperature on the process of auto-ignition and combustion of rape oil and its mixtures. Sustainability 2019, 11, 3451. [Google Scholar] [CrossRef]
- Figlus, T. A method for diagnosing gearboxes of means of transport using multi-stage filtering and entropy. Entropy 2019, 21, 441. [Google Scholar] [CrossRef]
- Harman, B.N.; Opalic, M.; Veres, M. Deterministic and probabilistic methods in determination of correct mating cylindrical teeth profiles. Strojarstvo 2011, 53, 191–197. [Google Scholar]
- Veres, M.; Nemcekova, M.; Marinkovic, A. Tooth flanks scoring resistance of non-involute teeth profiles in plane toothed cylindrical gears. FME Trans. 2009, 37, 103–106. [Google Scholar]
- Hlebanja, G.; Hlebanja, J. S-gears: From Metal to Polymer Solution. In Advanced Gear Engineering; Goldfarb, V., Trubachev, E., Barmina, N., Eds.; Springer International Publishing Switzerland: Cham, Switzerland, 2018; pp. 255–269. [Google Scholar] [CrossRef]
- Zorko, D.; Kulovec, S.; Tavcar, J.; Duhovnik, J. Different teeth profile shapes of polymer gears and comparison of their performance. J. Adv. Mech. Des. Syst. Manuf. 2017, 11, 1–5. [Google Scholar] [CrossRef]
- Hlebanja, G.; Kulovec, S. Development of a Planocentric Gear Box Based on S-Gear Geometry. Kolloqu. Getr. Garch. 2015, 11, 205–216. [Google Scholar]
- Arnaudov, K.; Karaivanov, D.P. Planetary Gear Trains; CRC Press: Boca Raton, FL, USA; New York, NY, USA; Taylor & Francis Group: London, UK, 2019. [Google Scholar]
- Fiorio, R.; Diez, S.V.; Sánchez, R.; D’hooge, D.R.; Cardon, L. Influence of Different Stabilization Systems and Multiple Ultraviolet A (UVA) Aging/Recycling Steps on Physicochemical, Mechanical, Colorimetric, and Thermal-Oxidative Properties of ABS. Materials 2020, 13, 212. [Google Scholar] [CrossRef]
- García-Domínguez, D.; Claver, J.; Camacho, A.M.; Sebastián, M.A. Considerations on the Applicability of Test Methods for Mechanical Characterization of Materials Manufactured by FDM. Materials 2020, 13, 28. [Google Scholar] [CrossRef]
- Gardyński, L.; Lonkwic, P. Testing polymer rollers memory in the context of passenger lift car comfort. J. Vibroeng. 2014, 16, 225–230. [Google Scholar]
- Borazjani, S.; Belingardi, G. Development of an innovative design of a composite-sandwich based vehicle roof structure. Compos. Struct. 2017, 168, 522–534. [Google Scholar] [CrossRef]
- Krzyżak, A.; Kucharczyk, W.; Gaska, J.; Szczepaniak, R. Ablative test of composites with epoxy resin and expanded perlite. Compos. Struct. 2018, 202, 978–987. [Google Scholar] [CrossRef]
- Krzyżak, A.; Valis, D. Selected reliability measures of composites with natural fibres tested in climatic environment. In Proceedings of the International Conference on Military Technologies (ICMT 2015), Brno, Czech, 19–21 May 2015; pp. 81–87. [Google Scholar]
- Pieniak, D.; Wit-Rusieck, A.M.; Krzyżak, A.; Gil, L.; Krzysiak, Z. Adhesion tests of varnish coatings used on the surface of carbon fiber reinforced polimer compositions. Przemysł Chem. 2019, 98, 1619–1622. [Google Scholar]
- Jiang, R.; Liu, T.; Xu, Z.; Park, C.B.; Zhao, L. Improving the Continuous Microcellular Extrusion Foaming Ability with Supercritical CO2 of Thermoplastic Polyether Ester Elastomer through In-Situ Fibrillation of Polytetrafluoroethylene. Polymers 2019, 11, 1983. [Google Scholar] [CrossRef] [PubMed]
- Gupta, K.; Jain, N.; Laubscher, R. Advanced Gear Manufacturing and Finishing; Academic Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Veres, M.; Bosansky, M.; Gadus, J. Theory of Convex-Concave and Plane Cylindrical Gearing; Slovak University of Technology: Bratislava, Slovak, 2006. [Google Scholar]
- Brumercik, F.; Lukac, M.; Majchrak, M.; Krzysiak, Z.; Krzywonos, L. Teeth geometry and contact pressure calculation of external cycloidal gears. Sci. J. Sil. Univ. Technol. Ser. Transp. 2018, 101, 27–35. [Google Scholar] [CrossRef]
- Wikimedia Commons. Available online: https://commons.wikimedia.org/wiki/File:Rearview_Mirror_Epicyclic_Gears.jpg (accessed on 1 June 2019).
- Looman, J. Zahnradgetriebe. Grundlagen, Konstruktionen, Anwendungen in Fahrzeugen; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Polymer Science. Typical Poisson’s Ratios of Polymers at Room Temperature. Available online: https://polymerdatabase.com/polymer%20physics/Poisson%20Table.html (accessed on 1 June 2019).
- MatWeb. Overview of Materials for Nylon 6, Cast. Available online: http://matweb.com/search/DataSheet.aspx?MatGUID=8d78f3cfcb6f49d595896ce6ce6a2ef1 (accessed on 1 June 2019).
- Erichello, R. Gear Sliding. In Encyclopedia of Tribology; Wang, Q.J., Chung, Y.-W., Eds.; Springer: Boston, MA, USA, 2013. [Google Scholar] [CrossRef]
- Orokocky, R.; Bosansky, M.; Veres, M. The influence of geometrical parameter to sliding speed in K-K gears. In Proceedings of the 44th Conference of the Departments of Machine Elements and Mechanisms, Prague, Czech Republic, 9–10 September 2003; pp. 240–243. [Google Scholar]



| Gear | Teeth Number z (-) | Module m (mm) |
|---|---|---|
| Sun gear 1 | 15 | 0.45 |
| Planet gear 2 | 18 | 0.45 |
| Ring gear 3 | 51 | 0.45 |
| Planet gear 4 | 18 | 0.50 |
| Ring gear 5 | 48 | 0.50 |
| Gearbox Element | Relative Speed ω (-) | Relative Torque T (-) | Relative Power P (-) |
|---|---|---|---|
| A | 1 | 1 | 1 |
| B | −0.0142 | 51.9269 | −0.7376 |
| C | 0.0000 | −52.9269 | 0.0000 |
| 1 | 1.0000 | −1.0000 | −1.0000 |
| 3 | 0.0000 | 52.9269 | 0.0000 |
| 5’ | −0.0142 | −48.8223 | 0.6935 |
| 5’’ | −0.0142 | −3.1046 | 0.0441 |
| 5 | −0.0142 | −51.9269 | 0.7376 |
| S1 | 0.2273 | −4.1046 | −0.9329 |
| S2 | 0.2273 | 4.1046 | 0.9329 |
| Gear Pair | Point of the Path of Contact | Contact Pressure p [MPa] | Flank Type Ratio pC-C/pINV (-) | |
|---|---|---|---|---|
| Involute Teeth Flanks | Convex–Concave Teeth Flanks | |||
| 1-2 | A | 12.3086 | 3.6178 | 0.2939 |
| B2/B1 | 5.9996/8.4645 | 3.8418/5.4372 | 0.6407/0.6423 | |
| C | 7.9379 | 7.9379 | 1.0000 | |
| D1/D2 | 7.9999/5.658 | 5.2443/3.6961 | 0.6555/0.6533 | |
| E | 7.6604 | 3.4491 | 0.4502 | |
| 2-3 | A | 42.9729 | 8.7852 | 0.2044 |
| B2/B1 | 14.2245/20.0888 | 9.1338/12.9432 | 0.6421/0.6443 | |
| C | 16.9851 | 16.9851 | 1.0000 | |
| D1/D2 | 16.2260/11.4516 | 9.5872/6.7698 | 0.5909/0.5912 | |
| E | 8.1294 | 6.3054 | 0.7756 | |
| 4-5 | A | 41.7424 | 7.7110 | 0.1847 |
| B2/B1 | 12.8809/18.0976 | 7.9674/11.2820 | 0.6185/0.6234 | |
| C | 15.3391 | 15.3391 | 1.000 | |
| D1/D2 | 14.7914/10.4142 | 8.4263/5.9422 | 0.5697/0.5706 | |
| E | 7.2949 | 5.6199 | 0.7704 | |
| Gear Pair | Point of the Path of Contact | Slide Ratio vss (-) | Flank Type Ratio vssC-C/vssINV (-) | ||||
|---|---|---|---|---|---|---|---|
| Involute Teeth Flanks | Convex–Concave Teeth Flanks | ||||||
| Pinion | Gear | Pinion | Gear | Pinion | Gear | ||
| 1-2 | A | −13.4628 | 0.9308 | −1.1526 | 0.5355 | 0.0856 | 0.5752 |
| E | 0.8436 | −5.3937 | 0.5079 | −1.0323 | 0.6021 | 0.1914 | |
| 2-3 | A | −5.0521 | −0.3770 | −0.2891 | −0.1869 | 0.0572 | 0.4958 |
| E | 0.2738 | 0.8348 | 0.1575 | 0.2242 | 0.5752 | 0.2686 | |
| 4-5 | A | −5.5229 | −0.3595 | −0.2574 | −0.1709 | 0.0466 | 0.4752 |
| E | 0.2645 | 0.8467 | 0.1459 | 0.2047 | 0.5518 | 0.2418 | |
| Gear Pair | Contact Ratio εα (-) | |
|---|---|---|
| Involute Teeth Flanks | Convex–Concave Teeth Flanks | |
| 1-2 | 1.5055 | 1.1567 |
| 2-3 | 1.6893 | 1.1251 |
| 4-5 | 1.7017 | 1.1025 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brumercik, F.; Lukac, M.; Caban, J.; Krzysiak, Z.; Glowacz, A. Comparison of Selected Parameters of a Planetary Gearbox with Involute and Convex–Concave Teeth Flank Profiles. Appl. Sci. 2020, 10, 1417. https://doi.org/10.3390/app10041417
Brumercik F, Lukac M, Caban J, Krzysiak Z, Glowacz A. Comparison of Selected Parameters of a Planetary Gearbox with Involute and Convex–Concave Teeth Flank Profiles. Applied Sciences. 2020; 10(4):1417. https://doi.org/10.3390/app10041417
Chicago/Turabian StyleBrumercik, Frantisek, Michal Lukac, Jacek Caban, Zbigniew Krzysiak, and Adam Glowacz. 2020. "Comparison of Selected Parameters of a Planetary Gearbox with Involute and Convex–Concave Teeth Flank Profiles" Applied Sciences 10, no. 4: 1417. https://doi.org/10.3390/app10041417
APA StyleBrumercik, F., Lukac, M., Caban, J., Krzysiak, Z., & Glowacz, A. (2020). Comparison of Selected Parameters of a Planetary Gearbox with Involute and Convex–Concave Teeth Flank Profiles. Applied Sciences, 10(4), 1417. https://doi.org/10.3390/app10041417






