Abstract
Soil-abutment or soil-pile interactions under cyclic static loads have been widely studied in integral abutment jointless bridges (IAJBs). However, the IAJB has the combinational interaction of soil-abutment and soil-pile, and the soil-abutment-pile interaction is lack of comprehensively study. Therefore, a reciprocating low-cycle pseudo-static test was carried out under an cyclic horizontal displacement load (DL) to gain insight into the mechanical behavior of the soil-abutment-pile system. Test results indicate that the earth pressure of backfill behind abutment has the ratcheting effect, which induced a large earth pressure. The soil-abutment-pile system has a favorable energy dissipation capacity and seismic behavior with relatively large equivalent viscous damping. The accumulative horizontal deformation in pile will be occurred by the effect of abutment and unbalance soil pressure of backfill. The test shows that the maximum horizontal deformation of pile occurs in the pile depth of 1.0b~3.0b of pile body rather than at the pile head due to the accumulative deformation of pile, which is significantly different from those of previous test results of soil-pile interaction. The time-history curve for abutment is relatively symmetrical and its accumulative deformation is small. However, the time-history curve of pile is asymmetrical and its accumulative deformation is dramatically large. The traditional theory of deformation applies only to the calculation of noncumulative deformation of pile, and the influence of accumulative deformation should be considered in practical engineering. A significant difference of inclinations in the positive and negative directions increases when the displacement load is relatively large. The rotation of abutment when bridge expands is larger than that when bridge contracts due to earth pressure of backfill.
1. Introduction
Jointless bridge has a continuous superstructure without moveable deck joint (MDJ), which includes integral abutment jointless bridge (IAJB), semi-integral abutment jointless bridge (SAJB) and deck-extension abutment jointless bridge (DAJB), etc. IAJB with the most favorable integrality has been widely used in North America, Europe and Australia [1,2,3,4,5]. Compared to the conventional bridges, the advantages of IAJBs involve: (1) decreasing cost of installation and maintenance of joints, (2) reducing impact and damage on bridge deck caused by bump, (3) enhancing the earthquake resistance with better redundancy. However, the superstructure would be moved (expansion/contraction) along the longitudinal direction of bridge under temperature variations, creep and shrinkage effects, or earthquake excitations [6]. These movements would inevitably cause the abutment and pile foundation to move back and forth and induce soil-structures interaction (including soil-pile, soil-abutment, abutment-pile, and soil-abutment-pile). It is well-known that when the abutment moves away from the embankment, it is subjected to active earth pressure; whereas when it moves towards the embankment, it is subjected to passive earth pressure.
The researches on interaction of soil-pile foundation in IAJB were widely and comprehensively studied [7,8,9,10]. The results indicate that the piles supporting on the abutment in IAJB should have reasonable flexibility to accommodate the horizontal movement. For the researches of soil-abutment interaction, some researchers carried out the tests in Lab or in filed to study the effects of temperature or seismic movements on IAJBs. Huang et al. [11] and Chen et al. [12] reported that when abutment moved towards the embankment, the earth pressure was equal to about two-thirds of the Rankine passive earth pressure after several cycles. England et al. [13] observed that the distribution of earth pressure was in the shape of a trapezoid under cyclic load, and suggested that the passive earth pressure coefficient was only related to the height and longitudinal displacement of abutment. Other researchers analyzed the interaction of soil-abutment by finite element model. Peng et al. [14,15] analyzed a 137-m-long IAJB using ANSYS software, and concluded that the earth pressure behind abutment was 0.478 times that of the Rankine passive earth pressure when temperature rose about 15 degrees Celsius. Peng et al. [16] also studied the ratcheting effect with the aid of the finite element model and concluded that the earth pressure behind the abutment increased year by year under the seasonal temperature cycling. For example, when the integral abutment bridge was subjected to a temperature increase of 30 degrees Celsius, the earth pressure increased by 23% after 5 years. Yu et al. [17] analyzed a computer model of a 64-m-long bridge using the TDV software [18], and inferred that the earth pressure behind abutment was 0.161 times the Rankine passive earth pressure when temperature rose about 20 degrees Celsius. David et al. [19] implemented a finite element model that incorporated nonlinear soil behavior and linear structural response considering various loading conditions and concluded that the depth of the pile would influence the behavior of the abutment.
The researchers indicate that the earth pressure behind the abutment in IAJBs increases gradually with the periodical and seasonal temperature over the years. This phenomenon of increasing earth pressure is called the ratcheting effect of soil [20]. Nevertheless, these studies were mainly focused on the soil-abutment interaction rather than the soil-abutment-pile interaction, which need to be further investigated. In addition, Frosch et al. [21] conducted a test of monolithic abutment integrated with steel H-pile to estimate the lateral displacement capacity and the seismic performance of integral abutment bridges. However, it is only focused on the interaction of abutment-pile, ignored the effect of soil. At present, few works about the experiments on the soil-abutment-pile interaction are reported. How does the existence of pile affect the soil-abutment interaction and how does the abutment affect the soil-pile interaction need to be researched. Since the earth pressure of soil has the accumulative (ratcheting) effect, whether the deformation of pile also has the ratcheting effect needs to be explored.
In order to further study the soil-abutment-pile interaction, a reciprocating low-cycle pseudo-static test on an soil-abutment-pile system was carried out under an horizontal displacement load. The earth pressure distribution behind the abutment was measured in the longitudinal and depth directions. Some conclusions about the hysteretic curve, skeleton curve and viscous damping analysis of the specimen were put forward. Horizontal deformation of the specimen along the depth direction, the time-history curve with or without considering the accumulative deformation and accumulative angle were studied in this paper.
2. Brief Introduction of Test
2.1. Specimen Design and Manufacturing
2.1.1. Specimen Design
The specimen design was based on an practical IAJB in Fujian Province, China. The total length of the bridge is 136 m, including four 30-m-long spans and two 8-m-long approach slabs. The thickness (longitudinal direction of bridge) and width (transverse direction of bridge) of abutment for one supported pile are 1.8 m and 2.12 m, respectively. The height of abutment (vertical direction) including girder and pile cap is 3.25 m. Four piles supported the abutment. The pile with the cross section of 0.7 m × 0.5 m was oriented in the weak axis under longitudinal bridge movement.
Considering the limitations of test equipment and Lab condition, the geometric scale ratio of the specimen was selected to be 0.31. Figure 1 shows the dimensions of the specimen. The height of specimen is 3.90 m, as shown in Figure 1a. Figure 1b,c show the dimensions of cross section of the abutment and steel H-pile. In Figure 1, the height of abutment (H) is 1000 mm. The thickness (T) and width (W) of scaled abutment in the transverse and longitudinal directions are 560 mm and 660 m, respectively. The cross-sectional widths of scaled pile (h and b) along the strong and weak axes are 217 mm and 155 mm, respectively. The flange and web of scaled pile (t1 and t2) are 10 mm and 6 mm, respectively. The total length of scaled steel H-pile (L) is 3.21 m. In Figure 1a, the depth of steel pile that embedded into the abutment is 0.31 m (2 times of b), which meets the requirement of consolidation according to the Reference [22]. The depth of steel pile (l0) buried in the soil is 2.9 m. The construction of the specimen was shown in Figure 1d.
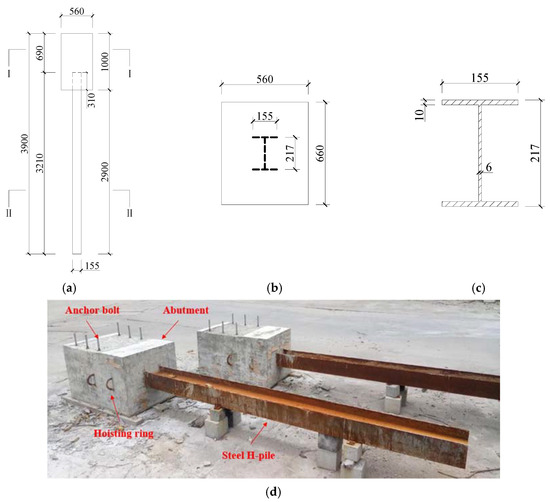
Figure 1.
Test specimen dimensions (unit: mm). (a) Abutment-pile specimen. (b) Section I-I. (c) Section II-II. (d) Photos of specimen after construction.
2.1.2. Specimen Material and Soil Properties
Specimen Material Characteristics
C40 (compressive strength of 40 MPa) was used in this abutment, which is consistent with the actual bridge. The 28-day compressive strength of the concrete cube was 43.5 MPa, and its elastic modulus was 32.5 GPa. HRB335 steel was employed. Its yield strength measured by tensile test was 337 MPa, and the ultimate tensile strength was 454 MPa.
Q235 steel was employed for Steel H-pile in the test. The yield strength and strain measured by tensile test were 238 MPa and 1151 με, respectively, and the elastic modulus was 208 GPa.
Soil Properties
The soil was obtained from Min-jiang River in Fujian Province, China. The nonuniformity coefficient (Cu) obtained by the diameter of sand was 3.15, which means that the soil is basically homogeneous [23]. Poisson’s ratio was calculated using the method of Kulhawy [24]. The parameters of sand are shown in Table 1.

Table 1.
Physical and mechanical parameters of soil.
2.1.3. Specimen Manufacturing
In order to facilitate the erection and casting, the specimen was fabricated in an inverted position, where the pile is up and abutment is down, as shown in Figure 2a,b. The details of specimen fabrication are as follows.
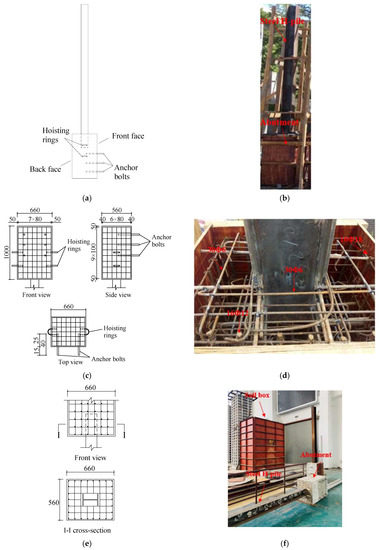
Figure 2.
Manufacturing of the specimen (unit: mm). (a) Layout of the specimen. (b) Construction of the specimen. (c) Reinforcement layout of abutment. (d) Photo of steel layout of pile and abutment. (e) Details of consolidation of pile and abutment. (f) Photo of Abutment-pile specimens and soil box.
The first step is to assemble the reinforcing bars of abutment. Three different types of steel reinforcing bar (with the diameters of 12 mm, 8 mm, 6 mm) are used for the reinforcement of abutment. Sixteen 12-mm bars are arranged at the front and back faces of the abutment with a spacing of 80 mm and cover thickness of 50 mm. Fourteen 8-mm bars are arranged along the transverse direction with a spacing of 80 mm and cover thickness of 40 mm, as shown in Figure 2c. Then, the steel H-pile is welded to the bars in the abutment, as shown in Figure 2d,e.
The second step is to install the abutment formwork. Six 25-mm anchor bolts are arranged longitudinally, which are connection with the actuator and transfer the longitudinal force to the abutment. The total length of anchor bolt is 40 cm, with an embedded length of 25 cm. Hoisting rings are arranged to facilitate the transport and installation of specimen, as shown in Figure 2c.
The last step is to pour the concrete of abutment to form a integrity with steel H-pile after the installation of formwork. Figure 2f shows the abutment-pile specimen after pouring.
2.2. Soil Box Design and Specimen Installation
2.2.1. Soil Box Design and Manufacturing
Since the test was carried out in the soil box of laboratory, the boundary effect of soil should be considered during the process of soil box design. The researches [25,26,27] indicate that, when the boundary for the abutment is larger at least two times the height of abutment and the boundary for the pile is larger about five times the diameter of pile, the boundary effect can be neglected. Based on the size of the test specimen and the boundary requirements, the distances from the pile and abutment to the soil box should be no less than 0.75 m and 2 m (total of 2.75 m), respectively. Therefore, the soil box was designed to be 3 m long (larger than 2.75 m), 2 m wide and 4 m high (Figure 2f), which is one of the largest testing soil boxes used in China. Figure 3 shows the top view and elevation view of specimen and soil box.
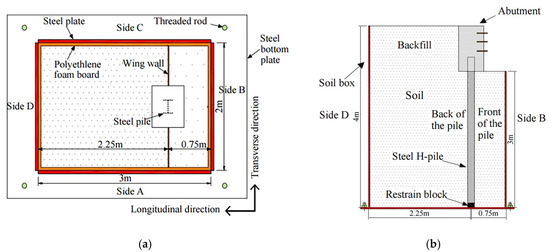
Figure 3.
Test layout (unit:m). (a) Top view of specimen and soil box. (b) Elevation view.
In addition, 5-cm-thick polyethylene foam boards were used to reduce the boundary effect, and two steel wing walls were arranged to prevent backfill sliding and keep the different height of soil between the front and back of abutment. The soil box was fixed on the Lab platform by 4 threaded rods. The heights of the soil box for Side A, Side C and Side D with soil are 4 m high, while Side B without soil is only 3 m high that can let MTS actuator to move and load.
2.2.2. Specimen Orientation and Soil Filling
Before the test, the specimen was moved into position and oriented with weak axial firstly, as shown in Figure 4a. Then its end was fixed by a device of restrain block (Figure 3b) that was assembled using several steel angles and bolts on the bottom plate of box as shown in Figure 4b.

Figure 4.
The process of soil filling. (a) The installation of specimen. (b) Details of the pile-toe. (c) The filling up to 3 m. (d) Photo for filling the soil of backfill. (e) Fully filled. (f) Photo for fully filled.
After that, the box began to fill into soil. The soil was compacted with each height increment of 25 cm and filled up to 3 m height (fully bury the pile), as shown in Figure 4c. Then, it continuously filled the soil behind the abutment as shown in Figure 4d. A 1.0 m height soil of backfill was filled making the total height of soil behind the abutment equal to 4 m, as shown in Figure 4e,f. Thus, the soil-abutment-pile system is formed, where the heights of soil in back and front of abutment are 4 m and 3 m respectively.
2.3. Layout of Measurement Points
Four types of sensors were used in the experiment: earth pressure cell, displacement meters (LVDT), inclinometer and strain gage, which were introduced as following.
2.3.1. Layout of Earth Pressure Cells
Figure 5a shows the layout of earth pressure cells. Thirty six earth pressure cells were arranged, one of seventeen were arranged for the abutment and nineteen for the steel pile. The earth pressure cells behind abutment were placed in 4 rows and 4 columns (T1~T16). The locations of four rows of earth pressure cells were buried with the depths of 0.125 m, 0.375 m, 0.625 m and 0.875 m, and the locations of four columns of earth pressure cells were embedded with the distances of 0H (the back face of abutment), 0.2H, 0.6H and 1.4H from the back of abutment (H is the height of abutment). The T1~T4 pressure cells were glued on the abutment while the T5~T16 pressure cells were embedded vertically in the soil, as shown in Figure 5b,c, respectively. In addition, the T17 earth pressure cell was adhered to the bottom back of the abutment.

Figure 5.
Layout of earth pressure cells (unit: mm). (a) Layout of earth pressure cells. (b) Cell on the abutment. (c) Cell behind the abutment. (d) Cell on the pile.
At the top of the pile, the T18 earth pressure cell was adhered to the pile head (Figure 5d). In the range of 0.2 m~1.2 m of pile depth, the T19~T30 pressure cells were arranged at 200-mm intervals. In the range of 1.2 m~2.4 m, the T31~T36 earth pressure cells were arranged at 400-mm intervals. There were no earth pressure cells beyond the depth of 2.4 m.
2.3.2. Layout of Displacement Gages and Inclinometers
Figure 6 shows the layout of displacement meters and inclinometers. Four displacement meters were arranged on the abutment and ten were arranged on the steel pile. For the abutment, the D1 displacement meter was arranged at the top of the abutment, and the D2~D4 displacement meter were located within the buried depth of 0.6 m~1 m at 200-mm intervals. For the pile, the D5~D13 displacement meter were arranged within the pile depth of 0 m~1.8 m at 200-mm intervals, and the D14 displacement meter was arranged at the pile depth of 2.4 m, as shown in Figure 6a. To assess the horizontal deformations of pile that is covered by soil accurately, a method from Huang [26] was implemented, which can directly measure the horizontal deformation, as shown in Figure 6b.
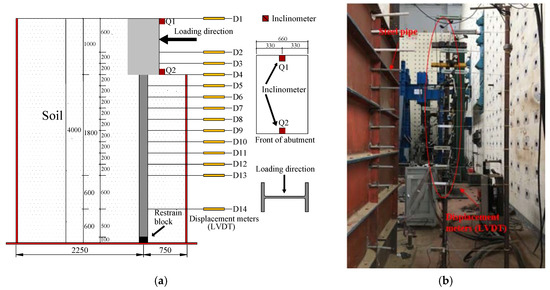
Figure 6.
Layout of displacement meters and inclinometers (unit: mm). (a) Layout. (b) Photo of displacement meters.
In addition, the Q1 and Q2 inclinometers were placed at the top center and bottom center of the front face of the abutment to measure the angle and curvature. As for the layout of strain gages of abutment and pile, it is not shown herein due to the strain results do not present.
2.4. Loading Test
2.4.1. Loads
Horizontal Displacement loads
The prototype bridge that the experiment was implemented is located in Fujian Province, and its maximum movement of expansion and contraction of the superstructure are estimated at 13 mm and 10 mm, respectively, when the temperature varies from +25 degrees Celsius to −20 degrees Celsius. To fully consider the thermal expansion and contraction of jointless bridge, the horizontal displacement load imposed by the MTS is ±16 mm in the test. The location of the horizontal displacement load was at the distance of 0.35 m below the top of the abutment.
Vertical Weight
To ensure the consistency of axial compression on the abutment-pile structure between the test specimen and the actual prototype bridge, a vertical load should be applied to the specimen. As the axial compression ratio for the original bridge was about 0.1, the vertical load (counterweight) of 25.02 kN was applied to the top of the abutment.
2.4.2. Loading Scheme
The loading arrangement is shown in Figure 7. Reciprocating low-cycle pseudo-static displacements were imposed during the test. The cyclical displacements started from ±2 mm and increased to ±16 mm with 2 mm increments. There were eight displacement steps and each step consisted of three displacement cycles, as shown in Figure 8. The movement speed for each displacement cycle was set at 1 mm/s, and the displacement was sustained for 30 s at each peak before changing direction. In addition, the test equipment include a 250 kN MTS hydraulic actuator and a data acquisition system. When the specimen pushed by the MTS moves towards the backfill (road embankment), the direction is defined as positive; when the specimen pulled by the MTS moves towards the reaction-wall (span of bridge), the direction is defined as negative, as shown in Figure 7.
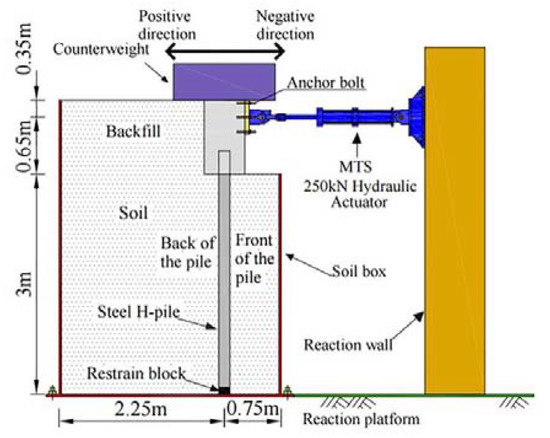
Figure 7.
Loading arrangement.
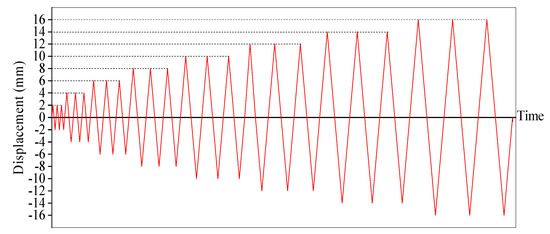
Figure 8.
Loading scheme (unit: mm).
3. Experimental Results and Analyses
3.1. Earth Pressure behind Abutment
3.1.1. Relationship between Earth Pressure and Displacement Load
As discussed earlier, the T1~T16 earth pressure cells were arranged on the back of the abutment in four rows and four columns. For the limit of space, results from four typical earth pressure cells (the third row of T3, T7, T11 and T15) are discussed in this section. Figure 9 shows the relationship between earth pressure and displacement load.
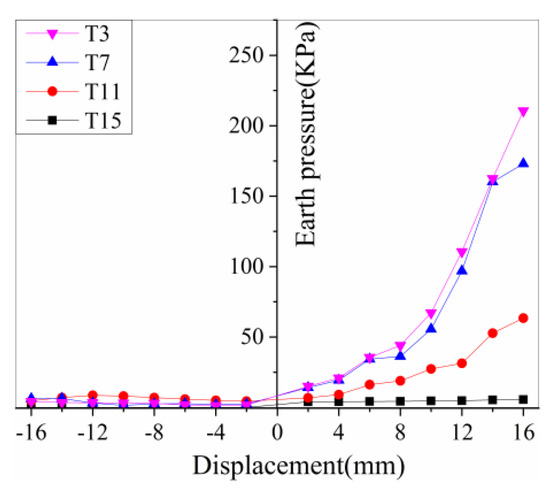
Figure 9.
Relationship between earth pressure and displacement load.
It can be seen from Figure 9 that the active earth pressures are occurred and nearly constant (about 5 kPa) when the abutment moves to the negative direction (pulled by MTS). In addition, the active earth pressure is also close to the earth pressure at rest. The passive earth pressures are occurred and increase rapidly with the increase of displacement load when the abutment moves to the positive direction (pushed by MTS), especially for the pressures near the abutment (T3 and T7) as shown in Figure 9. The maximum pressure for T3 reaches 214 kPa under the displacement of +16 mm. By comparison, the passive earth pressure of T3 is over 30 times of active earth pressure.
Figure 10 shows the relationships between the relative displacement ∆/H (∆ is the displacement at the top of the abutment) and the earth pressure coefficient K. The passive earth pressure coefficient Kp from Burke-Chen [12,28], England [13], Barker and NCHRP [29], Dicleli [30], Massachusetts [31], Rankine theory and Coulomb theory are compared with the test results.
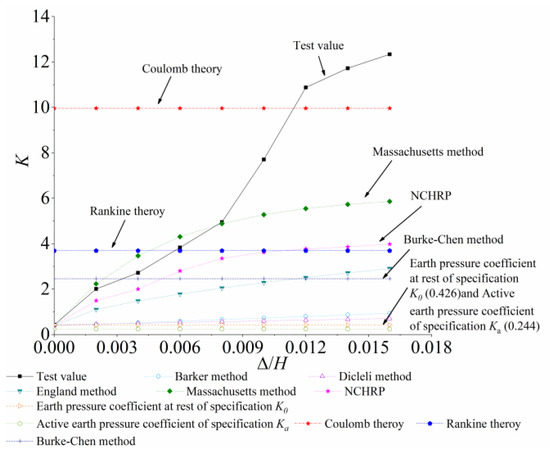
Figure 10.
Relationship between ∆/H and Kp.
It can be observed from Figure 10 that the test result of earth pressure coefficient is approximately equal to all Kp of Burke-Chen, England, Barker, NCHRP, Dicleli, Massachusetts when ∆/H is not larger than 0.004 (∆/H ≤ 0.004). Moreover, it is approximately equal to two thirds of earth pressure coefficient of Rankine theory, but it is far less than Coulomb theory. When ∆/H is larger than 0.004 and less than or equal to 0.006 (0.004 < ∆/H ≤ 0.006), the Kp from Burke-Chen, England, Barker, NCHRP and Dicleli are less than that of test. The Kp from Rankine theory is nearly close to the test result, but still significant lower that Coulomb theory when ∆/H reaches 0.006 (∆/H = 0.006). The test result is larger than all of those except Coulomb theory when ∆/H is between 0.006 and 0.012 (0.006 < ∆/H ≤ 0.012). However, it exceeds the Coulomb theory when ∆/H is larger than 0.012 (∆/H > 0.012). Therefore, the coefficient Kp obtained from this test is larger than all of them, which is demonstrated the ratcheting effect significantly. Moreover, the coefficient Kp from this test is 3.33 times as much as that of Rankine theory and 1.27 as much as that of Coulomb theory when ∆/H is equal to 0.016 (∆/H = 0.016). Therefore, the existing calculation method earth pressure of backfill behind abutment is not accurate for that of IAJB.
By the way, only the calculated methods of active earth pressure coefficient Ka and earth pressure coefficient at rest K0 were obtained from the code of General Specifications for Design of Highway Bridges and Culverts (JTG D60-2015) [32] in China, while how to calculate Kp was not given. The calculation of Ka and K0 by JTG D60-2015 was also shown in Figure 10. The coefficients of Ka and K0 are less than the Kp of test from Figure 10. The result further indicated that the calculation of the Ka and K0 in the Chinese code is not suitable for IAJBs, which need to be improved to consider the coefficient Kp.
3.1.2. Distribution of Earth Pressure
Distribution along the Height of Abutment
Since the active earth pressure is quite low compared to the passive earth pressure in Figure 9, the distribution of active earth pressure will not be discussed further in this paper. Figure 11 shows the distribution of passive earth pressure along the height of abutment when the abutment moves to the positive direction. Figure 11a shows the distribution of earth pressure for sensors T1~T4 and T17 at the back face of the abutment. Besides, Figure 11b–d show the distribution of earth pressures for sensors T5~T8, T9~T12 and T13~T16 at horizontal distances of 0.2H, 0.6H and 1.4H (0.2 m, 0.6 m and 1.4 m) from the back of the abutment, respectively.
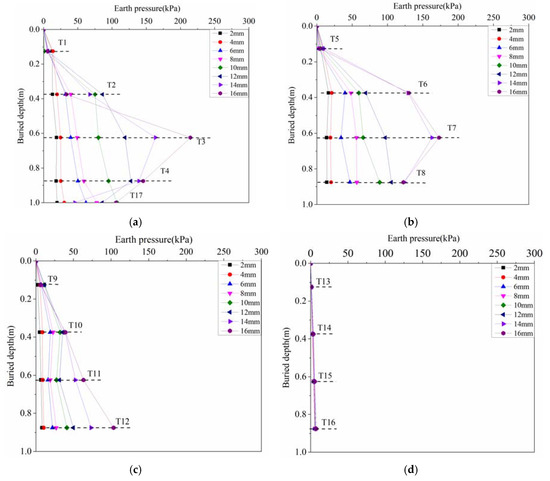
Figure 11.
Distribution of passive earth pressure along the height of abutment. (a) Cells at the back face of the abutment. (b) Cells at horizontal distance of 0.2H. (c) Cells at horizontal distance of 0.6H. (d) Cells at horizontal distance of 1.4H.
It is observed that the earth pressure behind abutment has a typical triangular distribution when the horizontal displacement is small (less than 8 mm) in Figure 11a,b, or when the soil is far away from abutment (larger than 0.6H) in Figure 11c,d. However, the earth pressure shows a trapezoid distribution when the soil is close to abutment under a large horizontal displacement (larger than 8 mm), as shown in Figure 11a,b. The reason of forming a trapezoid distribution is that the horizontal movement of the bottom of integral abutment is influenced by the constraint of steel H-pile when abutment is under the large displacement load, which reduces the horizontal deformation of the abutment and thus reduces the earth pressure. This trapezoid distribution is also consistent with the results of Dicleli [33]. In Figure 11c,d, the earth pressure at horizontal distances of 0.6H and 1.4H from the back of the abutment is triangular under different displacements, which indicates that the pile has little influence on the distribution of earth pressure when the soil is far away from the abutment.
Distribution along the Longitudinal Direction
Figure 12 shows the distribution of earth pressure along the longitudinal direction when abutment moves to the positive direction under different displacement steps. For brevity, results from four typical earth pressure cells (T3, T7, T11 and T15) are discussed in this section. In Figure 12, it is observed that the earth pressure decreases with the increases of the horizontal distance. The decreasing trend is similar to an exponential decay. Within the distance of 0H to 0.6H, the earth pressure drops significantly, especially under large displacement loads. Within the distance of 0.6H to 1.4H, the rate of reduction in earth pressure slows down. Finally, the earth pressure reduces to the earth pressure at rest under different displacement steps, which means the displacement loads have little influence on earth pressure when the horizontal distance is larger than 1.4H. This also illustrates that the soil box was sufficiently large that can be neglected the boundary effect on the development of earth pressure.
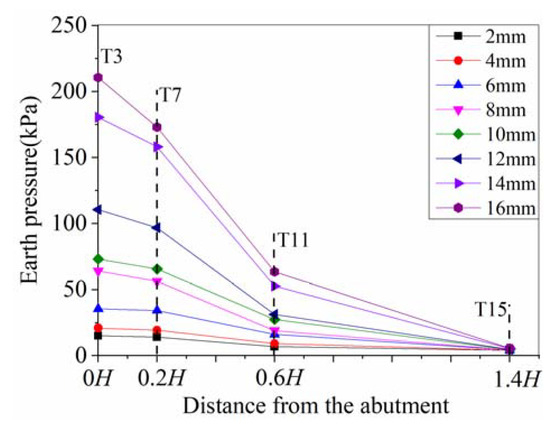
Figure 12.
Distribution of earth pressure along the longitudinal direction.
3.2. Hysteretic Curve and Skeleton Curve
3.2.1. Hysteretic Curve
Figure 13 shows the hysteretic curves of interaction of soil-abutment-pile system. Figure 13a shows the whole process of hysteretic curves, and Figure 13b only shows one cycle of hysteretic curve of ±14 mm displacement load as a typical demonstration case (ABCDEFA1 path shown in Figure 14). The hysteretic curves of soil-abutment-pile interaction in the first quadrant represent the abutment movements in the positive direction (From A to B in Figure 14), and the curves in the third quadrant represent the abutment movements in the negative direction (From D to E in Figure 14). Besides, the curves in the second quadrant represent the changing process from soil-pile interaction to soil-abutment-pile interaction (From B to D in Figure 14), and the curves in the fourth quadrant represent the changing process from soil-abutment-pile interaction to soil-pile interaction (From E to A1 in Figure 14).
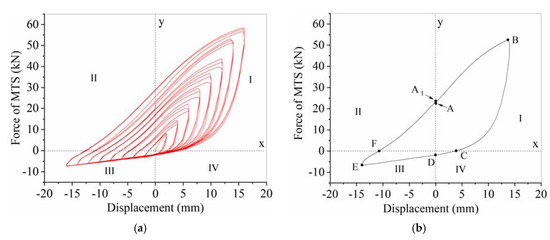
Figure 13.
Hysteresis curves. (a) Hysteretic curves for the entire process. (b) Hysteretic curve for one cycle.
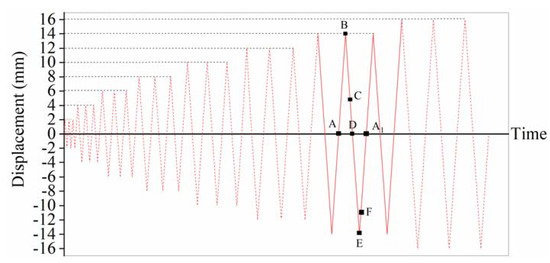
Figure 14.
Illustration of ±14 mm displacement load.
In Figure 13a, the hysteretic curves are dramatically asymmetrical that the first quadrant is plump and spindle-shaped, but other three quadrants are not spindle-shaped, which are greatly different from the traditional hysteretic curves of column or pile. As there are three cycles for each step of displacement load, it is found that the horizontal force shows an upward trend with the increase of cycle. Specifically, under the ±10 mm displacement load step, the horizontal push force is +32.54 kN in the first cycle, but +36.78 kN in the third cycle, showing an increase of about 13.0%. The reason is that the interaction of soil-abutment-pile system gets stronger by the reciprocating displacement, which makes the soil behind the abutment or around the pile become compacted. This result is consistent with the soil ratcheting phenomenon in which the earth pressure behind abutment increases year by year under seasonal temperature variations [34].
As mentioned when the abutment moves towards the embankment (the positive direction in Figure 7), the MTS actuator produces a horizontal push force, and when the abutment moves away from the embankment (the negative direction in Figure 7), the actuator provides horizontal pull force. However, after several displacement cycles, when the force of actuator reduces to 0 kN, the actuator would not go back to the initial position and the deviation of horizontal displacement is induced. As shown in Figure 13b, when the actuator goes back to the initial position and the displacement of abutment is 0 mm (Point A), the force in the actuator is 22.79 kN (an unbalanced force). As the abutment moves to the positive direction (Curve AB), the soil resistance behind abutment increases continuously. The force exerted by the actuator increases to 52.49 kN when the abutment reaches the displacement of +14 mm (Point B). Then, when the abutment changes its direction and moves to the negative direction (Curve BC), the force exerted by the actuator drops dramatically. When the force reduces to 0 kN (Point C), the remaining displacement of the abutment is +3.63 mm (Point C, as shown in Figure 14). Herein the remaining displacement is defined as residual deformation. The reason is that the soil is a plastic material, the skeleton curve of force-displacement (Curve BC) is nonlinear during unloading, which leads to the residual deformation. By the way, when the actuator displacement reduces to 0 mm, the actuator force and the deformation of pile that deviates from the vertical central axis would not be equal to zero. The force is called as the unbalanced force, and the deformation of steel H-pile is called as the accumulative deformation. When continuous to load, the pull force exerted by the actuator begins to increase and is up to −1.81 kN (Curve CD) when the actuator moves back to the initial position (Point D). After that, the abutment keeps moving in the negative direction (Curve DE). By the time the abutment reaches the displacement of −14 mm (Point E), the pull force climbs up to −6.61 kN.
After the abutment reaches the maximum displacement in the negative direction (Point E), its movement begin to return back to the positive direction (Curve EF), and the actuator force declines moderately. As the force decreases to 0 kN (Point F), the residual deformation in the negative direction is −10.81 mm (Point E, as shown in Figure 14), which is about 77.2% of the displacement load (−14 mm). Moreover, the negative residual deformation is far larger than the positive one (+3.63 mm). After that, the abutment keeps moving to the positive direction (Curve FA1) and arrives at the initial position (Point A1). Then, the unbalanced force of the actuator grows to +23.44 kN, which is also the initial force of third cycle of ±14 mm displacement load step, and slightly larger than that in the second cycle.
Generally, the energy dissipation capacity of the structure is represented by the area of hysteretic curve in the coordinate axis. In Figure 13b, the area of hysteresis curve in the first quadrant is larger than that of the third quadrant, which means the energy dissipation capacity of soil-abutment-pile interaction when test specimen moves to the positive direction is much larger than that of the soil-pile interaction when specimen moves to the negative direction. The area of hysteresis curve in the second quadrant is larger than that of the third quadrant, which indicates that the energy dissipation capacity when bridge expands is greater than that when the bridge contracts.
Many researchers also applied the equivalent viscous damping to evaluate the energy dissipation capacity of the system [35]. The equivalent viscous damping is calculated using the following equation [36], as shown in Figure 15.
where: Ah = area of a full cycle of force-displacement response, N·mm; F = Maximum force occurring within a cycle, N; Δ = Maximum displacement occurring within a cycle, mm.
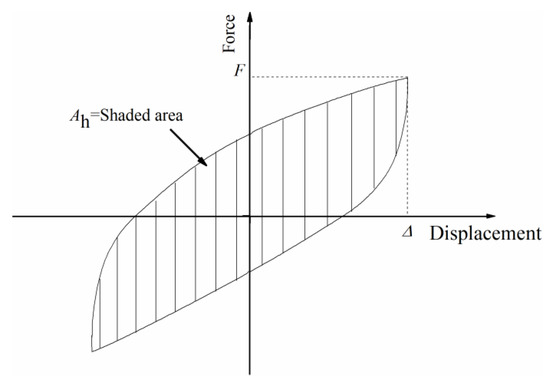
Figure 15.
Hysteretic area for damping calculation.
Figure 16 shows the equivalent viscous damping of the soil-abutment-pile and soil-pile interactions under different displacement steps. Generally, the larger the equivalent viscous damping is, the stronger of energy dissipation capacity and the better of seismic behavior are. As shown in Figure 16, the equivalent viscous damping of the soil-abutment-pile system grows rapidly when the displacement load increases from 0 mm to 8 mm. Then, when the displacement increases from 8 mm to 16 mm, the ratio tends to be stable and reaches a maximum value of 0.25. The equivalent viscous damping of soil-pile structure is about 0.17, which varies little under different displacement steps. According to Reference [37], the soil-abutment-pile system in IAJBs has favorable energy dissipation capacity and seismic behavior.
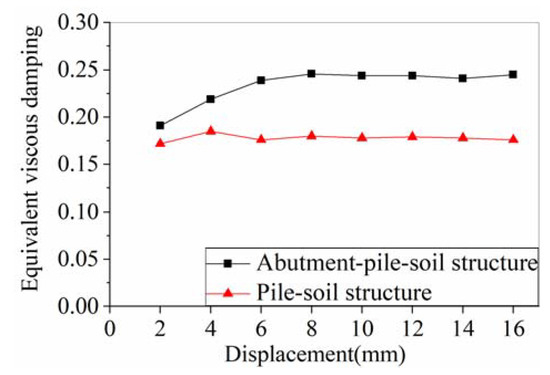
Figure 16.
Equivalent viscous damping.
3.2.2. Skeleton Curve
Figure 17 shows the skeleton curve for the test specimen. Whether the specimen moves to the positive or to the negative directions, the force-displacement curve almost shows a linear behaviour, which means that the specimen shows a linear elastic behavior during the test. The structural stiffness of the specimen is 3.21 kN/mm in the positive direction, and 0.41 kN/mm in the negative direction. The former is as much as 7.76 times of the latter, which is mainly due to the soil resistance behind the abutment.
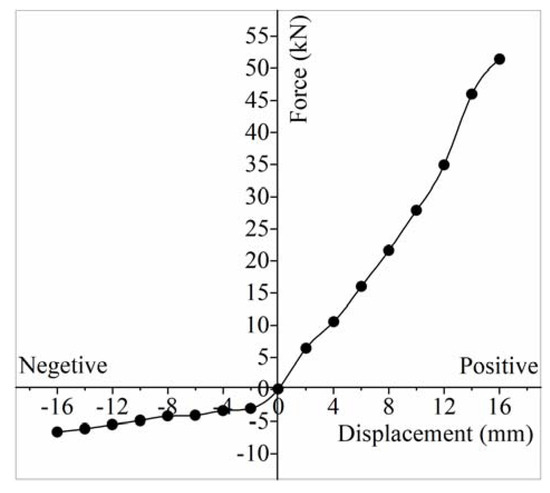
Figure 17.
Skeleton curve for the test specimen.
3.3. Horizontal Deformation
3.3.1. Time-History Curves of Horizontal Deformation
Time-History Curves Considering Accumulative Deformation
In order to further analyze the distribution of horizontal displacement of test specimen along the depth, the time-history curves of horizontal displacement of nine typical measurement points on the specimen are discussed in this section, as shown in Figure 18. Figure 18a shows the locations of nine measurement points and the distribution (red line) of the specimen considering accumulative deformation under ±16 mm displacement load. Time-history curves of horizontal deformation of measurement points, D1, D2, D4 (the buried depth of 0 m, 0.6 m, 1.0 m), D5, D6, D7, D8, D10, D13 (the pile depth of 0.2 m, 0.4 m, 0.6 m, 0.8 m, 1.2 m, 1.8 m) are presented in Figure 18b–j respectively. In Figure 18b–j, the purple lines are the accumulative deformation curves for each measurement point.
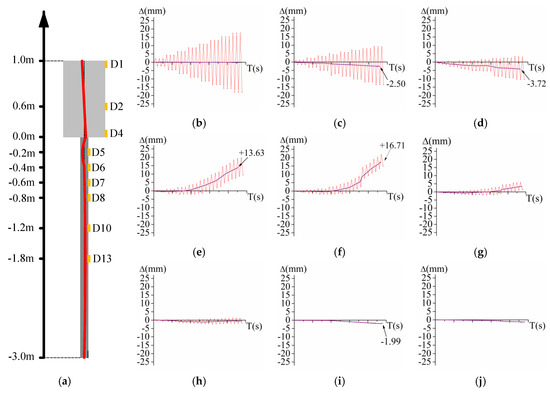
Figure 18.
Time-history curves considering accumulative deformation. (a) The locations of nine measurement points and the distribution (red line) of the specimen considering accumulative deformation. (b) D1. (c) D2. (d) D4. (e) D5. (f) D6. (g) D7. (h) D8. (i) D10. (j) D13.
For the measurement points of abutment, it can be seen that the time-history curve of horizontal deformation of D1 in Figure 18b is basically symmetrical and consistent with that of displacement load in Figure 8. Since the abutment revolves around the action point, the time-history curve of horizontal deformation of D1 is slightly larger than that of loading system. In Figure 18c,d, the time-history curves of horizontal displacement of D2 and D4 are smaller than that of the displacement loads, which are a little asymmetrical by the effect of steel H-pile.
For the measurement points of pile, the time-history curves of horizontal deformation of D5, D6, D7, D8, D10 and D13 vary widely. In Figure 18e, the accumulative deformation of D5 is almost neglected when the displacement is less than ±10 mm. But after that, the accumulative deformation increases rapidly, and goes up to +13.63 mm when the displacement load is ±16 mm. The accumulative deformation makes the displacement of measurement points no longer symmetrical with time axis. In Figure 18f,g, D6 and D7 have the similar phenomenon with D5. To be noted, in Figure 18h–j, the measurement points D8, D10 and D13 have the negative accumulative deformations, which means this range of pile body moves to the negative direction as the displacement load increases. Among these measurement points, the maximum positive accumulative deformation occurs at D6, about +16.71 mm, and the maximum negative accumulative deformation occurs at D10, about −1.99 mm.
Figure 19 shows the curves of accumulative deformation and displacement loads for each measurement point. It can be observed from Figure 19 that the accumulative deformation goes up with the increases of displacement load, and the growth rate is nonlinear and faster when the displacement load reaches 10 mm, especially for D5 and D6 of 1.0b~3.0b of pile depth.
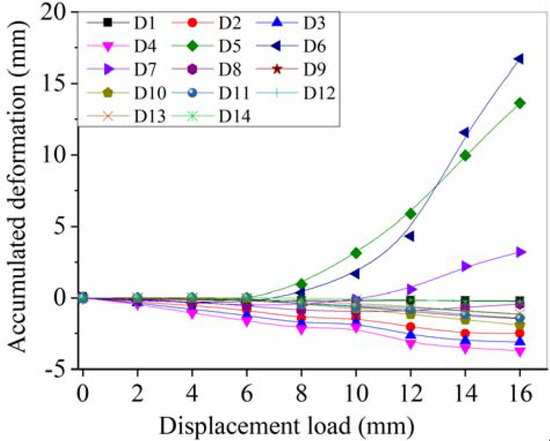
Figure 19.
Accumulative deformation of each measurement point.
Time-History Curves Deducting Accumulative Deformation
The noncumulative deformation is that the whole horizontal deformation of specimen deducts its accumulative deformation, thus it is symmetrical with the time axis. In order to further understand the distribution of horizontal deformation of specimen under each step of displacement load and compare with those of previous test and traditional theory of soil-pile, the time-history curves of horizontal deformation of nine typical measurement points deducting accumulative deformation are discussed in this section, as shown in Figure 20. Figure 20a shows the locations of nine measurement points and the distribution (red line) of the specimen deducting accumulative deformation under ±16 mm displacement load. Their time-history curves are presented in Figure 20b–j respectively.
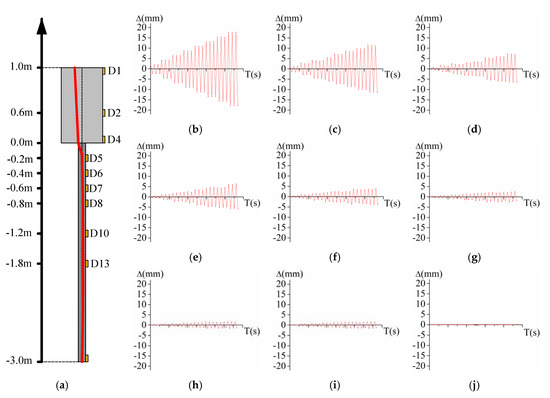
Figure 20.
Time-history curves deducting accumulative deformation. (a) The locations of nine measurement points and the distribution (red line) of the specimen deducting accumulative deformation. (b) D1. (c) D2. (d) D4. (e) D5. (f) D6. (g) D7. (h) D8. (i) D10. (j) D13.
For the measurement points on the abutment, the time-history curve of horizontal deformation is basically consistent with that of displacement load and symmetrical with time axis, as shown in Figure 20b. For the measurement points on the pile, the time-history curves of horizontal deformation of D5, D6, D7, D8, D10 and D13 are symmetrical. Their deformation values are not too large and all of them are smaller than that of pile head (D4), as shown in Figure 20e–j. The horizontal deformations of D4, D5 and D6 are +6.70 mm, +6.33 mm and +3.85 mm under the displacement of +16 mm. By comparison on Figure 18 that the accumulative deformations of D5 and D6 are +13.63 mm and +16.71 mm respectively under the displacement load of +16 mm, they are dramatically larger than the that noncumulative deformation. Therefore, the influence of accumulative deformation of pile should be considered in practical IAJB when the movement of abutment is larger than 10 mm.
3.3.2. Horizontal Deformation along the Depth
Horizontal Deformation under Positive Displacements
Figure 21 shows the distribution of horizontal deformation of specimen along the depth under the positive displacement loads. It can be observed from Figure 21 that the deformation of the abutment increases linearly from the bottom to the top of the abutment under different positive displacement steps, thus the abutment movement can be regarded as a rigid body motion with a certain rotation.
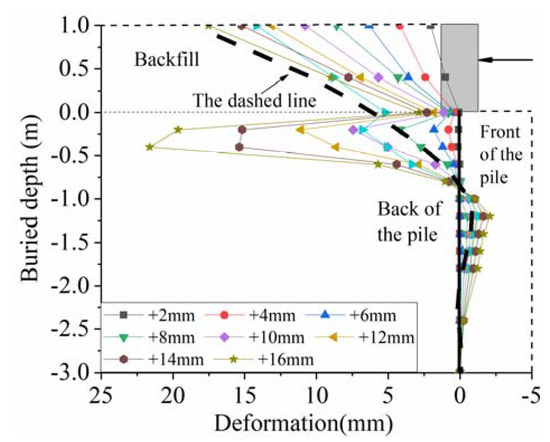
Figure 21.
Distribution of horizontal deformation of specimen under positive displacement loads.
In Figure 21, it can be also observed that the deformation of the pile along the depth increases firstly to maximum, then to decrease to zero and continuous to be a negative value. After the deformation reaches a maximum negative value, it begins to decrease to zero at the end of pile. The horizontal deformation of pile head is relatively small under the displacement loads, but the deformation of pile body grows rapidly at deeper depth along the pile and it reaches the maximum value at the pile depth of 0.4 m (2.58b). Then, the horizontal deformation of pile reduces to 0 mm at depth of 0.9 m (5.8b), where it begins to change into a negative value. The maximum negative deformation of the pile is observed at depth of 1.2 m (7.74b), and gradually diminishes to 0 mm as the depth increases.
It can be seen from Figure 21 that the distribution of horizontal deformation of the specimen is significantly different from the those of previous test and traditional theory of soil-pile system [38,39,40]. The traditional distribution assuming the maximum horizontal deformation is occurred at pile head, is also shown in Figure 21 with a dashed line. To be specific, the maximum horizontal deformation of pile in this test is occurred in the pile body rather than at the pile head. Under the displacement load of +12 mm, the maximum deformation of pile body reaches +11.08 mm, which is far larger than that of the pile head (+1.82 mm); under the displacement of +14 mm and +16 mm, they reach +15.38 mm and +21.62 mm respectively, which even exceed their displacement loads.
In Figure 21, the significant difference between the traditional theory and this test is caused by the unbalance of earth pressure on the front and back of the abutment and the movement of soil around the pile. When the specimen moves to the positive direction, then a gap is formed between the pile and front soil. The gap will be filled by the soil of backfill due to the difference earth pressure that is shown in Figure 22. This will induce the residual deformation greatly in the positive direction. The residual deformation grows constantly and accumulatively under the reciprocating loads. Here we define the growing phenomenon as the ratcheting effect of deformation or accumulative deformation.
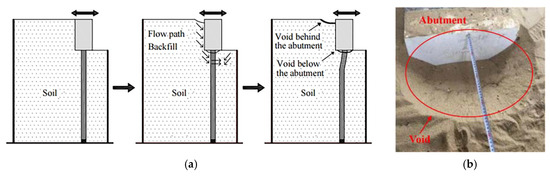
Figure 22.
Void formation. (a) Process of void formation. (b) Void behind the abutment.
In practical engineering, when the integral abutment moves towards the bridge span due to reduction in temperature or concrete shrinkage, a gap develops between the abutment and backfill. Then under the action of vehicle weight and dead weights of backfill, the soil will fill the gap, which leads to the development of a void below the approach slab. This phenomenon was also observed in this experiment when the test specimen moves to the negative direction. Figure 22a shows the process of void formation, and Figure 22b shows a photo of void behind the abutment. Therefore, the reasons for bumping at bridge-head and settlement of soil are also related to the mechanical behavior of the soil-abutment-pile interaction in addition to the properties of soil. Besides the soil, the void phenomenon also occurs around the interface between abutment and pile, as shown in Figure 22a, which is caused by the reciprocating movements of pile and soil.
Horizontal Deformation under Negative Displacements
Figure 23 shows the distribution of horizontal deformation of specimen along the depth under the negative displacement loads. Figure 23a,b show the deformation under displacements of −2 mm~−10 mm and −10 mm~−16 mm respectively. In Figure 23a, the horizontal deformation of pile reaches the maximum negative value at pile head when the displacement load is less than −10 mm, and gradually diminishes as the pile depth increases. The distribution of deformation is a little similar to the test and traditional theory of soil-pile. However, when the displacement load rises to −10 mm, a turning point appears at the pile depth of 0.4 m (2.58b), as shown in Figure 23b. With the increase of displacement load, the horizontal deformation at the depth of 0.4 m declines and changes from the negative to the positive, and finally goes up to +11.83 mm when the displacement load reaches −16 mm. The phenomenon in Figure 23b is caused by the accumulative deformation.
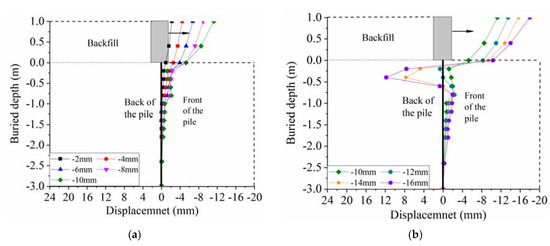
Figure 23.
Distribution of horizontal deformation of specimen under negative displacement loads. (a) Under displacement loads of −2 mm~−10 mm. (b) Under displacement loads of −10 mm~−16 mm.
3.4. Rotation of Abutment
Figure 24 shows the relationship between inclination and displacement of the abutment. In Figure 24, the inclinations basically linear increase with the increases of displacement load in both positive and negative directions. When the displacement load is relatively small, the inclinations are nearly the same. After the displacement load reaches ±8 mm, the significant difference of inclinations in the positive and negative directions begins to generate. Under the displacement of ±16 mm, the inclination is 0.75° in the positive direction, and 0.51° in the negative direction. The former is 1.47 times as much as the latter, which means the rotation of abutment when bridge expands is larger than that when bridge contracts. The mainly reason is caused by the earth pressure of backfill. When the abutment moves to positive direction, the earth pressure provide a resistant force at the low part of abutment. A moment generated by resistant force (earth pressure resultant force) and MTS push force makes the abutment rotate easily, as shown in Figure 25a. However, when the abutment moves to negative direction, the moment generated by the earth pressure is against the moment generated by MTS pull force, which will prevent abutment to rotate difficultly as shown in Figure 25b.
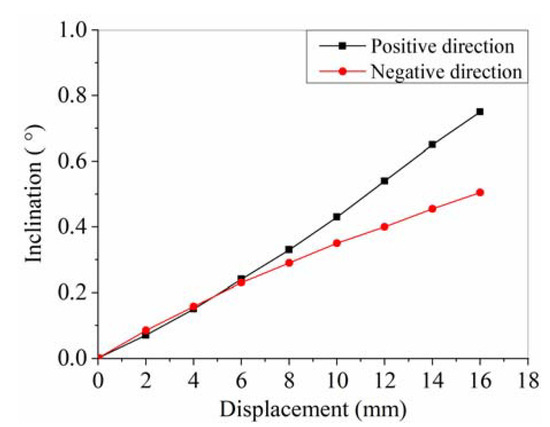
Figure 24.
Relationship between inclination and displacement of the abutment.
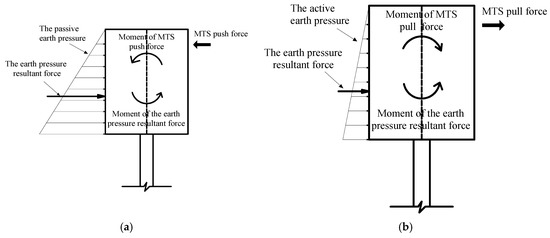
Figure 25.
Angle diagram. (a) Positive direction. (b) Negative direction.
4. Conclusions
A pseudo-static test combination with abutment, steel H-pile and soil was carried out to study the mechanical behavior of the soil-abutment-pile system under reciprocating low-cycle displacement load. The testing results were discussed and explored, including earth pressure behind abutment, hysteretic and skeleton curves, horizontal deformation of specimen and rotation of abutment. The typical observations and conclusions are described as follows.
- (1)
- The passive earth pressure of backfill is over 30 times of active earth pressure, and the passive earth pressure coefficient is larger than those by others (Burke-Chen, Barker, NCHRP, Dicleli, England, Massachusetts, Rankine theory, Coulomb theory and JTG D60-2015) due to the ratcheting effect of soil. The existing calculation method earth pressure of backfill behind abutment is not accurate for that of IAJB.
- (2)
- The earth pressure behind abutment has a typical triangular distribution when the horizontal displacement is small (less than 8 mm), and it shows a trapezoid distribution when the soil is close to abutment under a large horizontal displacement (larger than 8 mm). The earth pressure at horizontal distances of 0.6H and 1.4H from the back of the abutment is triangular under different displacements. The pile has little influence on the distribution of earth pressure when distance exceeds 1.4H.
- (3)
- The accumulative deformation is observed and the hysteretic curves are dramatically asymmetrical, but the soil-abutment-pile system shows a linear behavior yet.
- (4)
- The energy dissipation capacity when test specimen moves to the positive direction is much larger than that when specimen moves to the negative direction. The soil-abutment-pile system in IAJBs has favorable energy dissipation capacity and seismic behavior. The sum of horizontal deformation of abutment-pile-soil specimen are far larger than that of traditional pile-soil specimen due to the effect of accumulative deformation. Its maximum horizontal deformation occurs at the pile body rather than the pile head. The phenomenon of void is observed at the surface of the backfill and the interface between abutment and pile, which is also one of the reasons for bumping at bridge-end and settlement of soil.
- (5)
- The time-history horizontal accumulative deformation goes up with the increase of displacement load, and the growth rate becomes faster when the displacement load reaches 10 mm. The accumulative deformation is relatively small for the abutment, but it is large in the buried depth of 1.0b~3.0b for pile. The traditional calculated theory of deformation of pile is not appropriate to calculate the accumulative deformation. The noncumulative deformation is nearly the same as the deformation of traditional theory. The influence of accumulative deformation should be considered in practical engineering.
- (6)
- A significant difference of inclinations in the positive and negative directions increases when the displacement load is relatively large. The rotation of abutment when bridge expands is larger than that when bridge contracts.
Author Contributions
All authors substantially contributed to this work. Y.L. designed and fabricated the pile model. Y.L. and Y.S. designed the experiment. Y.S. and G.C. performed the experiments and analysis. Y.S. and F.H. wrote the paper. H.T. and B.B. revised and finalized the paper. All authors helped with the writing of the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China with Grant Numbers 51578161, and by the Fuzhou Technology Bureau with Grant Number 2018-G-63.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kunin, J.; Alampalli, S. Integral Abutment Bridges: Current Practice in United States and Canada. J. Perform. Constr. Facil. 2000, 14, 104–111. [Google Scholar] [CrossRef]
- Frangi, A.; Collin, P.; Geier, R. Bridges with Integral Abutments: Introduction. Struct. Eng. Int. 2011, 21, 144. [Google Scholar] [CrossRef]
- White, H.; Pétursson, H.; Collin, P. Integral Abutment Bridges: The European Way. Pract. Period. Struct. Des. Constr. 2010, 15, 201–208. [Google Scholar] [CrossRef]
- Hassiotis, S.; Roman, E. A survey of current issues on the use of integral abutment bridges. Bridge Struct. 2005, 1, 81–101. [Google Scholar] [CrossRef]
- Jimin, H.; Carol, S.; Catherine, F. Behavior of an Integral Abutment Bridge in Minnesota, US. Struct. Eng. Int. 2011, 21, 320–331. [Google Scholar]
- Chen, B.C.; Zhuang, Y.Z.; Huang, F.Y.; Briseghella, B. Jointless Bridges, 2nd ed.; China Communication Press: Beijing, China, 2019. [Google Scholar]
- Guo, P.X.; Xiao, Y.; Kunnath, S.K. Performance of laterally loaded H-piles in sand. Soil Dyn. Earthq. Eng. 2014, 67, 316–325. [Google Scholar] [CrossRef]
- Huntley, S.A.; Valsangkar, A.J. Behaviour of H-piles supporting an integral abutment bridge. Can. Geotechnol. J. 2014, 51, 713–734. [Google Scholar] [CrossRef]
- Burdette, E.; Ingram, E.; Tidwell, J.; Goodpasture, D.; Deatherage, J.; Howard, S. Behavior of Integral Abutments Supported by Steel H-Piles. Transp. Res. Rec. J. Transp. Res. Board 2004, 1892, 24–28. [Google Scholar] [CrossRef]
- Luo, X.Y.; Huang, F.Y.; Zhuang, Y.Z.; Wu, S.W.; Qian, H.M. Modified Calculations of Lateral Displacement and Soil Pressure of Pile Considering Pile-Soil Interaction under Cyclic Loads. J. Test. Eval. 2019, 49. [Google Scholar] [CrossRef]
- Huang, J.; Shield, C.K.; French, C.E.W. Parametric Study of Concrete Integral Abutment Bridges. J. Bridge Eng. 2008, 13, 511–526. [Google Scholar] [CrossRef]
- Chen, Y.F. Important Considerations, Guidelines, and Practical Details of Integral Bridges. J. Eng. Technol. 1997, 14, 16–19. [Google Scholar]
- England, G.L.; Tsang, N.C.M.; Bush, D.I. Integral Bridges: A Fundamental Approach to the Time–Temperature Loading Problem; Thomas Telford: London, UK, 2000; pp. 151–152. [Google Scholar]
- Hong, J.X.; Peng, D.W.; Wang, X.H. Passive Earth Pressure Behind Abutment of Integral Abutment Bridges. J. Fuzhou Univ. (Nat. Sci.) 2003, 31, 721–725. (In Chinese) [Google Scholar]
- Peng, D.W.; Hong, J.X. Research on Simplified Calculating Model of Integral Abutment Bridges. Highway 2009, 54, 34–39. (In Chinese) [Google Scholar]
- Peng, D.W.; Chen, X.D.; Yuan, Y. Study on Seasonal Fluctuation of Earth Pressure Behind the Abutment. Chin. J. Geotechnol. Eng. 2003, 25, 135–139. (In Chinese) [Google Scholar]
- Yu, T.L.; Zhou, T.; Jiang, L.D.; Zhang, J.H. Study of Calculating Methods for Earth Pressure Behind Abutment of Integral Abutment Bridge Under Action of Rising Temperatures. Bridge Constr. 2010, 1, 29–35. (In Chinese) [Google Scholar]
- Janjic, D.; Bokan, H. Erection Control, TDV’s unique tool solution for bridge design and construction. IABSE Symp. Rep. 2006, 92, 97–104. [Google Scholar] [CrossRef]
- David, T.K.; Forth, J.P. Implementation of linear numerical analysis for integral abutment bridge-soil interaction. IEEE Colloq. Humanit. Sci. Eng. 2011, 82–87. [Google Scholar] [CrossRef]
- Take, W.A.; Bolton, M.D. Seasonal ratcheting and softening in clay slopes, leading to first-time failure. Géotechnique 2011, 61, 757–769. [Google Scholar] [CrossRef]
- Frosch, R.J.; Kreger, M.E.; Talbot, A.M. Earthquake Resistance of Integral Abutment Bridges. Ph.D. Thesis, Purdue University, Purdue, Germany, 2009. [Google Scholar]
- Guo, C.; Fu, B.Y.; Yuan, H.; Gong, W.M. Application and Field Tests of Cap-Pile Combined Foundation with Reversed Construction. Chin. J. Geotechnol. Eng. 2016, 38, 2085–2092. (In Chinese) [Google Scholar]
- Test Method of Soils for Highway Engineering; JTG E40-2007; China Communications Press: Beijing, China, 2007.
- Kulhawy, F.H.; Phoon, K.K. On the Evolution from Deterministic to Reliability-Based Foundation Design; Thomas Telford: London, UK, 2003; pp. 27–36. [Google Scholar]
- Zhao, M.H.; Xiao, Y.; Chen, C.F.; He, W. Analysis of Deformation on Soft Subsoil Around Bridge Abutment Considering Soil Creep Property. China J. Highw. Transp. 2006, 19, 56–61. (In Chinese) [Google Scholar]
- Huang, F.Y.; Wu, S.W.; Luo, X.Y.; Chen, B.C.; Lin, Y.W. Pseudo-static low cycle test on the mechanical behavior of PHC pipe piles with consideration of soil-pile interaction. Eng. Struct. 2018, 171, 992–1006. [Google Scholar] [CrossRef]
- Lou, M.L.; Wang, W.J.; Zhu, T.; Mang, H.C. Soil lateral boundary effect in shaking table model test of soil-structure system. Earthq. Eng. Eng. Dyn. 2000, 20, 30–36. [Google Scholar]
- Burke, J.R.; Martin, P. Design of integral concrete bridges. Concr. Int. 1993, 15, 37–42. [Google Scholar]
- Barker, R.M.; Duncan, J.M.; Rojiani, K.B.; Ooi PS, K.; Tan, C.K.; Kim, S.G. Manuals for the Design of Bridge Foundations: Shallow Foundations, Driven Piles, Retaining Walls and Abutment, Drilled Shafts, Estimating Tolerable Movements, and Load Factor Design Specifications and Commentary; Transportation Research Board: Washington, DC, USA, 1991. [Google Scholar]
- Dicleli, M. A rational design approach for prestressed-concrete-girder integral bridges. Eng. Struct. 2000, 22, 230–245. [Google Scholar] [CrossRef]
- Helmut, E. Geotechnical aspects of the mass-highway guidelines for integral abutment Bridges. In Design of Integral Abutment Bridges, BSCE/ASCE Geotechnical and Structural Groups Seminar; Bentley College: Waltham, MA, USA, 1999; pp. 207–224. [Google Scholar]
- General Specifications for Design of Highway Bridges and Culverts; JTG D60-201; China Communications Press: Beijing, China, 2015.
- Dicleli, M.; Albhaisi, S.M. Performance of Abutment–Backfill System Under Thermal Variations in Integral Bridges Built on Clay. Eng. Struct. 2004, 26, 949–962. [Google Scholar] [CrossRef]
- England, G.L.; Dunstan, T.; Tsang, C.M. Ratcheting flow of granular materials. In Static and Dynamic Properties of Gravelly Soils; ASCE: Reston, VA, USA, 2014. [Google Scholar]
- Anagnostopoulos, S.A. Equivalent Viscous Damping for Modeling Inelastic Impacts in Earthquake Pounding Problems. Earthq. Eng. Struct. Dyn. 2010, 33, 897–902. [Google Scholar] [CrossRef]
- Wijesundara, K.K.; Nascimbene, R.; Sullivan, T.J. Equivalent viscous damping for steel concentrically braced frame structures. Bull. Earthq. Eng. 2011, 9, 1535–1558. [Google Scholar] [CrossRef]
- Huang, F.Y.; Qian, H.M.; Zhuang, Y.Z. Experimental Study on the Dynamic Response of PHC Pipe-Piles in Liquefiable Soil. J. Test. Eval. 2017, 45, 230–241. [Google Scholar] [CrossRef]
- Novak, M.; Nogami, T. Soil-pile interaction in horizontal vibration. Earthq. Eng. Struct. Dyn. 1977, 5, 263–281. [Google Scholar] [CrossRef]
- Allani, M.; Holeyman, A. Flexural analysis in dynamic pinned head pile testing. Geotechnol. Geol. Eng. 2014, 32, 59–70. [Google Scholar] [CrossRef]
- Makris, N.; Gazetas, G. Dynamic pile-soil-pile interaction. Part II: Lateral and seismic response. Earthq. Eng. Struct. Dyn. 2010, 21, 145–162. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).