Dynamic Stability of Bi-Directional Functionally Graded Porous Cylindrical Shells Embedded in an Elastic Foundation
Abstract
1. Introduction
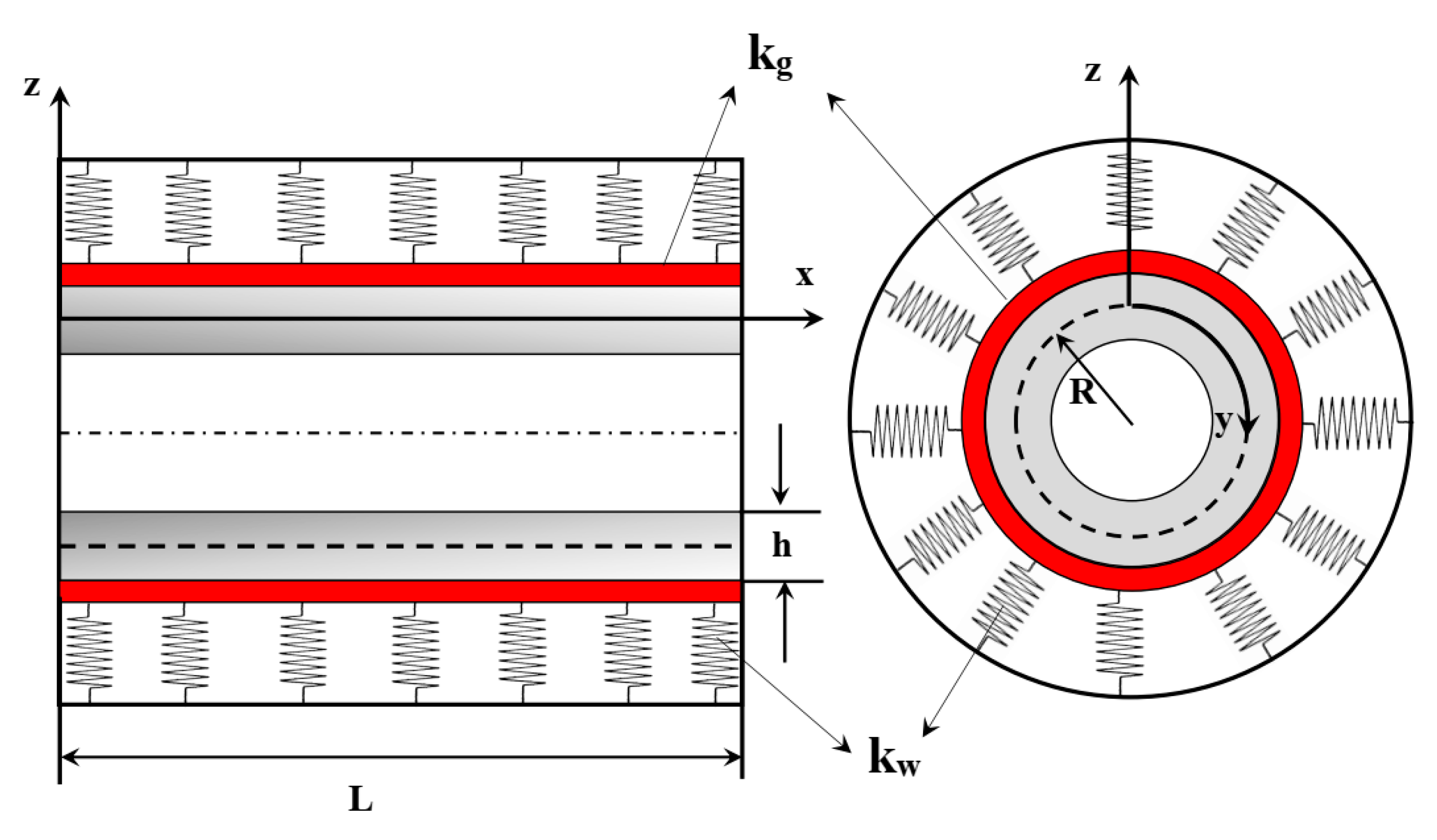
2. Governing Equations of the Problem
- ➢
- Simply-Simply (S-S) supports
- ➢
- Clamped-Clamped (C-C) supports
- ➢
- Clamped-simply (C-S) supports
3. Solution Procedure
3.1. The GDQ Method
3.2. Bolotin Method
4. Numerical Investigation
4.1. Validation
4.2. Parametric Study
5. Conclusions
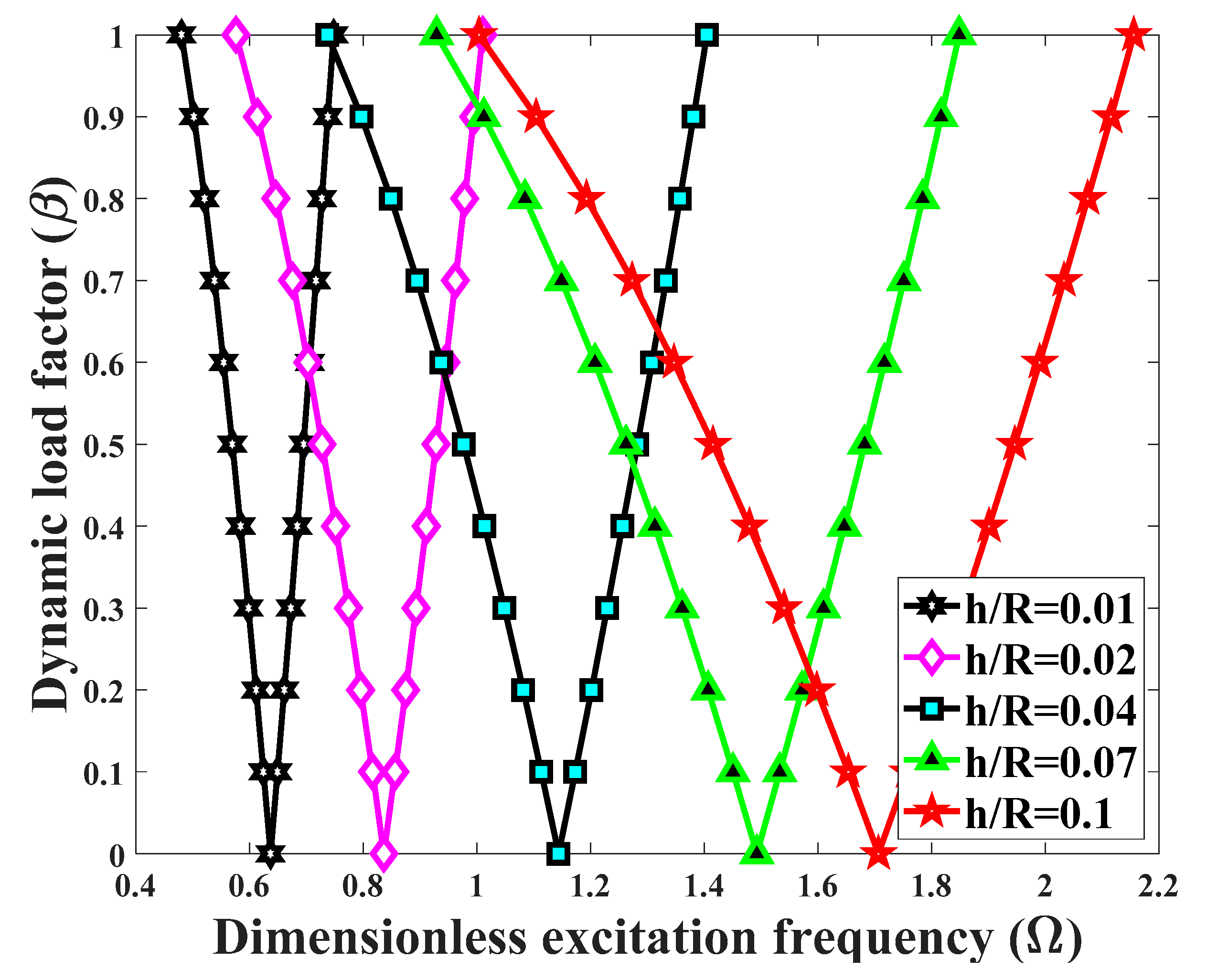
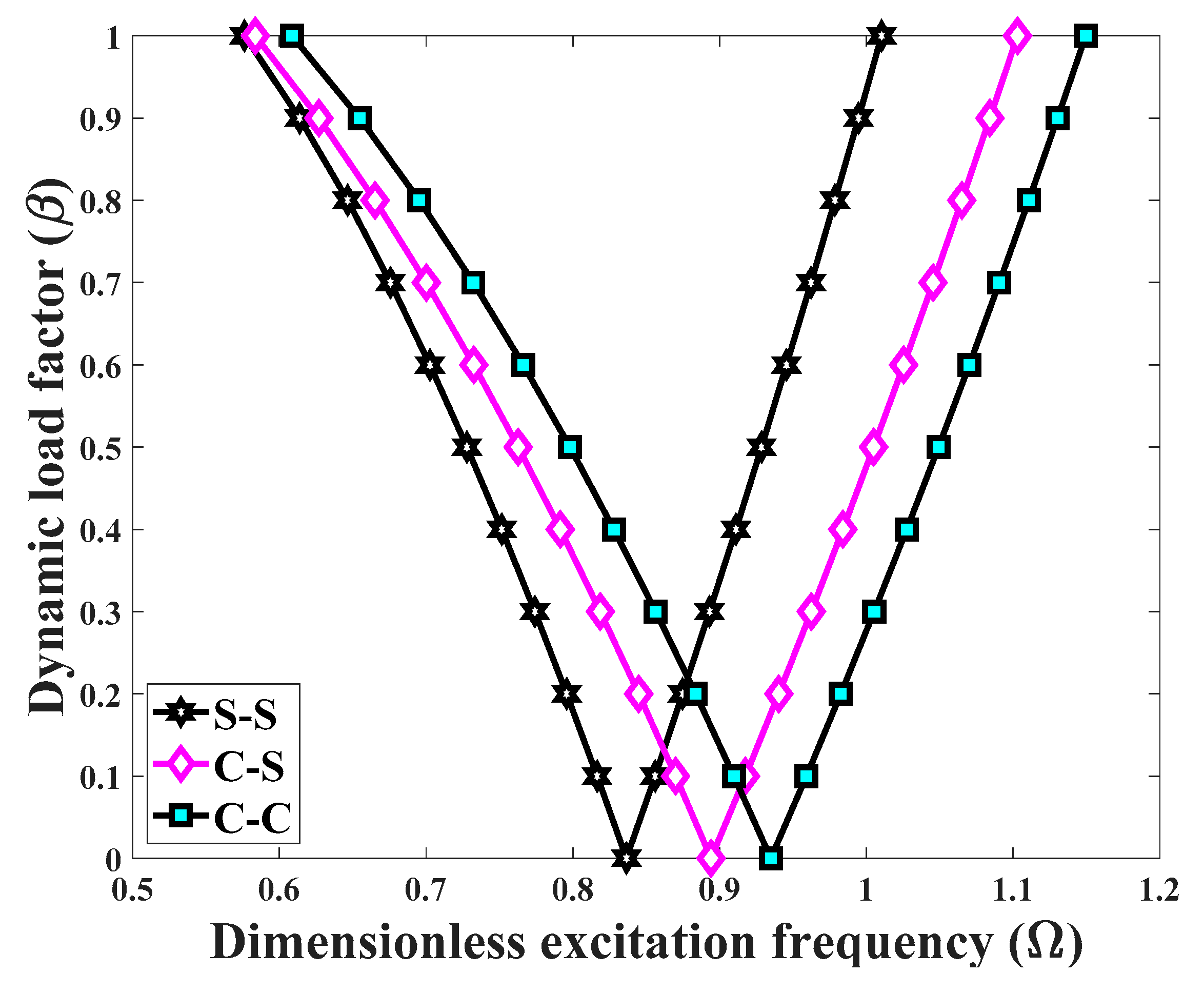
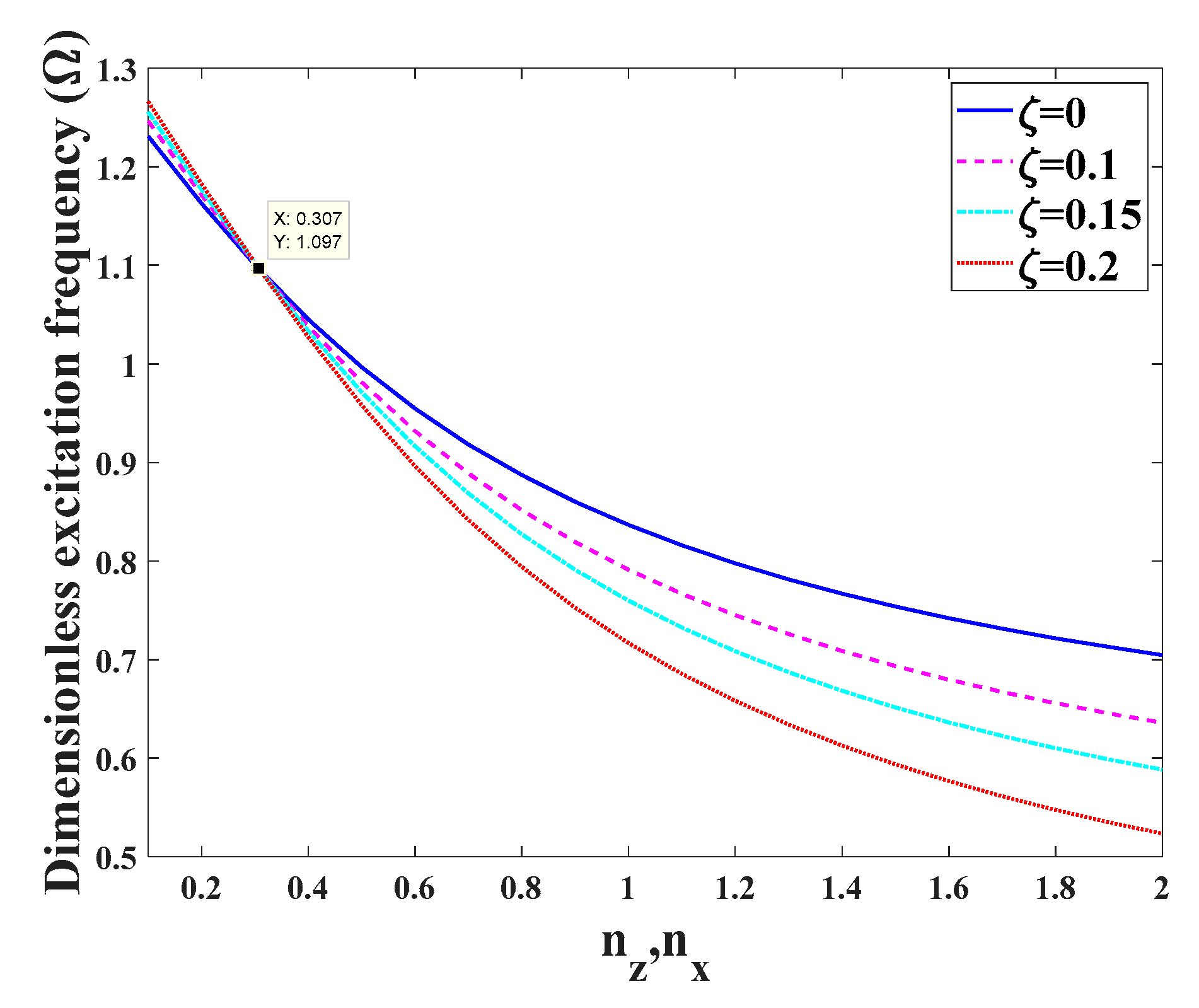
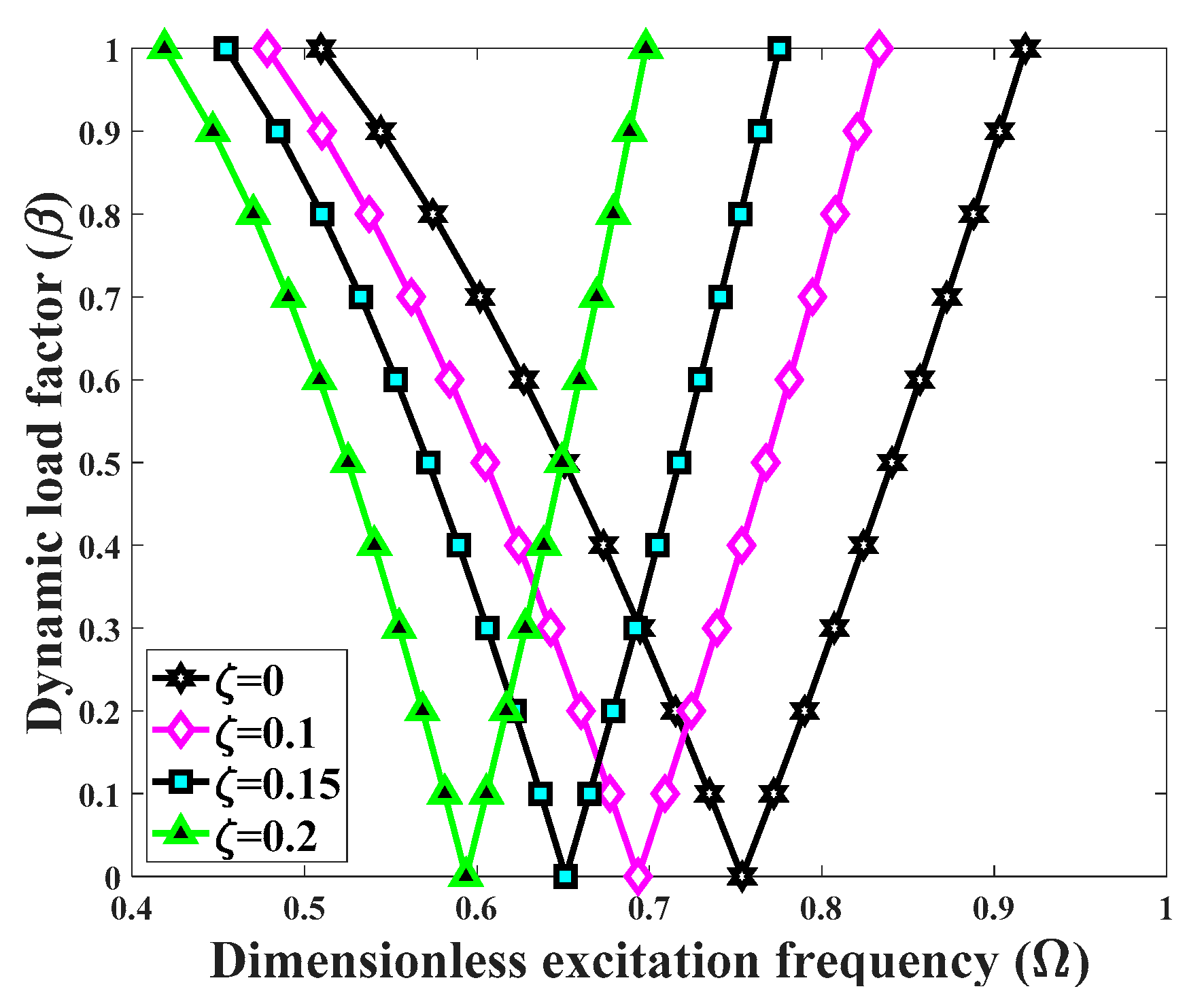
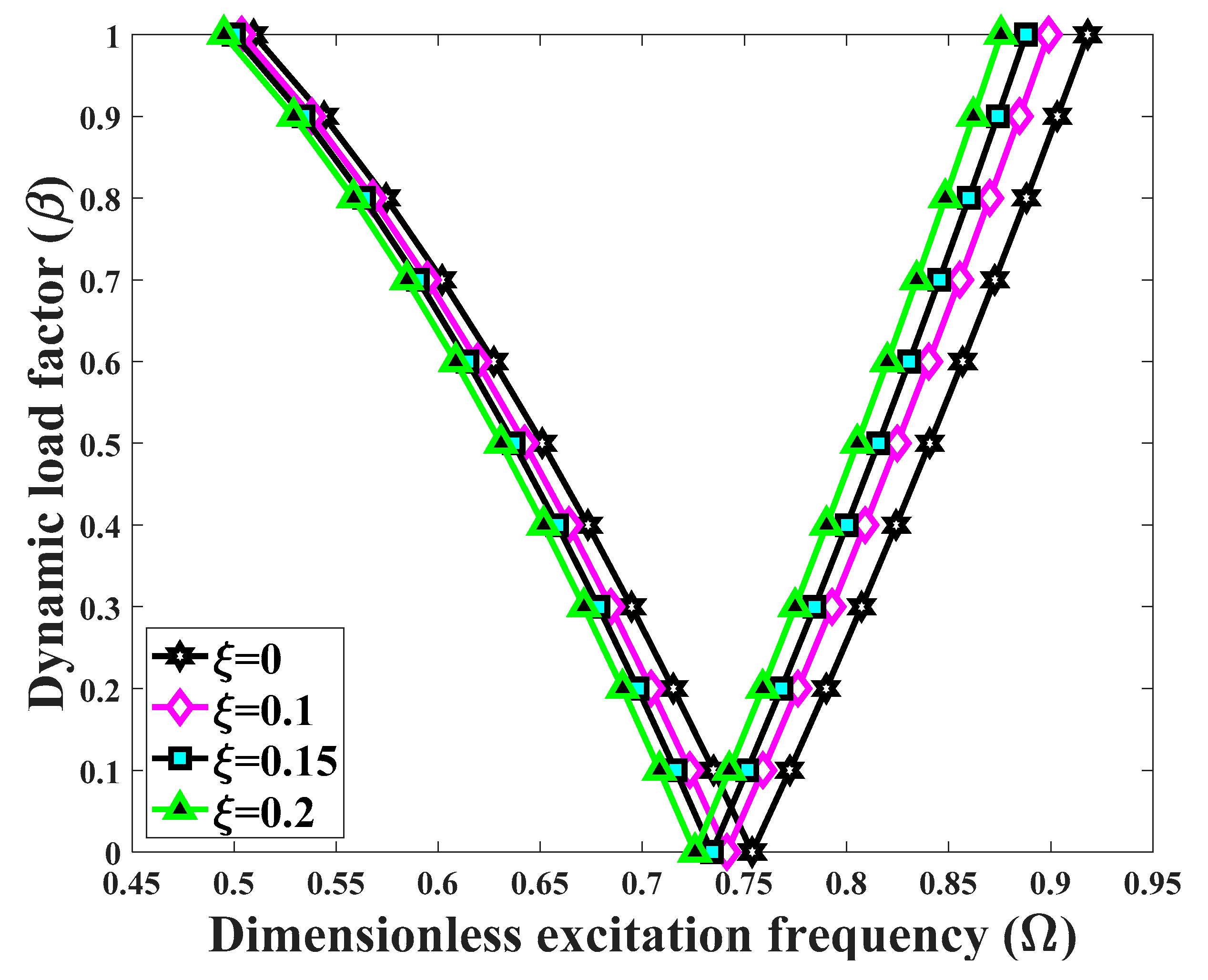
- An increased thickness-to-radius ratio causes a general shift of the DIR origin towards higher excitation frequencies. Moreover, the DIR gets wider at a certain value of the dynamic load factor.
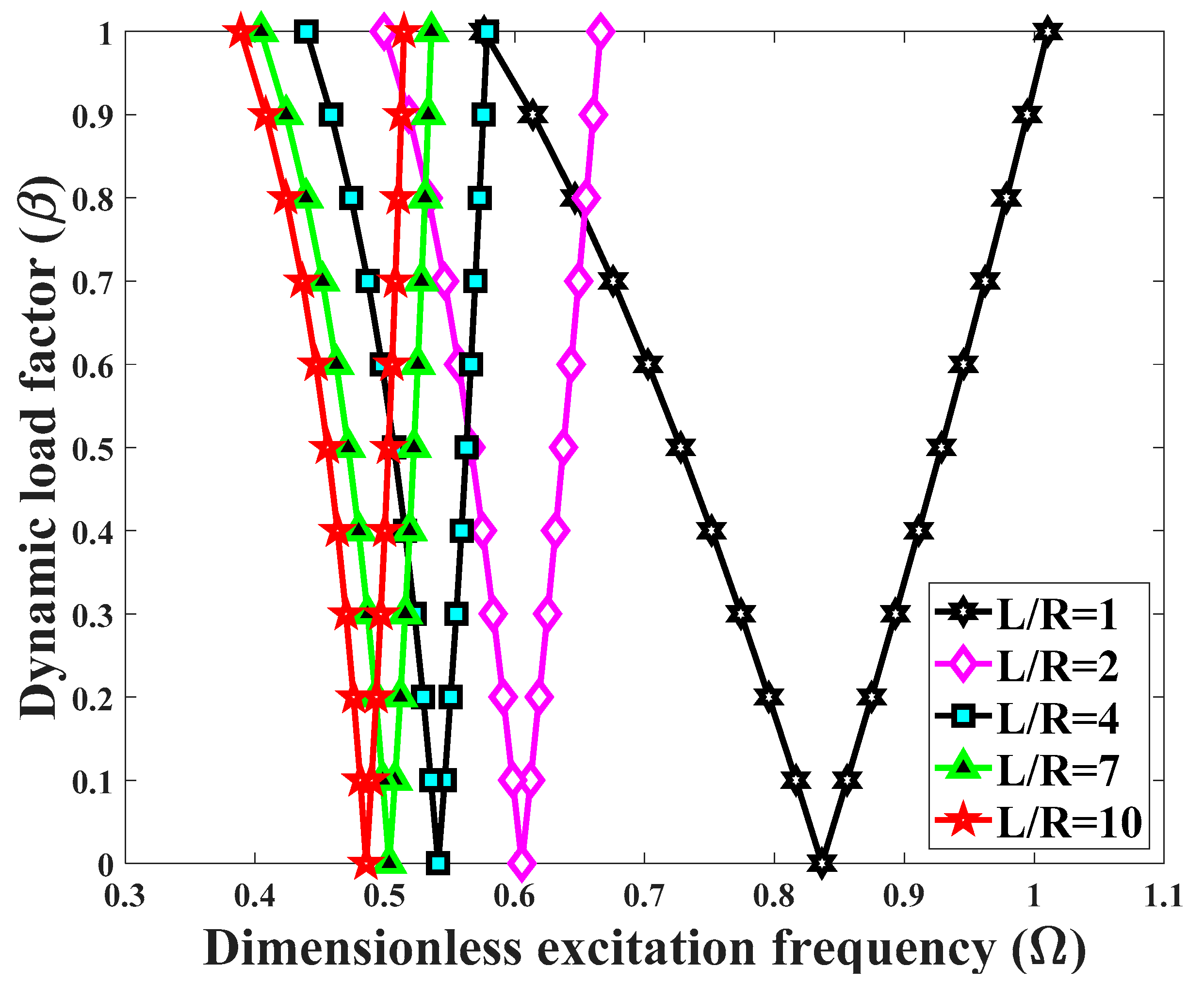
- An increased length-to-radius dimensionless ratio moves the DIR origin towards lower excitation frequencies, whereas the DIR gets smaller.
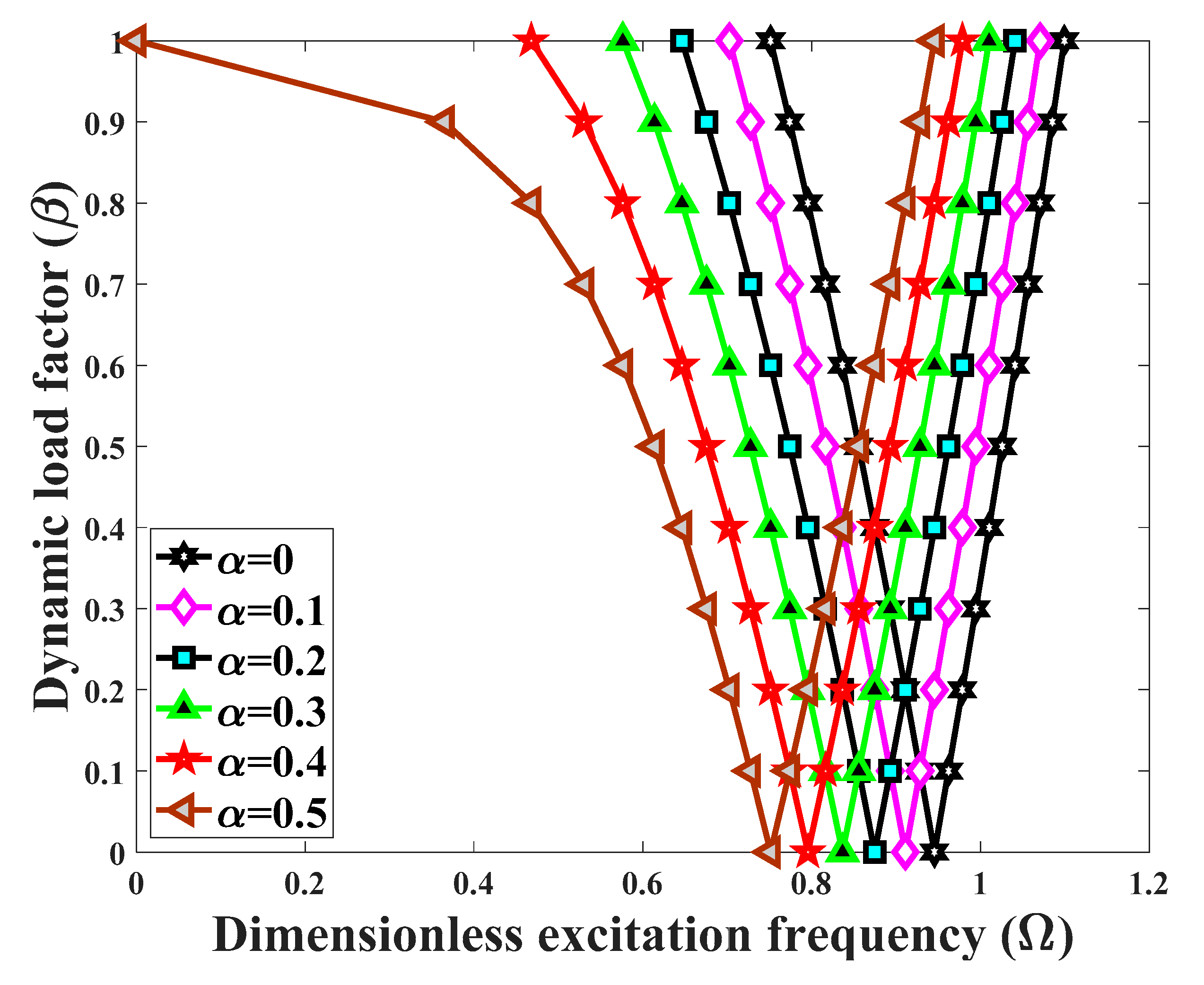
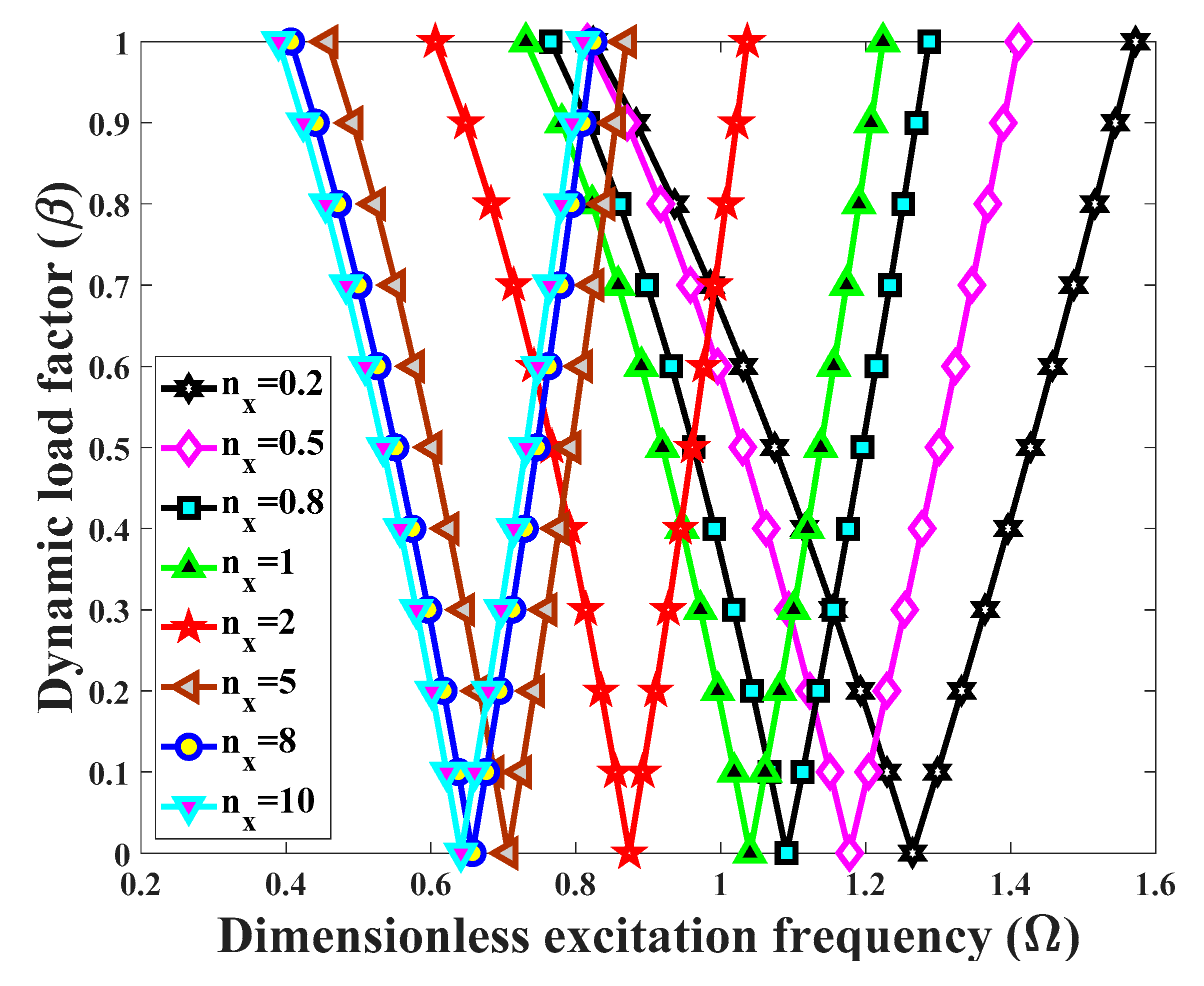
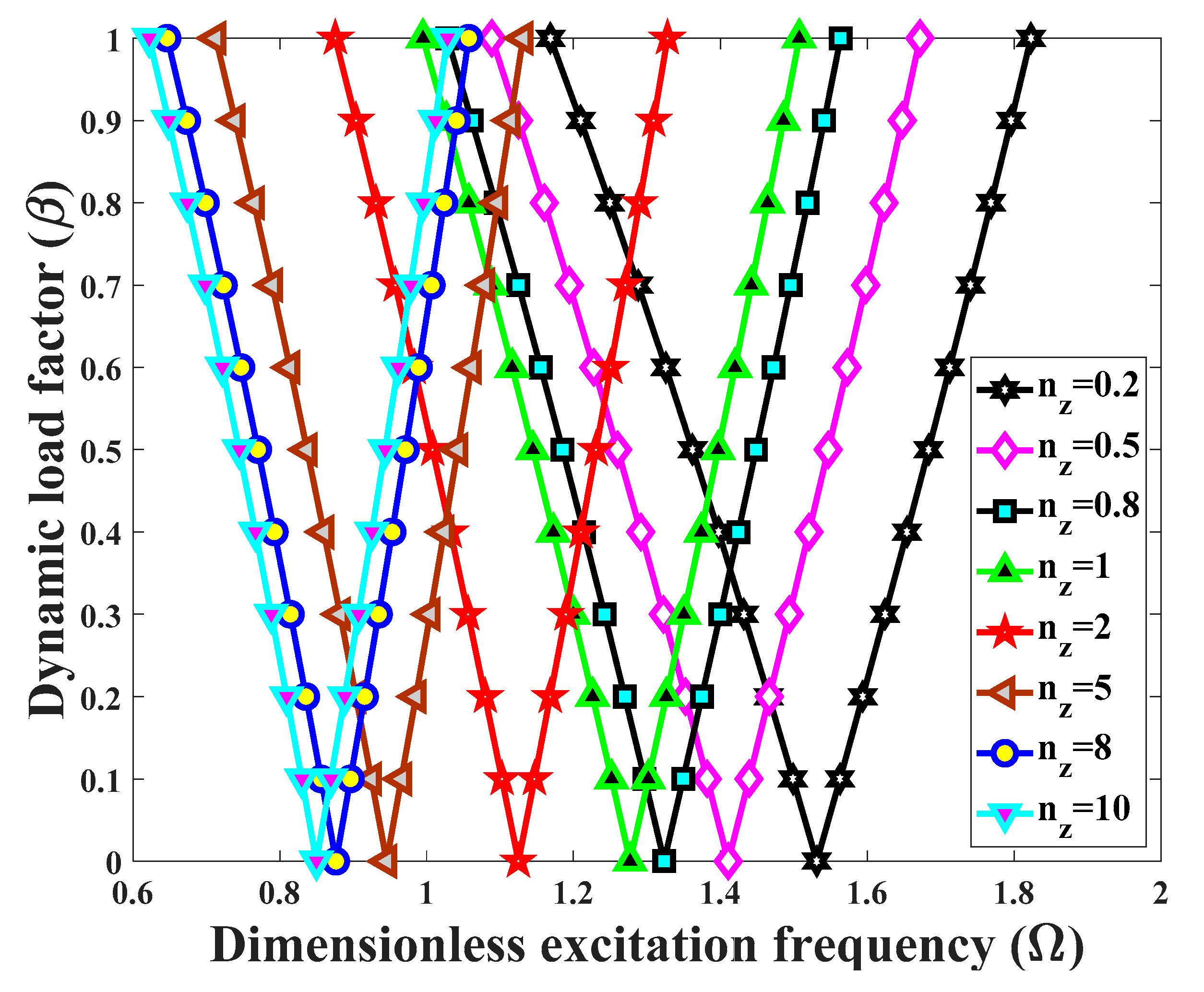
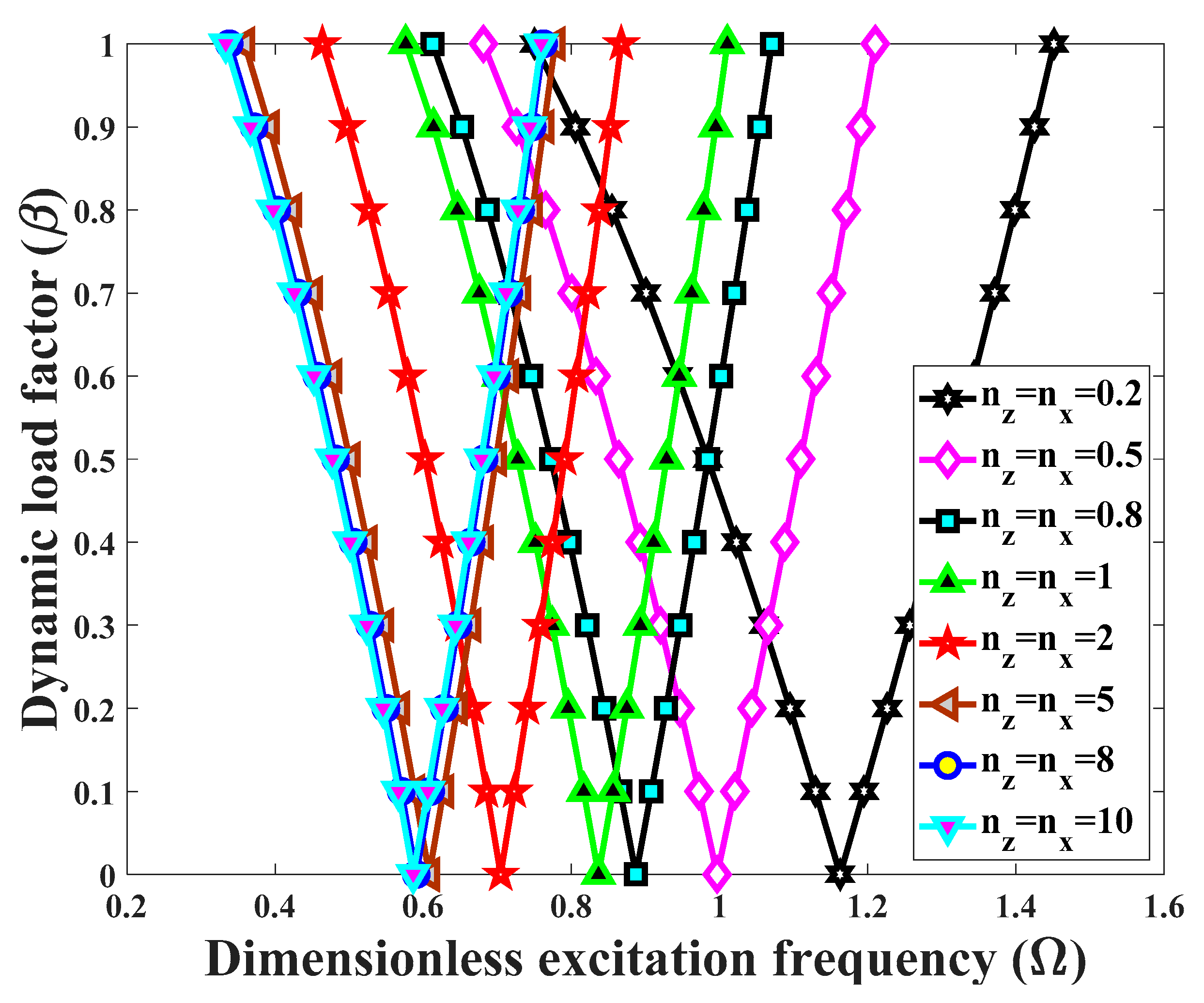
- A simultaneous increase of longitudinal and transverse power indexes yields an overall decrease in the excitation frequencies associated with the DIR origin.
- The control of the dynamic instability for a BD-FG cylindrical shell, is convenient for an appropriate selection of the power indexes.
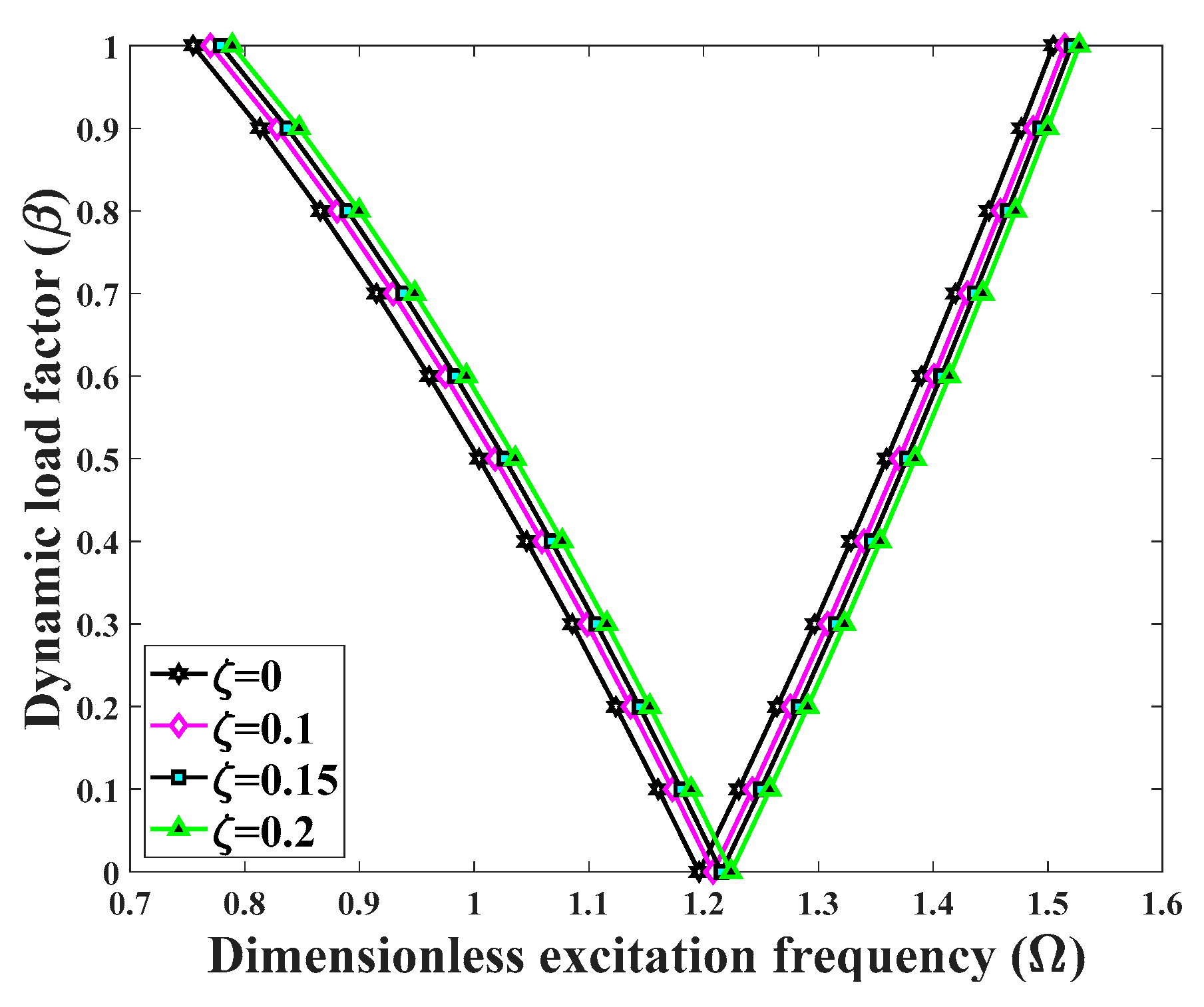
- BD-FG cylindrical shells with a simply support at both ends are more unstable than the clamped-clamped or clamped-simply supported structures, because of their higher deformability.
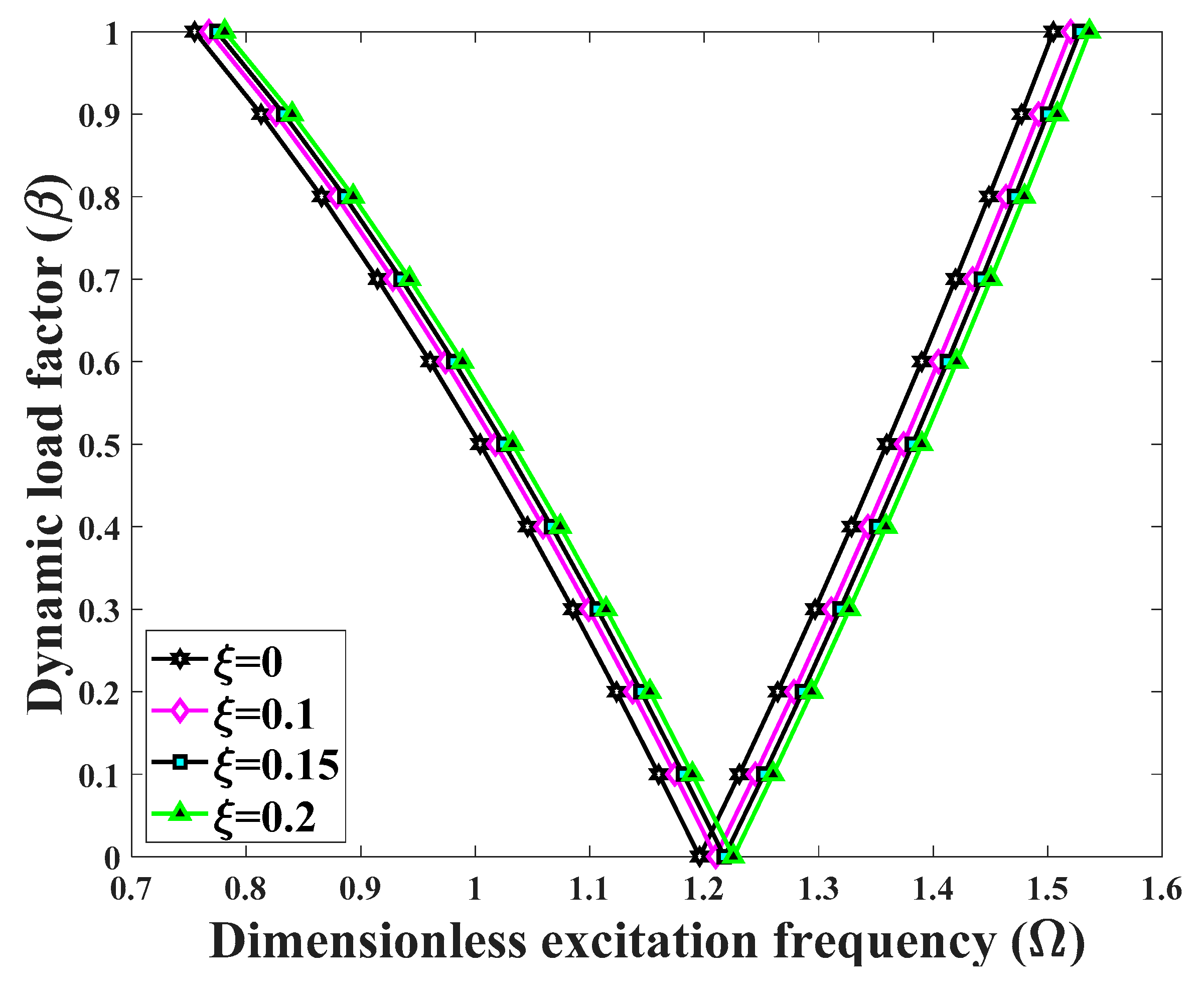
- The effect of coefficients and type of porosity on the structural DIR depend on the extent of the longitudinal and transverse power law indexes. There exists a certain value for these indexes, for which the excitation frequencies corresponding to the DIR can invert their behavior.
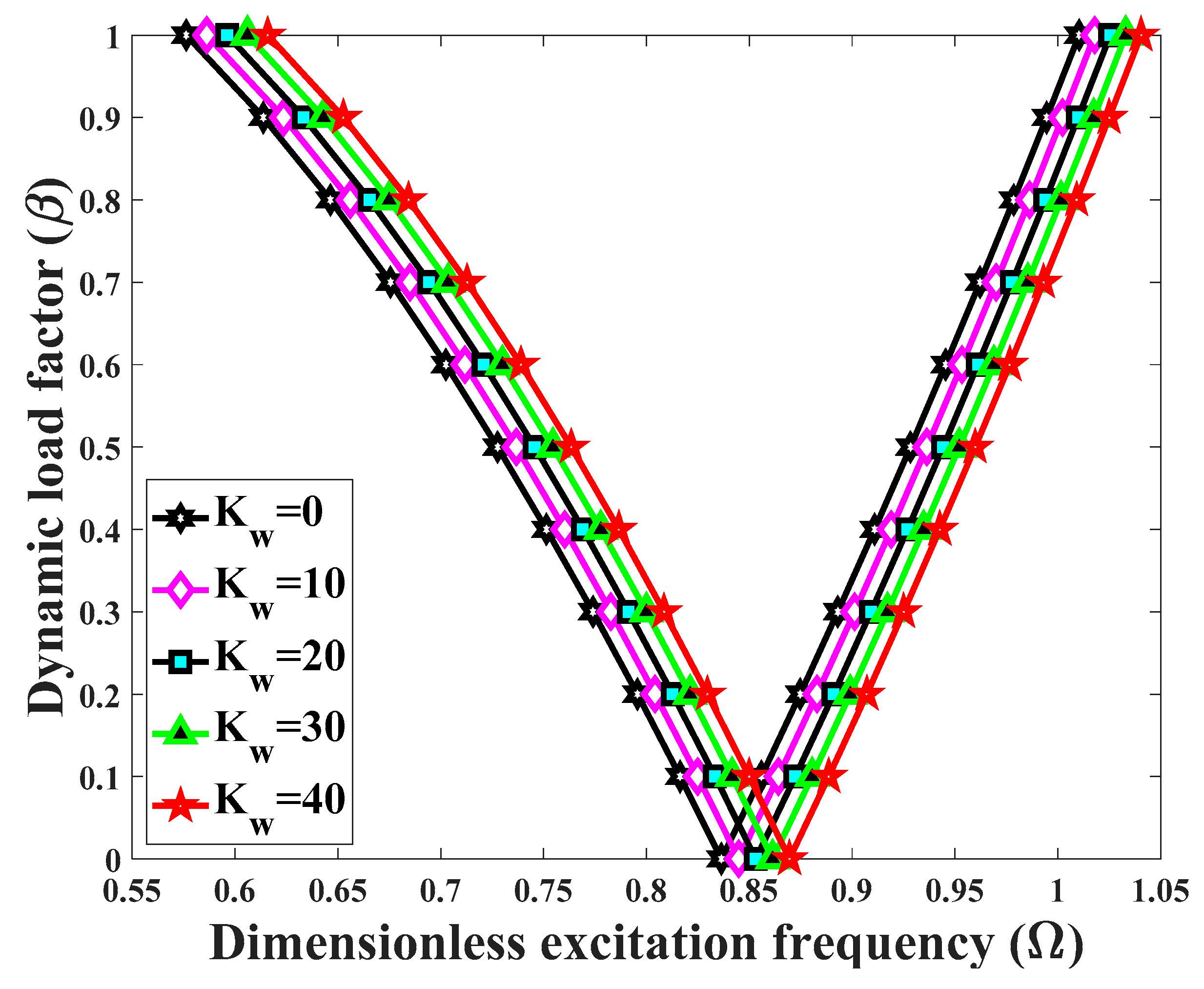
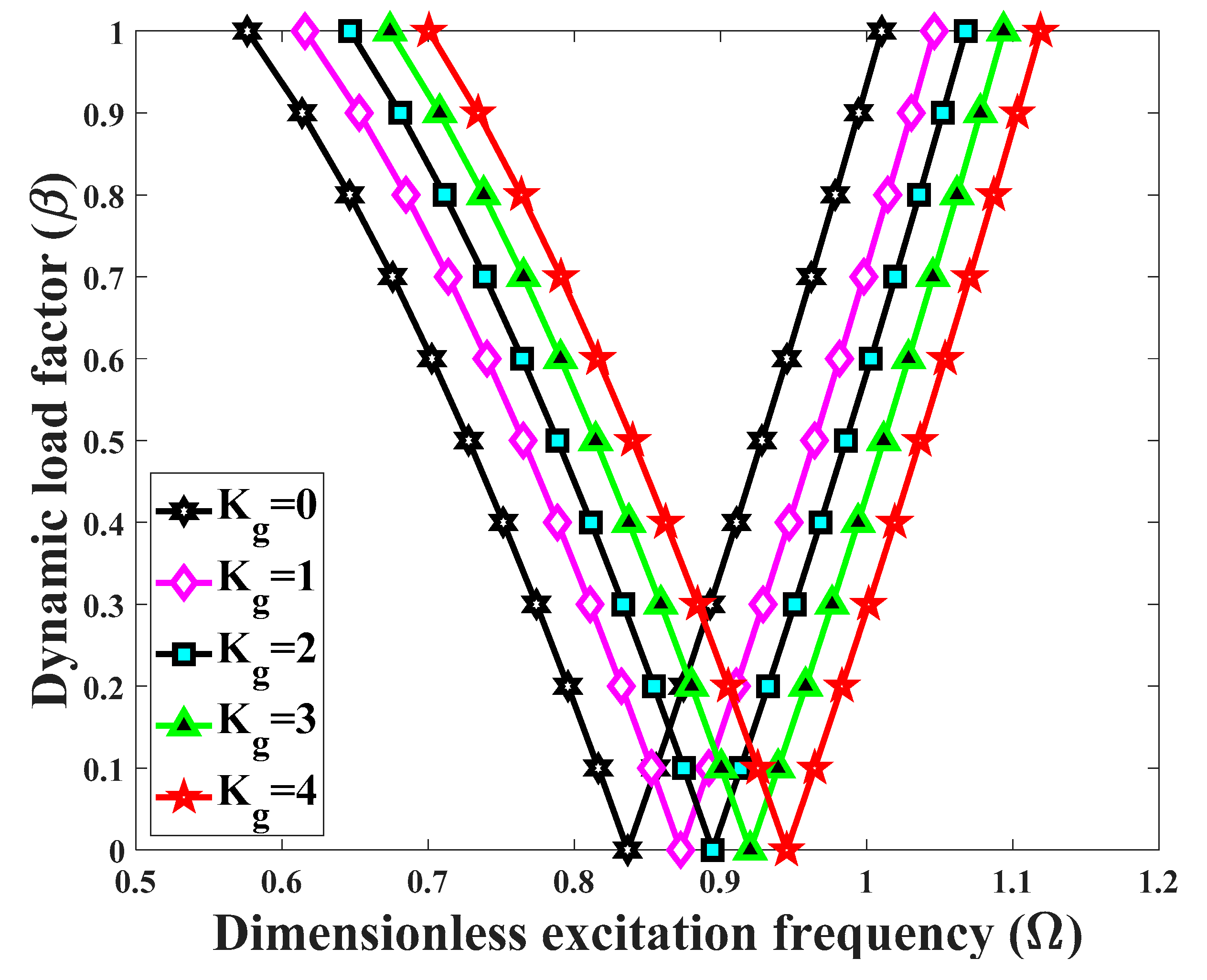
- A general increase in the elastic foundation coefficients yields higher excitation structural frequencies especially when a Pasternak foundation is assumed instead of a Winkler foundation. Anyway, the presence of an elastic foundation makes the structure stiffer and more stable.
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
References
- Birman, V.; Byrd, L.W. Modeling and analysis of functionally graded materials and structures. Appl. Mech. Rev. 2007, 60, 195–216. [Google Scholar] [CrossRef]
- Miyamoto, Y.; Kaysser, W.A.; Rabin, B.H.; Kawasaki, A.; Ford, R.G. Functionally Graded Materials: Design, Processing and Applications; Springer Science & Business Medi: New York, NY, USA, 2013. [Google Scholar]
- Noda, N. Thermal stresses in functionally graded materials. J. Therm. Stress. 1999, 22, 477–512. [Google Scholar] [CrossRef]
- Shen, H.S. Functionally Graded Materials: Nonlinear Analysis of Plates and Shells; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Du, C.; Li, Y.; Jin, X. Nonlinear forced vibration of functionally graded cylindrical thin shells. Thin-Walled Struct. 2014, 78, 26–36. [Google Scholar] [CrossRef]
- Rahimi, G.H.; Ansari, R.; Hemmatnezhad, M. Vibration of functionally graded cylindrical shells with ring support. Sci. Iran. 2011, 18, 1313–1320. [Google Scholar] [CrossRef]
- Ghasemi, A.R.; Mohandes, M.; Dimitri, R.; Tornabene, F. Agglomeration effects on the vibrations of CNTs/fiber/polymer/metal hybrid laminates cylindrical shell. Compos. Part B Eng. 2019, 167, 700–716. [Google Scholar] [CrossRef]
- Bich, D.H.; van Dung, D.; Nam, V.H.; Phuong, N.T. Nonlinear static and dynamic buckling analysis of imperfect eccentrically stiffened functionally graded circular cylindrical thin shells under axial compression. Int. J. Mech. Sci. 2013, 74, 190–200. [Google Scholar] [CrossRef]
- Beni, Y.T.; Mehralian, F.; Zeighampour, H. The modified couple stress functionally graded cylindrical thin shell formulation. Mech. Adv. Mater. Struct. 2016, 23, 791–801. [Google Scholar] [CrossRef]
- da Silva, F.M.A.; Montes, R.O.P.; Goncalves, P.B.; del Prado, Z.J.G.N. Nonlinear vibrations of fluid-filled functionally graded cylindrical shell considering a time-dependent lateral load and static preload. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 230, 102–119. [Google Scholar] [CrossRef]
- Bich, D.H.; Nguyen, N.X. Nonlinear vibration of functionally graded circular cylindrical shells based on improved Donnell equations. J. Sound Vib. 2012, 331, 5488–5501. [Google Scholar] [CrossRef]
- Ghannad, M.; Rahimi, G.H.; Nejad, M.Z. Elastic analysis of pressurized thick cylindrical shells with variable thickness made of functionally graded materials. Compos. Part B Eng. 2013, 45, 388–396. [Google Scholar] [CrossRef]
- Jafari, A.A.; Khalili, S.M.R.; Tavakolian, M. Nonlinear vibration of functionally graded cylindrical shells embedded with a piezoelectric layer. Thin-Walled Struct. 2014, 79, 8–15. [Google Scholar] [CrossRef]
- Jin, G.; Xie, X.; Liu, Z. The Haar wavelet method for free vibration analysis of functionally graded cylindrical shells based on the shear deformation theory. Compos. Struct. 2014, 108, 435–448. [Google Scholar] [CrossRef]
- Liu, Y.Z.; Hao, Y.X.; Zhang, W.; Chen, J.; Li, S.B. Nonlinear dynamics of initially imperfect functionally graded circular cylindrical shell under complex loads. J. Sound Vib. 2015, 348, 294–328. [Google Scholar] [CrossRef]
- Mehralian, F.; Beni, Y.T. Size-dependent torsional buckling analysis of functionally graded cylindrical shell. Compos. Part B Eng. 2016, 94, 11–25. [Google Scholar] [CrossRef]
- Sheng, G.G.; Wang, X. Nonlinear response of fluid-conveying functionally graded cylindrical shells subjected to mechanical and thermal loading conditions. Compos. Struct. 2017, 168, 675–684. [Google Scholar] [CrossRef]
- Sheng, G.G.; Wang, X. The dynamic stability and nonlinear vibration analysis of stiffened functionally graded cylindrical shells. Appl. Math. Model. 2018, 56, 389–403. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, H.; Han, Q. Buckling of elastoplastic functionally graded cylindrical shells under combined compression and pressure. Compos. Part B Eng. 2015, 69, 120–126. [Google Scholar] [CrossRef]
- Sofiyev, A.H.; Hui, D. On the vibration and stability of FGM cylindrical shells under external pressures with mixed boundary conditions by using FOSDT. Thin-Walled Struct. 2019, 134, 419–427. [Google Scholar] [CrossRef]
- Sun, J.; Xu, X.; Lim, C.W.; Qiao, W. Accurate buckling analysis for shear deformable FGM cylindrical shells under axial compression and thermal loads. Compos. Struct. 2015, 123, 246–256. [Google Scholar] [CrossRef]
- Huang, H.; Han, Q.; Wei, D. Buckling of FGM cylindrical shells subjected to pure bending load. Compos. Struct. 2011, 93, 2945–2952. [Google Scholar] [CrossRef]
- Wali, M.; Hentati, T.; Jarraya, A.; Dammak, F. Free vibration analysis of FGM shell structures with a discrete double directors shell element. Compos. Struct. 2015, 125, 295–303. [Google Scholar] [CrossRef]
- Mohammadi, M.; Arefi, M.; Dimitri, R.; Tornabene, F. Higher-Order Thermo-Elastic Analysis of FG-CNTRC Cylindrical Vessels Surrounded by a Pasternak Foundation. Nanomaterials 2019, 9, 79. [Google Scholar] [CrossRef] [PubMed]
- Tornabene, F.; Brischetto, S.; Fantuzzi, F.; Viola, E. Numerical and exact models for free vibration analysis of cylindrical and spherical shell panels. Compos. Part B Eng. 2015, 3675, 231–250. [Google Scholar] [CrossRef]
- Arefi, M.; Mohammadi, M.; Tabatabaeian, A.; Dimitri, R.; Tornabene, F. Two-dimensional thermo-elastic analysis of FG-CNTRC cylindrical pressure vessels. Steel Compos. Struct. 2018, 27, 525–536. [Google Scholar]
- Nejati, M.; Dimitri, R.; Tornabene, F.; Yas, M.H. Thermal buckling of nanocomposite stiffened cylindrical shells reinforced by functionally Graded wavy Carbon NanoTubes with temperature-dependent properties. Appl. Sci. 2017, 7, 1223. [Google Scholar] [CrossRef]
- Aragh, B.S.; Hedayati, H. Static response and free vibration of two-dimensional functionally graded metal/ceramic open cylindrical shells under various boundary conditions. Acta Mech. 2012, 223, 309–330. [Google Scholar] [CrossRef]
- Zafarmand, H.; Hassani, B. Analysis of two-dimensional functionally graded rotating thick disks with variable thickness. Acta Mech. 2014, 225, 453–464. [Google Scholar] [CrossRef]
- Ebrahimi, M.J.; Najafizadeh, M.M. Free vibration analysis of two-dimensional functionally graded cylindrical shells. Appl. Math. Model. 2014, 38, 308–324. [Google Scholar] [CrossRef]
- Allahkarami, F.; Satouri, S.; Najafizadeh, M.M. Mechanical buckling of two-dimensional functionally graded cylindrical shells surrounded by Winkler–Pasternak elastic foundation. Mech. Adv. Mater. Struct. 2016, 23, 873–887. [Google Scholar] [CrossRef]
- Satouri, S.; Kargarnovin, M.H.; Allahkarami, F.; Asanjarani, A. Application of third order shear deformation theory in buckling analysis of 2D-functionally graded cylindrical shell reinforced by axial stiffeners. Compos. Part B Eng. 2015, 79, 236–253. [Google Scholar] [CrossRef]
- Li, L.; Hu, Y. Torsional vibration of bi-directional functionally graded nanotubes based on nonlocal elasticity theory. Compos. Struct. 2017, 172, 242–250. [Google Scholar] [CrossRef]
- Kiran, M.C.; Kattimani, S.C. Assessment of porosity influence on vibration and static behaviour of functionally graded magneto-electro-elastic plate: A finite element study. Eur. J. Mech.-A/Solids 2018, 71, 258–277. [Google Scholar] [CrossRef]
- Kiran, M.C.; Kattimani, S.C.; Vinyas, M. Porosity influence on structural behaviour of skew functionally graded magneto-electro-elastic plate. Compos. Struct. 2018, 191, 36–77. [Google Scholar] [CrossRef]
- Barati, M.R.; Sadr, M.H.; Zenkour, A.M. Buckling analysis of higher order graded smart piezoelectric plates with porosities resting on elastic foundation. Int. J. Mech. Sci. 2016, 117, 309–320. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Wan, Y.H.; Zhang, Y.F. Vibrations of longitudinally traveling functionally graded material plates with porosities. Eur. J. Mech.-A/Solids 2017, 66, 55–68. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Zu, J.W. Vibration behaviors of functionally graded rectangular plates with porosities and moving in thermal environment. Aerosp. Sci. Technol. 2017, 69, 550–562. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, D. Free vibration of functionally graded porous cylindrical shell using a sinusoidal shear deformation theory. Aerosp. Sci. Technol. 2017, 66, 83–91. [Google Scholar] [CrossRef]
- Kiani, Y.; Dimitri, R.; Tornabene, F. Free vibration of FG-CNT reinforced composite skew cylindrical shells using the Chebyshev-Ritz formulation. Compos. Part B Eng. 2018, 147, 169–177. [Google Scholar] [CrossRef]
- Ghadiri, M.; SafarPour, H. Free vibration analysis of size-dependent functionally graded porous cylindrical microshells in thermal environment. J. Therm. Stress. 2017, 40, 55–71. [Google Scholar] [CrossRef]
- Barati, M.R.; Zenkour, A.M. Vibration analysis of functionally graded graphene platelet reinforced cylindrical shells with different porosity distributions. Mech. Adv. Mater. Struct. 2019, 26, 1580–1588. [Google Scholar] [CrossRef]
- Malikan, M.; Tornabene, F.; Dimitri, R. Nonlocal three-dimensional theory of elasticity for buckling behavior of functionally graded porous nanoplates using volume integrals. Mater. Res. Express 2018, 5, 095006. [Google Scholar] [CrossRef]
- Malikan, M.; Tornabene, F.; Dimitri, R. Effect of sinusoidal corrugated geometries on the vibrational response of viscoelastic nanoplates. Appl. Sci. 2018, 8, 1432. [Google Scholar] [CrossRef]
- Arefi, M.; Bidgoli, E.M.R.; Dimitri, R.; Tornabene, F. Free vibrations of functionally graded polymer composite nanoplates reinforced with graphene nanoplatelets. Aerosp. Sci. Technol. 2018, 81, 108–117. [Google Scholar] [CrossRef]
- Jouneghani, F.Z.; Dimitri, R.; Tornabene, F. Structural response of porous FG nanobeams under hygro-thermo-mechanical loadings. Compos. Part B Eng. 2018, 152, 71–78. [Google Scholar] [CrossRef]
- Arefi, M.; Bidgoli, E.M.R.; Dimitri, R.; Bacciocchi, M.; Tornabene, F. Nonlocal bending analysis of curved nanobeams reinforced by graphene nanoplatelets. Compos. Part B Eng. 2019, 166, 1–12. [Google Scholar] [CrossRef]
- Bagherizadeh, E.; Kiani, Y.; Eslami, M.R. Mechanical buckling of functionally graded material cylindrical shells surrounded by Pasternak elastic foundation. Compos. Struct. 2011, 93, 3063–3071. [Google Scholar] [CrossRef]
- Shu, C. Differential Quadrature and Its Application in Engineering; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Tornabene, F.; Fantuzzi, N.; Ubertini, F.; Viola, E. Strong formulation finite element method based on differential quadrature: A survey. Appl. Mech. Rev. 2015, 67, 1–55. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Dimitri, R. Free vibrations of composite oval and elliptic cylinders by the generalized differential quadrature method. Thin-Walled Struct. 2015, 97, 114–129. [Google Scholar] [CrossRef]
- Yas, M.; Nejati, M.; Asanjarani, A. Free vibration analysis of continuously graded fiber reinforced truncated conical shell via third-order shear deformation theory. J. Solid Mech. 2016, 8, 212–231. [Google Scholar]
- Kamarian, S.; Salim, M.; Dimitri, R.; Tornabene, F. Free vibration analysis conical shells reinforced with agglomerated Carbon Nanotubes. Int. J. Mech. Sci. 2016, 108–109, 157–165. [Google Scholar] [CrossRef]
- Liu, G.R.; Wu, T.Y. In-plane vibration analyses of circular arches by the generalized differential quadrature rule. Int. J. Mech. Sci. 2001, 43, 2597–2611. [Google Scholar] [CrossRef]
- Tornabene, F.; Dimitri, R. A numerical study of the seismic response of arched and vaulted structures made of isotropic or composite materials. Eng. Struct. 2018, 159, 332–366. [Google Scholar] [CrossRef]
- Dimitri, R.; Tornabene, F.; Zavarise, G. Analytical and numerical modeling of the mixed-mode delamination process for composite moment-loaded double cantilever beams. Compos. Struct. 2018, 187, 535–553. [Google Scholar] [CrossRef]
- Dimitri, R.; Tornabene, F. Numerical Study of the Mixed-Mode Delamination of Composite Specimens. J. Compos. Sci. 2018, 2, 30. [Google Scholar] [CrossRef]
- Tomasiello, S. Differential quadrature method: Application to initial-boundary-value problems. J. Sound Vib. 1998, 218, 573–585. [Google Scholar] [CrossRef]
- Tornabene, F.; Dimitri, R.; Viola, E. Transient dynamic response of generally-shaped arches based on a GDQ-time-stepping method. Int. J. Mech. Sci. 2016, 114, 277–314. [Google Scholar] [CrossRef]
- Bolotin, V.V. The dynamic stability of elastic systems. Am. J. Phys. 1965, 33, 752–753. [Google Scholar] [CrossRef]
- Khazaeinejad, P.; Najafizadeh, M.M. Mechanical buckling of cylindrical shells with varying material properties. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2010, 224, 1551–1557. [Google Scholar] [CrossRef]


| R/h | Khazaeinejad and Najafizadeh [61] | Present | |
|---|---|---|---|
| 5 | Alumina | 1.598 (1,1) | 1.5975 |
| nz = 1 | 0.853 (1,1) | 0.8532 | |
| nz = 2 | 0.662 (1,1) | 0.6624 | |
| nz = 5 | 0.520 (1,1) | 0.5197 | |
| nz = 10 | 0.450 (1,1) | 0.4500 | |
| Aluminum | 0.294 (1,1) | 0.2942 | |
| 10 | Alumina | 1.403 (1,1) | 1.4029 |
| nz = 1 | 0.759 (1,1) | 0.7589 | |
| nz = 2 | 0.589 (1,1) | 0.5885 | |
| nz = 5 | 0.456 (1,1) | 0.4557 | |
| nz = 10 | 0.393 (1,1) | 0.3931 | |
| Aluminum | 0.258 (1,1) | 0.2584 | |
| 20 | Alumina | 1.594 (1,1) | 1.5936 |
| nz = 1 | 0.903 (1,1) | 0.9029 | |
| nz = 2 | 0.698 (1,1) | 0.6977 | |
| nz = 5 | 0.514 (1,1) | 0.5140 | |
| nz = 10 | 0.430 (1,1) | 0.4295 | |
| Aluminum | 0.293 (1,1) | 0.2935 | |
| 30 | Alumina | 1.566 (2,1) | 1.5664 |
| nz = 1 | 0.826 (2,1) | 0.8262 | |
| nz = 2 | 0.642 (2,1) | 0.6419 | |
| nz = 5 | 0.511 (2,1) | 0.5108 | |
| nz = 10 | 0.449 (2,1) | 0.4486 | |
| Aluminum | 0.289 (2,1) | 0.2885 | |
| 100 | Alumina | 1.443 (3,1) | 1.4428 |
| nz = 1 | 0.782 (3,1) | 0.7822 | |
| nz = 2 | 0.606 (3,1) | 0.6064 | |
| nz = 5 | 0.469 (3,1) | 0.4681 | |
| nz = 10 | 0.404 (3,1) | 0.4008 | |
| Aluminum | 0.266 (3,1) | 0.2657 | |
| 300 | Alumina | 1.443 (5,1) | 1.4431 |
| nz = 1 | 0.787 (5,1) | 0.7841 | |
| nz = 2 | 0.610 (5,1) | 0.6079 | |
| nz = 5 | 0.468 (5,1) | 0.4683 | |
| nz = 10 | 0.402 (5,1) | 0.4017 | |
| Aluminum | 0.266 (5,1) | 0.2658 |
| Z | h/R | Bagherizadeh et al. [48] | Present |
|---|---|---|---|
| 50 | 0.01 | 79.9296 (4,5) | 79.9295 |
| 0.025 | 79.48684 (4,3) | 79.4868 | |
| 0.05 | 78.79842 (4,3) | 78.7984 | |
| 300 | 0.01 | 479.5066 (10,5) | 479.5065 |
| 0.025 | 476.3834 (10,3) | 476.3834 | |
| 0.05 | 470.8775 (11,1) | 470.8775 | |
| 900 | 0.01 | 1438.157 (18,3) | 1438.1576 |
| 0.025 | 1428.611 (18,2) | 1428.6108 | |
| 0.05 | 1412.380 (19,1) | 1412.3802 |
| Constituent Phases | Materi | Properties | ||
|---|---|---|---|---|
| E (GPa) | ρ (Kg/m3) | ν | ||
| c | SiC | 427 | 3100 | 0.17 |
| m | Al | 70 | 2702 | 0.3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Allahkarami, F.; Tohidi, H.; Dimitri, R.; Tornabene, F. Dynamic Stability of Bi-Directional Functionally Graded Porous Cylindrical Shells Embedded in an Elastic Foundation. Appl. Sci. 2020, 10, 1345. https://doi.org/10.3390/app10041345
Allahkarami F, Tohidi H, Dimitri R, Tornabene F. Dynamic Stability of Bi-Directional Functionally Graded Porous Cylindrical Shells Embedded in an Elastic Foundation. Applied Sciences. 2020; 10(4):1345. https://doi.org/10.3390/app10041345
Chicago/Turabian StyleAllahkarami, Farshid, Hasan Tohidi, Rossana Dimitri, and Francesco Tornabene. 2020. "Dynamic Stability of Bi-Directional Functionally Graded Porous Cylindrical Shells Embedded in an Elastic Foundation" Applied Sciences 10, no. 4: 1345. https://doi.org/10.3390/app10041345
APA StyleAllahkarami, F., Tohidi, H., Dimitri, R., & Tornabene, F. (2020). Dynamic Stability of Bi-Directional Functionally Graded Porous Cylindrical Shells Embedded in an Elastic Foundation. Applied Sciences, 10(4), 1345. https://doi.org/10.3390/app10041345







