Percolation and Transport Properties in The Mechanically Deformed Composites Filled with Carbon Nanotubes
Abstract
1. Introduction
2. Model and Simulation Details
3. Results and Discussion
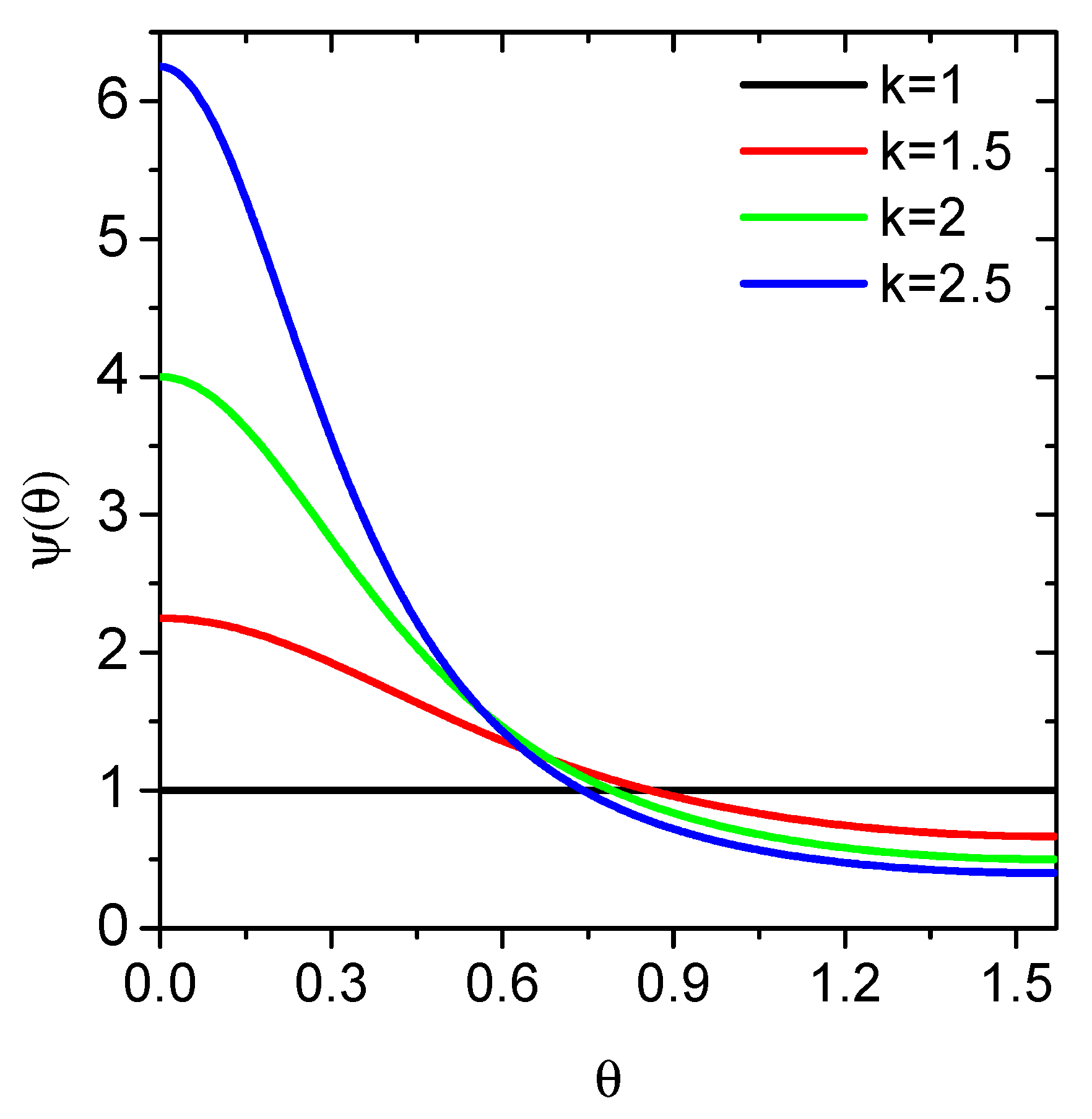
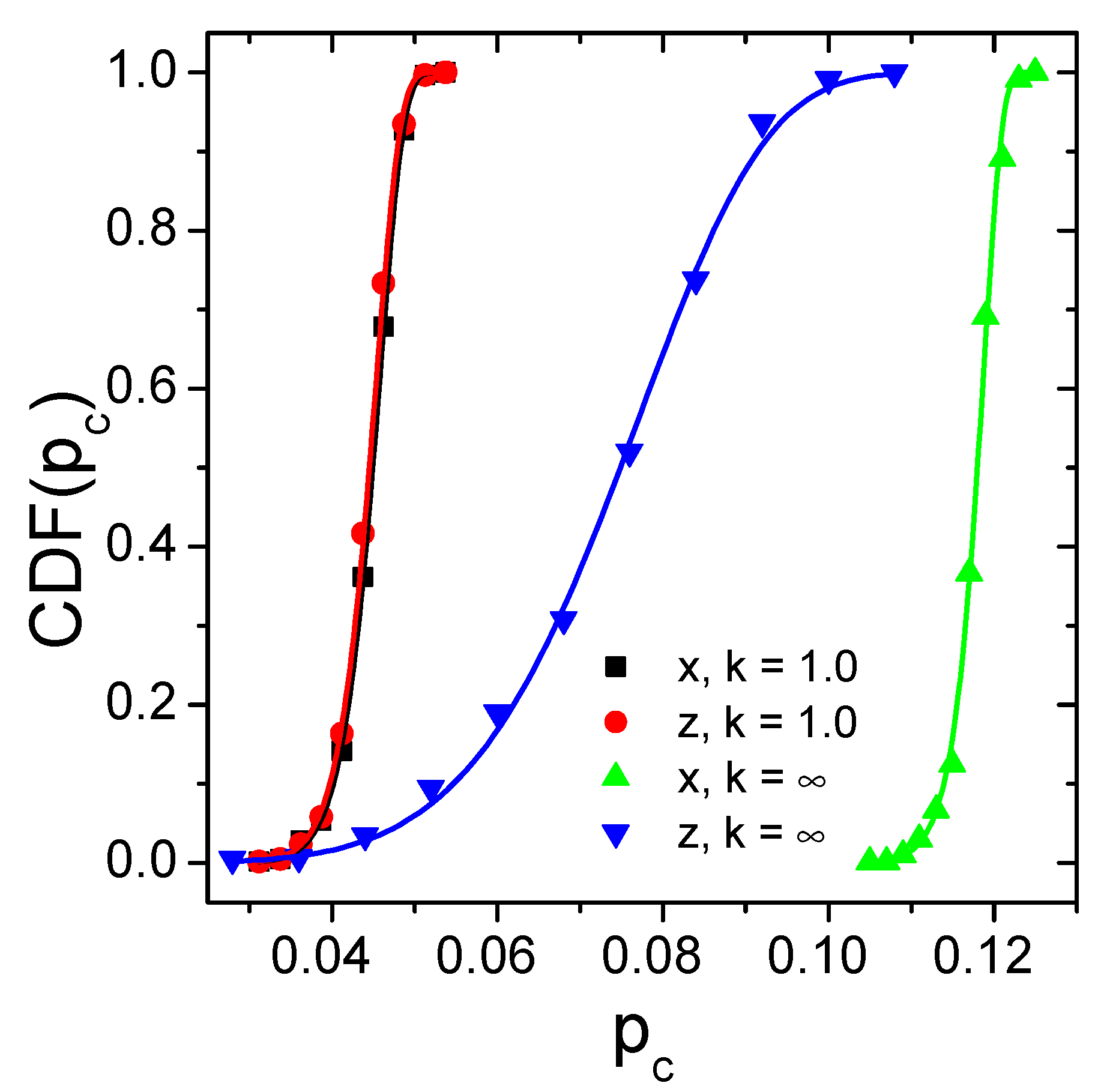
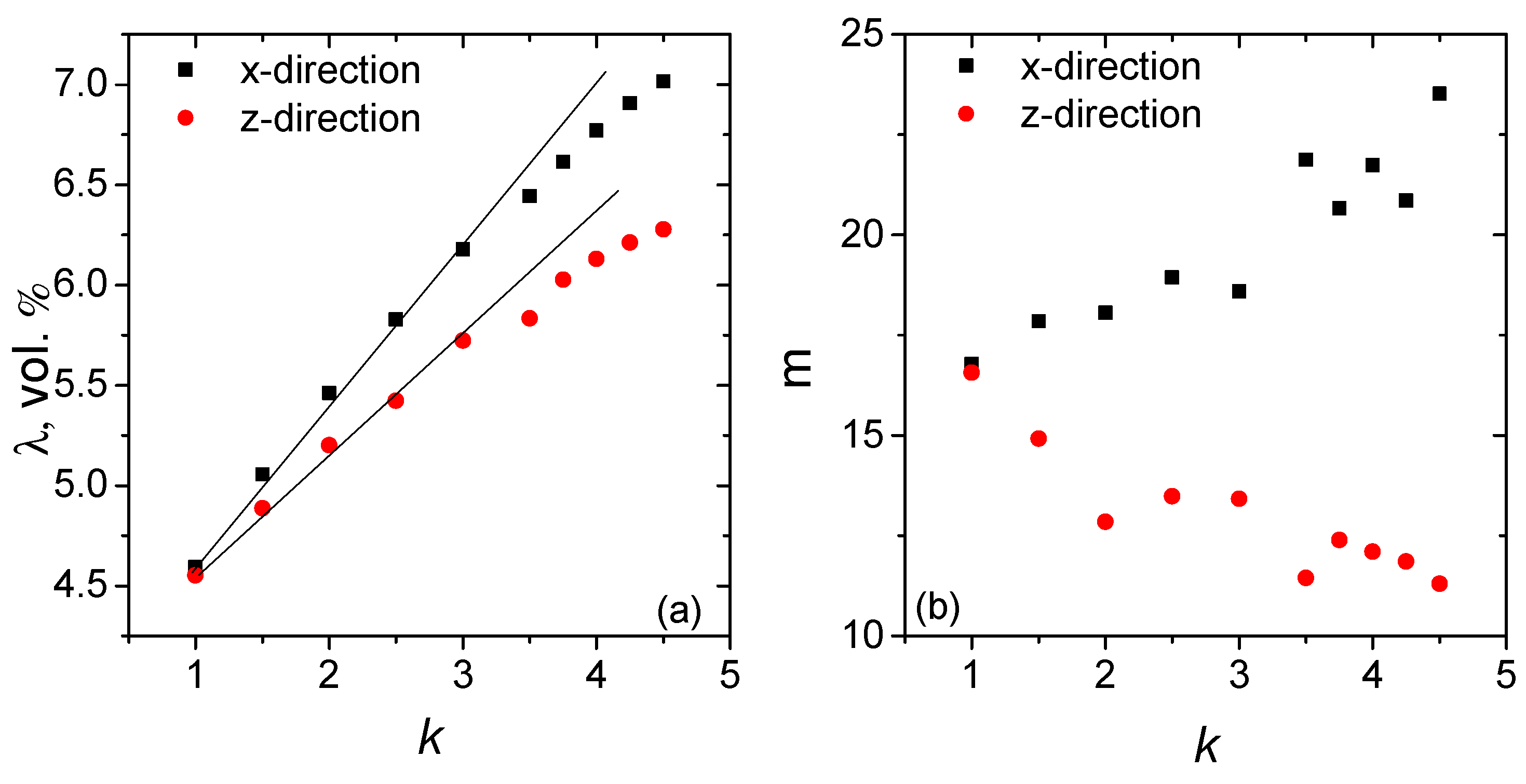
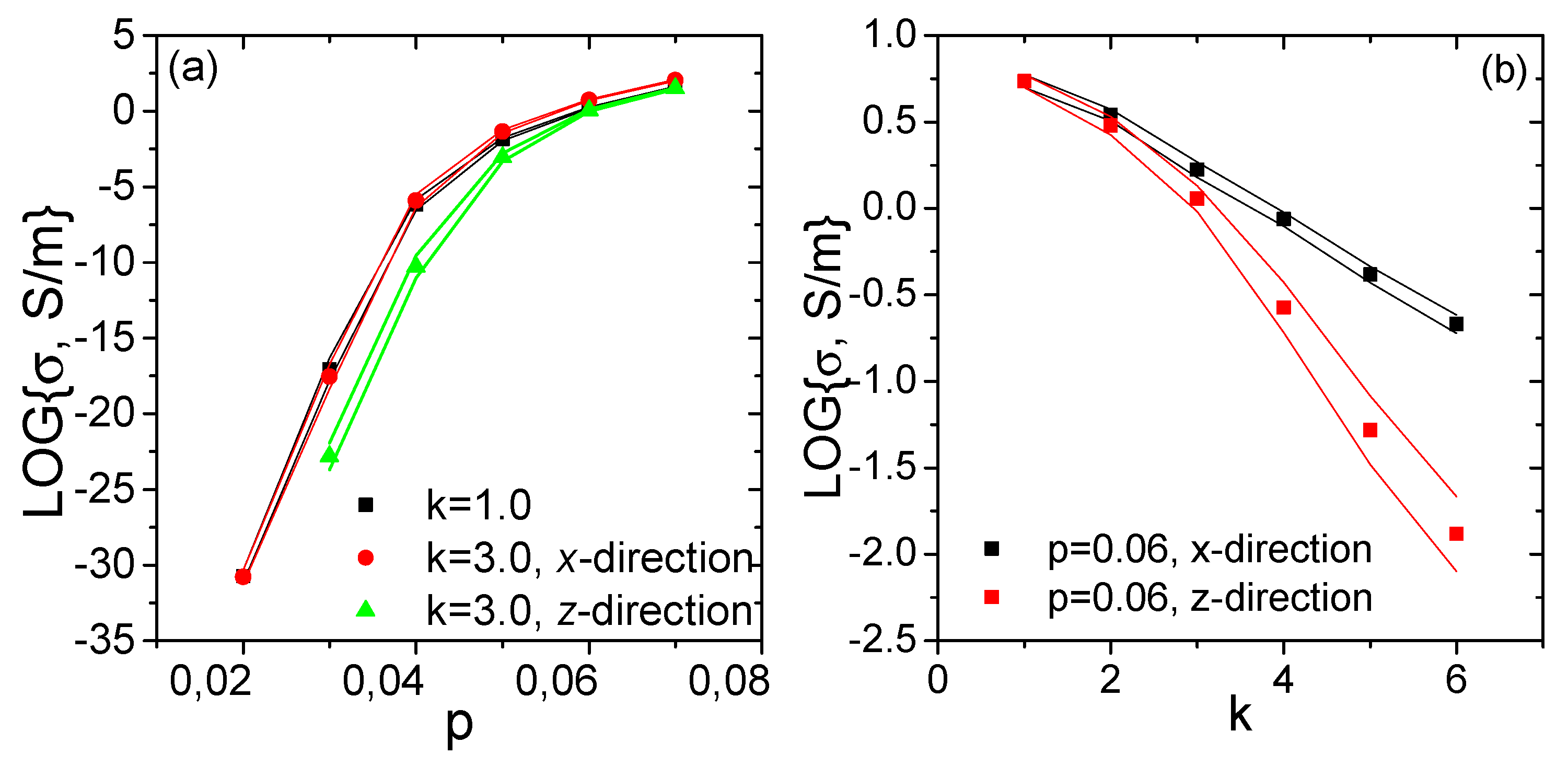
3.1. Percolation Computations
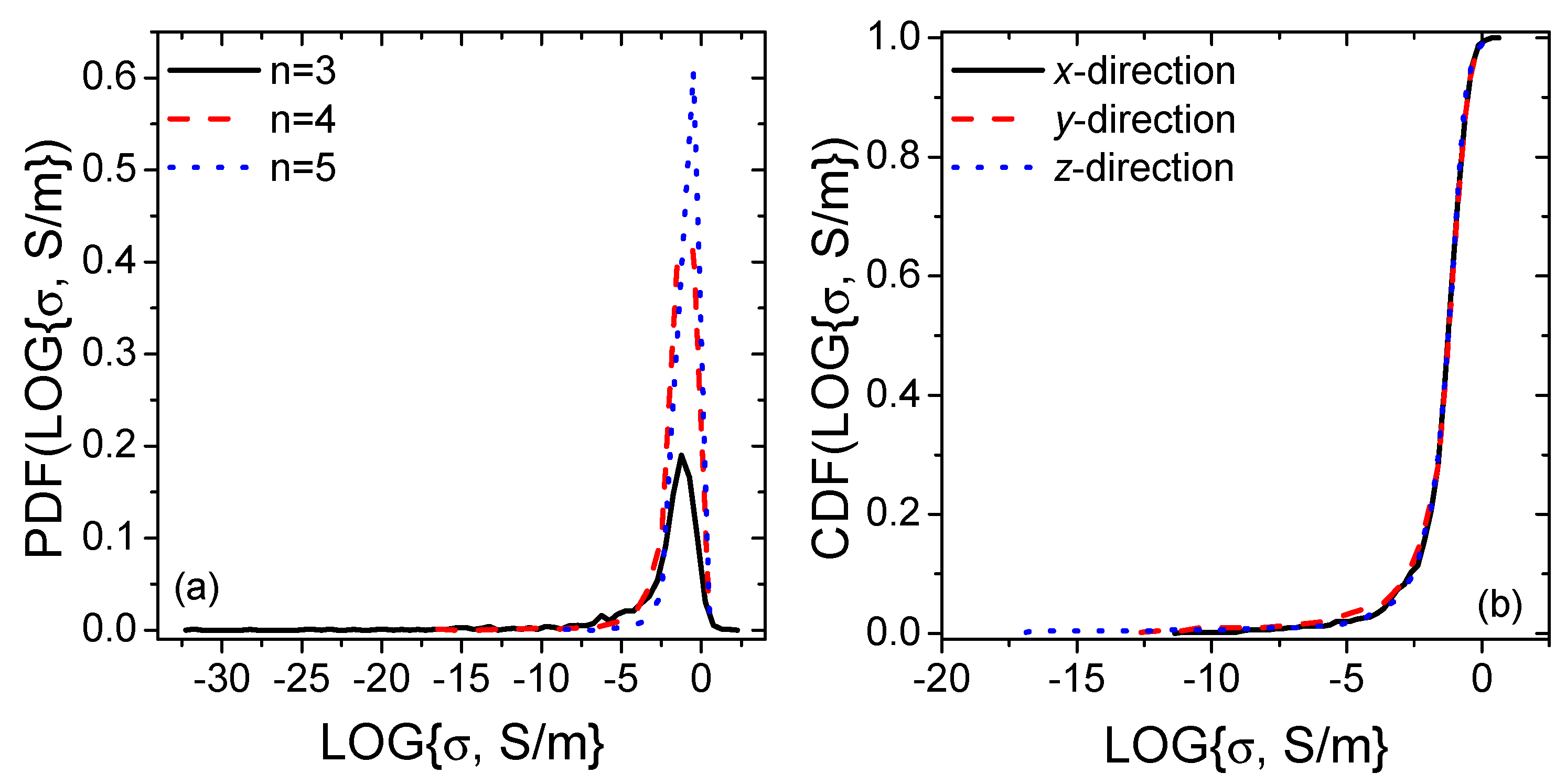
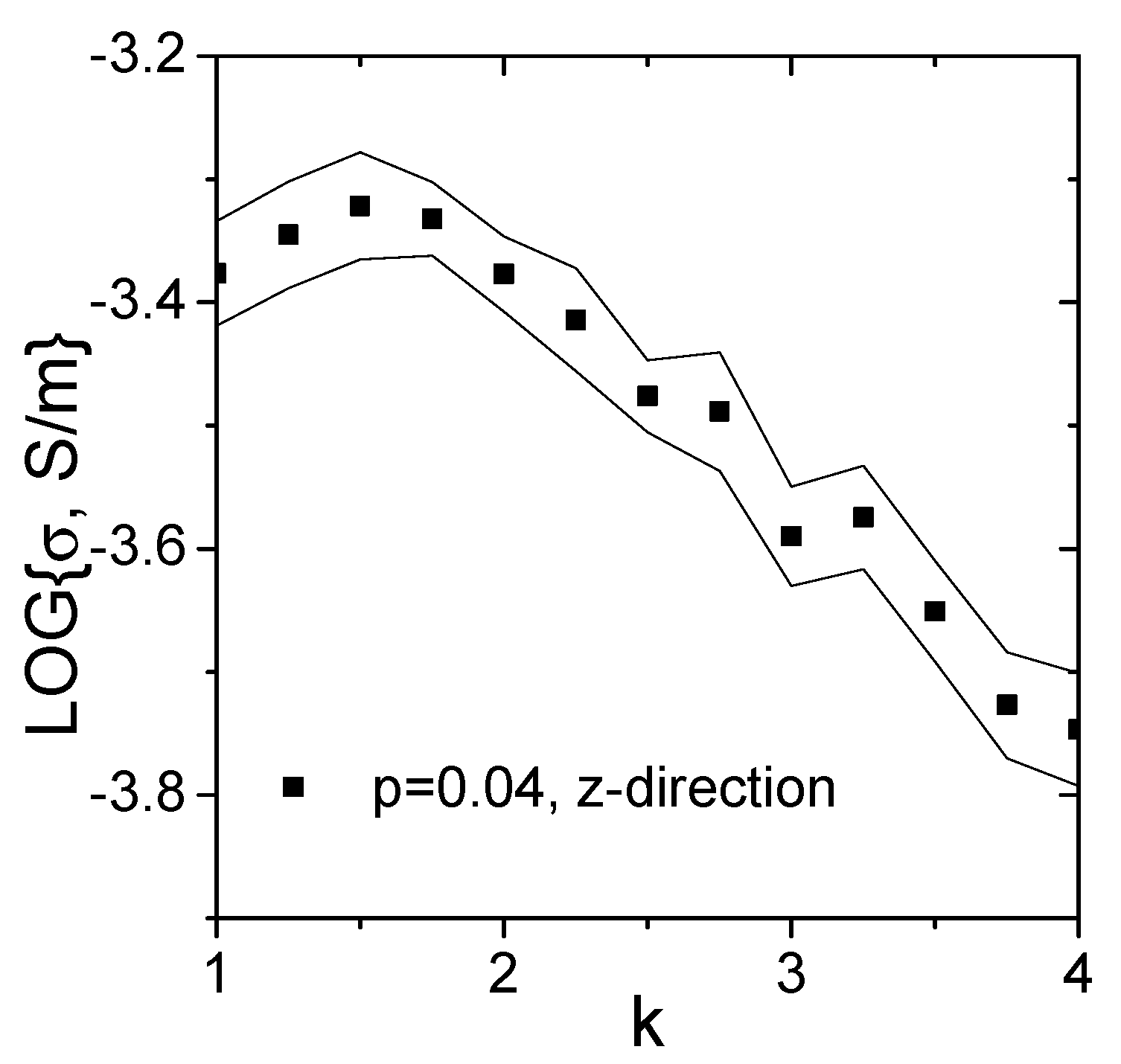
3.2. Piezoresistivity Computations
Boundary Conditions Impact
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| PBC | Periodic boundary conditions |
| CNT | Carbon nanotube |
| Probability density function | |
| CDF | Cumulative distribution function |
References
- Foygel, M.; Morris, R.; Anez, D.; French, S.; Sobolev, V. Theoretical and computational studies of carbon nanotube composites and suspensions: Electrical and thermal conductivity. Phys. Rev. B 2005, 71, 104201. [Google Scholar] [CrossRef]
- Fang, C.; Zhang, J.; Chen, X.; Weng, G.J. A monte carlo model with equipotential approximation and tunneling resistance for the electrical conductivity of carbon nanotube polymer composites. Carbon 2019, 146, 125–138. [Google Scholar] [CrossRef]
- Ni, X.; Hui, C.; Su, N.; Cutler, R.; Liu, F. A 3D percolation model for multicomponent nanocarbon composites: The critical role of nematic transition. Nanotechnology 2019, 30, 185302. [Google Scholar] [CrossRef]
- Hu, Y.; Huang, J.C. Mechanical Properties and Reinforcement Mechanisms of Carbon Nanotube Composites with Amine Functional Groups Based on Molecular Dynamics. J. Phys. Conf. Ser. 2019, 1176, 052054. [Google Scholar] [CrossRef]
- Liu, M.; Kinloch, I.A.; Young, R.J.; Papageorgiou, D.G. Modelling mechanical percolation in graphene-reinforced elastomer nanocomposites. Compos. Part B Eng. 2019, 178, 107506. [Google Scholar] [CrossRef]
- Sagalianov, I.; Vovchenko, L.; Matzui, L.; Lazarenko, O. Synergistic enhancement of the percolation threshold in hybrid polymeric nanocomposites based on carbon nanotubes and graphite nanoplatelets. Nanoscale Res. Lett. 2017, 12, 140. [Google Scholar] [CrossRef]
- Sagalianov, I.Y.; Lazarenko, O.A.; Vovchenko, L.L.; Matzui, L.Y. Monte-Carlo study of the percolation in a binary composites: Hardcore and softcore models comparison. In Proceedings of the 2017 IEEE 7th International Conference on Nanomaterials: Application & Properties (NAP), Zatoka, Ukraine, 10–15 September 2017. [Google Scholar]
- Oskouyi, A.; Sundararaj, U.; Mertiny, P. Tunneling conductivity and piezoresistivity of composites containing randomly dispersed conductive nano-platelets. Materials 2014, 7, 2501–2521. [Google Scholar] [CrossRef] [PubMed]
- Mai, C.K.; Liu, J.; Evans, C.M.; Segalman, R.A.; Chabinyc, M.L.; Cahill, D.G.; Bazan, G.C. Anisotropic thermal transport in thermoelectric composites of conjugated polyelectrolytes/single-walled carbon nanotubes. Macromolecules 2016, 49, 4957–4963. [Google Scholar] [CrossRef]
- Pan, T.W.; Kuo, W.S.; Tai, N.H. Tailoring anisotropic thermal properties of reduced graphene oxide/multi-walled carbon nanotube hybrid composite films. Compos. Sci. Technol. 2017, 151, 44–51. [Google Scholar] [CrossRef]
- Chen, J.; Wang, L.; Gui, X.; Lin, Z.; Ke, X.; Hao, F.; Li, Y.; Jiang, Y.; Wu, Y.; Shi, X.; et al. Strong anisotropy in thermoelectric properties of CNT/PANI composites. Carbon 2017, 114, 1–7. [Google Scholar] [CrossRef]
- Xie, X.L.; Mai, Y.W.; Zhou, X.P. Dispersion and alignment of carbon nanotubes in polymer matrix: A review. Mater. Sci. Eng. R Rep. 2005, 49, 89–112. [Google Scholar] [CrossRef]
- Radzuan, N.A.M.; Sulong, A.B.; Sahari, J. A review of electrical conductivity models for conductive polymer composite. Int. J. Hydrog. Energy 2017, 42, 9262–9273. [Google Scholar] [CrossRef]
- Sun, Y.; Bao, H.D.; Guo, Z.X.; Yu, J. Modeling of the electrical percolation of mixed carbon fillers in polymer-based composites. Macromolecules 2008, 42, 459–463. [Google Scholar] [CrossRef]
- Román, S.; Lund, F.; Bustos, J.; Palza, H. About the relevance of waviness, agglomeration, and strain on the electrical behavior of polymer composites filled with carbon nanotubes evaluated by a Monte-Carlo simulation. Mater. Res. Express 2018, 5, 015044. [Google Scholar] [CrossRef]
- Zhao, N.; Kim, Y.; Koo, J.H. 3D Monte Carlo simulation modeling for the electrical conductivity of carbon nanotube-incorporated polymer nanocomposite using resistance network formation. Mater. Sci. 2018, 2, 1. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, X. Continuum models of carbon nanotube-based composites using the boundary element method. Electron. J. Bound. Elem. 2003, 1. [Google Scholar] [CrossRef][Green Version]
- Liu, Y.; Nishimura, N.; Otani, Y. Large-scale modeling of carbon-nanotube composites by a fast multipole boundary element method. Comput. Mater. Sci. 2005, 34, 173–187. [Google Scholar] [CrossRef]
- Berhan, L.; Sastry, A. Modeling percolation in high-aspect-ratio fiber systems. I. Soft-core versus hard-core models. Phys. Rev. E 2007, 75, 041120. [Google Scholar] [CrossRef]
- Gong, S.; Zhu, Z.; Meguid, S. Anisotropic electrical conductivity of polymer composites with aligned carbon nanotubes. Polymer 2015, 56, 498–506. [Google Scholar] [CrossRef]
- Du, F.; Fischer, J.E.; Winey, K.I. Effect of nanotube alignment on percolation conductivity in carbon nanotube/polymer composites. Phys. Rev. B 2005, 72, 121404. [Google Scholar] [CrossRef]
- Zeng, X.; Xu, X.; Shenai, P.M.; Kovalev, E.; Baudot, C.; Mathews, N.; Zhao, Y. Characteristics of the electrical percolation in carbon nanotubes/polymer nanocomposites. J. Phys. Chem. C 2011, 115, 21685–21690. [Google Scholar] [CrossRef]
- Ghazavizadeh, A.; Baniassadi, M.; Safdari, M.; Atai, A.; Ahzi, S.; Patlazhan, S.; Gracio, J.; Ruch, D. Evaluating the effect of mechanical loading on the electrical percolation threshold of carbon nanotube reinforced polymers: A 3D Monte-Carlo study. J. Comput. Theor. Nanosci. 2011, 8, 2087–2099. [Google Scholar] [CrossRef]
- Li, C.; Chou, T.W. Electrical conductivities of composites with aligned carbon nanotubes. J. Nanosci. Nanotechnol. 2009, 9, 2518–2524. [Google Scholar] [CrossRef] [PubMed]
- Bao, W.; Meguid, S.; Zhu, Z.; Meguid, M. Modeling electrical conductivities of nanocomposites with aligned carbon nanotubes. Nanotechnology 2011, 22, 485704. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Glover, F. Tabu search—part II. ORSA J. Comput. 1990, 2, 4–32. [Google Scholar] [CrossRef]
- Glover, F. Tabu search—part I. ORSA J. Comput. 1989, 1, 190–206. [Google Scholar] [CrossRef]
- Glover, F.; Laguna, M. Tabu Search. In Handbook of Combinatorial Optimization; Springer: Berlin, Germany, 2013; pp. 3261–3362. [Google Scholar]
- Plyushch, A.; Lamberti, P.; Spinelli, G.; Macutkevič, J.; Kuzhir, P. Numerical Simulation of the Percolation Threshold in Non-Overlapping Ellipsoid Composites: Toward Bottom-Up Approach for Carbon Based Electromagnetic Components Realization. Appl. Sci. 2018, 8, 882. [Google Scholar] [CrossRef]
- Simmons, J.G. Generalized formula for the electric tunnel effect between similar electrodes separated by a thin insulating film. J. Appl. Phys. 1963, 34, 1793–1803. [Google Scholar] [CrossRef]
- Bychanok, D.; Kanygin, M.; Okotrub, A.V.; Shuba, M.; Paddubskaya, A.; Pliushch, A.; Kuzhir, P.; Maksimenko, S. Anisotropy of the electromagnetic properties of polymer composites based on multiwall carbon nanotubes in the gigahertz frequency range. Jetp Lett. 2011, 93, 607. [Google Scholar] [CrossRef]
- CUDA FORTRAN. Available online: https://developer.nvidia.com/cuda-fortran (accessed on 14 February 2020).
- Weibull, W. A statistical distribution function of wide applicability. J. Appl. Mech. 1951, 18, 293–297. [Google Scholar]
- Dagan, G. Higher-order correction of effective permeability of heterogeneous isotropic formations of lognormal conductivity distribution. Transp. Porous Media 1993, 12, 279–290. [Google Scholar] [CrossRef]
- Stauffer, D.; Aharony, A. Introduction to Percolation Theory; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Zhang, R.; Baxendale, M.; Peijs, T. Universal resistivity–strain dependence of carbon nanotube/polymer composites. Phys. Rev. B 2007, 76, 195433. [Google Scholar] [CrossRef]
- Alig, I.; Skipa, T.; Engel, M.; Lellinger, D.; Pegel, S.; Pötschke, P. Electrical conductivity recovery in carbon nanotube–polymer composites after transient shear. Phys. Status Solidi B 2007, 244, 4223–4226. [Google Scholar] [CrossRef]
- Hu, N.; Karube, Y.; Arai, M.; Watanabe, T.; Yan, C.; Li, Y.; Liu, Y.; Fukunaga, H. Investigation on sensitivity of a polymer/carbon nanotube composite strain sensor. Carbon 2010, 48, 680–687. [Google Scholar] [CrossRef]
- Bychanok, D.; Shuba, M.; Kuzhir, P.; Maksimenko, S.; Kubarev, V.; Kanygin, M.; Sedelnikova, O.; Bulusheva, L.; Okotrub, A. Anisotropic electromagnetic properties of polymer composites containing oriented multiwall carbon nanotubes in respect to terahertz polarizer applications. J. Appl. Phys. 2013, 114, 114304. [Google Scholar] [CrossRef]
- Shuba, M.; Slepyan, G.Y.; Maksimenko, S.; Thomsen, C.; Lakhtakia, A. Theory of multiwall carbon nanotubes as waveguides and antennas in the infrared and the visible regimes. Phys. Rev. B 2009, 79, 155403. [Google Scholar] [CrossRef]
- Li, C.; Thostenson, E.T.; Chou, T.W. Dominant role of tunneling resistance in the electrical conductivity of carbon nanotube–based composites. Appl. Phys. Lett. 2007, 91, 223114. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plyushch, A.; Lyakhov, D.; Šimėnas, M.; Bychanok, D.; Macutkevič, J.; Michels, D.; Banys, J.; Lamberti, P.; Kuzhir, P. Percolation and Transport Properties in The Mechanically Deformed Composites Filled with Carbon Nanotubes. Appl. Sci. 2020, 10, 1315. https://doi.org/10.3390/app10041315
Plyushch A, Lyakhov D, Šimėnas M, Bychanok D, Macutkevič J, Michels D, Banys J, Lamberti P, Kuzhir P. Percolation and Transport Properties in The Mechanically Deformed Composites Filled with Carbon Nanotubes. Applied Sciences. 2020; 10(4):1315. https://doi.org/10.3390/app10041315
Chicago/Turabian StylePlyushch, Artyom, Dmitry Lyakhov, Mantas Šimėnas, Dzmitry Bychanok, Jan Macutkevič, Dominik Michels, Jūras Banys, Patrizia Lamberti, and Polina Kuzhir. 2020. "Percolation and Transport Properties in The Mechanically Deformed Composites Filled with Carbon Nanotubes" Applied Sciences 10, no. 4: 1315. https://doi.org/10.3390/app10041315
APA StylePlyushch, A., Lyakhov, D., Šimėnas, M., Bychanok, D., Macutkevič, J., Michels, D., Banys, J., Lamberti, P., & Kuzhir, P. (2020). Percolation and Transport Properties in The Mechanically Deformed Composites Filled with Carbon Nanotubes. Applied Sciences, 10(4), 1315. https://doi.org/10.3390/app10041315








