Discrimination of Severity of Alzheimer’s Disease with Multiscale Entropy Analysis of EEG Dynamics
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.2. EEG Recordings and Preprocessing
2.3. Multiscale Entropy (MSE) Algorithm
2.4. Feature Extraction in Linear Discriminant Analysis (LDA)
2.5. Performance Matrix
2.6. Analysis Procedure
- Leave-one-out cross validation (LOOCV) method was used to test the performance of the LDA in differentiating 15 HC and 15 AD2 subjects.
- The expected AD severity indices were obtained by training 15 HC and 15 AD2 subjects using LDA. Then, the models obtained were applied to all the HC, AD1, and AD2 groups to compare their weighted sum values.
- The 69 AD1 subjects were divided into training and validation sets with 54 and 15 subjects, respectively, to obtain the AD severity indices. Then, the models obtained were applied to the 15 HC, 15 AD1, and 15 AD2 subjects to compare their weighted sum values.
3. Results
3.1. LOOCV Performance in Differentiating the HC from AD2 Subjects
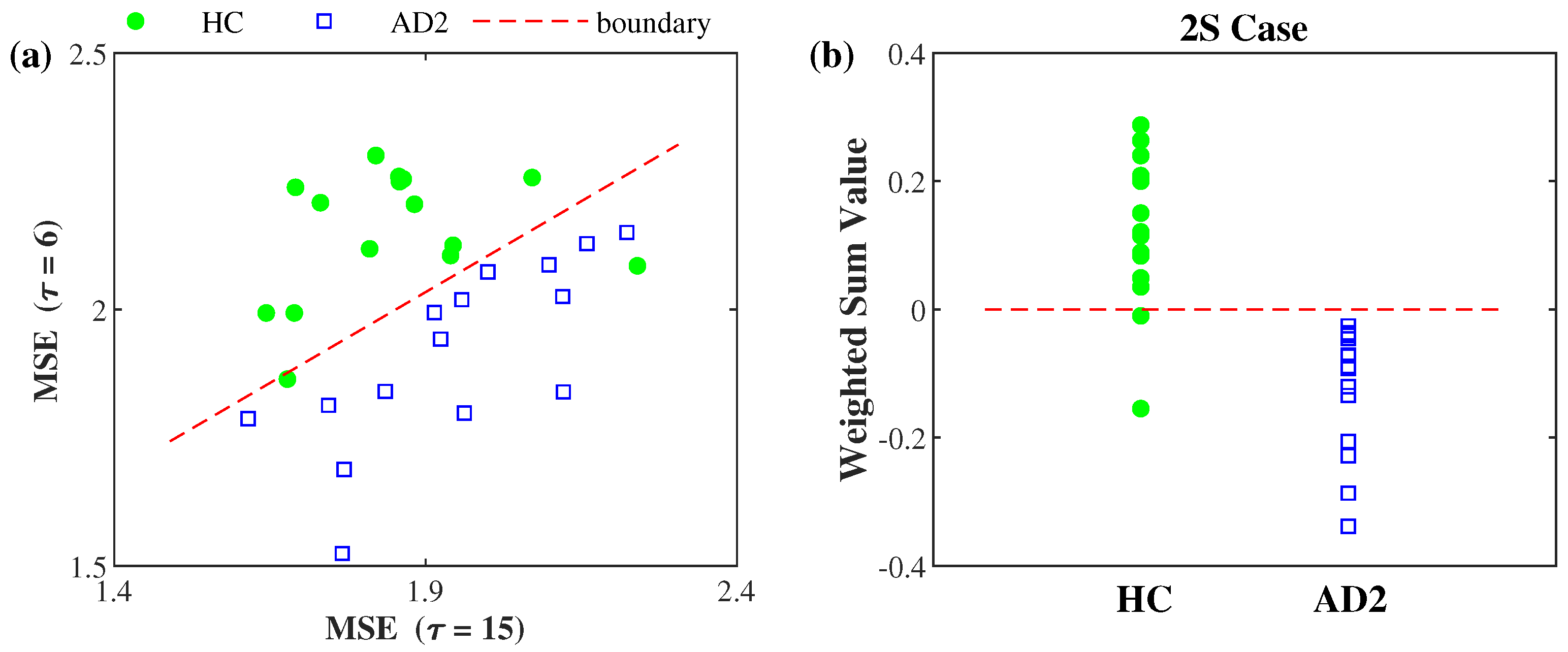
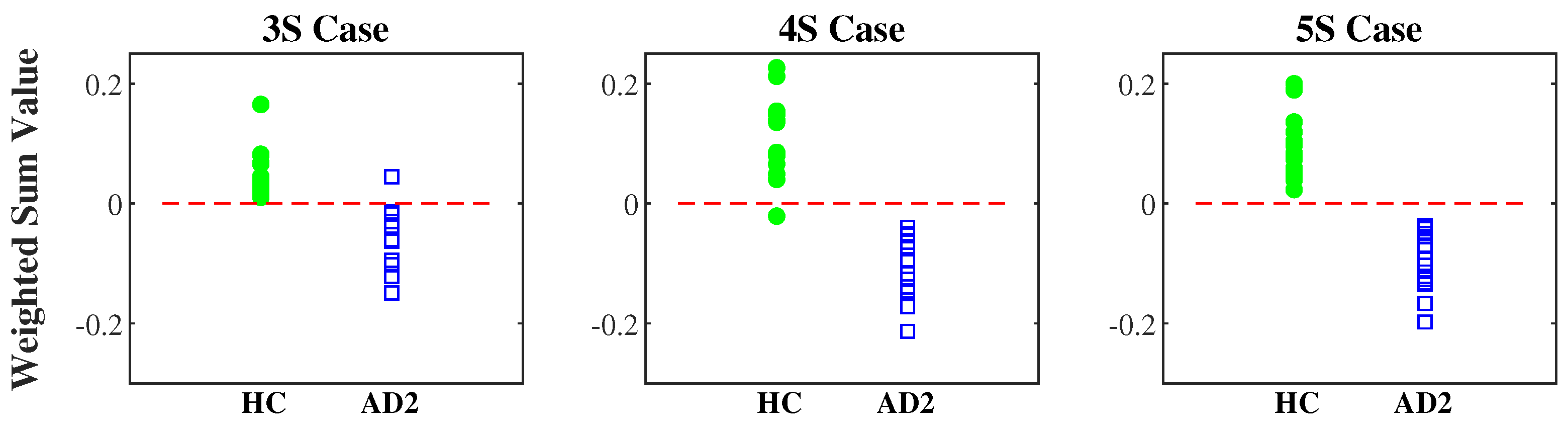
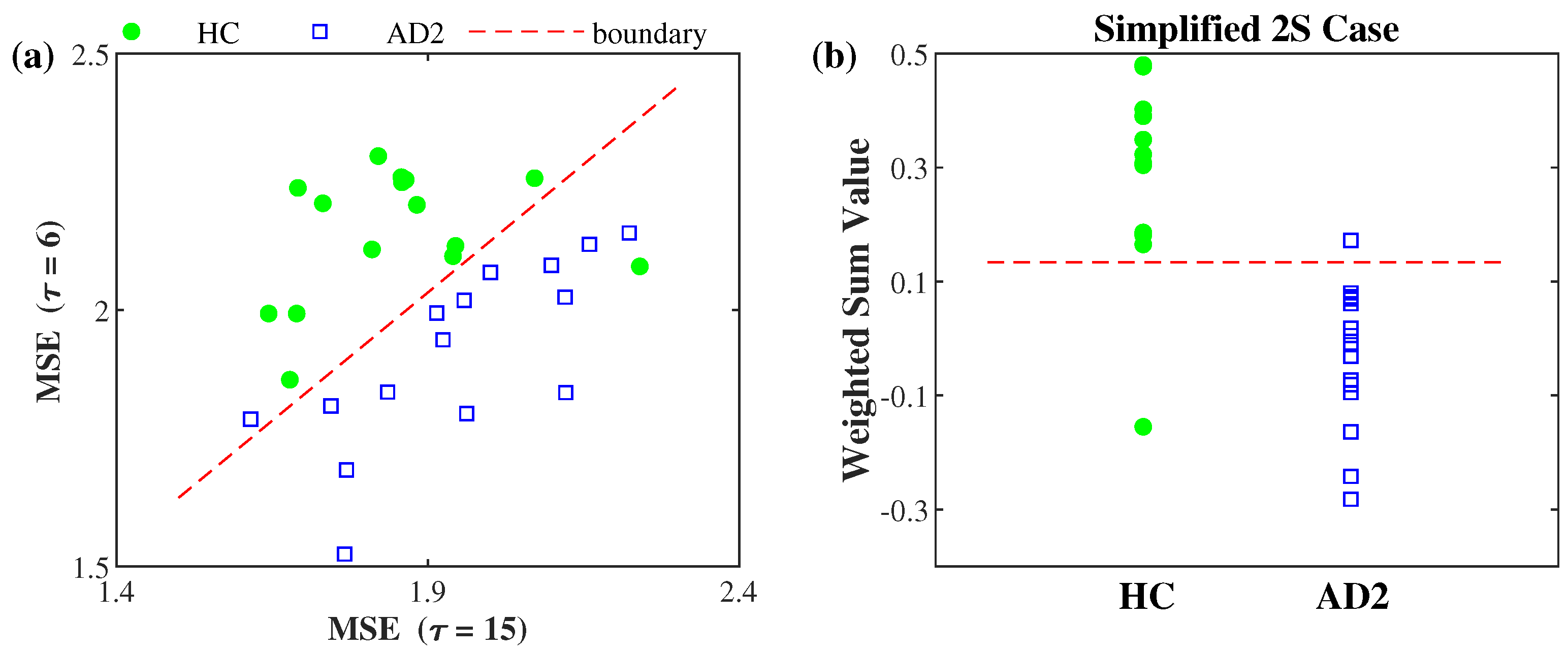
3.2. AD Severity Index Obtained by Training HC and AD2 Groups
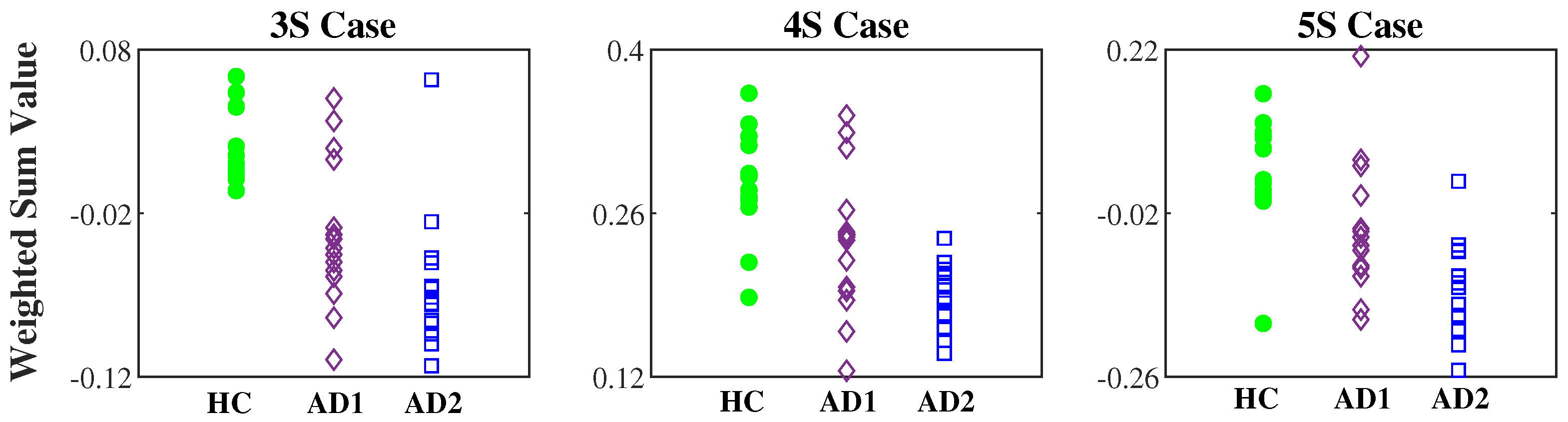
3.3. AD Severity Index Obtained by Training HC and AD1 Groups
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kulkarni, N.; Bairagi, V. EEG-Based Diagnosis of Alzheimer Disease: A Review and Novel Approaches for Feature Extraction and Classification Techniques; Academic Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Patterson, C. World Alzheimer Report 2018: The State of the Art of Dementia Research: New Frontiers; Alzheimer’s Disease International: London, UK, 2018. [Google Scholar]
- Mizuno, T.; Takahashi, T.; Cho, R.Y.; Kikuchi, M.; Murata, T.; Takahashi, K.; Wada, Y. Assessment of EEG dynamical complexity in Alzheimer’s disease using multiscale entropy. Clin. Neurophysiol. 2010, 121, 1438–1446. [Google Scholar] [CrossRef] [PubMed]
- Yang, A.C.; Wang, S.-J.; Lai, K.-L.; Tsai, C.-F.; Yang, C.-H.; Hwang, J.-P.; Lo, M.-T.; Huang, N.E.; Peng, C.-K.; Fuh, J.-L. Cognitive and neuropsychiatric correlates of EEG dynamic complexity in patients with Alzheimer’s disease. Prog. Neuropsychopharmacol. Biol. Psychiatry 2013, 47, 52–61. [Google Scholar] [CrossRef] [PubMed]
- Azami, H.; Abásolo, D.; Simons, S.; Escudero, J. Univariate and multivariate generalized multiscale entropy to characterise EEG signals in Alzheimer’s disease. Entropy 2017, 19, 31. [Google Scholar] [CrossRef]
- Escudero, J.; Abásolo, D.; Hornero, R.; Espino, P.; López, M. Analysis of electroencephalograms in Alzheimer’s disease patients with multiscale entropy. Physiol. Meas. 2006, 27, 1091. [Google Scholar] [CrossRef] [PubMed]
- Tzimourta, K.D.; Giannakeas, N.; Tzallas, A.T.; Astrakas, L.G.; Afrantou, T.; Ioannidis, P.; Grigoriadis, N.; Angelidis, P.; Tsalikakis, D.G.; Tsipouras, M.G. EEG window length evaluation for the detection of Alzheimer’s disease over different brain regions. Brain Sci. 2019, 9, 81. [Google Scholar] [CrossRef] [PubMed]
- Fan, M.; Yang, A.C.; Fuh, J.L.; Chou, C.A. Topological pattern recognition of severe Alzheimer’s disease via regularized supervised learning of EEG complexity. Front. Neurosci. 2018, 12, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Song, Z.; Deng, B.; Wang, J.; Wang, R. Biomarkers for Alzheimer’s Disease Defined by a Novel Brain Functional Network Measure. IEEE Trans. Biomed. Eng. 2019, 66, 41–49. [Google Scholar] [CrossRef] [PubMed]
- Tang, B. Comment on “analysis of electroencephalograms in Alzheimer’s disease patients with multiscale entropy”. Physiol. Meas. 2007, 28, 9–11. [Google Scholar] [CrossRef] [PubMed]
- Tsai, P.H.; Chang, S.C.; Liu, F.C.; Tsao, J.; Wang, Y.H.; Lo, M.T. A novel application of multiscale entropy in electroencephalography to predict the efficacy of acetylcholinesterase inhibitor in Alzheimer’s disease. Comput. Math. Methods Med. 2015, 2015. [Google Scholar] [CrossRef] [PubMed]
- Azami, H.; Fernández, A.; Escudero, J. Refined multiscale fuzzy entropy based on standard deviation for biomedical signal analysis. Med. Biol. Eng. Comput. 2017, 55, 2037–2052. [Google Scholar] [CrossRef] [PubMed]
- McBride, J.; Zhao, X.; Munro, N.; Jicha, G.; Smith, C.; Jiang, Y. EEG multiscale entropy dynamics in mild cognitive impairment and early Alzheimer’s disease. In Proceedings of the 2014 Biomedical Sciences and Engineering Conference, Oak Ridge, TN, USA, 6–8 May 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 68102. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 021906. [Google Scholar] [CrossRef] [PubMed]
- Richman, J.; Moorman, J. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol.-Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed]
- Fisher, R.A. The use of multiple measurements in taxonomic problems. Ann. Eugen. 1936, 7, 179–188. [Google Scholar] [CrossRef]
- Chao, H.-H.; Yeh, C.-W.; Hsu, C.F.; Hsu, L.; Chi, S. Multiscale Entropy Analysis with Low-Dimensional Exhaustive Search for Detecting Heart Failure. Appl. Sci. 2019, 9, 3496. [Google Scholar] [CrossRef]
- Hsu, C.F.; Lin, P.Y.; Chao, H.-H.; Hsu, L.; Chi, S. Average Entropy: Measurement of disorder for cardiac RR interval signals. Physica A 2019, 529, 121533. [Google Scholar] [CrossRef]
- Hsu, C.F.; Wei, S.-Y.; Huang, H.-P.; Hsu, L.; Chi, S.; Peng, C.K. Entropy of Entropy: Measurement of Dynamical Complexity for Biological Systems. Entropy 2017, 19, 550. [Google Scholar] [CrossRef]
| Case | 1S | 2S | 3S | 4S | 5S | |
|---|---|---|---|---|---|---|
| Electrode | ||||||
| Fp1 | 0.710 | 0.774 | 0.903 | 0.903 | 0.933 | |
| Fp2 | 0.733 | 0.759 | 0.815 | 0.857 | 0.857 | |
| F7 | 0.710 | 0.828 | 0.933 | 0.938 | 0.938 | |
| F3 | 0.710 | 0.800 | 0.889 | 0.889 | 0.889 | |
| Fz | 0.710 | 0.815 | 0.903 | 0.903 | 0.903 | |
| F4 | 0.714 | 0.800 | 0.828 | 0.897 | 0.897 | |
| F8 | 0.750 | 0.897 | 0.933 | 0.966 | 0.966 | |
| T3 | 0.733 | 0.786 | 0.867 | 0.867 | 0.857 | |
| C3 | 0.741 | 0.800 | 0.867 | 0.875 | 0.897 | |
| Cz | 0.750 | 0.774 | 0.867 | 0.839 | 0.857 | |
| F4 | 0.714 | 0.800 | 0.828 | 0.897 | 0.897 | |
| F8 | 0.750 | 0.897 | 0.933 | 0.966 | 0.966 | |
| T3 | 0.733 | 0.786 | 0.867 | 0.867 | 0.857 | |
| C3 | 0.741 | 0.800 | 0.867 | 0.875 | 0.897 | |
| Cz | 0.750 | 0.774 | 0.867 | 0.839 | 0.857 | |
| C4 | 0.800 | 0.867 | 0.867 | 0.897 | 0.933 | |
| T4 | 0.786 | 0.938 | 0.966 | 0.968 | 1.000 | |
| T5 | 0.828 | 0.903 | 0.903 | 0.903 | 0.933 | |
| P3 | 0.828 | 0.933 | 0.966 | 0.966 | 0.966 | |
| Pz | 0.786 | 0.897 | 0.903 | 0.903 | 0.903 | |
| P4 | 0.759 | 0.903 | 0.933 | 0.933 | 0.968 | |
| T6 | 0.621 | 0.750 | 0.750 | 0.774 | 0.774 | |
| O1 | 0.800 | 0.897 | 0.897 | 0.897 | 0.897 | |
| O2 | 0.667 | 0.690 | 0.667 | 0.667 | 0.645 | |
| Case | Electrode | Scales | F1 Score | Accuracy | Recall | Precision | Specificity |
|---|---|---|---|---|---|---|---|
| 1S | T5; P3 | {12}; {19} | 0.828 | 0.833 | 0.813 | 0.867 | 0.800 |
| 2S | T4 | {6, 15} | 0.938 | 0.933 | 0.882 | 1.000 | 0.867 |
| 3S | T4 | {2, 3, 14} | 0.966 | 0.967 | 1.000 | 0.933 | 1.000 |
| 4S | T4 | {6, 9, 12, 17} | 0.968 | 0.967 | 0.938 | 1.000 | 0.933 |
| 5S | T4 | {2, 8, 11, 15, 16} | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Case | Weighted Sum Model |
|---|---|
| 2S | 0.82 · MSE ( = 6) − 0.58 · MSE ( = 15) − 0.56 |
| 3S | 0.61 · MSE ( = 2) + 0.79 · MSE ( = 3) − 0.10 · MSE ( = 14) − 0.29 |
| 4S | 0.43 · MSE ( = 6) + 0.54 · MSE ( = 9) − 0.67 · MSE ( = 12) + 0.25 · MSE ( = 17) − 1.13 |
| 5S | 0.22 · MSE ( = 2) + 0.67 · MSE ( = 8) − 0.30 · MSE ( = 11) − 0.55 · MSE ( = 15) + 0.32 · MSE ( = 16) − 0.69 |
| Group | HC N = 15 | AD1 N = 69 | AD2 N = 15 | |
|---|---|---|---|---|
| Case | ||||
| 2S | 0.13 ± 0.12 | 0.05 ± 0.14 | −0.13 ± 010 | |
| 3S | 0.05 ± 0.04 | 0.00 ± 0.05 | −0.05 ± 0.05 | |
| 4S | 0.12 ± 0.08 | 0.06 ± 0.11 | −0.12 ± 0.08 | |
| 5S | 0.09 ± 0.05 | 0.03 ± 0.12 | −0.09 ± 0.05 | |
| Case | Electrode | Scales | F1 Score | Accuracy | Recall | Precision | Specificity |
|---|---|---|---|---|---|---|---|
| 3S | F8 | {2, 3, 12} | 0.854 | 0.797 | 0.976 | 0.759 | 0.933 |
| 4S | F7 | {2, 5, 6, 12} | 0.857 | 0.797 | 0.955 | 0.778 | 0.867 |
| 5S | F7 | {1, 2, 4, 15, 17} | 0.857 | 0.797 | 0.955 | 0.778 | 0.867 |
| Case | Weighted Sum Model |
|---|---|
| 3S | − 0.63 · MSE ( = 2) + 0.76 · MSE ( = 3) − 0.16 · MSE ( = 12) − 0.06 |
| 4S | − 0.31 · MSE ( = 2) + 0.86 · MSE ( = 5) − 0.36 · MSE ( = 6) − 0.21 · MSE ( = 12 − 0.06 |
| 5S | − 0.10 · MSE ( = 1) − 0.47 · MSE ( = 2) + 0.78 · MSE ( = 4) − 0.40 · MSE ( = 15) − 0.05 · MSE ( = 17) |
| Group | HC N = 15 | AD1 N = 15 | AD2 N = 15 | |
|---|---|---|---|---|
| Case | ||||
| 3S | 0.02 ± 0.02 | −0.03 ± 0.04 | −0.07 ± 0.04 | |
| 4S | 0.28 ± 0.04 | 0.24 ± 0.06 | −0.19 ± 0.03 | |
| 5S | 0.03 ± 0.08 | −0.05 ± 0.10 | −0.13 ± 0.07 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsu, C.F.; Chao, H.-H.; Yang, A.C.; Yeh, C.-W.; Hsu, L.; Chi, S. Discrimination of Severity of Alzheimer’s Disease with Multiscale Entropy Analysis of EEG Dynamics. Appl. Sci. 2020, 10, 1244. https://doi.org/10.3390/app10041244
Hsu CF, Chao H-H, Yang AC, Yeh C-W, Hsu L, Chi S. Discrimination of Severity of Alzheimer’s Disease with Multiscale Entropy Analysis of EEG Dynamics. Applied Sciences. 2020; 10(4):1244. https://doi.org/10.3390/app10041244
Chicago/Turabian StyleHsu, Chang Francis, Hsuan-Hao Chao, Albert C. Yang, Chih-Wei Yeh, Long Hsu, and Sien Chi. 2020. "Discrimination of Severity of Alzheimer’s Disease with Multiscale Entropy Analysis of EEG Dynamics" Applied Sciences 10, no. 4: 1244. https://doi.org/10.3390/app10041244
APA StyleHsu, C. F., Chao, H.-H., Yang, A. C., Yeh, C.-W., Hsu, L., & Chi, S. (2020). Discrimination of Severity of Alzheimer’s Disease with Multiscale Entropy Analysis of EEG Dynamics. Applied Sciences, 10(4), 1244. https://doi.org/10.3390/app10041244






