Adaptation of Conformable Residual Power Series Scheme in Solving Nonlinear Fractional Quantum Mechanics Problems

Abstract

In this paper, the general state of quantum mechanics equations that can be typically expressed by nonlinear fractional Schrödinger models will be solved based on an attractive efficient analytical technique, namely the conformable residual power series (CRPS). The fractional derivative is considered in a conformable sense. The desired analytical solution is obtained using conformable Taylor series expansion through substituting a truncated conformable fractional series and minimizing its residual errors to extract a supportive approximate solution in a rapidly convergent fractional series. This adaptation can be implemented as a novel alternative technique to deal with many nonlinear issues occurring in quantum physics. The effectiveness and feasibility of the CRPS procedures are illustrated by verifying three realistic applications. The obtained numerical results and graphical consequences indicate that the suggested method is a convenient and remarkably powerful tool in solving different types of fractional partial differential models.

1. Introduction

Modern physics was born after classical mechanics failed in explanation of various physical phenomena, including microscopic scales, like photoelectric effect, black body radiation, and the stability of the atoms depending on the fact that all physical quantities of a bound system are restricted to discrete values quantization. Quantum mechanics can successfully describe different modern physics phenomena in atomic and nuclear physics and other modern physics branches, where electrons’ behavior in atomic physics and nucleons in nuclear physics can be described quantum mechanically by the Schrödinger equation [1]. The discovery of the quantum mechanical path integral approach can be used as an alternative of the Schrödinger wave equation and Heisenberg matrix dynamics that originated to find what corresponds in quantum theory to the Lagrangian method of classical mechanics. Dirac searched in the role which classical mechanics fundamentals like Lagrangian and least-action principle, which effect quantum mechanics. Furthermore, Feynman developed this idea and called it path integral. Since then, the path integral approach and the perturbation technique based on it, Feynman diagrams, became powerful tools in quantum mechanics and quantum field theory, solid-state and quantum liquid theory, equilibrium and non-equilibrium statistical physics, theory of turbulence and chaotic phenomena, theory of random processes and polymer physics, mathematics, chemistry, and economic studies.

Several powerful analytical strategies are established and developed in the literature to solve the Schrödinger equation. For example, an analytic, accurate solution beyond adiabatic approximation by transferring the 1D Schrödinger equation into the Ricatti equation has been obtained in [2]. In [3], the position-dependent mass Schrödinger equation has been studied and solved by using an effective advanced analytical technique. While the analytic solution of the 3D stationary Schrödinger equation for any arbitrary potential was proposed in [4] by transforming the Schrödinger equation to the generalized Ricatti equation.

The fractional Schrödinger equation is a new fundamental equation of quantum physics, and it includes the space derivative of fractional order instead of a second-order space derivative in the standard Schrödinger equation. In this regard, the fractional Schrödinger equation is the fractional differential equation in accordance to modern terminology. In the limit of integer case, the fundamental equation of fractional quantum mechanics is transformed into the well-known equation of standard quantum mechanics [5]. Many elegant and fascinating models in quantum mechanics, fluid dynamics, and other physical fields were formulated by partial differential equations in a fractional sense, for instance, the nonlinear fractional Schrödinger equation, fractional wave equation, fractional fluid flow models, and fractional Boussinesq-like equation. The solution of partial differential equations (PDEs), in the sense of fractional, is very significant to describe the dynamic behavior of both linear and nonlinear physical systems such as the dynamics of nuclear reactors, randomized analytical models, fluid mechanics, viscoelastic damping, electromagnetism, and electrochemistry [6,7,8,9,10,11]. However, only a little research has been done on nonlinear systems, and few analytic-numeric techniques have been presented for solving the nonlinear PDE problems for fractional models. This gives us the motivation to look for numerical solutions for these systems. In this analysis, the application of conformable residual power series (CRPS) technique is extended to construct the approximate solution of the following nonlinear time-fractional Schrödinger equation (FSE):

$$i{T}_t^{\alpha }𝓊\left(x,t\right)+\xi {𝓊}_{xx}\left(x,t\right)+\psi \left(x\right)𝓊\left(x,t\right)+\eta {\left|𝓊\left(x,t\right)\right|}^2𝓊\left(x,t\right)=0,$$

(1)

along with the following initial conditions

$$𝓊\left(x,0\right)={𝓊}_0\left(x\right),$$

(2)

where $\xi ,\eta \in ℝ$; $0<\alpha \le 1$, $i^2=-1$; $T_t^{\alpha }$ indicates conformable fractional derivative of order $\alpha$; $𝓊\left(x,t\right)$ is unknown complex-valued function to be determined, $x\in ℝ$; $t\ge 0$, $\psi \left(x\right)$ is the trapping potential; $|𝓊|$ represents the modulus of $𝓊$; and ${𝓊}_0\left(x\right)$ is given smooth function. For $\alpha =1,$ Equation (1) reduces to classical nonlinear Schrödinger equation. The linear case occurs when $\eta =0$. Anyhow, the CRPS is applied for both linear and nonlinear cases with zero and nonzero trapping potential. In this light, it is assumed that fractional initial value problems (IVPs), Equations (1) and (2), have a unique and sufficiently smooth solution in the domain of interest.

The fractional calculus theory is a powerful generalization of classical calculus theory dealing with differentiation and integration of arbitrary order. It has recently attracted the attention of numerous researchers for its considerable importance in many applications, such as fluid dynamics, signal processing, viscoelasticity, bioengineering, finance, Hamiltonian chaos, and vibrations, which can be used to describe the memory and transmissibility for multiple types of materials [12,13,14,15,16]. Moreover, it has successfully proved to be a valuable tool due to the realistic modeling that does not depend only on the instant time, but also on the history of the previous time, which can be achieved using fractional calculus [17,18,19,20]. Unlike the classical calculus, which has unique definitions and clear geometrical and physical interpretations, there are numerous definitions for the operations of differentiation and integration of fractional order. Riemann–Liouville, Riesz, Grünwald–Letnikov, and Caputo are some examples of these definitions [21,22,23,24]. In this light, a novel definition of fractional derivative, the conformable fractional concept, was proposed in 2014 by Khalil et al. [25]. Since then, several studies have appeared in the literature. For more details see [26,27,28,29,30,31,32].

The mathematical construction of most natural phenomena leads us to nonlinear differential equations of integer or non-integer order. Typically, there is no general theory for finding a closed-form solution of these nonlinear differential equations. To avoid such difficulty associated with the nonlinear terms, computer transform techniques, linearization process, or simplifying assumptions can be used to obtain solutions and consider linear approximations, and then attempt to reach geometric and arithmetic interpretations that enable us to understand these phenomena further. Indeed, such assumptions lead to significant errors in the solution. Therefore, nonlinear differential equations must be solved in a way that represents the real nonlinear problem, particularly in the fractional case. Anyhow, the difficulty in solving the model depends on the degree of nonlinearity [33,34,35]. Furthermore, the computation of solution through the power series while attractive from the theoretical point of view is difficult to implement since the terms of the power series may become very high, provoking machine overflow. In this orientation, a truncated conformable power series approximation can be used to compute the solution based on a simple algorithm, which is acceptable over the interval of interest and has a wide range of applications, particularly in simulating nonlinear problems in a fractional sense.

This paper is structured as follow. The necessary definitions and properties of the conformable fractional derivative and fractional power series are shown in Section 2. The description of the suggested approach is introduced in Section 3 to provide the representation of CRPS solution for both linear and nonlinear FSEs. In Section 4, some numerical examples are performed to manifest the versatility, capability, and applicability of the CRPS algorithm. Section 5 is devoted to conclusions.

2. Notations and Preliminaries

In this section, the fundamentals resulting of conformable fractional calculus theory are presented briefly, and the most important definitions and theories of the fractional power series approach are also given in conformable sense.

Definition 1.

From [26], let $f$ be $n$-differentiable at $t>s$. The conformable fractional derivative starting from $s$ of a function $f:\left[s,\infty \right)\to ℝ$ of order $\alpha >0$ is defined by

$$T^{\alpha }f\left(t\right)=\underset{\epsilon \to 0}{\lim }\frac{f^{\left(\lceil \alpha \rceil -1\right)}\left(t+\epsilon {\left(t-s\right)}^{\lceil \alpha \rceil -\alpha }\right)-f^{\left(\lceil \alpha \rceil -1\right)}\left(t\right)}{\epsilon }, \alpha \in \left(n-1,n\right] , t>s,$$

(3)

and$T^{\alpha }f\left(s\right)=\underset{t\to s^{+}}{\lim }{T}^{\alpha }f\left(t\right)$provided$f\left(t\right)$is$\alpha$-differentiable in some$\left(0,s\right),$$s>0$, and$\underset{t\to s^{+}}{\lim }{T}^{\alpha }f\left(t\right)$exists, where$\lceil \alpha \rceil$is the smallest integer greater than or equal to$\alpha$. The function$f$is called$\alpha$-differentiable at a point$t$whenever$f$has a conformable fractional derivative of order$\alpha$at the point$t$.

Theorem 1.

From [26], let$\alpha \in \left(0, 1\right]$and assume$f$,$g$be$\alpha$-differentiable at a point$t>s$. Then

(1) 

$\frac{d^{\alpha }}{d{t}^{\alpha }}\left(kf +hg\right) = k f^{\left(\alpha \right)}+h g^{\left(\alpha \right)}$, $\forall k, h\in ℝ$.

(2) 

$\frac{d^{\alpha }}{d{t}^{\alpha }}\left(\lambda \right)=0$, $\lambda$ is a constant.

(3) 

$\frac{d^{\alpha }}{d{t}^{\alpha }}\left(\lambda f\right)=\lambda \frac{d^{\alpha }}{d{t}^{\alpha }}\left(f\right).$

(4) 

$\frac{d^{\alpha }}{d{t}^{\alpha }}\left({\left(t-a\right)}^p\right)= p{\left(t-a\right)}^{p-\alpha }$, $\forall p\in ℝ.$

(5) 

If$f$is differentiable, then$\frac{d^{\alpha }f}{d{t}^{\alpha }}\left(t\right)={\left(t-a\right)}^{1-\alpha }\frac{df}{dt}\left(t\right)$.

Remark 1.

For$\alpha \in \left(n-1,n\right]$, if$f$is$n$-differentiable at$t>s$, then$\frac{d^{\alpha }f}{d{t}^{\alpha }}\left(t\right)={\left(t-s\right)}^{n-\alpha }\frac{d^{n}f}{d{t}^n}\left(t\right)$.

Definition 2.

From [27], the conformable fractional integral starting from s of order$\alpha \in \left(n-1,n\right]$of$f\left(t\right)$is defined as

$$I_s^{\alpha }f\left(t\right)=\frac{1}{\left(n-1\right)!}{{\displaystyle \int }}_s^t\frac{{\left(t-\tau \right)}^{n-1}f\left(\tau \right)}{{\left(\tau -s\right)}^{n-\alpha }}d\tau ,t>\tau \ge s\ge 0.$$

(4)

Definition 3.

From [27], Let${\partial }^k𝓊/\partial t^k$and${\partial }^k𝓊/\partial x^k,$$k=1,2,\dots ,n-1,$be defined on$I\times \left[s,\infty \right)$, then the conformable time-fractional differential operator of order$\alpha$of a function$𝓊\left(x,t\right):I\times \left[s,\infty \right)\to ℝ$is defined by

$$\begin{gathered} T_t^{\alpha }𝓊\left(x,t\right)=\frac{{\partial }^{\alpha }𝓊\left(x,t\right)}{\partial t^{\alpha }}=\underset{\epsilon \to 0}{\lim }\frac{{𝓊}_t^{\left(n-1\right)}\left(x,t+\epsilon {\left(t-s\right)}^{n-\alpha }\right)-{𝓊}_t^{\left(n-1\right)}\left(x,t\right)}{\epsilon }, \alpha \in \left(n-1,n\right], \\ t\ge 0. \end{gathered}$$

(5)

Definition 4.

From [27], the conformable fractional integral starting from$s$of order$\alpha \in \left(n-1,n\right]$of a function$𝓊\left(x,t\right):I\times \left[s,\infty \right)\to ℝ$is defined by

$$I_s^{\alpha }𝓊\left(x,t\right)=\{\begin{array}{ll}\frac{1}{\left(n-1\right)!}{{\displaystyle \int }}_s^t\frac{{\left(t-\tau \right)}^{n-1}𝓊\left(x,\tau \right)}{{\left(\tau -s\right)}^{n-\alpha }}d\tau ,& x\in I, t>\tau \ge s\ge 0, \\ 𝓊\left(x,t\right),& \alpha =0.\end{array}$$

(6)

Definition 5.

From [29], for$0\le n-1<\alpha \le n$, a power series (PS) of the form

$$\begin{array}{c}{\displaystyle \sum _{k=0}^{\infty }}{f}_k\left(x\right)\left(t-t_0\right){ }^{k\alpha }=f_0\left(x\right)+f_1\left(x\right){\left(t-t_0\right)}^{\alpha }+f_2\left(x\right){\left(t-t_0\right)}^{2\alpha }+\dots , x\in I, t_0\le t\\ <t_0+R^{1/\alpha },R>0,\end{array}$$

(7)

is called a multiple fractional PS at$t=t_0$, where$t$is a variable and the function$f_k\left(x\right)$is called the coefficients of the PS.

As the classical power series [36,37,38,39,40,41], it is clear that all terms of the multiple fractional PS (Equation (7)) vanish as soon as $t=t_0$, except the first term, which means the multiple fractional PS is convergent when $t=t_0.$ Furthermore, for $t\ge t_0$, this multiple fractional series is definitely convergent for $\left|t-t_0\right|<R^{1/\alpha },$ ( $R>0$), where $R^{1/\alpha }$ is the radius of convergence of the series.

Theorem 2.

Let$0\le n-1<\alpha \le n$and assume$𝓊\left(x,t\right):I\times \left[t_0,t_0+R^{1/\alpha }\right)\to ℝ$can be expressed as the following multiple fractional PS about$t=t_0$:

$$𝓊\left(x,t\right)={\displaystyle \sum }_{k=0}^{\infty }{f}_k\left(x\right)\left(t-t_0\right){ }^{k\alpha }, x\in I, t_0\le t<t_0+R^{\frac{1}{\alpha }},R>0.$$

(8)

Let$𝓊\left(x,t\right)$becontinuous on$I \times \left[t_0,t_0+R^{1/\alpha }\right)$and$\frac{{\partial }^{k\alpha }}{\partial t^{k\alpha }}𝓊\left(x,t\right)=T_t^{k\alpha }𝓊\left(x,t\right)\in C\left(t_0,t_0+R^{1/\alpha }\right)$, for$k=1,2,\dots$, then the coefficients$f_k\left(x\right)$are given by$f_k\left(x\right)=\frac{T_t^{k\alpha }𝓊\left(x,t_0\right)}{{\alpha }^k\left(k\right)!},$where$T_t^{k\alpha }$stands for sequential conformable time-fractional derivative of order$k$that is defined by$T^{k\alpha }𝓊\left(x,t\right)=\underset{k-\mathrm{times}}{\underbrace{T^{\alpha }·T^{\alpha }\cdots T^{\alpha }𝓊\left(x,t\right)}}$.

The$n$th-partial sum of the multiple fractional PS (Equation (8)) is given by

$${𝓊}_n\left(x,t\right)={\displaystyle \sum }_{k=0}^n{f}_k\left(x\right)\left(t-t_0\right){ }^{k\alpha }, x\in I, t_0\le t<t_0+R^{\frac{1}{\alpha }},R>0.$$

(9)

Corollary 1.

Let$\alpha \in \left(n-1,n\right]$, $T_t^{k\alpha }𝓊\left(x,t\right)$exist at a neighborhood of a point$t_0$for$k=0,1,2,\dots ,n+1,$and$𝓊\left(x,t\right)$can be expressed by the multiple fractional PS (Equation (8)) about$t=t_0$such that$\left|T_t^{\left(n+1\right)\alpha }𝓊\left(x,t\right)\right|\le M\left(x\right)$, for some$n\in \mathbb{N}.$Then, for all$\left({\tau }_0,{\tau }_0+R^{1/\alpha }\right)$, the reminder${ℛ}_n\left(t\right)$of the multiple fractional PS satisfies

$$\left|{ℛ}_n\left(x,t\right)\right|\le \frac{M\left(x\right)}{{\alpha }^{n+1}\left(n+1\right)!}{\left(t-t_0\right)}^{\left(n+1\right)\alpha },$$

(10)

where${ℛ}_n\left(x,t\right)={\sum }_{k=n+1}^{\infty }\frac{T_t^{k\alpha }𝓊\left(x,t_0\right)}{{\alpha }^k\left(k\right)!}\left(t-t_0\right){ }^{k\alpha }=𝓊\left(x,t\right)-{\sum }_{k=0}^n\frac{T_t^{k\alpha }𝓊\left(x,t_0\right)}{{\alpha }^k\left(k\right)!}\left(t-t_0\right){ }^{k\alpha }$.

3. The Conformable RPS Approach

This section aims to construct the multiple CRPS solutions for Equations (1) and (2) based on fractional Taylor series in the sense of conformable derivative through substituting the series expansion within its truncated residual error functions. To achieve our goal, let $𝓊\left(x,t\right)=𝓋\left(x,t\right)+i𝓌\left(x,t\right)$ in Equation (1) so that the following equivalent coupled system can be obtained

$$\begin{gathered} T_t^{\alpha }𝓋\left(x,t\right)+\xi {𝓌}_{xx}\left(x,t\right)+\psi \left(x\right)𝓌\left(x,t\right)+\eta \left({𝓋}^2\left(x,t\right)𝓌\left(x,t\right)+{𝓌}^3\left(x,t\right)\right)=0, \\ {T}_t^{\alpha }𝓌\left(x,t\right)-\xi {𝓋}_{xx}\left(x,t\right)-\psi \left(x\right)𝓋\left(x,t\right)-\eta \left({𝓋}^3\left(x,t\right)+{𝓌}^2\left(x,t\right)𝓋\left(x,t\right)\right)=0, \end{gathered}$$

(11)

subject to the initial conditions

$$𝓋\left(x,0\right)={𝓋}_0\left(x\right), \mathrm{and} 𝓌\left(x,0\right)={𝓌}_0\left(x\right),$$

(12)

in which $𝓊\left(x,0\right)={𝓋}_0\left(x\right)+i{𝓌}_0\left(x\right)$.

Now, let us assume that the solutions of Equations (11) and (13) for $0\le t, x\in ℝ$, have the following multiple CRPS about $t_0=0$:

$$\begin{gathered} 𝓋\left(x,t\right)={\displaystyle \sum _{k=0}^{\infty }}{a}_k\left(x\right)\frac{t^{k\alpha }}{{\alpha }^{k}k!}, \\ 𝓌\left(x,t\right)={\displaystyle \sum _{k=0}^{\infty }}{b}_k\left(x\right)\frac{t^{k\alpha }}{{\alpha }^{k}k!}, \end{gathered}$$

(13)

Evidently, the $n$th-truncated series solutions can be defined as follows

$$\begin{gathered} {𝓋}_n\left(x,t\right)={𝓋}_0\left(x\right)+{\displaystyle \sum _{k=1}^n}{a}_k\left(x\right)\frac{t^{k\alpha }}{{\alpha }^{k}k!}, \\ {𝓌}_n\left(x,t\right)={𝓌}_0\left(x\right)+{\displaystyle \sum _{k=1}^n}{b}_k\left(x\right)\frac{t^{k\alpha }}{{\alpha }^{k}k!}, \end{gathered}$$

(14)

and the $n$th-residual functions can be defined as follows

$$\begin{array}{c}Re{s}_{𝓋}^n\left(x,t\right)=T_t^{\alpha }{𝓋}_n\left(x,t\right)+\xi {\left({𝓌}_n\right)}_{xx}\left(x,t\right)+\psi \left(x\right){𝓌}_n\left(x,t\right)+\eta ({𝓋}_n^2\left(x,t\right){𝓌}_n\left(x,t\right)+\\ {𝓌}_n^3\left(x,t\right)),\\ Re{s}_{𝓌}^n\left(x,t\right)=T_t^{\alpha }{𝓌}_n\left(x,t\right)-\xi {({𝓋}_n)}_{xx}\left(x,t\right)-\psi \left(x\right){𝓋}_n\left(x,t\right)\\ -\eta \left({𝓋}_n^3\left(x,t\right)+{𝓌}_n^2\left(x,t\right){𝓋}_n\left(x,t\right)\right),\end{array}$$

(15)

whereas the residual functions

$$Re{s}_{𝓋}\left(x,t\right)=\underset{n\to \infty }{\lim }Re{s}_{𝓋}^n\left(x,t\right) \mathrm{and} Re{s}_{𝓌}\left(x,t\right)=\underset{n\to \infty }{\lim }Re{s}_{𝓌}^n\left(x,t\right).$$

Consequently, it can be noted that $Res\left(x,t\right)$ is vanished for each $x\in ℝ$ and $0<t<\epsilon$, where $\epsilon$ is the convergence radius for the multiple PS. Also, $T_t^{n\alpha }Res\left(x,t\right)=0$ and $T_t^{\left(n-1\right)\alpha }Res{\left(x,t\right)}_{│t=0}=0$ for each $n=1,2,\dots$. Therefore, by solving the corresponding system $T_t^{\left(n-1\right)\alpha }Re{s}_{}^n{\left(x,t\right)}_{│t=0}=0$, $n=1,2,3,\dots$, the unknown coefficients of Equation (13) can be determined with the help of the fact that $T_t^{\alpha }{t}^p=0$ for $p>\alpha$ at $t=0$ after a little simplification. However, to find the unknown coefficients $a_k\left(x\right) \mathrm{and} b_k\left(x\right), k=1,2,\dots ,n,$ of $n\mathrm{th}$-truncated series (Equation (14)), do the following: Firstly, substitute the first truncated series ${𝓋}_1\left(x,t\right)={𝓋}_0\left(x\right)+a_1\left(x\right)\frac{t^{\alpha }}{\alpha }$ and ${𝓌}_1\left(x,t\right)={𝓌}_0\left(x\right)+b_1\left(x\right)\frac{t^{\alpha }}{\alpha }$ into the first truncated residual functions $Re{s}_{𝓋}^1\left(x,t\right)$ and $Re{s}_{𝓌}^1\left(x,t\right)$ such that

$$\begin{array}{cc}\hfill Re{s}_{𝓋}^1\left(x,t\right)=a_1\left(x\right)& +\xi \left({𝓌}_0^{″}\left(x\right)+\frac{b_1^{″}\left(x\right)t^{\alpha }}{\alpha }\right)+\psi \left(x\right)\left({𝓌}_0\left(x\right)+\frac{b_1\left(x\right)t^{\alpha }}{\alpha }\right),\hfill \\ & +\eta (\left({𝓋}_0^2\left(x\right)+2{𝓋}_0\left(x\right)a_1\left(x\right)\frac{t^{\alpha }}{\alpha }+\frac{a_1^2\left(x\right)t^{2\alpha }}{{\alpha }^2}\right)\left({𝓌}_0\left(x\right)+\frac{b_1\left(x\right)t^{\alpha }}{\alpha }\right)\hfill \\ & +\left({𝓌}_0^3\left(x\right)+3{𝓌}_0^2\left(x\right)b_1\left(x\right)\frac{t^{\alpha }}{\alpha }+\dots +\frac{b_1^3\left(x\right)t^{3\alpha }}{{\alpha }^3}\right)),\hfill \\ \hfill Re{s}_{𝓌}^1\left(x,t\right)=b_1\left(x\right)& -\xi \left({𝓋}_0^{″}\left(x\right)+\frac{a_1^{″}\left(x\right)t^{\alpha }}{\alpha }\right)-\psi \left(x\right)\left({𝓋}_0\left(x\right)+\frac{a_1\left(x\right)t^{\alpha }}{\alpha }\right)\hfill \\ & -\eta (\left({𝓋}_0^3\left(x\right)+3{𝓋}_0^2\left(x\right)a_1\left(x\right)\frac{t^{\alpha }}{\alpha }+\dots +\frac{a_1^3\left(x\right)t^{3\alpha }}{{\alpha }^3}\right)\hfill \\ & +\left({𝓌}_0^2\left(x\right)+2{𝓌}_0\left(x\right)b_1\left(x\right)\frac{t^{\alpha }}{\alpha }+\frac{b_1^2\left(x\right)t^{2\alpha }}{{\alpha }^2}\right)\left({𝓋}_0\left(x\right)+\frac{a_1\left(x\right)t^{\alpha }}{\alpha }\right)).\hfill \end{array}$$

(16)

Using $Re{s}_{𝓋}^1\left(x,0\right)=0$ and $Re{s}_{𝓌}^1\left(x,0\right)=0$, one can get

$$a_1\left(x\right)=-\left(\xi {𝓌}_0^{″}\left(x\right)+\psi \left(x\right){𝓌}_0\left(x\right)+\eta \left({𝓋}_0^2\left(x\right){𝓌}_0\left(x\right)+{𝓌}_0^3\left(x\right)\right)\right),$$

$$b_1\left(x\right)=\xi {𝓋}_0^{″}\left(x\right)+\psi \left(x\right){𝓋}_0\left(x\right)+\eta \left({𝓌}_0^2\left(x\right){𝓋}_0\left(x\right)+{𝓋}_0^3\left(x\right)\right).$$

Therefore, the first CRPS approximation of Equations (11) and (12) can be expressed as follows

$$\begin{array}{l}{𝓋}_1\left(x,t\right)={𝓋}_0\left(x\right)-\left(\xi {𝓌}_0^{″}\left(x\right)+\psi \left(x\right){𝓌}_0\left(x\right)+\eta \left({𝓋}_0^2\left(x\right){𝓌}_0\left(x\right)+{𝓌}_0^3\left(x\right)\right)\right)\frac{t^{\alpha }}{\alpha },\\ {𝓌}_1\left(x,t\right)={𝓌}_0\left(x\right)+\left(\xi {𝓋}_0^{″}\left(x\right)+\psi \left(x\right){𝓋}_0\left(x\right)+\eta \left({𝓌}_0^2\left(x\right){𝓋}_0\left(x\right)+{𝓋}_0^3\left(x\right)\right)\right)\frac{t^{\alpha }}{\alpha }.\end{array}$$

(17)

To determine the second unknown coefficients $a_2\left(x\right)$ and $b_2\left(x\right)$, substitute the second truncated series solutions ${𝓋}_2\left(x,t\right)={𝓋}_0\left(x\right)+a_1\left(x\right)\frac{t^{\alpha }}{\alpha }+a_2\left(x\right)\frac{t^{2\alpha }}{2{\alpha }^2}$ and ${𝓌}_1\left(x,t\right)={𝓌}_0\left(x\right)+b_1\left(x\right)\frac{t^{\alpha }}{\alpha }+b_2\left(x\right)\frac{t^{2\alpha }}{2{\alpha }^2}$ into the second truncated residual functions $Re{s}_{𝓋}^2\left(x,t\right)$ and $Re{s}_{𝓌}^2\left(x,t\right)$ such that

$$\begin{array}{cc}\hfill Re{s}_{𝓋}^2\left(x,t\right)=& (a_1\left(x\right)+\frac{a_2\left(x\right)t^{\alpha }}{\alpha })+\xi \left({𝓌}_0^{″}\left(x\right)+\frac{b_1^{″}\left(x\right)t^{\alpha }}{\alpha }+\frac{b_2^{″}\left(x\right)t^{2\alpha }}{2{\alpha }^2}\right)\hfill \\ & \hspace{1em}\hspace{1em}+\psi \left(x\right)\left({𝓌}_0\left(x\right)+\frac{b_1\left(x\right)t^{\alpha }}{\alpha }+\frac{b_2\left(x\right)t^{2\alpha }}{2{\alpha }^2}\right)\hfill \\ & \hspace{1em}\hspace{1em}+\eta \left(\left({𝓋}_0^2\left(x\right)+\frac{2{𝓋}_0\left(x\right)a_1\left(x\right)t^{\alpha }}{\alpha }+\dots +\frac{a_2^2\left(x\right)t^{4\alpha }}{4{\alpha }^4}\right)\right({𝓌}_0\left(x\right)+\frac{b_1\left(x\right)t^{\alpha }}{\alpha }\hfill \\ & \hspace{1em}\hspace{1em}+\frac{b_2\left(x\right)t^{2\alpha }}{2{\alpha }^2})+\left({𝓌}_0^3\left(x\right)+\frac{3{𝓌}_0^2\left(x\right)b_1\left(x\right)t^{\alpha }}{\alpha }+\dots +\frac{b_2^3\left(x\right)t^{6\alpha }}{2^3{\alpha }^6}\right)),\hfill \\ \hfill Re{s}_{𝓌}^2\left(x,t\right)=& \left(b_1\left(x\right)+\frac{b_2\left(x\right)t^{\alpha }}{\alpha }\right)-\xi \left({𝓋}_0^{″}\left(x\right)+\frac{a_1^{″}\left(x\right)t^{\alpha }}{\alpha }+\frac{a_2^{″}\left(x\right)t^{2\alpha }}{2{\alpha }^2}\right)\hfill \\ & \hspace{1em}\hspace{1em}-\psi \left(x\right)\left({𝓋}_0\left(x\right)+\frac{a_1\left(x\right)t^{\alpha }}{\alpha }+\frac{a_2\left(x\right)t^{2\alpha }}{2{\alpha }^2}\right)\hfill \\ & \hspace{1em}\hspace{1em}-\eta (\left({𝓋}_0^3\left(x\right)+\frac{3{𝓋}_0^2\left(x\right)a_1\left(x\right)t^{\alpha }}{\alpha }+\dots +\frac{a_2^3\left(x\right)t^{6\alpha }}{2^3{\alpha }^6}\right)\hfill \\ & \hspace{1em}\hspace{1em}+\left({𝓌}_0^2\left(x\right)+\frac{2{𝓌}_0\left(x\right)b_1\left(x\right)t^{\alpha }}{\alpha }+\dots +\frac{b_2^2\left(x\right)t^{4\alpha }}{4{\alpha }^4}\right)({𝓋}_0\left(x\right)+\frac{a_1\left(x\right)t^{\alpha }}{\alpha }\hfill \\ & \hspace{1em}\hspace{1em}+\frac{a_2\left(x\right)t^{2\alpha }}{2{\alpha }^2})).\hfill \end{array}$$

(18)

Now, by operating $T_t^{\alpha }$ on both sides of Equation (18), using the fact that $T_t^{\alpha }{t}^p=0$ for $p>\alpha$ at $t=0$ and equating the resulting equations to zero at $t=0$ yields

$$\begin{array}{ll}{T}_t^{\alpha }Re{s}_{𝓋}^2{\left(x,t\right)}_{│t=0}& \\ & =a_2\left(x\right)+\xi b_1^{″}\left(x\right)+\psi \left(x\right)b_1\left(x\right)\\ & +\eta \left(\left(2{𝓌}_0\left(x\right){𝓋}_0\left(x\right)a_1\left(x\right)+{𝓋}_0^2\left(x\right)b_1\left(x\right)\right)+\left(3{𝓌}_0^2\left(x\right)b_1\left(x\right)\right)\right)=0,\end{array}$$

$$\begin{array}{ll}{T}_t^{\alpha }Re{s}_{𝓌}^2{\left(x,t\right)}_{│t=0}& \\ & =a_2\left(x\right)+\xi b_1^{″}\left(x\right)+\psi \left(x\right)b_1\left(x\right)& \\ & =b_2\left(x\right)-\xi a_1^{″}\left(x\right)-\psi \left(x\right)a_1\left(x\right)\\ & -\eta \left(\left(3{𝓋}_0^2\left(x\right)a_1\left(x\right)\right)+\left(2{𝓌}_0\left(x\right){𝓋}_0\left(x\right)b_1\left(x\right)+{𝓌}_0^2\left(x\right)a_1\left(x\right)\right)\right)=0.\end{array}$$

Thus, the send unknown coefficients $a_2\left(x\right)$ and $b_2\left(x\right)$ are given by

$$a_2\left(x\right)=-\left(\xi b_1^{″}\left(x\right)+\psi \left(x\right)b_1\left(x\right)+\eta \left(2{𝓌}_0\left(x\right){𝓋}_0\left(x\right)a_1\left(x\right)+\left({𝓋}_0^2\left(x\right)+3{𝓌}_0^2\left(x\right)\right)b_1\left(x\right)\right)\right),$$

$$b_2\left(x\right)=\xi a_1^{″}\left(x\right)+\psi \left(x\right)a_1\left(x\right)+\eta \left(\left(3{𝓋}_0^2\left(x\right)+{𝓌}_0^2\left(x\right)\right)a_1\left(x\right)+2{𝓌}_0\left(x\right){𝓋}_0\left(x\right)b_1\left(x\right)\right).$$

Therefore, the second CRPS approximation of Equations (11) and (12) can be expressed as follows

$$\begin{array}{cc}\hfill {𝓋}_2\left(x,t\right)={𝓌}_0\left(x\right)& -\left(\xi {𝓌}_0^{″}\left(x\right)+\psi \left(x\right){𝓌}_0\left(x\right)+\eta \left({𝓋}_0^2\left(x\right){𝓌}_0\left(x\right)+{𝓌}_0^3\left(x\right)\right)\right)\frac{t^{\alpha }}{\alpha }\hfill \\ & -(\xi b_1^{″}\left(x\right)+\psi \left(x\right)b_1\left(x\right)\hfill \\ & +\eta \left(2{𝓌}_0\left(x\right){𝓋}_0\left(x\right)a_1\left(x\right)+\left({𝓋}_0^2\left(x\right)+3{𝓌}_0^2\left(x\right)\right)b_1\left(x\right)\right))\frac{t^{2\alpha }}{2{\alpha }^2},\hfill \\ \hfill {𝓌}_2\left(x,t\right)={𝓌}_0\left(x\right)& +(\xi {𝓋}_0^{″}\left(x\right)+\psi \left(x\right){𝓋}_0\left(x\right)+\eta \left({𝓌}_0^2\left(x\right){𝓋}_0\left(x\right)+{𝓋}_0^3\left(x\right)\right))\frac{t^{\alpha }}{\alpha }\hfill \\ & +(\xi a_1^{″}\left(x\right)+\psi \left(x\right)a_1\left(x\right)\hfill \\ & +\eta \left(\left(3{𝓋}_0^2\left(x\right)+{𝓌}_0^2\left(x\right)\right)a_1\left(x\right)+2{𝓌}_0\left(x\right){𝓋}_0\left(x\right)b_1\left(x\right)\right))\frac{t^{2\alpha }}{2{\alpha }^2}.\hfill \end{array}$$

(19)

As the former, the third unknown coefficients $a_3\left(x\right)$ and $b_3\left(x\right)$ can be obtained using $T_t^{2\alpha }Re{s}_{𝓋}^3\left(x,0\right)=T_t^{2\alpha }Re{s}_{𝓌}^3\left(x,0\right)=0$. However, without losing the generality, by continuing the same argument of CRPS algorithm up to arbitrary order $\mathrm{n}$, the multiple CRPS solution ${𝓊}_n\left(x,t\right)$ of Equations (1) and (2) can be directly obtained. Furthermore, high accuracy can be accomplished by calculating more components of the CRPS solution.

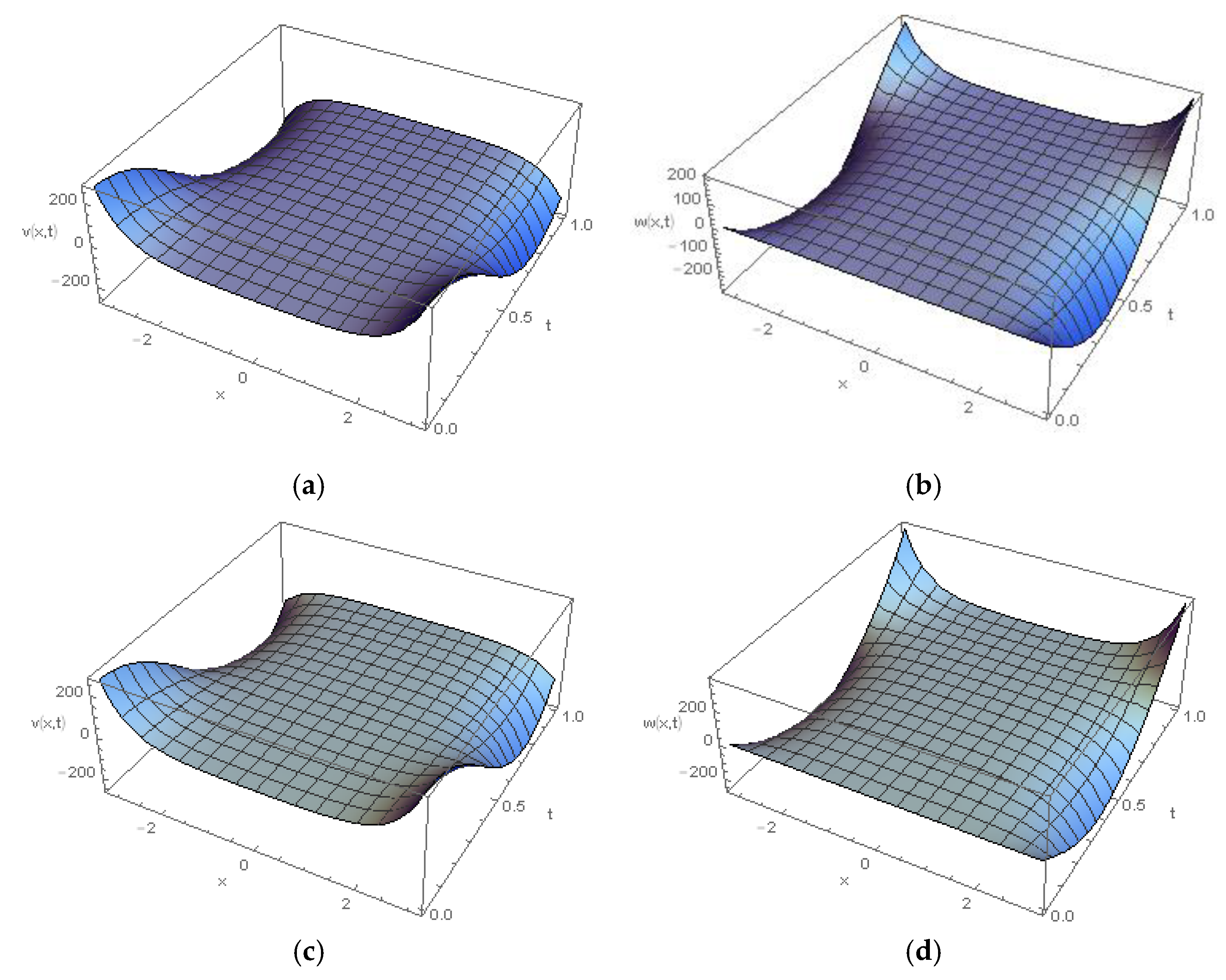
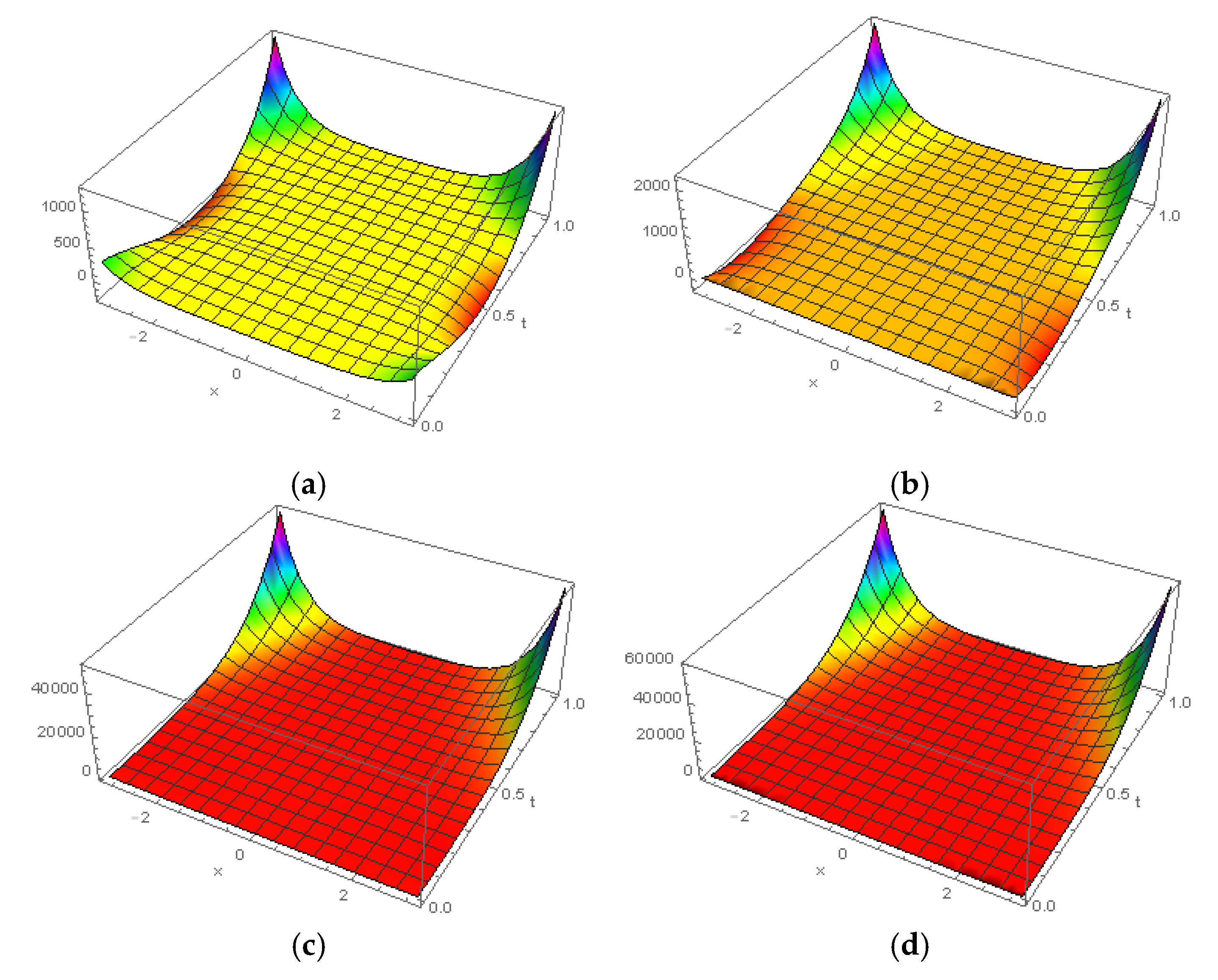
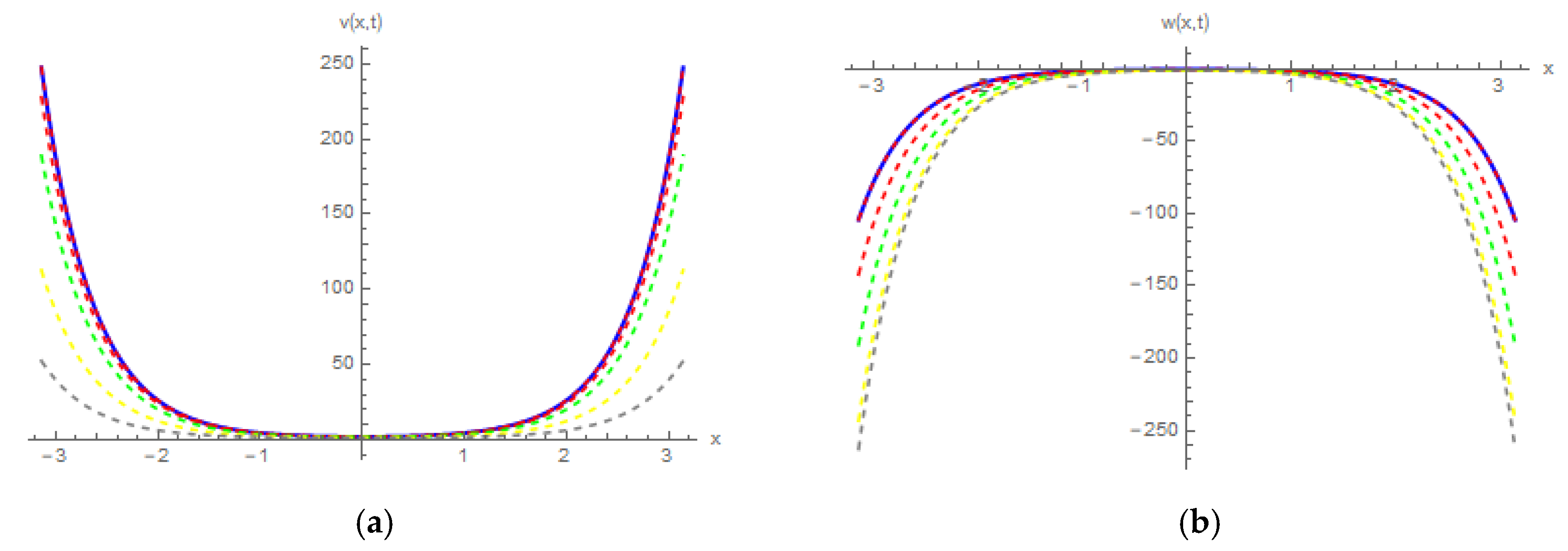
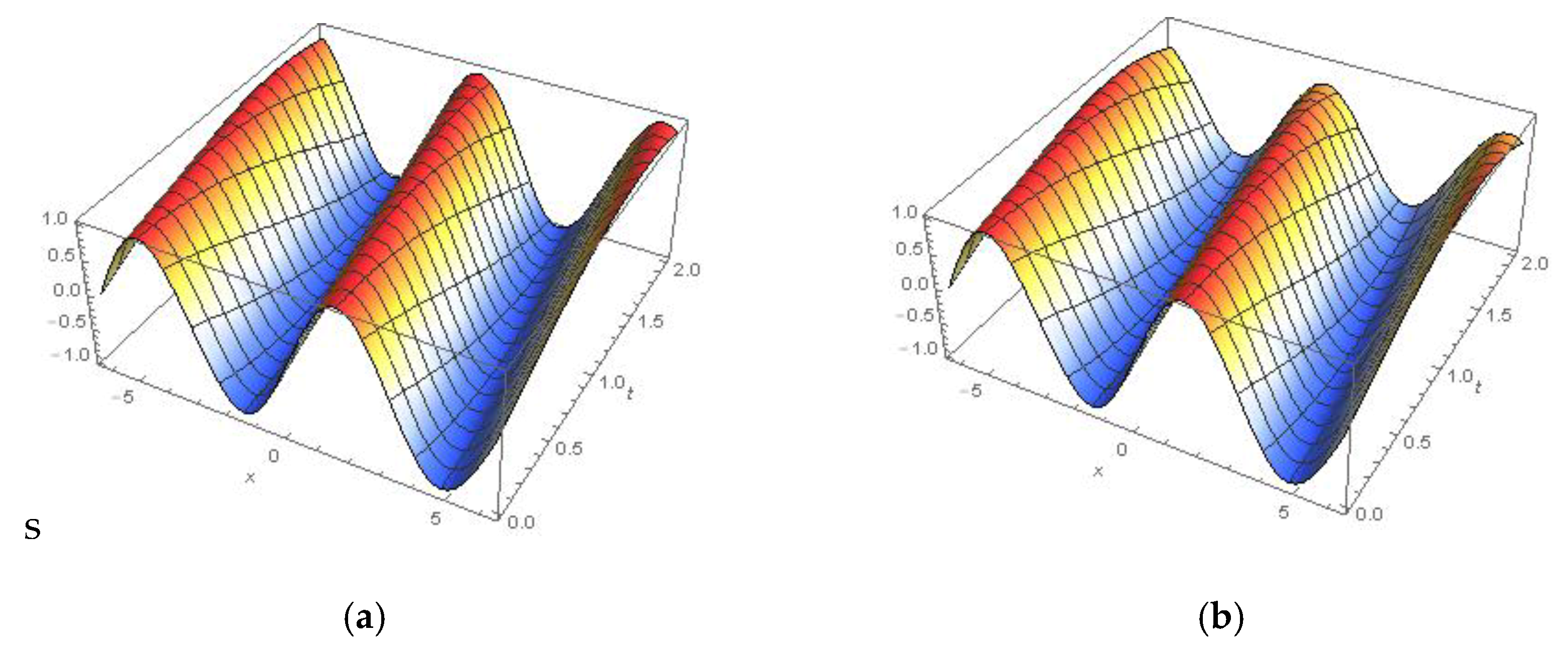
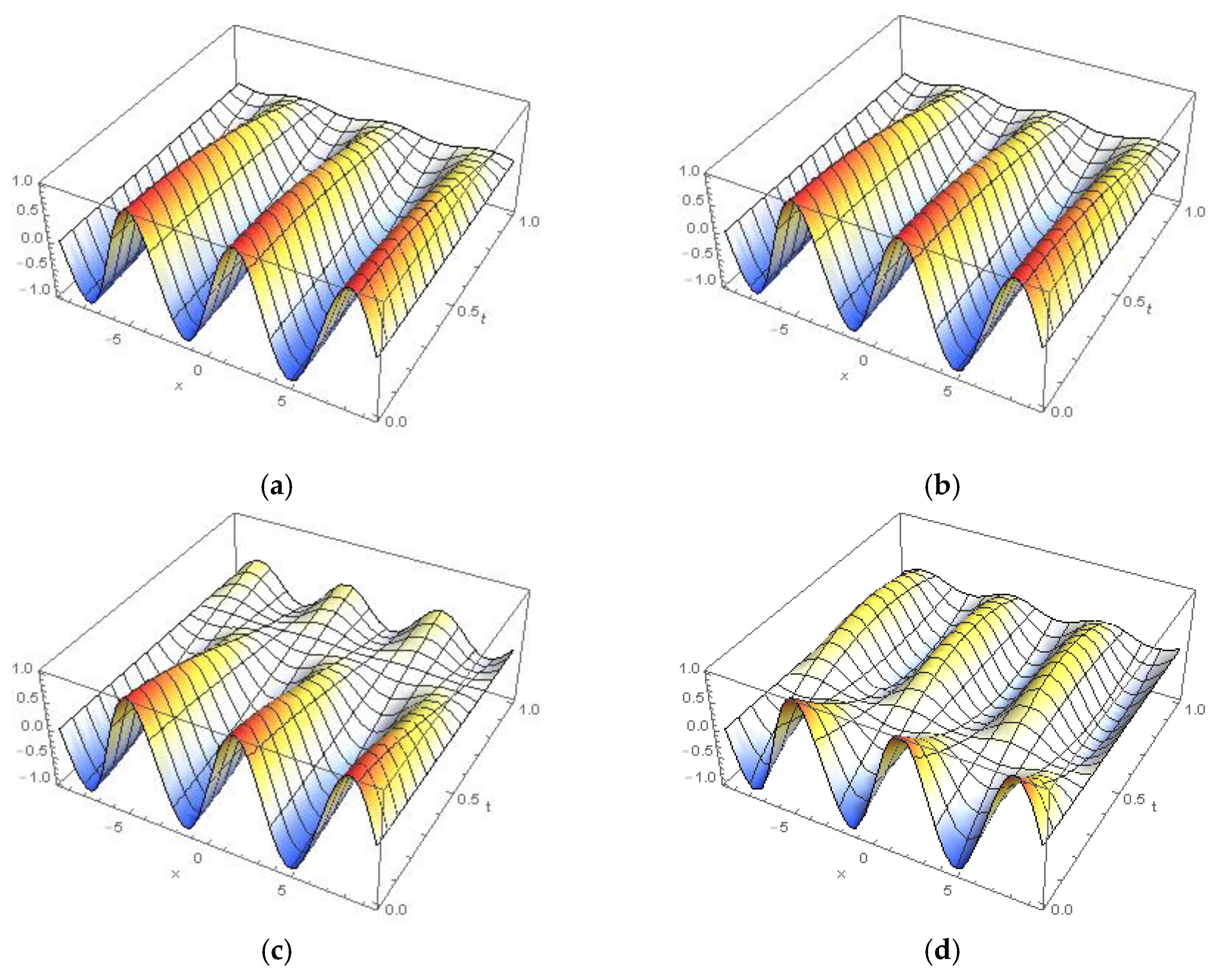
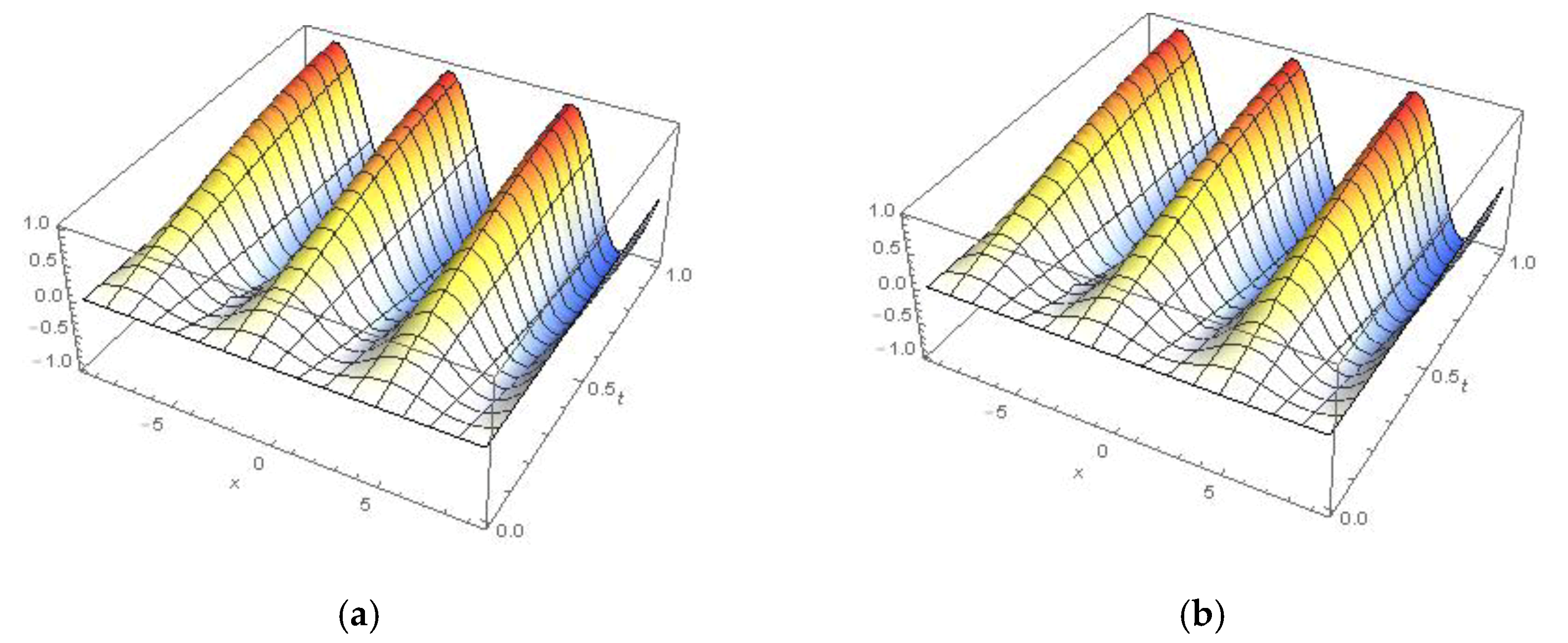
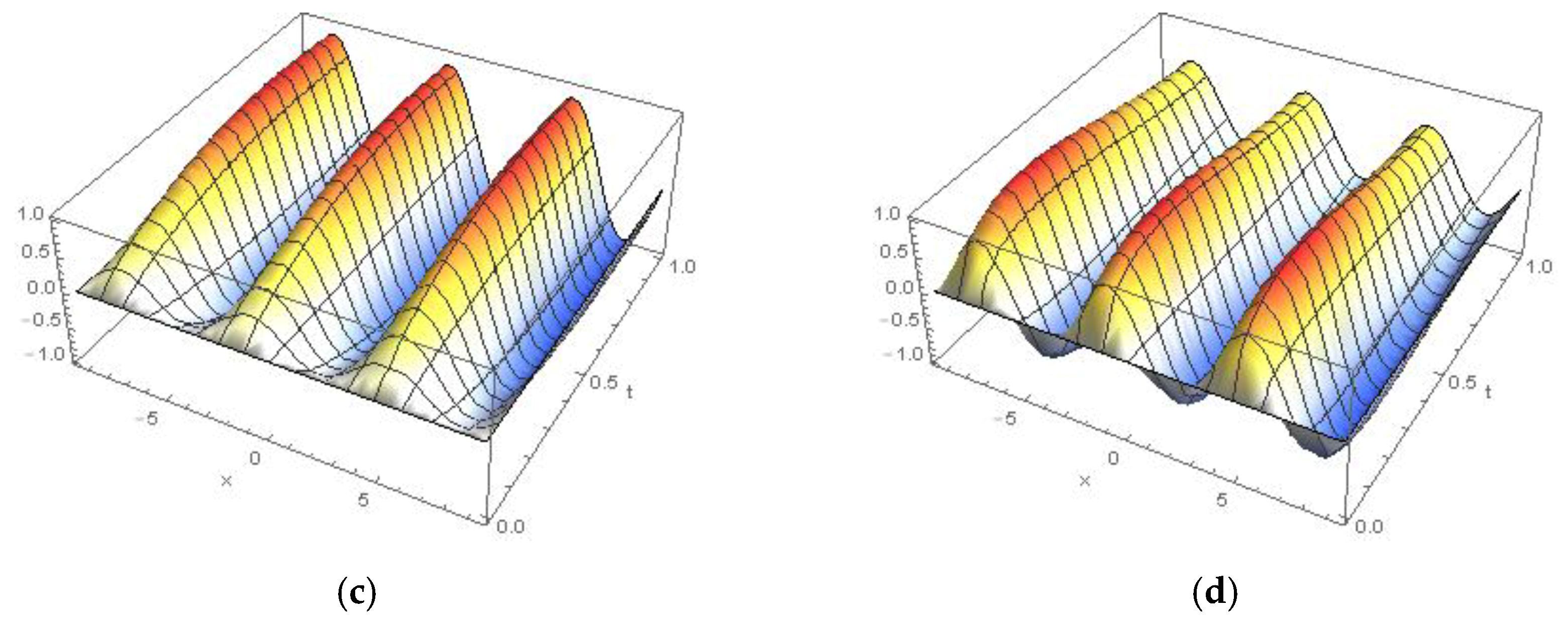
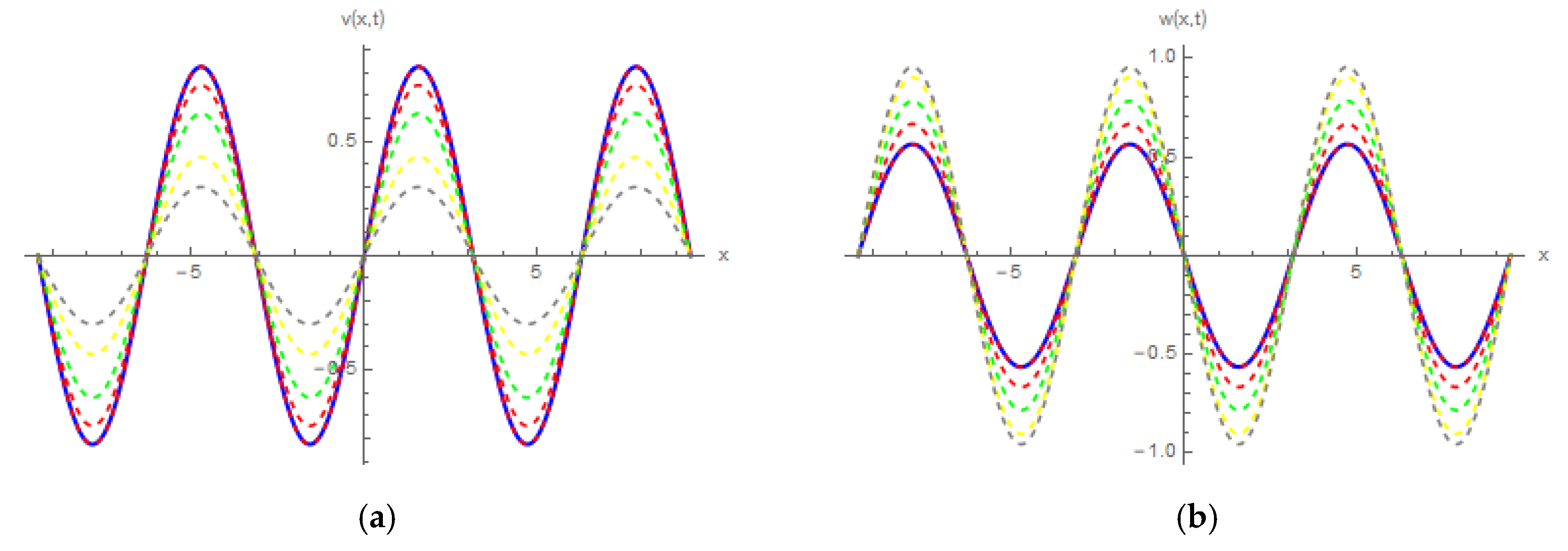
4. Physical Numerical Applications

The fractional quantum mechanics based on the Levy path integral generalizes the standard quantum mechanics based on the well-known Feynman path integral. It has been realized that the understanding of complex quantum and classical physics phenomena requires the implementation of the Levy fights random process instead of Brownian motion. The motivation behind the involvement of Levy fights into consideration is that if the path integral over Brownian trajectories leads to the well-known Schrödinger equation, then the path integral over Levy trajectories leads to the fractional Schrödinger equation. This section is intended for displaying some numerical applications to show the efficiency, reliability, and simplicity of the proposed method in finding conformable series coefficients for both linear and nonlinear FSEs associated with trapping potential. Wolfram’s Mathematica software package was used in all computational processes.

Example 1.

Consider the following linear fractional Schrödinger equation with zero trapping potential [42,43]:

$$i{T}_t^{\alpha }𝓊\left(x,t\right)-{𝓊}_{xx}\left(x,t\right)=0, t\ge 0, 0<\alpha \le 1,$$

(20)

subject to the initial condition

$$𝓊\left(x,0\right)=1+\cosh \left(2x\right),x\in ℝ.$$

(21)

This model is a special case of FSE that arises in the modeling of free particle state, where the particle moves without any potential energy. In particular, the exact solution of this model at $\alpha =1$ is $\begin{array}{c}𝓊\left(x,t\right)\end{array}=1+\cosh \left(2x\right)e^{-4it}$.

To achieve our goal, let $𝓊\left(x,t\right)=𝓋\left(x,t\right)+i𝓌\left(x,t\right)$ so that $𝓊\left(x,0\right)={𝓋}_0\left(x\right)+i{𝓌}_0\left(x\right)$. Then, the corresponding coupled system is given by

$$\begin{gathered} T_t^{\alpha }𝓋\left(x,t\right)-{𝓌}_{xx}\left(x,t\right)=0, \\ {T}_t^{\alpha }𝓌\left(x,t\right)+{𝓋}_{xx}\left(x,t\right)=0, \end{gathered}$$

(22)

subject to the following initial conditions

$$𝓋\left(x,0\right)=1+\cosh \left(2x\right) \mathrm{and} 𝓌\left(x,0\right)=0.$$

(23)

According to CRPS algorithm, the $n$th-truncated series solutions are given by

$$\begin{array}{l}{𝓋}_n\left(x,t\right)=1+\cosh \left(2x\right)+{\displaystyle {\displaystyle \sum }_{k=1}^n}{a}_k\left(x\right)\frac{t^{k\alpha }}{{\alpha }^{k}k!},\\ {𝓌}_n\left(x,t\right)={\displaystyle {\displaystyle \sum }_{k=1}^n}{b}_k\left(x\right)\frac{t^{k\alpha }}{{\alpha }^{k}k!},\end{array}$$

(24)

while the $n$th-residual functions can be defined by

$$\begin{array}{l}Re{s}_{𝓋}^n\left(x,t\right)=T_t^{\alpha }{𝓋}_n\left(x,t\right)-{\left({𝓌}_n\right)}_{xx}\left(x,t\right),\\ Re{s}_{𝓌}^n\left(x,t\right)=T_t^{\alpha }{𝓌}_n\left(x,t\right)+{({𝓋}_n)}_{xx}\left(x,t\right).\end{array}$$

(25)

For $n=1$, substitute the first truncated series ${𝓋}_1\left(x,t\right)=1+\cosh \left(2x\right)+a_1\left(x\right)\frac{t^{\alpha }}{\alpha }$ and ${𝓌}_1\left(x,t\right)=b_1\left(x\right)\frac{t^{\alpha }}{\alpha }$ into the first truncated residual functions $Re{s}_{𝓋}^1\left(x,t\right)$ and $Re{s}_{𝓌}^1\left(x,t\right)$ such that

$$\begin{array}{l}Re{s}_{𝓋}^1\left(x,t\right)=a_1\left(x\right)-\frac{b_1^{″}\left(x\right)t^{\alpha }}{\alpha },\\ Re{s}_{𝓌}^1\left(x,t\right)=b_1\left(x\right)+\left(4\cosh \left(2x\right)+\frac{a_1^{″}\left(x\right)t^{\alpha }}{\alpha }\right).\end{array}$$

(26)

By using $Re{s}_{𝓋}^1\left(x,0\right)=0$ and $Re{s}_{𝓌}^1\left(x,0\right)=0$, one can get

$$a_1\left(x\right)=0 \mathrm{and} b_1\left(x\right)=-4\cosh \left(2x\right).$$

Therefore, the first CRPS approximations of Equations (22) and (23) are

$${𝓋}_1\left(x,t\right)=1+\cosh \left(2x\right) \mathrm{and} {𝓌}_1\left(x,t\right)=-4\cosh \left(2x\right)\frac{t^{\alpha }}{\alpha }.$$

For $n=2$, substitute the second truncated series solutions ${𝓋}_2\left(x,t\right)=1+\cosh \left(2x\right)+a_2\left(x\right)\frac{t^{2\alpha }}{2{\alpha }^2}$ and ${𝓌}_2\left(x,t\right)=-4\cosh \left(2x\right)\frac{t^{\alpha }}{\alpha }+b_2\left(x\right)\frac{t^{2\alpha }}{2{\alpha }^2}$ into the second truncated residual functions $Re{s}_{𝓋}^2\left(x,t\right)$ and $Re{s}_{𝓌}^2\left(x,t\right)$ such that

$$\begin{array}{l}Re{s}_{𝓋}^2\left(x,t\right)=\frac{a_2\left(x\right)t^{\alpha }}{\alpha }+\left(\frac{16\cosh \left(2x\right)t^{\alpha }}{\alpha }-\frac{b_2^{″}\left(x\right)t^{2\alpha }}{2{\alpha }^2}\right),\\ Re{s}_{𝓌}^2\left(x,t\right)=\frac{b_2\left(x\right)t^{\alpha }}{\alpha }+\frac{a_2^{″}\left(x\right)t^{2\alpha }}{2{\alpha }^2}.\end{array}$$

(27)

Consequently, by operating $T_t^{\alpha }$ on both sides of Equation (27), using the fact that $T_t^{\alpha }{t}^p=0$ for $p>\alpha$ at $t=0$ and equating the resulting equations to zero at $t=0$ yields

$$\begin{array}{l}{T}_t^{\alpha }Re{s}_{𝓋}^2{\left(x,t\right)}_{│t=0}=a_2\left(x\right)+{\left(16\mathit{cosh}\left(2x\right)-\frac{b_2^{″}\left(x\right)t^{\alpha }}{\alpha }\right)}_{│t=0}=0,\\ T_t^{\alpha }Re{s}_{𝓌}^2{\left(x,t\right)}_{│t=0}=b_2\left(x\right)+{\left(\frac{a_2^{″}\left(x\right)t^{\alpha }}{\alpha }\right)}_{│t=0}=0.\end{array}$$

That is, $a_2\left(x\right)=-16\cosh \left(2x\right)$ and $b_2\left(x\right)=0.$ Therefore, the second CPS approximate solutions of Equations (22) and (23) are

$${𝓋}_2\left(x,t\right)=1+\cosh \left(2x\right)-8\cosh \left(2x\right)\frac{t^{2\alpha }}{{\alpha }^2} \mathrm{and} {𝓌}_2\left(x,t\right)=-4\cosh \left(2x\right)\frac{t^{\alpha }}{\alpha }.$$

For $n=3$, substitute the third truncated series solutions ${𝓋}_3\left(x,t\right)=1+\cosh \left(2x\right)-8\cosh \left(2x\right)\frac{t^{2\alpha }}{{\alpha }^2}+a_3\left(x\right)\frac{t^{3\alpha }}{3!{\alpha }^3}$ and ${𝓌}_3\left(x,t\right)=-4\cosh \left(2x\right)\frac{t^{\alpha }}{\alpha }+b_3\left(x\right)\frac{t^{3\alpha }}{3!{\alpha }^3}$ into the third truncated residual functions $Re{s}_{𝓋}^3\left(x,t\right)$ and $Re{s}_{𝓌}^3\left(x,t\right)$ such that

$$\begin{array}{l}Re{s}_{𝓋}^3\left(x,t\right)=\left(\frac{-8\cosh \left(2x\right)t^{\alpha }}{\alpha }+\frac{a_3\left(x\right)t^{2\alpha }}{2{\alpha }^2}\right)+\left(\frac{16\cosh \left(2x\right)t^{\alpha }}{\alpha }-\frac{b_3^{″}\left(x\right)t^{3\alpha }}{3!{\alpha }^3}\right),\\ Re{s}_{𝓌}^3\left(x,t\right)=\frac{b_3\left(x\right)t^{2\alpha }}{2{\alpha }^2}-\frac{32\cos \mathrm{h}\left(2x\right)t^{2\alpha }}{{\alpha }^2}+\frac{a_3^{″}\left(x\right)t^{3\alpha }}{3!{\alpha }^3}.\end{array}$$

(28)

Consequently, by operating $T_t^{\alpha }$ twice on both sides of Equation (28) and equating the resulting equations to zero at $t=0$ such that

$$\begin{array}{l}{T}_t^{2\alpha }Re{s}_{𝓋}^3{\left(x,t\right)}_{│t=0}=a_3\left(x\right)-{\left(\frac{b_3^{″}\left(x\right)t^{\alpha }}{\alpha }\right)}_{│t=0}=0,\\ T_t^{2\alpha }Re{s}_{𝓌}^3{\left(x,t\right)}_{│t=0}=b_3\left(x\right)-{\left(64\cosh \left(2x\right)+\frac{a_3^{″}\left(x\right)t^{\alpha }}{\alpha }\right)}_{│t=0}=0.\end{array}$$

That is, $a_3\left(x\right)=0$ and $b_3\left(x\right)=64\cosh \left(2x\right).$ Therefore, the third FPS approximate solutions of Equations (22) and (23) are

$$\begin{array}{l}{𝓋}_3\left(x,t\right)=1+\cosh \left(2\mathrm{x}\right)-8\cos \mathrm{h}\left(2x\right)\frac{t^{2\alpha }}{{\alpha }^2}, \\ {𝓌}_3\left(x,t\right)=-4\cosh \left(2x\right)\frac{t^{\alpha }}{\alpha }+32\cos \mathrm{h}\left(2x\right)\frac{t^{3\alpha }}{3{\alpha }^3} .\end{array}$$

As the former, the fourth unknown coefficients $a_4\left(x\right)$ and $b_4\left(x\right)$ can be obtained using the same procedure of CRPS with the help of the fact that $T_t^{3\alpha }Re{s}_{𝓋}^4\left(x,0\right)=$ $T_t^{3\alpha }Re{s}_{𝓌}^4\left(x,0\right)=0$ such that $a_4\left(x\right)=256\cosh \left(2x\right)$ and $b_4\left(x\right)=0$. Thus, the fourth FPS approximate solutions of Equations (22) and (23) are

$$\begin{array}{l}{𝓋}_4\left(x,t\right)=1+\cosh \left(2x\right)-8\cosh \left(2x\right)\frac{t^{2\alpha }}{{\alpha }^2}+32\cosh \left(2x\right)\frac{t^{4\alpha }}{3{\alpha }^4},\\ {𝓌}_4\left(x,t\right)=-4\cosh \left(2x\right)\frac{t^{\alpha }}{\alpha }+32\cosh \left(2x\right)\frac{t^{3\alpha }}{3{\alpha }^3}.\end{array}$$

Hence, the first few CRPS solutions for Equations (20) and (21) are given as follows:

$$\begin{array}{l}{𝓊}_1\left(x,t\right)=1+\cosh \left(2x\right)-4i\cosh \left(2x\right)\frac{t^{\alpha }}{\alpha },\\ {𝓊}_2\left(x,t\right)=1+\cosh \left(2x\right)\left(1-\frac{8t^{2\alpha }}{{\alpha }^2}-i\frac{4t^{\alpha }}{\alpha }\right),\\ {𝓊}_3\left(x,t\right)=1+\cosh \left(2x\right)\left(\left(1-\frac{8t^{2\alpha }}{{\alpha }^2}\right)+i\left(\frac{-4t^{\alpha }}{\alpha }+\frac{32t^{3\alpha }}{3{\alpha }^3}\right)\right),\\ {𝓊}_4\left(x,t\right)=1+\cosh \left(2x\right)\left(\left(1-\frac{8t^{2\alpha }}{{\alpha }^2}+\frac{32t^{4\alpha }}{3{\alpha }^4}\right)+i\left(\frac{-4t^{\alpha }}{\alpha }+\frac{32t^{3\alpha }}{3{\alpha }^3}\right)\right),\\ ⋮\end{array}$$

(29)

by continuing this procedure, the multiple CFPS solution $𝓊\left(x,t\right)$ in term of infinite series can be obtained by

$$\begin{array}{cc}\hfill 𝓊\left(x,t\right)& =\left(1+\cosh \left(2x\right)-\frac{8\cosh \left(2x\right)}{{\alpha }^2}{t}^{2\alpha }+\frac{32\cosh \left(2x\right)}{3{\alpha }^4}{t}^{4\alpha }+\dots \right)\hfill \\ & +i\left(\frac{-4\cosh \left(2x\right)}{\alpha }{t}^{\alpha }+\frac{32\cosh \left(2x\right)}{3{\alpha }^3}{t}^{3\alpha }-\frac{128\cosh \left(2x\right)}{15{\alpha }^5}{t}^{5\alpha }+\dots \right)\hfill \\ & =1+\cosh \left(2x\right)\left(\begin{array}{c}\left(1-\frac{4^2{t}^{2\alpha }}{2!{\alpha }^2}+\frac{4^4{t}^{4\alpha }}{4!{\alpha }^4}+\dots \right)\end{array}-i\left(\frac{4t^{\alpha }}{\alpha }-\frac{4^3{t}^{3\alpha }}{3!{\alpha }^3}+\frac{4^5{t}^{5\alpha }}{5!{\alpha }^5}-\dots \right)\right)\hfill \\ & =1+\cosh \left(2x\right)\left(\begin{array}{c}{\displaystyle {\displaystyle \sum }_{n=0}^{\infty }}\frac{{\left(-1\right)}^n}{\left(2n\right)!}\end{array}{\left(\frac{4t^{\alpha }}{\alpha }\right)}^{2n}-i\left(\begin{array}{c}{\displaystyle {\displaystyle \sum }_{n=0}^{\infty }}\frac{{\left(-1\right)}^n}{\left(2n+1\right)!}\end{array}{\left(\frac{4t^{\alpha }}{\alpha }\right)}^{2n+1}\right)\right).\hfill \end{array}$$

In particular, the CFPS solution of Equations (20) and (21) at $\alpha =1$ is $\begin{array}{c}𝓊\left(x,t\right)\end{array}=1+\cosh \left(2x\right)e^{-4it}$, which is exactly in accordance with the results obtained by homotopy perturbation method [42], variational iteration method [43], and Adomian decomposition method [44].

In the light of showing the agreement between the exact solutions and CRPS solutions at $\alpha =1$ of Equations (20) and (21), the absolute and relative errors are listed in

Table A1. Error analysis of the ninth CRPS solutions for Example 1 at $\alpha =1$.

$\left({\mathit{x}}_{\mathit{i}},{\mathit{t}}_{\mathit{i}}\right)$	$𝓋\left(\mathit{x},\mathit{t}\right) \mathbf{Solution}$		$𝓌\left(\mathit{x},\mathit{t}\right) \mathbf{Solution}$
	Absolute Error	Relative Error	Absolute Error	Relative Error
$\left(0.1,0.1\right)$	$2.22045\times {10}^{-16}$	$1.14483\times {10}^{-16}$	$0.00$	$0.00$
$\left(0.2,0.2\right)$	$0.00$	$0.00$	$0.00$	$0.00$
$\left(0.3,0.3\right)$	$0.00$	$0.00$	$4.44089\times {10}^{-16}$	$4.01927\times {10}^{-16}$
$\left(0.4,0.4\right)$	$6.77236\times {10}^{-15}$	$7.04759\times {10}^{-15}$	$8.28226\times {10}^{-14}$	$6.19529\times {10}^{-14}$
$\left(0.5,0.5\right)$	$6.59361\times {10}^{-13}$	$1.84255\times {10}^{-12}$	$6.58784\times {10}^{-12}$	$4.69514\times {10}^{-12}$
$\left(0.6,0.6\right)$	$2.95495\times {10}^{-11}$	$8.81637\times {10}^{-11}$	$2.45938\times {10}^{-10}$	$2.01089\times {10}^{-10}$
$\left(0.7,0.7\right)$	$7.62655\times {10}^{-10}$	$7.42876\times {10}^{-10}$	$5.43840\times {10}^{-9}$	$7.54782\times {10}^{-9}$
$\left(0.8,0.8\right)$	$1.31375\times {10}^{-8}$	$8.35151\times {10}^{-9}$	$8.19302\times {10}^{-8}$	$5.44541\times {10}^{-7}$
$\left(0.9,0.9\right)$	$1.66060\times {10}^{-7}$	$9.29446\times {10}^{-8}$	$9.20014\times {10}^{-7}$	$6.69043\times {10}^{-7}$

(Appendix A) for $n=9$ and at some selected grid points $\left(x_i,t_i\right)$ in the domain $\left[0,1\right]\times \left[0,1\right]$ with step-size $0.1$ for time and space directions. From the table, it can be noted that the CRPS approximate solutions are in good agreement with the exact solutions over the domain of interest. Figure A1 (Appendix B) shows the three-dimensional surface plots of the exact and CRPS solutions at $\alpha =1$ and $n=6$ for $t\in \left[0,1\right]$ and $x\in \left[-\pi ,\pi \right]$.

Figure A2 depicts the surface plots behavior of CRPS solutions of Example 1 at different levels of fractional order $\alpha$ for each $t\in \left[0,1\right]$ and $x\in \left[-\pi ,\pi \right]$ such that $\alpha =0.5$ and $\alpha =0.75$. Further, the curves of CRPS solutions for Example 1 at different values of $\alpha$ for each $x\in \left[-\pi ,\pi \right]$ with $t=0.1$ are shown in Figure A3, where blue, red, green, yellow, and gray indicate the solution curve when $\alpha =1$, $0.9, 0.8$, $0.7$, and $\alpha =0.6$, respectively. From these graphs, it can be indicated that the behavior of the approximate solutions for Equations (20) and (21) smoothly correspond to each other for different values of the fractional order $\alpha$.

Example 2.

Consider the following linear fractional Schrödinger equation with zero trapping potential [45,46]:

$$i{T}_t^{\alpha }𝓊\left(x,t\right)+{𝓊}_{xx}\left(x,t\right)+2{\left|𝓋\left(x,t\right)\right|}^2𝓋\left(x,t\right)=0, t\ge 0, 0<\alpha \le 1,$$

(30)

subject to the initial condition

$$𝓊\left(x,0\right)=e^{ix},x\in ℝ.$$

(31)

This model arises in the modeling of free particle state, where the particle moves without any potential energy. In particular, the exact solution of this model at $\alpha =1$ is $\begin{array}{c}𝓊\left(\mathrm{x},\mathrm{t}\right)\end{array}=e^{i\left(x+t\right)}$.

Evidently, the corresponding coupled system of Equations (30) and (31) is given by

$$\begin{array}{l}{T}_t^{\alpha }𝓋\left(x,t\right)+{𝓌}_{xx}\left(x,t\right)+2\left({𝓋}^2\left(x,t\right)𝓌\left(x,t\right)+{𝓌}^3\left(x,t\right)\right)=0,\\ T_t^{\alpha }𝓌\left(x,t\right)-{𝓋}_{xx}\left(x,t\right)-2\left({𝓋}^3\left(x,t\right)+{𝓌}^2\left(x,t\right)𝓋\left(x,t\right)\right)=0,\end{array}$$

(32)

subject to the following initial conditions

$$𝓋\left(x,0\right)=\cos \left(x\right) \mathrm{and} 𝓌\left(x,0\right)=\sin \left(x\right).$$

(33)

According to CRPS algorithm, the $n$th-truncated series solutions are

$$\begin{gathered} {𝓋}_n\left(x,t\right)=\cos \left(x\right)+{\displaystyle \sum }_{k=1}^n{a}_k\left(x\right)\frac{t^{k\alpha }}{{\alpha }^{k}k!}, \\ {𝓌}_n\left(x,t\right)=\sin \left(x\right)+{\displaystyle \sum }_{k=1}^n{b}_k\left(x\right)\frac{t^{k\alpha }}{{\alpha }^{k}k!}, \end{gathered}$$

(34)

and the $n$th-residual functions are

$$\begin{gathered} Re{s}_{𝓋}^n\left(x,t\right)=T_t^{\alpha }{𝓋}_n\left(x,t\right)+{\left({𝓌}_n\right)}_{xx}\left(x,t\right)+2\left({𝓋}_n^2\left(x,t\right){𝓌}_n\left(x,t\right)+{𝓌}_n^3\left(x,t\right)\right), \\ Re{s}_{𝓌}^n\left(x,t\right)=T_t^{\alpha }{𝓌}_n\left(x,t\right)-{({𝓋}_n)}_{xx}\left(x,t\right)-2\left({𝓌}_n^2\left(x,t\right){𝓋}_n\left(x,t\right)+{𝓋}_n^3\left(x,t\right)\right). \end{gathered}$$

(35)

For $n=1$, substitute the first truncated series ${𝓋}_1\left(x,t\right)=\cos \left(x\right)+a_1\left(x\right)\frac{t^{\alpha }}{\alpha }$ and ${𝓌}_1\left(x,t\right)=\sin \left(x\right)+b_1\left(x\right)\frac{t^{\alpha }}{\alpha }$ into the first truncated residual functions $Re{s}_{𝓋}^1\left(x,t\right)$ and $Re{s}_{𝓌}^1\left(x,t\right)$ and equating the resulting equations to zero at $t=0$ such that

$$\begin{array}{cc}\hfill Re{s}_{𝓋}^1{\left(x,t\right)}_{│t=0}=& a_1\left(x\right)+{\left(-\sin \left(x\right)+\frac{b_1^{″}\left(x\right)t^{\alpha }}{\alpha }\right)}_{│t=0}\hfill \\ & +2({\left(\cos \left(x\right)+a_1\left(x\right)\frac{t^{\alpha }}{\alpha }\right)}^2\left(\sin \left(x\right)+b_1\left(x\right)\frac{t^{\alpha }}{\alpha }\right)\hfill \\ & +{\left(\sin \left(x\right)+b_1\left(x\right)\frac{t^{\alpha }}{\alpha }\right)}^3{)}_{│t=0}=0,\hfill \\ \hfill Re{s}_{𝓌}^1{\left(x,t\right)}_{│t=0}=& b_1\left(x\right)-{\left(-\cos \left(x\right)+\frac{a_1^{″}\left(x\right)t^{\alpha }}{\alpha }\right)}_{│t=0}\hfill \\ & -2({\left(\sin \left(x\right)+b_1\left(x\right)\frac{t^{\alpha }}{\alpha }\right)}^2\left(\cos \left(x\right)+a_1\left(x\right)\frac{t^{\alpha }}{\alpha }\right)\hfill \\ & +{\left(\cos \left(x\right)+a_1\left(x\right)\frac{t^{\alpha }}{\alpha }\right)}^3{)}_{│t=0}=0.\hfill \end{array}$$

(36)

Here, it can be observed that

$$a_1\left(x\right)=-\sin \left(x\right) \mathrm{and} b_1\left(x\right)=\cos \left(x\right).$$

Therefore, the first CRPS approximations of Equations (32) and (33) are

$${𝓋}_1\left(x,t\right)=\cos \left(x\right)-\sin \left(x\right)\frac{t^{\alpha }}{\alpha } \mathrm{and} {𝓌}_1\left(x,t\right)=\sin \left(x\right)+\cos \left(x\right)\frac{t^{\alpha }}{\alpha }.$$

For $n=2$, substitute the second truncated series solutions ${𝓋}_2\left(x,t\right)=\cos \left(x\right)-\sin \left(x\right)\frac{t^{\alpha }}{\alpha }+a_2\left(x\right)\frac{t^{2\alpha }}{2{\alpha }^2}$ and ${𝓌}_2\left(x,t\right)=\sin \left(x\right)+\cos \left(x\right)\frac{t^{\alpha }}{\alpha }+b_2\left(x\right)\frac{t^{2\alpha }}{2{\alpha }^2}$ into the second truncated residual functions $Re{s}_{𝓋}^2\left(x,t\right)$ and $Re{s}_{𝓌}^2\left(x,t\right)$ such that

$$\begin{array}{cc}\hfill Re{s}_{𝓋}^2\left(x,t\right)=& \left(-\sin \left(x\right)+\frac{a_2\left(x\right)t^{\alpha }}{\alpha }\right)+\left(-\sin \left(x\right)-\frac{\cos \left(x\right)t^{\alpha }}{\alpha }+\frac{b_2^{″}\left(x\right)t^{2\alpha }}{2{\alpha }^2}\right)\hfill \\ & +2({\left(\cos \left(x\right)-\frac{\sin \left(x\right)t^{\alpha }}{\alpha }+\frac{a_2\left(x\right)t^{2\alpha }}{2{\alpha }^2}\right)}^2(\sin \left(x\right)+\frac{\cos \left(x\right)t^{\alpha }}{\alpha }\hfill \\ & +\frac{b_2\left(x\right)t^{2\alpha }}{2{\alpha }^2})+{\left(\sin \left(x\right)+\frac{\cos \left(x\right)t^{\alpha }}{\alpha }+\frac{b_2\left(x\right)t^{2\alpha }}{2{\alpha }^2}\right)}^3),\hfill \\ \hfill Re{s}_{𝓌}^2\left(x,t\right)=& \left(\cos \left(x\right)+\frac{b_2\left(x\right)t^{\alpha }}{\alpha }\right)-\left(-\cos \left(x\right)+\frac{\sin \left(x\right)t^{\alpha }}{\alpha }+\frac{a_2^{″}\left(x\right)t^{2\alpha }}{2{\alpha }^2}\right)\hfill \\ & -2\left({\left(\sin \left(x\right)+\frac{\cos \left(x\right)t^{\alpha }}{\alpha }+\frac{b_2\left(x\right)t^{2\alpha }}{2{\alpha }^2}\right)}^2\right(\cos \left(x\right)-\frac{sin\left(x\right)t^{\alpha }}{\alpha }\hfill \\ & +\frac{a_2\left(x\right)t^{2\alpha }}{2{\alpha }^2})+{\left(\cos \left(x\right)-\frac{sin\left(x\right)t^{\alpha }}{\alpha }+\frac{a_2\left(x\right)t^{2\alpha }}{2{\alpha }^2}\right)}^3)\hfill \end{array}$$

(37)

Consequently, by operating $T_t^{\alpha }$ on both sides of Equation (37), using the fact that $T_t^{\alpha }{t}^p=0$ for $p>\alpha$ at $t=0$ and equating the resulting equations to zero at $t=0$ yields

$$\begin{array}{ll}{T}_t^{\alpha }Re{s}_{𝓋}^2{\left(x,t\right)}_{│t=0}& \\ & =a_2\left(x\right)+{\left(-\cos \left(x\right)+\frac{b_2^{″}\left(x\right)t^{\alpha }}{\alpha }\right)}_{│t=0}\\ & +2\left(\right({\cos }^3\left(x\right)-2\cos \left(x\right){\sin }^2\left(x\right)+\frac{2{\sin }^3\left(x\right)t^{\alpha }}{\alpha }+\dots \\ & +\frac{3a_2^2\left(x\right)b_2\left(x\right)t^{5\alpha }}{4{\alpha }^5}{)}_{│t=0}\\ & +{\left(3\cos \left(x\right){\sin }^2\left(x\right)+\frac{6\sin \left(x\right){\cos }^2\left(x\right)t^{\alpha }}{\alpha }+\dots +\frac{3b_2^3\left(x\right)t^{5\alpha }}{4{\alpha }^5}\right)}_{│t=0})\\ & =0,\\ T_t^{\alpha }Re{s}_{𝓌}^2{\left(x,t\right)}_{│t=0}& \\ & =b_2\left(x\right)-{\left(\sin \left(x\right)+\frac{a_2^{″}\left(x\right)t^{\alpha }}{\alpha }\right)}_{│t=0}\\ & -2\left(\right(-{\sin }^3\left(x\right)+2\sin \left(x\right){\cos }^2\left(x\right)+\frac{2{\cos }^3\left(x\right)t^{\alpha }}{\alpha }+\dots \\ & {+\frac{3b_2^2\left(x\right)a_2\left(x\right)t^{5\alpha }}{4{\alpha }^5})}_{│t=0}\\ & +{\left(-3\sin \left(x\right){\cos }^2\left(x\right)+\frac{6\cos \left(x\right){\sin }^2\left(x\right)t^{\alpha }}{\alpha }+\dots +\frac{3a_2^3\left(x\right)t^{5\alpha }}{4{\alpha }^5}\right)}_{│t=0})\\ & =0.\end{array}$$

That is, $a_2\left(x\right)=-\cos \left(x\right)$ and $b_2\left(x\right)=-\sin \left(x\right).$ Therefore, the second CPS approximate solutions of Equations (32) and (33) are

$$\begin{gathered} {𝓋}_2\left(x,t\right)=\cos \left(x\right)-\sin \left(x\right)\frac{t^{\alpha }}{\alpha }-\cos \left(x\right)\frac{t^{2\alpha }}{2{\alpha }^2}, \\ {𝓌}_2\left(x,t\right)=\sin \left(x\right)+\cos \left(x\right)\frac{t^{\alpha }}{\alpha }-\sin \left(x\right)\frac{t^{2\alpha }}{2{\alpha }^2}. \end{gathered}$$

For $n=3$, by substituting the third truncated series solutions ${𝓋}_3\left(x,t\right)=\cos \left(x\right)-\sin \left(x\right)\frac{t^{\alpha }}{\alpha }-\cos \left(x\right)\frac{t^{2\alpha }}{2{\alpha }^2}+a_3\left(x\right)\frac{t^{3\alpha }}{3!{\alpha }^3}$ and ${𝓌}_3\left(x,t\right)=\sin \left(x\right)+\cos \left(x\right)\frac{t^{\alpha }}{\alpha }-\sin \left(x\right)\frac{t^{2\alpha }}{2{\alpha }^2}+b_3\left(x\right)\frac{t^{3\alpha }}{3!{\alpha }^3}$ into the third truncated residual functions $Re{s}_{𝓋}^3\left(x,t\right)$ and $Re{s}_{𝓌}^3\left(x,t\right)$, then applying $T_t^{\alpha }$ twice on both sides of the resulting equations and equating to zero at $t=0$, one can get $a_3\left(x\right)=\sin \left(x\right)$ and $b_2\left(x\right)=-\cos \left(x\right).$ Therefore, the third FPS approximate solutions of Equations (32) and (33) are

$${𝓋}_3\left(x,t\right)=\cos \left(x\right)-\sin \left(x\right)\frac{t^{\alpha }}{\alpha }-\cos \left(x\right)\frac{t^{2\alpha }}{2{\alpha }^2}+\sin \left(x\right)\frac{t^{3\alpha }}{3!{\alpha }^3},$$

$${𝓌}_3\left(x,t\right)=\sin \left(x\right)+\cos \left(x\right)\frac{t^{\alpha }}{\alpha }-\sin \left(x\right)\frac{t^{2\alpha }}{2{\alpha }^2}-\cos \left(x\right)\frac{t^{3\alpha }}{3!{\alpha }^3}.$$

As the former, the fourth unknown coefficients $a_4\left(x\right)$ and $b_4\left(x\right)$ can be obtained using the same procedure of CRPS with the help of the fact that $T_t^{3\alpha }Re{s}_{𝓋}^4\left(x,0\right)=$ $T_t^{3\alpha }Re{s}_{𝓌}^4\left(x,0\right)=0$ such that $a_4\left(x\right)=\cos \left(x\right)$ and $b_4\left(x\right)=\sin \left(x\right)$. Thus, the fourth FPS approximate solutions of Equations (32) and (33) are

$${𝓋}_4\left(x,t\right)=\cos \left(x\right)-\frac{\sin \left(x\right)t^{\alpha }}{\alpha }-\frac{\cos \left(x\right)t^{2\alpha }}{2{\alpha }^2}+\frac{\sin \left(x\right)t^{3\alpha }}{3!{\alpha }^3}+\frac{\cos \left(x\right)t^{4\alpha }}{4!{\alpha }^4},$$

$${𝓌}_4\left(x,t\right)=\sin \left(x\right)+\frac{\cos \left(x\right)t^{\alpha }}{\alpha }-\frac{\sin \left(x\right)t^{2\alpha }}{2{\alpha }^2}-\frac{\cos \left(x\right)t^{3\alpha }}{3!{\alpha }^3}+\frac{\sin \left(x\right)t^{4\alpha }}{4!{\alpha }^4}.$$

Hence, the first few CRPS solutions for Equations (30) and (31) are given as follows:

$$\begin{array}{cc}\hfill {𝓊}_1\left(x,t\right)=& (\cos \left(x\right)-\sin \left(x\right)\frac{t^{\alpha }}{\alpha })+i\left(\sin \left(x\right)+\cos \left(x\right)\frac{t^{\alpha }}{\alpha }\right),\hfill \\ \hfill {𝓊}_2\left(x,t\right)=& \left(\cos \left(x\right)-\frac{\sin \left(x\right)t^{\alpha }}{\alpha }-\frac{\cos \left(x\right)t^{2\alpha }}{2{\alpha }^2}\right)+i\left(\sin \left(x\right)+\frac{\cos \left(x\right)t^{\alpha }}{\alpha }-\frac{\sin \left(x\right)t^{2\alpha }}{2{\alpha }^2}\right),\hfill \\ \hfill {𝓊}_3\left(x,t\right)=& \left(\cos \left(x\right)-\frac{\sin \left(x\right)t^{\alpha }}{\alpha }-\frac{\cos \left(x\right)t^{2\alpha }}{2{\alpha }^2}+\frac{\sin \left(x\right)t^{3\alpha }}{3!{\alpha }^3}\right)\hfill \\ & +i\left(\sin \left(x\right)+\frac{\cos \left(x\right)t^{\alpha }}{\alpha }-\frac{\sin \left(x\right)t^{2\alpha }}{2{\alpha }^2}-\frac{\cos \left(x\right)t^{3\alpha }}{3!{\alpha }^3}\right),\hfill \\ \hfill {𝓊}_4\left(x,t\right)=& (\cos \left(x\right)-\frac{\sin \left(x\right)t^{\alpha }}{\alpha }-\frac{\cos \left(x\right)t^{2\alpha }}{2{\alpha }^2}+\frac{\sin \left(x\right)t^{3\alpha }}{3!{\alpha }^3}+\frac{\cos \left(x\right)t^{4\alpha }}{4!{\alpha }^4})\hfill \\ & +i(\sin \left(x\right)+\frac{\cos \left(x\right)t^{\alpha }}{\alpha }-\frac{\sin \left(x\right)t^{2\alpha }}{2{\alpha }^2}-\frac{\cos \left(x\right)t^{3\alpha }}{3!{\alpha }^3}+\frac{\sin \left(x\right)t^{4\alpha }}{4!{\alpha }^4}),\hfill \end{array}$$

(38)

By continuing this procedure, the multiple CFPS solution $𝓊\left(x,t\right)$ in term of infinite series can be obtained by

$$\begin{array}{cc}\hfill 𝓊\left(x,t\right)=& \left(\cos \left(x\right)-\frac{\sin \left(x\right)t^{\alpha }}{\alpha }-\frac{\cos \left(x\right)t^{2\alpha }}{2!{\alpha }^2}+\frac{\sin \left(x\right)t^{3\alpha }}{3!{\alpha }^3}+\frac{\cos \left(x\right)t^{4\alpha }}{4!{\alpha }^4}+\dots \right)\hfill \\ & +i\left(\sin \left(x\right)+\frac{\cos \left(x\right)t^{\alpha }}{\alpha }-\frac{\sin \left(x\right)t^{2\alpha }}{2!{\alpha }^2}-\frac{\cos \left(x\right)t^{3\alpha }}{3!{\alpha }^3}+\frac{\sin \left(x\right)t^{4\alpha }}{4!{\alpha }^4}+\dots \right)\hfill \\ & =\left(\cos \left(x\right)+i\sin \left(x\right)\right)\left(\begin{array}{c}{\displaystyle {\displaystyle \sum }_{n=0}^{\infty }}\frac{1}{n!}\end{array}{\left(\frac{i{t}^{\alpha }}{\alpha }\right)}^n\right).\hfill \end{array}$$

In particular, the CFPS solution of Equations (30) and (31) at $\alpha =1$ is $𝓊\left(x,t\right)=e^{i\left(x+\frac{t^{\alpha }}{\alpha }\right)}$, which is fully compatible with solutions found in other existing methods [42,43,44].

To show the geometric behaviors of the fourth CFPS approximations of Equations (30) and (31), the numerical comparison of exact and approximate solutions at different values of $\alpha$ such that $\alpha \in \left\{1,0.9,0.8,0.7\right\}$ is presented in

Table A2. Numerical results of fifth approximate solutions for Example 2 at $x=0.1$.

𝓋(x,t)	ti	Exact	CRPS	Absolute Error	CRPS
					α = 0.9	α = 0.8	α = 0.7
	0.1	0.980067	0.980067	1.37972 × 10−9	0.971366	0.955893	0.926785
	0.3	0.921061	0.921062	1.00150 × 10−6	0.888847	0.838066	0.755156
	0.5	0.825336	0.825357	2.13426 × 10−5	0.767839	0.683914	0.558152
	0.7	0.696707	0.696866	1.59550 × 10−4	0.617253	0.507404	0.352798
	0.9	0.540302	0.541017	7.14529 × 10−4	0.445556	0.319365	0.150472
𝓌(x,t)	ti	Exact	CRPS	Absolute Error		CRPS
					α = 0.9	α = 0.8	α = 0.7
	$0.1$	$0.198669$	$0.198669$	$1.58372\times {10}^{-10}$	$0.237587$	$0.293716$	$0.375594$
	$0.3$	$0.389418$	$0.389418$	$1.44041\times {10}^{-7}$	$0.458212$	$0.545596$	$0.655644$
	$0.5$	$0.564642$	$0.564646$	$3.69389\times {10}^{-6}$	$0.640727$	$0.729775$	$0.830299$
	$0.7$	$0.717356$	$0.717388$	$3.23193\times {10}^{-5}$	$0.787136$	$0.862472$	$0.937317$
	$0.9$	$0.841471$	$0.841637$	$1.66004\times {10}^{-4}$	$0.896316$	$0.949479$	$0.991809$

for each value of $t_i$ in $\left[0,1\right]$ with step-size $0.2$ when $x=0.1$ and $n=5$. From these numerical comparisons, it can be concluded that the results obtained by the proposed method are excellent in comparison with the exact solution. For further analysis, the surface plots of the exact $𝓋\left(x,t\right)$ and $𝓌\left(x,t\right)$ of Example 2 and fourth CRPS solutions ${𝓋}_4\left(x,t\right)$ and ${𝓌}_4\left(x,t\right)$ at different values of fractional order $\alpha$ for each $t\in \left[0,2\right]$ and $x\in \left[-2\pi ,2\pi \right]$ are illustrated in Figure A4 and Figure A5, respectively. From these figures, it can be seen that the behavior of the fourth CRPS approximate solutions is in good agreement with each other at different values of $\alpha$.

Example 3.

Consider the following linear fractional Schrödinger equation with nonzero trapping potential [45,46]:

$$i{T}_t^{\alpha }𝓊\left(x,t\right)+\frac{1}{2}{𝓊}_{xx}\left(x,t\right)-{\cos }^2\left(x\right)𝓊\left(x,t\right)-{\left|𝓊\left(x,t\right)\right|}^2𝓊\left(x,t\right)=0, t\ge 0, 0<\alpha \le 1$$

(39)

subject to the initial condition

$$𝓊\left(x,0\right)=\sin \left(x\right),x\in ℝ.$$

(40)

The exact solution of this model at α = 1 is $𝓊\left(x,t\right)=\sin \left(x\right)e^{-3it/2}$.

Evidently, the corresponding coupled system of Equations (39) and (40) is given by

$$\begin{gathered} T_t^{\alpha }𝓊\left(x,t\right)+\frac{1}{2}{𝓌}_{xx}\left(x,t\right)-{\cos }^2\left(x\right)𝓌\left(x,t\right)-\left({𝓋}^2\left(x,t\right)𝓌\left(x,t\right)+{𝓌}^3\left(x,t\right)\right)=0, \\ {T}_t^{\alpha }𝓌\left(x,t\right)-\frac{1}{2}{𝓋}_{xx}\left(x,t\right)+{\cos }^2\left(x\right)𝓋\left(x,t\right)+\left({𝓌}^2\left(x,t\right)𝓋\left(x,t\right)+{𝓋}^3\left(x,t\right)\right)=0, \end{gathered}$$

(41)

subject to the following initial conditions

$$𝓋\left(x,0\right)=\sin \left(x\right) \mathrm{and} 𝓌\left(x,0\right)=0.$$

(42)

According to CRPS algorithm, the $n$th-truncated series solutions are

$$\begin{array}{l}{𝓋}_n\left(x,t\right)=\sin \left(x\right)+{\displaystyle {\displaystyle \sum }_{k=1}^n}{a}_k\left(x\right)\frac{t^{k\alpha }}{{\alpha }^{k}k!},\\ {𝓌}_n\left(x,t\right)={\displaystyle {\displaystyle \sum }_{k=1}^n}{b}_k\left(x\right)\frac{t^{k\alpha }}{{\alpha }^{k}k!},\end{array}$$

(43)

and the $n$th-residual functions are

$$Re{s}_{𝓋}^n\left(x,t\right)=T_t^{\alpha }{𝓋}_n\left(x,t\right)+\frac{1}{2}{\left({𝓌}_n\right)}_{xx}\left(x,t\right)-co{s}^2\left(x\right){𝓌}_n\left(x,t\right)-\left({𝓋}_n^2\left(x,t\right){𝓌}_n\left(x,t\right)+{𝓌}_n^3\left(x,t\right)\right),$$

$$Re{s}_{𝓌}^n\left(x,t\right)=T_t^{\alpha }{𝓋}_n\left(x,t\right)-\frac{1}{2}{({𝓋}_n)}_{xx}\left(x,t\right)+co{s}^2\left(x\right){𝓋}_n\left(x,t\right)+\left({𝓌}_n^2\left(x,t\right){𝓋}_n\left(x,t\right)+{𝓋}_n^3\left(x,t\right)\right).$$

By applying the former iteration process of CRPS algorithm, the first few terms of Equation (43) are given as follows:

$$\begin{array}{l}{a}_1\left(x\right)=0, b_1\left(x\right)=-\frac{3}{2}\sin \left(x\right),\\ a_2\left(x\right)=-\frac{9}{4}\sin \left(x\right), b_2\left(x\right)=0,\\ a_3\left(x\right)=0, b_3\left(x\right)=\frac{27}{8}\sin \left(x\right),\end{array}$$

Hence, the first few CRPS solutions for Equations (39) and (40) are given as follows:

$$\begin{array}{l}{𝓊}_1\left(x,t\right)=\sin \left(x\right)-\frac{3i}{2}\sin \left(x\right)\frac{t^{\alpha }}{\alpha },\\ {𝓊}_2\left(x,t\right)=\left(\sin \left(x\right)-\frac{9}{8}\frac{\sin \left(x\right)t^{2\alpha }}{{\alpha }^2}\right)-\frac{3i}{2}\sin \left(x\right)\frac{t^{\alpha }}{\alpha },\\ {𝓊}_3\left(x,t\right)=\left(\sin \left(x\right)-\frac{9}{8}\frac{\sin \left(x\right)t^{2\alpha }}{{\alpha }^2}\right)+i\left(-\frac{3}{2}\frac{\sin \left(x\right)t^{\alpha }}{\alpha }+\frac{9}{16}\frac{\sin \left(x\right)t^{3\alpha }}{{\alpha }^3}\right),\end{array}$$

(44)

in which the multiple CFPS solution $𝓊\left(x,t\right)$ in term of infinite series can be obtained by

$$\begin{array}{cc}\hfill 𝓊\left(x,t\right)& =\left(\sin \left(x\right)-\frac{9}{8}\frac{\sin \left(x\right)t^{2\alpha }}{{\alpha }^2}+\dots \right)+i\left(-\frac{3}{2}\frac{\sin \left(x\right)t^{\alpha }}{\alpha }+\frac{9}{16}\frac{\sin \left(x\right)t^{3\alpha }}{{\alpha }^3}+\dots \right)\hfill \\ & =\sin \left(x\right)\left(\left(1-\frac{1}{2!}{\left(\frac{3t^{\alpha }}{2\alpha }\right)}^2+\dots \right)-i\left(\left(\frac{3t^{\alpha }}{2\alpha }\right)-\frac{1}{3!}{\left(\frac{3t^{\alpha }}{2\alpha }\right)}^3+\dots \right)\right)\hfill \\ & =\sin \left(x\right)\left(\begin{array}{c}{\displaystyle {\displaystyle \sum }_{n=0}^{\infty }}\frac{1}{\left(2n\right)!}\end{array}{\left(\frac{3t^{\alpha }}{2\alpha }\right)}^{2n}-i\begin{array}{c}{\displaystyle {\displaystyle \sum }_{n=0}^{\infty }}\frac{1}{\left(2n+1\right)!}\end{array}{\left(\frac{3t^{\alpha }}{2\alpha }\right)}^{2n+1}\right).\hfill \end{array}$$

In particular, the CFPS solution of Equations (39) and (40) at $\alpha =1$ is $\begin{array}{c}𝓊\left(x,t\right)\end{array}=\sin \left(x\right)e^{-3it/2}$, which is fully compatible with solutions found in other existing methods [42,43,44].

To demonstrate the effectiveness of the CRPS algorithm in handling Equations (39) and (40), the numerical comparison between the third CRPS solutions and other existing numerical methods including homotopy perturbation method (HPM) [45] and homotopy analysis method (HAM) [46] for each $\left(x_i,t_i\right)$ in the domain $\left[0,1\right]\times \left[0,1\right]$ with step-size $0.2$ for time and space directions. From

Table A3. Comparison of third approximations of Example 3 at $\alpha =1$.

𝓋(x,t)	(xi,ti)	Exact	CRPS	HPM [45]	HAM [46]
	$\left(0.2,0.2\right)$	$0.189796$	$0.189729$	$0.189729$	$0.189729$
	$\left(0.4,0.4\right)$	$0.321401$	$0.319323$	$0.319323$	$0.319323$
	$\left(0.6,0.6\right)$	$0.350987$	$0.335962$	$0.335962$	$0.335962$
	$\left(0.8,0.8\right)$	$0.259940$	$0.200860$	$0.200860$	$0.200860$
𝓌(x,t)	(xi,ti)	Exact	CRPS	HPM [45]	HAM [46]
	$\left(0.2,0.2\right)$	$-0.058711$	$-0.058707$	$-0.059899$	$-0.058552$
	$\left(0.4,0.4\right)$	$-0.219882$	$-0.219632$	$-0.238324$	$-0.209943$
	$\left(0.6,0.6\right)$	$-0.442300$	$-0.439574$	$-0.531046$	$-0.333908$
	$\left(0.8,0.8\right)$	$-0.668604$	$-0.654229$	$-0.929693$	$-0.101207$

, it can be seen that the numerical results obtained by the CRPS method are better than those obtained by other methods. While the three-dimensional plots of the exact, $𝓋\left(x,t\right)$ and $𝓌\left(x,t\right)$, and fifth CRPS approximate solutions for different values of fractional order $\alpha$ such that $\alpha \in \left\{1,0.75,0.5\right\}$ are given respectively in Figure A6 and Figure A7 for $t\in \left[0,1\right]$ and $x\in \left[-3\pi ,3\pi \right]$. Anyhow, fractional level curves of fifth CRPS solutions of Example 3 are shown in Figure A8 at different values of $\alpha$ for each $x\in \left[-3\pi ,3\pi \right]$ with $t=0.4$.

5. Conclusions

In this article, the application of the CFPS algorithm was extended in obtaining approximate solutions for both linear and nonlinear time-fractional Schrödinger equations associated with potential energy and suitable initial guesses in the sense of conformable fractional derivative. The proposed method has been utilized directly to solve three fractional models without being linearized, discretized, or perturbation. Meanwhile, such illustrative examples are presented to show the effectiveness and ability of the proposed approach. Graphical results revealed the validity and reliability of CRPS technique with a great potential in scientific applications. The CFPS method is considered a valuable tool, effective and straightforward, to predict and construct numeric-analytic solutions of many problems related to fractional partial differential equations arising in physics and applied sciences.