An Uncertainties Simulation Model Applied to an Automated Laminar Flowmeter

Abstract

Aircraft oxygen regulators are a normally used specialized test bench designed to perform tests to the regulators during its work conditions. The tests are performed placing the regulator in the barometric chamber, where low pressure conditions are forced to simulate altitude conditions and then a flow is forced on the output of the regulator to simulate the inhalation of the user. The relevant test flows are measured by laminar flowmeters. These flowmeters are meant to measure the flowrate at pressures correspondent to altitudes between sea level altitude and fifty thousand feet. In this work a way was studied to automate laminar flowmeters used on oxygen regulator test benches. For this purpose, was developed a data acquisition system (DAS) using a microcontroller board and two microelectromechanical systems—MEMSs (a pressure and temperature sensor and a differential pressure sensor). Since these MEMSs did not have factory calibration, they were calibrated in this study. The automated flowmeter was also calibrated. To estimate the error of flow rate measured by this solution, an uncertainties simulation model based on the Monte Carlo method and several calibrations were performed. According to the automated flowmeter calibration, the uncertainty obtained (±0.45% fs) is accepted, but the authors only recommend its use for actual volumetric flowrate measurements.

1. Introduction

The oxygen equipment of an aircraft is the first line of defense against the potentially lethal effects of hypoxia and carbon monoxide poisoning. It is the pilot’s responsibility that all aboard the aircraft—crewmembers and passengers—know how to use this life-saving equipment safely and efficiently [1].

Most oxygen systems are composed of a storage system (containers), delivery system and mask or nasal cannula. The oxygen delivery system, also known as an oxygen regulator can be one of three types: continuous flow—delivering continuous flow of oxygen from the storage to the mask (28,000 feet and lower); diluter demand: giving the user oxygen on-demand (during inhalation) stopping the flow when the demand ceases (during exhalation) to conserve oxygen (altitudes up to 40,000) and pressure demand—providing oxygen under positive pressure to over-inflate the lungs (altitudes above 40,000 feet) [2,3].

Aircraft components require periodical maintenance, repair and overhaul (MRO) activity. For oxygen regulators MRO is normally used a specialized test bench designed to perform tests to the regulators during its work conditions. The test bench is composed of a barometric chamber, a vacuum pump, an altimeter and several flowmeters [4]. The tests are performed placing the regulator in the barometric chamber, where low pressure conditions are forced to simulate altitude conditions and then a flow is forced on the output of the regulator to simulate the inhalation of the user [5]. The relevant test flows are measured by laminar flowmeters [6].

In this work a way was studied to automate laminar flowmeters used on oxygen regulator test benches. The flowmeters studied have particular requirements of accuracy established by the technical documentation delivered by the test bench manufacturer (1% full scale—fs). This flowmeter is meant to measure flowrate at pressures correspondent to altitudes between sea level altitude and fifty thousand feet. So, in order to achieve precise measurements, they should be corrected considering the pressure and temperature changes. At the core of this work, the correspondence between altitude and pressure was made in accordance to the U.S. Standard Atmosphere [3]. To estimate the error of the flow rate measured by this solution, an uncertainties simulation model and several calibrations were performed. The simulation model was based on the Monte Carlo method. These calibrations were made in accordance with the Guide to the Expression of Uncertainty in Measurement—GUM [7]. In this work, was also developed a data acquisition system (DAS) using a microcontroller board and two microelectromechanical systems—MEMSs. Since these MEMS did not have factory calibration, the uncertainty measurement study was performed. A methodology was developed to test the accuracy of the automated laminar flowmeter.

2. Theoretical Fundaments: Laminar Flowmeters

Laminar flowmeters are a well-known kind of differential pressure-based flow measurement devices mainly used for measuring low flow rates of gases and liquids.

A laminar flowmeter is composed of a laminar flow element and a differential pressure gauge or transducer. The laminar flow element ensures that the flow passing through the flowmeter is in laminar condition. In this condition the viscous forces, generated by internal friction of the fluid, overcome the inertial forces and therefore the dominant mechanism for resistance to fluid motion is friction against the surrounding walls [8].

The pressure drop $\left(\Delta p\right)$ caused by fluid friction between two points separated by a distance $\Delta x$ along a pipe in a laminar flow regime is quantifiable, and can be expressed by the Hagen–Poiseuille equation (Equation (1)) [9].

$$\Delta p=\frac{128\mu Q\Delta x}{\pi D^4},$$

(1)

where $D$ is the pipe internal diameter, $\mu$ the fluid’s viscosity and $Q$ the volumetric flow rate.

Equation (1) establishes that for a laminar flow there is a linear relationship between the flow rate and developed pressure drop. A major drawback of this type of flowmeter, however, is its dependence on fluid viscosity, which in turn is mostly dependent on fluid temperature. Thus, any laminar flowmeter requires some form of temperature compensation to obtain precise measurements [4]. In Figure 1 there is a scheme of a longitudinal and a transversal cut of a laminar flowmeter.

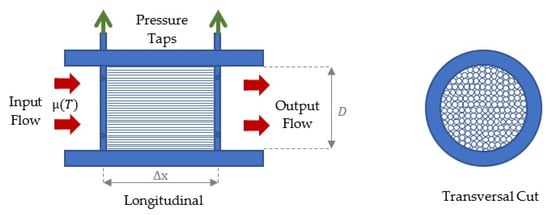
Figure 1. Laminar flowmeter.

The assumptions of the Hagen–Poiseuille equation (Equation (1)) [10] are:

• The flow has negligible kinetic energy,
• The flow is laminar and steady,
• The capillary is straight and has a uniform, circular cross section,
• The fluid is incompressible and its density is constant,
• The fluid is Newtonian,
• The temperature of the fluid is constant and viscous heating is negligible,
• There is no slip at the wall of the capillary.

This is a simplistic model.

In real situations, it is natural that some of these conditions cannot be met and therefore errors arise in the flow measurement. The practical models used by experimentalists must correct errors arising from a breach of the conditions listed. According to the practical model adopted in this work, each laminar flowmeter has its calibration curve that is generated using a quadratic Equation (2) [11]. This equation is only valid for temperature and pressure at standard conditions (at sea level: $T=15°\mathrm{C}$ and $p=1013,25\mathrm{mbar})$.

$$Q=\left[B\times \Delta p+C\times {\left(\Delta p\right)}^2\right],$$

(2)

where B and C are calibration constants.

The actual volumetric flowrate, $Q_a$, can be obtained by measuring the differential pressure ($\Delta p$) across the laminar flow element and the temperature $\left(T\right)$ of the inlet fluid. This flow rate can be obtained by the Equation (3).

$$Q_a=\left[B\times \Delta p+C\times {\left(\Delta p\right)}^2\right]\ast \frac{{\mu }_{std}}{{\mu }_a},$$

(3)

where ${\mu }_a$ is the actual viscosity of the fluid and ${\mu }_{std}$ the viscosity of the fluid at standard temperature.

The word “standard” when associated with flow rate, means that the flow rate has been normalized to an assigned standard pressure and temperature [7]. If the standard volumetric flowrate is desired it can be obtained by multiplying the actual volumetric flowrate by the pressure and temperature ratios:

-

$standard temperature \left(T_{std}\right)/actual temperature \left(T_a\right)$,

-

and $actual pressure \left(p_a\right)/standard pressure \left(p_{std}\right)$.

This way, the standard volumetric flowrate can be obtained by Equation (4).

$$Qstd=\left[B\times \Delta p+C\times {\left(\Delta p\right)}^2\right]\times \frac{{\mu }_{std}}{{\mu }_a}\times \frac{T_{std}}{T_a}\times \frac{p_a}{p_{std}}.$$

(4)

3. Experimental Proceeding

The process of measuring an electrical or physical phenomenon is called data acquisition (DAQ). A DAQ system is normally composed by one or more sensors, a DAQ measurement device or hardware and a computer with programmable software as shown in Figure 2 [4].

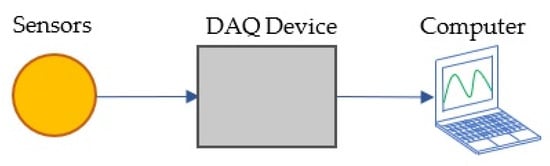
Figure 2. Parts of a data acquisition (DAQ) system.

The DAQ system used to automate the laminar flowmeters in this work was composed by: two sensors (an absolute pressure and temperature sensor and a differential pressure sensor), an Arduino microcontroller board and a computer (Figure 2).

In Figure 3 the solution’s is presented with all the components: The MEMS capture the three input variables ($p$,$T \mathrm{and} \Delta p$). The Arduino acquires the signals from the sensors, stabilizes them if necessary and converts them. These signals are sent to the computer where they are processed according to information programmed in LabVIEW and finally the desired outputs $\left(Q,Q_a\mathrm{and}Qstd\right)$ are obtained.

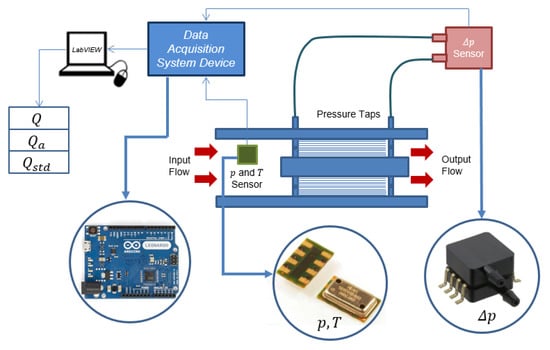
Figure 3. Solution’s setup.

A MS5611-01BA03 barometric pressure sensor, with a stainless steel cap [12] was used, to measure pressure and temperature (see Figure 3). This is a new generation of a high resolution altimeter sensor, which the specifications are presented in Table 1. A differential and gauge, integrated pressure sensor, MPXV5004DP, was used to measure the pressure drop [13], and the respective specifications are presented in Table 2. The MPXV5004DP MEMS combines a highly sensitive implanted strain gauge with advanced micromachining techniques, thin-film metallization and bipolar processing to provide an accurate, high level analog output sign that is proportional to the applied pressure [13]. The data acquisition system used the micro controller board Arduino Leonardo [14] based on the Atmega32u4 microprocessor [15]. The Arduino Leonardo has 20 digital input/output pins, 16 MHz crystal oscillator, a micro USB connection [14]. In Table 3 are presented the Atmega32u4 principal specifications.

Table 1. MS5611-01BA03 technical data.

Sensor Performance $({\mathit{V}}_{\mathit{S}}=3\mathbf{V})$	Minimum	Maximum	Unit
Pressure Range	10	1200	mbar
Pressure Accuracy (25 °C; 750 mbar)	−1.5	+1.5	mbar
Error Band ([−20, +85] °C, [450, 1100] mbar)	−2.5	+2.5	mbar
Temperature Range	−40	+85	°C
Temperature Accuracy	−0.8	+0.8	°C

Table 2. MPXV5004DP technical data.

Operating Characteristics $({\mathit{V}}_{\mathit{S}}=5.0\mathbf{V})$	Minimum	Tipic	Maximum	Unit
Pressure Range	0	-	400	mm H2O
Full Scale Span ($V_{FSS}$)	-	3	-	V
Accuracy [0, 100] mm H2O [10, 60] °C	−1.5	-	+1.5	% $V_{FSS}$ (with autozero)
Accuracy [100, 400] mm H2O [10, 60] °C	−2.5	-	+2.5	% $V_{FSS}$ (with autozero)
Accuracy [0, 400] mm H2O [10, 60] °C	−6.25	-	+6.25	% $V_{FSS}$ (without autozero)

Table 3. Atmega32u4 technical data.

Features
Work Voltage	5V
Input Voltage (recommended)	7–12V
Input Voltage (limit)	6–20V
Digital I/O Pin	20 (7 PWM)
Analogic Input pin	12
Intensity by pin	40 mA
Intensity in pin 3.3 V	50 mA
Flash Memory	32 KB (4 KB $bootloade{r}^2$)
SRAM	25 KB
EEPROM	1 KB
Maximum Frequency	16 MHz at 4.5 V

Calibrations

In order to determinate the real uncertainty of measurement associated with each MEMS and to with automated flowmeter, calibrations were performed to each device separately.

The calibrations were performed according to the Guide to the Expression of Uncertainty in Measurement—GUM [7].

A Ruska 7750i Air Data Test Set (ADTS) [16] was used, for absolute and differential pressure calibration and a thermal mass flowmeter for volumetric flow rate calibration. The model 7750i is indicated for avionics instrumentation and represented the latest generation ADTS, having unequalled precision and long term stability with the latest pressure control technology, provides high performance measurement and control of all air data parameters [16].

For the calibration of the absolute pressure sensor, the sensor was placed in a barometric chamber where standard pressures were forced by the vacuum pump of the ADTS (see Figure 4). Five different pressures were forced inside the chamber, which, according to the U.S. Standard Atmosphere [3], refer to the altitude of: sea level, 10, 20, 30, 40 and 50 feet. Table 4 represents the calibration sheet of this sensor.

Figure 4. Calibration’ setup: (a) barometric chamber; (b) laptop computer; (c) Air Data Test Set (ADTS) and (d) vacuum pump.

Table 4. Absolute pressure sensor calibration sheet.

Reference Pressure (mbar)	Sensor Reading (mbar)	k	Uncertainty (±mbar)
1013.250	1013.18	2.02	0.16
696.817	696.32	2.07	0.15
465.633	464.49	2.03	0.1
300.896	299.18	2.17	0.13
187.539	185.43	2.52	0.13
155.972	113.66	2.2	0.08

Considering the calibration of the differential pressure sensor the same ADTS was used, connected to the positive pressure tap. This calibration is expressed in Table 5.

Table 5. Differential pressure sensor calibration sheet.

Reference Pressure (in H2O)	Sensor Reading (in H2O)	k	Uncertainty (±in H2O)
1	0.97	2.65	0.03
5	4.94	2.2	0.04
10	9.93	2.28	0.04
14	13.91	2.65	0.03

The calibration of the automated flowmeter was performed placing the two flowmeters in series (the thermal mass flowmeter and the automated flowmeter). The tests were performed with air at three different pressures: sea level, 30 kft and 50 kft. In Table 6 the calibration sheet at sea level is presented. At this pressure was obtained the maximum uncertainty of measurement.

Table 6. Automated flowmeter calibration sheet at sea level pressure.

Reference Flowrate (slpm)	Flowmeter Reading (slpm)	k	Uncertainty (±slpm)
5.953	5.7	2.01	0.65
50.05	49.6	2.01	0.59
95.975	96.5	2.04	0.6
137.85	138.4	2.18	0.67

The maximum flowrate uncertainty of measurement obtained was ±0.67 standard litters per minute that correspond to a relative uncertainty of ±0.45% full scale.

4. Uncertainties Simulation Model

In order to predict the measurement error of the automated flowmeter several simulations were executed. For that purpose, was performed an uncertainty simulation model, based on the Monte Carlo method, taking as premises two different scenarios for the MEMS uncertainties of the measurement: one based on the manufacturers information (Simulation 1) and another based on the results of the calibrations performed (Simulation 2). The software used for these simulations was Matlab.

In these simulations random values were generated for the input variables ($p$,$T\mathrm{and} \Delta p$) and their respective errors $\left(u_T, u_p\mathrm{and}{u}_{\Delta p}\right)$, within their established ranges, and subsequently values of the output data were calculated $\left(Q_a\mathrm{and}{Q}_{std}\right)$ and also their respective errors ($u_{Q_a}\mathrm{and}{u}_{Q_{std}})$.

In each simulation were selected the maximum errors observed for the output data.

A non-air-conditioned room where there were established ranges for the input variables and for their respective error was ensured (Table 7). As has been said before, in simulation 1 the ranges of error were established according to the data sheets of the MEMS, provided by its manufacturers; in simulation 2 the ranges of error were established according to the results obtained on MEMS calibrations. For the generation of the input variables and respective errors the rand function of Matlab was used. This function uses rectangular distribution in the generation of random value within its established range.

Table 7. Input variables and respective errors.

Variables	Min	Max	Unit
$p$	11,597	102,000	$\mathrm{Pa}$
$T$	263.15	313.15	$°\mathrm{K}$
$\Delta p$	0	10	$\mathrm{inH}2\mathrm{O}$
Errors (Manufacturers)	Min	Max	Unit
$u_T$	−0.8	0.8	$°\mathrm{K}$
$u_p$	−250	250	$\mathrm{Pa}$
$u_{\Delta p} (\Delta p<3.94 inH2O)$	−0.18	0.18	$\mathrm{inH}2\mathrm{O}$
$u_{\Delta p} (\Delta p>3.94 inH2O)$	−0.3	0.3	$\mathrm{inH}2\mathrm{O}$
Errors (Calibrations)	Min	Max	Unit
$u_p$	−16	16	$\mathrm{Pa}$
$u_{\Delta p}$	−0.04	0.04	$\mathrm{inH}2\mathrm{O}$

5. Results and Discussion

Table 8 and Table 9 express the results of simulation 1, based on the manufacturing uncertainty, that maximize the actual volumetric flow rate and the standard volumetric flow rate, respectively.

Table 8. Simulation 1: actual volumetric flow rate.

$\mathit{i}$	$\Delta \mathit{p}$	${\mathit{u}}_{\Delta \mathit{p}}$	$\mathit{T}$	${\mathit{u}}_{\mathit{T}}$	${\mathit{Q}}_{\mathit{a}}$	${\mathit{u}}_{{\mathit{Q}}_{\mathit{a}}}$
Number of Iterations	$\left(\mathbf{i}\mathbf{n}\mathbf{H}2\mathbf{O}\right)$	$\left(\mathbf{i}\mathbf{n}\mathbf{H}2\mathbf{O}\right)$	$\left(\mathbf{K}\right)$	$\left(\mathbf{K}\right)$	$\left(\mathbf{l}\mathbf{p}\mathbf{m}\right)$	$\left(\mathit{\%} \mathbf{f}\mathbf{s}\right)$
10 M	3.96	−0.299	265.45	0.791	72.633	3.559
-	3.94	−0.300	263.15	0.800	72.782	3.598

Table 9. Simulation 1: standard volumetric flow rate.

$\mathit{i}$	$\Delta \mathit{p}$	${\mathit{u}}_{\Delta \mathit{p}}$	$\mathit{T}$	${\mathit{u}}_{\mathit{T}}$	$\mathit{p}$	${\mathit{u}}_{\mathit{p}}$	${\mathit{Q}}_{\mathit{s}\mathit{t}\mathit{d}}$	${\mathit{u}}_{{\mathit{Q}}_{\mathit{s}\mathit{t}\mathit{d}}}$
	$\left(\mathbf{i}\mathbf{n}\mathbf{H}2\mathbf{O}\right)$	$\left(\mathbf{i}\mathbf{n}\mathbf{H}2\mathbf{O}\right)$	$\left(\mathbf{K}\right)$	$\left(\mathbf{K}\right)$	$\left(\mathbf{P}\mathbf{a}\right)$	$\left(\mathbf{P}\mathbf{a}\right)$	$\left(\mathbf{s}\mathbf{l}\mathbf{p}\mathbf{m}\right)$	$\left(\mathit{\%} \mathbf{f}\mathbf{s}\right)$
10 M	6.14	0.297	263.32	−0.608	101,730	173.68	120.301	3.984
-	3.94	0.300	263.15	−0.800	102,000	250.00	80.235	4.265

Based on the calibrations uncertainty, Table 10 and Table 11 express the results of simulation 2 that maximize the actual volumetric flow rate and the standard volumetric flow rate, respectively.

Table 10. Simulation 2: actual volumetric flow rate.

$\mathit{i}$	$\Delta \mathit{p}$	${\mathit{u}}_{\Delta \mathit{p}}$	$\mathit{T}$	${\mathit{u}}_{\mathit{T}}$	${\mathit{Q}}_{\mathit{a}}$	${\mathit{u}}_{{\mathit{Q}}_{\mathit{a}}}$
	$\left(\mathbf{i}\mathbf{n}\mathbf{H}2\mathbf{O}\right)$	$\left(\mathbf{i}\mathbf{n}\mathbf{H}2\mathbf{O}\right)$	$\left(\mathbf{K}\right)$	$\left(\mathbf{K}\right)$	$\left(\mathbf{l}\mathbf{p}\mathbf{m}\right)$	$\left(\mathit{\%} \mathbf{f}\mathbf{s}\right)$
10 M	9.94	0.039	263.15	−0.778	166.89	0.636
-	10.00	0.040	263.15	−0.800	167.67	0.644

Table 11. Simulation 2: standard volumetric flow rate.

$\mathit{i}$	$\Delta \mathit{p}$	${\mathit{u}}_{\Delta \mathit{p}}$	$\mathit{T}$	${\mathit{u}}_{\mathit{T}}$	$\mathit{p}$	${\mathit{u}}_{\mathit{p}}$	${\mathit{Q}}_{\mathit{s}\mathit{t}\mathit{d}}$	${\mathit{u}}_{{\mathit{Q}}_{\mathit{s}\mathit{t}\mathit{d}}}$
	$\left(\mathbf{i}\mathbf{n}\mathbf{H}2\mathbf{O}\right)$	$\left(\mathbf{i}\mathbf{n}\mathbf{H}2\mathbf{O}\right)$	$\left(\mathbf{K}\right)$	$\left(\mathbf{K}\right)$	$\left(\mathbf{P}\mathbf{a}\right)$	$\left(\mathbf{P}\mathbf{a}\right)$	$\left(\mathbf{s}\mathbf{l}\mathbf{p}\mathbf{m}\right)$	$\left(\mathit{\%} \mathbf{f}\mathbf{s}\right)$
10 M	9.34	0.035	264.79	−0.799	100,410	12.57	178.95	1.016
-	10.00	0.040	263.15	−0.800	102,000	16.00	184.84	1.107

The results of the MEMS calibration and the maximum errors that their manufactures claim to occur are presented in Table 12. Note that this MEMS do not have factory calibration, so it is natural that their manufacturers supply data with higher values of measurement errors in order to guarantee their clients medium/long time satisfaction.

Table 12. Uncertainty of microelectromechanical systems (MEMSs).

MEMS	Calibration	Manufacturer
Pressure	±0.16 mbar	±2.50 mbar
Differential Pressure	±0.040 inH2O	±0.30 inH2O

The maximum output errors were obtained in simulations that used ten million iterations. However, by analyzing the trend of the variables over each simulation, it was verified that the maximum output errors were obtained when the input values and respective errors take the limit values of their range. So, for this case, the iteration number (i) was negligible.

In Table 13 there are presented the results obtained by the two simulations and by the calibration for the uncertainty of actual and standard volumetric flowrate. As has been said before, this flowmeter had a particular accuracy requirement established by the technical documentation delivered by the test bench manufacturer (±1% full scale).

Table 13. Uncertainty of the actual and standard volumetric flowrate.

	Simulation 1	Simulation 2	Calibration
Actual Volumetric Flowrate	±3.56% fs	±0.64% fs	±0.45% fs
Standard Volumetric Flowrate	±4.27% fs	±1.11% fs	±0.45% fs

So, according to the MEMS manufacturing uncertainty, the automated flowmeter measurement uncertainty was $u_{Q_a}\approx \pm 3.6\%\mathrm{fs}$ and $u_{Q_{std}}\approx \pm 4.3\%\mathrm{fs}$. According to the MEMS calibrations uncertainty, the automated flowmeter measurement uncertainty was $u_{Q_a}\approx \pm 0.6\%\mathrm{fs}$ and $u_{Q_{std}}\approx \pm 1.1\%\mathrm{fs}$.

6. Conclusions

The conclusions taken from the various stages of this work are:

• The data measurement uncertainty given by the sensors manufacturers was higher than the obtained by the calibrations, so all MEMS must be calibrated before installed in the setup.
• The iteration number for simulation 1 and simulation 2 was negligible, because the maximum output errors were obtained when the input values and respective errors took the limit values of their range.
• In simulation 1, it was observed that both the actual volumetric flowrate and standard volumetric flowrate largely exceeded the accuracy requirement (±1% full scale). So, in coherence with the data measurement uncertainty given by the manufacturer this simulation was very conservative.
• In simulation 2 the actual volumetric flowrates maximum error was lower than the accuracy requirement established by the technical documentation delivered by the test bench manufacturer (±1% full scale).
• The maximum error of the standard volumetric flowrate, obtained by simulation 2, slightly exceeded the accuracy requirement established by the test bench technical manual.
• The automated flowmeter calibration performed according to the Guide to the Expression of Uncertainty in Measurement shows the lowest uncertainty values.
• The measurement uncertainty given by the calibration was lower than the values obtained by both simulations.
• According to the automated flowmeter calibration, the uncertainty obtained (±0.45% fs) was accepted by the requirement and therefore recommended for this application.

By analyzing all the results, this automated flowmeter can be used in this test bench, but the authors only recommended its use for actual volumetric flowrate measurements.