Double Slit with an Einstein–Podolsky–Rosen Pair
Abstract
1. Introduction
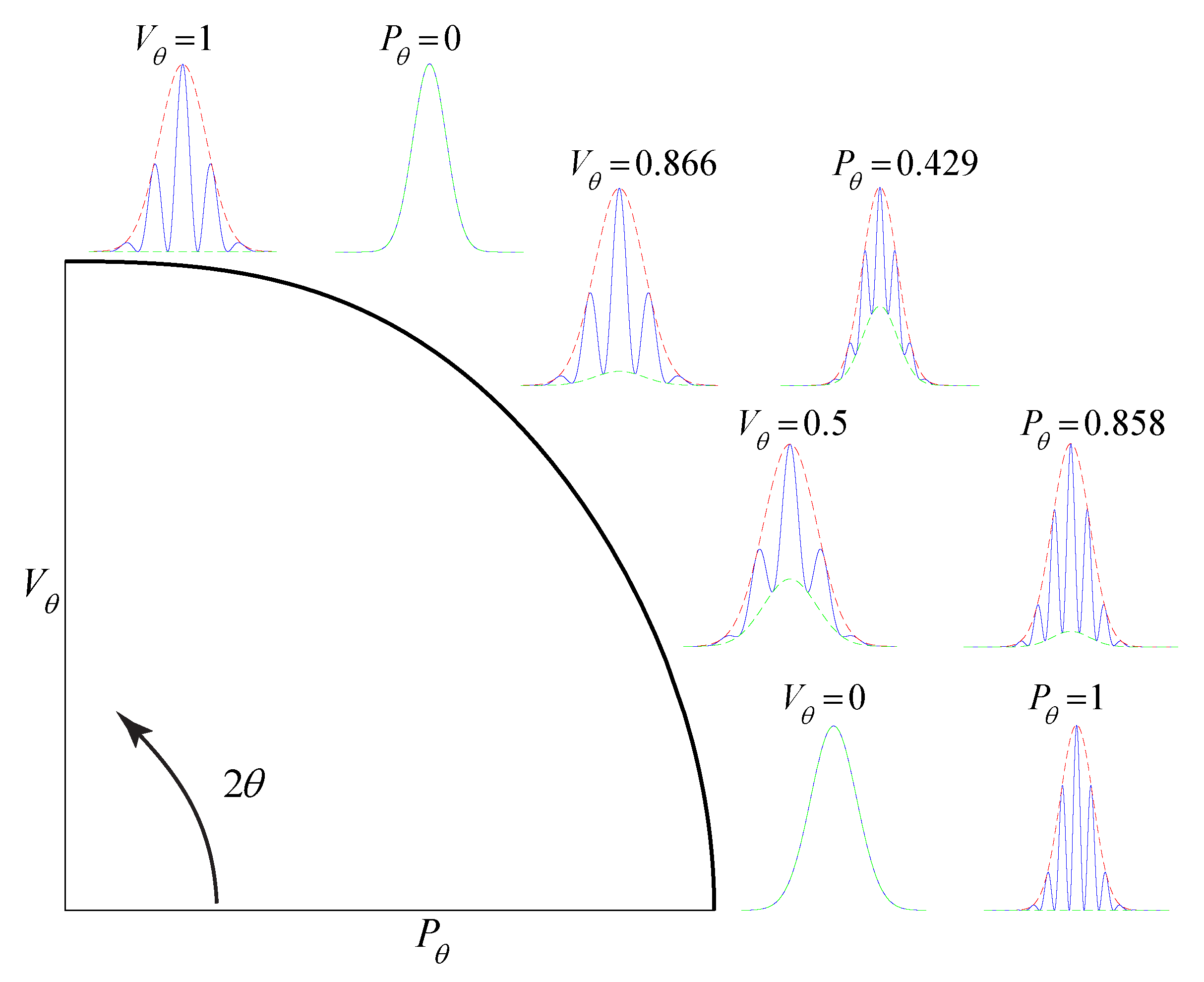
2. Model for Entangled Double-Slit Experiment Using Gaussian Wave Packets
3. A Partially Entangled Double-Slit Experiment
4. Model for Asymmetric Entangled Double-Slit Experiment
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Complementary Quantum Measures and Relations
Appendix B. Computations and Wigner Functions
Appendix B.1. The Wigner Function for a Partially Entangled Double-Slit Experiment
Appendix B.2. The Wigner Function for an Asymmetric Double-Slit Experiment
Appendix B.3. Purification of Alice’s Subsystem
References
- Jaeger, G.; Horne, M.A.; Shimony, A. Complementarity of one-particle and two-particle interference. Phys. Rev. A 1993, 48, 1023–1027. [Google Scholar] [CrossRef] [PubMed]
- Greenberger, D.M.; Yasin, A. Simultaneous wave and particle knowledge in a neutron interferometer. Phys. Lett. A 1988, 128, 391–394. [Google Scholar] [CrossRef]
- Jaeger, G.; Shimony, A.; Vaidman, L. Two interferometric complementarities. Phys. Rev. A 1995, 51, 54–67. [Google Scholar] [CrossRef] [PubMed]
- Englert, B.G. Fringe visibility and which-way information: An inequality. Phys. Rev. Lett. 1996, 77, 2154–2157. [Google Scholar] [CrossRef] [PubMed]
- Franson, J.D. Bell inequality for position and time. Phys. Rev. Lett. 1989, 62, 2205–2208. [Google Scholar] [CrossRef] [PubMed]
- Einstein, A.; Podolsky, B.; Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 1935, 47, 777–780. [Google Scholar] [CrossRef]
- Schrödinger, E. Discussion of probability relations between separated systems. Math. Proc. Camb. Philos. Soc. 1935, 31, 555–563. [Google Scholar] [CrossRef]
- Masada, G.; Miyata, K.; Politi, A.; Hashimoto, T.; O’Brien, J.L.; Furusawa, A. Continuous-variable entanglement on a chip. Nat. Photonics 2015, 9, 316–319. [Google Scholar] [CrossRef]
- Pirandola, S.; Eisert, J.; Weedbrook, C.; Furusawa, A.; Braunstein, S.L. Advances in quantum teleportation. Nat. Photonics 2015, 9, 641–652. [Google Scholar] [CrossRef]
- Braunstein, S.L.; van Loock, P. Quantum information with continuous variables. Rev. Mod. Phys. 2005, 77, 513–577. [Google Scholar] [CrossRef]
- Eisert, J.; Plenio, M.B. Introduction to the basics of entanglement theory in continuous-variable systems. Int. J. Quantum Inf. 2003, 1, 479–506. [Google Scholar] [CrossRef]
- Serafini, A. Entanglement of continuous variable systems. In Quantum Continuous Variables: A Primer of Theoretical Methods; CRC Press: Boca Raton, FL, USA, 2017; Chapter 7; pp. 171–222. [Google Scholar] [CrossRef]
- Adesso, G.; Illuminati, F. Entanglement in continuous-variable systems: recent advances and current perspectives. J. Phys. A 2007, 40, 7821–7880. [Google Scholar] [CrossRef]
- Scully, M.O.; Englert, B.G.; Walther, H. Quantum optical tests of complementarity. Nature 1991, 351, 111–116. [Google Scholar] [CrossRef]
- Englert, B.G.; Walther, H.; Scully, M.O. Quantum optical Ramsey fringes and complementarity. Appl. Phys. B 1992, 54, 366–368. [Google Scholar] [CrossRef]
- Herzog, T.J.; Kwiat, P.G.; Weinfurter, H.; Zeilinger, A. Complementarity and the quantum eraser. Phys. Rev. Lett. 1995, 75, 3034–3037. [Google Scholar] [CrossRef]
- Bertet, P.; Osnaghi, S.; Rauschenbeutel, A.; Nogues, G.; Auffeves, A.; Brune, M.; Raimond, J.M.; Haroche, S. A complementarity experiment with an interferometer at the quantum—Classical boundary. Nature 2001, 411, 166–170. [Google Scholar] [CrossRef]
- Braig, C.; Zarda, P.; Kurtsiefer, C.; Weinfurter, H. Experimental demonstration of complementarity with single photons. Appl. Phys. B 2003, 76, 113–116. [Google Scholar] [CrossRef]
- Jacques, V.; Lai, N.D.; Dréau, A.; Zheng, D.; Chauvat, D.; Treussart, F.; Grangier, P.; Roch, J.F. Illustration of quantum complementarity using single photons interfering on a grating. New J. Phys. 2008, 10, 123009. [Google Scholar] [CrossRef]
- Gao, L.; Zhang, Y.; Cohen, E.; Elitzur, A.C.; Karimi, E. Nonlocal quantum erasure of phase objects. Appl. Phys. Lett. 2019, 115, 051102. [Google Scholar] [CrossRef]
- Carmi, A.; Cohen, E. Relativistic independence bounds nonlocality. Sci. Adv. 2019, 5, eaav8370. [Google Scholar] [CrossRef]
- Pan, Y.; Cohen, E.; Karimi, E.; Gover, A.; Kaminer, I.; Aharonov, Y. Weak measurement, projective measurement and quantum-to-classical transitions in electron-photon interactions. arXiv 2019, arXiv:1910.11685. [Google Scholar]
- Pan, Y.; Zhang, J.; Cohen, E.; Wu, C.W.; Chen, P.X.; Davidson, N. Observation of the weak-to-strong transition of quantum measurement in trapped ions. arXiv 2019, arXiv:1910.11684. [Google Scholar]
- Aharonov, Y.; Albert, D.Z.; Vaidman, L. How the result of a measurement of a component of the spin of a spin- particle can turn out to be 100. Phys. Rev. Lett. 1988, 60, 1351–1354. [Google Scholar] [CrossRef] [PubMed]
- Tamir, B.; Cohen, E. Introduction to weak measurements and weak values. Quanta 2013, 2, 7–17. [Google Scholar] [CrossRef]
- Dressel, J.; Malik, M.; Miatto, F.M.; Jordan, A.N.; Boyd, R.W. Understanding quantum weak values: basics and applications. Rev. Mod. Phys. 2014, 86, 307–316. [Google Scholar] [CrossRef]
- Vaidman, L.; Ben-Israel, A.; Dziewior, J.; Knips, L.; Weißl, M.; Meinecke, J.; Schwemmer, C.; Ber, R.; Weinfurter, H. Weak value beyond conditional expectation value of the pointer readings. Phys. Rev. A 2017, 96, 032114. [Google Scholar] [CrossRef]
- Piacentini, F.; Avella, A.; Gramegna, M.; Lussana, R.; Villa, F.; Tosi, A.; Brida, G.; Degiovanni, I.P.; Genovese, M. Investigating the effects of the interaction intensity in a weak measurement. Sci. Rep. 2017, 8, 6959. [Google Scholar] [CrossRef]
- Dziewior, J.; Knips, L.; Farfurnik, D.; Senkalla, K.; Benshalom, N.; Efroni, J.; Meinecke, J.; Bar-Ad, S.; Weinfurter, H.; Vaidman, L. Universality of local weak interactions and its application for interferometric alignment. Proc. Natl. Acad. Sci. USA 2019, 116, 2881–2890. [Google Scholar] [CrossRef]
- Carmi, A.; Cohen, E. On the significance of the quantum mechanical covariance matrix. Entropy 2018, 20, 500. [Google Scholar] [CrossRef]
- Carmi, A.; Herasymenko, Y.; Cohen, E.; Snizhko, K. Bounds on nonlocal correlations in the presence of signaling and their application to topological zero modes. New J. Phys. 2019, 21, 073032. [Google Scholar] [CrossRef]
- Georgiev, D.; Cohen, E. Probing finite coarse-grained virtual Feynman histories with sequential weak values. Phys. Rev. A 2018, 97, 052102. [Google Scholar] [CrossRef]
- Zhang, S.; Feng, Y.; Sun, X.; Ying, M. Upper bound for the success probability of unambiguous discrimination among quantum states. Phys. Rev. A 2001, 64, 062103. [Google Scholar] [CrossRef]
- Qiu, D. Upper bound on the success probability for unambiguous discrimination. Phys. Lett. A 2002, 303, 140–146. [Google Scholar] [CrossRef]
- Bera, M.N.; Qureshi, T.; Siddiqui, M.A.; Pati, A.K. Duality of quantum coherence and path distinguishability. Phys. Rev. A 2015, 92, 012118. [Google Scholar] [CrossRef]
- Qureshi, T.; Siddiqui, M.A. Wave-particle duality in N-path interference. Ann. Phys. 2017, 385, 598–604. [Google Scholar] [CrossRef]
- Siddiqui, M.A.; Qureshi, T. A nonlocal wave-particle duality. Quantum Stud. Math. Found. 2016, 3, 115–122. [Google Scholar] [CrossRef][Green Version]
- Roy, P.; Qureshi, T. Path predictability and quantum coherence in multi-slit interference. Phys. Scr. 2019, 94, 095004. [Google Scholar] [CrossRef]
- Qureshi, T. Coherence, interference and visibility. Quanta 2019, 8, 24–35. [Google Scholar] [CrossRef]
- Qureshi, T. Interference visibility and wave-particle duality in multipath interference. Phys. Rev. A 2019, 100, 042105. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peled, B.Y.; Te’eni, A.; Georgiev, D.; Cohen, E.; Carmi, A. Double Slit with an Einstein–Podolsky–Rosen Pair. Appl. Sci. 2020, 10, 792. https://doi.org/10.3390/app10030792
Peled BY, Te’eni A, Georgiev D, Cohen E, Carmi A. Double Slit with an Einstein–Podolsky–Rosen Pair. Applied Sciences. 2020; 10(3):792. https://doi.org/10.3390/app10030792
Chicago/Turabian StylePeled, Bar Y., Amit Te’eni, Danko Georgiev, Eliahu Cohen, and Avishy Carmi. 2020. "Double Slit with an Einstein–Podolsky–Rosen Pair" Applied Sciences 10, no. 3: 792. https://doi.org/10.3390/app10030792
APA StylePeled, B. Y., Te’eni, A., Georgiev, D., Cohen, E., & Carmi, A. (2020). Double Slit with an Einstein–Podolsky–Rosen Pair. Applied Sciences, 10(3), 792. https://doi.org/10.3390/app10030792







