Abstract
The emergence of the uncertainty principle has celebrated its 90th anniversary recently. For this occasion, the latest experimental results of uncertainty relations quantified in terms of Shannon entropies are presented, concentrating only on outcomes in neutron optics. The focus is on the type of measurement uncertainties that describe the inability to obtain the respective individual results from joint measurement statistics. For this purpose, the neutron spin of two non-commuting directions is analyzed. Two sub-categories of measurement uncertainty relations are considered: noise–noise and noise–disturbance uncertainty relations. In the first case, it will be shown that the lowest boundary can be obtained and the uncertainty relations be saturated by implementing a simple positive operator-valued measure (POVM). For the second category, an analysis for projective measurements is made and error correction procedures are presented.
1. Introduction
According to quantum mechanics, any single observable or a set of compatible observables can be measured with arbitrary accuracy. However, the physical scenario changes when jointly (i.e., simultaneously or successively) measuring non-commuting observables. Heisenberg’s seminal paper from 1927 [1] predicts a lower bound on the uncertainty of a joint measurement of incompatible observables, more precisely of the canonically conjugate variables position and momentum. On the other hand, it also sets an upper bound on the accuracy with which the values of non-commuting observables can be simultaneously prepared.
While in the past these two statements have often been mixed, they are now clearly distinguished as measurement uncertainty and preparation uncertainty relations. When we consider the quantities position and momentum, as in Heisenberg’s original argument, the well-known inequality states that it is impossible to prepare a quantum system for which both, position and momentum, are arbitrarily sharply defined. Operationally this is achieved by an apparatus that prepares many copies of a quantum particle in the same way, which is schematically illustrated in Figure 1. On one part of the ensemble, the position is measured and on the other part the momentum. From the statistical distribution of these two measurements, the preparation uncertainty can be determined. What is the correct way to interpret these distributions? While Heisenberg’s paper only presented his idea heuristically, the first rigorously-proven uncertainty relation for position Q and momentum P was provided by Kennard [2] in terms of standard deviations expressed as
where the standard deviation is defined as . This relation can be generalized to other pairs of incompatible observables, including the phase and excitation number of a harmonic oscillator, the angle and the orbital angular momentum of a particle, and orthogonal components of spin angular momentum [3,4,5]. In 1929, Robertson [6] extended Kennard’s relation Equation (1) to an arbitrary pair of observables A and B as
with the commutator . Robertson’s uncertainty relation in turn follows from a slightly stronger inequality namely the Schrödinger uncertainty relation [7] which is given by
introducing the anti-commutator .
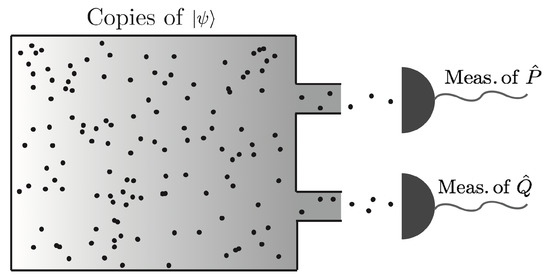
Figure 1.
Experimental procedure to measure preparation uncertainty relations. Each particle that is emitted by the source preparing identical states either undergoes a measurement of observable A or B.
In Kennard’s and Robertson’s uncertainty relations Equations (1) and (2) the uncertainty is expressed in terms of standard deviations. This is, however, not the only way to express uncertainties and sometimes not a well-suited measure [8]. For illustration consider the well-known single-slit experiment, which is schematically illustrated in Figure 2a. An incoming monochromatic plane wave represents an incoming beam of particles. The particles with momentum pass a slit of width and are detected on a screen (or photographic plate) placed at a distance l. The diffraction of particles by such a single slit is frequently used as an illustration of the uncertainty principle [9,10]. The wave function at the screen () may be represented by the following Fourier transform pair illustrated in Figure 2b (for and this is a good approximation of a Fourier transform). The uncertainty in momentum corresponds to the width of the central peak, which contains about 95 of the total probability. Therefore is a very reasonable measure of uncertainty. The standard deviations are then defined as and , where and , which gives and . So if we take these as measures of uncertainty, we have to say that the momentum is completely uncertain (independent of a). The problem stems from the definition of where the probability density is multiplied by a factor , giving increasing weight to the distant parts of the probability distribution. Although the tails of the momentum distribution contain very little probability, they fall off too slowly for to be finite, which illustrates that the standard deviation is not a proper measure of the width of a general probability distribution (even if its good for Gaussians).
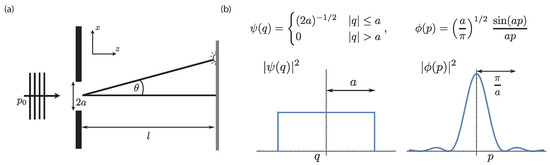
Figure 2.
Experimental procedure to measure preparation uncertainty relations, where each particle undergoes a measurement of observable A or B. (a) schematic illustration of the single-slit configuration. (b) Distributions of the canonical conjugated variables position q and momentum p.
The uncertainty relation as formulated by Robertson in terms of standard deviations has two flaws: (i) the standard deviation is not an optimal measure for all states, as discussed above. (ii) the boundary (right-hand side of any uncertainty relation) can become zero for non-commuting observables (this is also the case for our neutron spins for a combination of and ). At this point, it should be mentioned, that the reason for the existence of that bound is the well known canonical commutation relations (CCR) of position and momentum of a quantum particle. An algebraic structure in the form (in words: the uncertainty of the observables for a quantum state, must always be larger than some state-independent bound ) is desirable for an uncertainty relation. Note that Heisenberg’s (and Kennard’s) inequality has that form, but its generalization Equation (2) does not. In order to represent a quantitative physical notion of uncertainty, must at least possess the following elementary property: If and only if is a simultaneous eigenstate of A and B may become zero. From this, we can infer a property of , namely that it must vanish if and only if A and B have an eigenstate in common.
One way to avoid just mentioned problems is to use another measure of statistical dispersion. The first entropic uncertainty relation was formulated by Hirschman [11] in 1957 for the position and momentum observables, which was later improved in 1975 by Beckner [12] and Bialynicki–Birula and Mycielski [13] resulting in
where h is the differential entropy defined as , with probability density . Equation (4) actually implies Kennard’s relation Equation (1). The extension to non-degenerate observables on a finite-dimensional Hilbert space was given by Deutsch in 1983 [14] and later improved by Maassen and Uffink [15] yielding the well-known entropic uncertainty relation
where H denotes the Shannon entropy and c is the maximal overlap between the eigenvectors.
At this point we want to turn to the main topic of the present review article, that is measurement uncertainty relations, which include (1) joint measurability, i.e., the fact that certain pairs of observables cannot be measured simultaneously, and (2) measurement disturbance, i.e., the concept that in successive setups there exist certain pairs of observables that cause a disturbance on the second measured operator as shown in Figure 3. Measurement uncertainty is a topic gaining much attention in current research, both from the theoretic [16,17,18,19,20] and experimental view [21,22,23,24,25,26,27,28,29]. In light of these recent developments Buscemi and Hall proposed information-theoretic definitions for noise and disturbance in quantum measurements and a state-independent noise–disturbance uncertainty relation—an entropic formulation of measurement uncertainty relations [30].
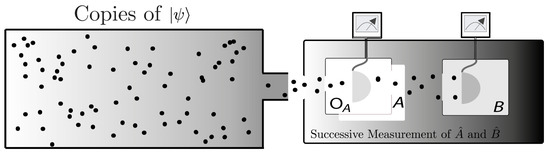
Figure 3.
Experimental procedure to measure observables A or B in a successive manner. Instead of precisely measuring A an approximate measure of A, denoted as is performed in order to reduce the disturbance on B.
The distinction between the two kinds of uncertainty types led to a resurgence of the corresponding research, in particular for qubits. In the first noise–disturbance investigations, an experiment is performed which successively measures the neutron spin in two maximally non-commuting directions [31]. The obtained result brings important insights, first that it is possible to improve the uncertainty relation by reverting some of the correlation losses, and second that it is difficult to find out which measurement configuration allows us to reach the lowest uncertainty. In fact, a little later, a violation of the presented noise–disturbance inequality was found [32]. Because a mathematical analysis of the noise–disturbance case is very difficult, an experimental investigation of the simpler noise–noise case is made [33]. In the following, a concise overview of the theory and a detailed picture of the neutron optical experiments is offered.
2. Theory
For an observable A with finite, non-degenerate spectrum the expectation value is defined by where the probability is given by Born’s rule. The standard deviation quantifies the statistical dispersion around the mean in many repetitions of the same configuration, written out as
There are of course other quantities that can describe the dispersion, peakedness or uniformity of probability measures. Associate to the outcomes the random variable , then the Shannon entropy [34] of the distribution is defined by
This entropy quantifies the average information content of probabilistic data and becomes larger the more uniform the distribution is. The striking difference between the standard deviation and the Shannon entropy is that the former explicitly depends on the outcome value , while the latter depends on nothing but the probabilities . Considering a probability distribution as a pair of values , it is quickly realized that the Shannon entropy is not affected by any relabeling or shuffling of .
The entropic noise operator quantifies the average information that the apparatus [35] gains in a measurement of the operator A. For that purpose an a priori distribution of eigenstates is considered which are prepared with uniform probability , where d denotes the dimension of the system state. This source of equiprobable input states is then sent to the instrument , modeled as a completely positive, trace non-increasing quantum operation with outcomes belonging to . The noise operator is defined as the conditional entropy ,
This is to be interpreted as the possibility to infer the unknown eigenstates of A by the instrument. If the outcomes are perfectly correlated to , then a certain guess of the initial state can be made, otherwise, if the instrument can not discriminate the input states perfectly then the measurement is considered as noisy and not well calibrated.
Let the observable B be an operator that generally does not commute with A. The entropic disturbance operator is modeled similar to the noise operator. Uniformly distributed eigenstates with eigenvalues associated with random variable are fed to the same instrument from which a post-measurement state emerges. In the disturbance configuration there is, however, an additional subsequent measurement of observable B with outcomes . Due to the disturbing nature of the measurement apparatus , generally, a loss of correlation occurs. A subtle, yet important addendum to the concept of disturbance are error corrections. After measurement by , the state decomposed to the eigenstates of the measurement observables can be further transformed by a quantum operation dependent on the pointer value of the apparatus. The disturbance operator is defined as the conditional entropy ,
The error correction is hidden in the probabilities
The entropic disturbance is to be interpreted as the possibility to infer the unknown eigenvalues of B from the outcomes of after the intermediate apparatus induced a disturbance on the initial state and an appropriate correction transformation is made. If a perfect guess is possible from the measurement results there is no disturbance, else if the instrument has reduced the correlation to some extent the inference of the initially unknown eigenstates is faulty. The optimal error correction is defined as the transformation that, for a given measurement , minimizes the disturbance .
From the definitions of the entropic noise and disturbance it becomes apparent that if , it is not possible to make noiseless and disturbance-free joint measurements. Generally, two different kinds of uncertainty relations arise in this framework, first derived in [30].
- Noise–noise uncertainty relationThis tradeoff expresses the inability for the device to jointly discriminate the eigenstates and to arbitrary precision.
- Noise–disturbance uncertainty relationThis inequality implies that the measurement apparatus cannot be noise and disturbance-free for both eigenstates of the non-commuting operators A and B.
At this point, it makes sense to point out a difference in the uncertainty relations involving entropy or standard deviations, respectively. From Equations (6) it is apparent that the formula depends generally on the input state , while the definitions of noise and disturbance involve only the observables’ eigenstates which makes Equation (11) and (12) state independent. Furthermore, the noise–noise and noise–disturbance inequalities look identical to the well-known Maassen–Uffink [15] relation which describes preparation uncertainties.
One of the biggest challenges in exploring uncertainty relations is finding the smallest boundary and the saturation conditions, i.e., the conditions under which the uncertainty relations acquire equality. Optimization studies are rather tough and therefore tight solutions have been proven only for a few selected cases. The Maassen–Uffink relation, for example, is only saturated for mutually unbiased (MUB) states and can not reach equality for other states. In the approach [32] the region of obtainable values is written out as
Finding this set of points reachable by joint measurements is an ongoing task. For two-dimensional quantum systems promising results have been derived in the first instance.
Entropic Measurement Uncertainty Relation for Qubits
The principle idea behind the optimization of the uncertainty relation is based on finding the minimum of the sum of entropies . For dichotomic observables there are only two outcomes and the binary Shannon entropy in its symmetric form can be compactly written as
Let and then calculation of the extreme values [36,37] for qubit systems show that for an analytic expression of the uncertainty relation can be provided. According to the details of [32] the noise–noise uncertainty relation is expressed as
where g is the inverse function of the binary entropy Equation (15), hence . However for , not all obtainable values by joint measurements are contained in the region demarcated by relation Equation (16). Geometrically, when the modulus of the inner product of the two Bloch vectors is larger than the critical angle the shape of the area becomes non-convex. According to the proposition [32] the entire region of obtainable values for qubits is given by the convex hull of the subset constituted by Equation (16), i.e.,
Let be two-dimensional, orthogonal projectors, where the Bloch sphere coordinates are used to parametrize by the polar and azimuthal angle . The entire region including the lower boundary of can be obtained by measuring four-outcome POVMs corresponding to a statistical mixture of two projectors weighted by q and ,
A generally valid and optimal uncertainty relation between the entropic noise and the disturbance has not been found so far, not even for two-dimensional quantum systems. At least for two Pauli observables which are orthogonal and a measurement apparatus that performs projective measurements the following inequality does hold
Apart from this special case, an entropic uncertainty relation for - has yet to be found. For a detailed survey and conjectures see [32].
3. Measurement of Entropic Noise–Noise Uncertainty Relation
3.1. Set-Up
The experiments presented here use neutrons generated by a nuclear reaction at the TRIGA Mark II reactor in Vienna. The neutrons, after being monochromatized, arrive at the experimental site through an outlet of the shielding in the reactor wall. A polarizer at the beginning of the beamline eliminates one spin component, leaving only monoenergetic neutrons with up spin. A schematic view of the experimental setup is depicted in Figure 4.
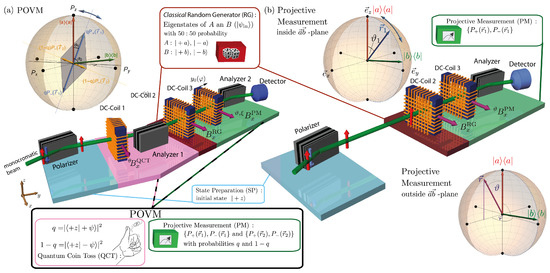
Figure 4.
Experimental arrangement for determining the noises and thus the uncertainty relation. In (a) the full set-up is shown. In the projective case in (b), the configuration consists of 2 coils, DC-Coil 2 generating one of the possible eigenstates () uniformly at random and DC-Coil 3 adjusted to make a selection of the state with orientation . For the positive operator-valued measure (POVM), the four-outcomes are implemented by ‘splitting’ the total neutron counts to two partitions in the rose colored area. For that purpose, the DC-Coil 1 changes the angle incident to Analyzer 1 and reduces the probability to be transmitted to the experimental backstage to . Whenever the experiment is set to q, Analyzer 1 makes a projection onto , but when the probability of transmission is inverted to , the second stage is conditioned to analyze .
Neutron spins can be manipulated precisely with static magnetic field generated by solenoid coils. When a neutron propagates in the y-direction and has a spin-up , then a magnet field in the perpendicular x-direction creates a unitary Larmor precession by an angle
The angle of rotation is proportional to the magnetic field strength and the time of passage of the neutron through the coil , being the gyromagnetic ratio. Since the transition time t is constant, the spin state is entirely controlled by the electric current that generates the magnetic field . Because the neutron is sensitive to magnetic fields, there are also unwanted disturbances from the earth’s magnetic field or magnetic materials in the vicinity of the setup. To avoid irritations of the neutron spin, the entire beamline is surrounded by a 13G vertical guide field. In order to leave the field’s axis in the coils unchanged in x-direction, the external field is compensated by a local field in the opposite direction.
A supermirror analyzer makes a spin-dependent projection by taking in the input quantum system and producing the outcome . The use of a coil placed in front of an analyzer, working according to Equation (20), allows any state to be generated before entry. A coil after the analyzer, in turn, allows an arbitrary initial state to be re-established. A measurement in the analyzer, therefore, consists of a combination of coil and supermirror, the usual sequence is the following: the state is generated by DC-Coil 1 and fed to the analyzer 1, the outcome appears with probability , which in turn is transformed by DC-Coil 2 after the analyzer to .
The idea for the realization of the POVM Equation (18) is as follows. At the neutrons, as indicated on the right of Figure 4, propagate along the y-axis with and are transformed by DC-Coil 2 to the eigenstates , respectively . The entropic concept of the noise demands that the two eigenstates are initially unknown and equally likely . For this purpose, the coils are driven by a power supply whose current is controlled by a random number generator (RG) operated by a computer. This RG will produce the desired eigenstates with equal probability distribution at random. In DC-Coil 3 the current is adjusted to make an analysis of the eigenstates in the direction , i.e., the probability to pass the Analyzer 2 before the detector is (likewise for ). The angle is controlled once more by the current in the coil while the azimuthal angle is a function of the distance between DC-Coil 2 and DC-Coil 3. In the case , the pink-colored section in Figure 4 is integrated into the setup. The incoming neutron is set to pass to the second stage of the instrument with probability , where is generated according to Equation (20) by DC-Coil 1. Then, as usual, the second coil produces one of the eigenstates of at random before analysis in direction . After some time, however, the incoming state is inverted and changes the probability of passing to . If that is the case, DC-Coil 3 is conditioned to make a measurement along .
At the end of the beamline, a count rate of about 40 neutrons per second remains, whereby all particles are registered in the detector independently of the spin. The efficiency of the detector is close to 1 owing to the high absorption cross-section of boron for thermal neutrons. The statistics of the counting rate follows a Poissonian distribution, hence the error of one standard deviation is equal to the mean value. The largest systematic error stems from the limited efficiency of resolving the polarization at the supermirror analyzers which causes a loss of state fidelity from 1 to approx. 0.98. To deal with the error, the insufficiency is compensated by marginally rescaling the values such that they cover the full range from 0 to 1.
3.2. Measurement Results
To determine the noise, all probabilities must be measured. This was done by counting the neutrons in a certain configuration each. The frequency of occurrence of an event in relation to all other possible events gives the probability. The Figure 5 and Figure 6 show the raw form of the measured data in the case of the input state , respectively . Each bar in the chart corresponds to the counted neutrons for a particular m and either an angle or a weighting q. If one denotes the counted neutrons as and then measuring the count rate for all combinations , and allows to obtain all necessary probabilities via
and
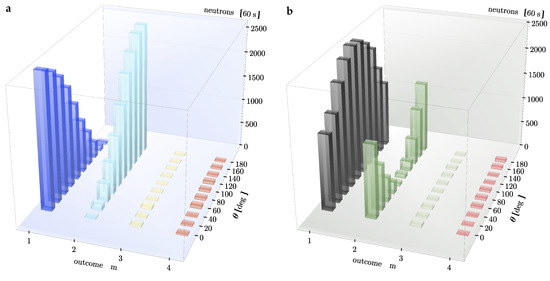
Figure 5.
The neutron count rate for (a) and (b) of the four-outcome POVM at a probability weighting of in the case and . Each histogram illustrates the change of counted neutrons depending on the angle of the measurement direction with an increment of . The maximal height in the 60s measurement are approximately 2500. At the initial angle , outcome corresponds to the projector and therefore a maximal count rate occurs in (a), while is associated with and no neutrons are detected. A rotation of the projectors by angle leads to a decrease of counts in and an increase of measured events in for the input state . Likewise, (b) shows the histogram for an input state , which is a distribution phase-shifted to by . Outcomes and from Equation (18) do not occur in the projective limit .
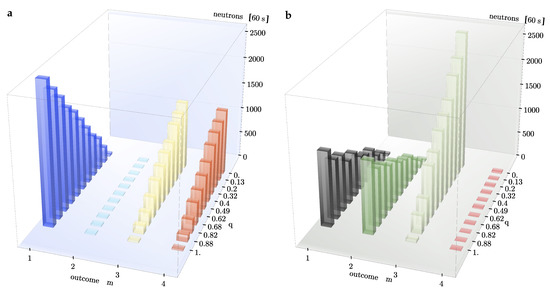
Figure 6.
The neutron count rate for (a) and (b) of the four-outcome POVM at polar angles and in the case and . Both histograms display a variation in the count rate depending on the probability weighting q with an approximate change rate of . In (a) the measurement start with the projective case and therefore is measured perfectly by . Alternation of the statistical mixture means that outcomes and measuring in direction contribute more and more to the statistics the more q decreases. As for (b), the measurement of A with the eigenstate of starts with half the count rate and then decreases equiprobably the more q is decreased. Meanwhile corresponing to registers more neutrons the closer q gets to 0, while associated with remains practically zero for the input state .
The regarded observable are and , the second operator is therefore only varied over the y-z plane. The first measurement was made in the projective case so that Equation (18) becomes . The Bloch vector is rotated from 0 to , hence depending on how close is to or the count rate is either large or small. Figure 5 shows the neutron count rate in the MUB case for the input states Figure 5a and Figure 5b . In order to obtain the total noise, the intensity distribution for the negative eigenstates is also necessary, which is not shown here. For each angle the four outcomes are detected each for the positive and negative eigenvectors with a total of 2500 neutrons recorded in 60 seconds.
In contrast to Figure 5 the bar chart in Figure 6 illustrates the alteration of count rates for varying statistical mixture q in Equation (18) but with static, unchanged measurement directions and . This means that if q is 0.7 for example, the neutron spins were measured by the operators and with a prefactor of 0.3, hence all four outcome slots are contributing to the statistics.
Putting the results together using Equation (8) for both observables A and B, the noise is plotted as a function of the rotation angle in Figure 7. The noises vary between 0 and 1; for a perfect measurement of A is made by which results in a noisefree determination of the eigenstates given by the blue data points, while on the other hand are maximally unpredictable at this point. When the projectors are rotated closer towards observable B, a trade-off between the noises occurs making the discrimination of more difficult and the differentiation of easier. This impossibility of jointly distinguishing the two eigenstates of the non-commuting observables of is known as the measurement uncertainty principle.
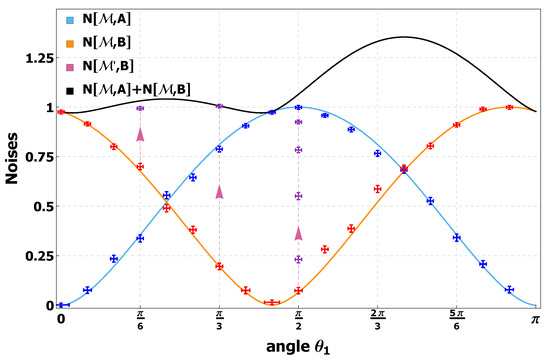
Figure 7.
The measurement results of noises in blue and in red for and together with the theoretical predictions given by the solid curves in the projective case. In addition, the purple data points show how variation of the azimuthal angle , which moves the measurement operator out of the plane spanned by , increases the total noise and makes the noise-noise trade-off worse. The black curve is equal to the sum and has two notable minima in the interval , which are necessary to identify the optimal values for the POVM.
Generally, we were interested in the region Equation (13) of all obtainable pairs of noise values. For that purpose, an analytic approach to finding the minimal and maximal values was necessary. The idea behind maximizing the noise is simple: since are confined to the y-z plane, rotating the measurement operator such that it lies outside the plane increases the entropy. The purple points at , and in Figure 7 are lifted to the maximal value through this procedure. To understand the strategy of finding the minimal value, it is necessary to look at the black curve representing the sum . Apparently, the sum of the entropic noises has two local minima in Figure 7 at and in the region 0-, calculable from the first derivative. The idea to obtain the lowest bound of the uncertainty region is to build the convex combination of the projectors and at exactly these minima. The linear progression of the noises as a function of the scalar parameter q is shown in Figure 8. The statistical weighting varies by about 0.1 and the two noises run with opposite proportionality, the sum always being at the minimum value of 0.96 (the same minima as in Figure 7).
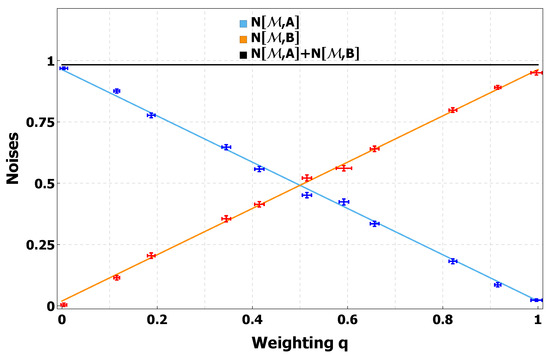
Figure 8.
Theoretical lines plus measurement points of in blue and in red for and for varying statistical weighting q. To obtain this plot the operators and are fixed to the extreme values and corresponding to the minima in Figure 7. The black line shows that the sum of the entropy remains constant at the lowest value of Figure 7. As a result, realizing the POVM Equation (18) reduces the overall noise.
Uncertainty relations are best viewed through a parametric representation as exhibited in Figure 9. The figure shows for Bloch vector and varying how the uncertainty region gradually changes. The white hatched part marks all the points which are not reachable by a joint measurement. Starting from the MUB case given in the first picture, it is seen that the amount of achievable points is sinking ever lower. On the other hand, the green area marks the POVM region, which only becomes relevant for far-off observables A and B.
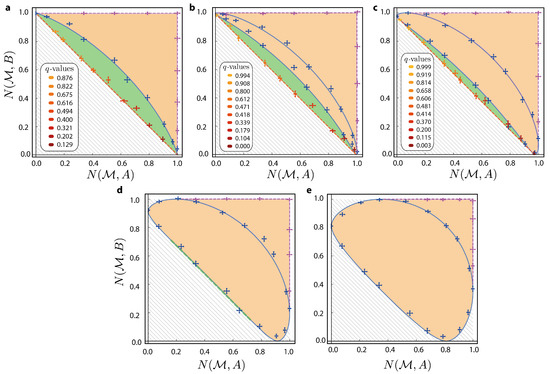
Figure 9.
Parametric plots of noises in observable and which indicate the accessible joint measurement uncertainty region , with the blue curve being the result of projective measurements in the plane spanned by -, the orange colored region obtainable by arbitrary projectors and finally the green area demarcating the lowest pairs of noise values only reached by POVMs. The upper panel shows the improvement on the uncertainty relation by choosing the convex combination of the operators and controlled by q, whose color coding is listed for (a) , (b) and (c) . In the lower panel, the included angle is very close or below the critical value of . Apparently the orange region is already becoming convex and further improvements by POVMs are not feasible for (d) or possible for (e) .
4. Measurement of Entropic Noise–Disturbance Uncertainty Relation
4.1. Set-Up
The setup bears some resemblance to the configuration shown in Figure 4. In the first stage of the set-up the necessary eigenstates of the observables under consideration are prepared in DC-1, which makes up four states in total. Afterwards, a successive measurement is conducted, first, the M-measurement in the middle, purple colored section shown in Figure 10 and then the B-measurement at the end of the set-up. The projection M is given by the combination DC-2 + Analyzer + DC-3: first, the initially prepared state is transformed to the eigenstate in DC-2, which interacts with the analyzer and is then recovered by DC-3 preparing the post-measurement state with the probability of occurrence being . Both coils adjacent to the first analyzer control the polar angle of the spin according to Equation (20) and are used to prepare and then conditionally recreate a particular state. The procedure for the B-measurement is analogous, i.e., the fourth coil DC-4 is set to transmit state maximally through the 2nd-analyzer and the orthogonal state with minimum probability. The reconstruction of the state before the detector is irrelevant since the registration of the neutron in the counting tube is spin-insensitive.
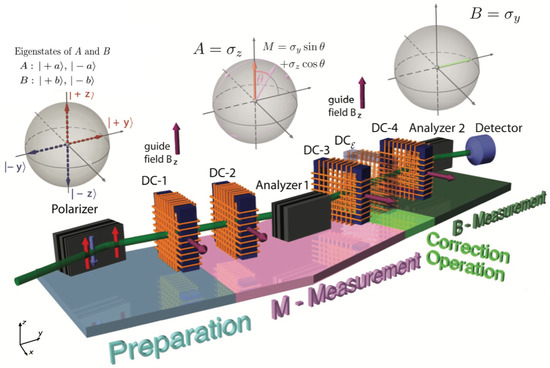
Figure 10.
Experimental realization for the measurement of noise and disturbance . In the preparation phase, the monochromatic neutrons are transformed to the observables’ eigenstates, indicated by the left Bloch sphere. DC-2 controls the incident angle of the spin. As noted in the middle Bloch sphere, the analyzer transmits best in the z-direction and gets worse as the operator turns away from the poles. DC-3 can either be used to produce the uncorrected eigenstates or perform the optimal correction and generate the spins . This different mode of operation is characterized by the light green color mark. In the dark green area, the second, subsequent projection takes place, in which DC-4 transforms the incoming vectors in such a way that B is measured optimally.
The error correction is a decisive aspect of the considerations of optimal noise–disturbance uncertainty relations. Practically, it is implemented by DC-3 which can not only be used to generate , but any other state. As it turns out, the optimal error-correction can be achieved by unitarily transforming the post-measurement state to the eigenvectors of observable B.
4.2. Measurement Results
The evaluation of the data is similar to the methods of the last section. However, each count rate has now three subscripts , as well as , the first index denoting the prepared eigenstate and the latter two indicate the result of the outcomes of the m and -measurements. The conditional and marginal probabilities required for the entropies are
Unlike for noise–noise uncertainty relations, an error correction procedure of the post measurement state must be taken into account which can drastically change the degree of disturbance. Setting the experimental observable to , and the oscillation of the conditional probabilities depending on the angle have been recorded and are plotted in Figure 11. The left panel Figure 11a illustrates a sine/cosine behavior as expected for the probability of preparing the input state corresponding to the eigenvalue a and receiving measurement outcome m. Based on the course of the conditional probabilities, one realizes for that , that is the modulus of the probability (centered at ) when leaving the post measurement state as is surpassed by the curve, where the optimal error correction is employed.
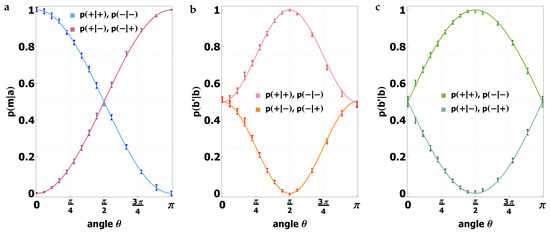
Figure 11.
Measurement results of the conditional probabilities for (a) , (b) and (c) . From to the increment is and changes to from on. At the angle the measurement operator is and the probability to receive given the value of the initial eigenvector is is maximal in (a), while the results with opposite signs are impossible to occur. Rotating the measurement direction leads to a sinusoidal change of the probabilities. The center (b) and right graph (c) show the probabilities for receiving given state b. The maxima and minima are shifted in phase to the first panel by . The uncorrected curve in the middle has not the same wide arc form compared to the curve where the optimal correction procedure is conducted.
The comparison of the respective curves and the shape of the noise can be seen well in Figure 12. The theoretical prediction of noise and uncorrected/optimally corrected disturbance for projective measurements are
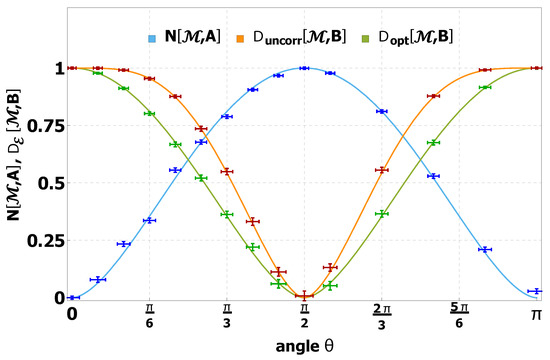
Figure 12.
Entropic noise in blue and uncorrected/optimally corrected disturbance in green/red as a function of the angle of the measurement operator. The noise for observable at is minimal, while the eigenstates of are maximally disturbed at this angle. Rotating the polar angle closer to the observable reduces the disturbance at the expanse of increasing the noise. After the first apparatus an additional rotation of the output state onto the closest eigenvector of B reduces the loss of correlation in parts and reduces the disturbance furthermore. At the measurement apparatus makes a perfect measurement of B inducing no disturbance, being however maximally noisy with respect to a measurement of .
The interpretation of the blue noise curve is all clear by now: the measurement starts perfectly correlated leading to vanishing noise and loses its correlation the closer M is to observable B before further rotation increases the anti-correlation and makes smaller again. The disturbance has a reciprocal form to the noise. The information about the initial states is maximally destroyed by the first apparatus and there is no certainty about the second measurement outcome. The more approximate B is measured in the first apparatus the better the correlations are conserved. The red-colored data points show , the disturbance when no correction is made and the -measurement is made on . However, as the green curve in Figure 12 implies, the situation can be improved by correlating the random variable of the second apparatus with the random output variable of the first measurement instrument. In terms of complete positive trace-preserving maps, this can be written as the operation
The green-colored result, therefore, shows the minimal disturbance, where the second apparatus makes a measurement on the state , the state rotated onto the closest eigenvector of B. Finally, it remains to have a look at the plot of noise vs. disturbance. In Figure 13 three curves are shown. The red curve corresponds to the uncorrected uncertainty relation and the green one to the corrected in accordance with the color-coding of Figure 12. The white-hatched area is the region not reachable by sharp, projective, joint measurements M of the two non-commuting observables . The green boundary of the uncertainty region Equation (19) is saturated for this particular case, while the Maassen–Uffink like relation , given by the black line, displays an underestimation of the obtainable noise–disturbance values.
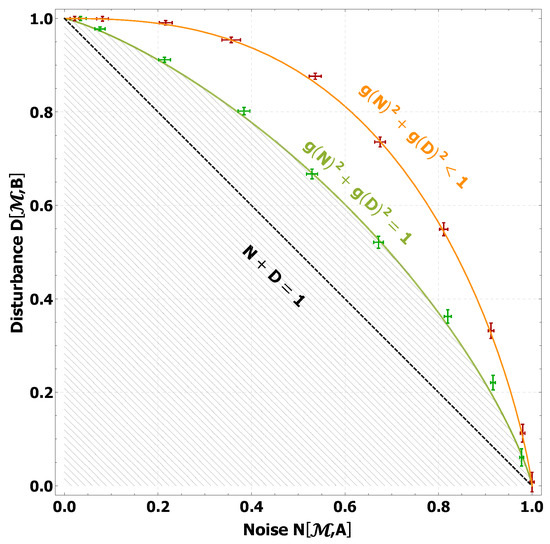
Figure 13.
Noise disturbance uncertainty relation for projective measurements for the uncorrected case in red and the corrected set-up in green. The data points are either on the green curve Equation (19) or above. It is apparent that the generally predicted Equation (12), given by the black dashed line, is not saturated for qubits except for the case where either noise or disturbance is maximal.
However, the inequality Equation (19) is to be treated with caution, as it is indeed possible to violate it when loosening some of the restrictions made in the presented measurements. Indeed, Abbott et al. [32] have proven that for POVMs the noise–disturbance uncertainty relation for two-dimensional quantum systems can be further improved and is possible. A generally tight, entropic noise–disturbance uncertainty relation for arbitrary pairs of non-commuting observables in two dimensions has however not been found or tested so far.
5. Conclusions
We have shown that uncertainty relations can be described very well by means of Shannon entropies and are well tested in neutron optics. The impossibility of the simultaneous distribution concentration in measurements of non-commuting observables is expressed by the trade-offs of information-theoretical noise and disturbance. After the theoretical basics were briefly explained in Section 2, we presented the experiments and the corresponding results in Section 3 and Section 4. In the simpler case of noise–noise uncertainty, POVMs are used to get the lowest boundary. Physically, this was realized by putting together a stochastic filter and a spin-dependent measurement. It is shown that, depending on the angle between the Bloch vectors, the region of accessible values can be obtained by projective measurements depicted in Figure 9d,e or by the formation of the convex hull as shown in Figure 9a–c, which corresponds to the statistical mixture of the projectors. In the more complex case of the noise–disturbance relation, the study was limited to dichotomic, projective measurements for MUB states. An essential difference in the case of successive measurements is that the quantum state is affected by the first measuring device, so that corresponding corrections are possible afterwards. The effects of error correction are clearly shown in the Figure 12 and Figure 13. In this regard, the investigation of the noise–disturbance relation for non-projective measurements will remain as an important task in the future, especially because it has been shown that it is possible to find pairs of measurement operators that are further below the green curve in Figure 13.
The presented experiments show an extract from a large catalog of entropic uncertainty relations. In information theory, many similar definitions of information gain or loss are known to exist, e.g., the Rényi entropy [38,39], Tsallis entropy [40,41], the Kullback–Leibler divergence [42] and many more. A good entropic measure for uncertainty relations must satisfy many requirements, in particular, it should allow a saturable generalization to uncertainty relations in higher dimensions, for three and more observables, mixed and entangled states, systems with memory, projective and non-projective measurements. In addition, information entropies are also applied in related topics such as complementarity [43], non-locality [44,45] and quantum correlations [46,47] in general. We think that neutron optics can make a big contribution to the testing and development of these various concepts.
Author Contributions
B.D. and S.S. wrote the paper. B.D., S.S. and Y.H. conceived and carried out the experiments. All authors have read and agreed to the published version of the manuscript.
Funding
We acknowledge the support by the Austrian science fund (FWF) Projects No. 30677-N20 and No. P27666-N36.
Acknowledgments
We also thank Alastair A. Abbott, Cyril Branciard, Georg Sulyok, Francesco Buscemi, Michael J.W. Hall and Masanao Ozawa for their involvement and dedication to the experimental researches.
Conflicts of Interest
The author declares no conflict of interest.
References
- Heisenberg, W. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z. Phys. 1927, 43, 172–198. [Google Scholar] [CrossRef]
- Kennard, E.H. Zur Quantenmechanik einfacher Bewegungstypen. Z. Phys. 1927, 44, 326–352. [Google Scholar] [CrossRef]
- Honarasa, G.; Tavassoly, M.; Hatami, M. Number-phase entropic uncertainty relations and Wigner functions for solvable quantum systems with discrete spectra. Physics Letters A 2009, 373, 3931–3936. [Google Scholar] [CrossRef]
- Mandilara, A.; Cerf, N.J. Quantum uncertainty relation saturated by the eigenstates of the harmonic oscillator. Phys. Rev. A 2012, 86, 030102. [Google Scholar] [CrossRef]
- Dammeier, L.; Schwonnek, R.; Werner, R.F. Uncertainty relations for angular momentum. New J. Phys. 2015, 17, 093046. [Google Scholar] [CrossRef]
- Robertson, H.P. The Uncertainty Principle. Phys. Rev. 1929, 34, 163–164. [Google Scholar] [CrossRef]
- Schrödinger, E. Zum Heisenbergschen Unschärfeprinzip. Sitzungsberichte der Preussischen Akademie der Wissenschaften, Physikalisch-mathematische Klasse 1930, 14, 296–303. Available online: http://arxiv.org/abs/quant-ph/9903100 (accessed on 25 December 2019).
- Coles, P.J.; Berta, M.; Tomamichel, M.; Wehner, S. Entropic uncertainty relations and their applications. Rev. Mod. Phys. 2017, 89, 015002. [Google Scholar] [CrossRef]
- Uffink, J.B.M.; Hilgevoord, J. Uncertainty principle and uncertainty relations. Found. Phys. 1985, 15, 925–944. [Google Scholar] [CrossRef]
- Hilgevoord, J. The standard deviation is not an adequate measure of quantum uncertainty. Am. J. Phys. 2002, 70, 983. [Google Scholar] [CrossRef]
- Hirschman, I.I. A Note on Entropy. Am. J. Math. 1957, 79, 152. [Google Scholar] [CrossRef]
- Beckner, W. Inequalities in Fourier Analysis. Ann. Math. 1975, 102, 159–182. [Google Scholar] [CrossRef]
- Biaynicki-Birula, I.; Mycielski, J. Uncertainty relations for information entropy in wave mechanics. Commun. Math. Phys. 1975, 44, 129. [Google Scholar] [CrossRef]
- Deutsch, D. Uncertainty in Quantum Measurements. Phys. Rev. Lett. 1983, 50, 631–633. [Google Scholar] [CrossRef]
- Maassen, H.; Uffink, J.B.M. Generalized entropic uncertainty relations. Phys. Rev. Lett. 1988, 60, 1103–1106. [Google Scholar] [CrossRef]
- Ozawa, M. Universally valid reformulation of the Heisenberg uncertainty principle on noise and disturbance in measurement. Phys. Rev. A 2003, 67, 042105. [Google Scholar] [CrossRef]
- Ozawa, M. Uncertainty relations for noise and disturbance in generalized quantum measurements. Ann. Phys. 2004, 311, 350–416. [Google Scholar] [CrossRef]
- Busch, P.; Lahti, P.; Werner, R.F. Proof of Heisenberg’s Error-Disturbance Relation. Phys. Rev. Lett. 2013, 111, 160405. [Google Scholar] [CrossRef]
- Busch, P.; Lahti, P.; Werner, R.F. Colloquium: Quantum root-mean-square error and measurement uncertainty relations. Rev. Mod. Phys. 2014, 86, 1261–1281. [Google Scholar] [CrossRef]
- Dressel, J.; Nori, F. Certainty in Heisenberg’s uncertainty principle: Revisiting definitions for estimation errors and disturbance. Phys. Rev. A 2014, 89, 022106. [Google Scholar] [CrossRef]
- Erhart, J.; Sponar, S.; Sulyok, G.; Badurek, G.; Ozawa, M.; Hasegawa, Y. Experimental demonstration of a universally valid error-disturbance uncertainty relation in spin-measurements. Nat. Phys. 2012, 8, 185–189. [Google Scholar] [CrossRef]
- Rozema, L.A.; Darabi, A.; Mahler, D.H.; Hayat, A.; Soudagar, Y.; Steinberg, A.M. Violation of Heisenberg’s Measurement-Disturbance Relationship by Weak Measurements. Phys. Rev. Lett. 2012, 109, 100404. [Google Scholar] [CrossRef]
- Sulyok, G.; Sponar, S.; Erhart, J.; Badurek, G.; Ozawa, M.; Hasegawa, Y. Violation of Heisenberg’s error-disturbance uncertainty relation in neutron-spin measurements. Phys. Rev. A 2013, 88, 022110. [Google Scholar] [CrossRef]
- Baek, S.Y.; Kaneda, F.; Ozawa, M.; Edamatsu, K. Experimental violation and reformulation of the Heisenberg’s error-disturbance uncertainty relation. Sci. Rep. 2013, 3, 2221. [Google Scholar] [CrossRef]
- Kaneda, F.; Baek, S.Y.; Ozawa, M.; Edamatsu, K. Experimental Test of Error-Disturbance Uncertainty Relations by Weak Measurement. Phys. Rev. Lett. 2014, 112, 020402. [Google Scholar] [CrossRef]
- Ringbauer, M.; Biggerstaff, D.N.; Broome, M.A.; Fedrizzi, A.; Branciard, C.; White, A.G. Experimental Joint Quantum Measurements with Minimum Uncertainty. Phys. Rev. Lett. 2014, 112, 020401. [Google Scholar] [CrossRef]
- Ma, W.; Ma, Z.; Wang, H.; Chen, Z.; Liu, Y.; Kong, F.; Li, Z.; Peng, X.; Shi, M.; Shi, F.; et al. Experimental Test of Heisenberg’s Measurement Uncertainty Relation Based on Statistical Distances. Phys. Rev. Lett. 2016, 116, 160405. [Google Scholar] [CrossRef]
- Demirel, B.; Sponar, S.; Sulyok, G.; Ozawa, M.; Hasegawa, Y. Experimental Test of Residual Error-Disturbance Uncertainty Relations for Mixed Spin-1/2 States. Phys. Rev. Lett. 2016, 117, 140402. [Google Scholar] [CrossRef]
- Sulyok, G.; Sponar, S. Heisenberg’s error-disturbance uncertainty relation: Experimental study of competing approaches. Phys. Rev. A 2017, 96, 022137. [Google Scholar] [CrossRef]
- Buscemi, F.; Hall, M.J.W.; Ozawa, M.; Wilde, M.M. Noise and Disturbance in Quantum Measurements: An Information-Theoretic Approach. Phys. Rev. Lett. 2014, 112, 050401. [Google Scholar] [CrossRef]
- Sulyok, G.; Sponar, S.; Demirel, B.; Buscemi, F.; Hall, M.J.W.; Ozawa, M.; Hasegawa, Y. Experimental Test of Entropic Noise-Disturbance Uncertainty Relations for Spin-1/2 Measurements. Phys. Rev. Lett. 2015, 115, 030401. [Google Scholar] [CrossRef]
- Abbott, A.A.; Branciard, C. Noise and disturbance of qubit measurements: An information-theoretic characterization. Phys. Rev. A 2016, 94, 062110. [Google Scholar] [CrossRef]
- Demirel, B.; Sponar, S.; Abbott, A.A.; Branciard, C.; Hasegawa, Y. Experimental test of an entropic measurement uncertainty relation for arbitrary qubit observables. New J. Phys. 2019, 21, 013038. Available online: https://arxiv.org/abs/1711.05023 (accessed on 25 December 2019). [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Davies, E.B.; Lewis, J.T. An operational approach to quantum probability. Comm. Math. Phys. 1970, 17, 239–260. [Google Scholar] [CrossRef]
- Sánches-Ruiz, J. Optimal entropic uncertainty relation in two-dimensional Hilbert space. Phys. Lett. A 1998, 244, 189–195. [Google Scholar] [CrossRef]
- Ghirardi, G.; Marinatto, L.; Romano, R. An optimal entropic uncertainty relation in a two-dimensional Hilbert space. Phys. Lett. A 2003, 317, 32–36. [Google Scholar] [CrossRef]
- Bialynicki-Birula, I. Rényi Entropy and the Uncertainty Relations. AIP Conf. Proc. 2007, 889, 52–61. [Google Scholar] [CrossRef]
- Coles, P.J.; Colbeck, R.; Yu, L.; Zwolak, M. Uncertainty Relations from Simple Entropic Properties. Phys. Rev. Lett. 2012, 108, 210405. [Google Scholar] [CrossRef]
- Wilk, G.; Włodarczyk, Z. Uncertainty relations in terms of the Tsallis entropy. Phys. Rev. A 2009, 79, 062108. [Google Scholar] [CrossRef]
- Rastegin, A.E. Uncertainty and certainty relations for complementary qubit observables in terms of Tsallis’ entropies. Quantum Inf. Process. 2013, 12, 2947–2963. [Google Scholar] [CrossRef]
- Barchielli, A.; Gregoratti, M.; Toigo, A. Measurement Uncertainty Relations for Position and Momentum: Relative Entropy Formulation. Entropy 2017, 19, 301. [Google Scholar] [CrossRef]
- Coles, P.J.; Kaniewski, J.; Wehner, S. Equivalence of wave-particle duality to entropic uncertainty. Nat. Commun. 2014, 5, 5814. [Google Scholar] [CrossRef]
- Horodecki, R.; Horodecki, P.; Horodecki, M. Quantum α-entropy inequalities: independent condition for local realism? Phys. Lett. A 1996, 210, 377–381. [Google Scholar] [CrossRef]
- Cerf, N.J.; Adami, C. Entropic Bell inequalities. Phys. Rev. A 1997, 55, 3371–3374. [Google Scholar] [CrossRef]
- Ollivier, H.; Zurek, W.H. Quantum Discord: A Measure of the Quantumness of Correlations. Phys. Rev. Lett. 2001, 88, 017901. [Google Scholar] [CrossRef] [PubMed]
- Winter, A.; Yang, D. Operational Resource Theory of Coherence. Phys. Rev. Lett. 2016, 116, 120404. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).