Average Error Probability of an Optically Pre-Amplified Pulse-Position Modulation Multichannel Receiver under Malaga-ℳ Fading
Abstract
1. Introduction
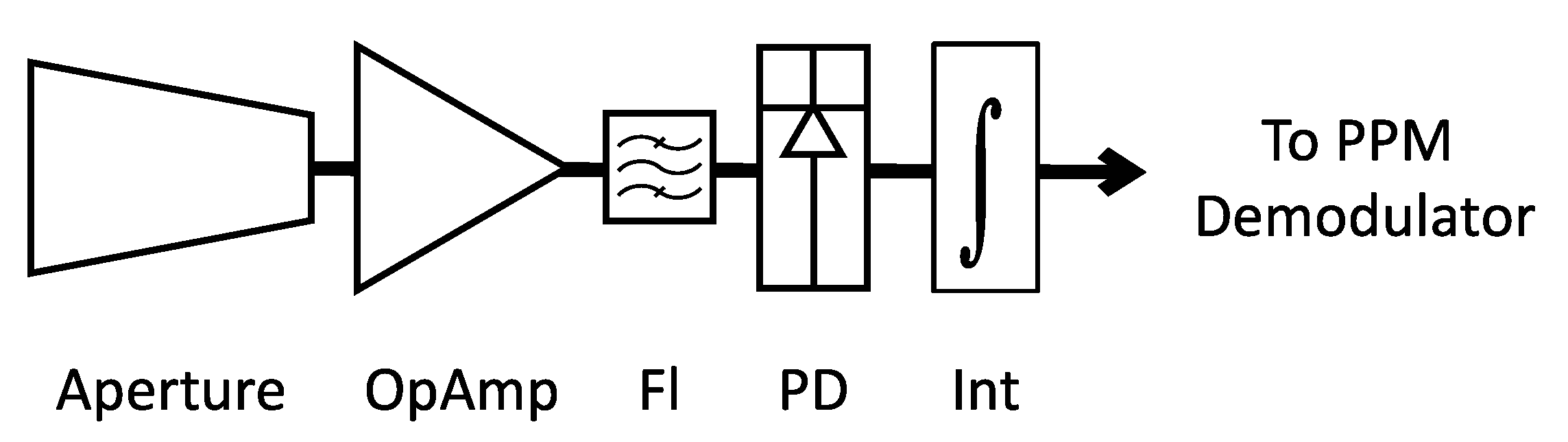
2. Optically Pre-Amplified PPM Receiver
3. PPM Probability of Error
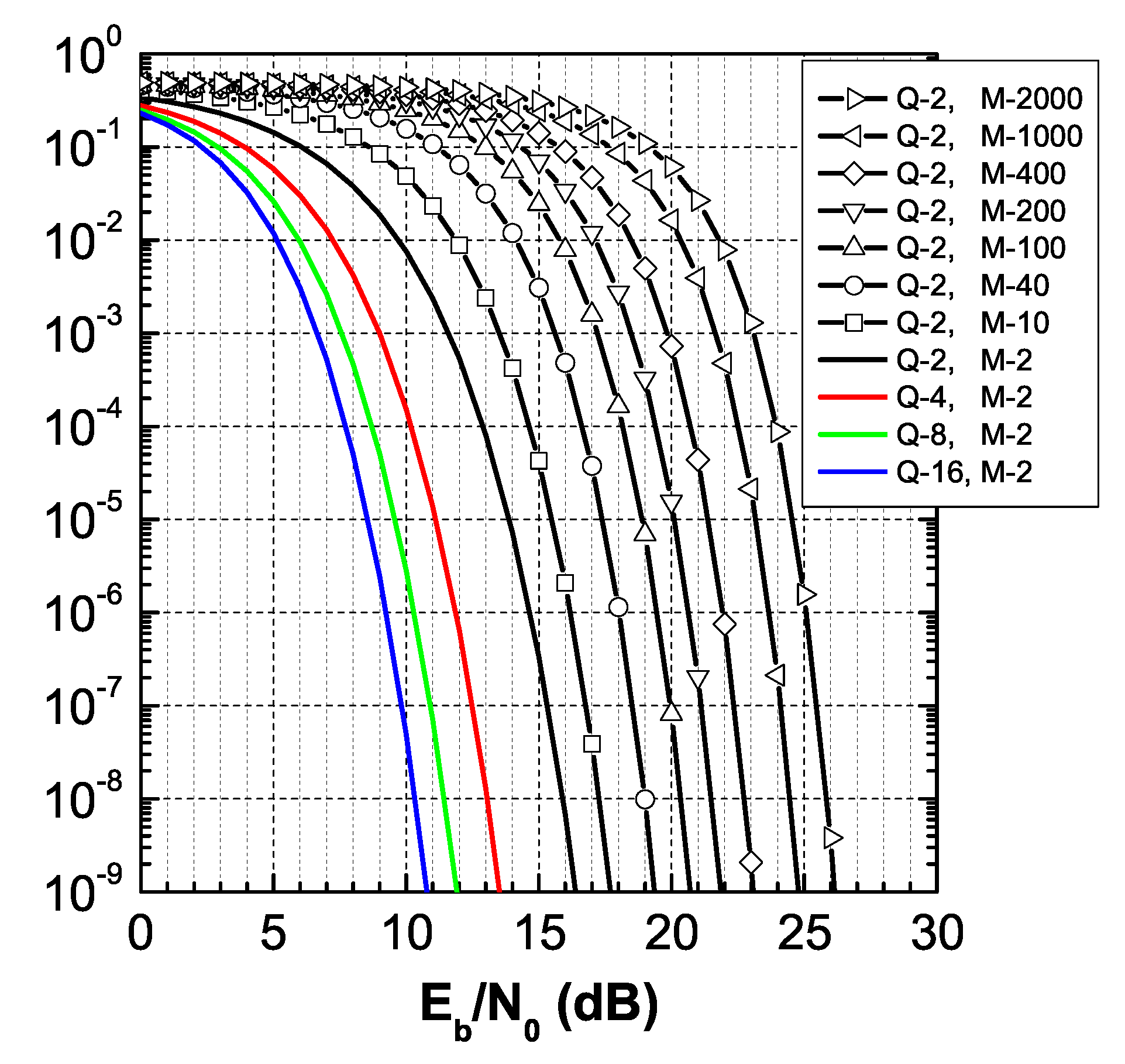
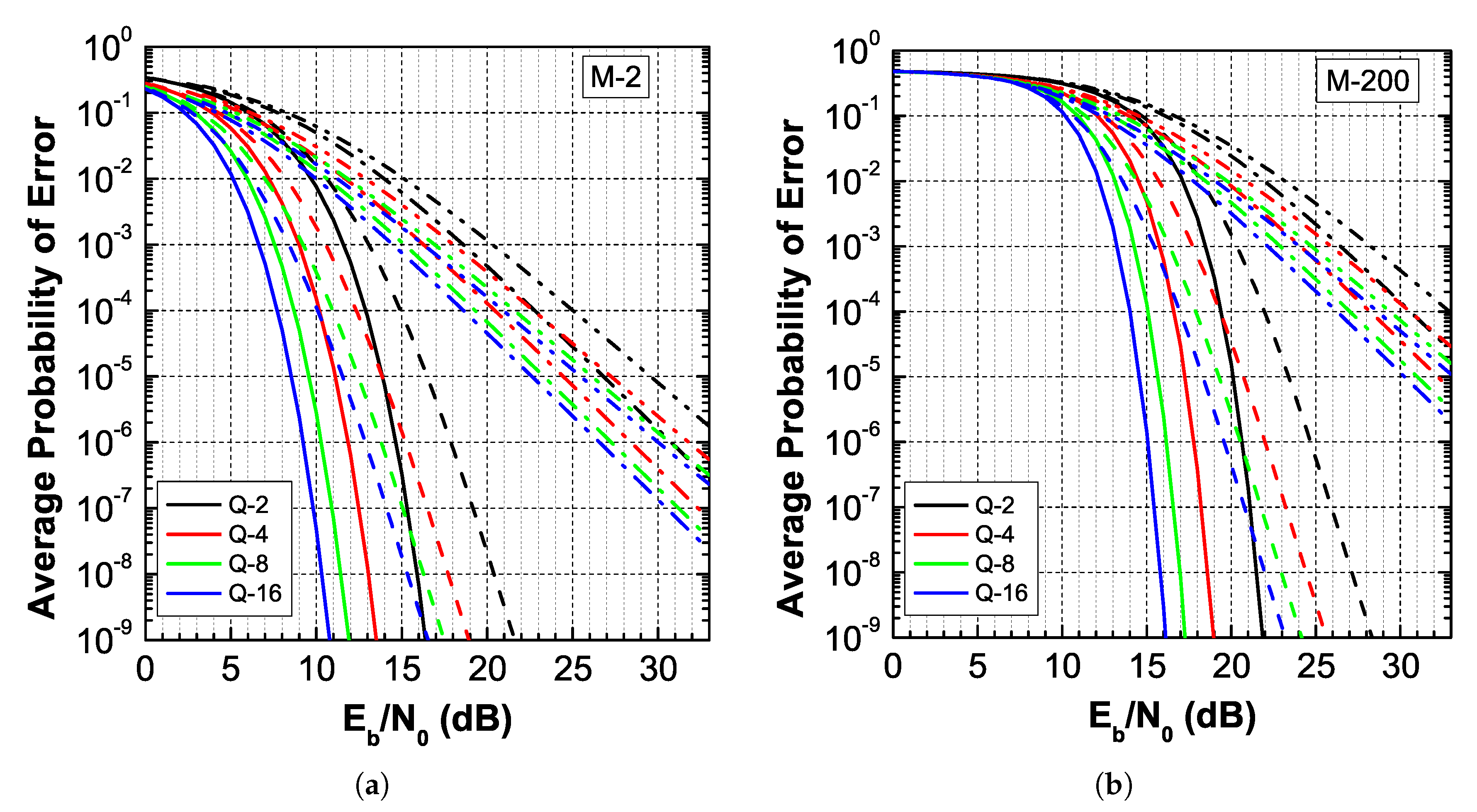
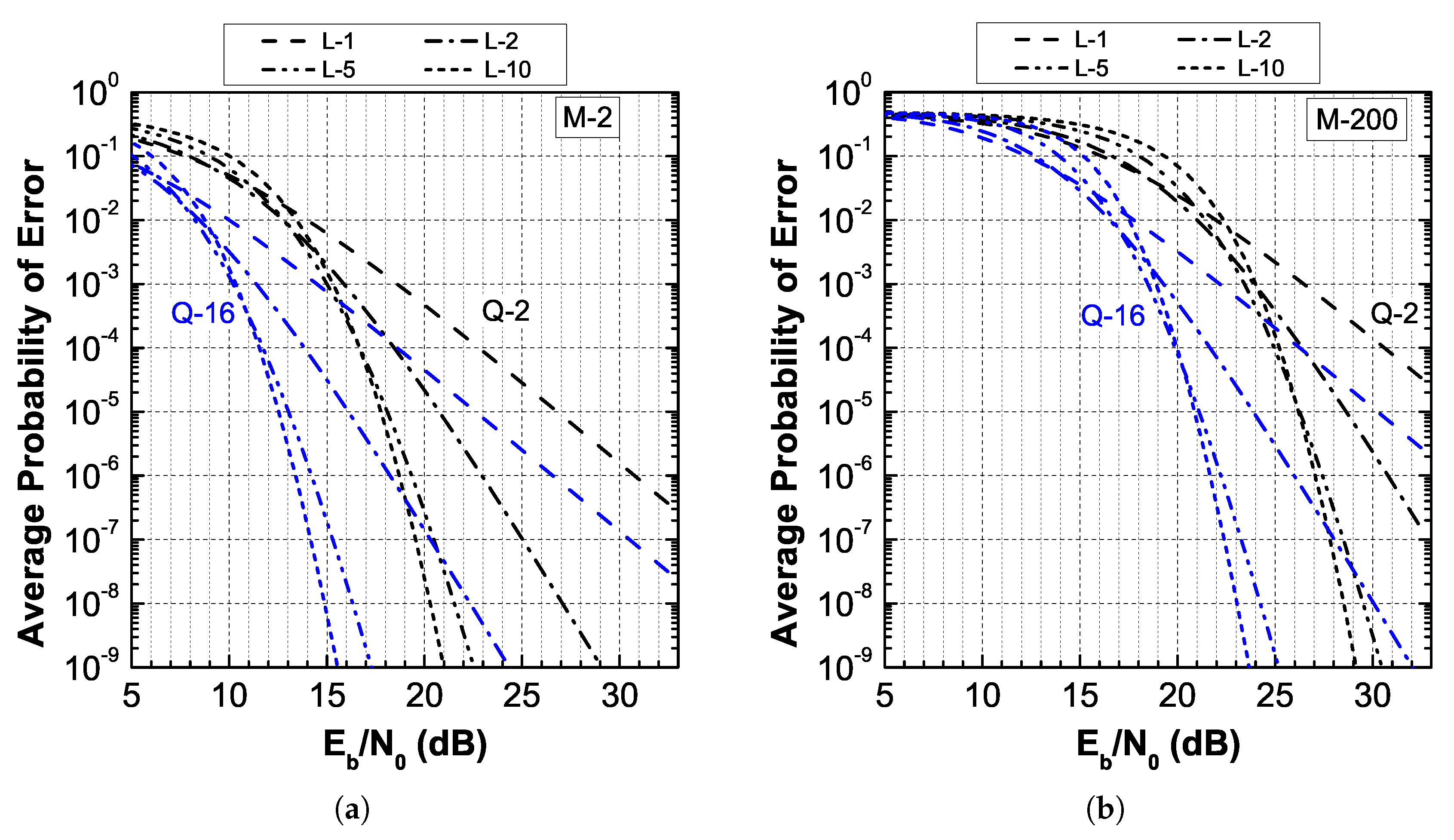
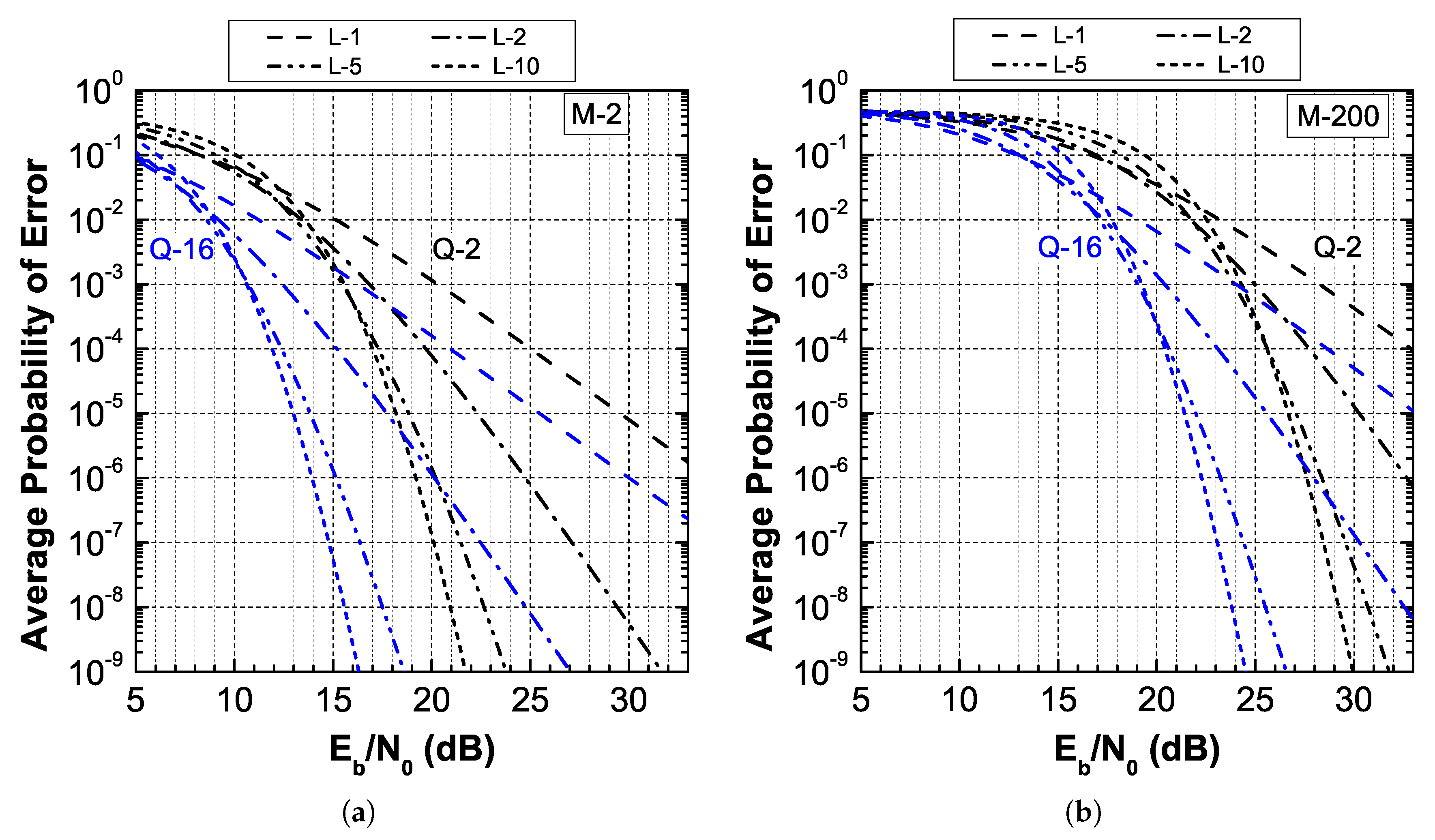
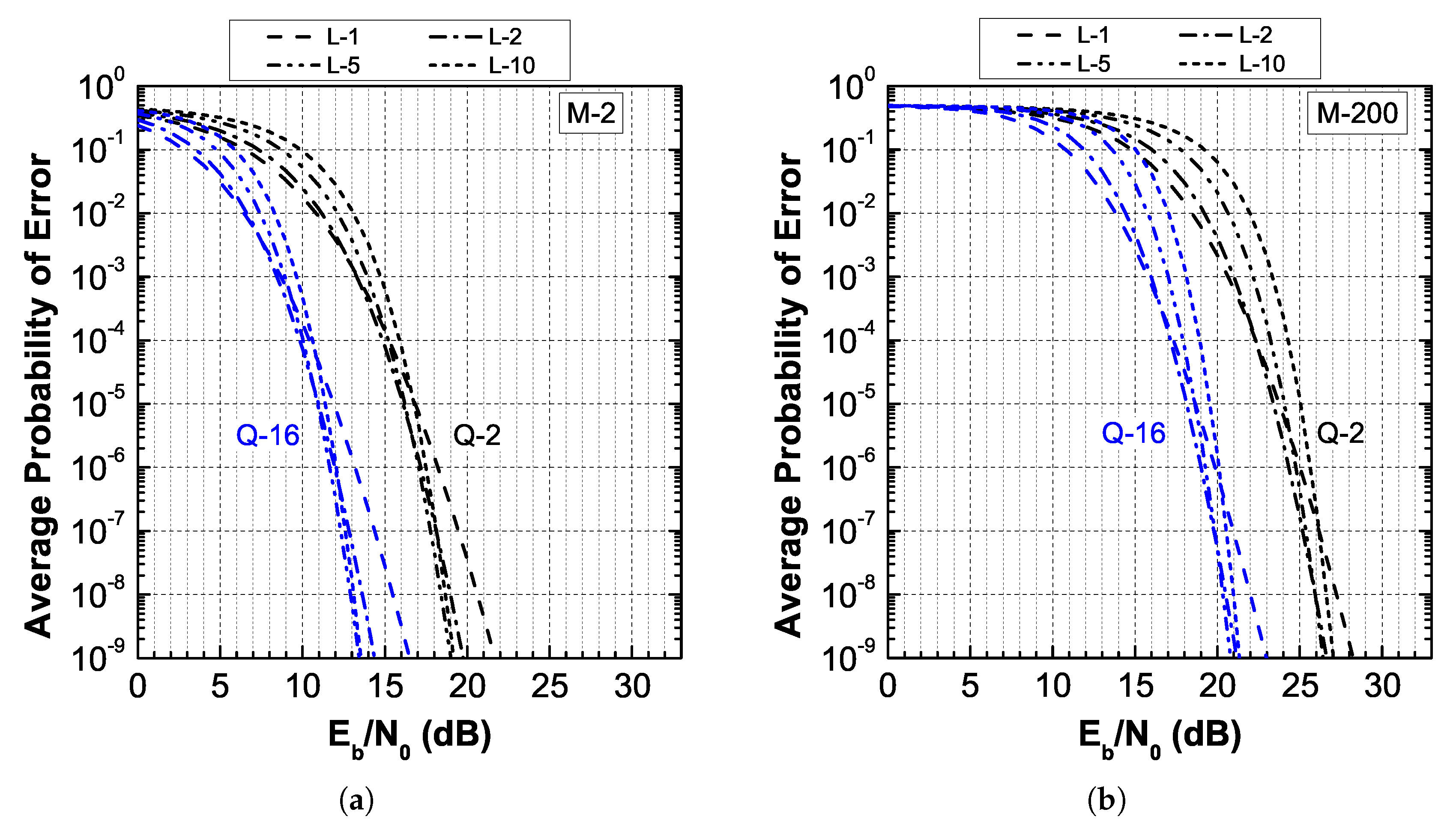
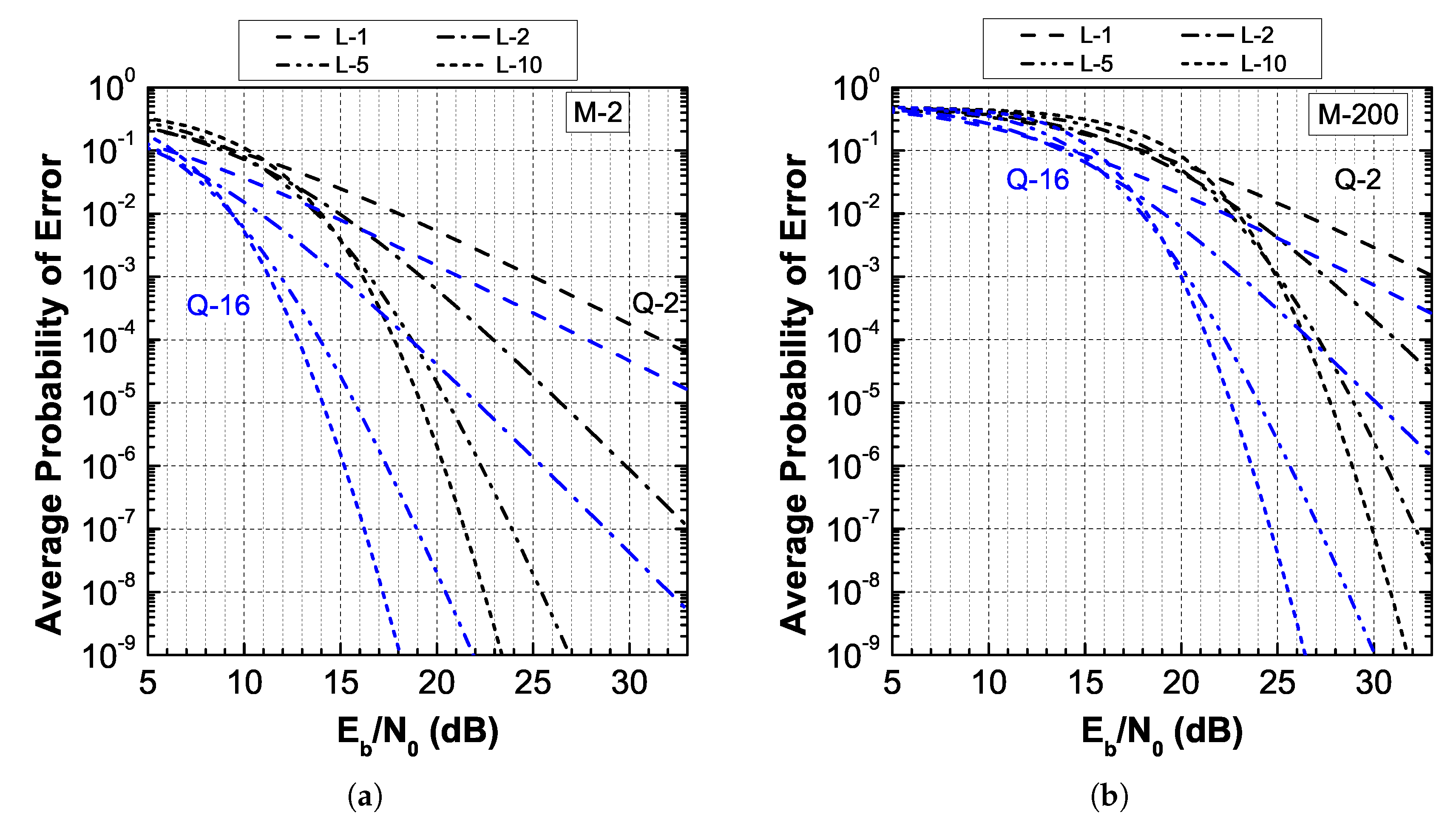
4. Average PER in Malaga- Fading
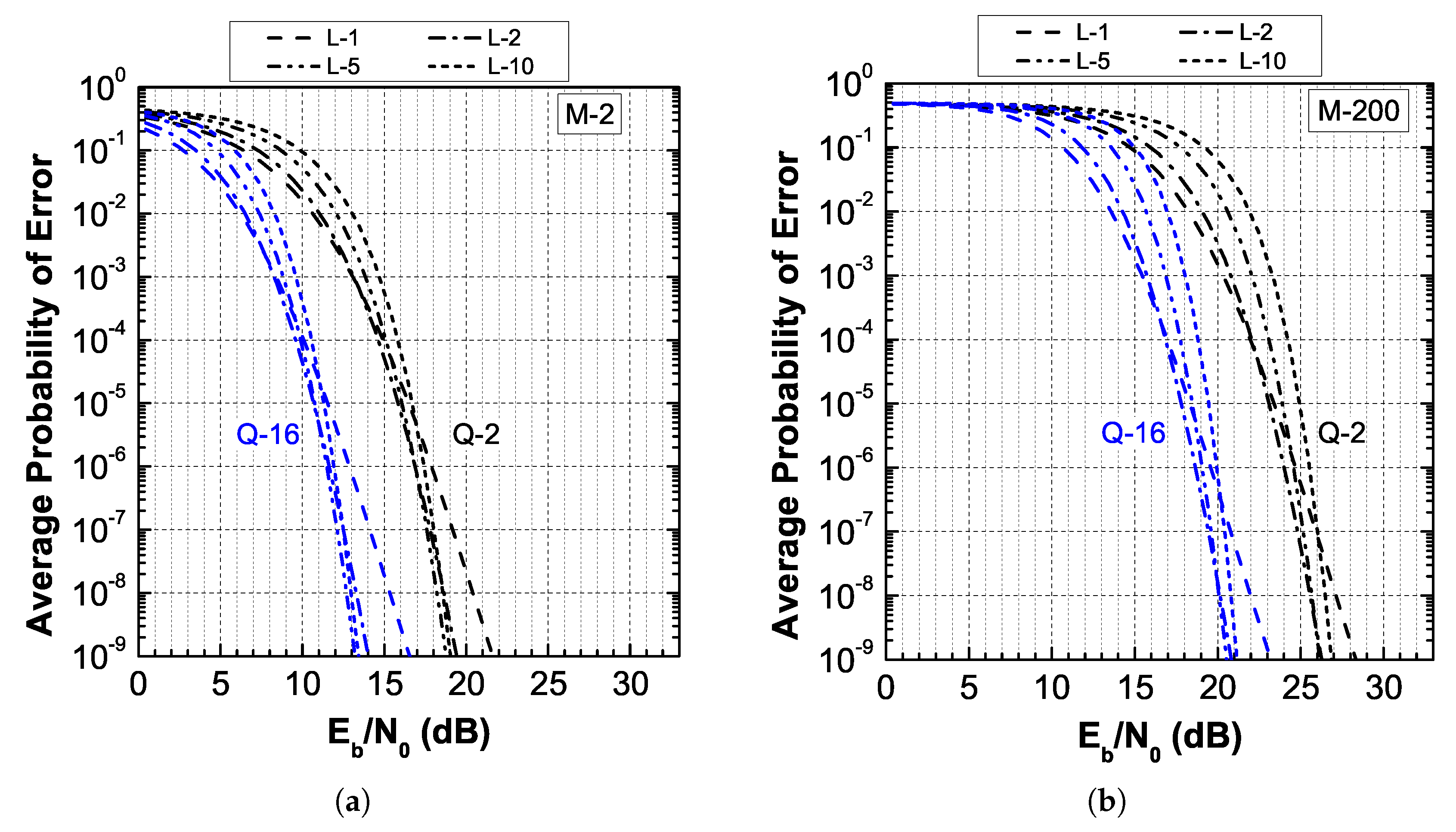
5. Diversity Reception in Malaga- Fading
6. Results on Other Distributions
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| EDFA | Erbium doped fiber amplifier |
| EGC | Equal-gain combiner |
| OWC | Optical wireless communication |
| PER | Probability of error |
| PPM | Pulse-position modulation |
| RV | Random variable |
| SEP | Symbol error probability |
| SOA | Semiconductor optical amplifier |
References
- Li, J.; Uysal, M. Optical wireless communications: System model, capacity and coding. In Proceedings of the 2003 IEEE 58th Vehicular Technology Conference, Orlando, FL, USA, 6–9 October 2003; Volume 1, pp. 168–172. [Google Scholar]
- Djordjevic, I.B. Adaptive Modulation and Coding for Free-Space Optical Channels. J. Opt. Commun. Netw. 2010, 2, 221–229. [Google Scholar] [CrossRef]
- Sandalidis, H.G. Coded Free-Space Optical Links over Strong Turbulence and Misalignment Fading Channels. IEEE Trans. Commun. 2011, 59, 669–674. [Google Scholar] [CrossRef]
- Safari, M.; Uysal, M. Relay-assisted free-space optical communication. IEEE Trans. Wirel. Commun. 2008, 7, 5441–5449. [Google Scholar] [CrossRef]
- Kazemlou, S.; Hranilovic, S.; Kumar, S. All-Optical Multihop Free-Space Optical Communication Systems. J. Light. Technol. 2011, 29, 2663–2669. [Google Scholar] [CrossRef]
- Chatzidiamantis, N.D.; Michalopoulos, D.S.; Kriezis, E.E.; Karagiannidis, G.K.; Schober, R. Relay selection protocols for relay-assisted free-space optical systems. IEEE/OSA J. Opt. Commun. Netw. 2013, 5, 92–103. [Google Scholar] [CrossRef]
- Peppas, K.P.; Stassinakis, A.N.; Nistazakis, H.E.; Tombras, G.S. Capacity analysis of dual amplify-and-forward relayed free-space optical communication systems over turbulence channels with pointing errors. IEEE/OSA J. Opt. Commun. Netw. 2013, 5, 1032–1042. [Google Scholar] [CrossRef]
- Xu, F.; Khalighi, A.; Caussé, P.; Bourennane, S. Channel coding and time-diversity for optical wireless links. Opt. Express 2009, 17, 872–887. [Google Scholar] [CrossRef]
- Tsiftsis, T.A.; Sandalidis, H.G.; Karagiannidis, G.K.; Uysal, M. Optical wireless links with spatial diversity over strong atmospheric turbulence channels. IEEE Trans. Wirel. Commun. 2009, 8, 951–957. [Google Scholar] [CrossRef]
- Nistazakis, H.E.; Tombras, G.S. On the use of wavelength and time diversity in optical wireless communication systems over gamma–gamma turbulence channels. Opt. Laser Technol. 2012, 44, 2088–2094. [Google Scholar] [CrossRef]
- Yang, L.; Gao, X.; Alouini, M. Performance Analysis of Free-Space Optical Communication Systems With Multiuser Diversity Over Atmospheric Turbulence Channels. IEEE Photonics J. 2014, 6, 1–17. [Google Scholar] [CrossRef]
- Yiannopoulos, K.; Sagias, N.C.; Boucouvalas, A.C.; Peppas, K. Optimal Combining for Optical Wireless Systems With Amplification: The χ2 Noise Regime. IEEE Photonics Technol. Lett. 2018, 30, 119–122. [Google Scholar] [CrossRef]
- Razavi, M.; Shapiro, J.H. Wireless optical communications via diversity reception and optical preamplification. IEEE Trans. Wirel. Commun. 2005, 4, 975–983. [Google Scholar] [CrossRef]
- Bayaki, E.; Michalopoulos, D.S.; Schober, R. EDFA-Based All-Optical Relaying in Free-Space Optical Systems. IEEE Trans. Commun. 2012, 60, 3797–3807. [Google Scholar] [CrossRef]
- Abtahi, M.; Lemieux, P.; Mathlouthi, W.; Rusch, L.A. Suppression of Turbulence-Induced Scintillation in Free-Space Optical Communication Systems Using Saturated Optical Amplifiers. J. Light. Technol. 2006, 24, 4966–4973. [Google Scholar] [CrossRef]
- Rizou, Z.V.; Zoiros, K.E.; Hatziefremidis, A. Signal amplitude and phase equalization technique for free space optical communications. In Proceedings of the 2013 15th International Conference on Transparent Optical Networks (ICTON), Cartagena, Spain, 23–27 June 2013. [Google Scholar]
- Yiannopoulos, K.; Sagias, N.C.; Boucouvalas, A.C. Fade Mitigation Based on Semiconductor Optical Amplifiers. J. Light. Technol. 2013, 31, 3621–3630. [Google Scholar] [CrossRef]
- Yiannopoulos, K.; Sagias, N.C.; Boucouvalas, A.C. On the Performance of Semiconductor Optical Amplifier-Assisted Outdoor Optical Wireless Links. IEEE J. Sel. Areas Commun. 2015, 33, 1869–1876. [Google Scholar] [CrossRef]
- Wilson, S.G.; Brandt-Pearce, M.; Cao, Q.; Leveque, J.H. Free-space optical MIMO transmission with Q-ary PPM. IEEE Trans. Commun. 2005, 53, 1402–1412. [Google Scholar] [CrossRef]
- Caplan, D.O.; Robinson, B.S.; Murphy, R.J.; Stevens, M.L. Demonstration of 2.5-Gslot/s optically-preamplified M-PPM with 4 photons/bit receiver sensitivity. In Proceedings of the Optical Fiber Communication Conference and Exposition and The National Fiber Optic Engineers Conference, Anaheim, CA, USA, 6 March 2005. [Google Scholar]
- Stevens, M.L.; Boroson, D.M. A simple delay-line 4-PPM demodulator with near-optimum performance. Opt. Express 2012, 20, 5270–5280. [Google Scholar] [CrossRef]
- Aladeloba, A. Performance evaluation of optically preamplified digital pulse position modulation turbulent free-space optical communication systems. IET Optoelectron. 2012, 6, 66–74. [Google Scholar] [CrossRef]
- Zhao, W.; Han, Y.; Yi, X. Error performance analysis for FSO systems with diversity reception and optical preamplification over gamma–gamma atmospheric turbulence channels. J. Mod. Opt. 2013, 60, 1060–1068. [Google Scholar] [CrossRef]
- Humblet, P.A.; Azizoglu, M. On the bit error rate of lightwave systems with optical amplifiers. J. Light. Technol. 1991, 9, 1576–1582. [Google Scholar] [CrossRef]
- Boucouvalas, A.C.; Sagias, N.C.; Yiannopoulos, K. Accurate Evaluation of the Average Probability of Error of Pulse Position Modulation in Amplified Optical Wireless Communications under Turbulence. Appl. Sci. 2019, 9, 749. [Google Scholar] [CrossRef]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation through Random Media, 2nd ed.; SPIE Press: Bellingham, WA, USA, 2005. [Google Scholar]
- Jurado-Navas, A.; Garrido-Balsells, J.M.; Paris, J.F.; Puerta-Notario, A. A Unifying Statistical Model for Atmospheric Optical Scintillation. In Numerical Simulations of Physical and Engineering Processes; Awrejcewicz, J., Ed.; IntechOpen: Rijeka, Croatia, 2011; Chapter 8. [Google Scholar]
- Samimi, H. New statistical model for atmospheric optical scintillation and its application. IET Optoelectron. 2013, 7, 31–37. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, 7th ed.; Elsevier/Academic Press: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Hughes, L.W. A simple upper bound on the error probability for orthogonal signals in white noise. IEEE Trans. Commun. 1992, 40, 670. [Google Scholar] [CrossRef]
- Truesdell, C. On the Addition and Multiplication Theorems for Special Functions. Proc. Natl. Acad. Sci. USA 1950, 36, 752–755. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; Dover: New York, NY, USA, 1964. [Google Scholar]
- Eger, S. Some Elementary Congruences for the Number of Weighted Integer Compositions. J. Integer Seq. 2015, 18, 1–18. [Google Scholar]

| Irradiance Fluctuations | |||
|---|---|---|---|
| Parameter | Weak | Moderate | Strong |
| 50 | 2.55 | 2.2814 | |
| 14 | 22 | 33 | |
| 1.0621 | 0.4618 | 1.33 | |
| 0.0216 | 0.6525 | 0.4231 | |
| 0.86 | 0.988 | 0.84 | |
| Parameter | l–100 m | l–500 m |
|---|---|---|
| 16.53 | 4.04 | |
| 14.91 | 1.53 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yiannopoulos, K.; Sagias, N.C.; Boucouvalas, A.C. Average Error Probability of an Optically Pre-Amplified Pulse-Position Modulation Multichannel Receiver under Malaga-ℳ Fading. Appl. Sci. 2020, 10, 1141. https://doi.org/10.3390/app10031141
Yiannopoulos K, Sagias NC, Boucouvalas AC. Average Error Probability of an Optically Pre-Amplified Pulse-Position Modulation Multichannel Receiver under Malaga-ℳ Fading. Applied Sciences. 2020; 10(3):1141. https://doi.org/10.3390/app10031141
Chicago/Turabian StyleYiannopoulos, Konstantinos, Nikos C. Sagias, and Anthony C. Boucouvalas. 2020. "Average Error Probability of an Optically Pre-Amplified Pulse-Position Modulation Multichannel Receiver under Malaga-ℳ Fading" Applied Sciences 10, no. 3: 1141. https://doi.org/10.3390/app10031141
APA StyleYiannopoulos, K., Sagias, N. C., & Boucouvalas, A. C. (2020). Average Error Probability of an Optically Pre-Amplified Pulse-Position Modulation Multichannel Receiver under Malaga-ℳ Fading. Applied Sciences, 10(3), 1141. https://doi.org/10.3390/app10031141







