Two-Dimensional Impact Modelling with Three Degrees of Freedom and Its Application in the Dynamics of Planing Hulls
Abstract
1. Introduction
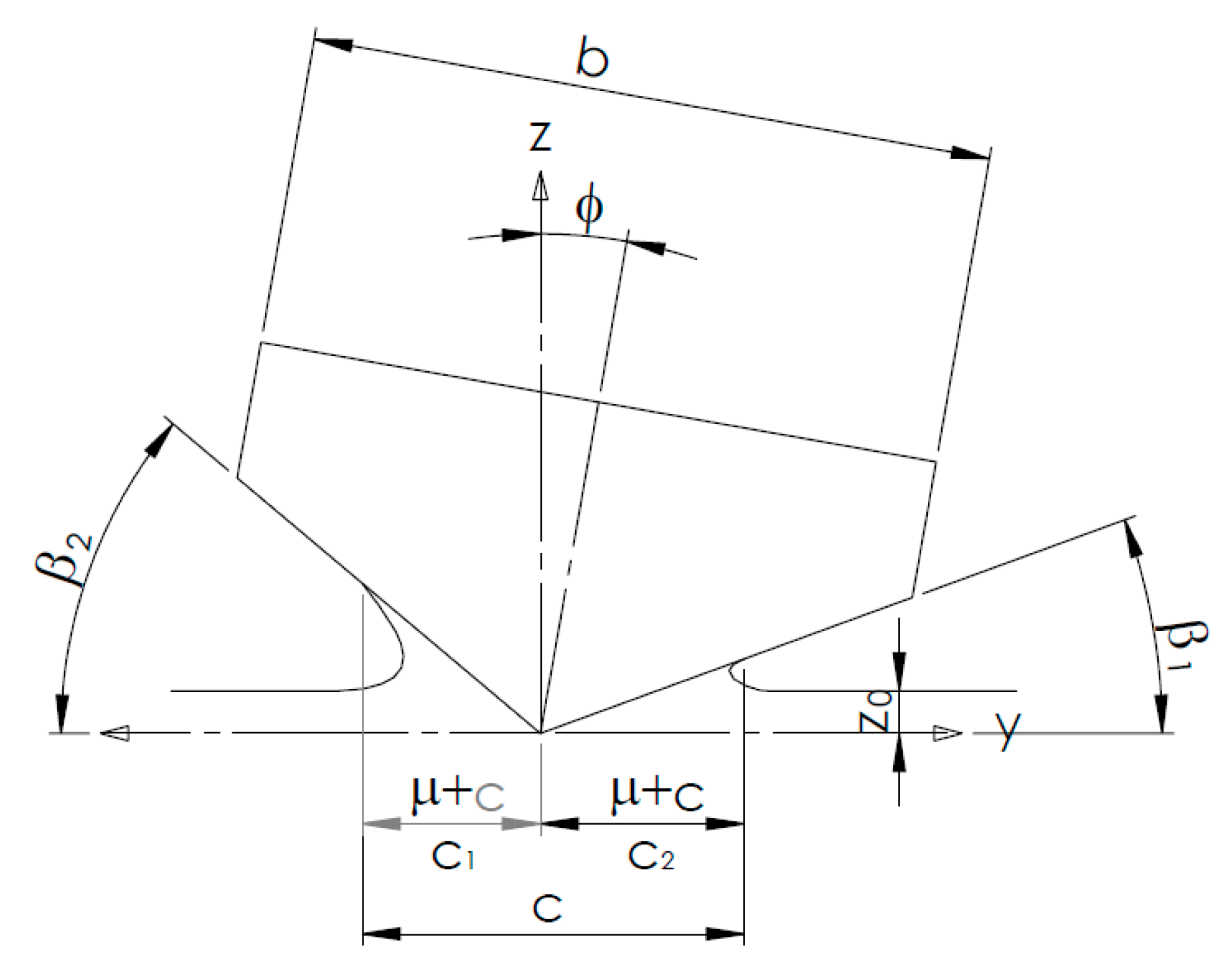
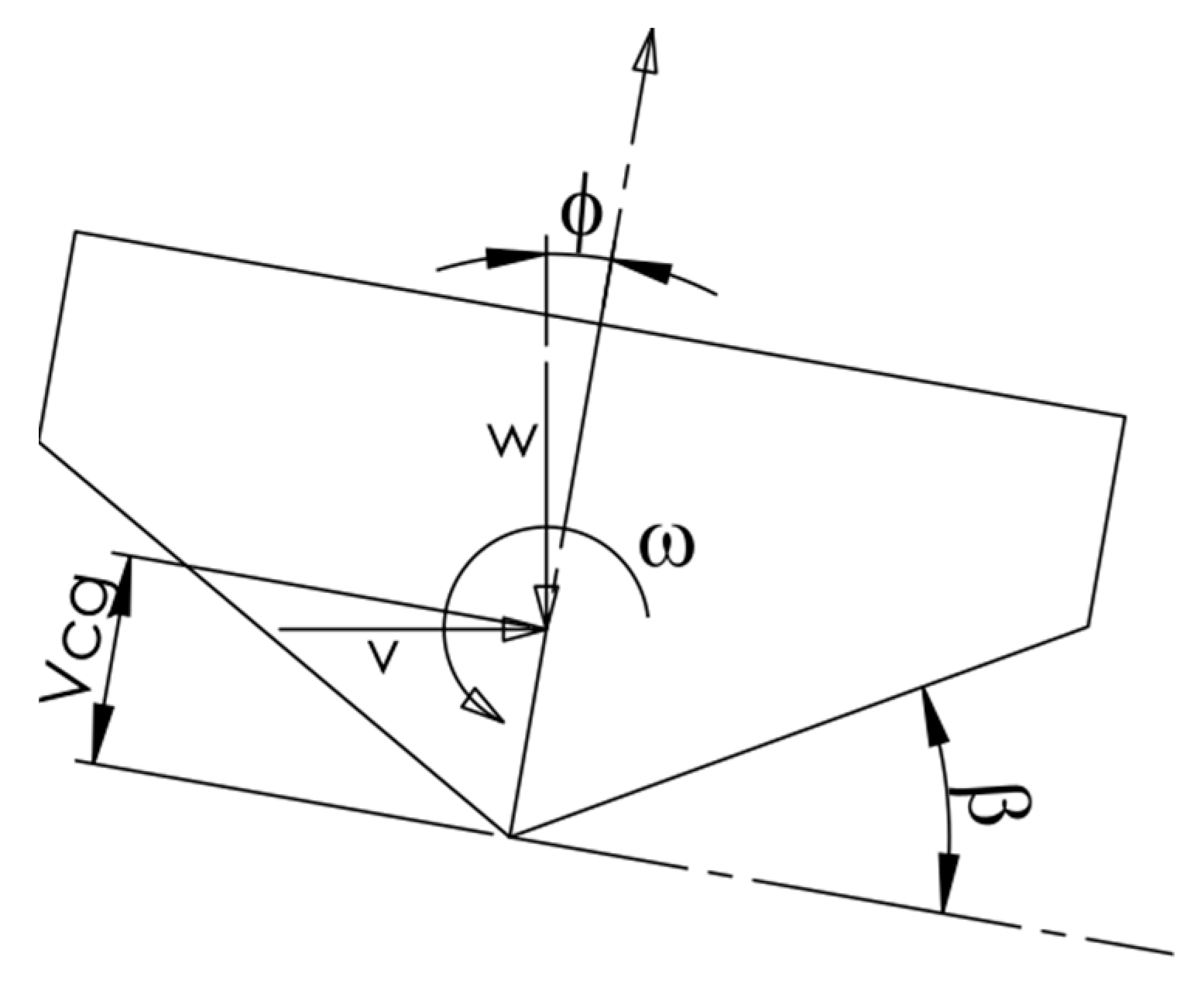
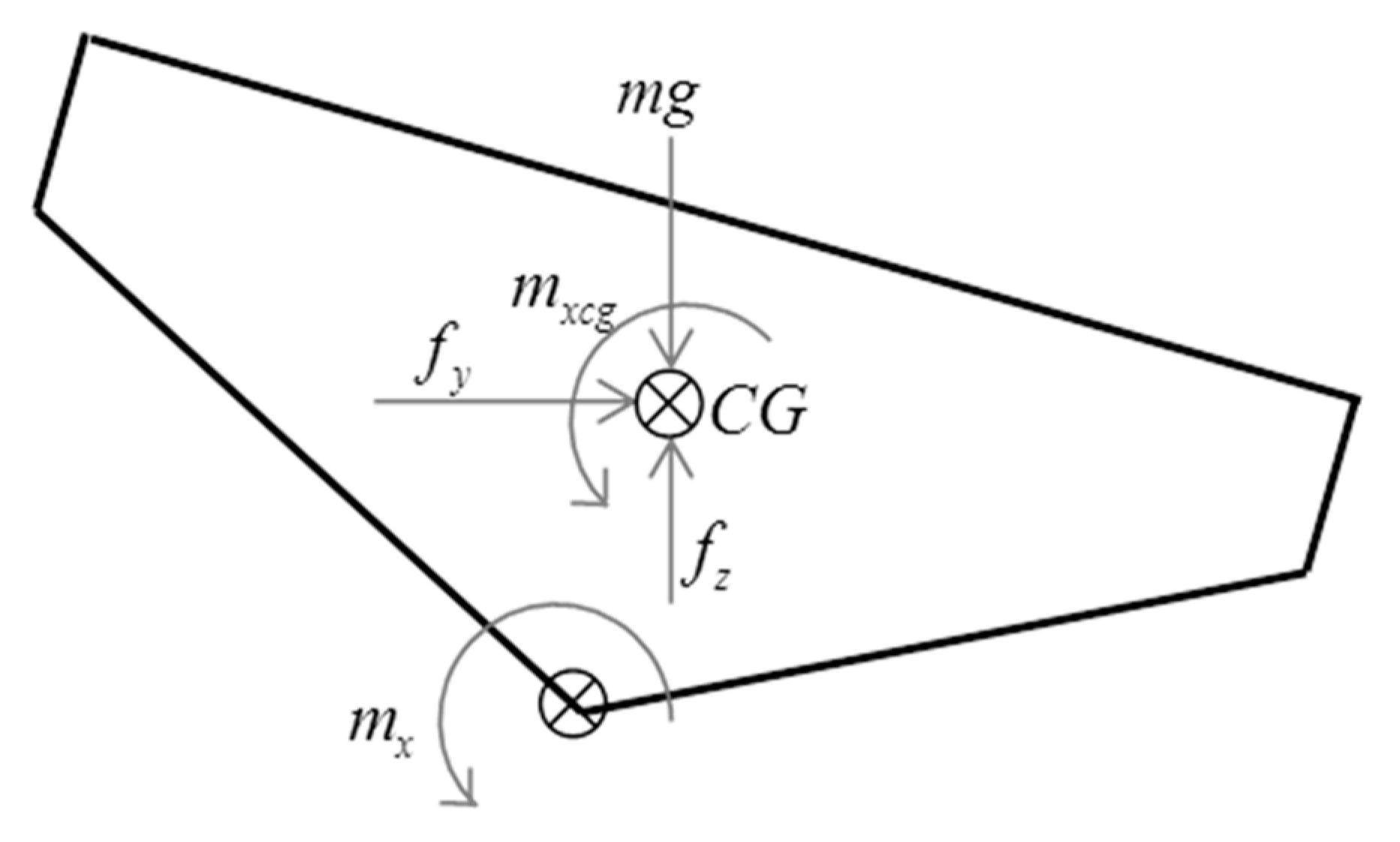
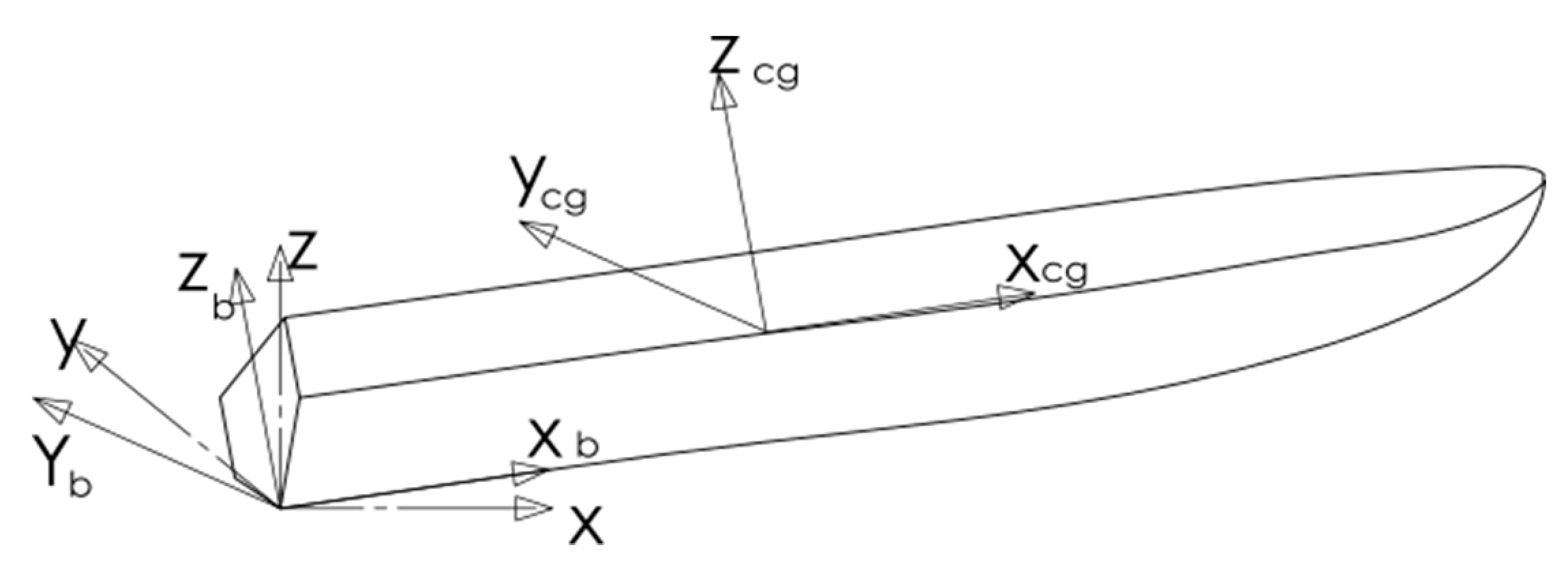
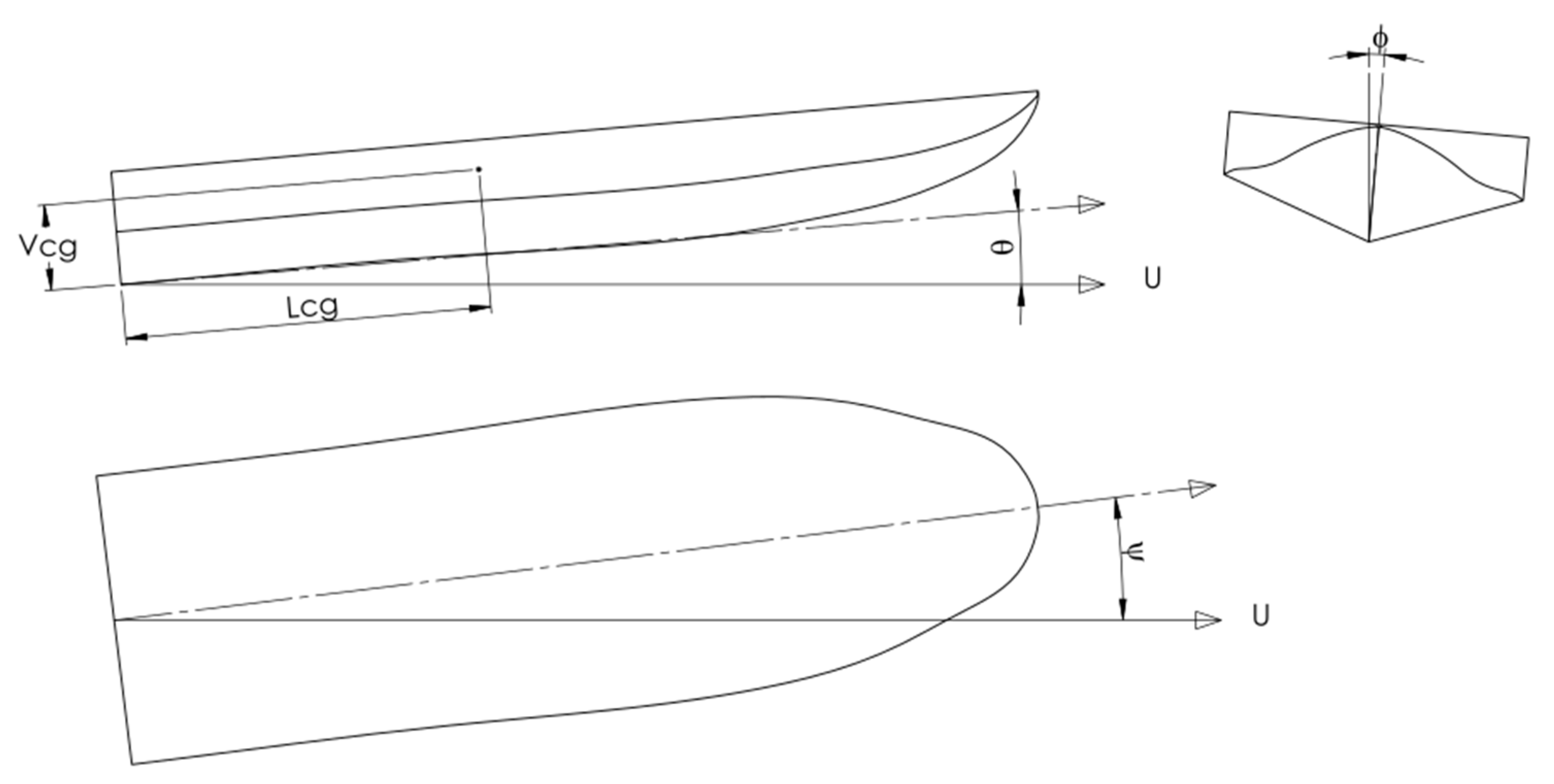
2. Mathematical Formulation
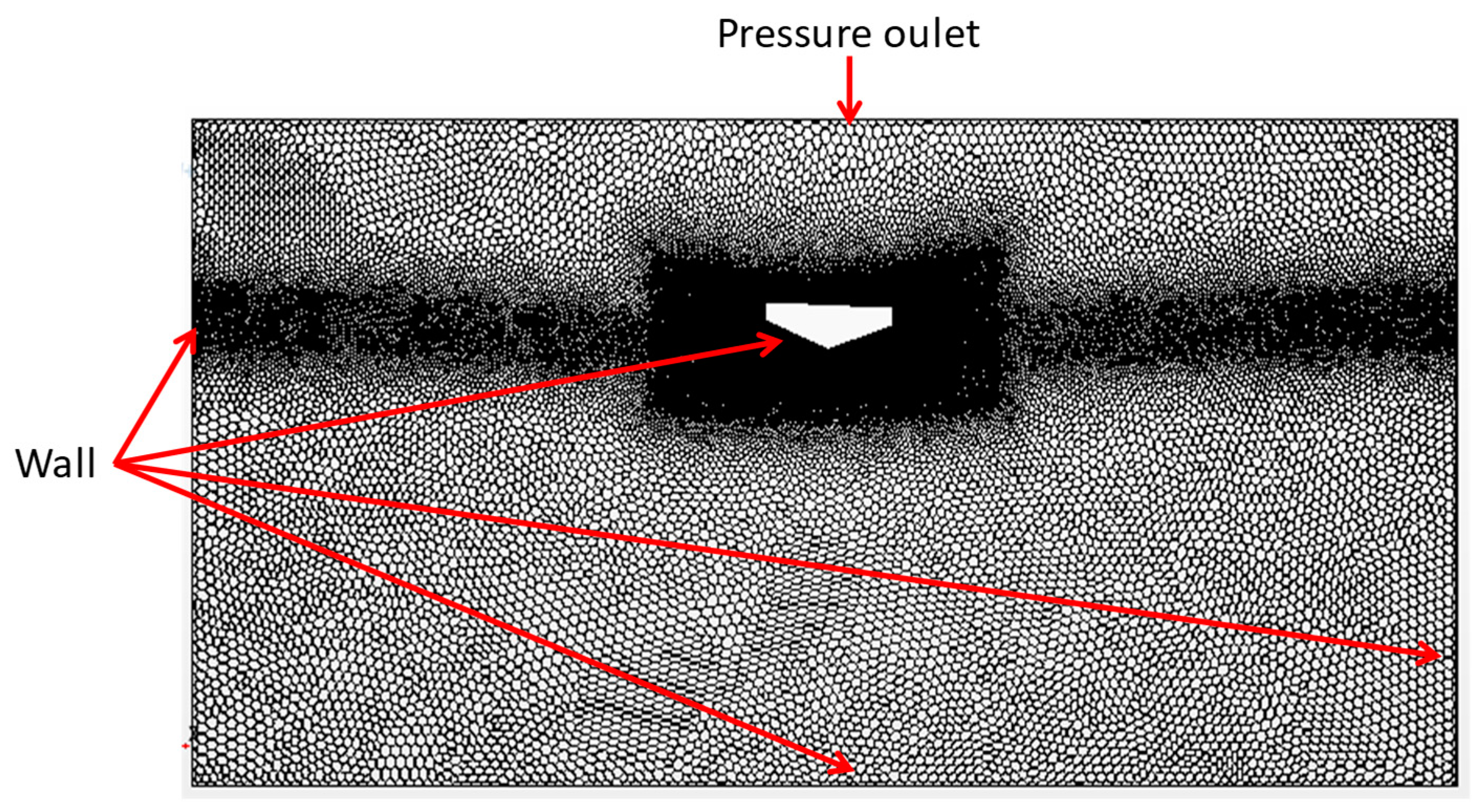
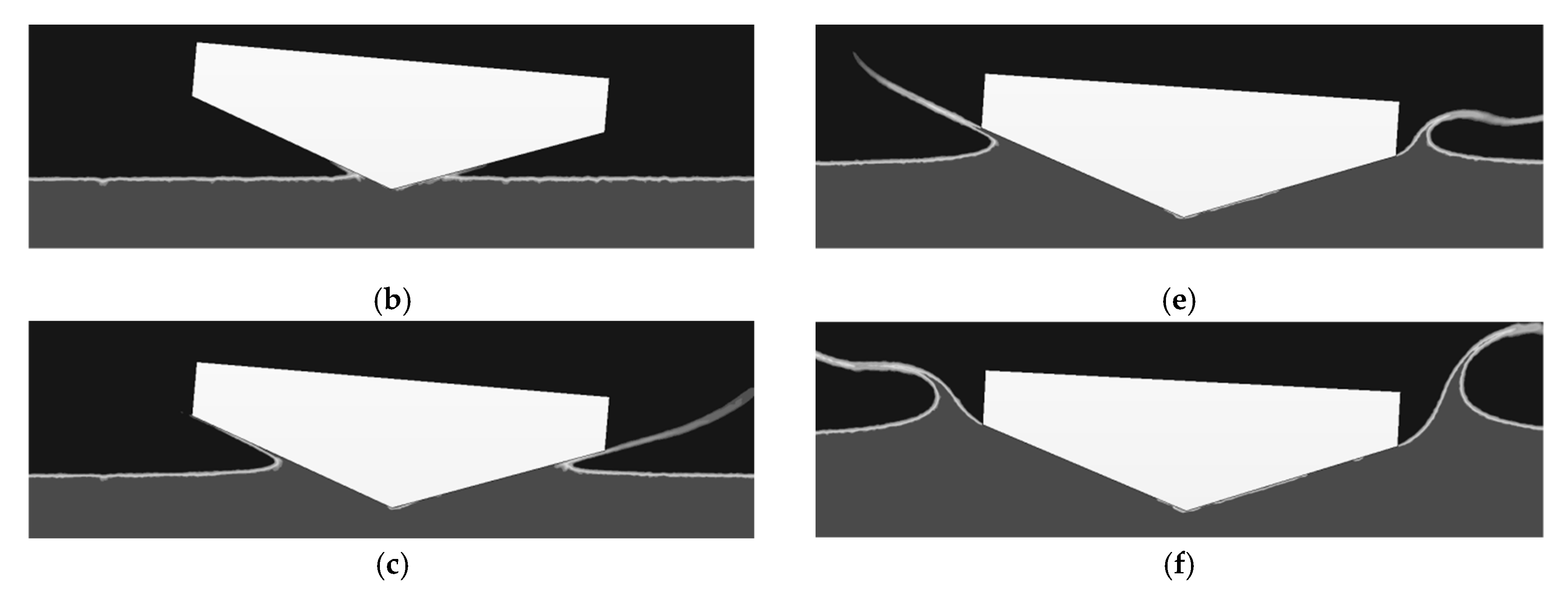
3. CFD Modelling
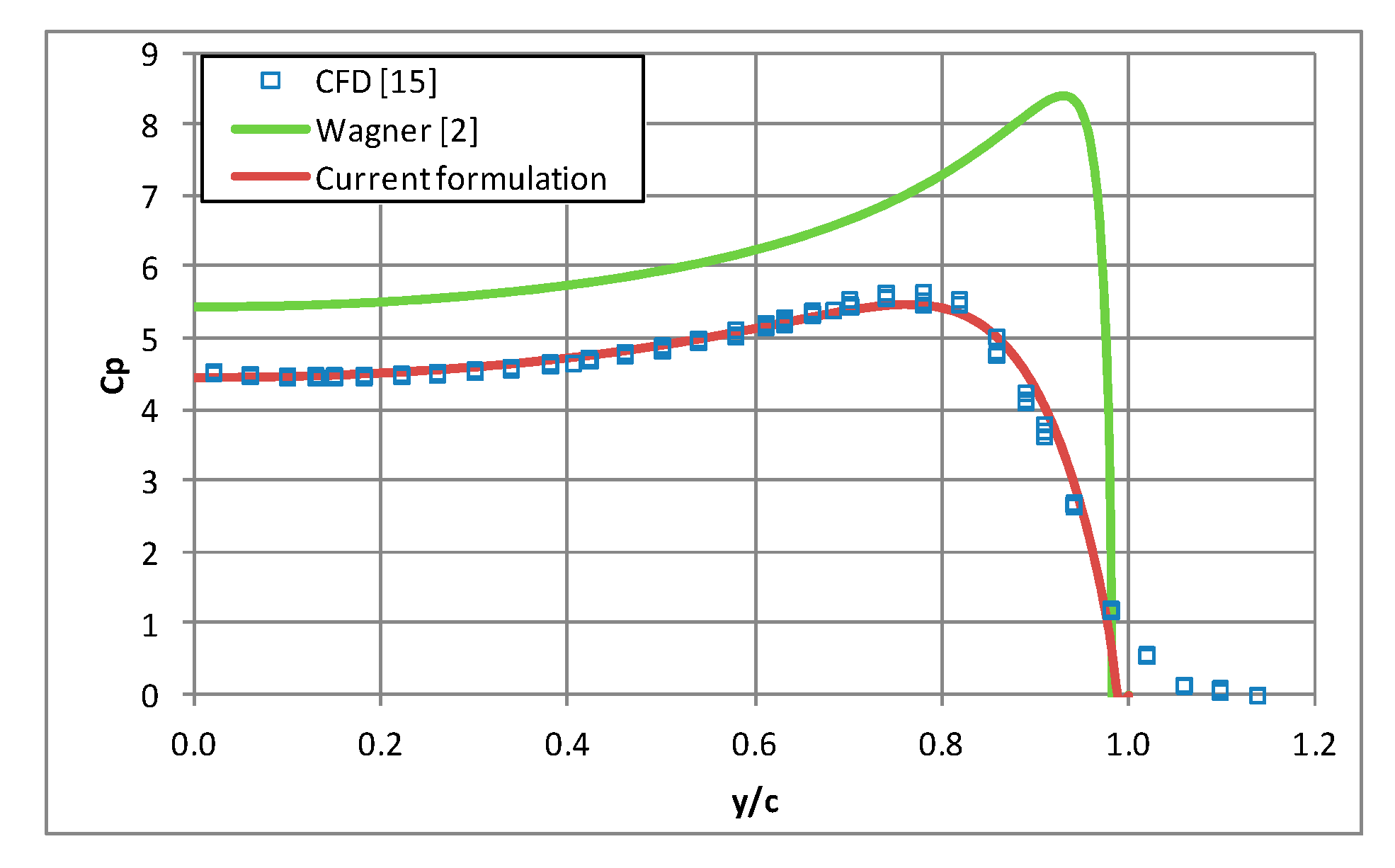
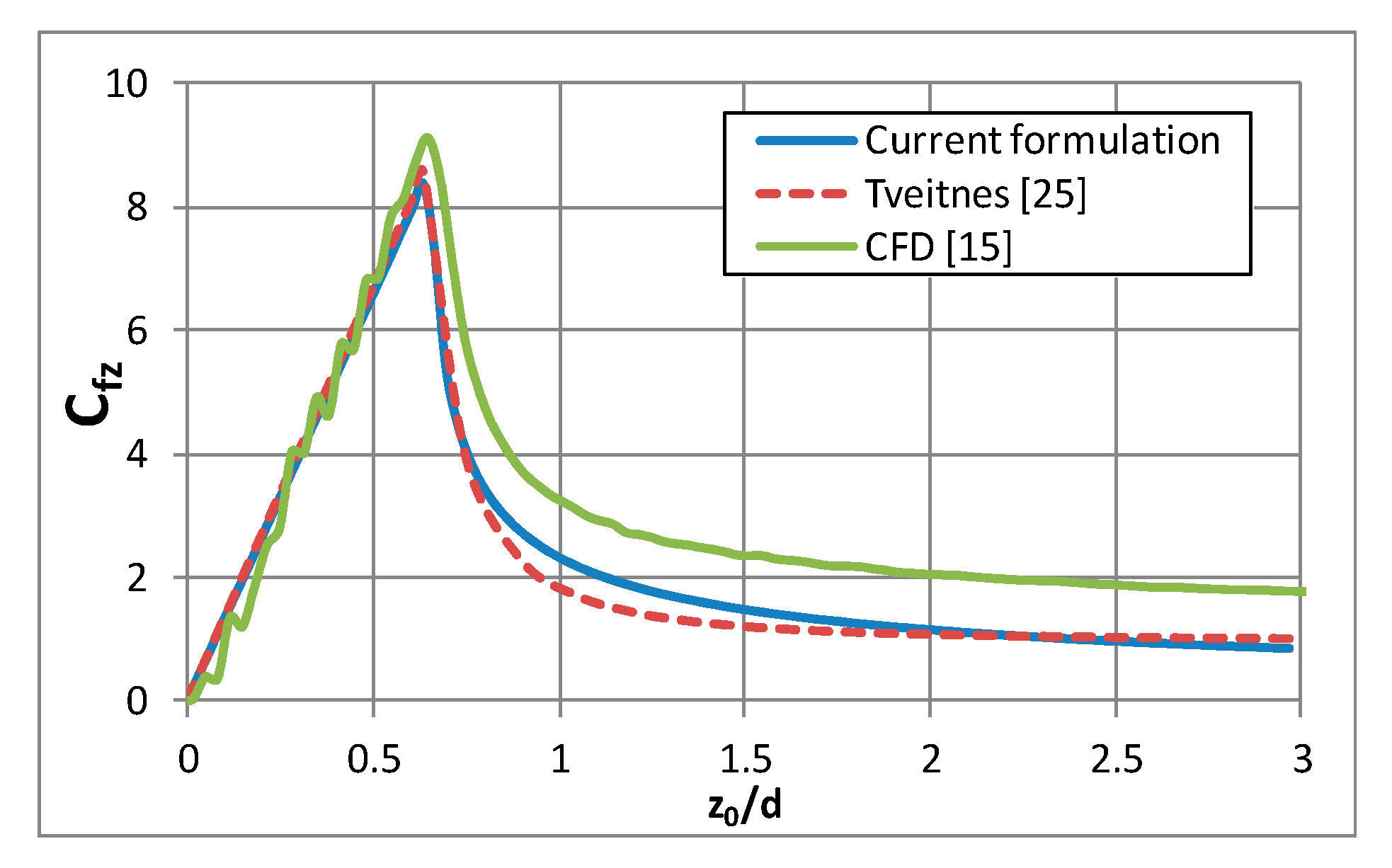
4. Results and Analysis
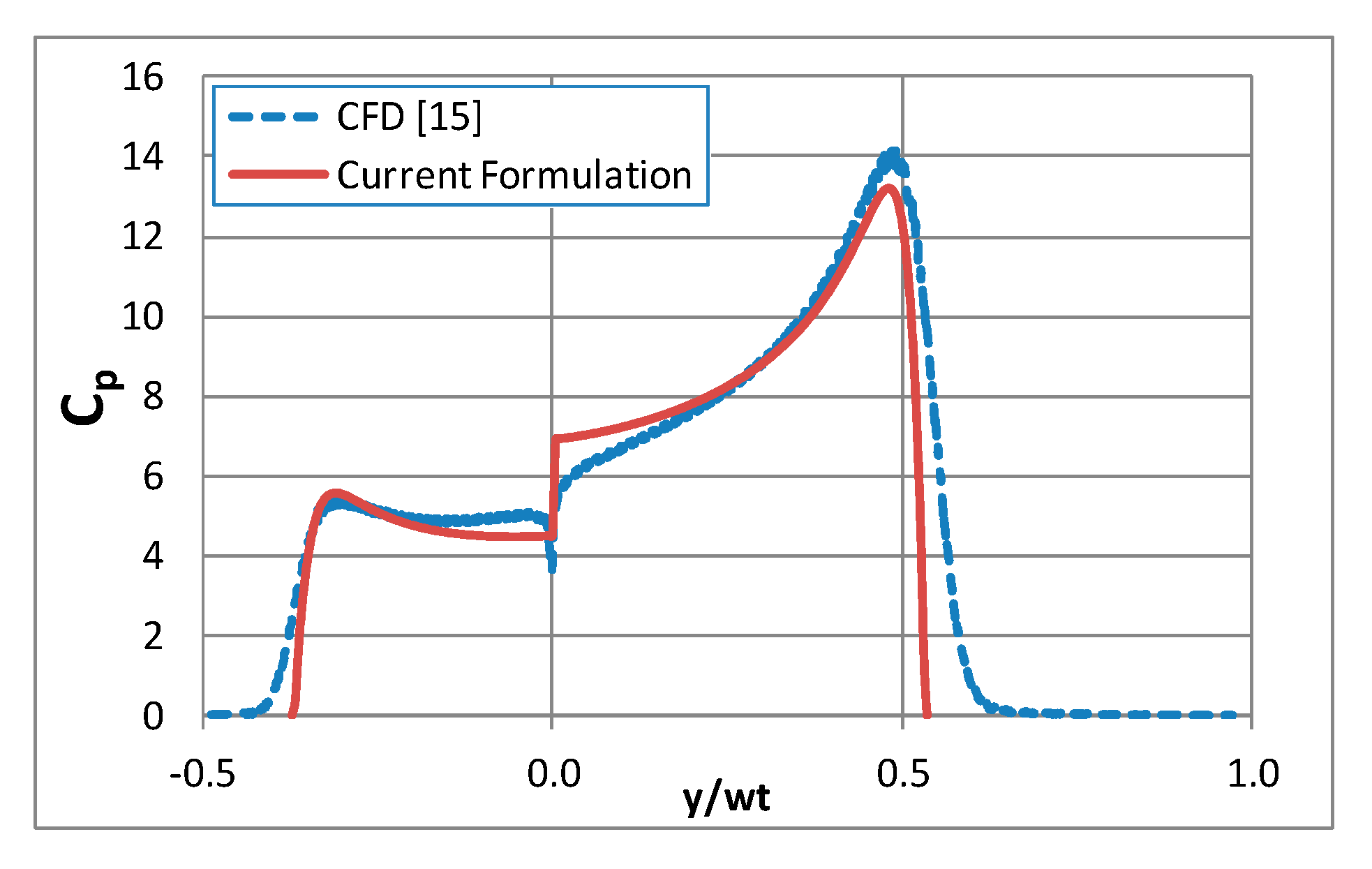
4.1. Impact with One Degree of Freedom
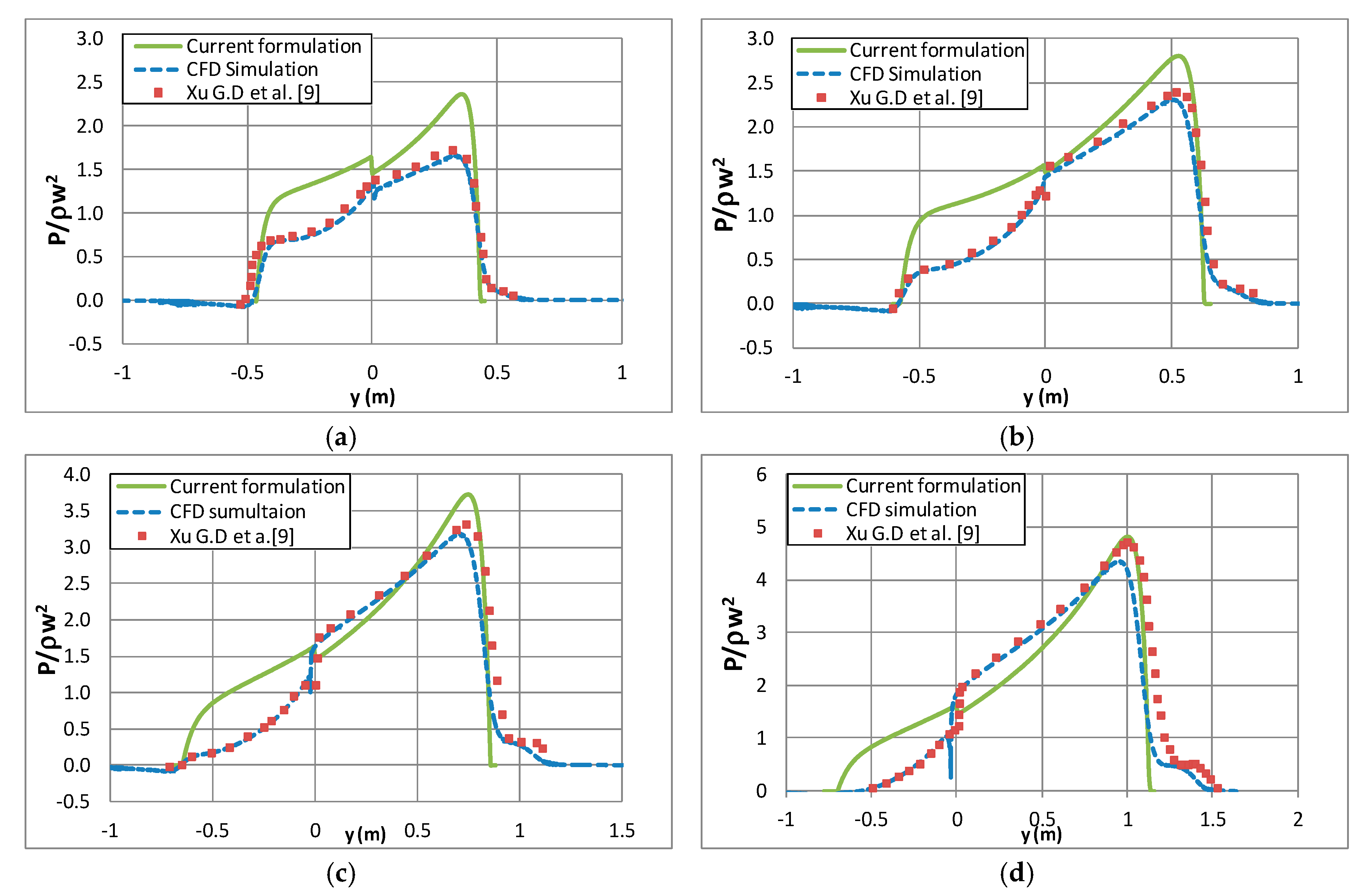
4.2. Impact with Two Degrees of Freedom
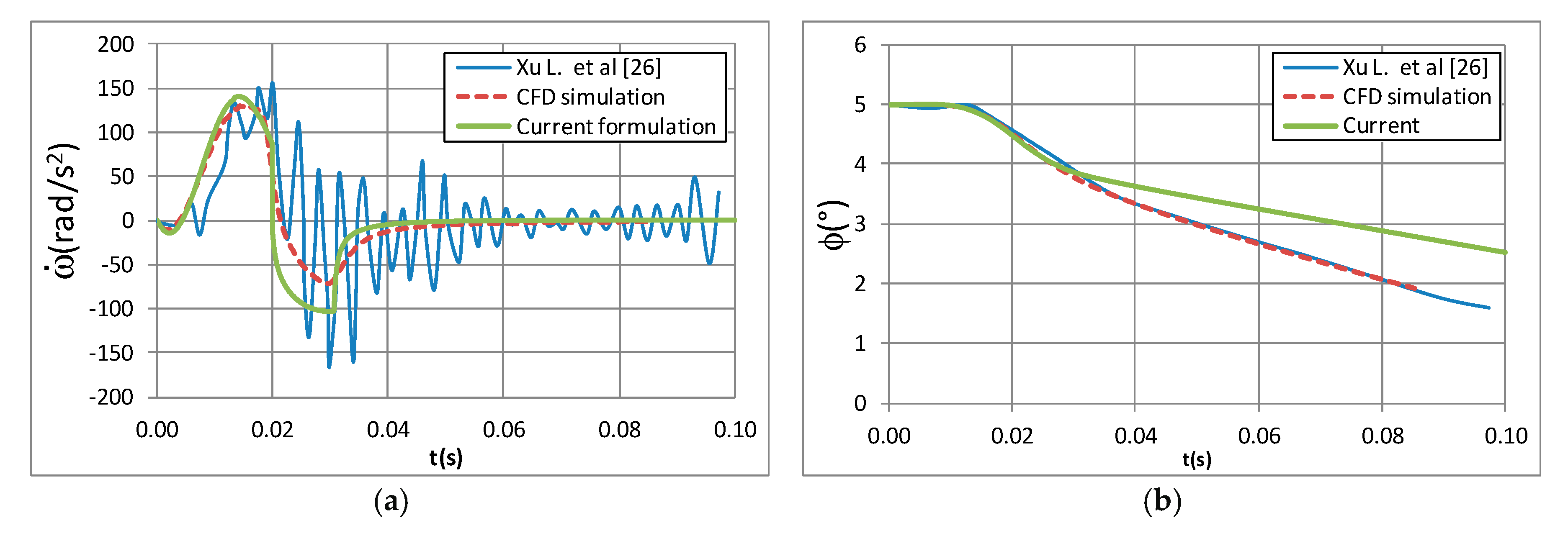
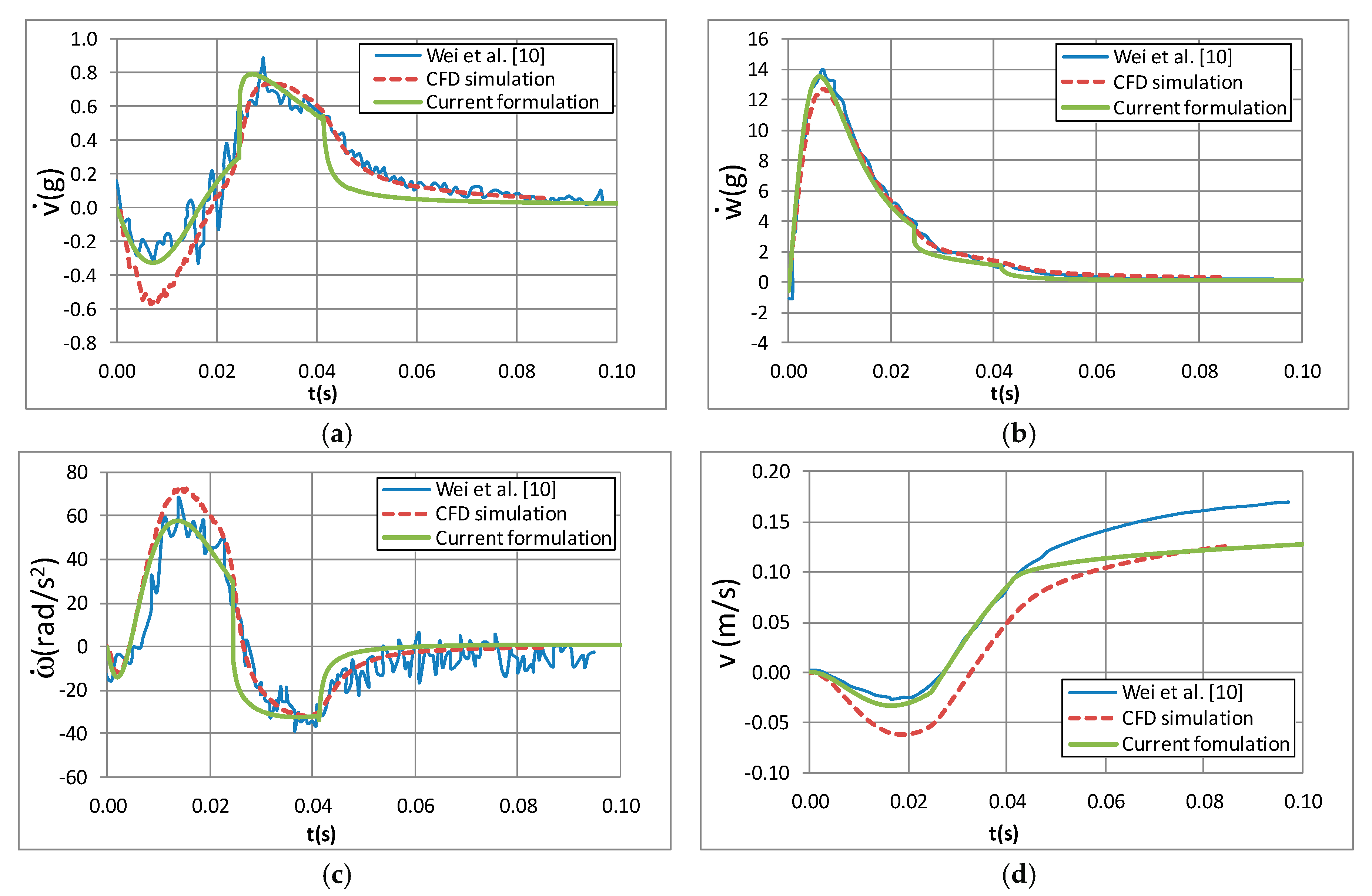
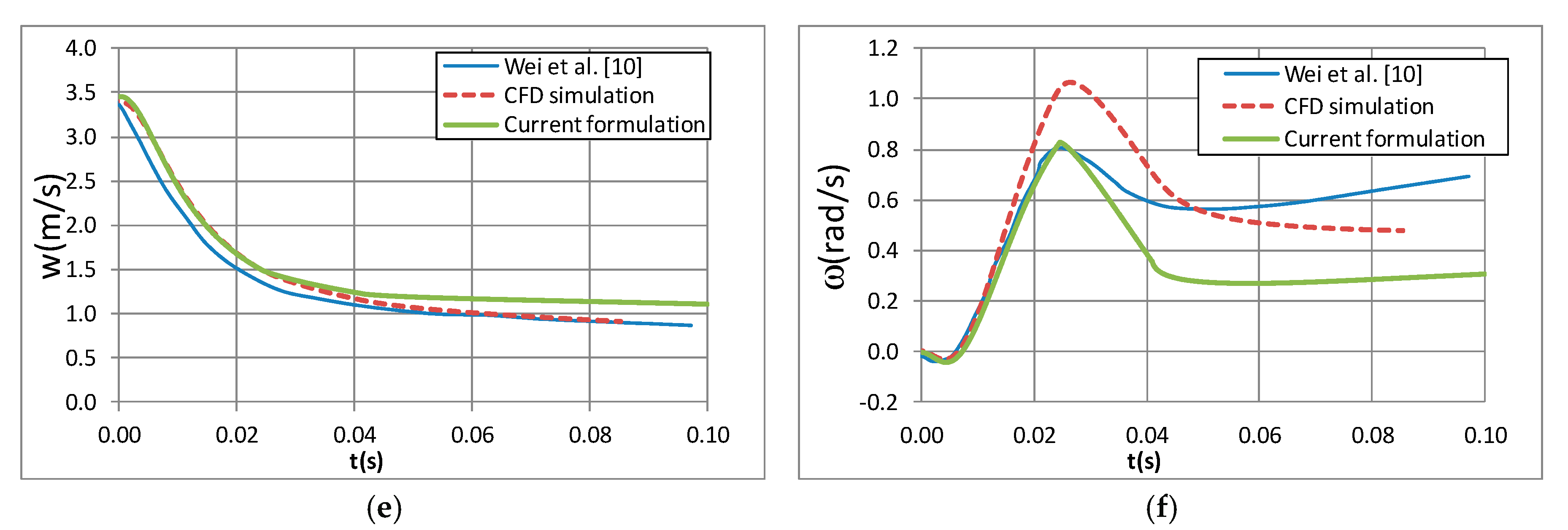
4.3. Impact with Three Degrees of Freedom
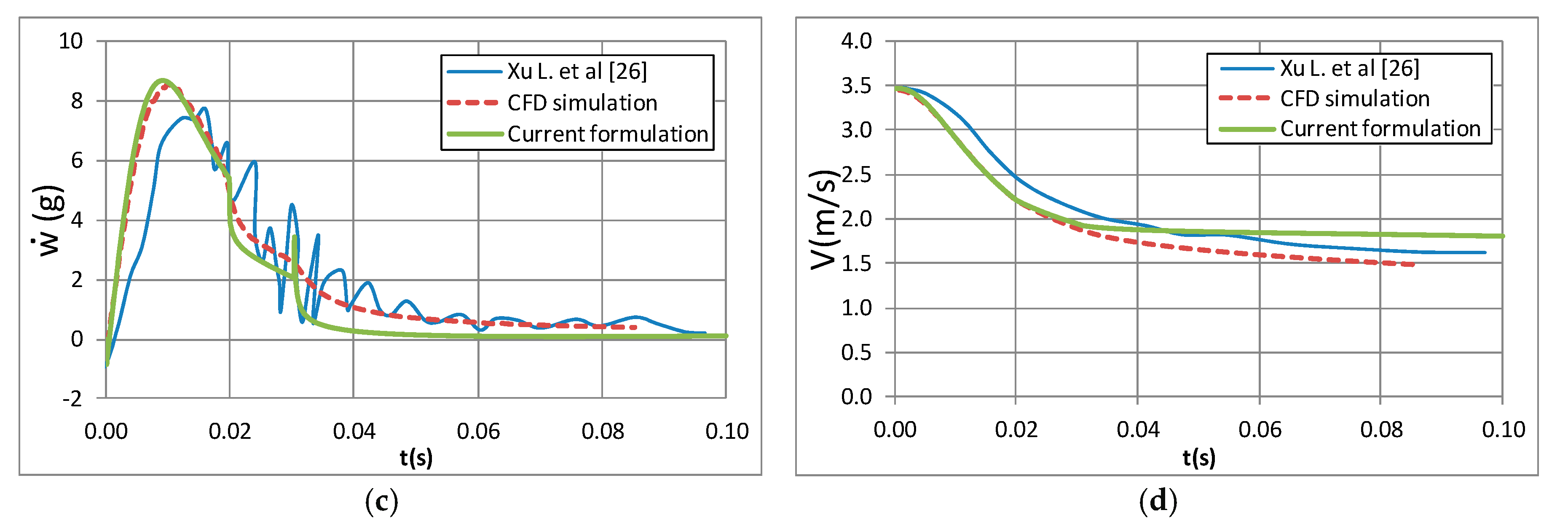
4.4. Free Fall Impact
4.5. Application to Planing Boats
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| deadrise angle of the wedge | |
| deadrise angle in the right side | |
| deadrise angle in the left side | |
| θ | trim angle |
| Ψ | drift angle |
| density of the fluid | |
| potential function of the fluid | |
| heel angle | |
| angular velocity | |
| angular acceleration | |
| μ | asymmetry parameter |
| μ0 | non-dimensional asymmetry parameter |
| asymmetry parameter variation with the time | |
| non-dimensional time | |
| correction factor of the deadrise angle | |
| wetted area of the hull | |
| b | beam section |
| horizontal distance between the keel and knuckle in the right side. | |
| horizontal distance between the keel and knuckle in the left side. | |
| B | beam boat |
| half wetted beam | |
| half wetted beam in the right side. | |
| half wetted beam in the left side | |
| half wetted beam variation in the time | |
| pressure coefficient | |
| frictional coefficient | |
| vertical force coefficient | |
| horizontal force coefficient | |
| roll moment coefficient | |
| velocity coefficient | |
| correction factor for the jet energy | |
| correction due to aft suction | |
| inertia of the wedge | |
| mass of the wedge | |
| horizontal position of cg | |
| keel wetted length | |
| asymmetry ratio | |
| horizontal axis | |
| vertical axis | |
| wedge immersion | |
| hydrostatic horizontal force | |
| hydrostatic vertical force | |
| horizontal force | |
| horizontal sectional force | |
| vertical force | |
| vertical sectional force | |
| roll moment in the keel | |
| hydrostatic roll moment | |
| roll moment in the cg | |
| roll sectional moment | |
| pressure of the fluid | |
| horizontal velocity | |
| horizontal acceleration | |
| tangential velocity in the right side | |
| tangential velocity in the left side | |
| horizontal velocity in the boat section | |
| vertical position of cg | |
| vertical velocity impact | |
| vertical acceleration | |
| vertical velocity in the right side | |
| vertical velocity in the left side | |
| vertical velocity in the boat section | |
| hull force in the x axis on BFCS | |
| hull force in the y axis on BFCS | |
| hull force in the z axis on BFCS | |
| hull moment in the x axis on BFCS | |
| hull moment in the y axis on BFCS | |
| hull moment in the z axis on BFCS | |
| hull force coefficient in the x axis on BFCS | |
| hull force coefficient in the y axis on BFCS | |
| hull force coefficient in the z axis on BFCS | |
| hull moment coefficient in the x axis on BFCS | |
| hull moment coefficient in the y axis on BFCS | |
| hull moment coefficient in the z axis on BFCS |
References
- Ullman Dynamics. Available online: https://ullmandynamics.com/ullman-dynamics-featured-in-ihs-janes-360-a-safe-seat (accessed on 19 December 2019).
- Wagner, H. Über stoss—Und Gleitvorgänge an der Oberfläshe von Flüssigkeiten. Z. Angew. Math. Mech. 1932, 12, 193–215. [Google Scholar] [CrossRef]
- Toyama, Y. Two-dimensional water impact of unsymmetrical bodies. J. Soc. Nav. Arch. Jpn. 1993, 173, 285–291. [Google Scholar] [CrossRef]
- Vorus, W.S. A flat cylinder theory for vessel impact and steady planing resistance. J. Ship Res. 1996, 40, 89–106. [Google Scholar]
- Xu, L.; Troesch, A.; Vorus, W. Asymmetric Vessel Impact and Planing Hydrodynamics. J. Ship Res. 1998, 42, 187–198. [Google Scholar]
- Judge, C.; Troesch, A. Asymmetry and horizontal velocity during water impact. In Proceedings of the International Workshop on Waters Waves and Floating Bodies, Tel Aviv, Israel, 27 February–1 March 2000. [Google Scholar]
- Xu, G.D. Numerical simulation of oblique water entry of an asymmetrical wedge. J. Ocean Eng. 2008, 35, 1597–1603. [Google Scholar] [CrossRef]
- Semenov, Y.A.; Iafrati, A. On the nonlinear water entry problem of asymmetric wedges. J. Fluid Mech. 2006, 547, 231–256. [Google Scholar] [CrossRef]
- Xu, G.D.; Duan, W.Y.; Wu, G.X. Simulation of water entry of a wedge through free fall in three degrees of freedom. Proc. R. Soc. A 2010, 466, 2219–2239. [Google Scholar] [CrossRef]
- Wei, Z.Y.; Xiao, H.Y.; Wang, Z.D.; Shi, X.H. Numerical Simulation of Water Entry of Wedges Based on the Cip Method. J. Mar. Sci. Technol. 2015, 23, 142–150. [Google Scholar]
- Bao, C.M.; Wu, G.X.; Xu, G. Simulation of free fall water entry of a finite wedge with flow detachment. Appl. Ocean Reach. 2017, 65, 62–278. [Google Scholar]
- Seif, M.; Mousaviraad, S.; Saddathosseini, S.; Bertram, V. Numerical Modeling of 2-D Water Impact in One degree of Freedom. Síntesis Tecnológica 2005, 2, 79–83. [Google Scholar] [CrossRef]
- Bilandi, R.; Jamei, S.; Roshan, F.; Azizi, M. Numerical simulation of vertical water impact of asymmetric wedges by using a finite volume method combined with a volume-of-fluid technique. Ocean Eng. 2018, 160, 119–131. [Google Scholar] [CrossRef]
- Tascón, O.; Troesch, A.W.; Maki, K.J. Numerical computation of the hydrodynamic forces acting on a manoeuvring planing hull slender body theory—SBT and 2-D impact theory. In Proceedings of the 10th International Conference on Fast Sea Transportation, Athens, Greece, 5–8 October 2009. [Google Scholar]
- Algarín, R. Modelamiento Del Impacto En Dos Dimensiones De Secciones Asimétricas Con Velocidad Horizontal Con Aplicaciones En El Diseño De Botes De PLANEO. Master’s Thesis, Universidad del Norte, Programa de Ingeniería Mecánica, Barranquilla, Colombia, 2010. [Google Scholar]
- Algarín, R.; Tascón, O. Hydrodynamic Modelling of Planing Boats with Asymmetry and Steady Condition. In Proceedings of the 11th International Symposium on High Speed Marine Vehicle, Naples, Italy, 25–27 May 2011. [Google Scholar]
- Bilandi, R.; Mancini, S.; Vitiello, L.; Miranda, S.; De Carlini, M. A Validation of Symmetric 2D + T Model Based on Single-Stepped Planing Hull Towing Tank Tests. J. Mar. Sci. Eng. 2018, 6, 136. [Google Scholar] [CrossRef]
- Tascón, O.; Algarín, R. Numerical computation of the added mass and damping coefficients of planing hulls in roll via slender body the 2D impact theory. In Proceedings of the 12th International Conference on Fast Sea Transportation, Amsterdam, The Netherland, 2–5 December 2013. [Google Scholar]
- Tavakoli, S.; Dashtimanesh, A.; Mancini, S. A theoretical method to explore influence of free roll motion on behavior of a high speed planing vessel through steady yawed motion. Trans. RINA Int. J. Small Craft Technol. 2018, 160, 25–26. [Google Scholar]
- Zarnick, E.E. A Nonlinear Mathematical Model of Motions of a Planing Boat in Regular Waves, SHIP Performance Department Research and Development Report DTNSRDC-78/032; David, W. Taylor Naval Ship Research and Development Center: Washington, DC, USA, 1978. [Google Scholar]
- Garmé, K. Improved time domain simulation of planing hulls in waves by correction of the near-transom lift. Int. Shipbuild. Prog. 2005, 52, 201–230. [Google Scholar]
- Olausson, K.; Garme, K. Simulation-based assessment of HSC crew exposure to vibration and shock. In Proceedings of the 12th International Conference on Fast Sea Transportation, Amsterdam, The Netherlands, 2–5 December 2013. [Google Scholar]
- ITTC. Recommended Procedures and Guidelines 7.5-03-01. In Uncertainty Analysis in CFD Verification and Validation Methodology and Procedures; 2017; Available online: https://www.ittc.info/media/8153/75-03-01-01.pdf (accessed on 21 November 2019).
- Roache, P.J. Quantification of uncertainty in computational fluid dynamics. Annu. Rev. Fluid Mech. 1997, 29, 123–160. [Google Scholar] [CrossRef]
- Tveitnes, T. Application of Added Mass Theory in Planning. Ph.D. Thesis, Department of Naval Architecture and Ocean Engineering, University of Glasgow, Glasgow, UK, 2001. [Google Scholar]
- Xu, L.; Troesch, A. A study on hydrodynamics of asymmetric planing surfaces. In Proceedings of the 5th International Conference on Fast Sea Transportation, Washington, DC, USA, 31 August–2 September 1999. [Google Scholar]
- ITTC. Concluding technical session. In Proceedings of the 8th International Towing Test Conference, Madrid, Spain, September 1957; Available online: https://ittc.info/media/3089/index.pdf (accessed on 21 November 2019).
- Brown, P.W.; Klosinski, W.E. Directional Stability Tests of Two Prismatic Planing Hulls, Technical Report USCG-D-11-9; Davidson Laboratory, Stevens Institute of Technology Hoboken: Hoboken, NJ, USA, 1994. [Google Scholar]


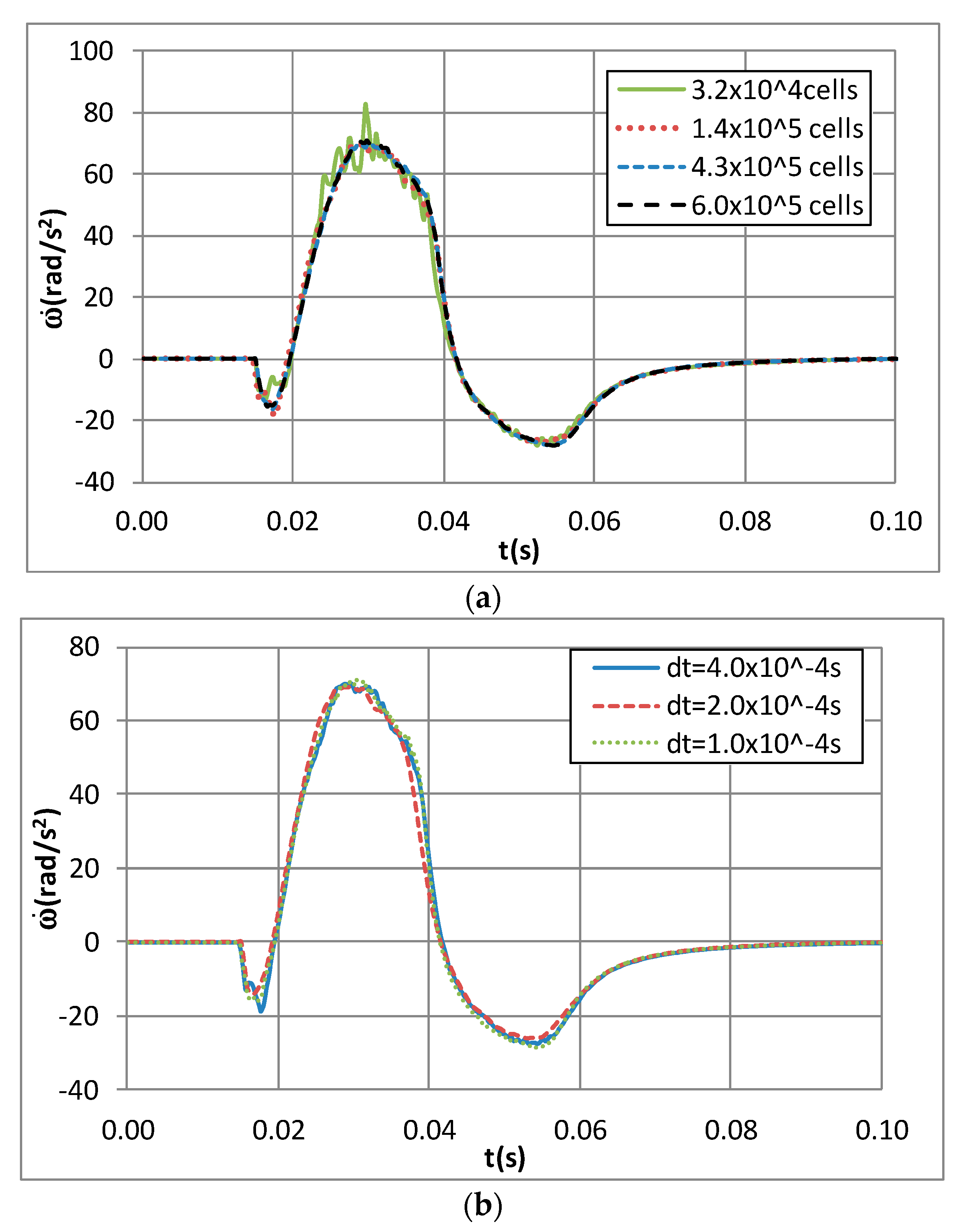




| Mesh | h (m) | Cells | Rg | pg | |1-Cg| | Ug % |
|---|---|---|---|---|---|---|
| 3 | 1.00 | 3.2 × 104 | ||||
| 2 | 0.45 | 1.4 × 105 | 0.341 | 0.647 | 0.25 | 28.14% |
| 1 | 0.30 | 4.4 × 105 |
| Cv | β (°) | θ (°) | ϕ (°) | Ψ (°) | 2Lk/B |
|---|---|---|---|---|---|
| 3 | 20 | 6 | 0 | 0 | 0.4788 |
| 3 | 20 | 6 | 0 | 5 | 0.4958 |
| 3 | 20 | 6 | 0 | 10 | 0.5199 |
| 3 | 20 | 6 | 0 | 15 | 0.5662 |
| 3 | 20 | 6 | −10 | 0 | 0.4925 |
| 3 | 20 | 6 | −10 | 5 | 0.4318 |
| 3 | 20 | 6 | −10 | 10 | 0.3858 |
| 3 | 20 | 6 | −10 | 15 | 0.3663 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Algarín, R.; Bula, A. Two-Dimensional Impact Modelling with Three Degrees of Freedom and Its Application in the Dynamics of Planing Hulls. Appl. Sci. 2020, 10, 1072. https://doi.org/10.3390/app10031072
Algarín R, Bula A. Two-Dimensional Impact Modelling with Three Degrees of Freedom and Its Application in the Dynamics of Planing Hulls. Applied Sciences. 2020; 10(3):1072. https://doi.org/10.3390/app10031072
Chicago/Turabian StyleAlgarín, Roberto, and Antonio Bula. 2020. "Two-Dimensional Impact Modelling with Three Degrees of Freedom and Its Application in the Dynamics of Planing Hulls" Applied Sciences 10, no. 3: 1072. https://doi.org/10.3390/app10031072
APA StyleAlgarín, R., & Bula, A. (2020). Two-Dimensional Impact Modelling with Three Degrees of Freedom and Its Application in the Dynamics of Planing Hulls. Applied Sciences, 10(3), 1072. https://doi.org/10.3390/app10031072





