Decentralized Bioinspired Non-Discrete Model for Autonomous Swarm Aggregation Dynamics
Abstract
1. Introduction
2. Model Presentation
2.1. Stigmergy
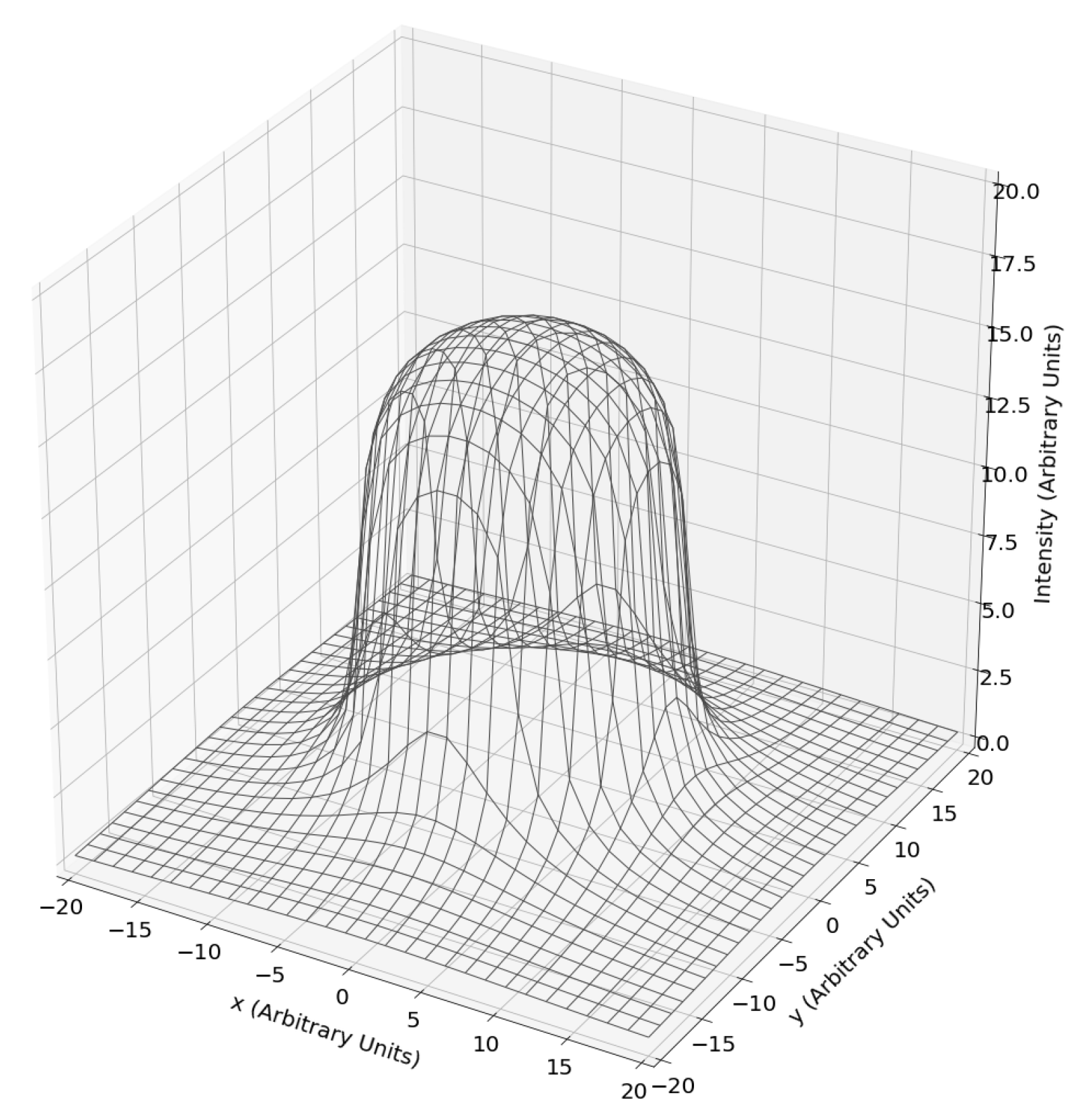
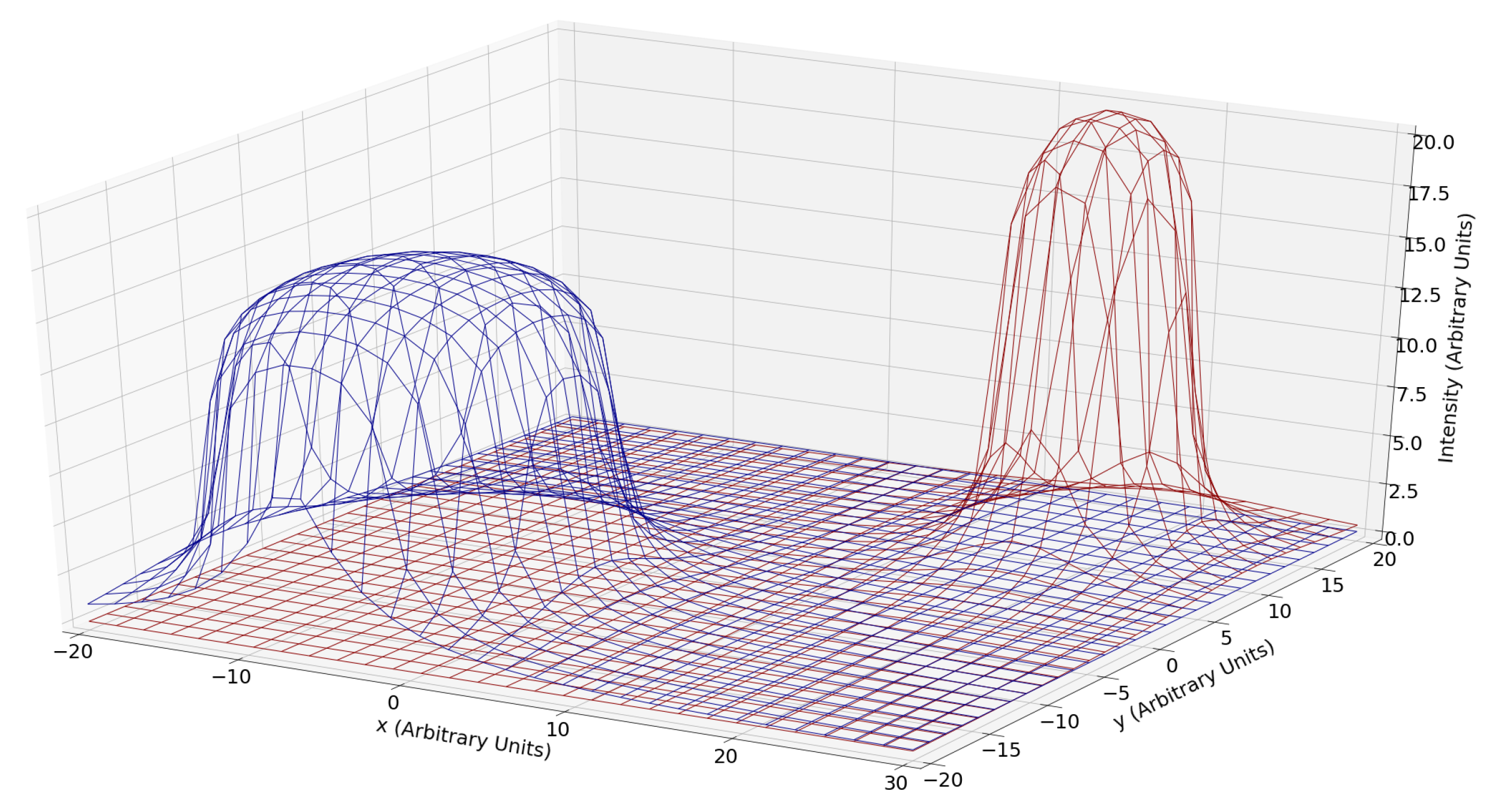
2.2. Task
2.3. Node
3. Simulation Methodology
3.1. Assumptions
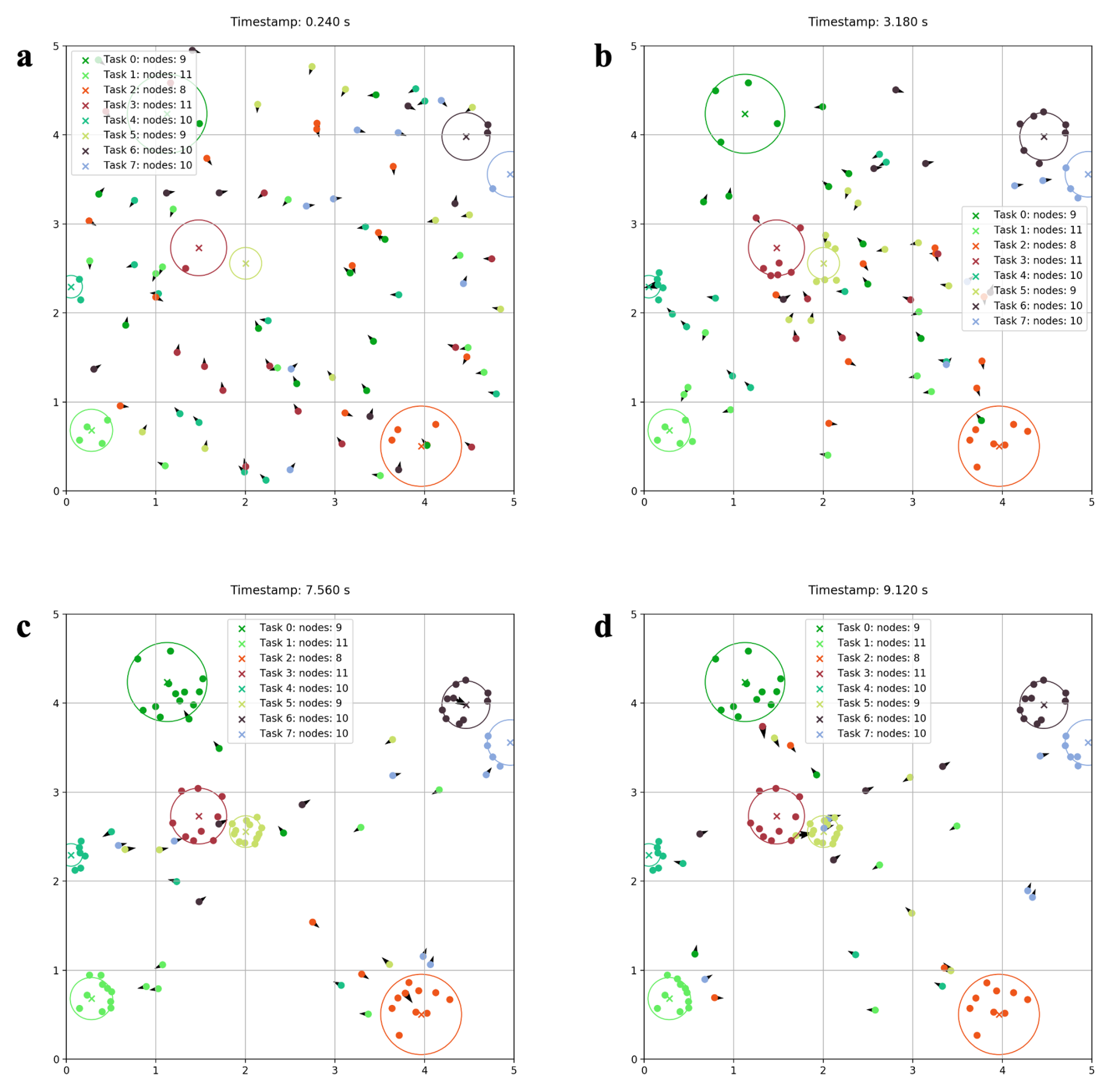
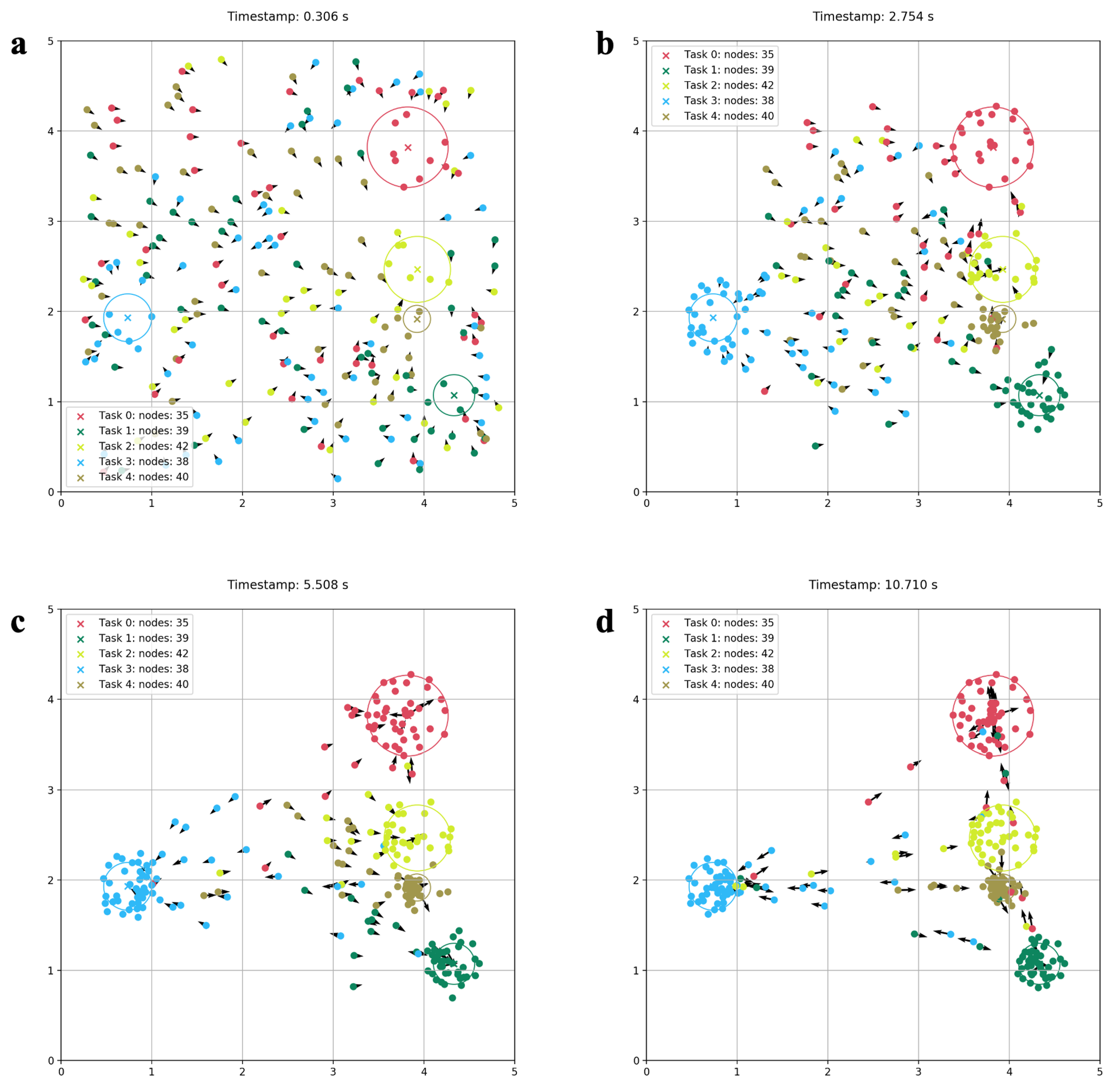
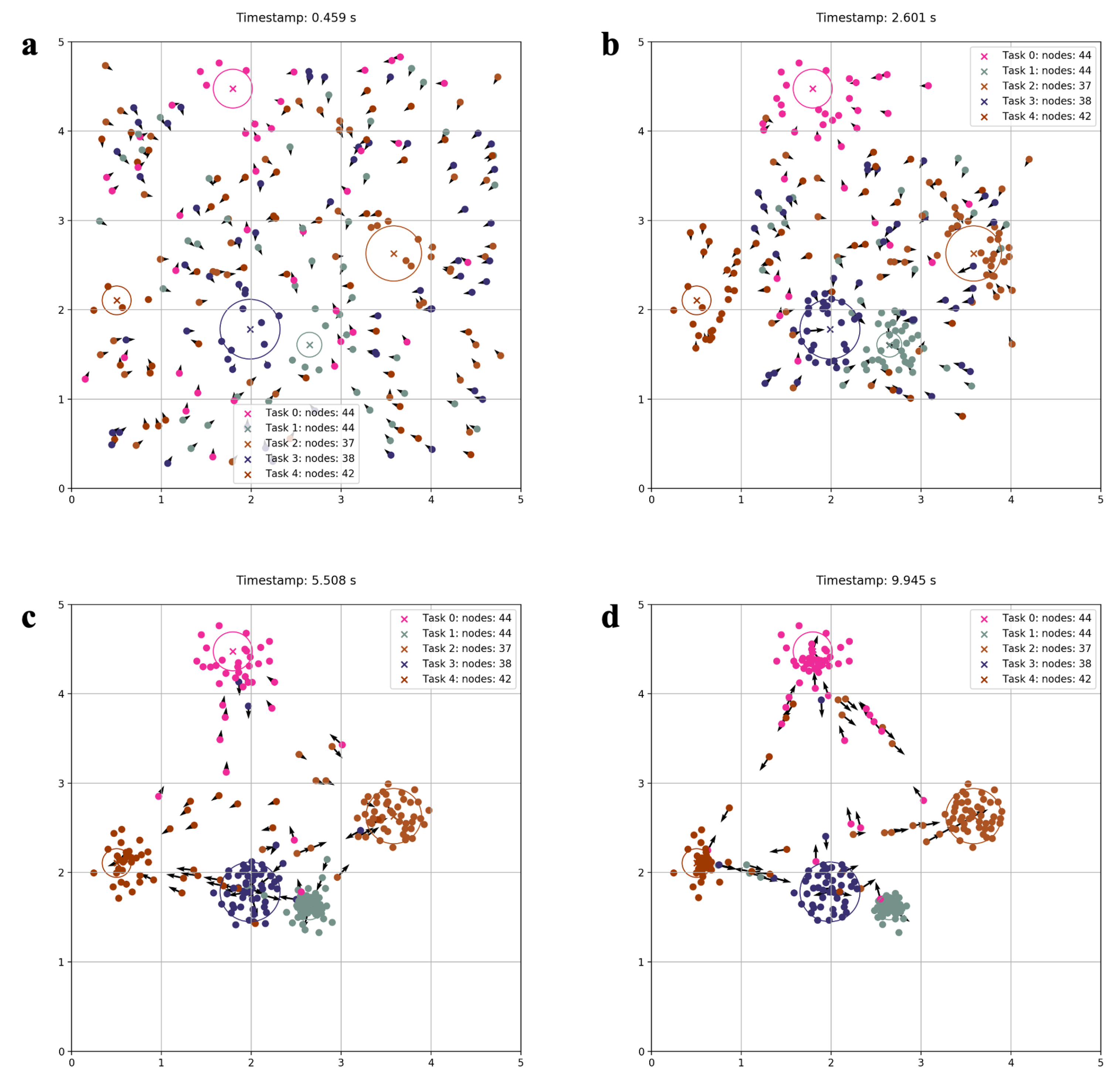
3.2. Qualitative Simulation Results
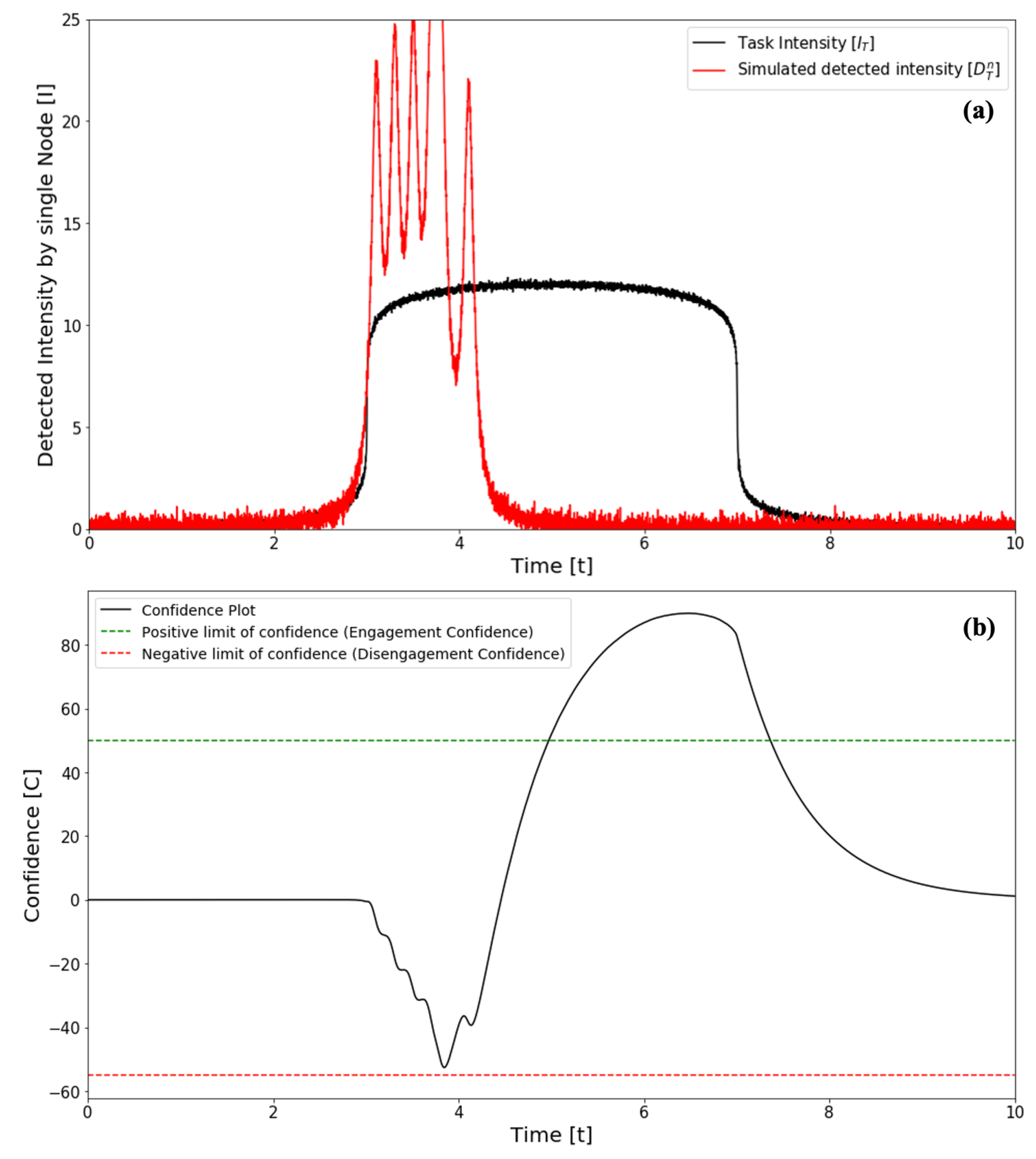
4. Aggregation Evaluation Metrics
- The center of mass of the nodes in an aggregate must coincide with the center of mass for the targeted task.
- The smallest circle enclosing all the nodes in a task, must have an area equal to the area of the task.
- The average distance between one node to all nodes in an aggregate must be equal for every node in said aggregate.
- The number of nodes that are inside the area of a task must be the number of nodes required for that task.
5. Optimization Methodology
5.1. Linear Multivariable Polynomial Regression
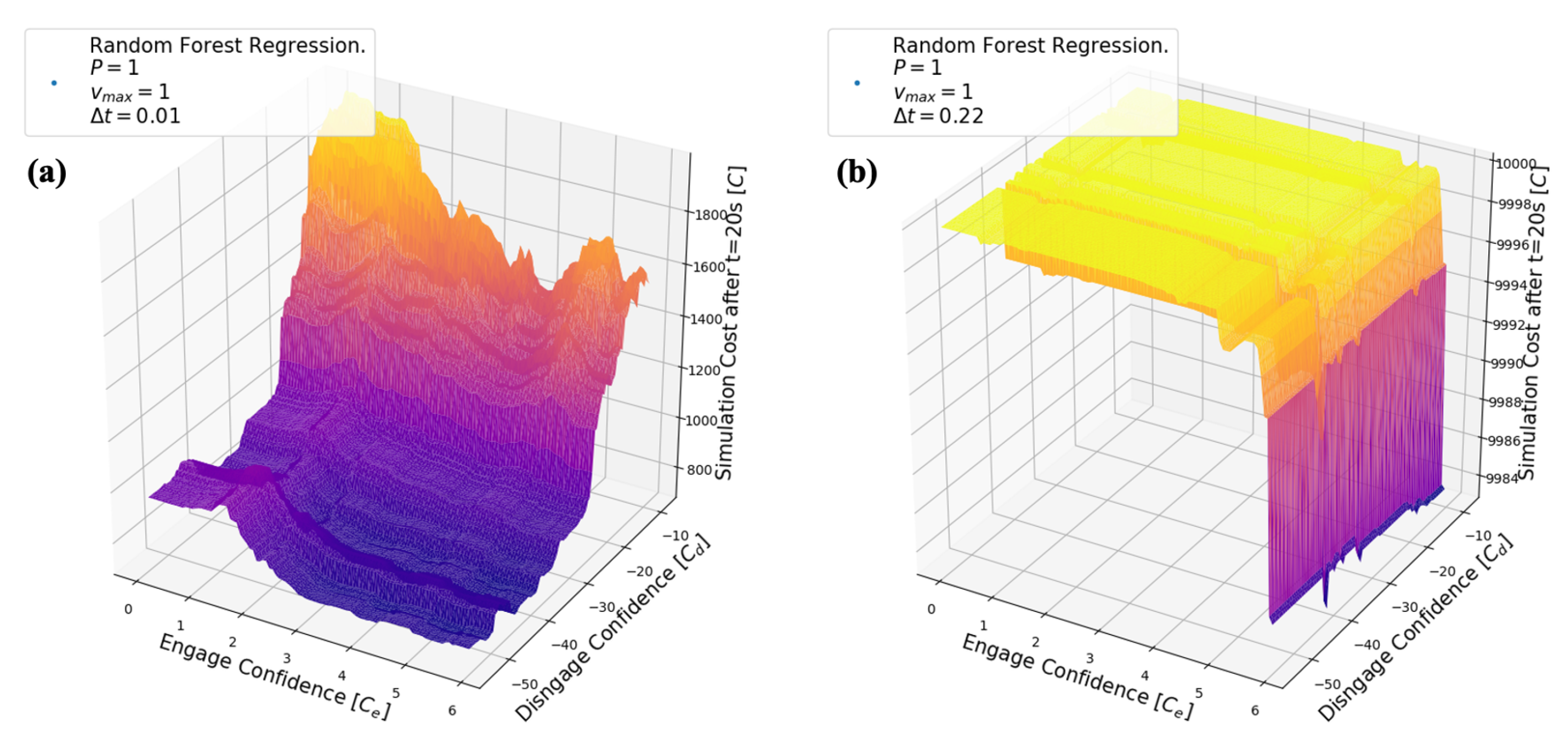
5.2. Random Forest Regression
6. Results
6.1. Linear Regression Results
6.2. Random Forest Results
7. Discussion
7.1. Model Novelty
7.2. Limitations and Future Research
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tan, Y.; Zheng, Z.Y. Research Advance in Swarm Robotics. Def. Technol. 2013, 9, 18–39. [Google Scholar] [CrossRef]
- Mohan, Y.; Ponnambalam, S.G. An extensive review of research in swarm robotics. In Proceedings of the World Congress on Nature and Biologically Inspired Computing, NABIC 2009, Coimbatore, India, 9–11 December 2009; pp. 140–145. [Google Scholar] [CrossRef]
- Sharkey, A.J.C.; Sharkey, N. The application of swarm intelligence to collective robots. In Advances in Applied Artificial Intelligence; IGI Global: Hershey, PA, USA, 2006; pp. 157–185. [Google Scholar] [CrossRef]
- Nedjah, N.; Junior, L.S. Review of methodologies and tasks in swarm robotics towards standardization. Swarm Evol. Comput. 2019, 50, 100565. [Google Scholar] [CrossRef]
- Barca, J.C.; Sekercioglu, Y.A. Swarm robotics reviewed. Robotica 2013, 31, 345–359. [Google Scholar] [CrossRef]
- Elston, J.; Frew, E.W. Hierarchical distributed control for search and tracking by heterogeneous aerial robot networks. In Proceedings of the IEEE International Conference on Robotics and Automation, ICRA, Pasadena, CA, USA, 19–23 May 2008; pp. 170–175. [Google Scholar] [CrossRef]
- Yu, J.; Wang, B.; Du, X.; Wang, Q.; Zhang, L. Ultra-extensible ribbon-like magnetic microswarm. Nat. Commun. 2018, 9, 3260. [Google Scholar] [CrossRef] [PubMed]
- Bayindir, L. A review of swarm robotics tasks. Neurocomputing 2016, 172, 292–321. [Google Scholar] [CrossRef]
- Rambabu, B.; Venugopal Reddy, A.; Janakiraman, S. Hybrid Artificial Bee Colony and Monarchy Butterfly Optimization Algorithm (HABC-MBOA)-based cluster head selection for WSNs. J. King Saud Univ. Comput. Inf. Sci. 2019. [Google Scholar] [CrossRef]
- Varughese, J.C.; Thenius, R.; Leitgeb, P.; Wotawa, F.; Schmickl, T. A Model for Bio-Inspired Underwater Swarm Robotic Exploration. IFAC-PapersOnLine 2018, 51, 385–390. [Google Scholar] [CrossRef]
- Zhao, H.; Zhang, C. A decomposition-based many-objective artificial bee colony algorithm with reinforcement learning. Appl. Soft Comput. 2020, 86, 105879. [Google Scholar] [CrossRef]
- Correll, N.; Martinoli, A. Modeling and designing self-organized aggregation in a swarm of miniature robots. Int. J. Robot. Res. 2011, 30, 615–626. [Google Scholar] [CrossRef]
- Garnier, S.; Gautrais, J.; Asadpour, M.; Jost, C.; Theraulaz, G. Self-Organized Aggregation Triggers Collective Decision Making in a Group of Cockroach-Like Robots. Adapt. Behav. 2009, 17, 109–133. [Google Scholar] [CrossRef]
- Garnier, S.; Jost, C.; Jeanson, R.; Gautrais, J.; Asadpour, M.; Caprari, G.; Theraulaz, G. Aggregation Behaviour as a Source of Collective Decision in a Group of Cockroach-Like-Robots. In Advances in Artificial Life; Capcarrère, M.S., Freitas, A.A., Bentley, P.J., Johnson, C.G., Timmis, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 169–178. [Google Scholar]
- Hamilton, W. Geometry for the selfish herd. J. Theor. Biol. 1971, 31, 295–311. [Google Scholar] [CrossRef]
- Hoare, D.; Couzin, I.; Godin, J.G.; Krause, J. Context-dependent group size choice in fish. Anim. Behav. 2004, 67, 155–164. [Google Scholar] [CrossRef]
- Romano, D.; Elayan, H.; Benelli, G.; Stefanini, C. Together We Stand–Analyzing Schooling Behavior in Naive Newborn Guppies through Biorobotic Predators. J. Bionic Eng. 2020, 17, 174–184. [Google Scholar] [CrossRef]
- Valentini, G.; Brambilla, D.; Hamann, H.; Dorigo, M. Collective Perception of Environmental Features in a Robot Swarm. In Swarm Intelligence; Dorigo, M., Birattari, M., Li, X., López-Ibáñez, M., Ohkura, K., Pinciroli, C., Stützle, T., Eds.; Springer International Publishing: Berlin, Germany, 2016; pp. 65–76. [Google Scholar]
- Arvin, F.; Turgut, A.E.; Krajník, T.; Yue, S. Investigation of cue-based aggregation in static and dynamic environments with a mobile robot swarm. Adapt. Behav. 2016, 24, 102–118. [Google Scholar] [CrossRef]
- Brambilla, M.; Ferrante, E.; Birattari, M.; Dorigo, M. Swarm robotics: A review from the swarm engineering perspective. Swarm Intell. 2013, 7, 1–41. [Google Scholar] [CrossRef]
- Dorigo, M.; Bonabeau, E.; Theraulaz, G. Ant algorithms and stigmergy. Future Gener. Comput. Syst. 2000, 16, 851–871. [Google Scholar] [CrossRef]
- Babaoglu, O.; Canright, G.; Deutsch, A.; Di Caro, G.A.; Ducatelle, F.; Gambardella, L.M.; Ganguly, N.; Jelasity, M.; Montemanni, R.; Montresor, A.; et al. Design patterns from biology for distributed computing. ACM Trans. Auton. Adapt. Syst. 2006, 1, 26–66. [Google Scholar] [CrossRef]
- Di Caro, G.; Dorigo, M. AntNet: Distributed stigmergetic control for communications networks. J. Artif. Intell. Res. 1998, 9, 317–365. [Google Scholar] [CrossRef]
- Gordon, D.M. Local Regulation of Trail Networks of the Arboreal Turtle Ant, Cephalotes goniodontus. Am. Nat. 2017, 190, E156–E169. [Google Scholar] [CrossRef]
- Gordon, D.M.; Goodwin, B.C.; Trainor, L.E.H. A parallel distributed model of the behaviour of ant colonies. J. Theor. Biol. 1992, 156, 293–307. [Google Scholar] [CrossRef]
- Gordon, D.M. From division of labor to the collective behavior of social insects. Behav. Ecol. Sociobiol. 2016, 70, 1101–1108. [Google Scholar] [CrossRef] [PubMed]
- Dorigo, M.; Blum, C. Ant colony optimization theory: A survey. Theor. Comput. Sci. 2005, 344, 243–278. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stützle, T. Ant colony optimization artificial ants as a computational intelligence technique. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Socha, K.; Dorigo, M. Ant colony optimization for continuous domains. Eur. J. Oper. Res. 2008, 185, 1155–1173. [Google Scholar] [CrossRef]
- Shlyakhov, N.E.; Vatamaniuk, I.V.; Ronzhin, A.L. Survey of Methods and Algorithms of Robot Swarm Aggregation. J. Physics Conf. Ser. 2017, 803, 012146. [Google Scholar] [CrossRef]
- Abu-Shikhah, N.; Elkarmi, F.; Aloquili, O.M. Medium-term electric load forecasting using multivariable linear and non-linear regression. Smart Grid Renew. Energy 2011, 2, 126. [Google Scholar] [CrossRef]
- Sauerbrei, W.; Meier-Hirmer, C.; Benner, A.; Royston, P. Multivariable regression model building by using fractional polynomials: Description of SAS, STATA and R programs. Comput. Stat. Data Anal. 2006, 50, 3464–3485. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Segal, M.R. Machine Learning Benchmarks and Random Forest Regression; University of California: San Francisco, CA, USA, 2004. [Google Scholar]
- Fei, Y.; Rong, G.; Wang, B.; Wang, W. Parallel L-BFGS-B algorithm on GPU. Comput. Graph. 2014, 40, 1–9. [Google Scholar] [CrossRef]
- Liu, D.C.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef]
- Iwamatsu, M.; Okabe, Y. Basin hopping with occasional jumping. Chem. Phys. Lett. 2004, 399, 396–400. [Google Scholar] [CrossRef]
- Verma, A.; Schug, A.; Lee, K.H.; Wenzel, W. Basin hopping simulations for all-atom protein folding. J. Chem. Phys. 2006, 124, 044515. [Google Scholar] [CrossRef] [PubMed]
- Wales, D.J.; Doye, J.P.K. Global Optimization by Basin-Hopping and the Lowest Energy Structures of Lennard-Jones Clusters Containing up to 110 Atoms. J. Phys. Chem. A 1997, 101, 5111–5116. [Google Scholar] [CrossRef]


| Variable | Inclusive Bounds | |
|---|---|---|
| From Value [au] | To Value [au] | |
| P | 1.00 | 1.00 |
| 1.00 | 1.00 | |
| 0.02 | 3.00 | |
| 0.00 | 10.00 | |
| −54 | 0.00 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oikonomou, P.; Pappas, S. Decentralized Bioinspired Non-Discrete Model for Autonomous Swarm Aggregation Dynamics. Appl. Sci. 2020, 10, 1067. https://doi.org/10.3390/app10031067
Oikonomou P, Pappas S. Decentralized Bioinspired Non-Discrete Model for Autonomous Swarm Aggregation Dynamics. Applied Sciences. 2020; 10(3):1067. https://doi.org/10.3390/app10031067
Chicago/Turabian StyleOikonomou, Panagiotis, and Stylianos Pappas. 2020. "Decentralized Bioinspired Non-Discrete Model for Autonomous Swarm Aggregation Dynamics" Applied Sciences 10, no. 3: 1067. https://doi.org/10.3390/app10031067
APA StyleOikonomou, P., & Pappas, S. (2020). Decentralized Bioinspired Non-Discrete Model for Autonomous Swarm Aggregation Dynamics. Applied Sciences, 10(3), 1067. https://doi.org/10.3390/app10031067






