Applicability of a Design Assessment and Management for the Current Ammunition Depots in Taiwan
Abstract
:Featured Application
Abstract
1. Introduction
2. The Power of Internal Blast
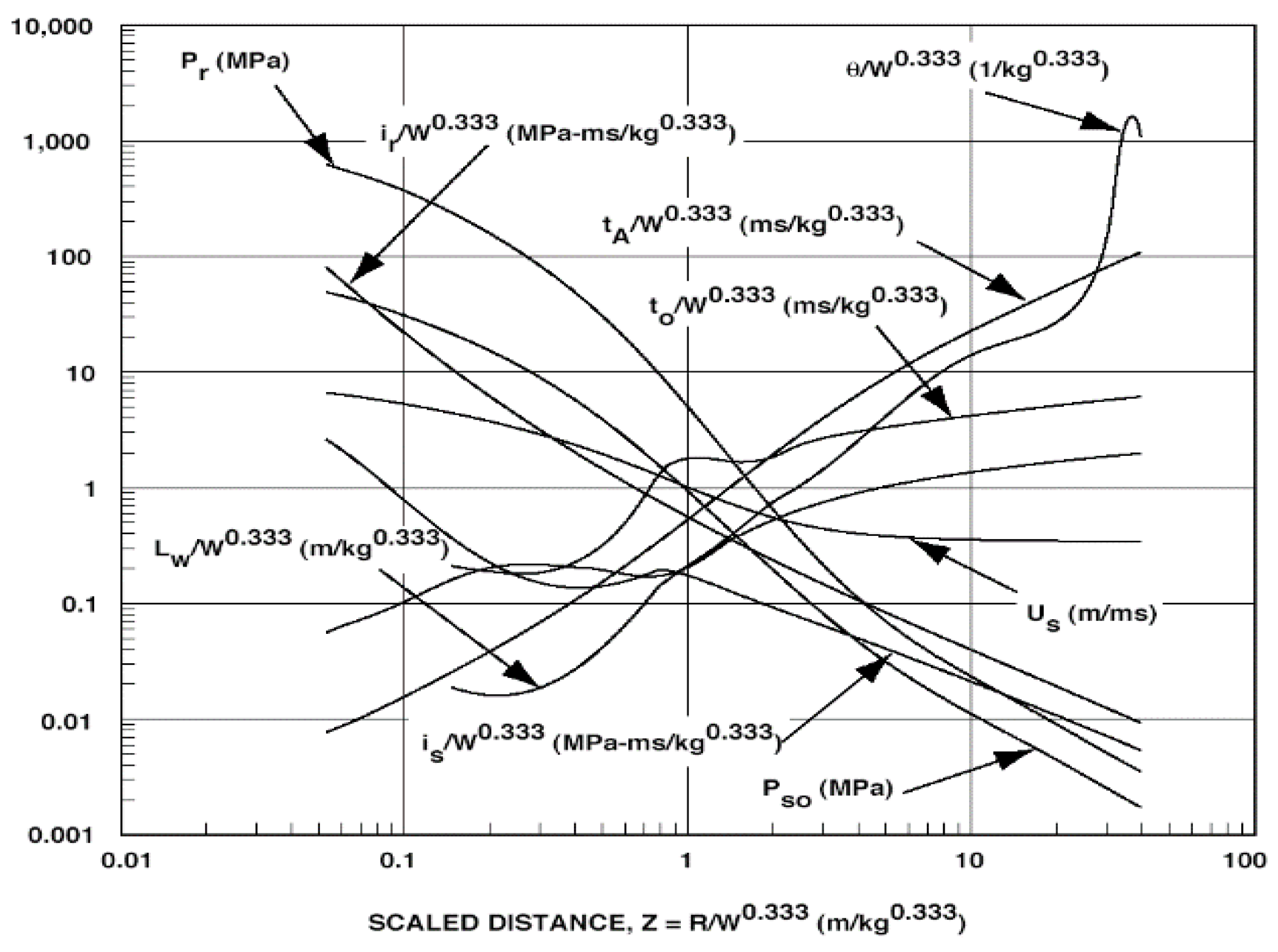
2.1. Shock Pressure
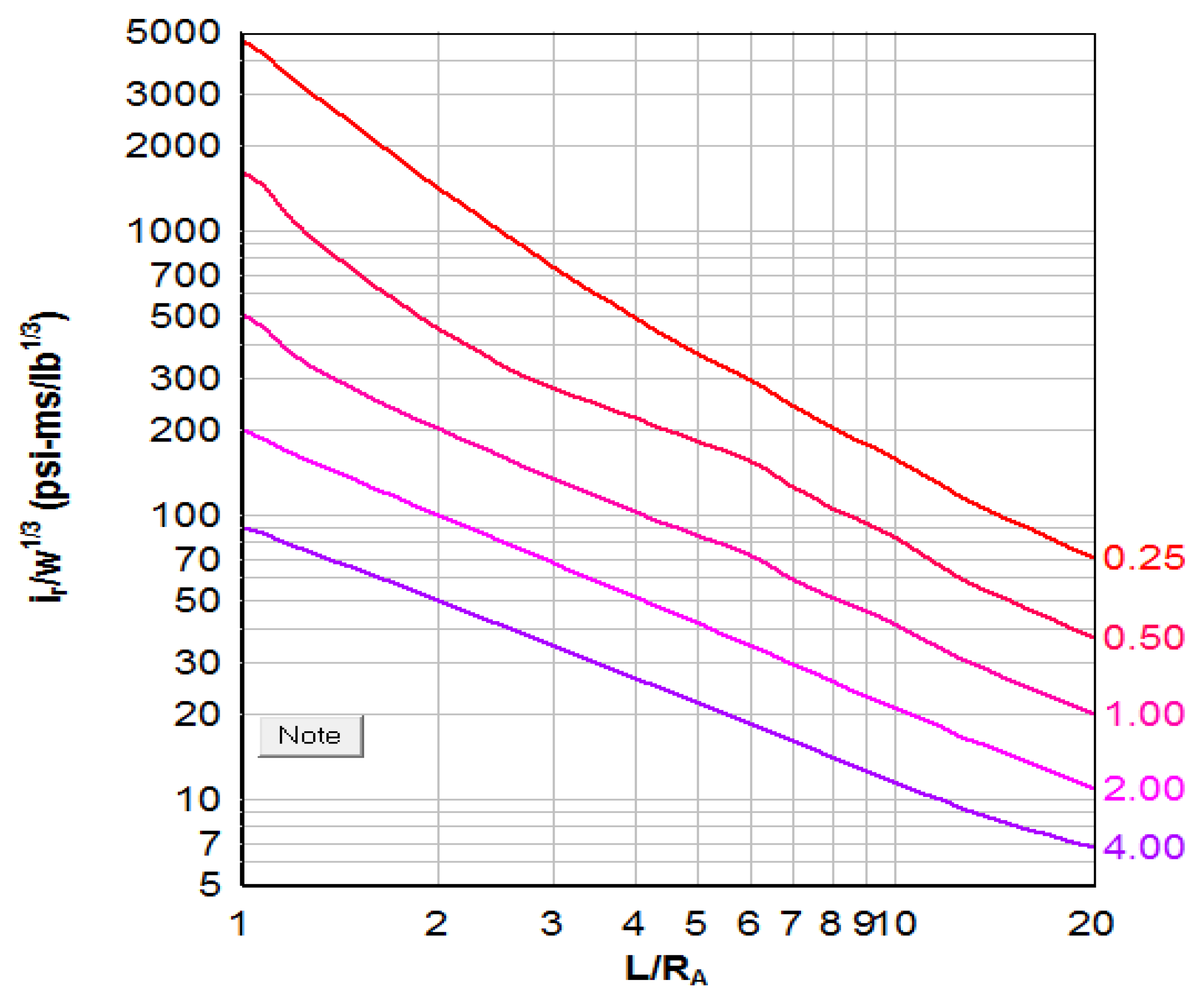
2.2. Gas Pressure
- tg = duration of gas pressure
- lg = total gas pressure impulse
- W = charge weight in pounds
- V = internal volume, cubic feet
- A = vent area, square feet
- a, b, c = constants (see below)
| a | b | c | |
| W/V < 0.015 | 1855 | 0.36 | 15.41135 |
| 0.015 < W/V < 0.15 | 409 | 0 | 13.89943 |
| W/V > 0.15 | 643 | 0.24 | 14.35186 |
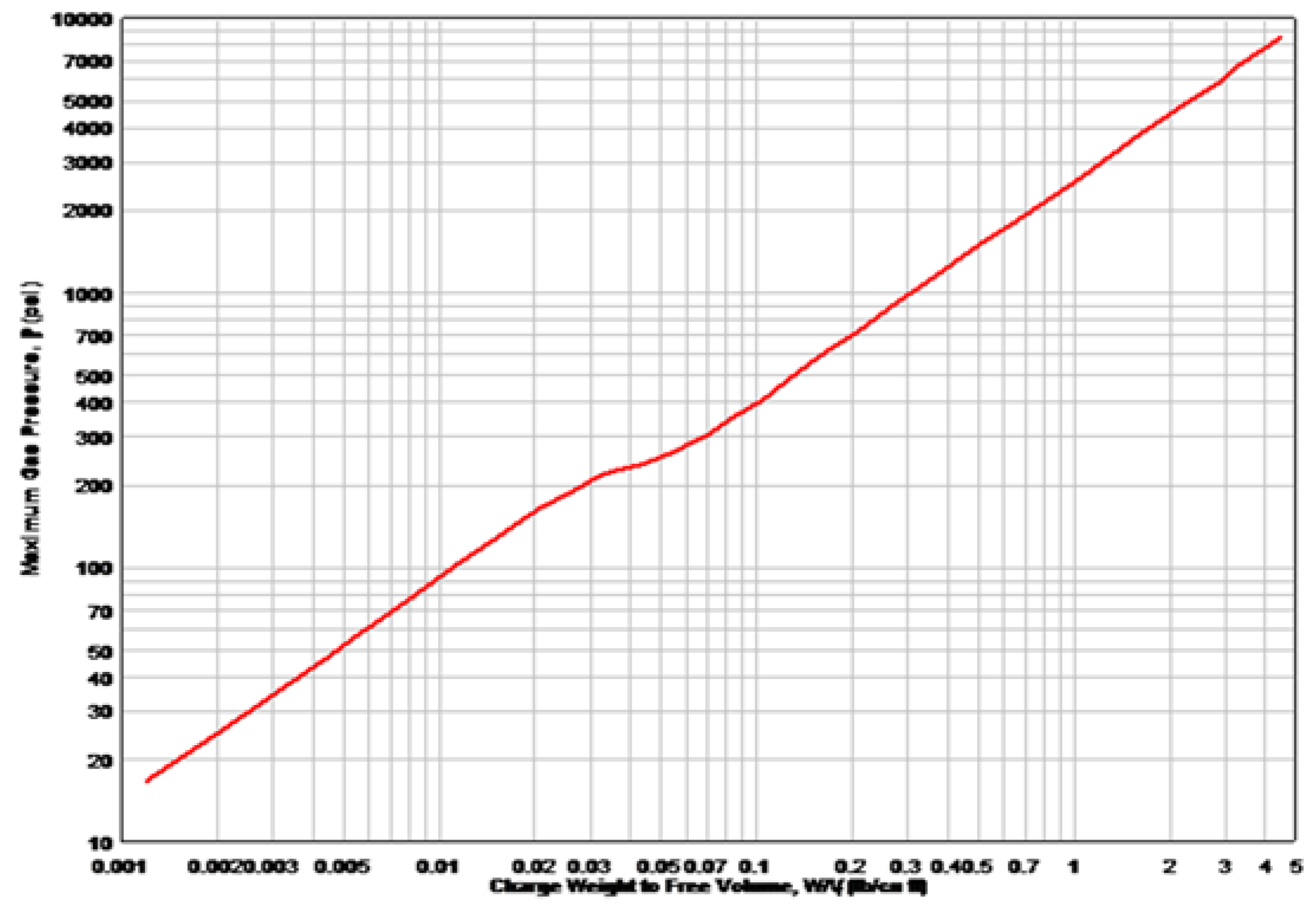
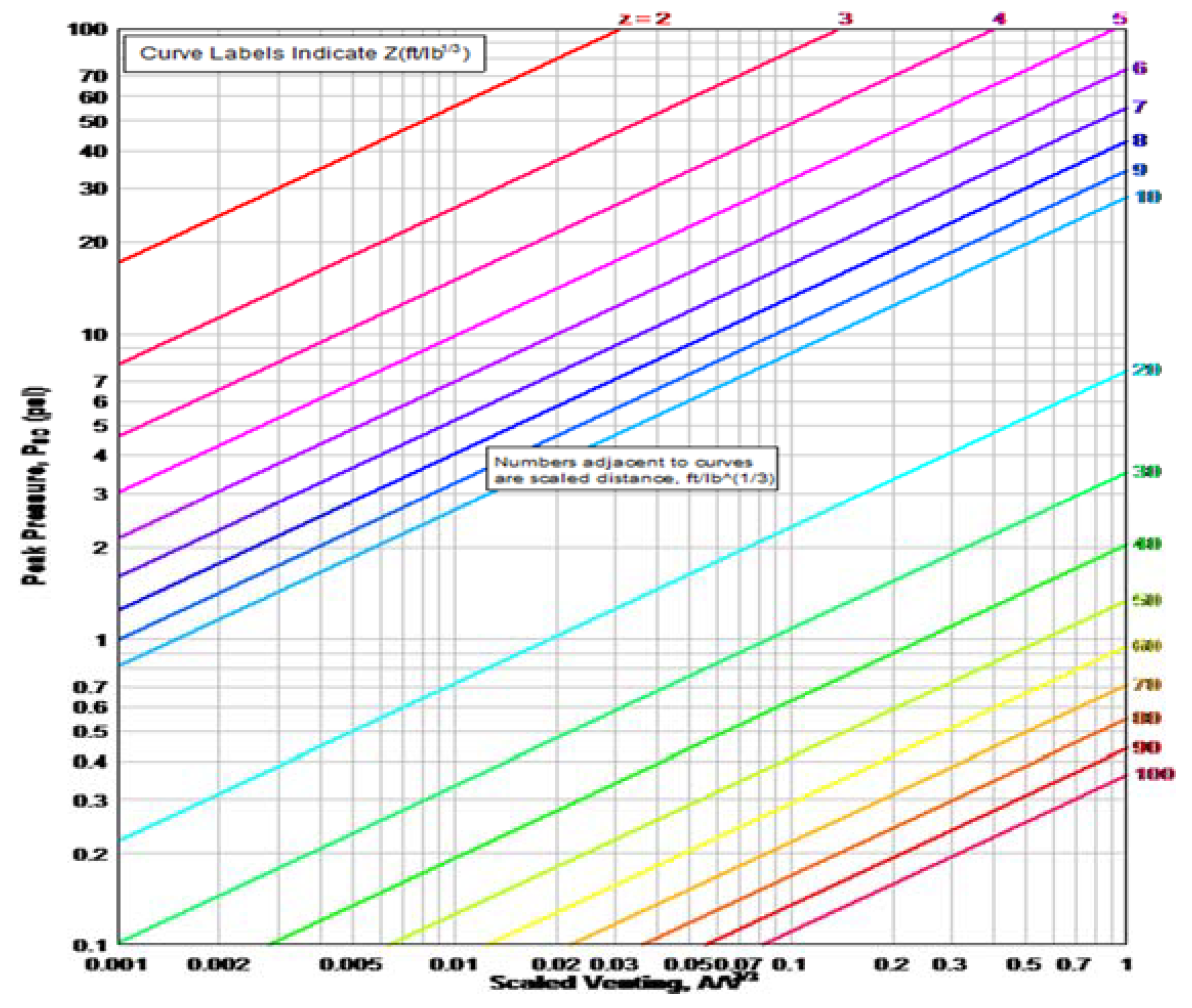
2.3. Leakage Pressure
3. Numerical Simulation
3.1. ALE Fluid–Structure Interaction Algorithm
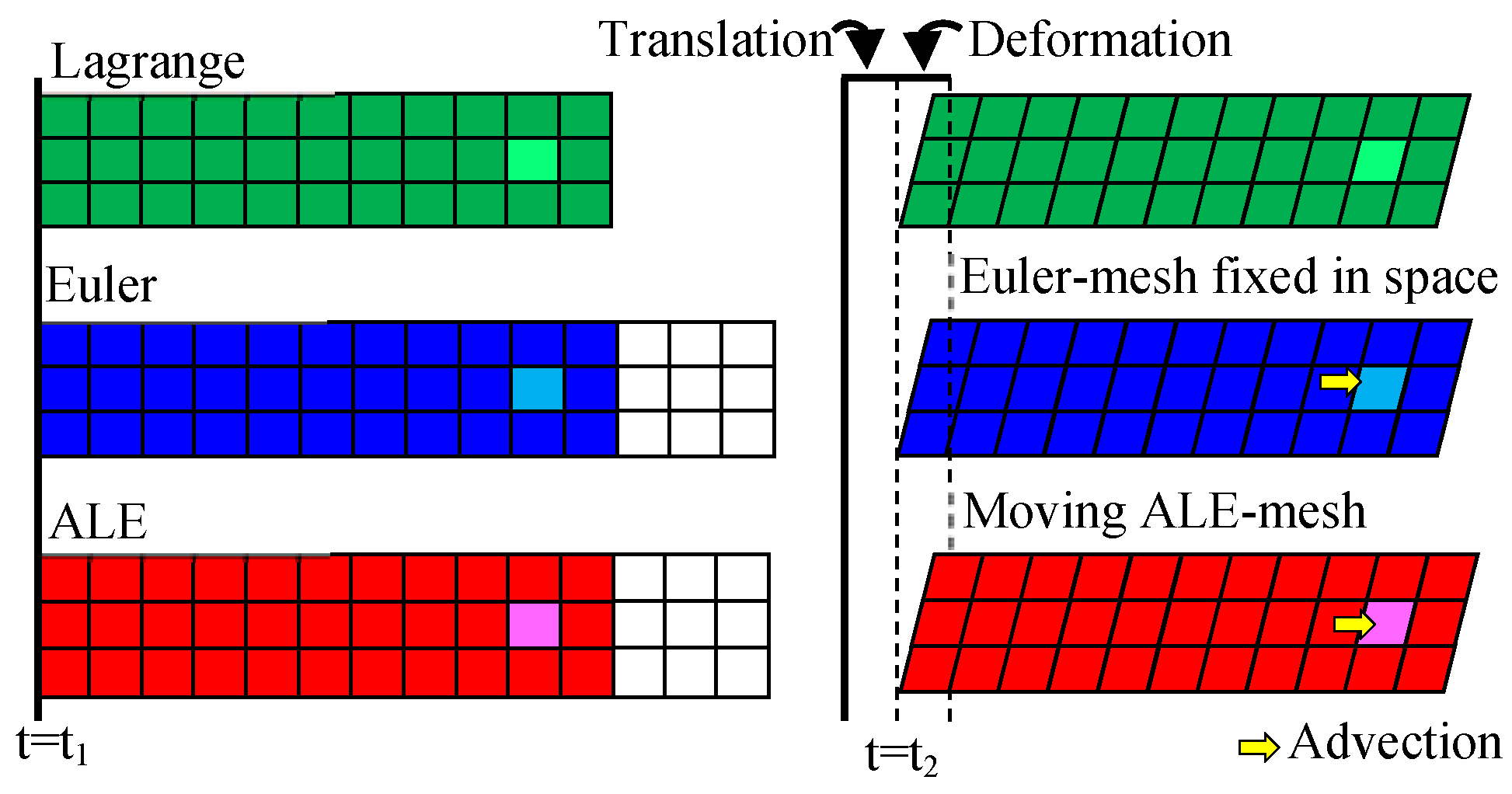
3.1.1. Lagrangian Description
3.1.2. Eulerian Description
3.1.3. ALE Description
3.2. Law of Material Composition
3.2.1. Air
3.2.2. Charge
3.2.3. Concrete
3.2.4. Rigid Body
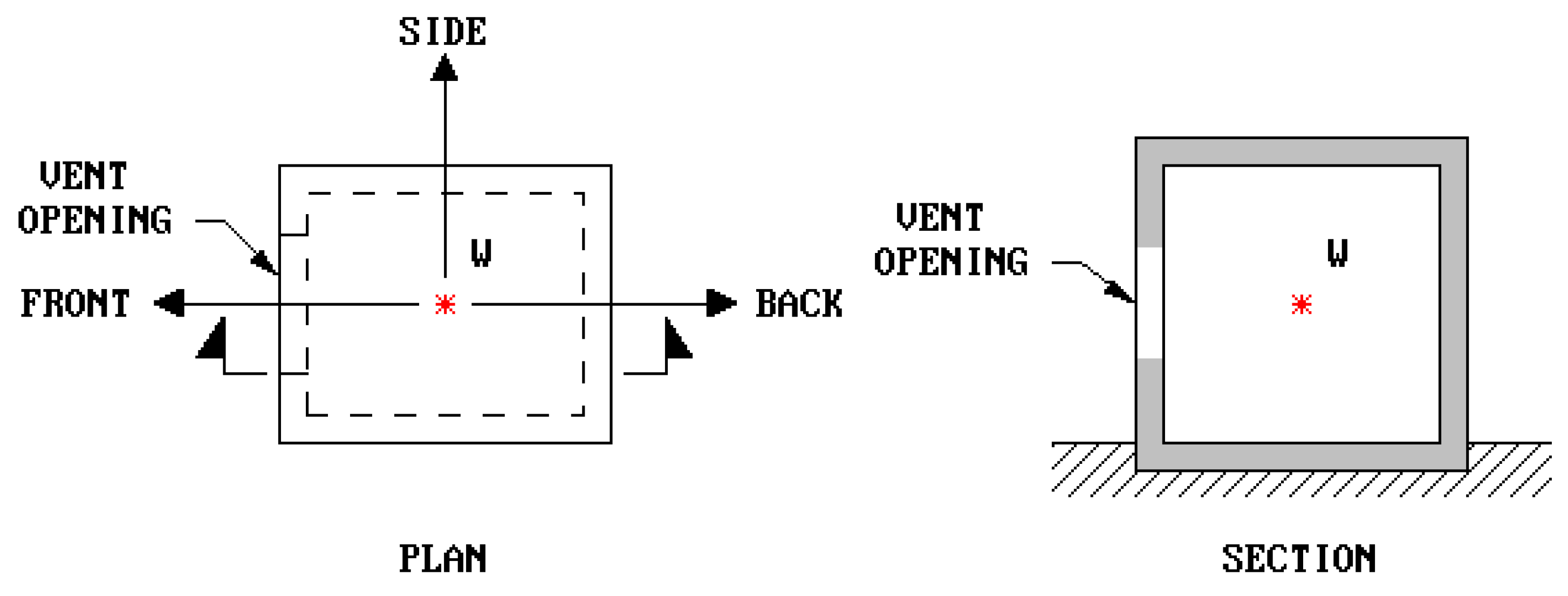
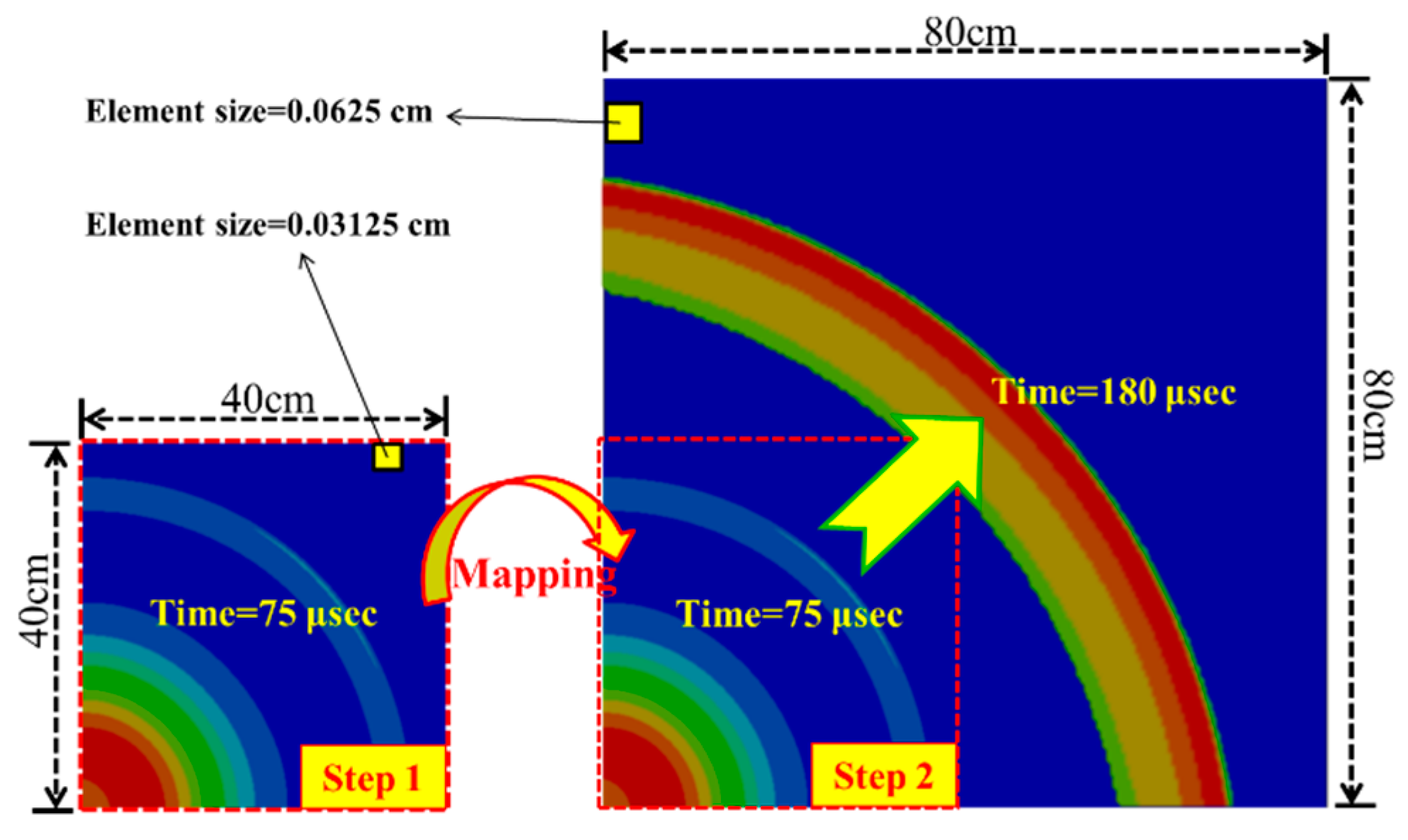
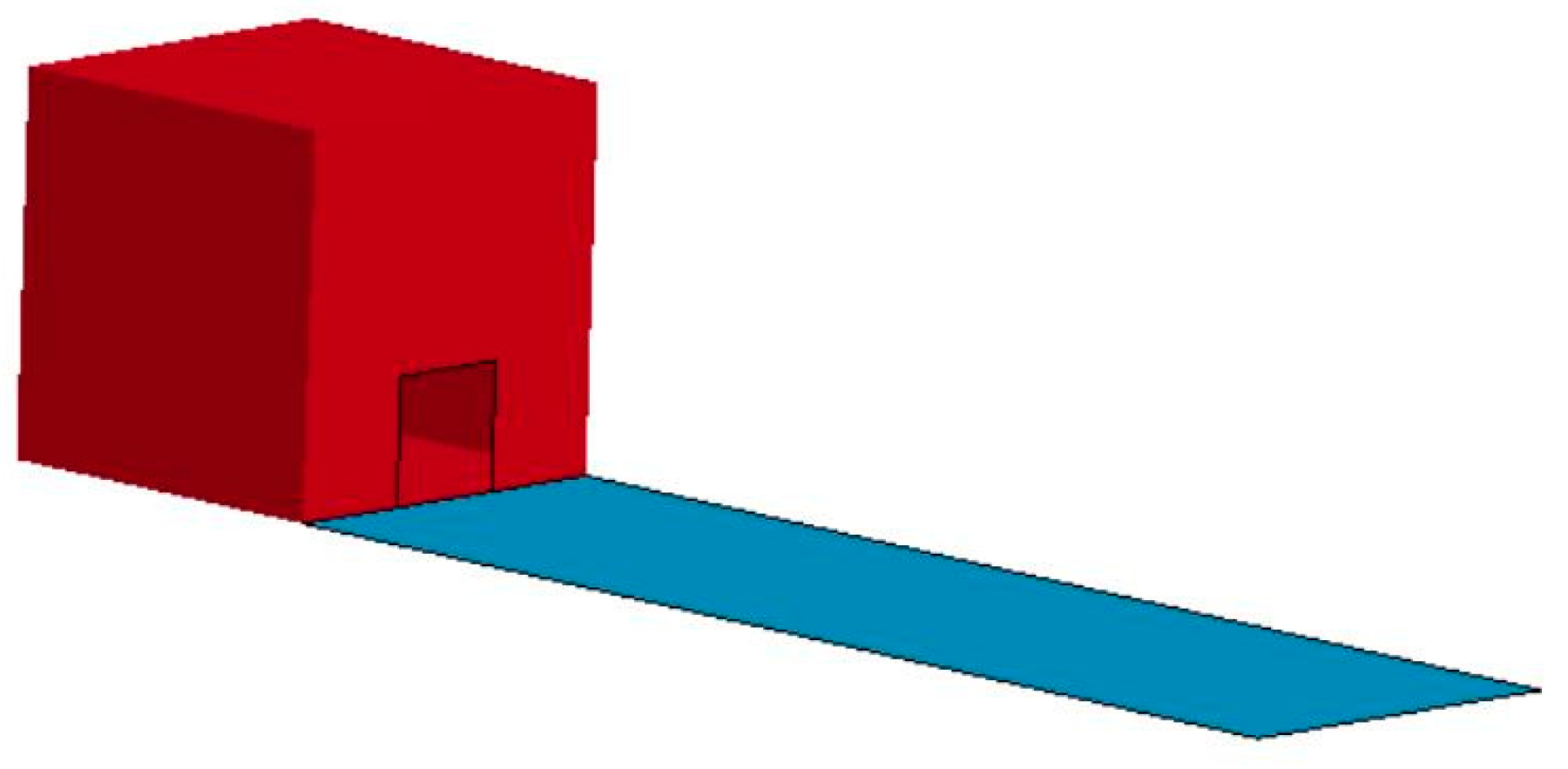
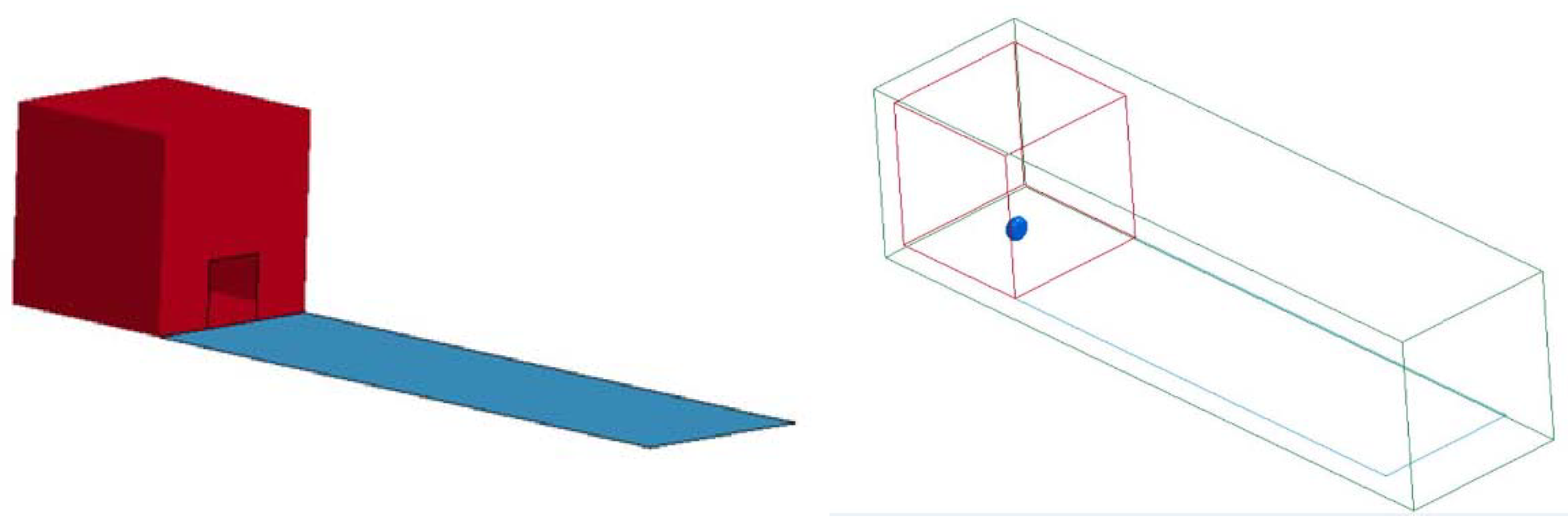
3.3. Application of Simulation Technique
4. Simulation Results
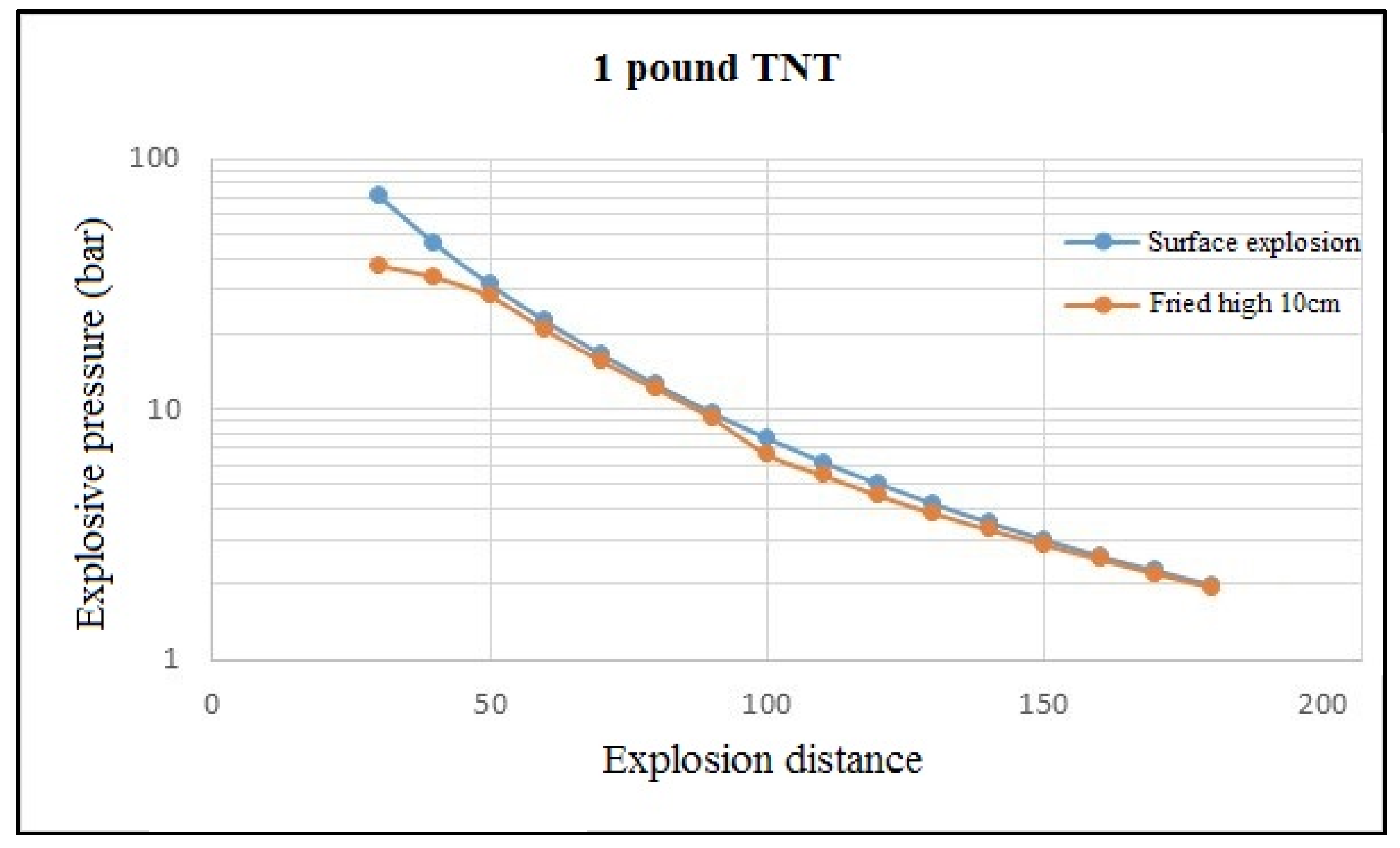
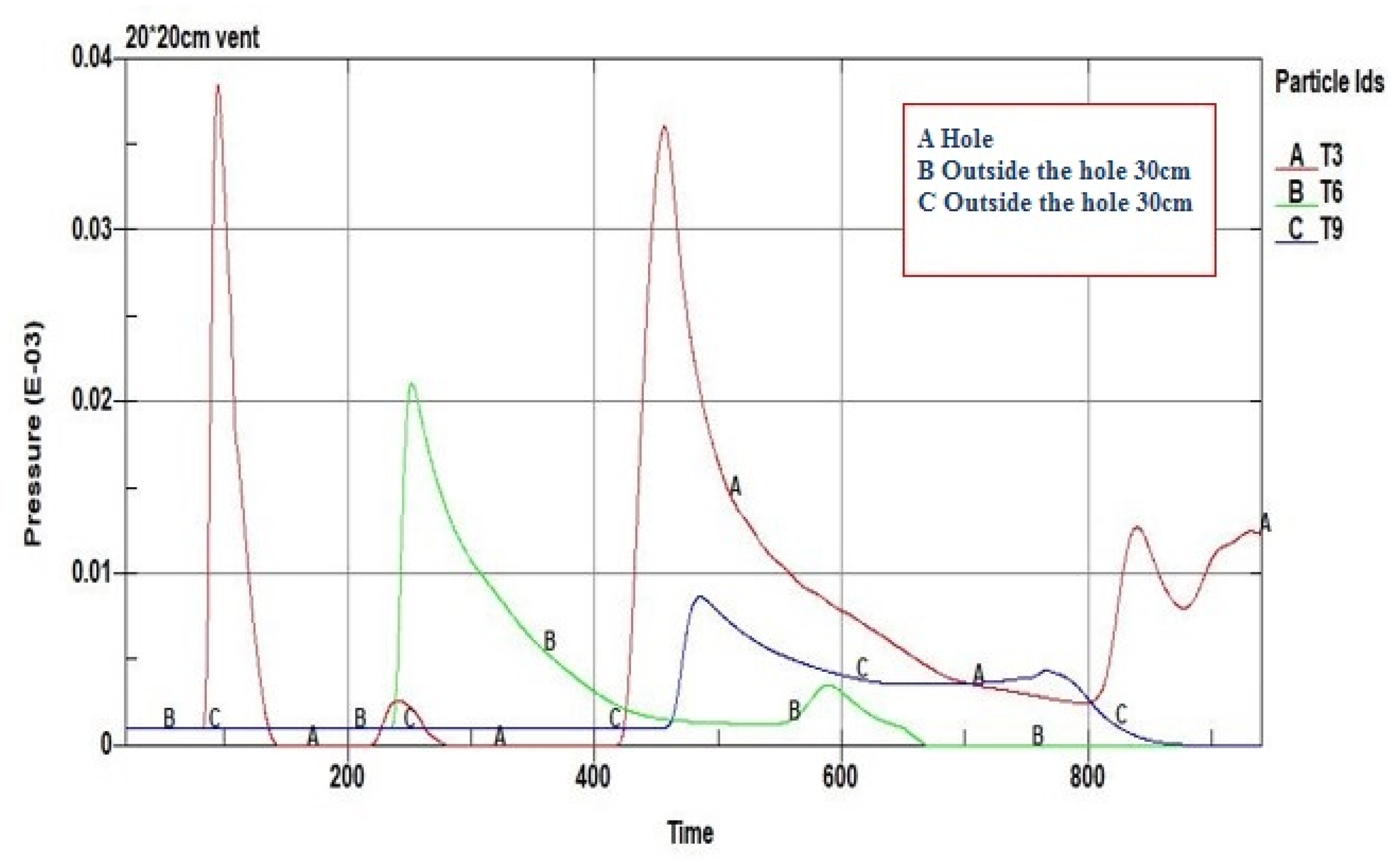
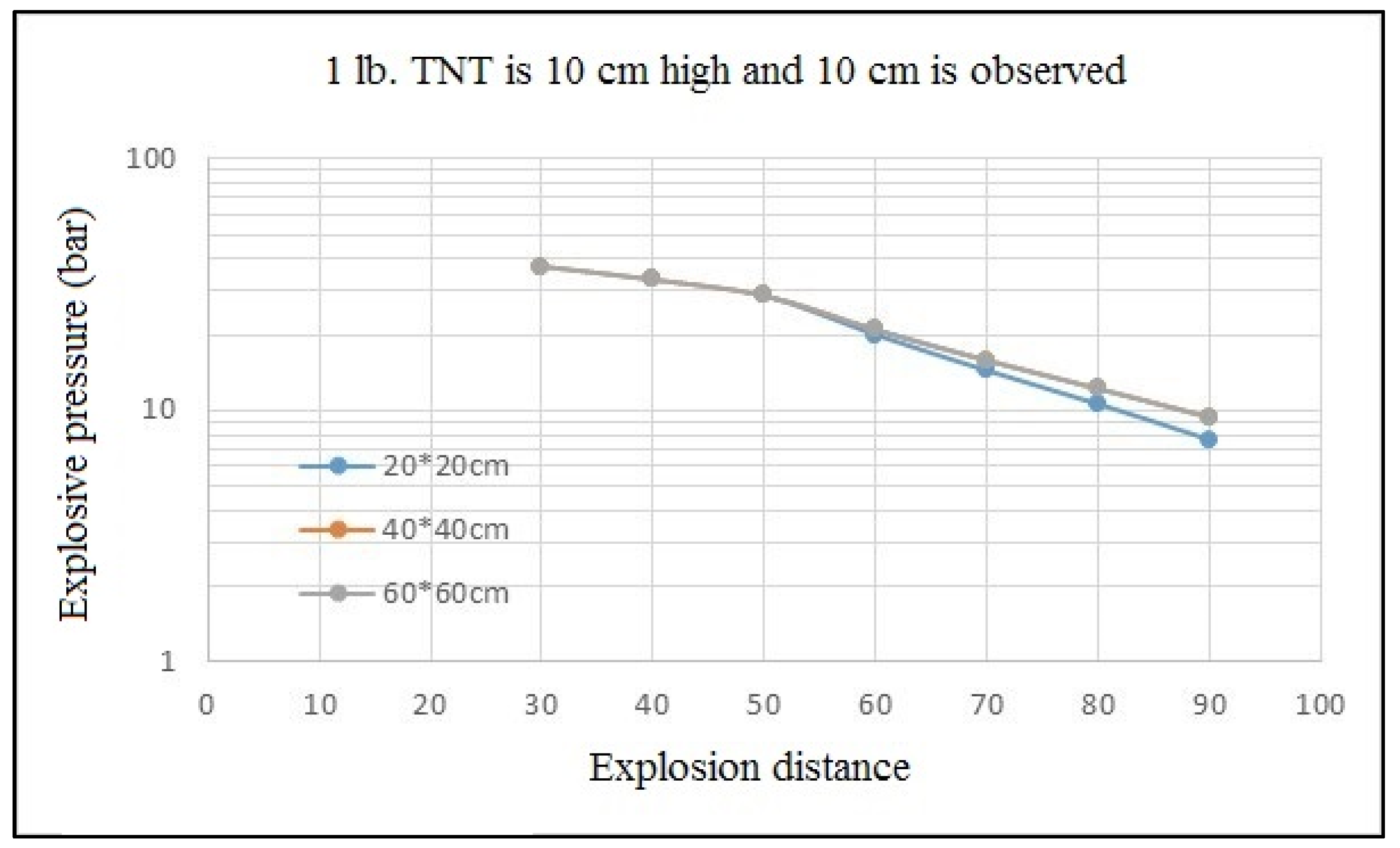
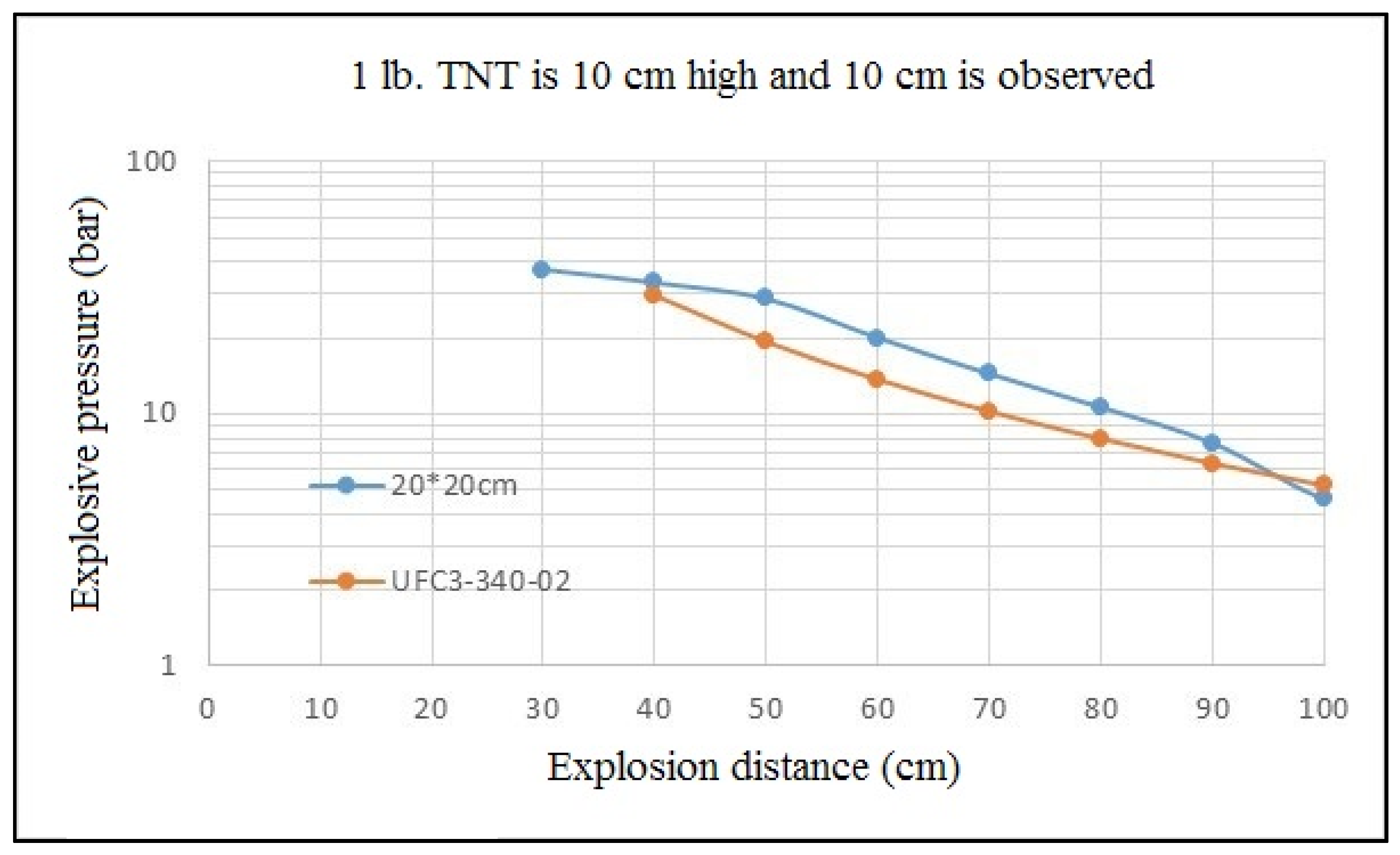
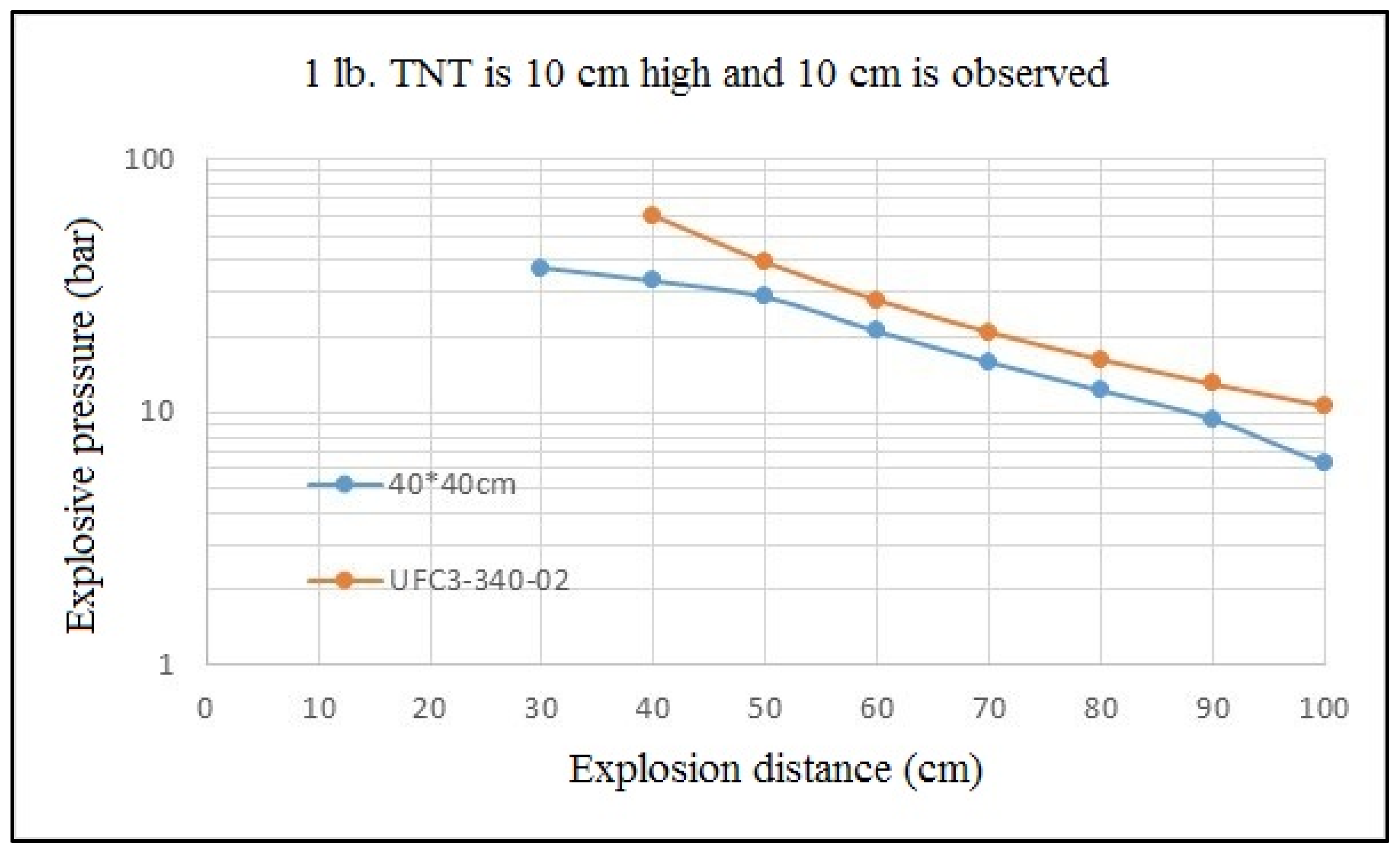
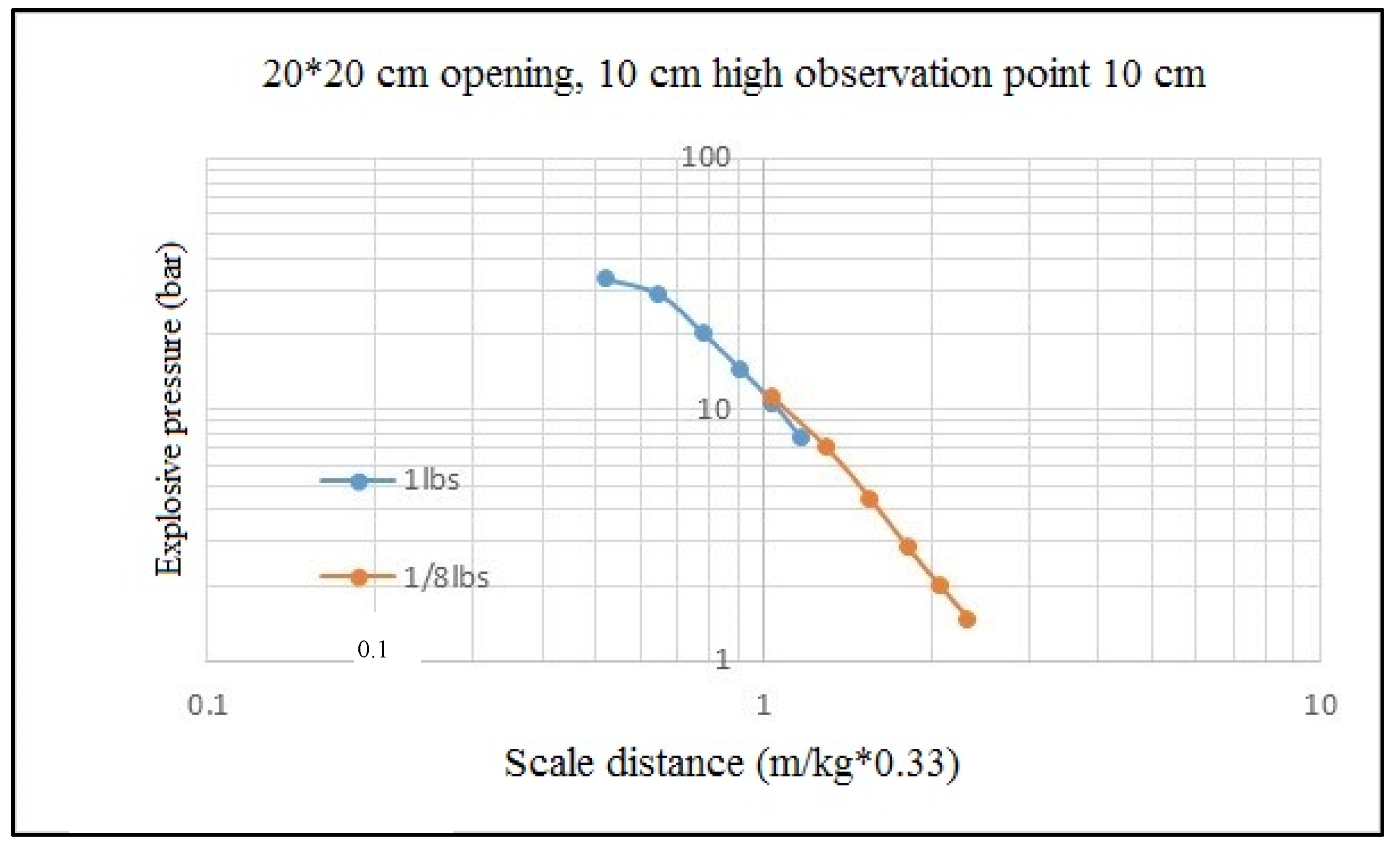
4.1. Impact of Vent Opening Size
4.2. Impact of the Location of Vent Opening
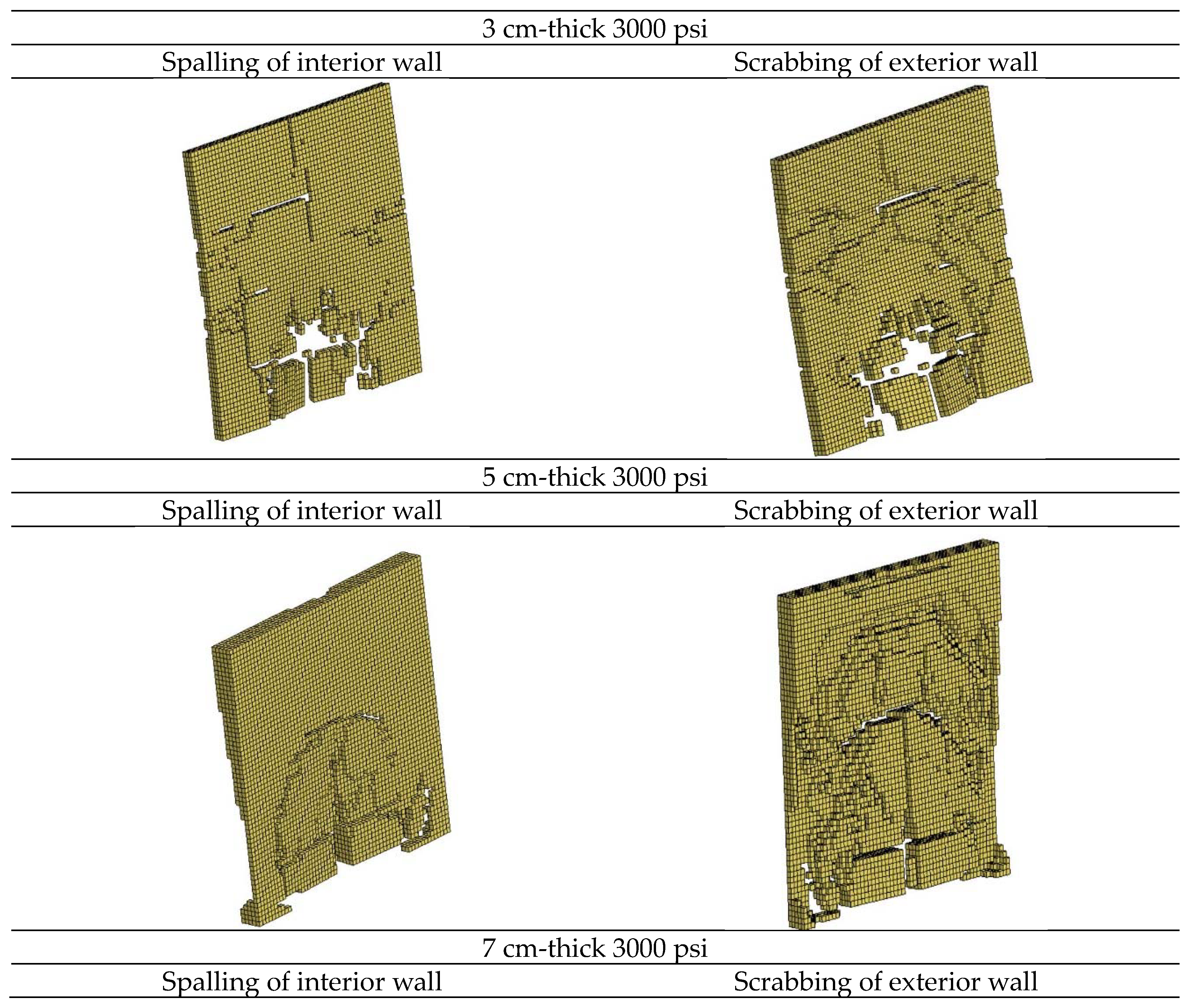
4.3. Impact of the Thickness of a Fragile Wall
4.4. Impact of the Strength of Fragile Wall
5. Conclusions and Suggestions
- I.
- Vent opening size has an impact on leakage pressure. The assessment method in the current UFC3-340-02 Specification is close to the computer simulation value, and thus, it can be applied in design. Leakage pressure is low and the internal impulse is large if the vent opening is small; with an increasing vent opening size, the leakage pressure increases and the internal impulse decreases; however, at the ideal vent opening size, leakage pressure does not increase.
- II.
- Vent opening location has an impact on leakage pressure. While the assessment method in the current UFC3-340-02 Specification is not available, the computer simulation is applicable instead. Where the blast point is beyond the range of the vent opening, the leakage decreases; thus, it would be relatively conservative when the effect is ignored in design.
- III.
- The thickness of the concrete wall has an impact on leakage pressure, as the blast energy will be absorbed by the wall. While the assessment method in the current UFC3-340-02 Specification is not available, the computer simulation is applicable instead. The accuracy of this simulation result should be subject to further validation through experiments. The thickness of the wall has an impact on vent opening size; when thickness is small, the resistance of the wall is small; when the vent opening size is small, leakage pressure is low, but the internal impulse is large. With increasing wall thickness, while the vent opening size and leakage pressure increase, the internal impulse decreases. However, at the ideal thickness, the vent opening decreases while the leakage pressure decreases. At an excessive wall thickness, there is no vent opening and no leakage pressure.
- IV.
- The strength of a concrete wall has an impact on leakage pressure, as the blast energy will be absorbed by the wall. While the assessment method in the current UFC3-340-02 Specification is not available, the computer simulation is applicable instead. However, the accuracy of the simulation result should be subject to further validation through experiments. While its behaviors are similar to the impact of the thickness of a wall, the impact of the strength of concrete is easily controlled due to the range limit of the strength of concrete.
Funding
Conflicts of Interest
References
- Department of Defense. Department of Defense Ammunition and Charge Safety Standards; Department of Defense: Washington, DC, USA, 2012.
- Keenan, W.A.; Tancreto, J.E. Design Criteria for Frangible Covers in Ordnance Facilities. In Proceedings of the Twentieth Department of Defense Safety Seminar, Norfolk, VA, USA, 24–26 August 1982. [Google Scholar]
- Wager, P.C. Yield, Line Analysis of Slabs with Covered Vents. In Proceedings of the 26th Department of Defense Explosives Safety Seminar, Miami, FL, USA, 16–18 August 1994. [Google Scholar]
- Department of Defense. Design and Analysis of Hardened Structures to Conventional Weapons Effects; UFC: Washington, DC, USA, 2002.
- Department of Defense. Structures to Resist the Effects of Accidental Blasts; UFC: Washington, DC, USA, 2014.
- Keenan, W.A.; Tancreto, J.E. Blast Environment from Fully and Partially Vented Blast in Cubicles. In US ARMY Report CEL-TR-828; DTIC: Fort Belvoir, VA, USA, 1975. [Google Scholar]
- Hokanson, J.C.; Esparza, E.D.; Baker, W.E.; Sandoval, N.R. Internal Blast Measurements in a Model of the Pantex Damaged Weapons Facility. In Proceedings of the Twentieth Department of Defense Safety Seminar, Norfolk, VA, USA, 24–26 August 1982. [Google Scholar]
- Tancreto, J.E.; Zehrt, W.H., Jr. Design for Internal Quasi-Static Pressures from Partially Confined Blasts. In Proceedings of the 28th Department of Defense Explosives Safety Seminar, Orlando, FL, USA, 18–20 August 1998. [Google Scholar]
- Chen, H.C. Applications of Arbitrary Lagrangian-Eulerian in Confined Blast Simulation. Master’s Thesis, Chung Cheng Institute of Technology, National Defense University, Taoyuan, Taiwan, 2008. [Google Scholar]
- Chung, C.N. Experiment and Numerical Simulation of External Tunnel Blast. Master’s Thesis, Chung Cheng Institute of Technology, National Defense University, Taoyuan, Taiwan, 2011. [Google Scholar]
- Hung, C.W. Prediction Model of Airblast Pressure for Ammunition depot Subjected to Near-Field Blast. Ph.D. Thesis, Chung Cheng Institute of Technology, National Defense University, Taoyuan, Taiwan, 2012. [Google Scholar]
- Pi, S.R. Experimental and Numerical Analyses of Underground Command Center Subjected to Near-Field Blast. Ph.D. Thesis, Chung Cheng Institute of Technology, National Defense University, Taoyuan, Taiwan, 2015. [Google Scholar]
- Hallquist, J.O. LS-DYNA Version 971 Theory’s Manual; Livermore Software Technology Corporation: Livermore, CA, USA, 2006; pp. 1–680. [Google Scholar]
- Haufe, A.; Weimar, K.; Gohner, U. Advanced Airbag Simulation Using Fluid-Structure-Interaction and the Eulerian Method in LS-DYNA; DYNAmore Gmbh: Deutschland, Germany, 2004. [Google Scholar]
- Gebbeken, N.; Ruppert, M. On the Safety and Reliability of High Dynamic Hydrocode Simulations. Int. J. Numer. Methods Eng. 1999, 46, 839–851. [Google Scholar] [CrossRef]
- Cheng, D.S.; Hung, C.W.; Pi, S.J. Numerical Simulation of Near-Field Blast. J. Appl. Sci. Eng. 2013, 16, 61–67. [Google Scholar]
- Schwer, L.E.; Malvar, L.J. Simplified concrete modeling with *MAT_ Concrete_ Damage_ Rel3. In JRI LS-Dyna User Week; Roadsafe LLC: Livermore, CA, USA, 2005. [Google Scholar]
- Akers, S.; Weed, R.; Rickman, D.; Danielson, K. Numerical simulations of explosive wall breaching. In Proceedings of the Users Group Conference, Nashville, TN, USA, 27–30 June 2005. [Google Scholar]





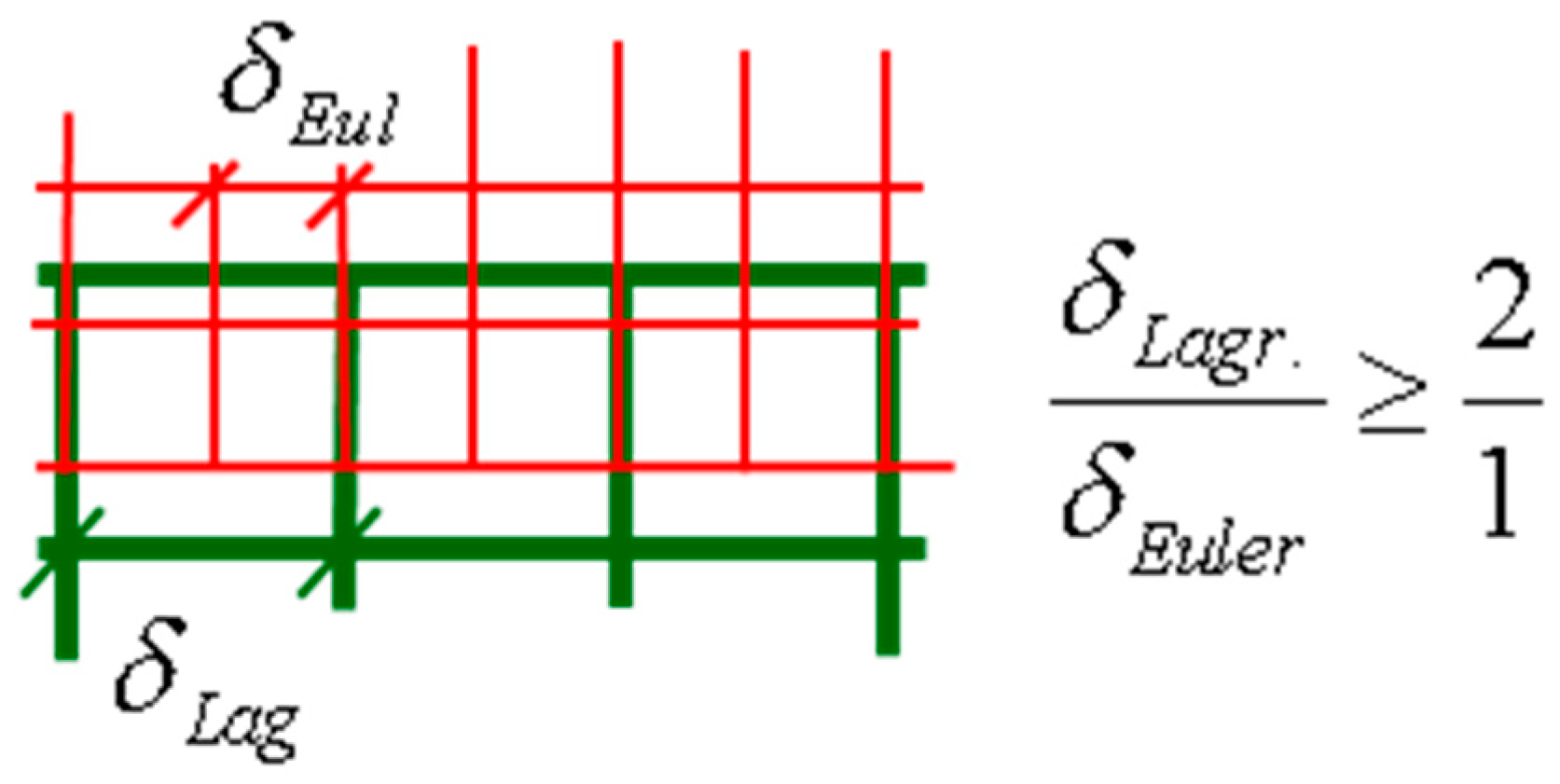



| h/H | l/L | Average Peak Reflected Pressure | Scaled Average Unit Reflected Impulse | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Number of Adjacent Reflecting Surfaces | |||||||||
| One | Two | Three | Four | One | Two | Three | Four | ||
| 0.10 | 0.10 | 2-52 | 2-64 | 2-80 | 2-92 | 2-101 | 2-113 | 2-129 | 2-141 |
| 0.25 | 2-53 | 2-65 | 2-81 | 2-93 | 2-102 | 2-114 | 2-130 | 2-142 | |
| 0.50 | 2-54 | 2-66 | 2-82 | 2-94 | 2-103 | 2-115 | 2-131 | 2-143 | |
| 0.75 | 2-53 | 2-67 | 2-81 | 2-93 | 2-102 | 2-116 | 2-130 | 2-142 | |
| 0.25 | 0.10 | 2-55 | 2-68 | 2-83 | 2-95 | 2-104 | 2-117 | 2-132 | 2-144 |
| 0.25 | 2-56 | 2-69 | 2-84 | 2-96 | 2-105 | 2-118 | 2-133 | 2-145 | |
| 0.50 | 2-57 | 2-70 | 2-85 | 2-97 | 2-106 | 2-119 | 2-134 | 2-146 | |
| 0.75 | 2-56 | 2-71 | 2-84 | 2-96 | 2-105 | 2-120 | 2-133 | 2-145 | |
| 0.50 | 0.10 | 2-58 | 2-72 | 2-86 | 2-98 | 2-107 | 2-121 | 2-135 | 2-147 |
| 0.25 | 2-59 | 2-73 | 2-87 | 2-99 | 2-108 | 2-122 | 2-136 | 2-148 | |
| 0.50 | 2-60 | 2-74 | 2-88 | 2-100 | 2-109 | 2-123 | 2-137 | 2-149 | |
| 0.75 | 2-59 | 2-75 | 2-87 | 2-99 | 2-108 | 2-124 | 2-136 | 2-148 | |
| 0.75 | 0.10 | 2-61 | 2-76 | 2-89 | 2-95 | 2-110 | 2-125 | 2-138 | 2-144 |
| 0.25 | 2-62 | 2-77 | 2-90 | 2-96 | 2-111 | 2-126 | 2-139 | 2-145 | |
| 0.50 | 2-63 | 2-78 | 2-91 | 2-97 | 2-112 | 2-127 | 2-140 | 2-146 | |
| 0.75 | 2-62 | 2-79 | 2-90 | 2-96 | 2-111 | 2-128 | 2-139 | 2-145 | |
| 1.4 | 1 | 1.29 | 0.7165 | 273.15 | 0 | |
| 288.15 | ||||||
| 1000 | ||||||
| 2000 | ||||||
| 3000 |
| Input values of air material and state equation (Unit = cm, g, μs, Mbar) | ||||||||
| Mat_Null (Air) | ||||||||
| Ro | Pc | Mu | Terod | Cerod | Ym | Pr | ||
| 0.00129 | - | 1.79 × 10−10 | - | - | - | - | ||
| Eos_Linear_Polynomial (State equation of air) | ||||||||
| C0 | C1 | C2 | C3 | C4 | C5 | C6 | E0 | V0 |
| −5.46 × 10−8 | 0 | 0 | 0 | 0.4 | 0.4 | 0 | 2.67 × 10−6 | 1 |
| Input values of TNT charge material and state equation (Unit = cm, g, μs, Mbar) | ||||||
| Mat_High_Explosive_Burn (Charge) | ||||||
| Ro | Dv | Pcj | Beta | K | G | Sigy |
| 1.63 | 0.693 | 0.21 | 0 | 0 | 0 | 0 |
| Eos_Jwl (State equation of charge) | ||||||
| A | B | R1 | R2 | Ω | Eo | Vo |
| 3.712 | 0.03231 | 4.15 | 0.95 | 0.3 | 0.070 | 1 |
| Parameter values of concrete (Unit = g, cm, μs, Mbar) | ||||
| Mat_Concrete_Damage_Rel3 | ||||
| Ro | Pr | A0 | Rsize | Ucf |
| 2.4 | 0.2 | −2.068 × 10−4 | 0.3973 | 1.45 × 107 |
| Strain Rate (1/μs) | Dynamic Amplification Coefficient | Strain Rate (1/μs) | Dynamic Amplification Coefficient |
|---|---|---|---|
| −3 × 10−2 | 9.70 | 3 × 10−11 | 1.00 |
| −3 × 10−4 | 9.70 | 1 × 10−10 | 1.03 |
| −1 × 10−4 | 6.72 | 1 × 10−09 | 1.08 |
| −3 × 10−5 | 4.50 | 1 × 10−08 | 1.14 |
| −1 × 10−5 | 3.12 | 1 × 10−07 | 1.20 |
| −3 × 10−6 | 2.09 | 1 × 10−06 | 1.26 |
| −1 × 10−6 | 1.45 | 3 × 10−06 | 1.29 |
| −1 × 10−7 | 1.36 | 1 × 10−05 | 1.33 |
| −1 × 10−8 | 1.28 | 3 × 10−05 | 1.36 |
| −1 × 10−9 | 1.20 | 1 × 10−04 | 2.04 |
| −1 × 10−10 | 1.13 | ||
| −1 × 10−11 | 1.06 | ||
| 0.00 | 1.00 |
| Parameter values of ground (Unit= g, cm, μs, Mbar) | ||
| MAT_Rigid | ||
| Ro | E | Rr |
| 1.8 | 1.916 × 10−3 | 0.3 |
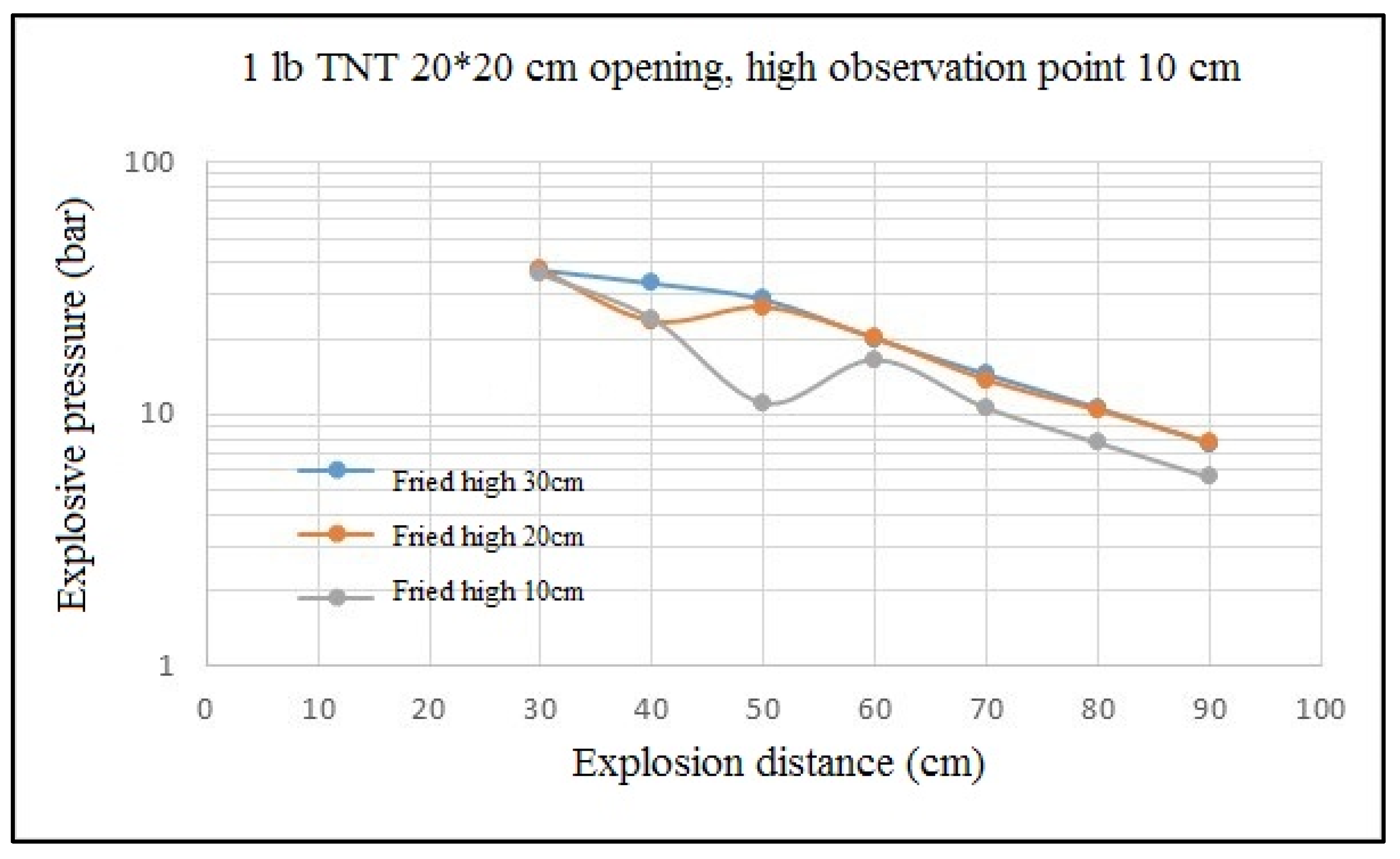
| Distance from Blast Point | 1-Pound TNT–20 × 20 cm Vent Opening Model (Blast Height 10 cm) | |||||
|---|---|---|---|---|---|---|
| Observation Point Height | ||||||
| 10 cm | 20 cm | 30 cm | ||||
| Blast Pressure Bar | Impulse Bar, ms | Blast pressure Bar | Impulse Bar, ms | Blast Pressure Bar | Impulse Bar, ms | |
| 30 cm | 37.4 | 0.799 | -- | -- | -- | -- |
| 40 cm | 33.1 | 1.990 | 17.3 | 0.601 | 5.24 | 0.320 |
| 50 cm | 28.6 | 2.420 | 13.2 | 1.470 | 6.7 | 0.489 |
| 60 cm | 20 | 1.610 | 15 | 1.060 | 8.89 | 0.771 |
| 70 cm | 14.4 | 1.120 | 11.2 | 1.000 | 7.7 | 0.921 |
| 80 cm | 10.6 | 1.110 | 8.7 | 1.070 | 6.6 | 0.939 |
| 90 cm | 7.65 | 1.230 | 6.63 | 1.410 | 5.36 | 1.140 |
| Center of the side wall of the ammunition depot | Center of the back wall of the ammunition depot | Center of the roof of the ammunition depot | ||||
| Blast pressure bar | Impulse bar, ms | Blast pressure bar | Impulse bar, ms | Blast pressure bar | Impulse bar, ms | |
| 128 | 36.717 | 119 | 36.227 | 59 | 13.748 | |
| Distance from Blast Point | 1-Pound TNT–40 × 40 cm vent Opening Model (Blast Height 10 cm) | |||||
|---|---|---|---|---|---|---|
| Observation Point Height | ||||||
| 10 cm | 20 cm | 30 cm | ||||
| Blast Pressure Bar | Impulse Bar, ms | Blast Pressure Bar | Impulse Bar, ms | Blast Pressure Bar | Impulse Bar, ms | |
| 30 cm | 37.4 | 0.782 | 38.7 | 0.919 | 35.3 | 1.040 |
| 40 cm | 33.1 | 1.900 | 23.9 | 1.060 | 22.7 | 1.100 |
| 50 cm | 28.6 | 1.711 | 16.2 | 1.660 | 15.4 | 1.230 |
| 60 cm | 20.9 | 1.650 | 19.9 | 2.180 | 11.2 | 2.080 |
| 70 cm | 15.8 | 1.900 | 14.6 | 2.150 | 13.8 | 2.070 |
| 80 cm | 12.2 | 2.050 | 11.6 | 1.970 | 10.7 | 1.860 |
| 90 cm | 9.4 | 1.850 | 9.1 | 1.880 | 8.58 | 1.840 |
| Center of the side wall of the ammunition depot | Center of the back wall of the ammunition depot | Center of the roof of the ammunition depot | ||||
| Blast pressure bar | Impulse bar, ms | Blast pressure bar | Impulse bar, ms | Blast pressure bar | Impulse bar, ms | |
| 128 | 30.010 | 119 | 35.502 | 39.8 | 9.592 | |
| Distance from Blast Point | 1-Pound TNT–Full Vent Model (Blast Height 10 cm) | |||||
|---|---|---|---|---|---|---|
| Observation Point Height | ||||||
| 10 cm | 20 cm | 30 cm | ||||
| Blast Pressure Bar | Impulse Bar, ms | Blast Pressure Bar | Impulse Bar, ms | Blast Pressure Bar | Impulse Bar, ms | |
| 30 cm | 37.4 | 0.903 | 38.7 | 0.927 | 35.3 | 0.995 |
| 40 cm | 33.1 | 1.920 | 23.9 | 1.060 | 22.7 | 1.100 |
| 50 cm | 28.6 | 1.720 | 16.2 | 1.660 | 15.4 | 1.220 |
| 60 cm | 20.9 | 1.640 | 19.9 | 1.820 | 11.3 | 1.670 |
| 70 cm | 15.8 | 1.760 | 14.6 | 1.680 | 13.8 | 2.570 |
| 80 cm | 12.2 | 2.660 | 11.6 | 2.830 | 10.7 | 3.100 |
| 90 cm | 9.4 | 2.720 | 9.1 | 3.100 | 8.6 | 3.390 |
| Center of the side wall of the ammunition depot | Center of the back wall of the ammunition depot | Center of the roof of the ammunition depot | ||||
| Blast pressure bar | Impulse bar, ms | Blast pressure bar | Impulse bar, ms | Blast pressure bar | Impulse bar, ms | |
| 127 | 19.193 | 118 | 22.415 | 26.4 | 4.382 | |
| Distance from Blast Point | 1-Pound TNT–20 × 20 cm Vent Opening Model (Blast Height 20 cm) | |||||
|---|---|---|---|---|---|---|
| Observation Point Height | ||||||
| 10 cm | 20 cm | 30 cm | ||||
| Blast Pressure Bar | Impulse Bar, ms | Blast Pressure Bar | Impulse Bar, ms | Blast Pressure Bar | Impulse Bar, ms | |
| 30 cm | 37.5 | 0.886 | ---- | ---- | ---- | ----- |
| 40 cm | 23.5 | 0.588 | 12.7 | 0.460 | 3.65 | 1.100 |
| 50 cm | 26.7 | 1.990 | 9.9 | 0.650 | 4.18 | 0.862 |
| 60 cm | 20.1 | 1.140 | 11.2 | 0.807 | 4.86 | 0.891 |
| 70 cm | 13.7 | 1.130 | 9.6 | 0.839 | 6.27 | 0.895 |
| 80 cm | 10.4 | 1.220 | 7.76 | 1.270 | 5.58 | 1.020 |
| 90 cm | 7.74 | 1.250 | 6.38 | 1.180 | 4.86 | 0.932 |
| Center of the side wall of the ammunition depot | Center of the back wall of the ammunition depot | Center of the roof of the ammunition depot | ||||
| Blast pressure bar | Impulse bar, ms | Blast pressure bar | Impulse bar, ms | Blast pressure bar | Impulse bar, ms | |
| 173 | 43.127 | 115 | 42.364 | 58.8 | 11.476 | |
| Distance from Blast Point | 1-Pound TNT–20 × 20 cm Vent Opening Model (Blast Height 30 cm) | |||||
|---|---|---|---|---|---|---|
| Observation Point Height | ||||||
| 10 cm | 20 cm | 30 cm | ||||
| Blast Pressure Bar | Impulse Bar, ms | Blast Pressure Bar | Impulse Bar, ms | Blast Pressure Bar | Impulse Bar, ms | |
| 30 cm | 36 | 1.630 | ---- | --- | --- | ---- |
| 40 cm | 24 | 0.905 | 8.49 | 0.331 | 3.95 | 0.273 |
| 50 cm | 11.1 | 1.110 | 6.12 | 0.937 | 2.7 | 1.280 |
| 60 cm | 16.5 | 1.050 | 6.8 | 1.200 | 5.83 | 1.150 |
| 70 cm | 10.6 | 1.010 | 7.9 | 1.130 | 5.03 | 0.967 |
| 80 cm | 7.7 | 1.410 | 6.2 | 1.150 | 4.48 | 0.876 |
| 90 cm | 5.62 | 1.420 | 4.79 | 1.130 | 3.81 | 0.921 |
| Center of the side wall of the ammunition depot | Center of the back wall of the ammunition depot | Center of the roof of the ammunition depot | ||||
| Blast pressure bar | Impulse bar, ms | Blast pressure bar | Impulse bar, ms | Blast pressure bar | Impulse bar, ms | |
| 181 | 47.611 | 121 | 46.490 | 174 | 15.025 | |
| 1-Pound TNT Blast Point 10 cm from 3000 psi Concrete Wall, Blast Height 10 cm Unit: Bar | |||
|---|---|---|---|
| Wall thickness 3 cm | |||
| Distance behind the wall | Measurement height 10 cm | Measurement height 20 cm | Measurement height 30 cm |
| 7 cm | 5.27 | 2.93 | 4.95 |
| 17 cm | 3.93 | 2.88 | 3.31 |
| 27 cm | 1.38 | 1.21 | 1.09 |
| Wall thickness 5 cm | |||
| Distance behind the wall | Measurement height 10 cm | Measurement height 20 cm | Measurement height 30 cm |
| 5 cm | 7.84 | 3.2 | 1.88 |
| 15 cm | 5.71 | 3.58 | 3.81 |
| 25 cm | 2.85 | 1.41 | 0.88 |
| Wall thickness 7 cm | |||
| Distance behind the wall | Measurement height 10 cm | Measurement height 20 cm | Measurement height 30 cm |
| 3 cm | 2.91 | 1.2 | 1.22 |
| 13 cm | 3.33 | 1.98 | 1.32 |
| 23 cm | 1.26 | 0.78 | 0.8 |
| 1-Pound TNT Blast Point 10 cm from Concrete Wall, 5 cm-Thick Wall, Blast Height 10 cm Unit: Bar | |||
|---|---|---|---|
| 3000 psi | |||
| Distance behind the wall | Measurement height 10 cm | Measurement height 20 cm | Measurement height 30 cm |
| 5 cm | 7.84 | 3.2 | 1.88 |
| 15 cm | 5.71 | 3.58 | 3.81 |
| 25 cm | 2.85 | 1.41 | 0.88 |
| 4500 psi | |||
| Distance behind the wall | Measurement height 10 cm | Measurement height 20 cm | Measurement height 30 cm |
| 5 cm | 7.47 | 3.79 | 2.06 |
| 15 cm | 5.98 | 3.91 | 2.75 |
| 25 cm | 2.87 | 1.43 | 0.89 |
| 6000 psi | |||
| Distance behind the wall | Measurement height 10cm | Measurement height 20cm | Measurement height 30cm |
| 5 cm | 5.91 | 3.03 | 2.0 |
| 15 cm | 5.53 | 3.67 | 2.66 |
| 25 cm | 2.53 | 1.32 | 0.81 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lai, H.-h. Applicability of a Design Assessment and Management for the Current Ammunition Depots in Taiwan. Appl. Sci. 2020, 10, 1041. https://doi.org/10.3390/app10031041
Lai H-h. Applicability of a Design Assessment and Management for the Current Ammunition Depots in Taiwan. Applied Sciences. 2020; 10(3):1041. https://doi.org/10.3390/app10031041
Chicago/Turabian StyleLai, Hsin-hung. 2020. "Applicability of a Design Assessment and Management for the Current Ammunition Depots in Taiwan" Applied Sciences 10, no. 3: 1041. https://doi.org/10.3390/app10031041
APA StyleLai, H.-h. (2020). Applicability of a Design Assessment and Management for the Current Ammunition Depots in Taiwan. Applied Sciences, 10(3), 1041. https://doi.org/10.3390/app10031041





