1. Introduction
Electromagnetic technology has a wide range of applications in various fields. Nasim (2019) proposed a metamaterial platform for solving integral equations using a monochromatic electromagnetic field [
1]. The application of electromagnetic technology in medical diagnosis equipment realizes the measurement of blood glucose and the detection of cancer stage [
2,
3]. In addition, it is necessary to consider electromagnetic fields in plasma electronics [
4,
5].
Here, we apply electromagnetic technology to geophysics. Grounded electrical-source airborne transient electromagnetic (GREATEM) is a useful detection geophysical method where the transmitter is set on the ground and the receiver is installed on the aircraft [
6]. Combining the ground and airborne electromagnetic systems, GREATEM has the advantages of large detection depth, high resolution, wide range, and fast speed. In particular, it has unique superiority in mountains, forest-covered areas, swamps, and other special areas [
7,
8]. Ji (2013) used an airship as the carrier and the two-dimensional finite difference method to calculate the time-domain GREATEM response with a long wire source [
9]. Ren (2017) investigated a three-dimensional time-domain airborne electromagnetic model based on the finite volume method, and then used the strategy of separating the primary field from the secondary field, which significantly saved on calculation time [
10]. For airborne transient electromagnetic measurement, a three-dimensional forward simulation method which considered attitude change was proposed, and the electromagnetic response of a shallow surface was analyzed in Reference [
11]. Later, the spectral element method (SE) was used to carry out three-dimensional modeling of GREATEM, effectively improving the modeling accuracy [
12].
To interpret GREATEM, researchers often make the assumption that the earth is just conductive or resistive. However, there is an induced polarization (IP)effect in the earth, which is usually reflected as a reverse signal. The existence of the IP effect has a great impact on the electromagnetic response [
13,
14]. The IP effect is related to conductivity and frequency, and its dispersion characteristics can be expressed by the Debye model and the Cole–Cole model [
15,
16]. At present, numerical simulations of the polarization effect are mainly conducted in the frequency domain. Most of the early studies simulated the IP effect by converting the electromagnetic field from the frequency domain to the time domain [
17,
18]. Unfortunately, when broadband frequency content is considered, the methods are not so efficient [
19]. In order to simulate the IP effect in the time domain, Kang (2015) proposed a method to generate a three-dimensional pseudo charge distribution using airborne time-domain electromagnetic data and effectively extracted the polarization signal [
20]. Wu (2017) used the FDTD (finite difference time-domain) method to simulate the IP effect with a small loop source [
21]. Commer (2017) expanded the finite difference time-domain scheme, modeled and analyzed the IP effect, and developed a simple calculation of the Cole–Cole model [
22].
However, three-dimensional (3D) numerical simulations of IP effects based on FDTD require a high computation load, when including the air layer. In addition, it is difficult to calculate the source in the FDTD method; thus, the upward continuation method is often used to avoid directly loading the emission source. Mittet (2010) put forward the theory of wave field transformation and successfully applied it to marine CSEM (controllable source electromagnetic method), increasing the calculation efficiency by nearly 10-fold [
23]. Mittet (2018) used the least squares fitting method to calculate the IP response of sea water in the fictitious wave field [
24]. Ji (2017) improved the emission source, applied the wave field transformation method to the ground transient electromagnetic simulation, and realized a three-dimensional transient electromagnetic numerical simulation including the air layer [
25]. However, it did not consider the IP effect of the earth. Therefore, here, we perform the wave field transformation in GREATEM, and we realize a three-dimensional numerical simulation in polarizable media using the Cole–Cole model. In addition, the computing efficiency is also improved.
The wave field transformation method is proposed for the grounded electrical-source airborne transient electromagnetic system in this paper. The Maxwell equations in the real diffusion field are transformed into the fictitious wave field by using the transformation relationship between the diffusion field and fictitious wave field. The fractional order Cole–Cole model is introduced into the fictitious wave field, and the Maxwell equations with the Cole–Cole model are solved using the finite difference time-domain method. Finally, an integral transformation method is used to transform the calculation results back to the real diffusion field. In the case of including polarized media, the two-field numerical simulation of the induction field and polarization field is realized. In addition, the computing efficiency is also improved.
2. Wave Field Transformation Theory Based on Fractional-Order Cole–Cole Model
2.1. Transformation from Real Diffusion Field to Fictitious Wave Field
The Maxwell equation in the frequency domain of the real diffusion field is written as follows:
where E and H are the electric and magnetic fields in the real diffusion field, respectively, J denotes the current density, and K denotes the magnetic current density.
is the angular frequency,
is permeability tensor, and σ is conductivity, while x is the direction.
The IP effect can be described by the Cole–Cole model [
16].
where
is the conductivity corresponding to infinite frequency,
is the characteristic time constant, and c and
are the frequency dependence and chargeability, respectively.
Applying Equation (3) to the frequency-domain Maxwell equation (Equation (1)), we can get
A fictitious dielectric constant is defined by the conductivity tensor (Mittet, 2010).
where
is the scaling parameter,
, and
is the fictitious dielectric permittivity tensor. Substituting Equation (5) into Equation (4), we can get
Multiplying both sides of Equation (6) by
gives
Equation (2) can be rewritten as
The relationship between the real diffusion field and fictitious wave field was given by Reference [
23].
where
is the scaling parameter,
is the angular frequency in the fictitious wave field,
and
are the current and magnetic current densities in the fictitious wave field, and
and
are the electric and magnetic fields in the fictitious wave domain.
Using Equations (9)–(13), Equations (7) and (8) can be written in terms of fictitious wave fields.
Because the appropriate kernel used to decompose the spectra is closer to a Cole–Cole function with an exponent c of 0.5 [
26], then
Assuming
, the time-domain expressions (Equations (16) and (17)) can be obtained through inverse Fourier transform.
By combining Equations (18) and (19), the electric and magnetic field x-components can be found as
where
Equation (22) can be solved by iteration, as shown in Equation (23).
where
, and the forward staggered time step is
.
2.2. Electrical Source Loading in Fictitious Wave Field
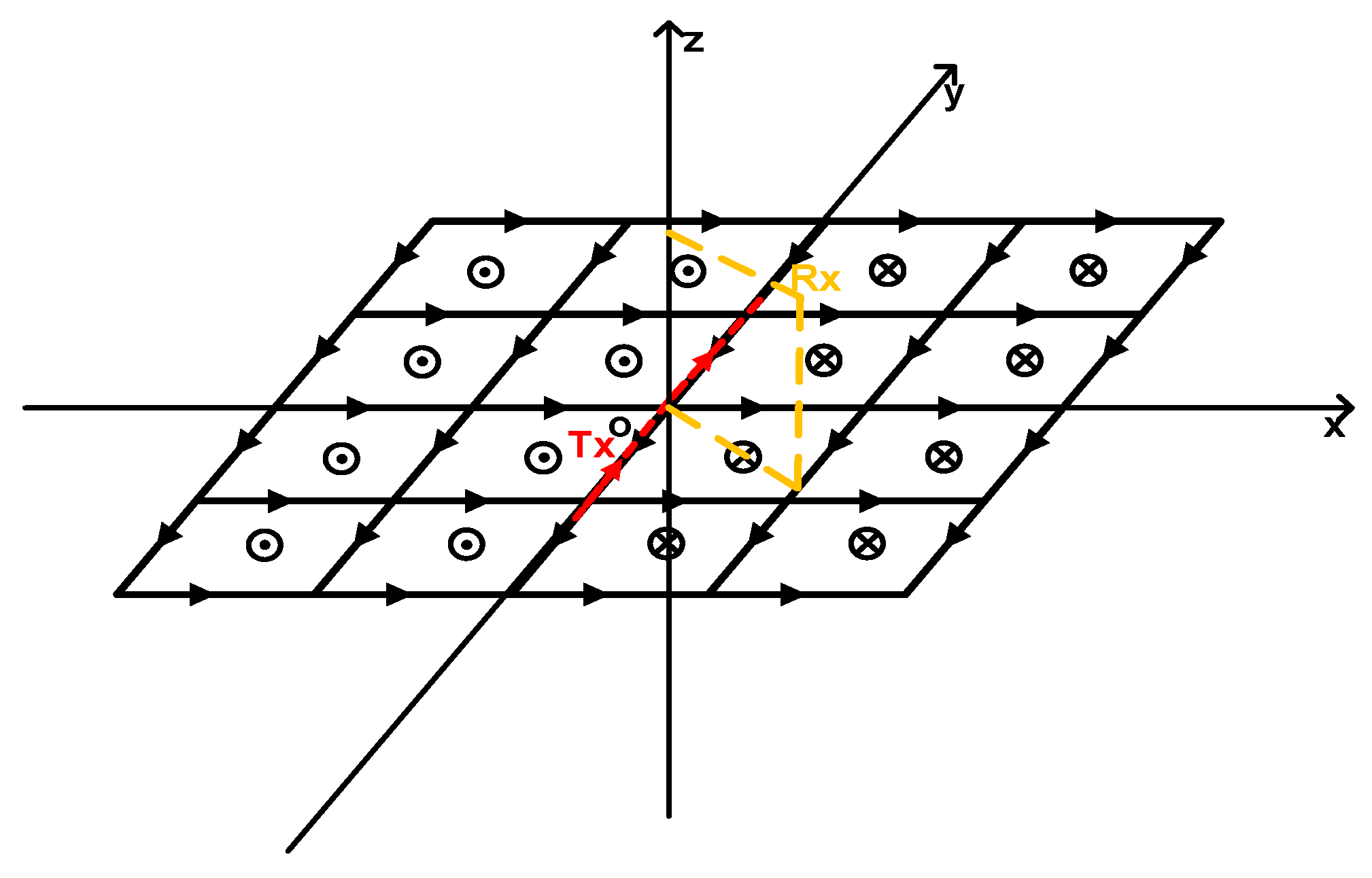
As shown in
Figure 1, Tx is the long wire source and Rx is the receiver. The fictitious emission source is only related to x- and y-components of the electric field, and the z-component is zero.
Here, the first-order Gaussian pulse is selected as the fictitious emitter, as shown in Equation (24).
where
,
is the maximum frequency in the fictitious wave field.
2.3. The Transformation from Fictitious Wave Field to Real Diffusion Field
It should be noted that the fictitious wave field is only used for the convenience of calculation, and it does not exist in reality. Therefore, we need to transform it back to the real diffusion field. The transformations are as follows [
23]:
where
is the total calculation time in the fictitious wave field, and
is the sample time.
2.4. Loading Complex Frequency Shifted Perfectly Matched Layer (CFS-PML) in Fictitious Wave Field
Roden (2000) proposed CFS-PML (complex frequency shifted perfectly matched layer) boundary conditions, which significantly saved on memory [
27]. The CFS-PML boundary conditions are introduced into the fictitious wave field to improve the absorption effect of the boundary on the low-frequency wave [
28].
In x-components, Maxwell’s curl equations are as follows:
It should be noted that is the imaginary unit in Maxwell equations, and i, j, and k are the three direction vectors of the coordinate system. , , and are the coordinate stretching factors, , , and . By setting , , we can get the original stretched coordinate metrics, which is the PML boundary condition.
Taking
as an example, and using Equations (29) and (30), we can get
Applying Laplace transform to (31) to the time domain, the iterative solution can be obtained.
On the boundary parameters,
and
, which depend on the relative positions of nodes and target areas, are not fixed, whereas
and
are two discrete variables.
where
indicates the intersection of the boundary and the target area boundary,
is the boundary thickness, and
is the polynomial parameter.
4. Calculation Results of the Three-Dimensional Chargeable Body Model
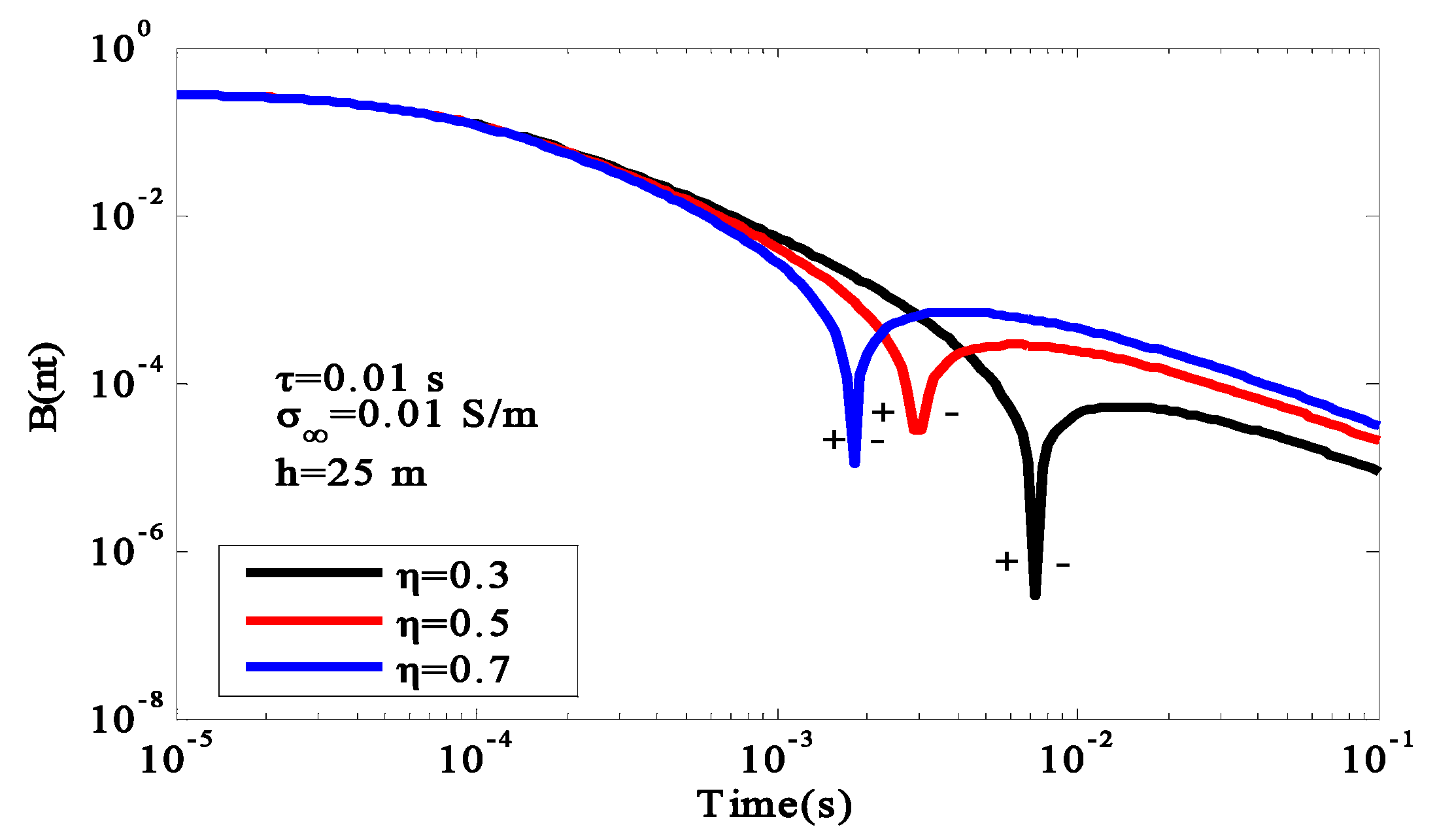
The phenomenon of the inverse sign (IP effect) often appears in GREATEM. Most researchers focused on the influence of the IP parameters. However, in addition to the IP parameters, the system parameters of GREATEM also have an impact on the IP effect. In this section, we mainly analyze the effect of the system parameters, and we provide a theoretical basis for the field measurements.
4.1. Forward Modeling Results of 3D Chargeable Body
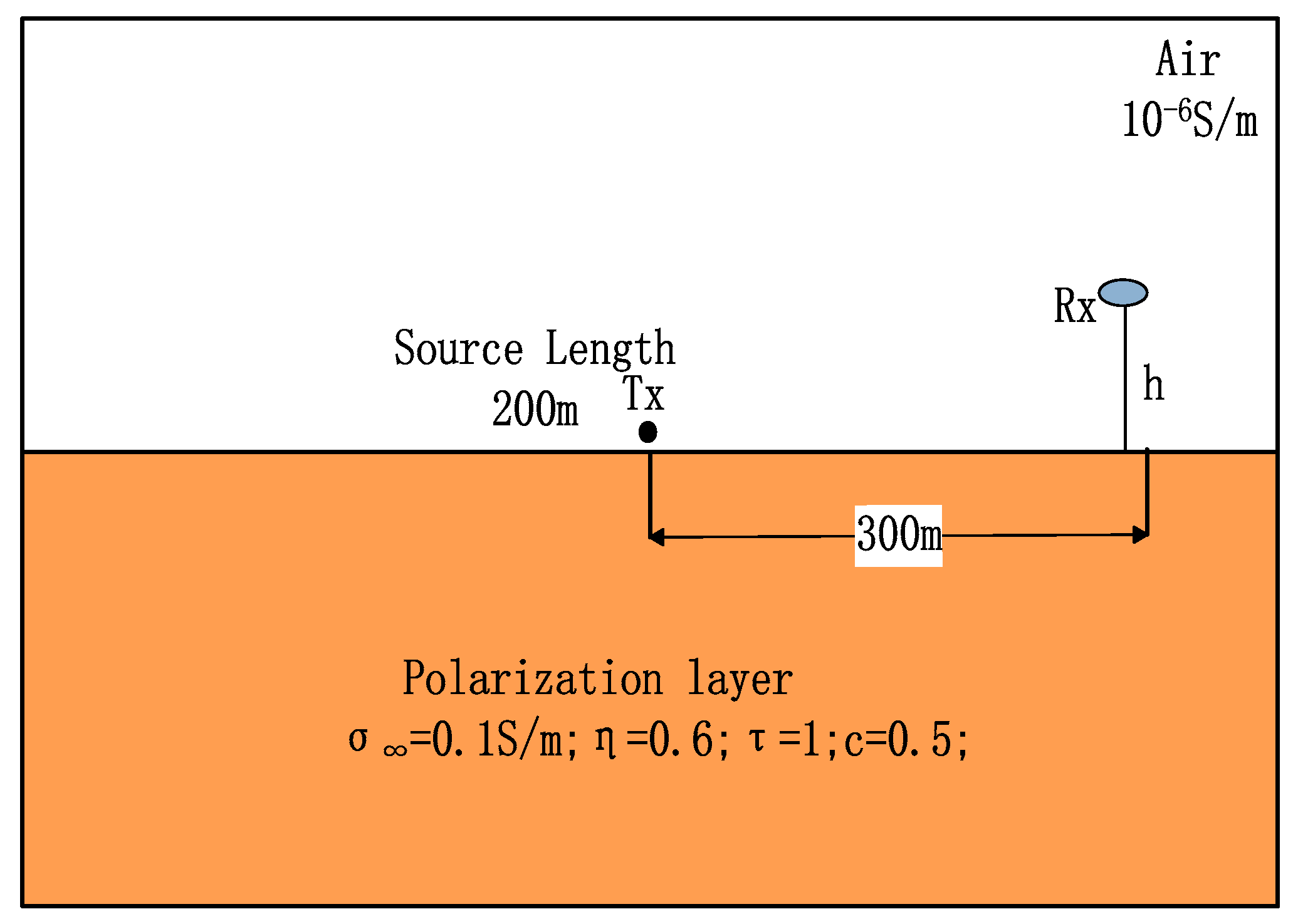
In order to analyze the influence of system parameters on the IP effect, we build a three-dimensional model with the consideration of a chargeable body, as shown in
Figure 8. The ground conductivity was
, the air layer conductivity was
, Tx was the long wire source, the length was
, Rx represents the receiving point, the height from the ground was
, and the offset distance was
. The dimensions of the chargeable body were
, which was 100 m below the surface. The model parameters of the chargeable body were selected as follows: chargeability
, frequency dependence
, and characteristic time constant
. The conductivities at infinite frequency were
,
, and
. The calculation results are shown in
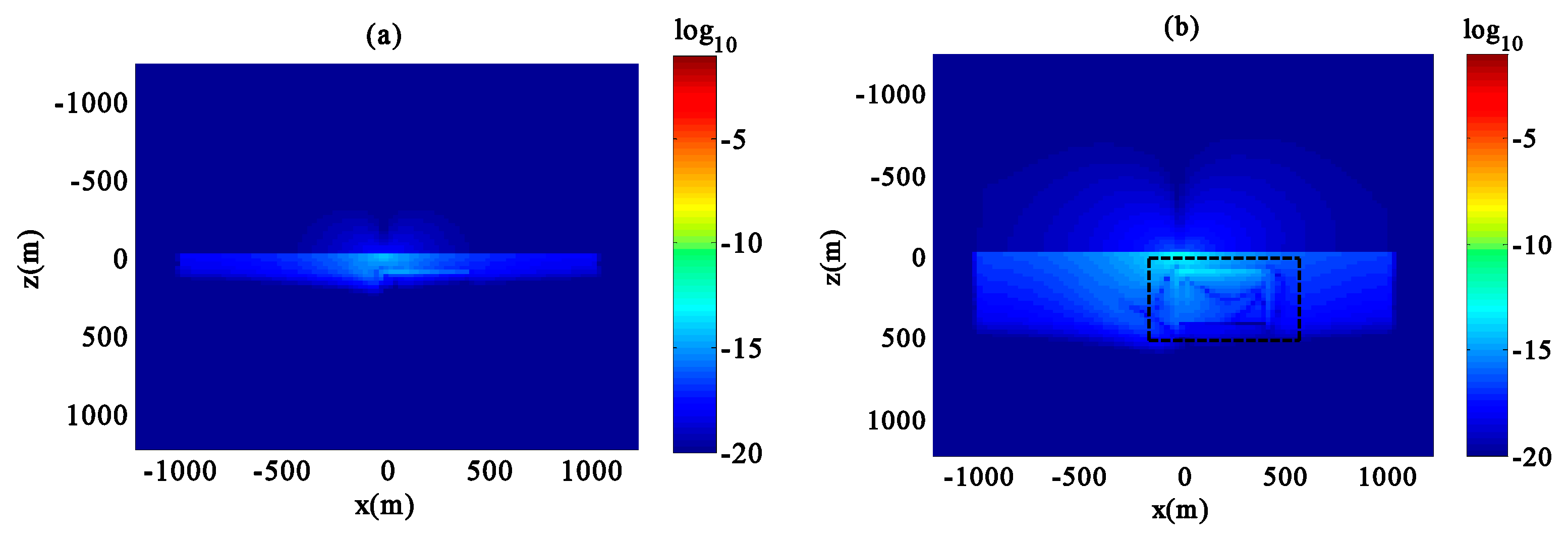
Figure 9. The snapshots of the induced current system in the fictitious wave field are shown in
Figure 10a,b.
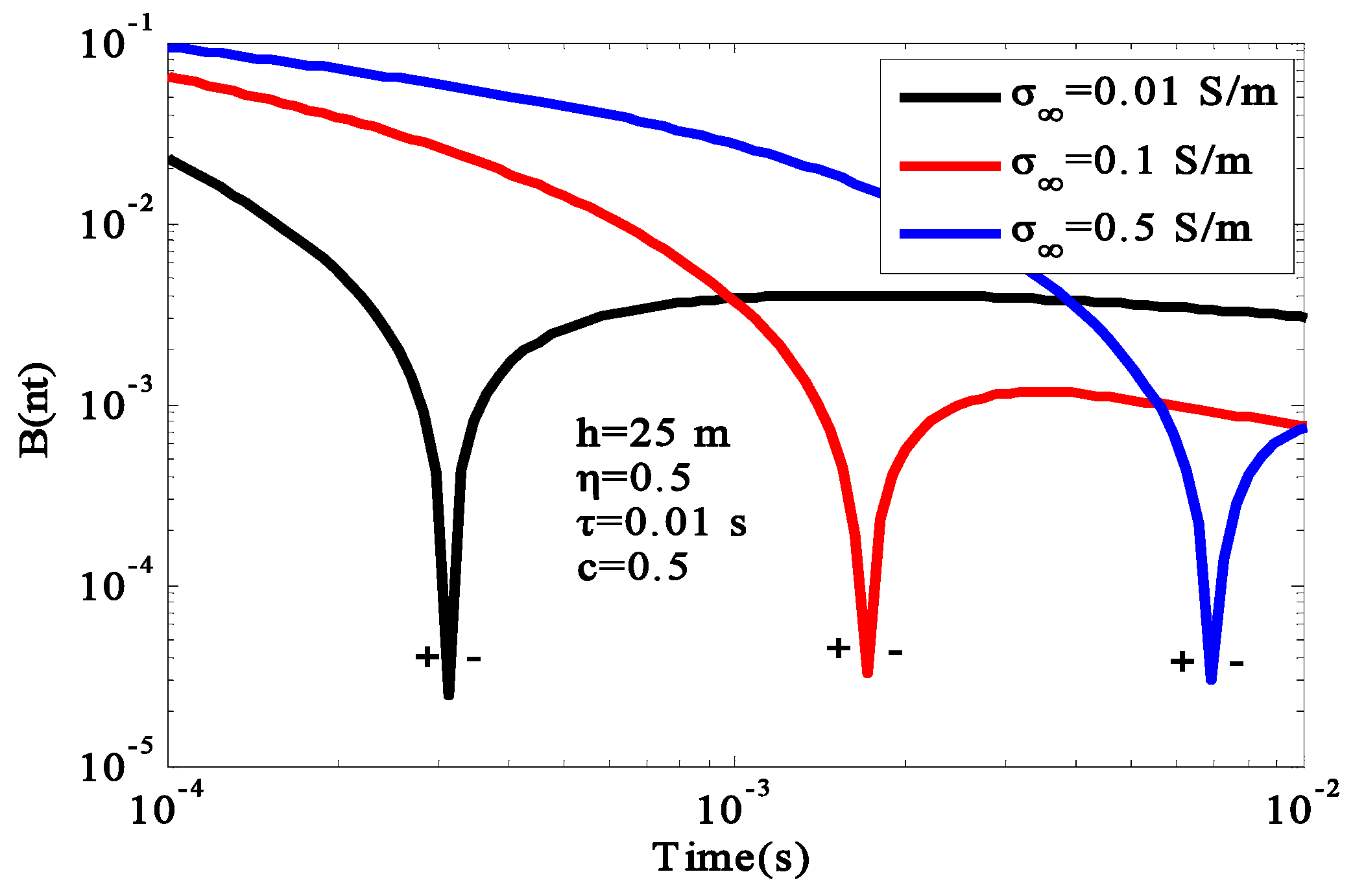
It can be seen from
Figure 9 that, with the increase in conductivity at the infinite frequency, the attenuation of the early induction field gradually decreased, the attenuation of the late IP response gradually quickened, and the occurrence time of the inverse sign gradually delayed. This is because the influence of the induction field of the low-resistance body was greater than that of the high-resistance body. Therefore, the second field decayed slowly, and the negative response appeared later. Thus, the polarization phenomenon was more easily observed on the high-resistance body. The chargeable body position can be clearly observed from
Figure 10, and the method of wave field transformation could effectively identify the polarizable body. Since we set the air layer as a finite high-resistance body, the conductivity was not zero, and the propagation of induced current in the air layer was not zero. In the fictitious wave field, due to the influence of the chargeable body, the propagation mode of the electromagnetic field changed, and it no longer propagated in the form of symmetry.
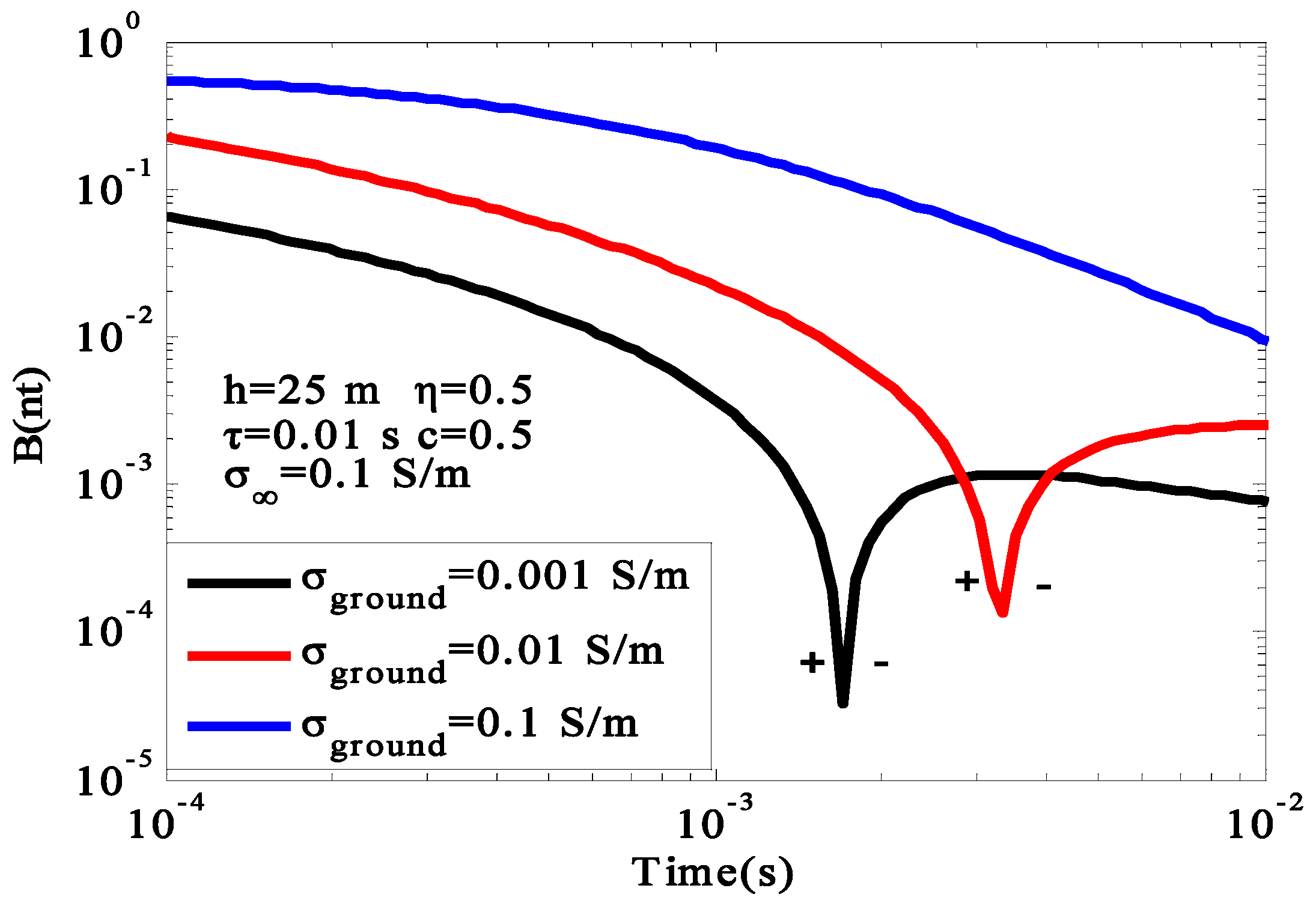
After setting
, as well as the ground conductivity
,
, and
, which are associated with high-, medium-, and low-resistance areas, the IP effects were calculated as shown in
Figure 11.
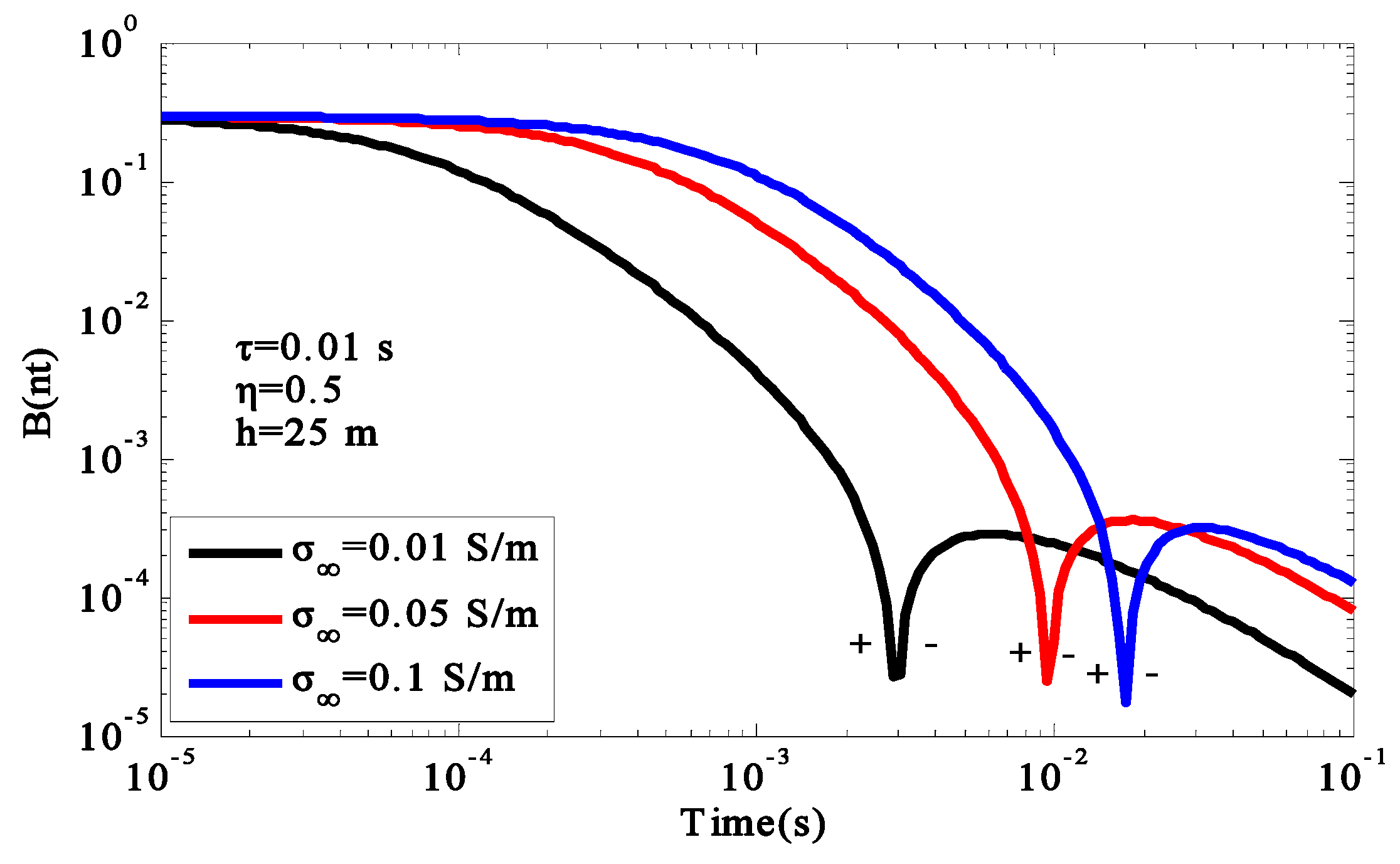
With the increase in ground conductivity, the amplitude of the early induction field and the late polarization field increased. In the high- and middle-resistance regions, the negative responses occurred at 1.7 ms and 3.3 ms. On the other hand, in the low-resistance region, the negative response could not be observed. When the negative value reached the minimum, the curve decayed approximately exponentially. The GREATEM had better resolution in the low-resistance region, but it is more suitable for the high-resistance region when measuring the IP effect.
4.2. The Influence of System Parameters on IP Response
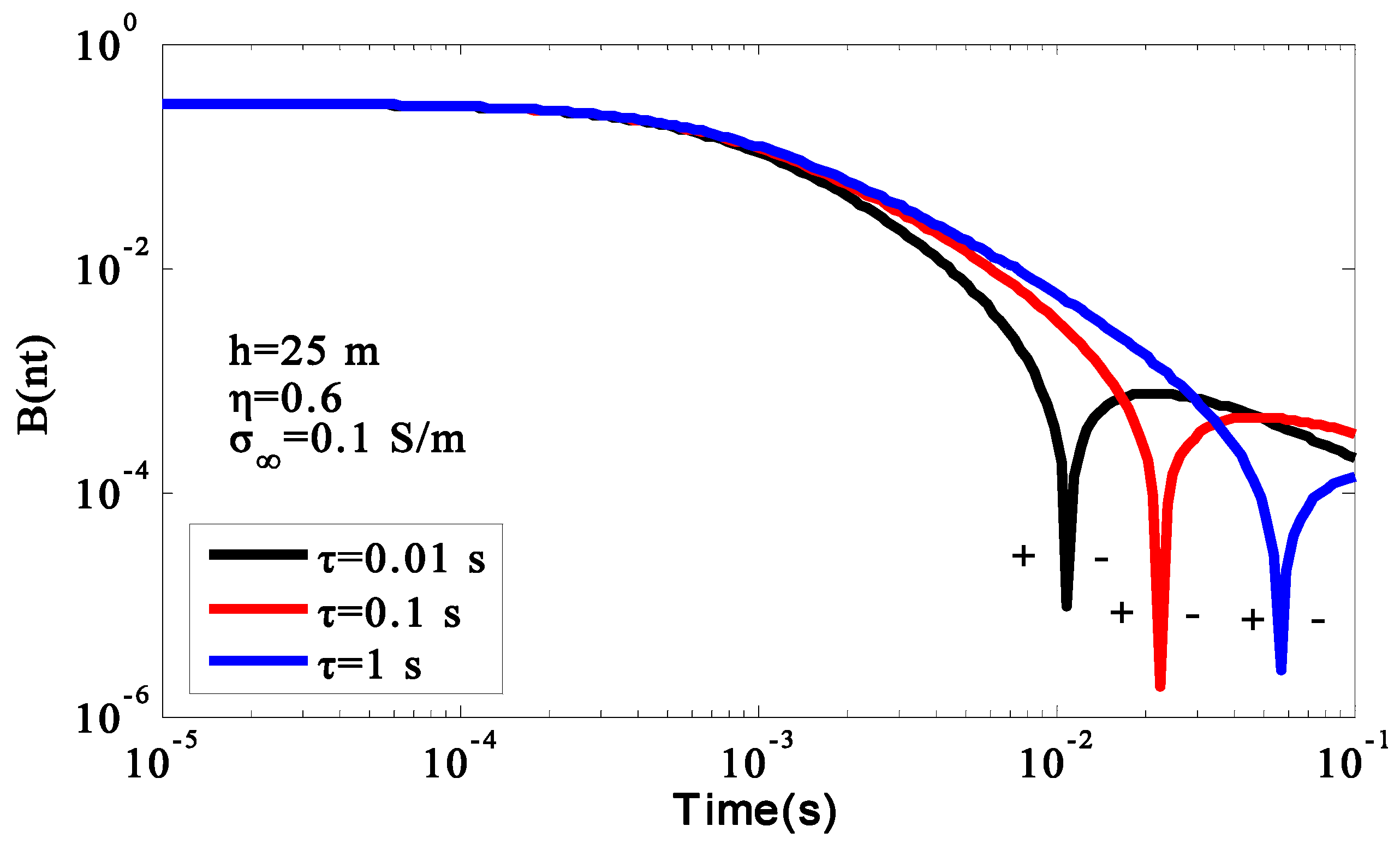
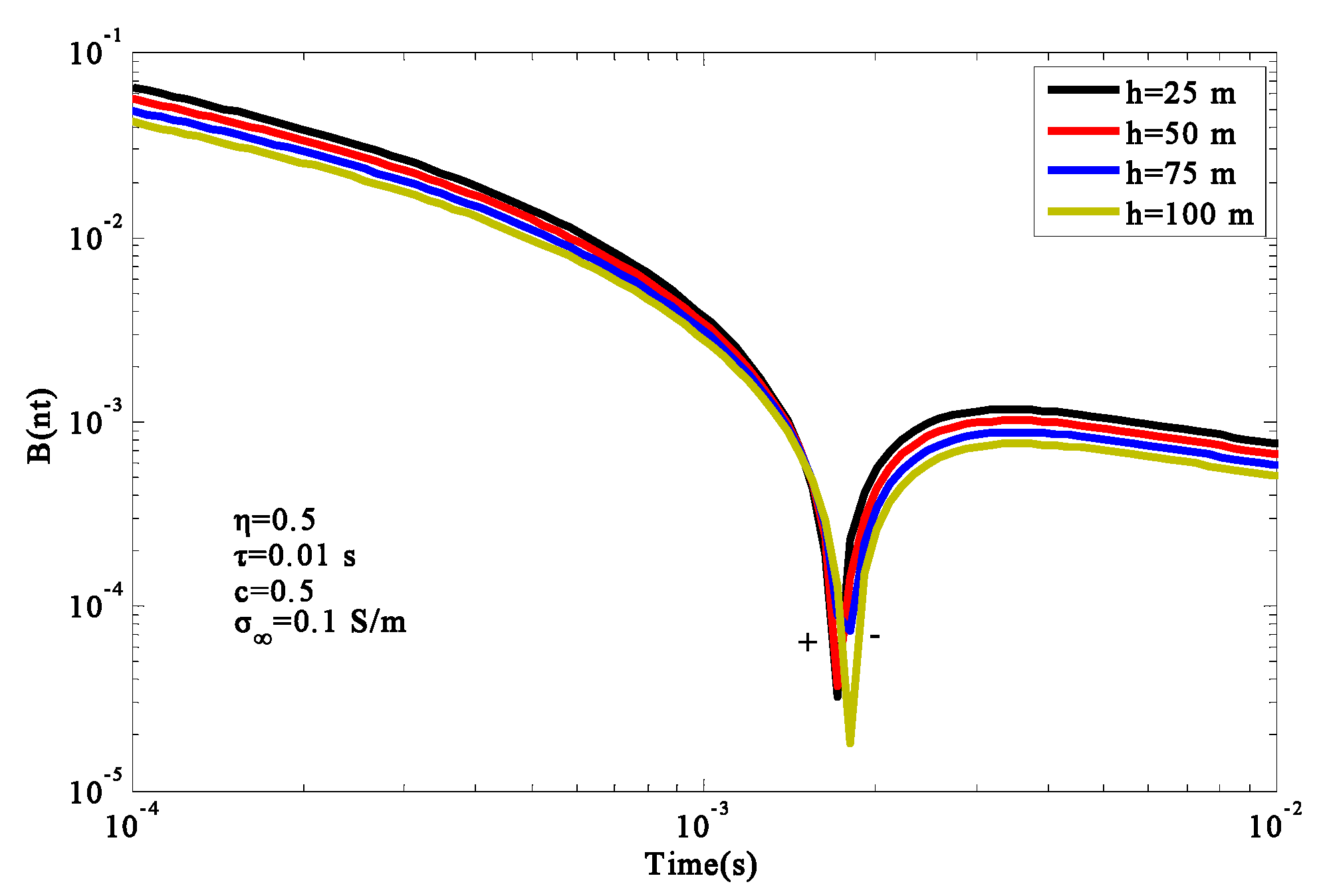
In the field measurements of GREATEM, due to the influence of airflow and environment, the flight height was not a constant. Therefore, it was necessary to analyze the influence of flight altitude on the IP effect. We take the 3D model (
Figure 8) as an example. The air layer conductivity was set to
and the earth conductivity was set to
, while the size of the chargeable body was
. The model parameters of the chargeable body were as follows: chargeability
, frequency dependence
, characteristic time constant
, conductivity at the infinite frequency
, offset distance
, and flight altitude
,
,
, and
. The induced polarization (IP) effect at different flight altitudes was calculated as depicted in
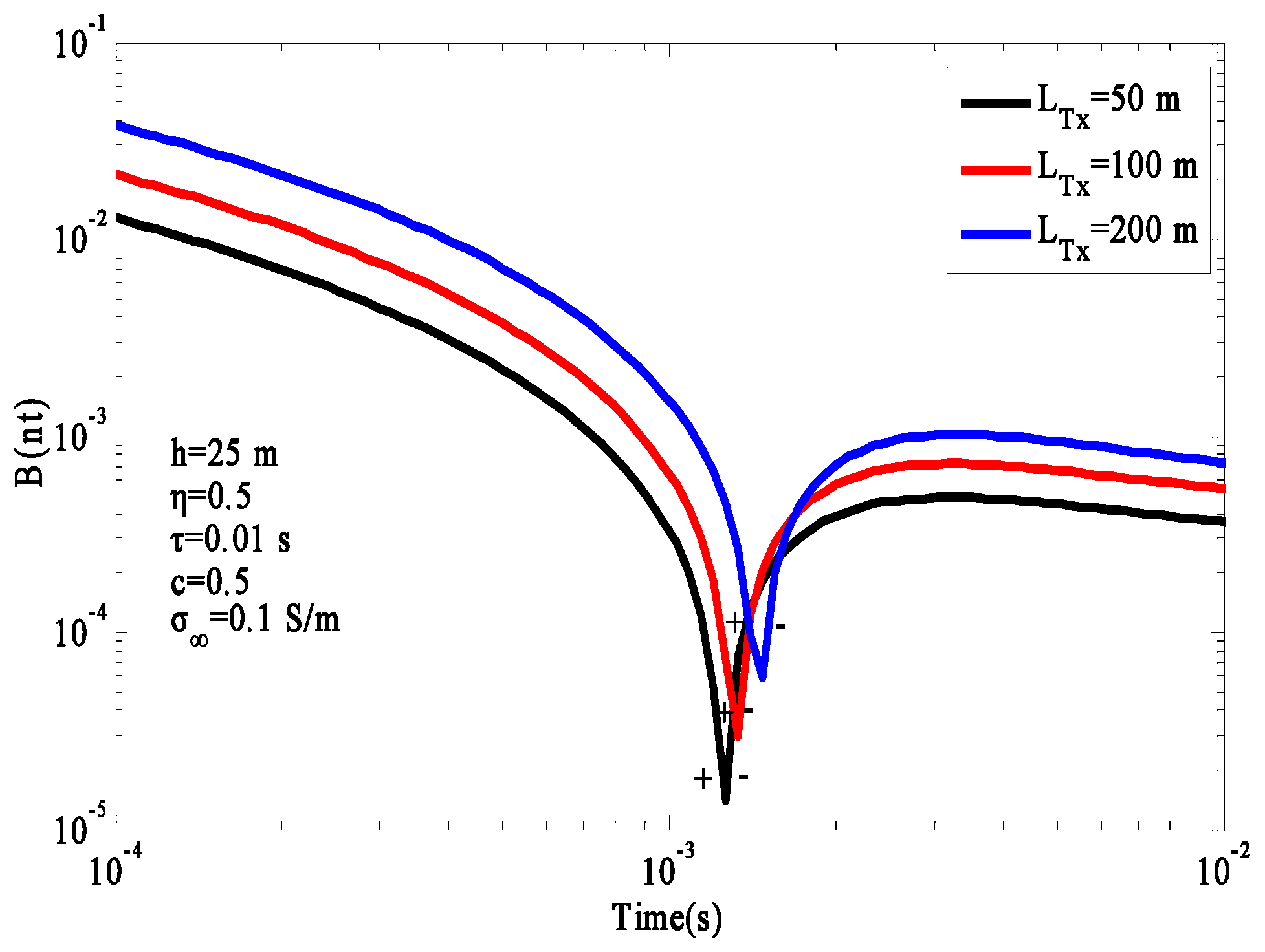
Figure 12. In order to understand the influence of the parameters of GREATEM on the IP response, other parameters remained unchanged, while the flight height was set to h = 25 m, and the emission source length was
,
, and
. The responses of different emission source lengths are shown in
Figure 13. Taking
and the offset distance
,
, and
, the responses of different offsets are shown in
Figure 14.
Based on
Figure 12, flight altitude mainly affected the amplitude of the response. The effect on the time of sign reversal was not obvious, and the sign reversal phenomenon was mainly concentrated in the range 1.5–2 ms. With the increase in flight altitude, the received electromagnetic response decreased gradually. It can be seen from
Figure 13 that the length of the emission source mainly affected the amplitude of the response. The length of emission source increased gradually, and the amplitude of response increased gradually, which also shows that a longer emission source resulted in a higher resolution of the polarizable body. In
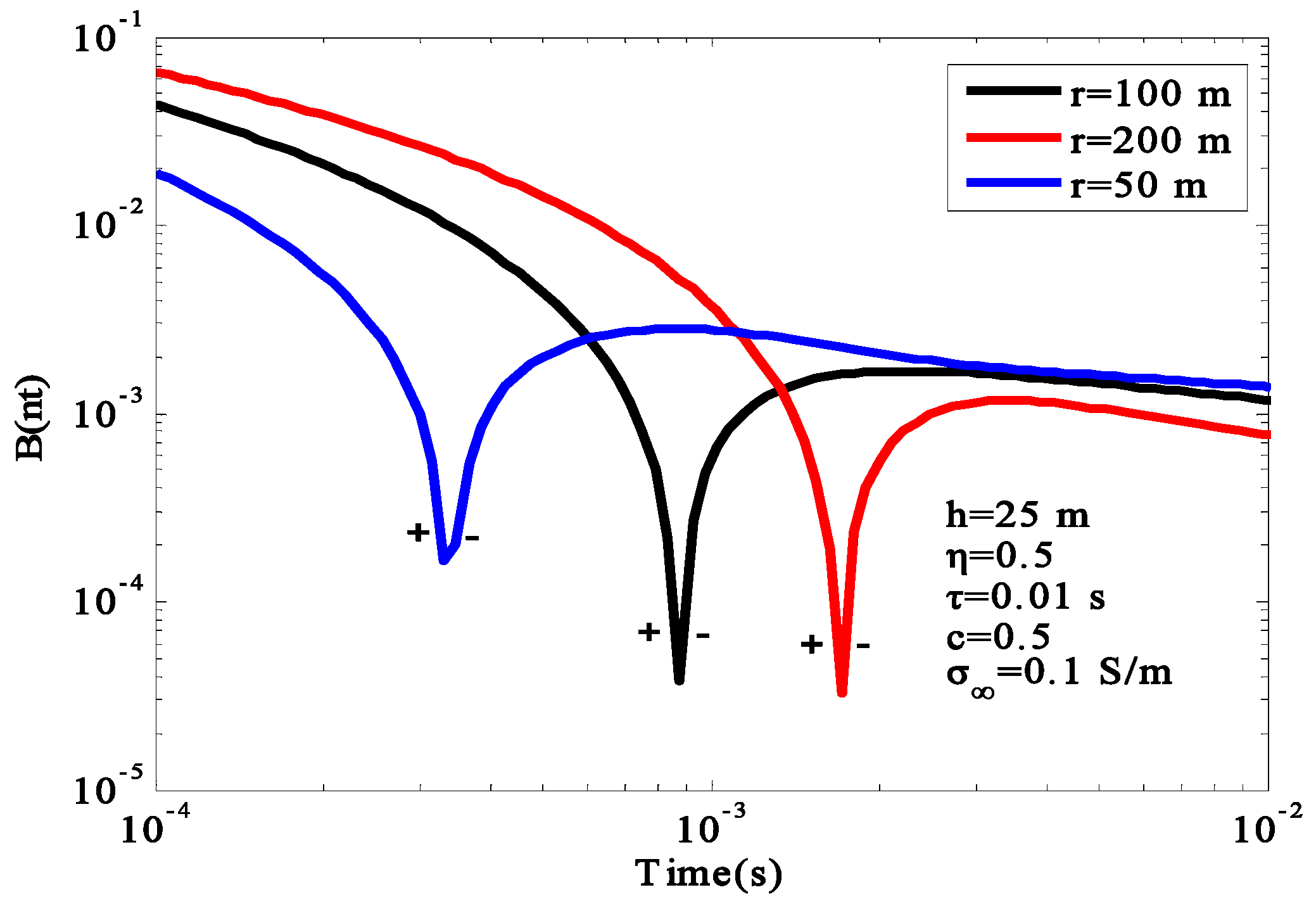
Figure 14, with the decrease in offset distance, the time of the sign reversal appeared earlier, and the polarization response became easier to observe at a short offset distance.
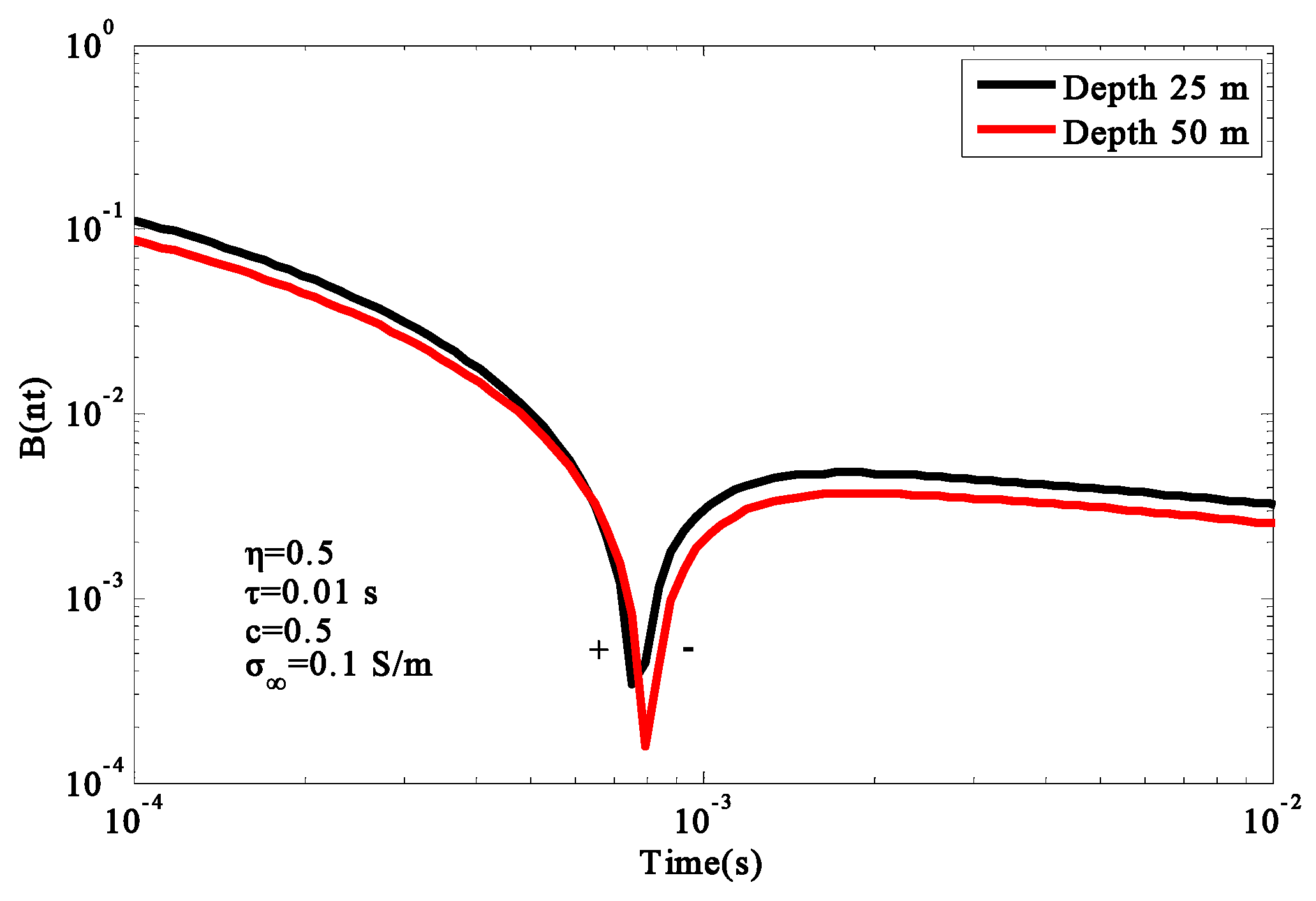
Next, we set the air layer conductivity to
and earth conductivity to
. The size of the chargeable body was
. The model parameters of the chargeable body were chosen as
,
,
,
, offset distance
, emission source length
, and flight altitude
. The chargeable body was buried
and
below the surface. The response curves of the chargeable body at different depths are shown in
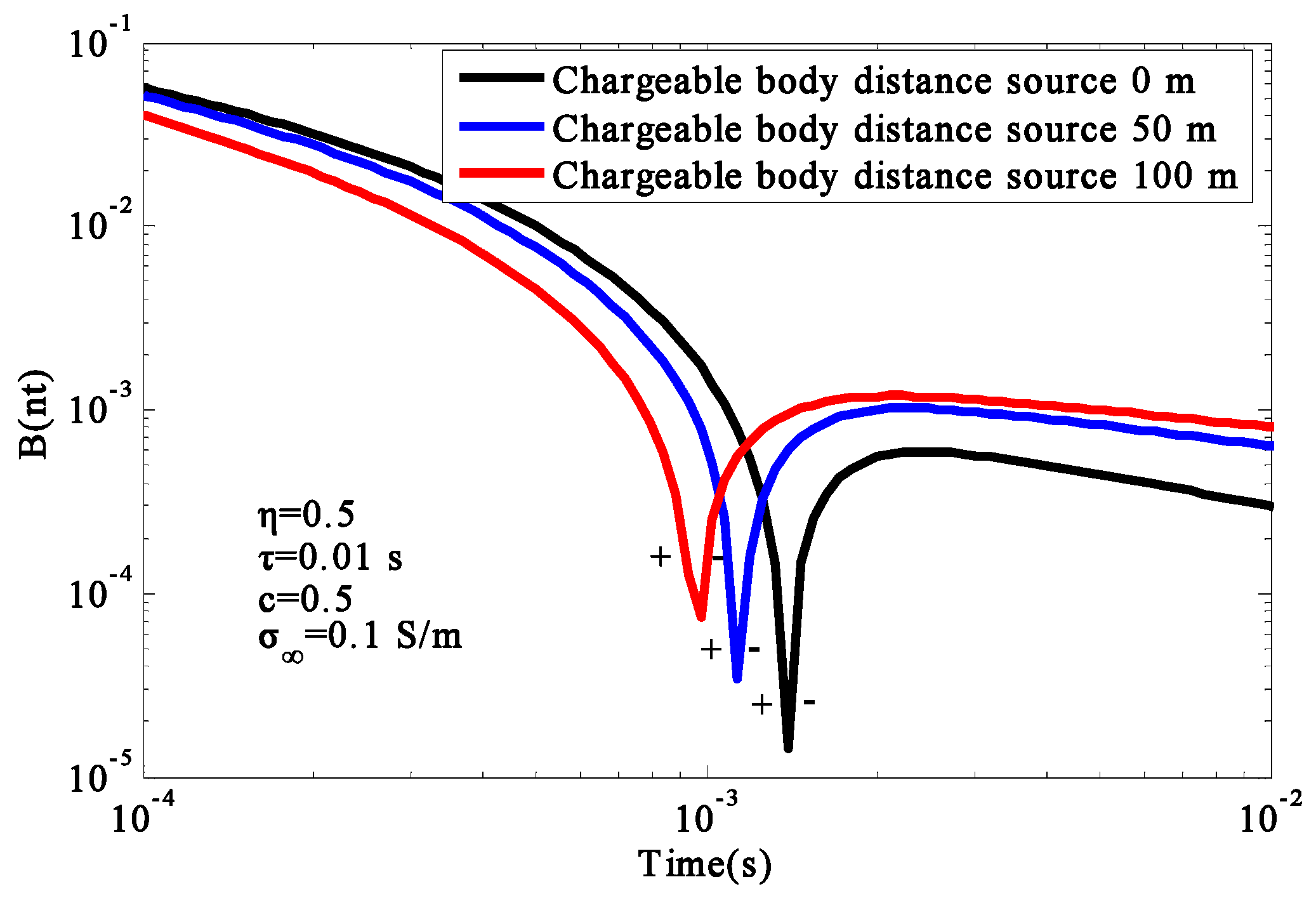
Figure 15. Moreover, we changed the size of the chargeable body to
and the chargeable body depth to
, while keeping other parameters the same, and setting the distance from the left boundary of the chargeable body to the emission source as
,
, and
. The response curves at different source positions are shown in
Figure 16.
From
Figure 15 and
Figure 16, it can be seen that all the amplitudes decreased, while the depth of chargeable body increased. However, the time of the reversal sign did not change. In the early stage, as the distance between the emitter source and the chargeable body decreased, the amplitude of the induced field increased, the attenuation of the curve was delayed. In the later stage, the time of sign reversal appeared later when the distance between the emitter and the chargeable body decreased.
5. Conclusions
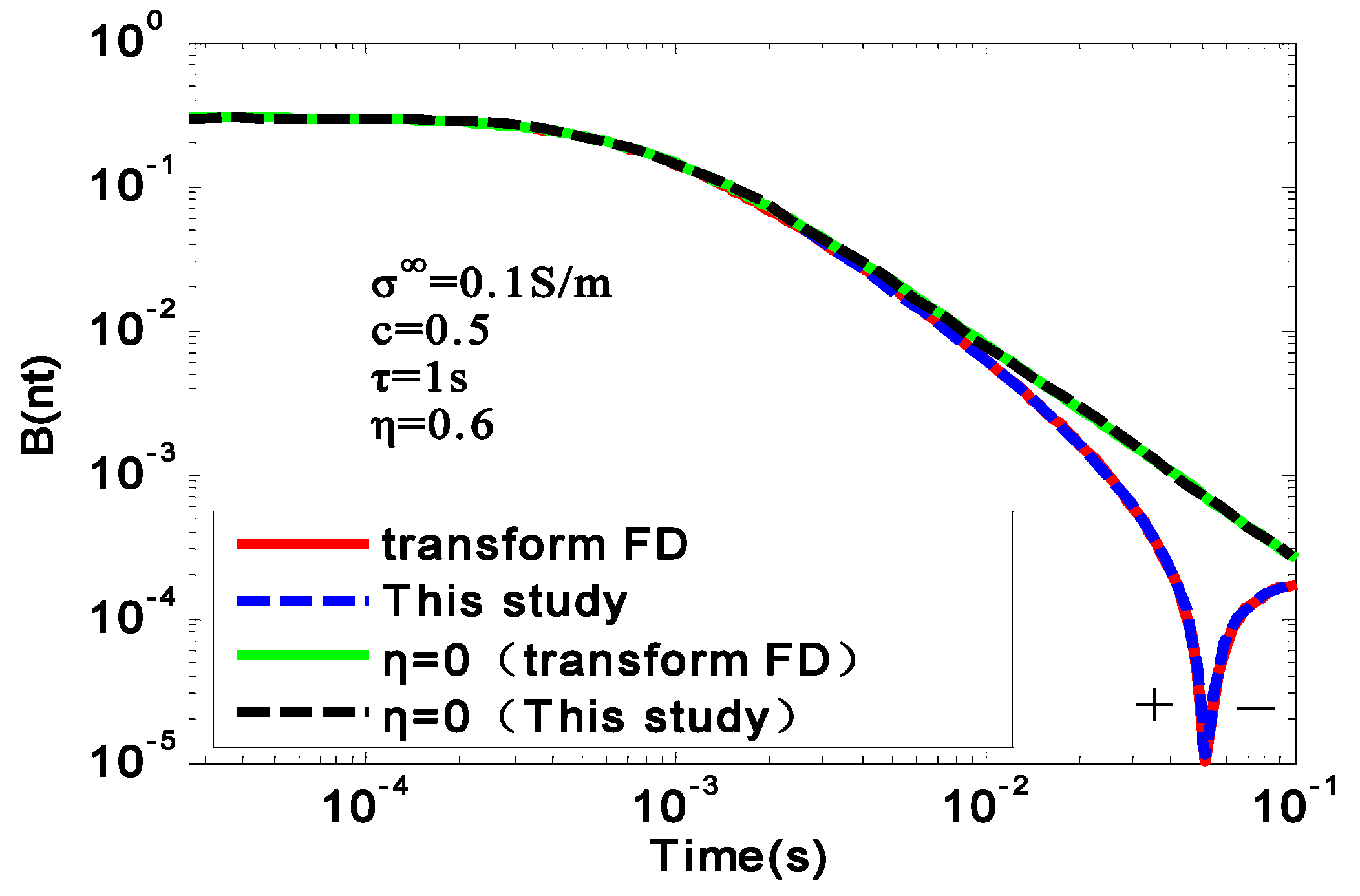
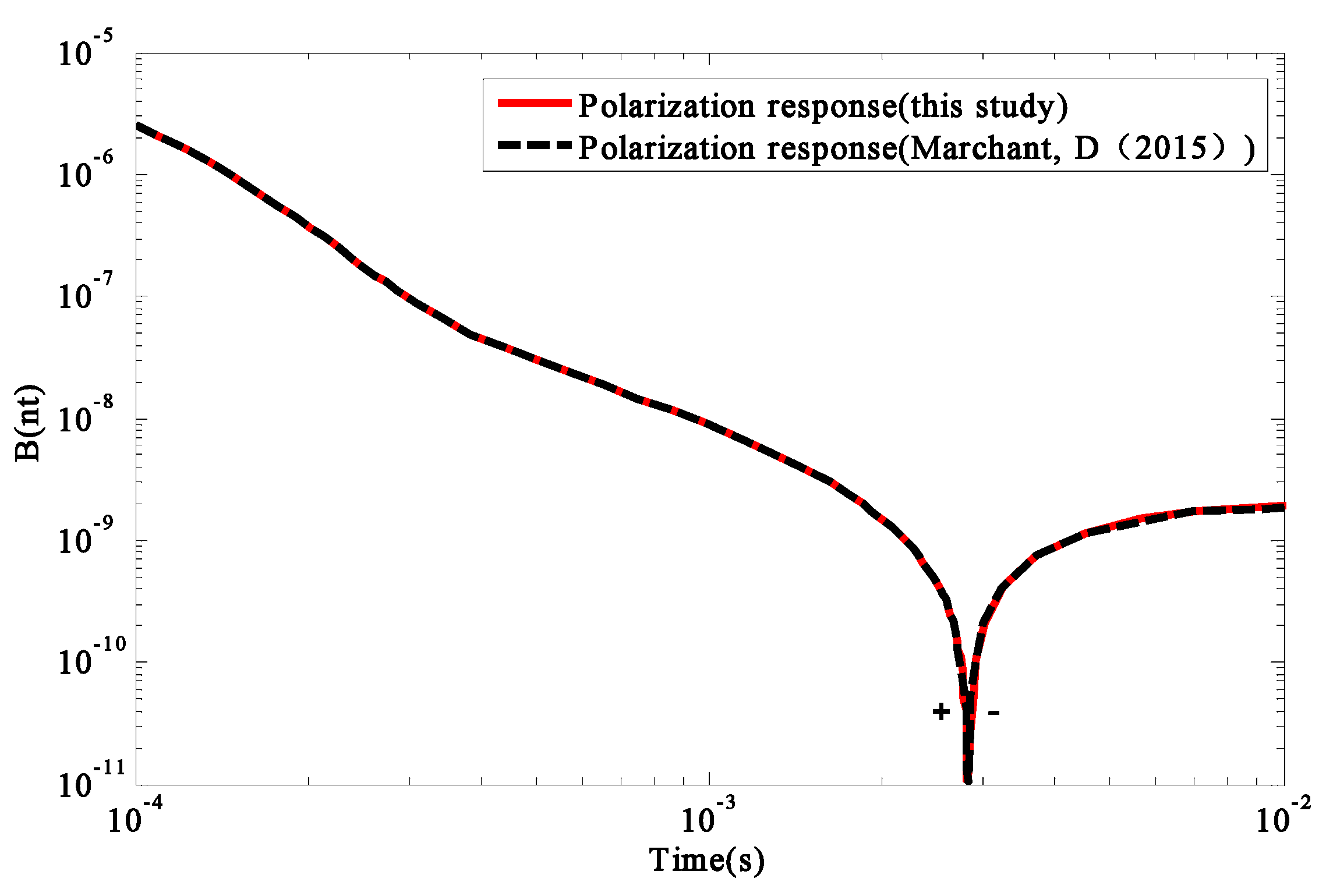
Three-dimensional numerical simulations are the basis of data interpretation and imaging. In this paper, a three-dimensional numerical simulation of underground polarized media was realized, which achieved simulation results closer to the actual mineral resources. In the actual measurement process with GREATEM, the geodetic model could be established using this method, and the optimal configuration structure of the equipment was obtained using the numerical simulation method. This not only provides the basis for the exploration of underground mineral resources, but also provides theoretical guidance for the design of detection instruments. Wave field transformation was proposed to calculate the response of the GREATEM system using the Cole–Cole model. The electromagnetic wave was absorbed by the boundary condition of CFS-PML in the fictitious wave field. Compared with the analytical solution and the transformed FD method, the relative error was less than 10%, satisfying the standard calculation requirements. Compared with the existing method, the calculation time was reduced five-fold. According to the simulations, the flight altitude, electrical source length, electrical source position, and the offset distance all affected the electromagnetic response monotonically. In the homogeneous half-space model, when the characteristic time constant () and conductivity at the infinite frequency () were too large, the negative response was likely overwhelmed by the noise; thus, the negative response could not be observed. Therefore, the occurrence time of the negative response could be enhanced by reducing the offset distance. Low-altitude flights can facilitate the recognition ability of the chargeable body, but they are often limited by geological conditions. The response of the GREATEM system had good recognition ability in the low-resistance area; however, the chargeable body could hardly be detected. Therefore, it is necessary to improve the detection accuracy of the GREATEM in low-resistance areas.
This paper realized a three-dimensional numerical simulation of polarized media based on the Cole–Cole model, and improved the calculation efficiency. However, in the actual measurement process, the underground medium is diverse. It is not comprehensive to only use the Cole–Cole model to describe the characteristics of polarized medium; the existence of the GEMTIP model in particular is a major problem in the field of geophysics. In future work, we need to consider the GEMTIP model in the numerical simulation, so as to improve the universality of this method.