Aeroaocustic Numerical Analysis of the Vehicle Model
Abstract
1. Introduction
2. Models and Methods
2.1. Mathematical Model
2.2. Numerical Model
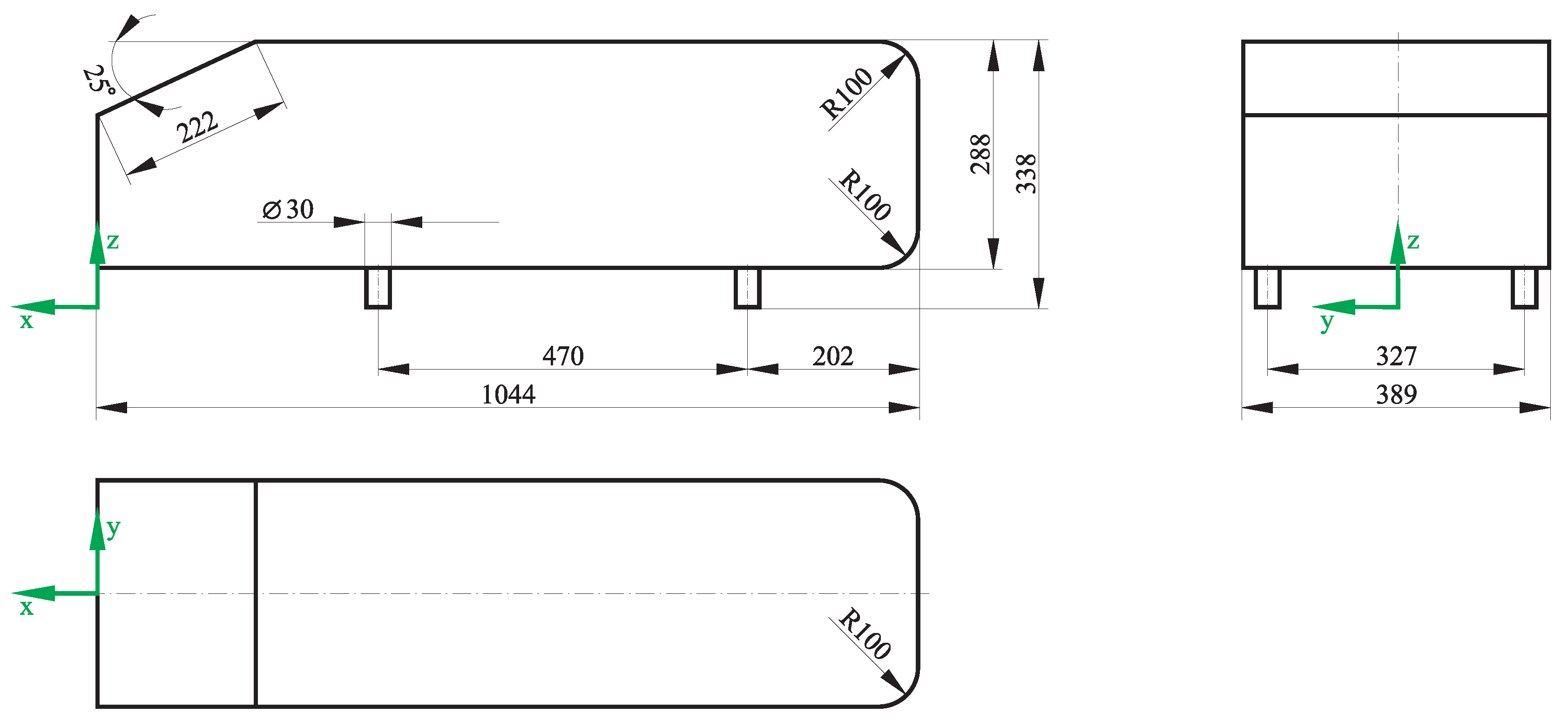
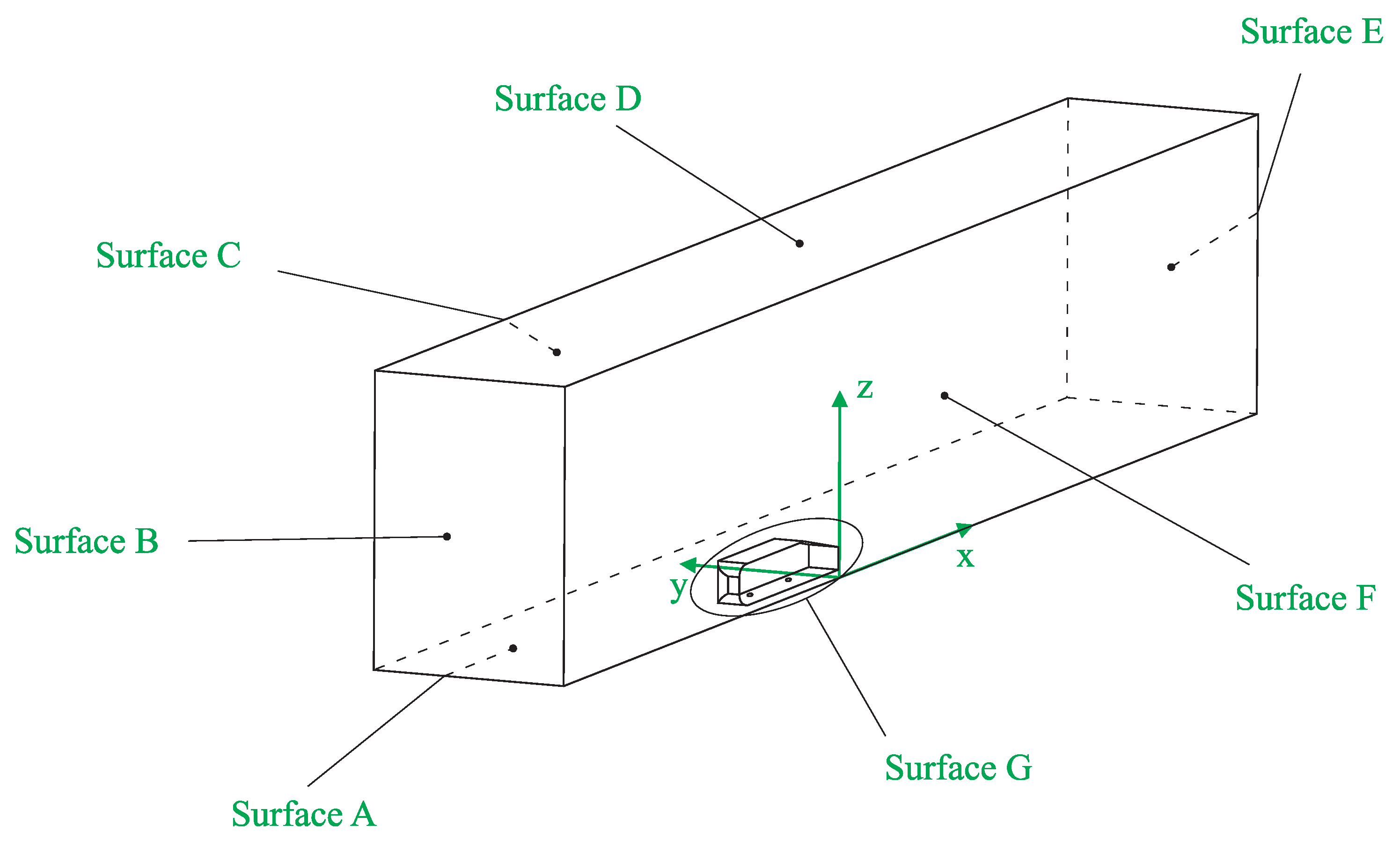
2.2.1. Geometry Model
2.2.2. Discretization
2.2.3. Boundary Conditions
2.2.4. Initial Condition
3. Results
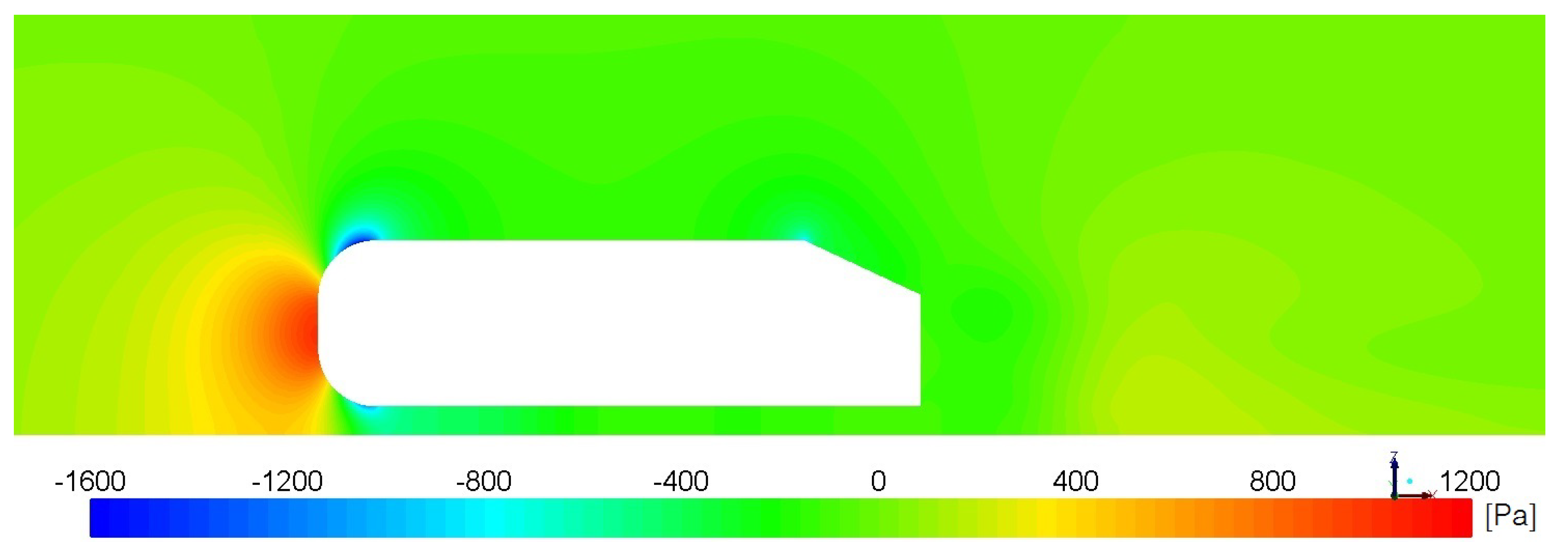
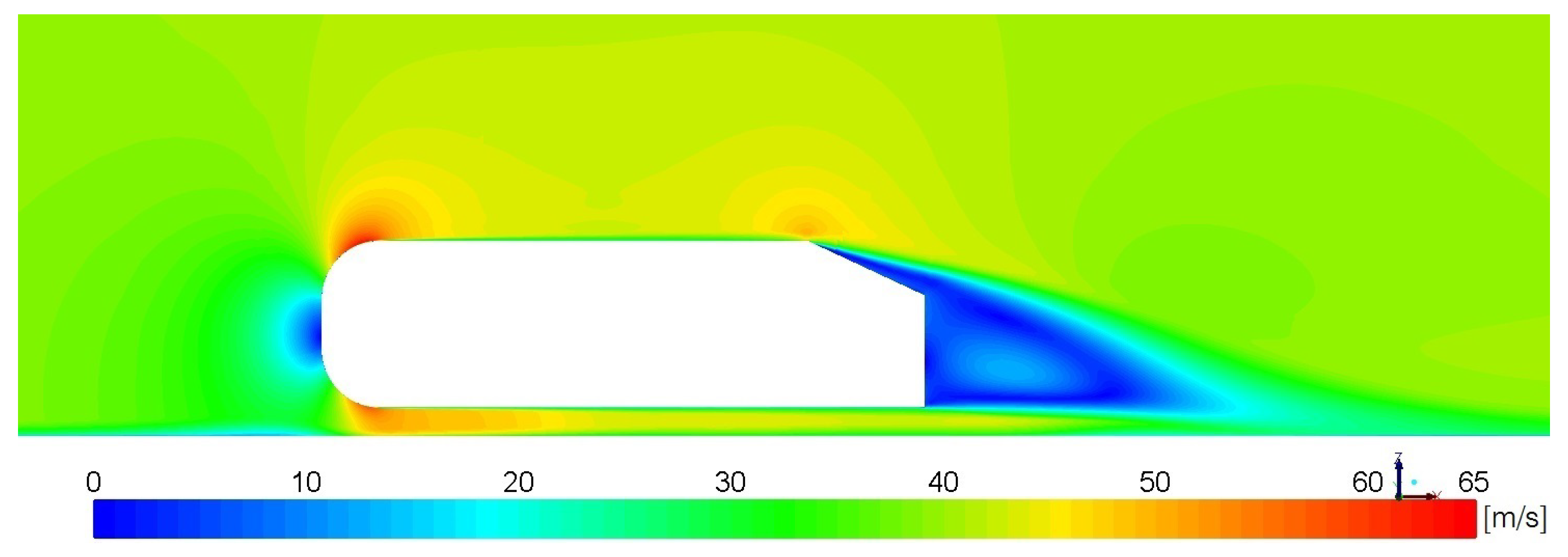
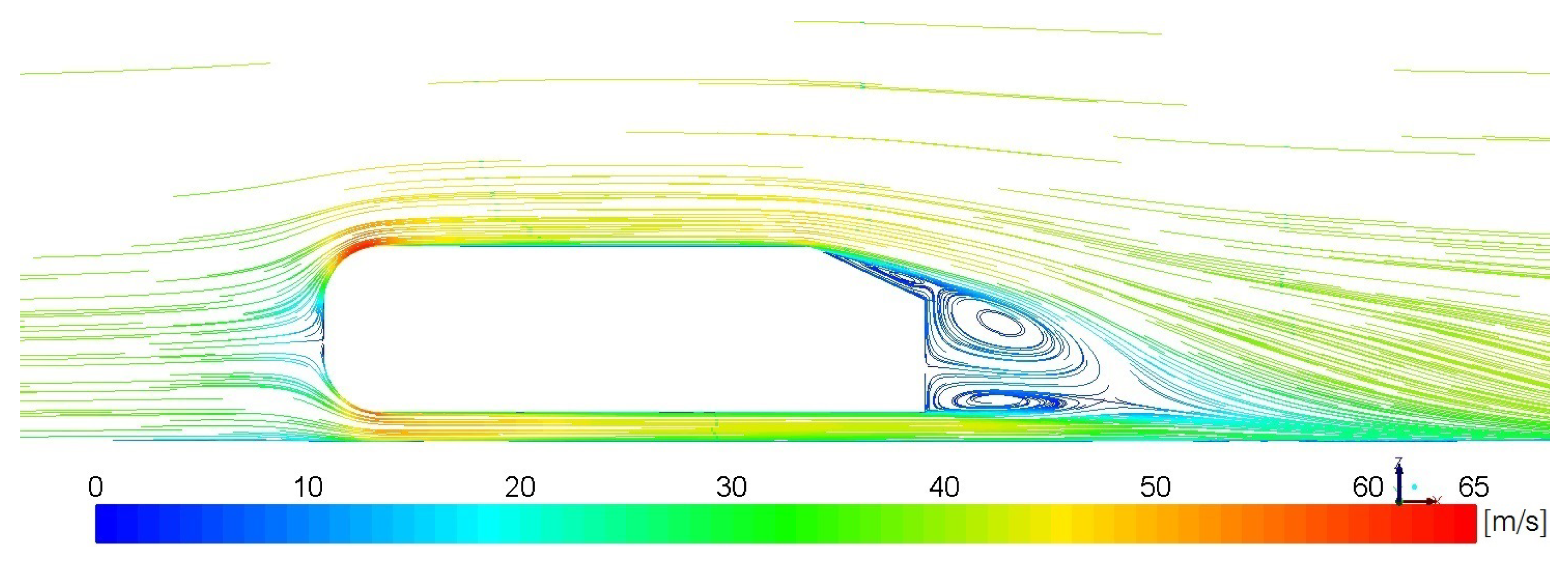
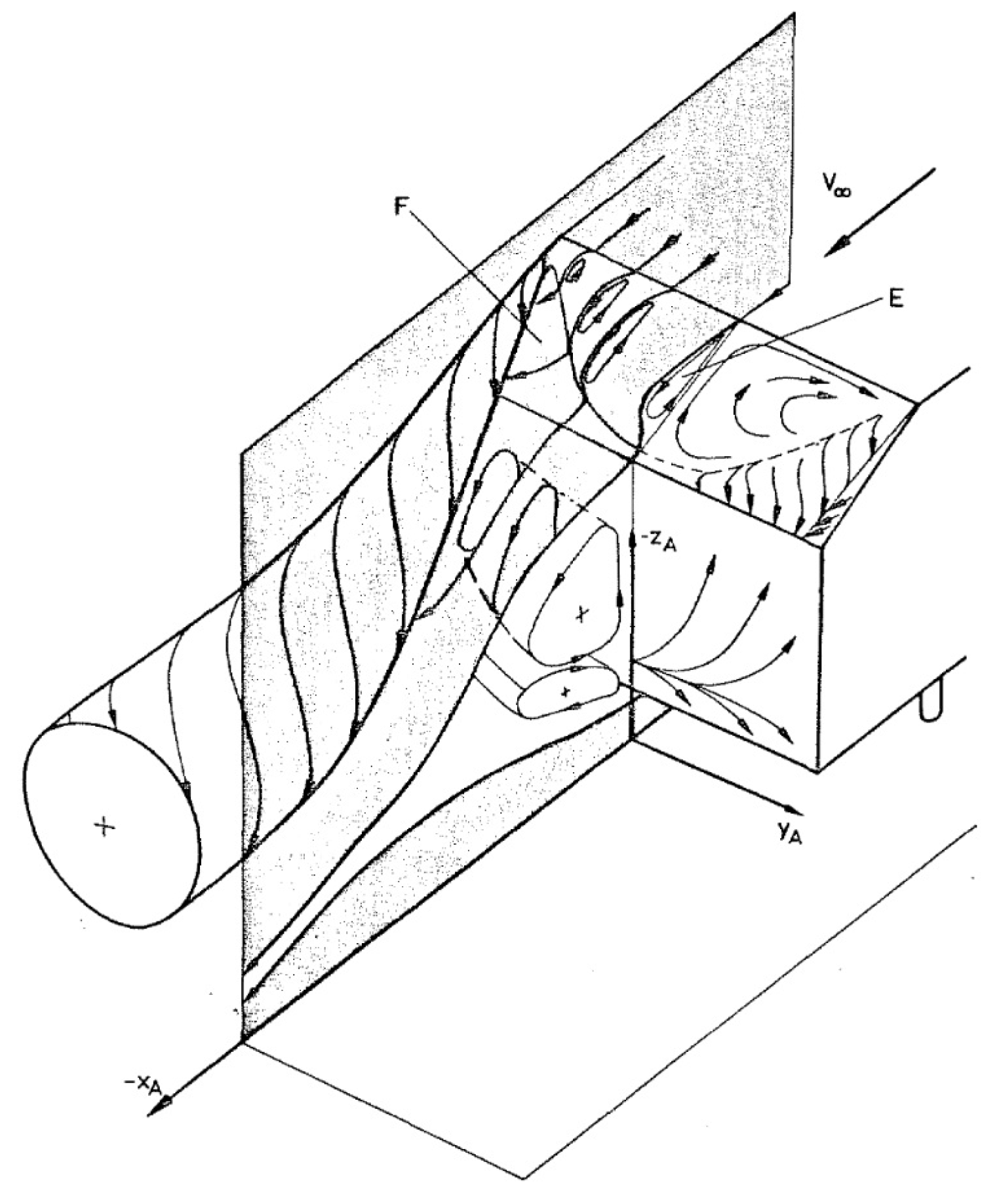
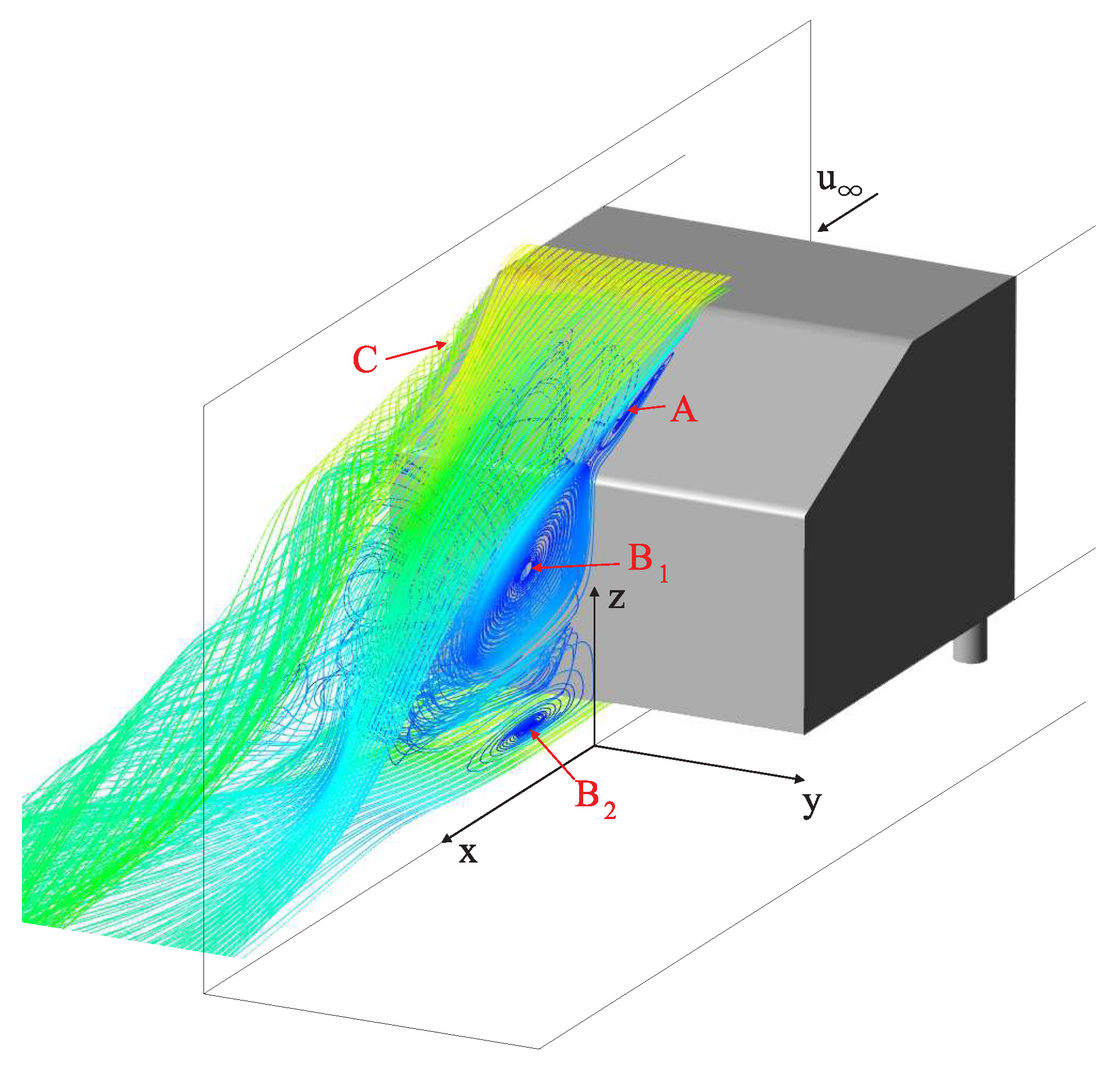
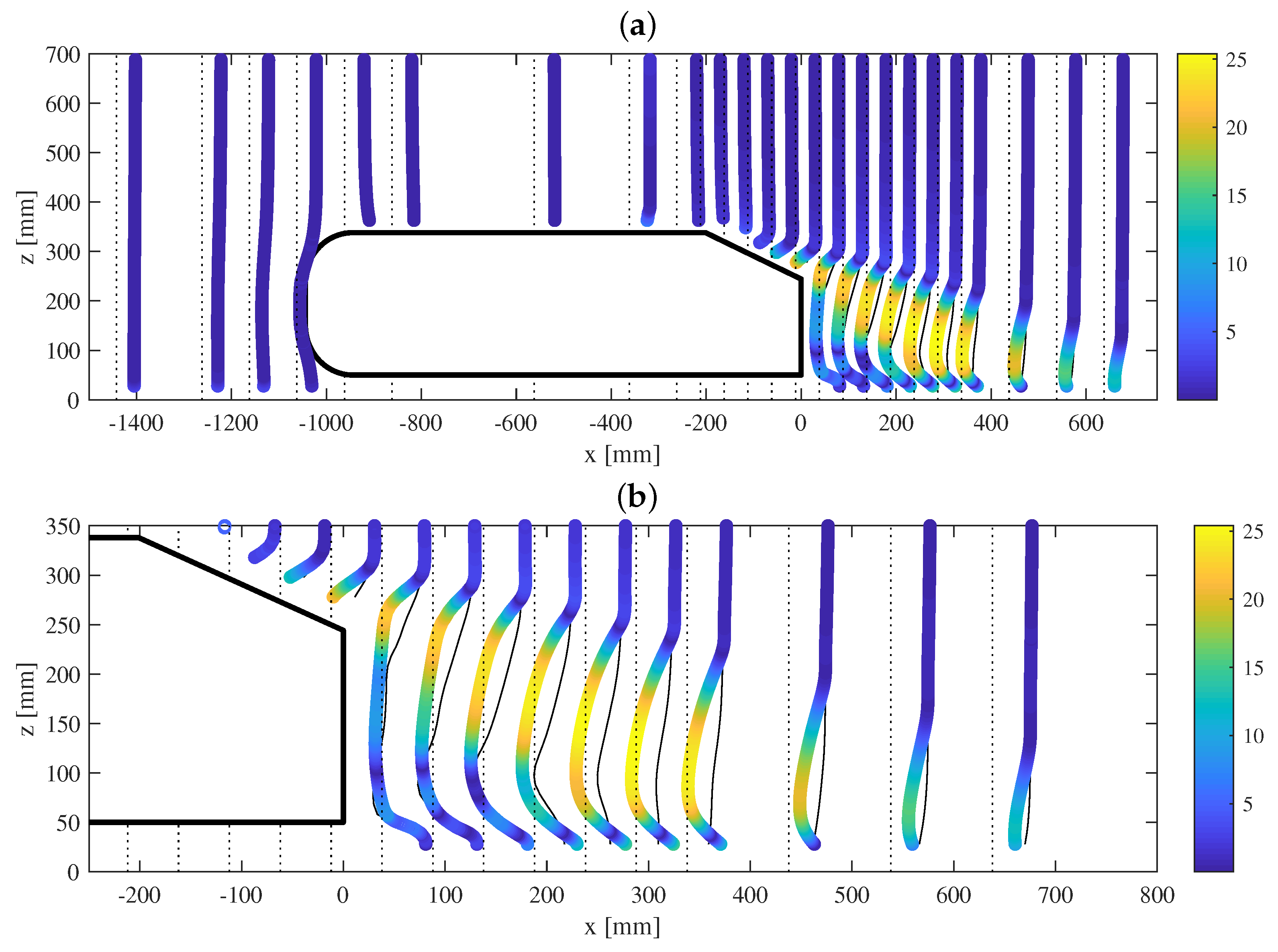
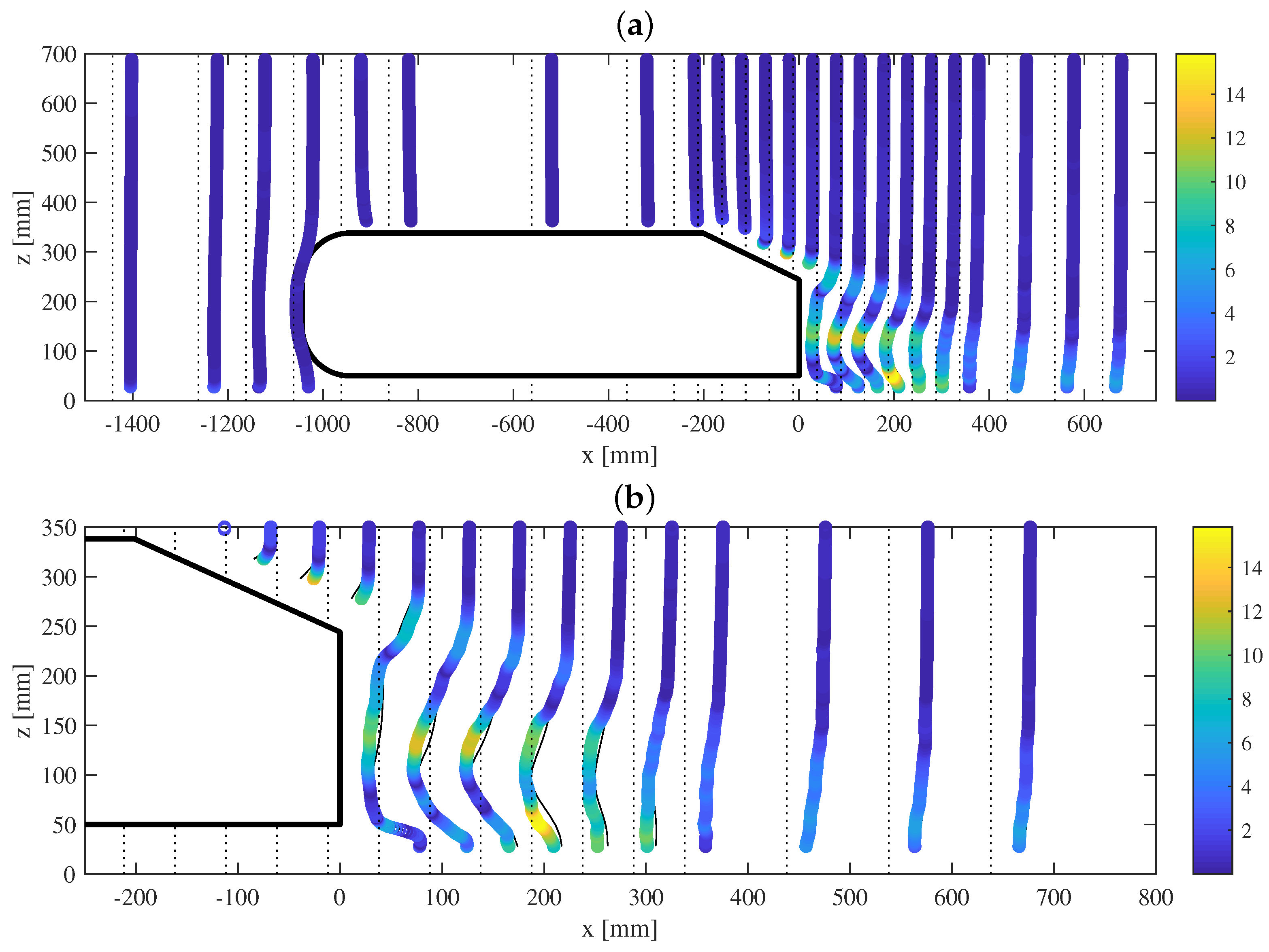
3.1. Velocity and Pressure Field in Symmetry Plane
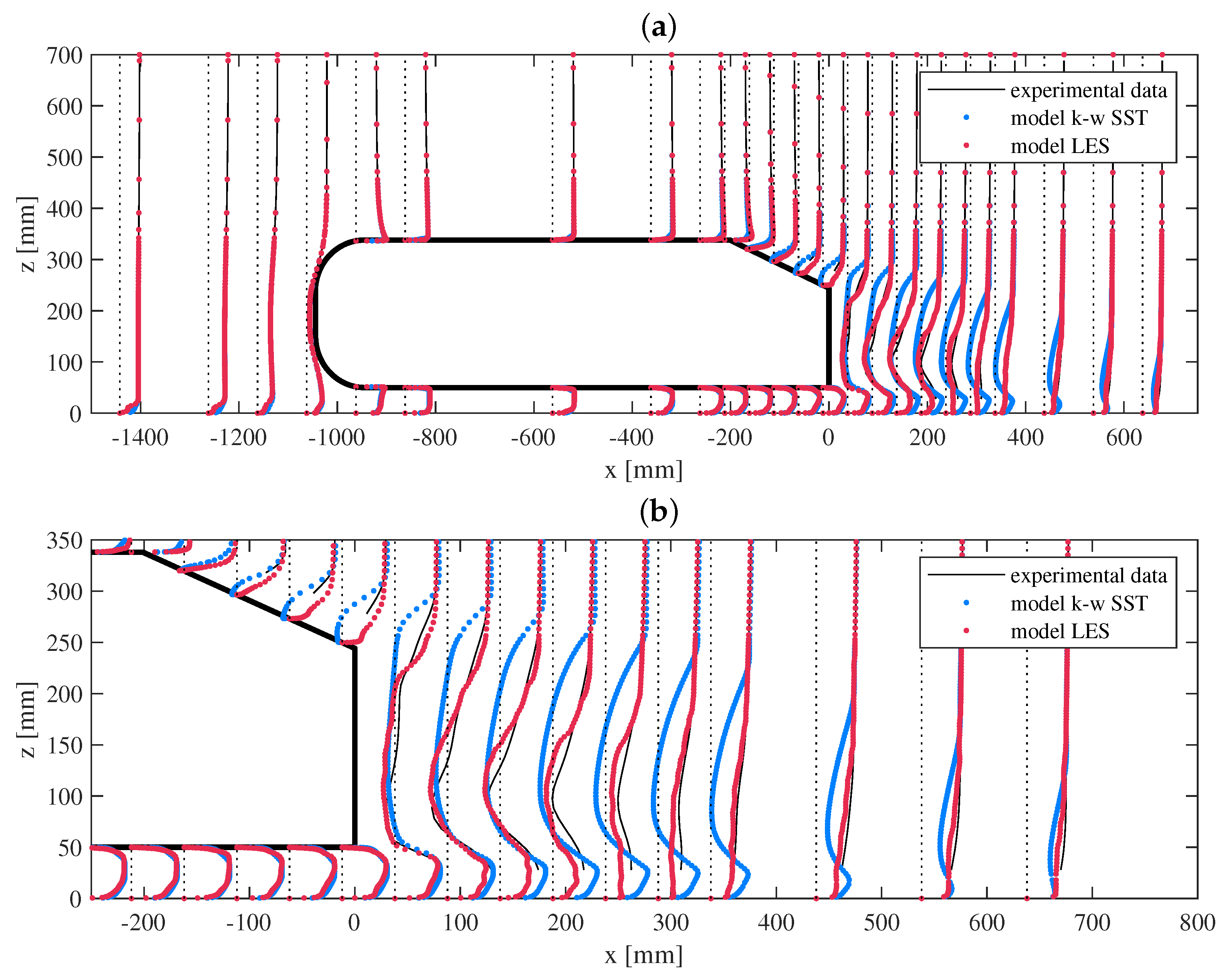
3.2. Steamwise Velocity Profile in Symmetry Plane
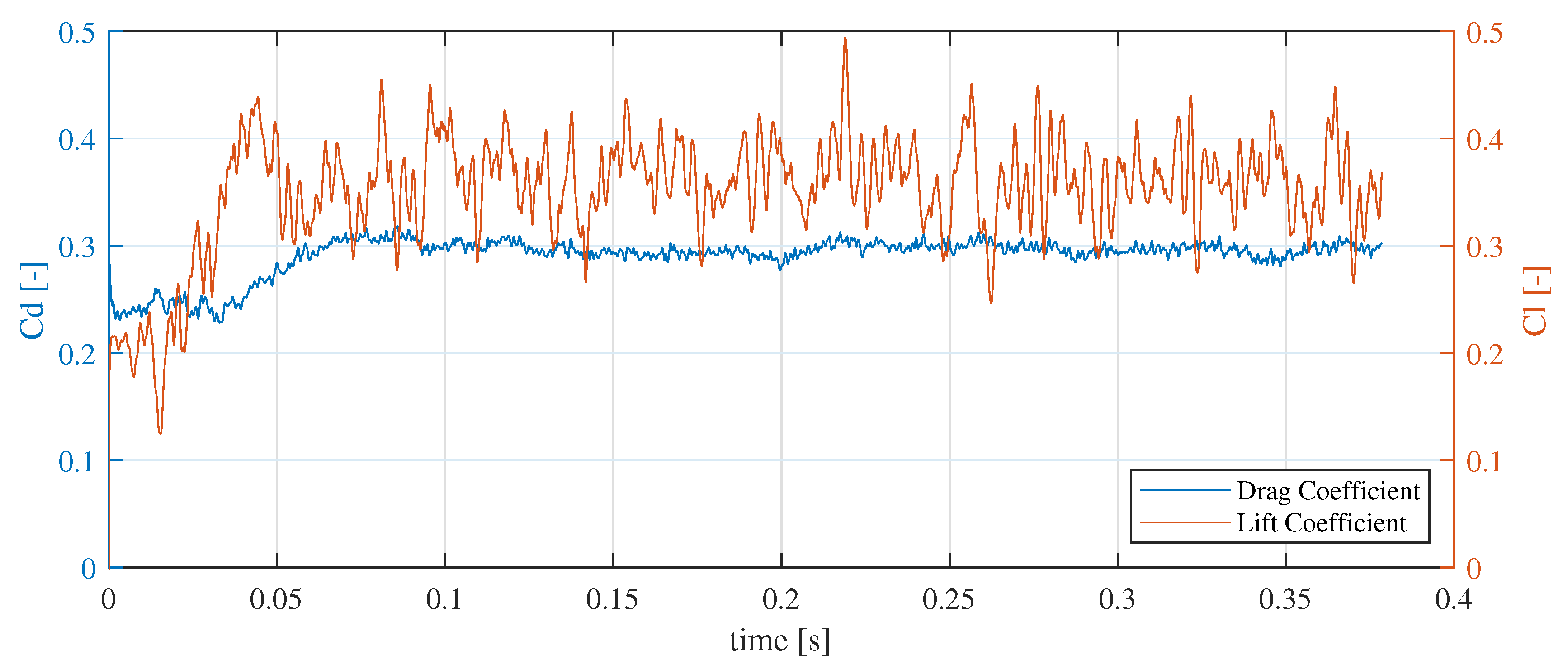
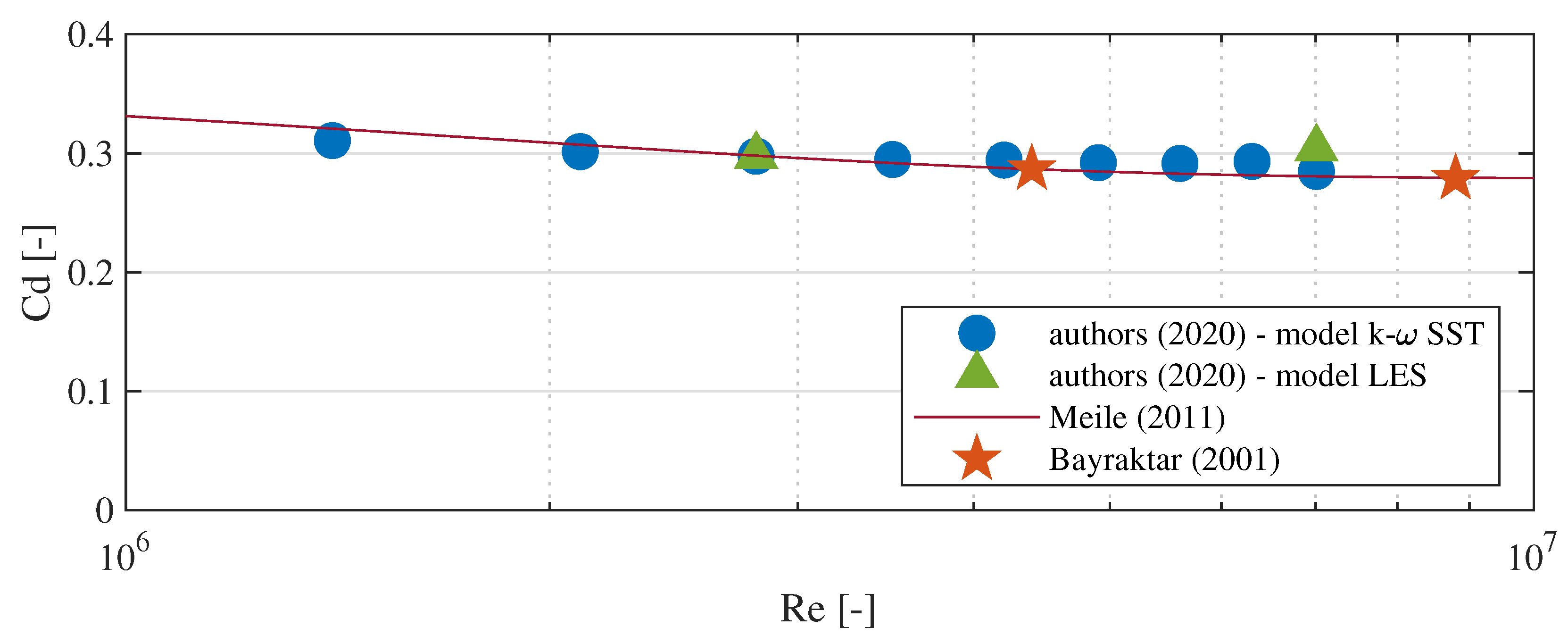
3.3. Drag Coefficient
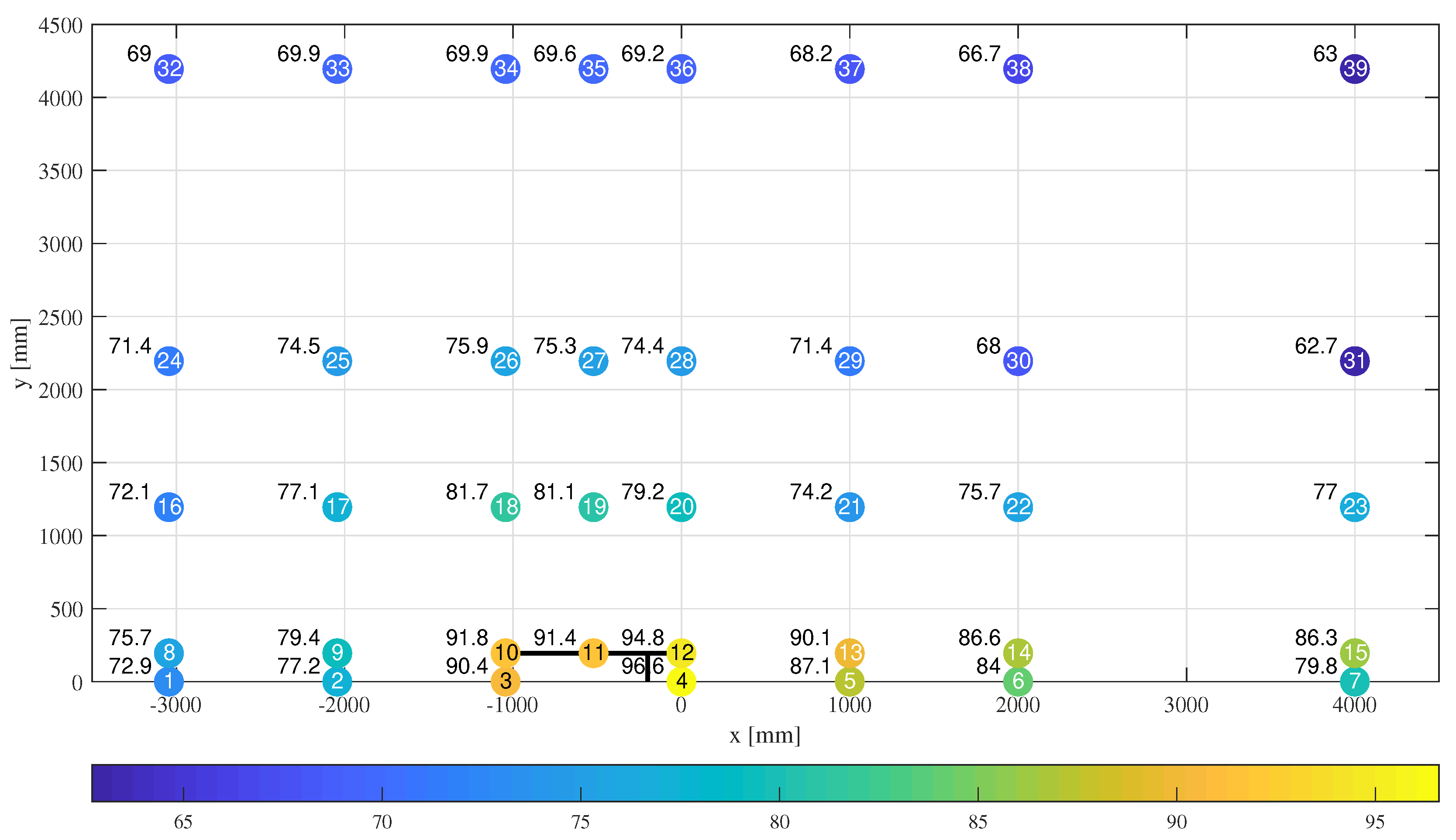
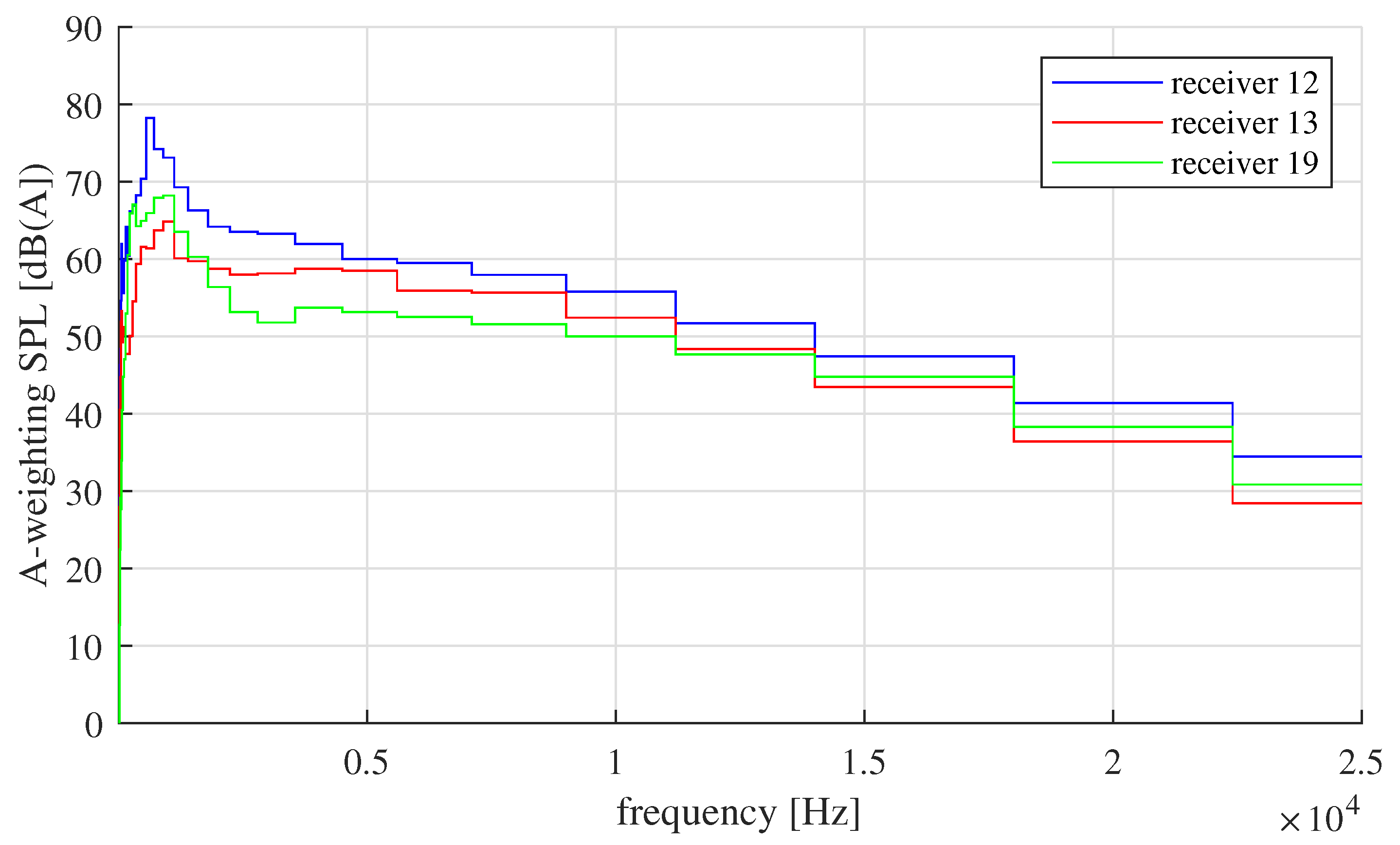
3.4. Sound Pressure Level (SPL)
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| CAA | Computational Aeroacoustics |
| FW-H | Ffowcs Williams–Hawkings |
| SST | Shear Stress Transport |
| LES | Large Eddy Simulation |
| FFT | Fast Fourier Transformation |
| VLES | Very Large Eddy Simulation |
| RANS | Reynolds-Averaged Navier–Stokes |
| EARSM | Explicit Algebraic Stress Model |
| DES | Detached Eddy Simulation |
| IDDES | Improved Delay Detached Eddy Simulation |
| RSM | Reynolds Stress Model |
| SA | Spalart–Allmaras |
| WA | Wray–Agarwal |
| RNG | Renormalization Group |
| PRESTO | Pressure Staggering Option |
| ERCOFTAC | European Research Community on Flow, Turbulence and Combustion |
| OASPL | Overall Sound Pressure Level |
References
- Helfer, M. General Aspects of Vehicle Aeroacoustics. In Proceedings of the Lecture Series on Road Vehicle Aerodynamics, Sint-Genesius-Rode, Belgium, 30 May–3 June 2005. [Google Scholar]
- Shi, X.; Sun, D.J.; Fu, S.; Zhao, Z.; Liu, J. Assessing On-Road Emission Flow Pattern under Car-Following Induced Turbulence Using Computational Fluid Dynamics (CFD) Numerical Simulation. Sustainability 2019, 11, 6705. [Google Scholar] [CrossRef]
- Żółtowski, P.; Piechna, J.; Żółtowski, K.; Zobel, H. Analysis of dynamic loads on lightweight footbridge caused by lorry passing underneath. Bull. Pol. Acad. Sci. Tech. Sci. 2006, 54, 33–43. [Google Scholar]
- Ahmet, A.; Tahsin, E.; Halit, Y.; Alper, Y.; Ahmet, H.P. Computational Fluid Dynamics Analysis of a Vehicle Radiator Using Porous Media Approach. Heat Transf. Eng. 2020, 1–13. [Google Scholar] [CrossRef]
- Mo, J.O.; Choi, J.H. Numerical investigation of unsteady flow and aerodynamic noise characteristics of an automotive axial cooling fan. Appl. Sci. 2020, 10, 5432. [Google Scholar] [CrossRef]
- Bergamini, P.; Casella, M.; Vitali, D.F. Computational Prediction of Vehicle Aerodynamic Noise by Integration of a CFD Technique with Lighthill’s Acoustic Analogy. SAE Int. 1997. [Google Scholar] [CrossRef]
- Tsai, C.-H.; Fu, L.-M.; Tai, C.-H.; Huang, Y.-L.; Leong, J.-C. Computational aero-acoustic analysis of a passenger car with a rear spoiler. Appl. Math. Model. 2009, 33, 3661–3673. [Google Scholar] [CrossRef]
- Duncan, B.D.; Sengupta, R.; Mallick, S.; Shock, R.; Sims-Williams, D.B. Numerical Simulation and Spectral Analysis of Pressure Fluctuations in Vehicle Aerodynamic Noise Generation. SAE Int. J. Passeng. Cars Mech. Syst. 2002, 111, 872–892. [Google Scholar]
- Ahmed, S.R.; Ramm, G.; Faltin, G. Some Salient Features Of The Time-Averaged Ground Vehicle Wake. SAE Int. 1984, 473–503. [Google Scholar] [CrossRef]
- Guilmineau, E.; Deng, G.B.; Leroyer, A.; Queutey, P.; Visonneau, M.; Wackers, J. Assessment of hybrid RANS-LES formulations for flow simulation around the Ahmed body. Comput. Fluids 2017, 176, 302–319. [Google Scholar] [CrossRef]
- Serre, E.; Minguez, M.; Pasquetti, R.; Guilmineau, E.; Deng, G.B.; Kornhaas, M.; Schäfer, M.; Fröhlich, J.; Hinterberger, C.; Rodi, W. On simulating the turbulent flow around the Ahmed body: A French–German collaborative evaluation of LES and DES. Comput. Fluids 2013, 78, 10–23. [Google Scholar] [CrossRef]
- Banga, S.; Zunaid, M.; Ansari, N.A.; Sharma, S.; Dungriyal, R.S. CFD Simulation of Flow around External Vehicle: Ahmed Body. IOSR J. Mech. Civ. Eng. 2015, 12, 87–94. [Google Scholar] [CrossRef]
- Meile, W.; Brenn, G.; Reppenhagen, A.; Lechner, B.; Fuchs, A. Experiments and numerical simulations on the aerodynamics of the Ahmed body. CFD Lett. 2011, 3, 32–39. [Google Scholar]
- Thomas, B.; Agarwal, R.K. Evaluation of Various RANS Turbulence Models for Predicting the Drag on an Ahmed Body. In Proceedings of the AIAA Aviation Forum, Dallas, TX, USA, 17–21 June 2019. [Google Scholar]
- Han, X.; Rahman, M.M.; Agarwal, R.K. Development and Application of a Wall Distance Free Wray-Agarwal Turbulence Model. In Proceedings of the AIAA SciTech Forum, Kissimmee, FA, USA, 8–12 January 2018. [Google Scholar]
- Dykas, S.; Wróblewski, W.; Rulik, S.; Chmielniak, T. Numerical Method for Modeling of Acoustic Waves Propagation. Arch. Acoust. 2010, 35, 35–48. [Google Scholar] [CrossRef]
- Sosnowski, M. The influence of computational domain discretization on CFD results concerning aerodynamics of a vehicle. J. Appl. Math. Comput. Mech. 2018, 17, 79–88. [Google Scholar] [CrossRef]
- Mansour, M.; Khot, P.; Kováts, P.; Thévenin, D.; Zähringer, K.; Janiga, G. Impact of computational domain discretization and gradient limiters on CFD results concerning liquid mixing in a helical pipe. Chem. Eng. J. 2020, 383, 123121. [Google Scholar] [CrossRef]
- Lienhart, H.; Becker, S.; Stoots, C. Flow and Turbulence Structures in the Wake of a Simplified Car Model (Ahmed Model). Notes Numer. Fluid Mech. 2002, 77, 1–8. [Google Scholar]
- Bayraktar, I.; Landman, D.; Baysal, O. Experimental and Computational Investigation of Ahmed Body for Ground Vehicle Aerodynamics. SAE Int. 2001, 321–331. [Google Scholar] [CrossRef]
- Murawski, K.; Lee, D. Numerical methods of solving equations of hydrodynamics from perspectives of the code FLASH. Bull. Pol. Acad. Sci. 2011, 59, 81–91. [Google Scholar] [CrossRef][Green Version]
| Stage | I | II | III |
|---|---|---|---|
| Convergence criteria | Residuals | Residuals | Residuals + steady value of drag and lift coefficient with fluctuation around mean |
| Number of iterations required to achieve the convergence criteria | 411 | 821 | 7500 |
| Turbulence model | SST | SST | LES |
| Pressure equation | Second Order | Second Order | Pressure Staggering Option (PRESTO) |
| Momentum equation | First Order | Second Order | Bounded Central Differencing |
| Relaxation Factor—Pressure | 0.25 | 0.25 | 0.5 |
| Relaxation Factor—Momentum | 0.25 | 0.25 | 0.5 |
| Drag Coefficient | 0.4409 | 0.3097 | 0.2979 (mean value) |
| Lift Coefficient | 0.4177 | 0.2066 | 0.3637 (mean value) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamiga, W.M.; Ciesielka, W.B. Aeroaocustic Numerical Analysis of the Vehicle Model. Appl. Sci. 2020, 10, 9066. https://doi.org/10.3390/app10249066
Hamiga WM, Ciesielka WB. Aeroaocustic Numerical Analysis of the Vehicle Model. Applied Sciences. 2020; 10(24):9066. https://doi.org/10.3390/app10249066
Chicago/Turabian StyleHamiga, Władysław Marek, and Wojciech Bronisław Ciesielka. 2020. "Aeroaocustic Numerical Analysis of the Vehicle Model" Applied Sciences 10, no. 24: 9066. https://doi.org/10.3390/app10249066
APA StyleHamiga, W. M., & Ciesielka, W. B. (2020). Aeroaocustic Numerical Analysis of the Vehicle Model. Applied Sciences, 10(24), 9066. https://doi.org/10.3390/app10249066




