2. Materials and Methods
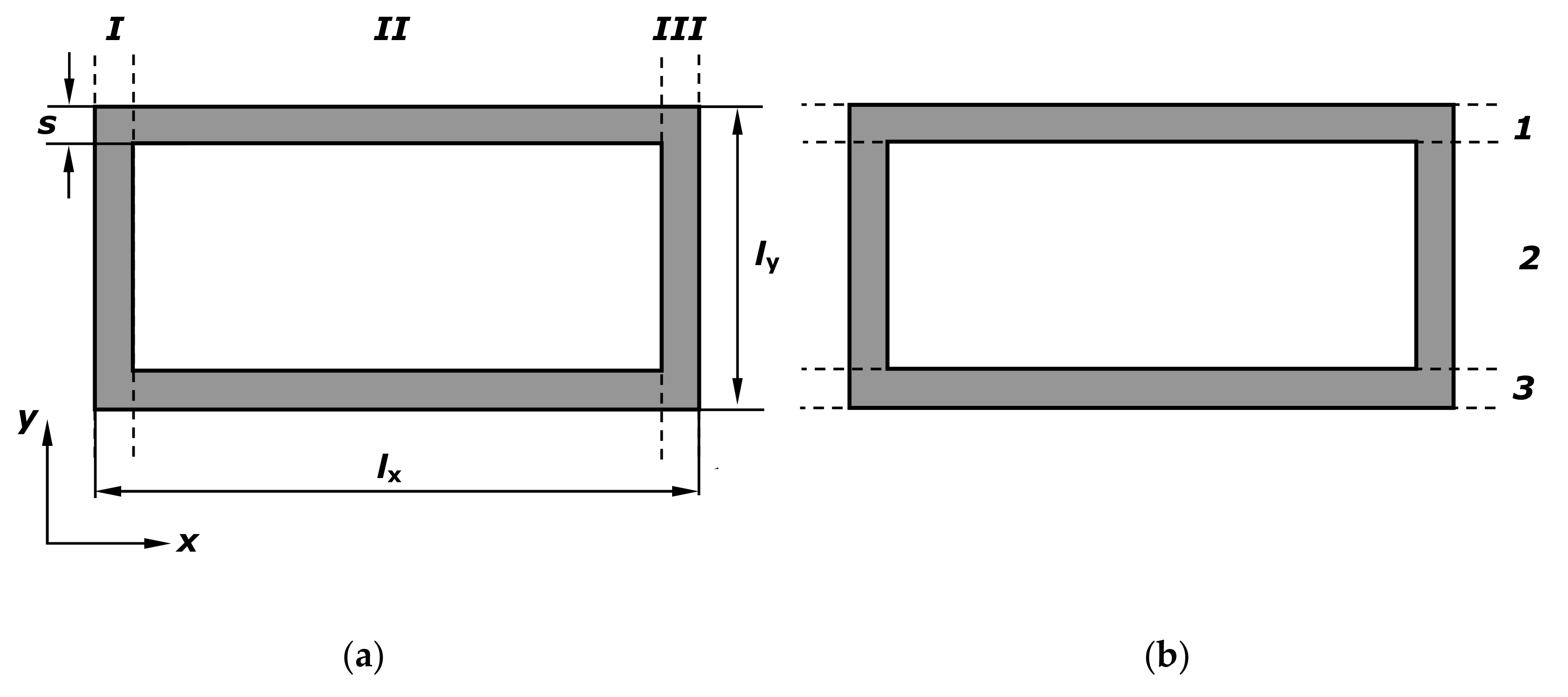
The starting point for the introduction of appropriate relationships is a physical model of the considered phenomenon. This model, as shown in
Figure 2, is a regularly packed package of rectangular sections in which a steady one-dimensional heat flow occurs.
The total thermal resistance of the system presented in
Figure 2 can be broadly considered as a serial connection of two resistances: heat resistance of sections
Rst and thermal contact resistance
Rct, which occurs between the consecutive layers of the package:
The resistances in Equation (1) refer to the unit surface area; therefore, their unit is (m2·K)/W. This unit has all the resistances included in the discussed model. The value of thermal resistance depends on the dimension of the considered layer. The resistance calculated according to the relationship (1) relates to the dimension that is equal to the height of a single layer of sections.
To determine the resistance
Rst, it is necessary to consider all the mechanisms of heat transfer that occur within the sections. The heat is transmitted as a result of conduction in steel walls, conduction and natural convection of gas inside the sections, as well as heat radiation occurring between the inner surfaces of a section. The model considers the changes in the intensity of those mechanisms caused by the increase in temperature. Each of the mentioned mechanisms of heat transfer is assigned a corresponding thermal resistance. This means that when determining the value of
Rst, it is necessary to consider the following: conduction resistances in steel, conduction resistance
Rgs in the gas area, and heat radiation resistance
Rrd. The solution is obtained by assuming one-dimensional heat transfer represented by heat flux q. When solving complex multidimensional heat transfer problems by regarding them as one-dimensional, two assumptions are commonly used: any plane wall normal to the direction of heat flow is isothermal and any plane parallel to the direction of heat flow is adiabatic [
6]. These assumptions lead to two different resistance networks, and thus to different values for the total thermal resistance
Rst-a and
Rst-b. The resistance
Rst-a relates to the division of the section into three vertical zones (I–III) parallel to the direction of heat flow, as shown in
Figure 3a. The resistance
Rst-b relates to the division of the section into three horizontal layers 1–3 (
Figure 3b).
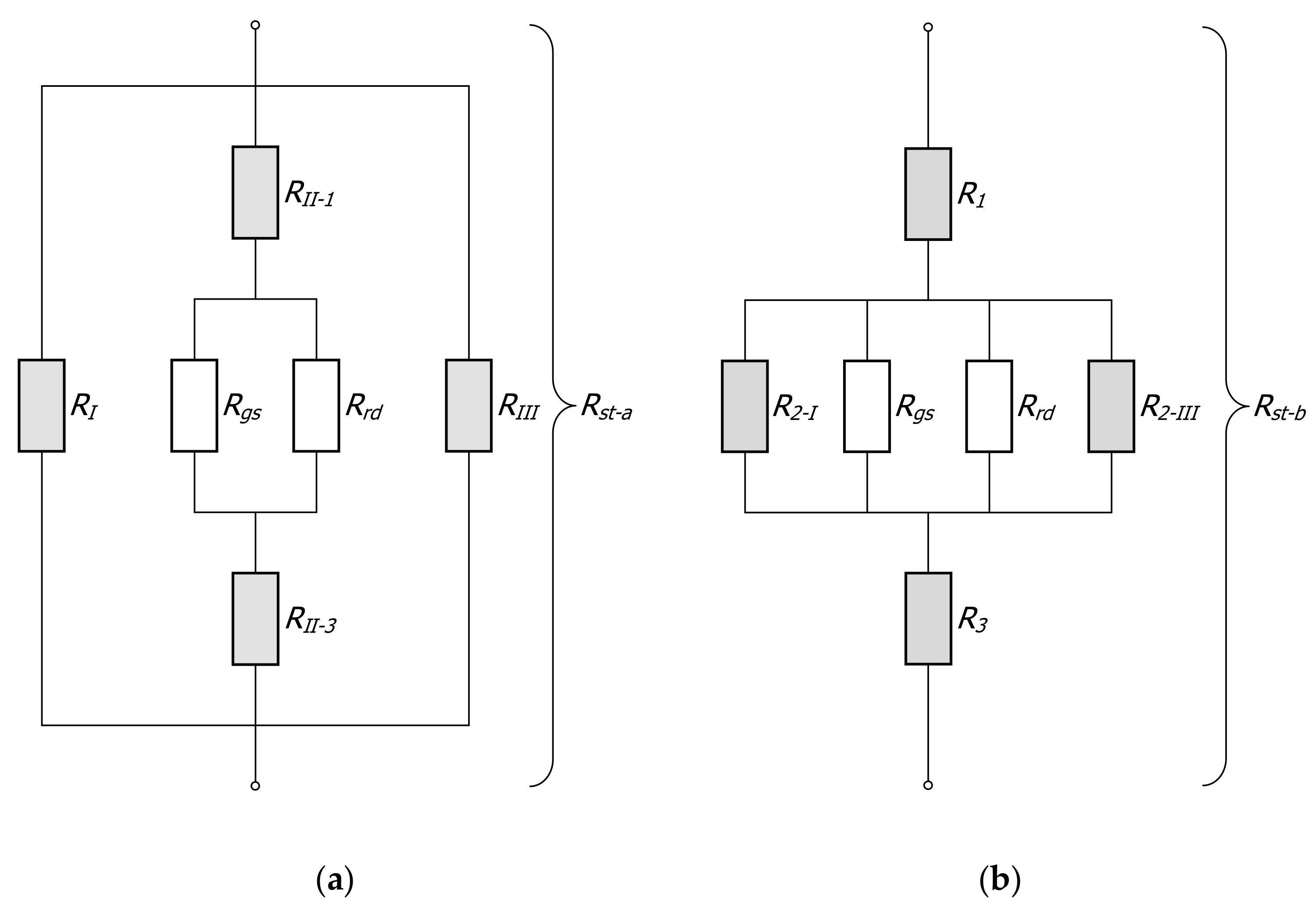
The thermal resistance networks corresponding to the individual divisions of the section are shown in
Figure 4. On this basis, we obtain:
As each division of a section considers different assumptions about the temperature field, the value of
Rst-a is slightly bigger than the value of
Rst-b. This result follows the above-mentioned different properties of the division planes. In the case of division into vertical zones, the division planes are adiabatic, whereas in the case of division into horizontal zones, the division planes are excellent conductors, which underrates the value of resistance. Hence, the final value of the section thermal resistance
Rst is calculated using [
7]:
The resistances occurring in the Equations (2) and (3), which apply to conduction in section walls (they are marked grey in
Figure 4), are described with the following relationships:
where
ks is the thermal conductivity of steel.
The resistance
Rgs applies to the heat flow in the gas area, which is connected with the conduction and the natural convection in a horizontal enclosure occurring at the same time. Both phenomena can be treated jointly as an intensified heat conduction expressed quantitatively by equivalent gas thermal conductivity
keg [
7]:
where
kg is the thermal conductivity of gas and
Nu is the Nusselt number.
The following correlations are recommended for horizontal enclosures that contain air [
6]:
For 4 × 10
5 <
Ra < 10
7:
where
Ra is the Rayleigh number. For an enclosure, this number is defined as:
where
g is gravitational acceleration,
β is the coefficient of volume expansion, Δ
t is the temperature difference between hot and cold surfaces of the enclosure,
Lc is the characteristic length of the geometry (in the section case, this is the distance between the hot and the cold surface),
v is the kinematic viscosity of the fluid, and
Pr is the Prandtl number. For air,
Pr = 0.71 [
6].
Based on the research described in [
8,
9], the values of the Rayleigh number for square 60 mm and 80 mm sections were calculated. The research consisted of heating the sections with a one-dimensional (oriented vertically from the bottom to the top), steady heat flux and measuring the temperature difference Δ
t between their hot (lower—with
th temperature) surface and their cold (upper—with temperature
tc) surface with the use of jacked thermocouples. The research was conducted for the temperatures ranging from room temperature to 750 °C. The values of the Δ
t parameter in the function of the mean temperature of a section
tm = 0,5(
th +
tc) obtained this way are presented in
Figure 5a. Then, the values of the Nusselt number (
Figure 5b) for the above-mentioned sections were calculated using Equations (10)–(12). Depending on the size of a section, natural convection in relation to pure conduction can increase the intensity of heat transfer four to seven times. However, this effect decreases significantly with the temperature increase.
The highest values of the
Nu occur for the temperature of 100 °C. This is mainly caused by changes in the temperature difference Δ
t observed in the area of sections and changes in kinematic viscosity of air. The increase in the
Nu value at the initial stage is attributable to changes in the parameter Δ
t. After exceeding 100 °C, the main effect on convection is from changes in air viscosity. Thus, with a further increase in temperature, the Nusselt number starts to decline rapidly despite a further rise in the difference in temperature. At the same time, the value of parameter Δ
t depends on the other heat transfer mechanisms that are present in the section. All these mechanisms are interrelated and, as a result, the course of convection and the Nusselt value depend on the section geometry and the thermal properties of the steel [
10].
Based on the curves in
Figure 5b for calculating the change in the Nusselt number in relation to temperature, the following relationships were derived.
In case of sections with dimensions smaller than 60 mm, the Nu number does not exceed the value of 1.2. Therefore, for such sections, the influence of natural convection of gas in the model calculations is ignored.
Considering Equation (9), resistance
Rgs can be described by:
Radiation resistance
Rrd can be solved through analysis of the thermal radiation transfer in the system of four flat surfaces that close a space. The methodology for the determination of resistance
Rrd for this system was described in [
11]. When the temperature drop Δ
T in the system is much smaller than its mean absolute temperature
Tm [K], radiation resistance can be described by:
where σ
c is the Stefan–Boltzmann constant and
ε is the emissivity of the section surface.
According to Equation (1), the intensity of heat flow in the package area also depends on the thermal contact resistance
Rct. This resistance expresses the heat transmitted between subsequent layers of the package in a quantitative way. Due to shape errors of the sections, contact between adjacent layers does not occur across the entire surface of the package, but only on small discrete contour areas whose sizes and spacing are completely random. This is the reason why the thermal contact resistance cannot be described by the commonly used analytical relationships [
12,
13,
14]. Furthermore, the experimental investigation of this resistance also proves difficult due to the hollow interior of the sections, which makes it impossible to measure the temperature distribution along those elements. To overcome this problem, we assumed that the thermal contact resistance of the adjacent sections is similar to the thermal contact resistance in the packed bed of square or flat bars. The pictorial photographs of these type of beds are shown in
Figure 6.
The total thermal resistance
Rto of such beds was determined experimentally using a guarded hot plate apparatus. The operating principle of this device is described in the standards [
15,
16]. During these tests, the beds of bars were heated with a one-dimensional, steady heat flux rate. The moment the fixed state was reached, the temperature difference Δ
t between the surfaces of the sample perpendicular to the direction of heat flow was measured. The thermal resistance of the sample relating to the dimension equal to a single layer of bars was calculated from the relationship:
where
qs is the heat flux in the sample,
lb is the dimension of the layer of bars, and
lsp is the dimension of the tested sample (the dimensions
lb and
lsp relate to the direction congruent with the heat flow).
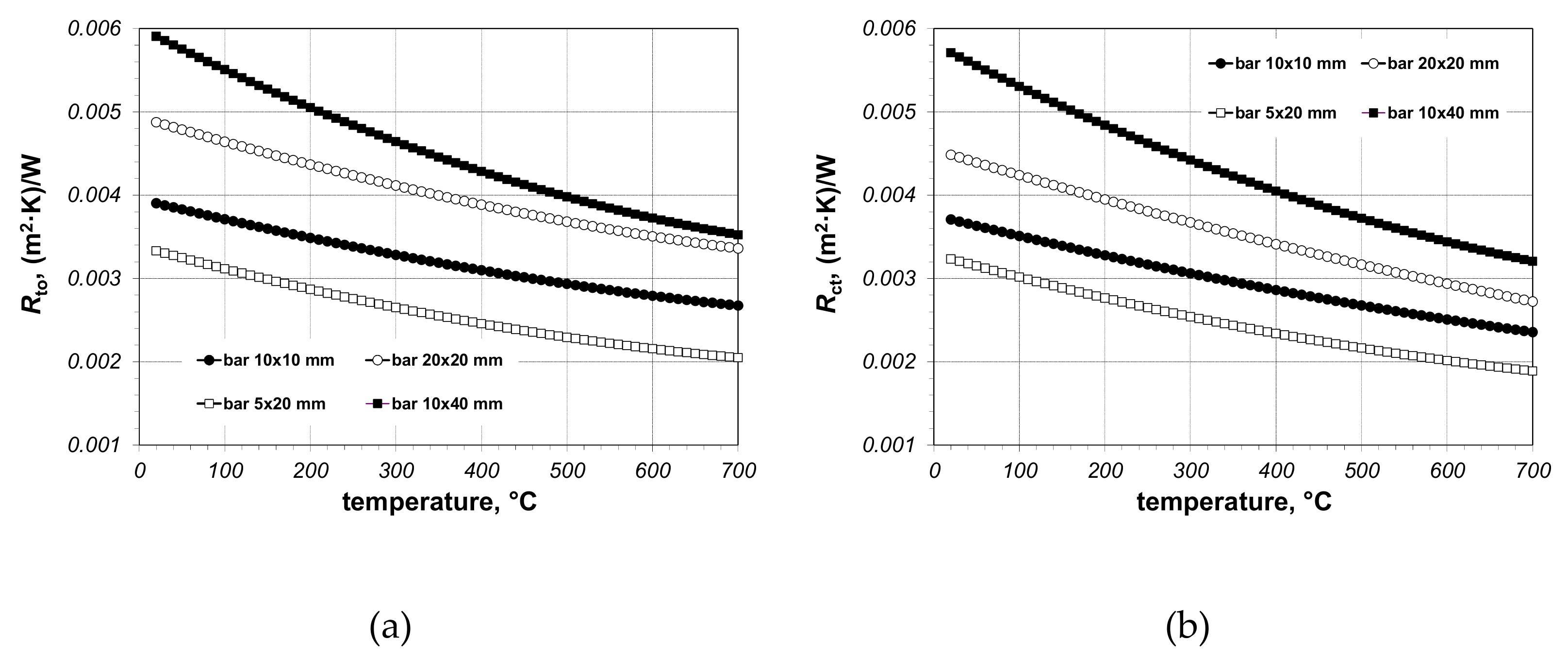
Due to a series of measurements for bigger and bigger values of
qs, it is possible to determine the change in resistance
Rto for a set temperature range. In the described tests, the resistance
Rto was set for four samples (two beds of rectangular 10 mm × 10 mm and 20 × 20 mm bars, two beds of flat 5 × 20 mm and 10 × 40 mm bars) in the temperature range of 50–650 °C. The smoothed results of these measurements are presented in
Figure 7a.
If the bar thermal conductivity
kb is known, the thermal contact resistance of such samples can be calculated from the following relation:
The
lb dimension for individual samples took the following values: 0.01, 0.02 and 0.005 m. The results of the
Rct resistance calculations according to the Equation (18) are presented in
Figure 7b.
The changes in the
Rct resistance for all the tested samples with respect to temperature
t can be approximated by the polynomial:
The lowest and highest values of the thermal contact resistance
Rct are described by the following equations:
where
Rct-min resistance corresponds to the bed of 5 × 20 mm bars and
Rct-max resistance corresponds to the bed of 10 × 40 mm bars.
Using Equations (20) and (21), two limiting values of the resistance Rto can be determined. The total thermal resistance of a given section package should remain between these values. This approach appears to be reasonable because the resistance Rto expressing the ability of a given package to transfer heat. For the considered system, this ability is largely dependent on the contact conditions in adjacent sections layers, which may vary between different section types.
3. Results and Discussion
In the presented model, the following parameters are used as input data: section dimensions (width
lx, height
ly, and wall thickness
s), emissivity of the section surface
ε, Nusselt number
Nu, thermal conductivities of steel
ks, and gas
kg. The last two parameters with respect to temperature are described by the following equations [
17]:
Equation (22) refers to steel with a carbon content of 0.2%, whereas Equation (23) refers to the air. For the emissivity of section surface, a value of 0.5 was assumed, which relates to the rolled carbon steel [
18].
The presented model enables the analysis of the process of heat flow in the area of the package of sections, both in a quantitative and qualitative manner. The quantitative analysis relates to determining the value of individual resistances, whereas the quantitative analysis consists of determining the share of the individual mechanisms in the heat transfer that occurs while heating the package. The results of the calculations presented below relate to four packages of the following sections: 20 × 40 × (2.5) mm, 40 × 40 × (3) mm, 60 × 60 × (3) mm, and 80 × 80 × (3) mm, where the number in parentheses is the thickness of a section wall.
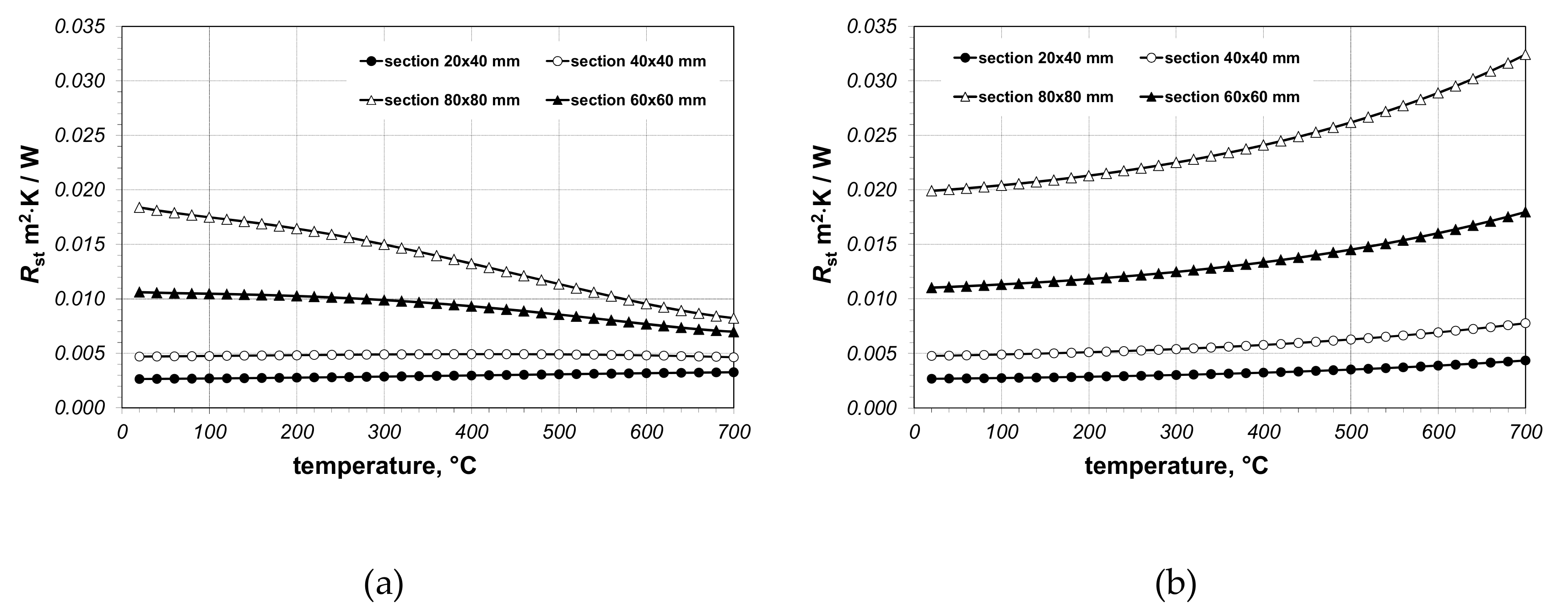
First, the results of the calculations of the
Rst resistance of the sections are presented. This parameter was calculated for two cases. Case I applies to the situations when all the types of heat transfer (conduction, radiation and convection) occur within a section; the results of these calculations are presented in
Figure 8a. Case II applies to the situations when only heat conduction occurs within a section (gas convection and heat radiation between the inner surfaces of a section were ignored); the results of these calculations are presented in
Figure 8b. By comparing the diagrams, it is possible to notice that the difference between the values of
Rst resistance for both cases increases with temperature; the bigger the size of a section, the bigger this difference. This effect is caused by the intensity of heat radiation increasing with the temperature function (proportional to the third power of
Tm) and the distance between the surfaces that exchange heat.
To quantitatively express the differences in the value of
Rst resistance between case I and case II, a relative percentage difference Δ
Rst was calculated, which was defined by the following relationship:
where
Rst-I is the value of resistance of a section in case I and
Rst-II is the value of resistance of a section in case II.
The values of the Δ
Rst parameter obtained for individual sections for chosen temperature values are collated in
Table 1. The maximum value of Δ
Rst was nearly 300%.
In the case of the performed analysis, the shape of the relationship between the
Rst resistance of individual sections and the
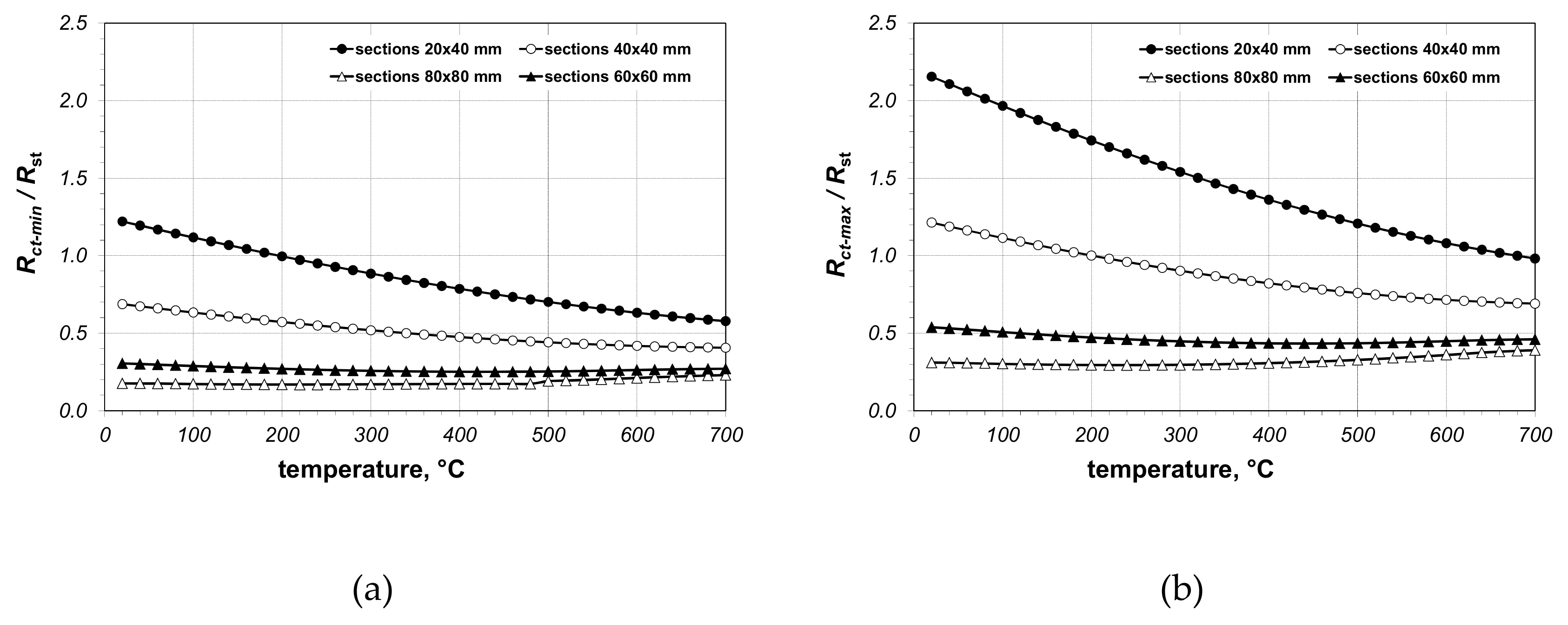
Rct resistance of contact conduction is interesting. To show the problem from the quantitative perspective, the quotient of resistances
Rct/Rst was calculated for each section. The calculations were run both for the maximal and the minimal value of
Rct. The results of these calculations are collated in
Figure 9. In most cases, the
Rst resistance was characterized by a higher value.
At the end of the performed analysis, the results of calculations of
Rto resistance of packages will be discussed. These results are presented in
Figure 10. The total thermal resistance value as well as its changes in the temperature function depend significantly on the section geometry. The larger the sections size, the greater the changes of
Rto. The values of
Rto-min and
Rto-max obtained for each package for 20 and 700 °C are presented in
Table 2. The minimal and maximal values for all packages were 0.0051 and 0.0238 (m
2·K)/W, respectively. This means that the resistance
Rto varies more than four and a half times.
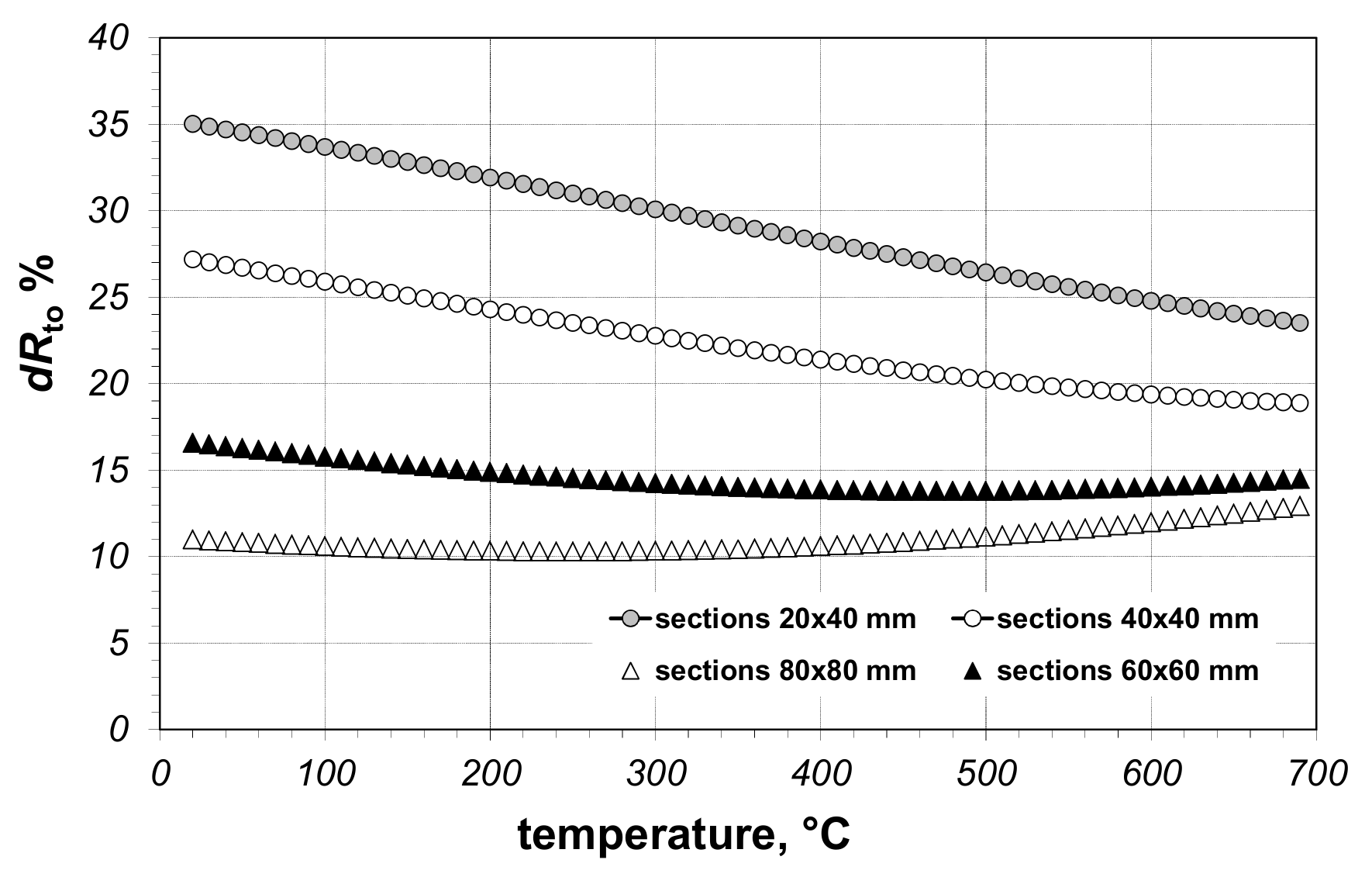
To perform a more detailed analysis, one additional parameter was calculated. This parameter, denoted as
dRto, describes percentage changes in the resistance
Rto in relation to its mean value and is expressed as:
The values of the parameter
dRto are shown in
Figure 11. The larger the section’s dimensions, the smaller the values of the considered parameter. At the same time, with the increase in dimensions of the sections in the package, we observe smaller changes in
dRto in the temperature function. The values of the parameter
dRto obtained for the extreme temperatures are summarized in
Table 3.
To evaluate the correctness of the presented model, the computed values of
Rto were compared with the experimental results. The experimental values of
Rto were measured using a guarded hot plate apparatus [
19]. The device works according to the principles described in the standards [
15,
16]. The measurement data also apply to the same sections that were analyzed in the calculations. The tests consisted of heating flat beds of sections (see
Figure 2) with a steady, one-dimensional heat flux rate. The moment the fixed state was reached, the temperature difference Δ
ts between the outer layers of the sample perpendicular to the direction of heat flow was measured. The thermal resistance of the sample relating to the dimension of a single layer of section was calculated from the relationship:
where
qs is the heat flux in the sample,
lst is the dimension of a layer of sections, and
lsp is the dimension of the tested sample (the
lst and
lsp dimensions relate to the direction congruent with the direction of heat flow).
The experimental values of
Rto are shown in
Figure 10 with the use of black dots. In case of the 20 × 40 and 60 × 60 mm sections, the measurement values of
Rto almost exactly coincided with the modelled values
Rto-min, while for the 40 × 40 mm sections, experimental data were very close to the modelled values
Rto-max. For these three cases, the considered model reflects the temperature changes in the
Rto values relatively well. A different situation was observed for the 80 × 80 mm sections. In this case, all the measured results were distinctly lower than the calculated values. This discrepancy, however, diminished with temperature increase.
For the sections of 20 × 40 and 60 × 60 mm, the maximum differences between the measured and the model Rto-min values were 6.1% and 5.2%, respectively. These differences are similar to measurement uncertainty, which, for the used experimental stand, is about 5%. For the 80 × 80 mm sections, the maximum discrepancy between the modelled and experimental values was 26%. The lack of consistent results for this package can be explained by the excessive measurement error. The samples investigated in a guarded hot plate apparatus should have a suitable proportion of dimensions: the height of the sample cannot be too large in relation to its transverse dimensions. In the case of the sample from 80 × 80 mm sections (due to their large dimensions), this condition was not fulfilled. This situation caused undesirable heat loss from the side surface of the sample. As a consequence of these losses, the values of the measured parameter were characterized by an additional error. This caused the measured values to be too low, but it is very difficult to estimate this inaccuracy. For this reason, the values of total thermal resistance measured for this package cannot be used for model evaluation.