Estimation of the High-Frequency Attenuation Parameter Kappa for the Zagreb (Croatia) Seismic Stations
Abstract
Featured Application
Abstract
1. Introduction
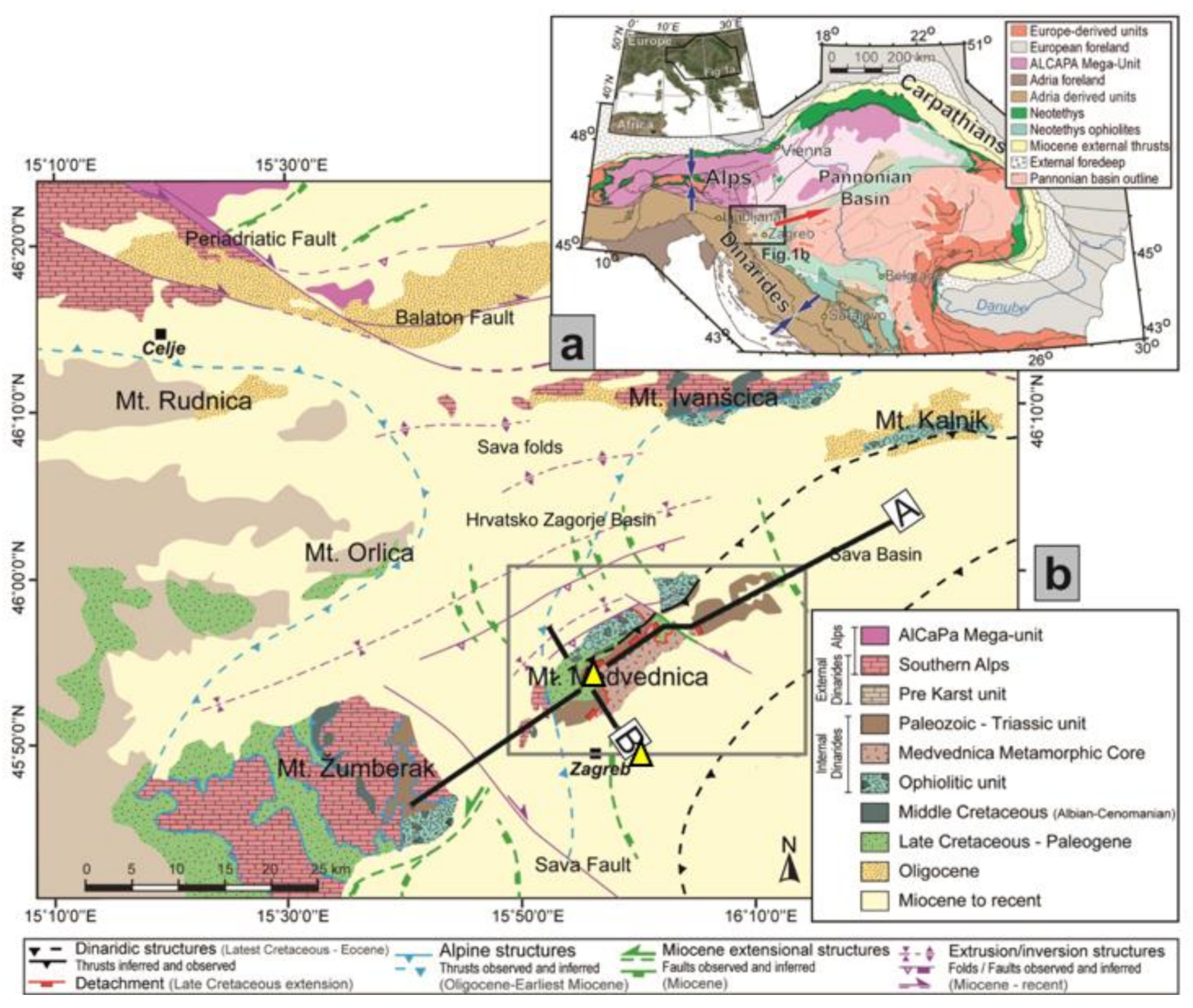
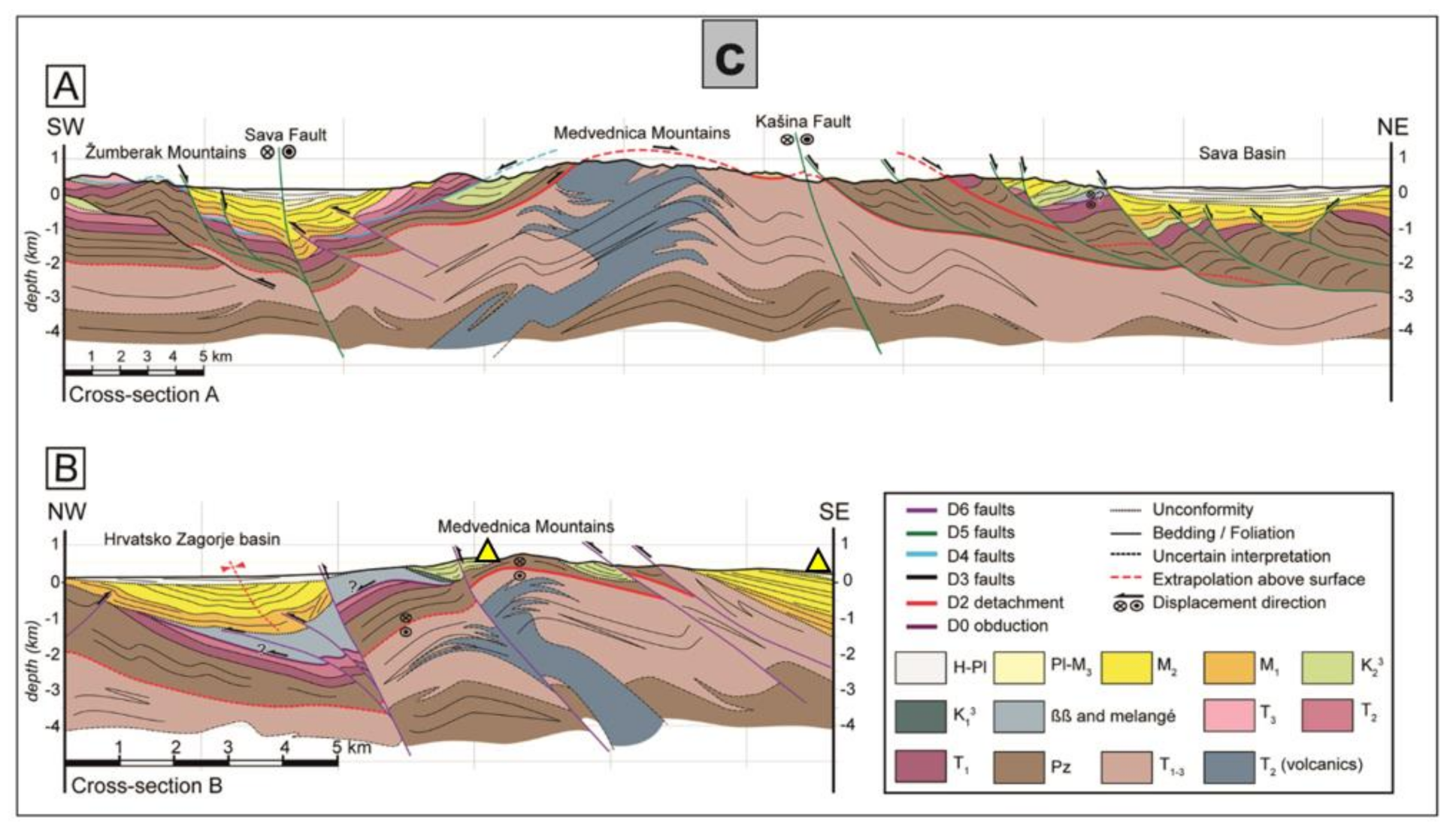
2. Study Area: Geological Features and Seismicity
2.1. Geological Features of the Zagreb Area
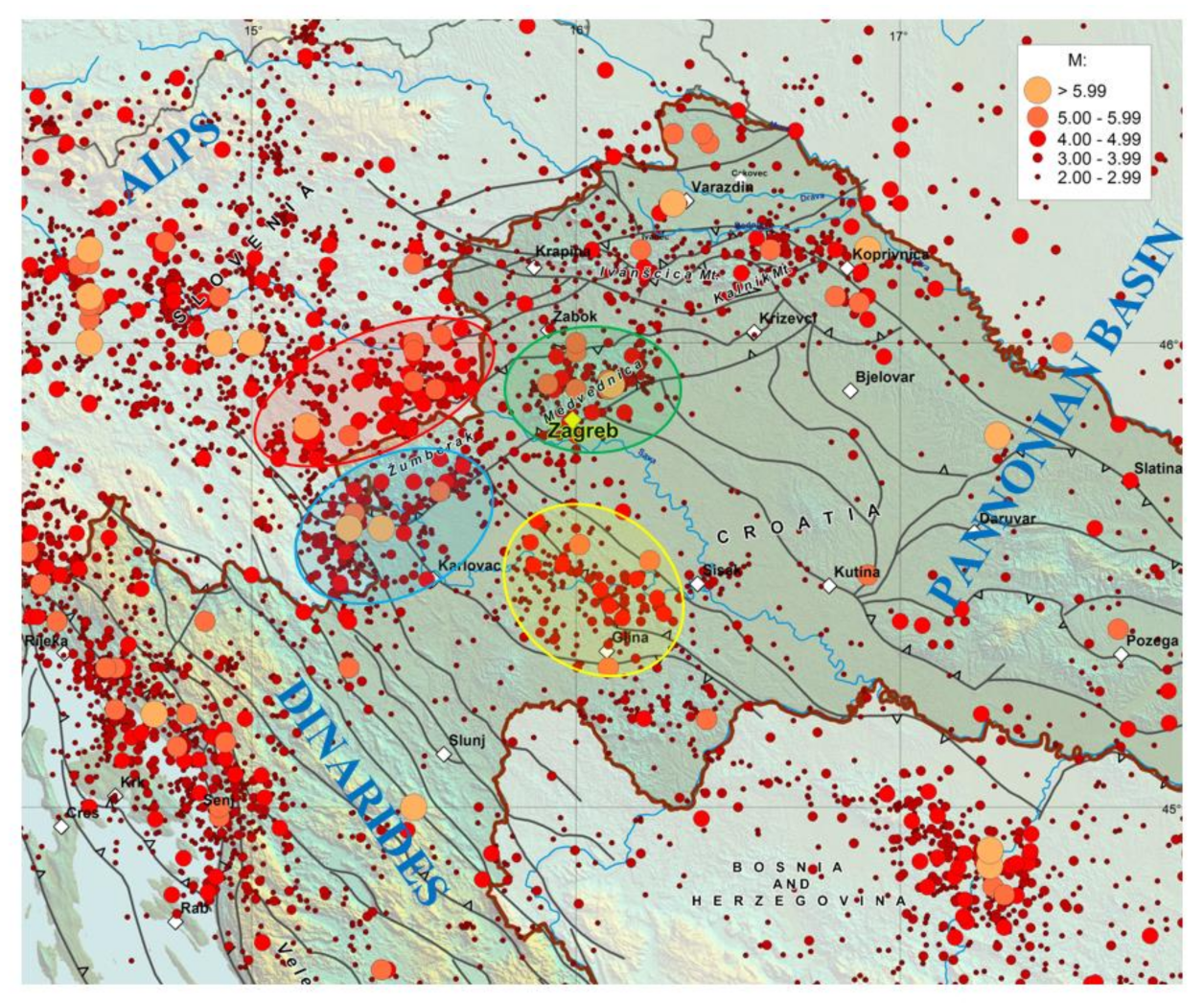
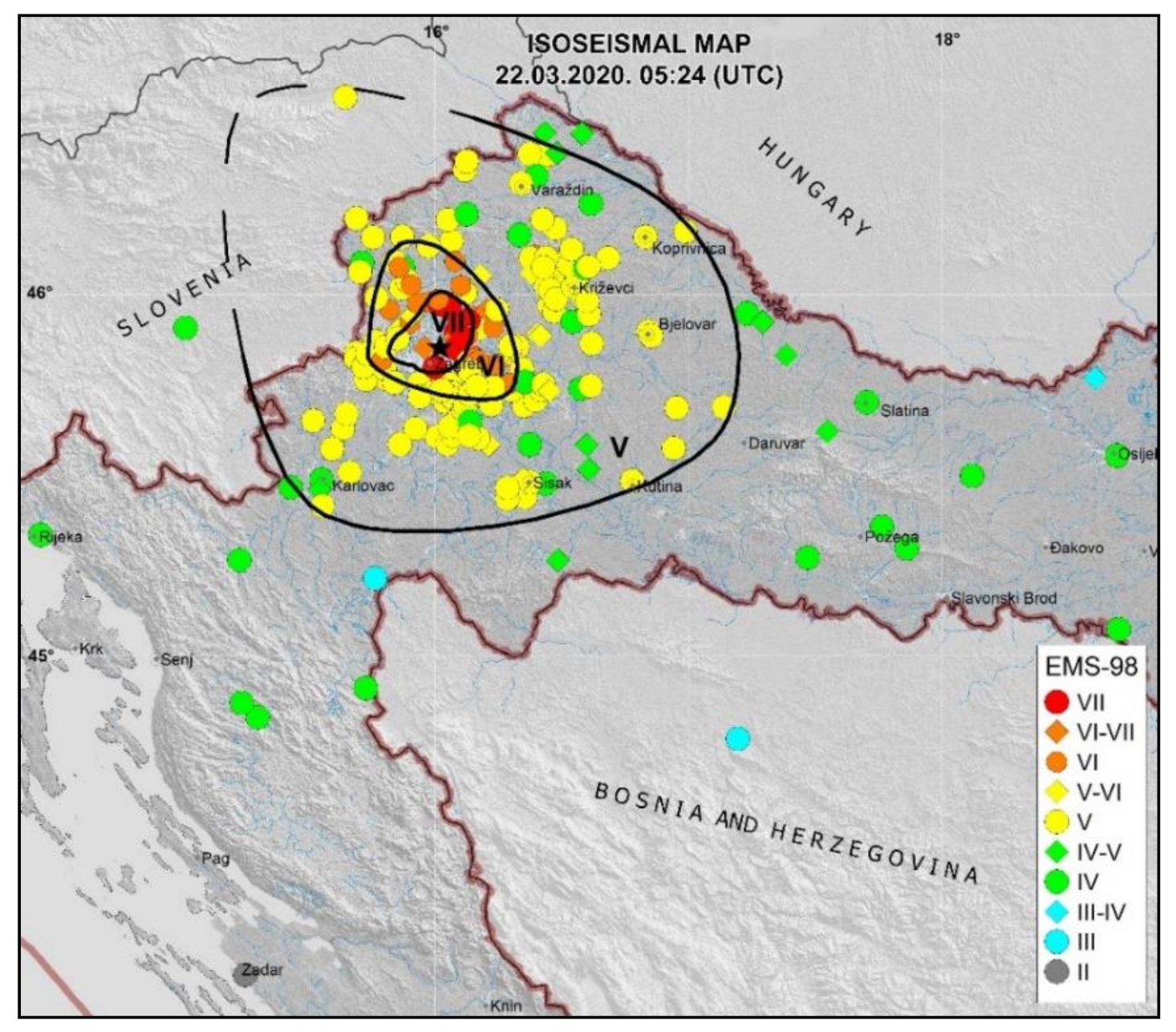
2.2. Seismicity of the Zagreb Area
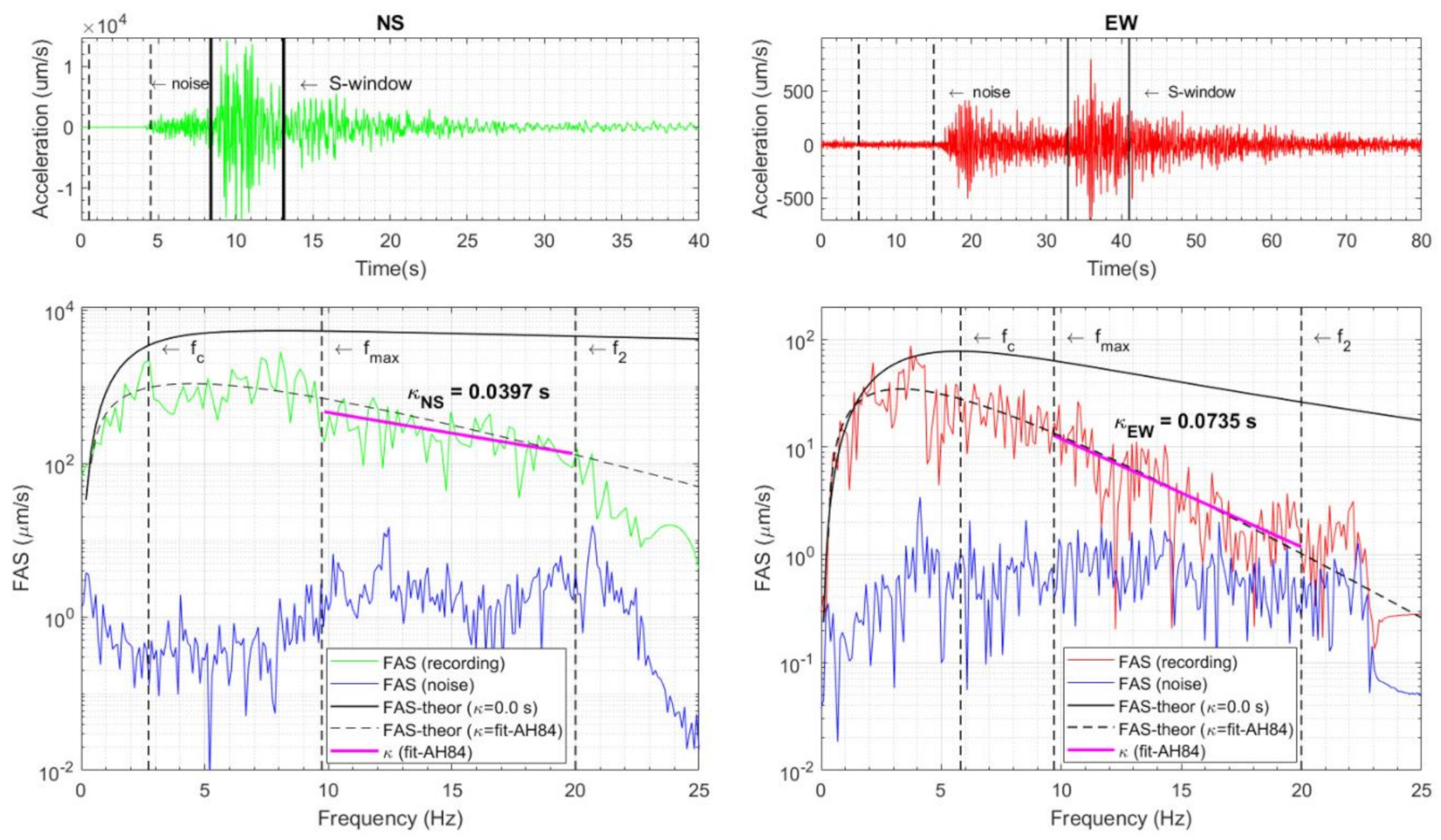
3. Methods and Data
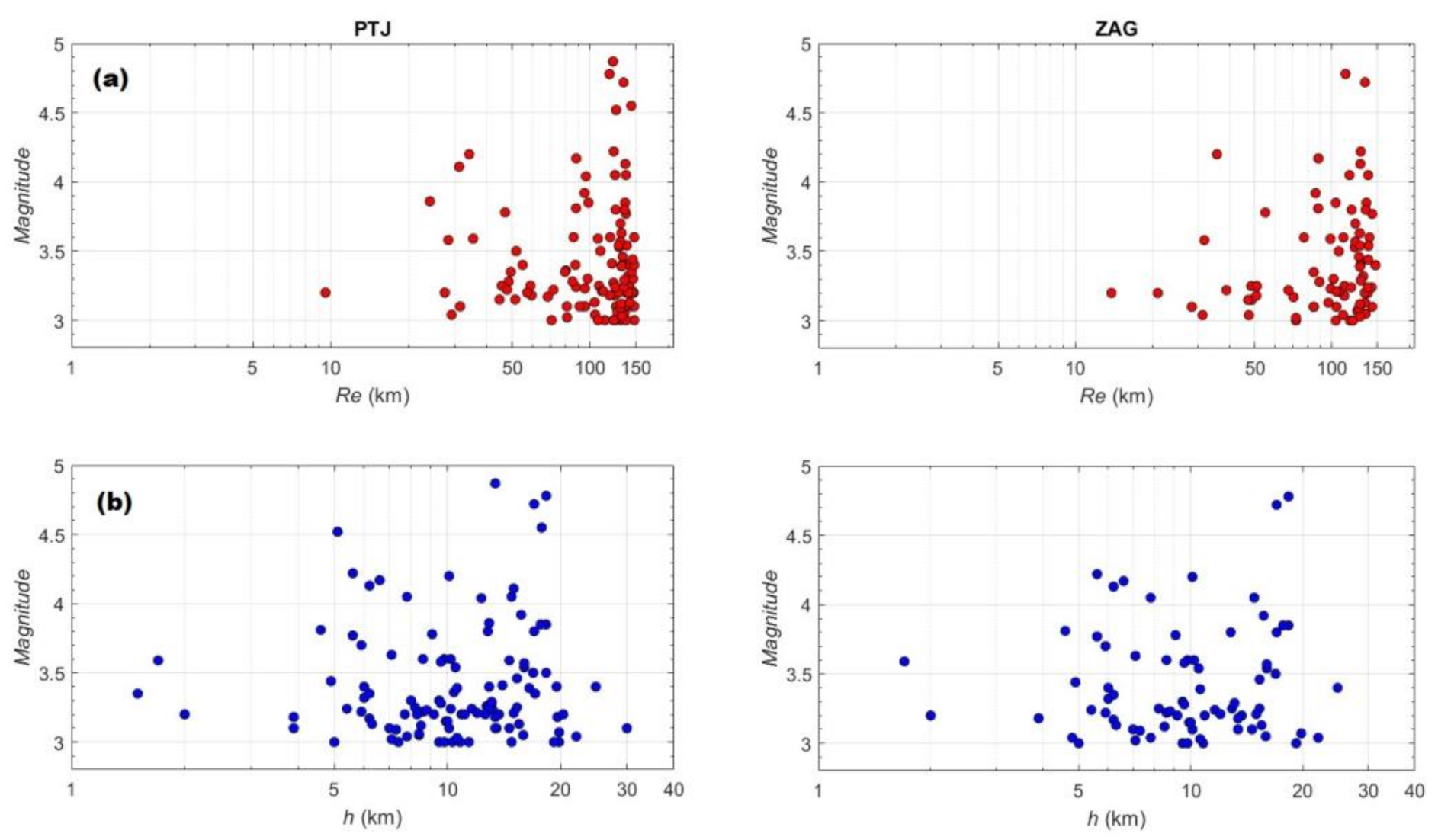
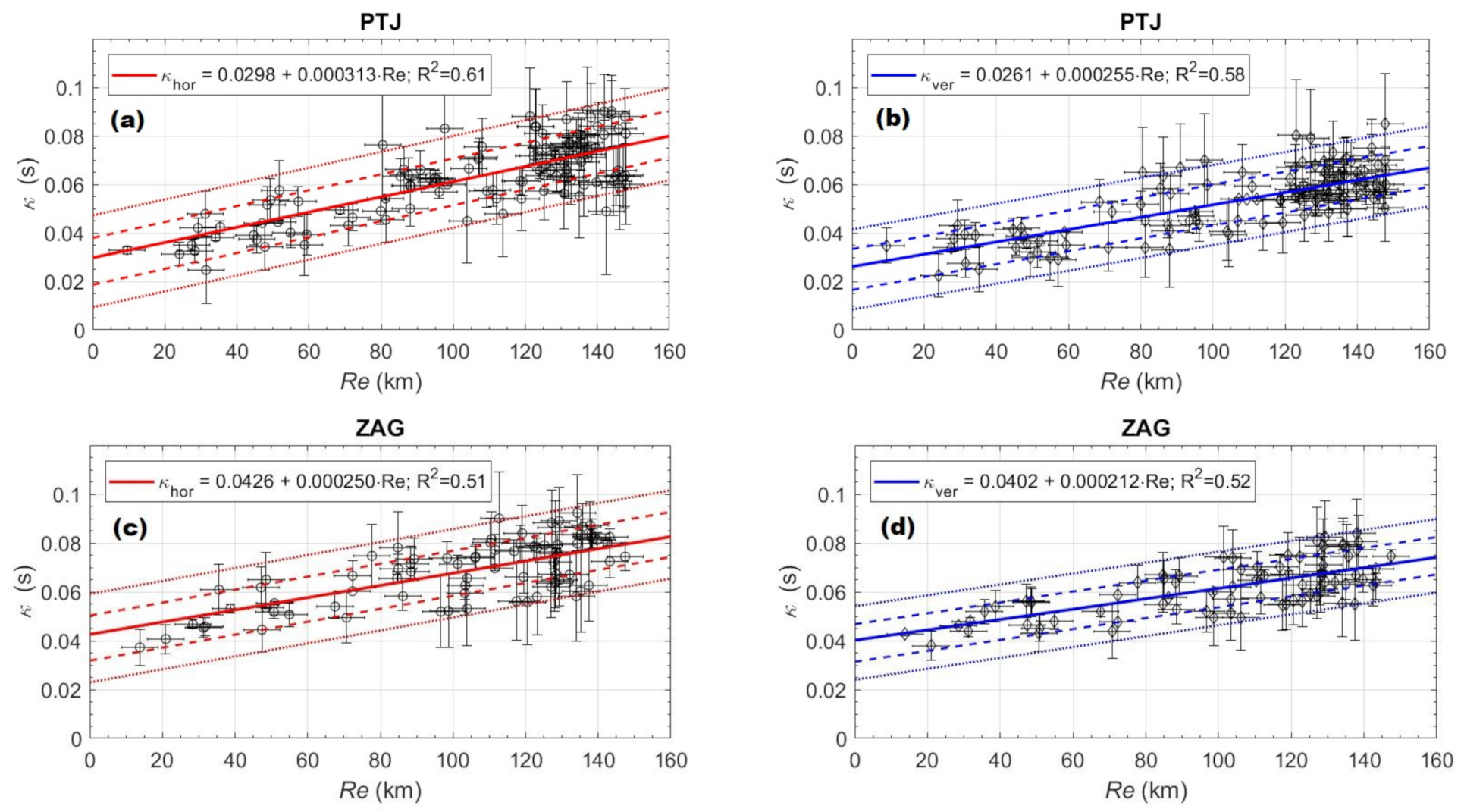
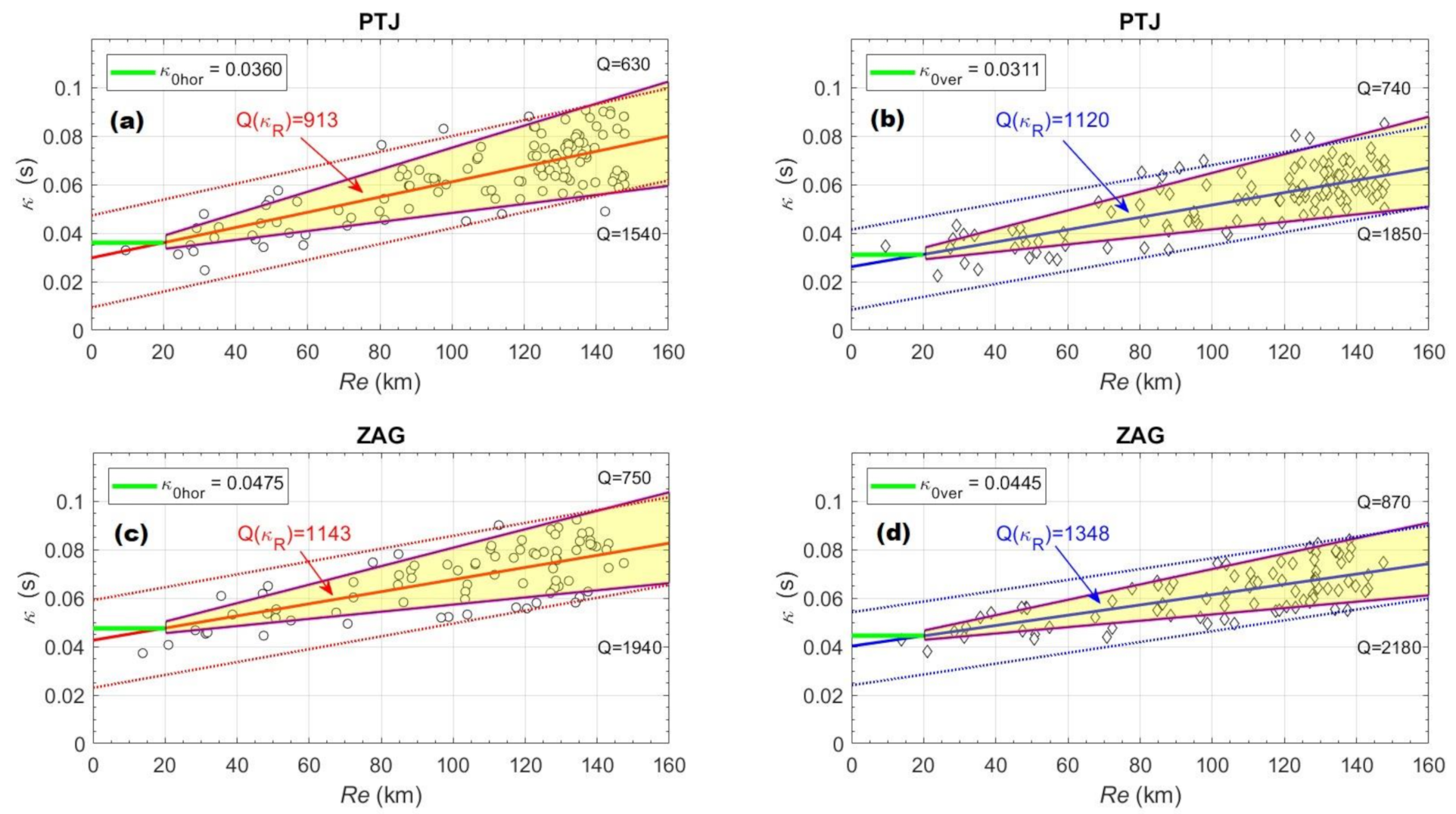
4. Results
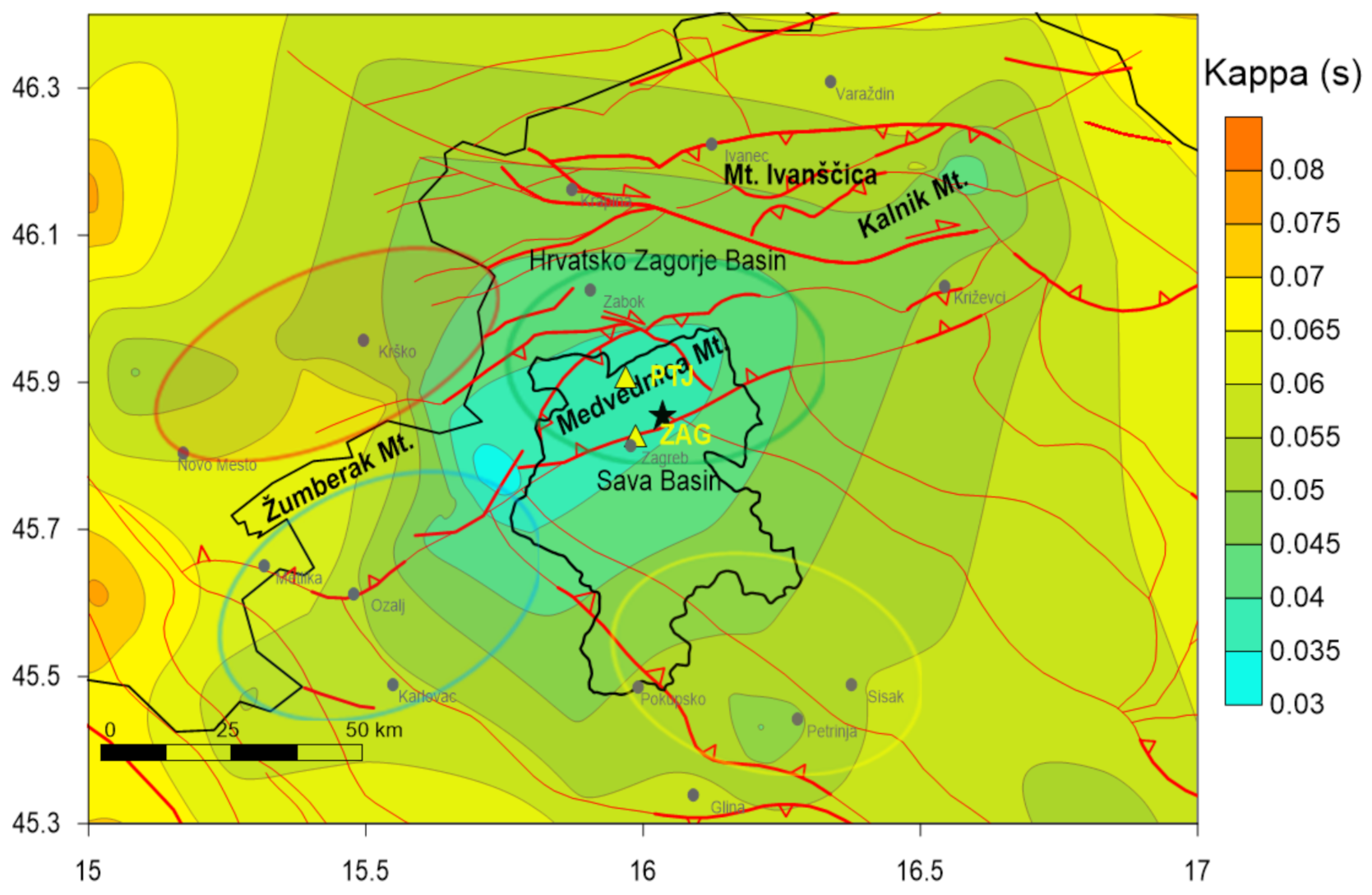
5. Discussion
6. Conclusions
- Site κ0 values estimated from the extrapolation to zero distance (using traditional linear regression and error-in-variables regression) are within the range of the uncertainty (±1 standard deviation) with a constrained κ0 value;
- Estimated κ0 values for PTJ (0.0283–0.0360 s) and ZAG (0.0411–0.4750 s) correlated with VS30 values are within the range of existing κ0‒VS30 correlations, showing that κ0 has lower values for sites on harder rocks (lower attenuation) and higher κ0 values on softer rocks (higher attenuation);
- Comparison of the high-frequency coda attenuation values with frequency independent, Qc(f) and Q(κR) for both stations can be considered comparable when looking at average values with the assumption that they are affected by the same regional characteristics;
- The lowest values are spatially distributed within a few kilometres around the stations due to near-site effects;
- Variations in observed distribution between lower and higher attenuation subset areas is clearly under the influence of local and regional geological structures that are distributed predominantly within regional active faults and complex tectonic structure.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Markušić, S.; Stanko, D.; Korbar, T.; Sović, I. Estimation of near-surface attenuation in the tectonically complex contact area of the northwestern External Dinarides and the Adriatic foreland. Nat. Hazards Earth Syst. Sci. 2019, 19, 2701–2714. [Google Scholar] [CrossRef]
- Brune, J.N. Tectonic stress and the spectra of seismic shear waves from earthquakes. J. Geophys. Res. 1970, 75, 4997–5009. [Google Scholar] [CrossRef]
- Hanks, T.C. fmax. Bull. Seismol. Soc. Am. 1982, 72, 1867–1879. [Google Scholar]
- Cormier, V.F. The Effect of Attenuation on Seismic Body Waves. Bull. Seismol. Soc. Am. 1982, 72, 169–200. [Google Scholar]
- Anderson, J.G.; Hough, S.E. A model for the shape of the Fourier amplitude spectrum of acceleration at high frequencies. Bull. Seismol. Soc. Am. 1984, 74, 1969–1993. [Google Scholar]
- Edwards, B.; Fäh, D.; Giardini, D. Attenuation of seismic shear wave energy in Switzerland. Geophys. J. Int. 2011, 185, 967–984. [Google Scholar] [CrossRef]
- Ktenidou, O.J.; Gélis, C.; Bonilla, L.F. A study on the variability of Kappa (κ) in a Borehole: Implications of the computation process. Bull. Seismol. Soc. Am. 2013, 103, 1048–1068. [Google Scholar] [CrossRef]
- Hanks, T.C.; McGuire, R.K. The character of high-frequency strong ground motion. Bull. Seismol. Soc. Am. 1981, 71, 2071–2095. [Google Scholar]
- Boore, D.M. Stochastic simulation of high-frequency ground motions based on seismological models of the radiated spectra. Bull. Seismol. Soc. Am. 1983, 73, 1865–1894. [Google Scholar]
- Boore, D.M. Simulation of Ground Motion Using the Stochastic Method. Pure Appl. Geophys. 2003, 160, 635–676. [Google Scholar] [CrossRef]
- Ktenidou, O.-J.; Cotton, F.; Abrahamson, N.A.; Anderson, J.G. Taxonomy of κ: A review of definitions and estimation approaches targeted to applications. Seismol. Res. Lett. 2014, 85, 135–146. [Google Scholar] [CrossRef]
- Biro, Y.; Renault, P. Importance and impact of host-to-target conversions for ground motion prediction equations in PSHA. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012. [Google Scholar]
- Delavaud, E.; Cotton, F.; Akkar, S.; Scherbaum, F.; Danciu, L.; Beauval, C.; Drouet, S.; Douglas, J.; Basili, R.; Sandikkaya, M.A.; et al. Toward a ground-motion logic tree for probabilistic seismic hazard assessment in Europe. J. Seismol. 2012, 16, 451–473. [Google Scholar] [CrossRef]
- Rathje, E.M.; Ozbey, M.C. Site-Specific Validation of Random Vibration Theory-Based Seismic Site Response Analysis. J. Geotech. Geoenviron. Eng. 2006, 132, 911–922. [Google Scholar] [CrossRef]
- Markušić, S.; Stanko, D.; Korbar, T.; Belić, N.; Penava, D.; Kordić, B. The Zagreb (Croatia) M5.5 earthquake on 22 March 2020. Geosciences 2020, 10, 252. [Google Scholar] [CrossRef]
- Tomljenović, B.; Csontos, L. Neogene-quaternary structures in the border zone between Alps, Dinarides and Pannonian Basin (Hrvatsko zagorje and Karlovac Basins, Croatia). Int. J. Earth Sci. 2001, 90, 560–578. [Google Scholar] [CrossRef]
- Schmid, S.M.; Bernoulli, D.; Fügenschuh, B.; Matenco, L.; Schefer, S.; Schuster, R.; Tischler, M.; Ustaszewski, K. The Alpine-Carpathian-Dinaridic orogenic system: Correlation and evolution of tectonic units. Swiss J. Geosci. 2008, 101, 139–183. [Google Scholar] [CrossRef]
- Herak, D.; Herak, M.; Tomljenović, B. Seismicity and earthquake focal mechanisms in North-Western Croatia. Tectonophysics 2009, 465, 212–220. [Google Scholar] [CrossRef]
- van Gelder, I.E.; Matenco, L.; Willingshofer, E.; Tomljenović, B.; Andriessen, P.A.M.; Ducea, M.N.; Beniest, A.; Gruić, A. The tectonic evolution of a critical segment of the Dinarides-Alps connection: Kinematic and geochronological inferences from the Medvednica Mountains, NE Croatia. Tectonics 2015, 34, 1952–1978. [Google Scholar] [CrossRef]
- Basch, O. Basic Geological Map 1:100 000, Sheet Ivanić-Grad; Institute of Geology: Zagreb, Croatia; Federal Geological Institute: Belgrade, Serbia, 1981. (In Croatian) [Google Scholar]
- Šikić, K.; Basch, O.; Šimunić, A. Basic Geological Map 1:100.000, Sheet Zagreb; Institute of Geology: Zagreb, Croatia; Federal Geological Institute: Belgrade, Serbia, 1977. (In Croatian) [Google Scholar]
- HGI. Geological Map of the Republic of Croatia in Scale 1:300.000; Hrvatski Geološki Institut—Croatian Geological Survey: Zagreb, Croatia, 1999; Available online: http://webgis.hgi-cgs.hr/gk300/default.aspx (accessed on 3 October 2020).
- Matoš, B.; Tomljenović, B.; Trenc, N. Identification of tectonically active areas using DEM: A quantitative morphometric analysis of Mt. Medvednica, NW Croatia. Geol. Q. 2014, 58, 51–70. [Google Scholar] [CrossRef][Green Version]
- Vrabec, M. Style of post-sedimentary deformation in the Plio-Quaternary Velenje basin, Slovenia. Neues Jahrb. Geol. Paläontol. 1999, 8, 449–463. [Google Scholar]
- Kuk, V.; Prelogović, E.; Sović, I.; Kuk, K.; Šariri, K. Seismological and seismo-tectonical properties of the wider Zagreb area. Građevinar 2000, 52, 647–653. Zagreb (In Croatian) [Google Scholar]
- Torbar, J. Report on the Zagreb Earthquake of November 9, 1880; Book I; Yugoslav Academy of Sciences and Arts: Zagreb, Croatia, 1882; pp. 1–144. (In Croatian) [Google Scholar]
- Herak, M.; Herak, D.; Markušić, S. Revision of the earthquake catalogue and seismicity of Croatia, 1908–1992. Terra Nova 1996, 8, 86–94. [Google Scholar] [CrossRef]
- Ivančić, I.; Herak, D.; Markušić, S.; Sović, I.; Herak, M. Seismicity of Croatia in the period 2002–2005. Geofizika 2006, 23, 87–103. [Google Scholar]
- Ivančić, I.; Herak, D.; Herak, M.; Allegretti, I.; Fiket, T.; Kuk, K.; Markušić, S.; Prevolnik, S.; Sović, I.; Dasović, I.; et al. Seismicity of Croatia in the period 2006–2015. Geofizika 2018, 35, 69–98. [Google Scholar] [CrossRef]
- Van Houtte, C.; Drouet, S.; Cotton, F. Analysis of the origins of κ (kappa) to compute hard rock to rock adjustment factors for GMPEs. Bull. Seismol. Soc. Am. 2011, 101, 2926–2941. [Google Scholar] [CrossRef]
- Van Houtte, C.; Ktenidou, O.J.; Larkin, T.; Holden, C. Hard-site κ0 (kappa) calculations for Christchurch, New Zealand, and comparison with local ground-motion prediction models. Bull. Seismol. Soc. Am. 2014, 104, 1899–1913. [Google Scholar] [CrossRef]
- Ktenidou, O.J.; Abrahamson, N.A.; Drouet, S.; Cotton, F. Understanding the physics of kappa (κ): Insights from a downhole array. Geophys. J. Int. 2015, 203, 678–691. [Google Scholar] [CrossRef]
- Perron, V.; Hollender, F.; Bard, P.Y.; Gélis, C.; Guyonnet-Benaize, C.; Hernandez, B.; Ktenidou, O.J. Robustness of kappa (κ) measurement in low-to-moderate seismicity areas: Insight from a site-specific study in provence, France. Bull. Seismol. Soc. Am. 2017, 107, 2272–2292. [Google Scholar] [CrossRef]
- Dasović, I.; Herak, M.; Herak, D. Coda-Q and its lapse time dependence analysis in the interaction zone of the Dinarides, the Alps and the Pannonian basin. Phys. Chem. Earth 2013, 63, 47–54. [Google Scholar] [CrossRef]
- York, D.; Evenson, N.; Martinez, M.; Delgado, J. Unified equations for the slope, intercept, and standard errors of the best straight line. Am. J. Phys. 2004, 72, 367–375. [Google Scholar] [CrossRef]
- Ktenidou, O.J.; Silva, W.; Darragh, R.; Abrahamson, N.; Kishida, T. Squeezing kappa (κ) out of the transportable array: A strategy for using bandlimited data in regions of sparse seismicity. Bull. Seismol. Soc. Am. 2017, 107, 256–275. [Google Scholar] [CrossRef]
- Palmer, S.M.; Atkinson, G.M. The High-Frequency decay slope of spectra (kappa) for M ≥ 3.5 earthquakes on rock sites in Eastern and Western Canada. Bull. Seismol. Soc. Am. 2020, 110, 471–488. [Google Scholar] [CrossRef]
- Chung, D.H.; Bernreuter, D.L. The Effect of Regional Variation of Seismic Wave Attenuation on the Strong Ground Motion from Earthquakes; Technical Report: NUREG/CR-1655; UCRL-53004; INIS-XA-N-048; U.S. Nuclear Regulatory Commission: Washington, DC, USA, 1981. [Google Scholar]
- Allen, T.I.; Wald, D.J. Topographic Slope as a Proxy for Global Seismic Site Conditions (VS30) and Amplification around the Globe; U.S. Geological Survey Open-File Report 2007-1357; U.S. Geological Survey: Tallahassee, FL, USA, 2007; p. 69. [Google Scholar]
- Vs30 Models and Data–Earthquake Hazards Program–USGS. Available online: https://earthquake.usgs.gov/data/vs30/ (accessed on 24 March 2020).
- EN 1998-1 (2004) Eurocode 8: Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Buildings (EN 1998-1:2004); European Committee for Standardization (CEN), European Union: Brussels, Belgium, 2004.
- Douglas, J.; Gehl, P.; Bonilla, L.F.; Ǵlis, C. A κ model for mainland France. Pure Appl. Geophys. 2010, 167, 1303–1315. [Google Scholar] [CrossRef]
- Reiter, L. Earthquake Hazard. Analysis: Issues and Insights; Columbia University Press: New York, NY, USA, 1990; p. 254. [Google Scholar]
- Stipčević, J.; Herak, M.; Molinari, I.; Dasović, I.; Tkalčić, H.; Gosar, A. Crustal Thickness Beneath the Dinarides and Surrounding Areas from Receiver Functions. Tectonics 2020, 37, 1–15. [Google Scholar] [CrossRef]
| PTJ Station | |||||||||
| HOR | VER | ||||||||
| κ0 (s) | SE-κ0 | κR (skm−1) | SE-κR | κ0 (s) | SE-κ0 | κR (skm−1) | SE-κR | ||
| LSE → | 0.0283 | 0.0028 | 0.000327 | 0.000024 | 0.0249 | 0.0024 | 0.000265 | 0.000021 | |
| Error Set | York et al. [35] Regression Test | ||||||||
| ±1 std | R = 2 km | 0.0287 | 0.0054 | 0.000323 | 0.000048 | 0.0252 | 0.0054 | 0.000263 | 0.000048 |
| R = 5 km | 0.0291 | 0.0053 | 0.000319 | 0.000047 | 0.0256 | 0.0053 | 0.000259 | 0.000047 | |
| R = 10 km | 0.0298 | 0.0051 | 0.000314 | 0.000045 | 0.0261 | 0.0005 | 0.000254 | 0.000046 | |
| Diff. % | R = 2 km | 1.39 | 1.24 | 1.19 | 0.80 | ||||
| R = 5 km | 2.75 | 2.51 | 2.73 | 2.36 | |||||
| R = 10 km | 5.03 | 4.14 | 4.60 | 4.37 | |||||
| ±2 std | R = 2 km | 0.0290 | 0.0027 | 0.000321 | 0.000023 | 0.0255 | 0.0027 | 0.000261 | 0.000024 |
| R = 5 km | 0.0298 | 0.0026 | 0.000313 | 0.000022 | 0.0261 | 0.0026 | 0.000255 | 0.000023 | |
| R = 10 km | 0.0300 | 0.0024 | 0.000311 | 0.000021 | 0.0266 | 0.0025 | 0.000250 | 0.000022 | |
| Diff. % | R = 2 km | 2.41 | 1.87 | 2.35 | 1.57 | ||||
| R = 5 km | 5.03 | 4.47 | 4.60 | 4.37 | |||||
| R = 10 km | 5.67 | 5.14 | 6.39 | 6.04 | |||||
| ZAG Station | |||||||||
| HOR | VER | ||||||||
| κ0 | SE-κ0 | κR | SE-κR | κ0 | SE-κ0 | κR | SE-κR | ||
| LSE → | 0.0411 | 0.0032 | 0.000265 | 0.000029 | 0.0391 | 0.0026 | 0.000223 | 0.000024 | |
| Error Set | York et al. [35] Regression Test | ||||||||
| ±1 std | R = 2 km | 0.0414 | 0.0063 | 0.000262 | 0.000058 | 0.0393 | 0.0063 | 0.000221 | 0.000058 |
| R = 5 km | 0.0419 | 0.0062 | 0.000256 | 0.000057 | 0.0397 | 0.0062 | 0.000217 | 0.000057 | |
| R = 10 km | 0.0426 | 0.0060 | 0.000250 | 0.000054 | 0.0402 | 0.0060 | 0.000213 | 0.000055 | |
| Diff. % | R = 2 km | 0.72 | 1.15 | 0.51 | 0.90 | ||||
| R = 5 km | 1.91 | 3.52 | 1.51 | 2.76 | |||||
| R = 10 km | 3.52 | 6.00 | 2.74 | 4.69 | |||||
| ±2 std | R = 2 km | 0.0418 | 0.0031 | 0.000258 | 0.000029 | 0.0396 | 0.0031 | 0.000218 | 0.000028 |
| R = 5 km | 0.0426 | 0.0030 | 0.000250 | 0.000027 | 0.0402 | 0.0030 | 0.000212 | 0.000027 | |
| R = 10 km | 0.0433 | 0.0029 | 0.000244 | 0.000026 | 0.0408 | 0.0029 | 0.000206 | 0.000026 | |
| Diff. % | R = 2 km | 1.67 | 2.71 | 1.26 | 2.29 | ||||
| R = 5 km | 3.52 | 6.00 | 2.74 | 5.19 | |||||
| R = 10 km | 5.08 | 8.61 | 4.17 | 8.25 | |||||
| Station | Method | HOR | VER | Vs30 EC8 Site Class | ||
|---|---|---|---|---|---|---|
| κ0 (s) | SE-κ0 | κ0 (s) | SE-κ0 | |||
| PTJ | LSE | 0.0283 | 0.0028 | 0.0249 | 0.0024 | 800 m/s A |
| Error-in-variable regression | 0.0298 | 0.0026 | 0.0261 | 0.0026 | ||
| Constrained κ0 | 0.0360 | 0.0097 | 0.0311 | 0.0084 | ||
| ZAG | LSE | 0.0411 | 0.0032 | 0.0391 | 0.0026 | 360–800 m/s B |
| Error-in-variable regression | 0.0426 | 0.0030 | 0.0402 | 0.0030 | ||
| Constrained κ0 | 0.0475 | 0.0092 | 0.0445 | 0.0077 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stanko, D.; Markušić, S.; Korbar, T.; Ivančić, J. Estimation of the High-Frequency Attenuation Parameter Kappa for the Zagreb (Croatia) Seismic Stations. Appl. Sci. 2020, 10, 8974. https://doi.org/10.3390/app10248974
Stanko D, Markušić S, Korbar T, Ivančić J. Estimation of the High-Frequency Attenuation Parameter Kappa for the Zagreb (Croatia) Seismic Stations. Applied Sciences. 2020; 10(24):8974. https://doi.org/10.3390/app10248974
Chicago/Turabian StyleStanko, Davor, Snježana Markušić, Tvrtko Korbar, and Josip Ivančić. 2020. "Estimation of the High-Frequency Attenuation Parameter Kappa for the Zagreb (Croatia) Seismic Stations" Applied Sciences 10, no. 24: 8974. https://doi.org/10.3390/app10248974
APA StyleStanko, D., Markušić, S., Korbar, T., & Ivančić, J. (2020). Estimation of the High-Frequency Attenuation Parameter Kappa for the Zagreb (Croatia) Seismic Stations. Applied Sciences, 10(24), 8974. https://doi.org/10.3390/app10248974






