A Parametric Computational Study of RC Building Structures under Corner-Column Removal Situations
Abstract
1. Introduction
2. Description of the Study
2.1. Description of the Building and Test
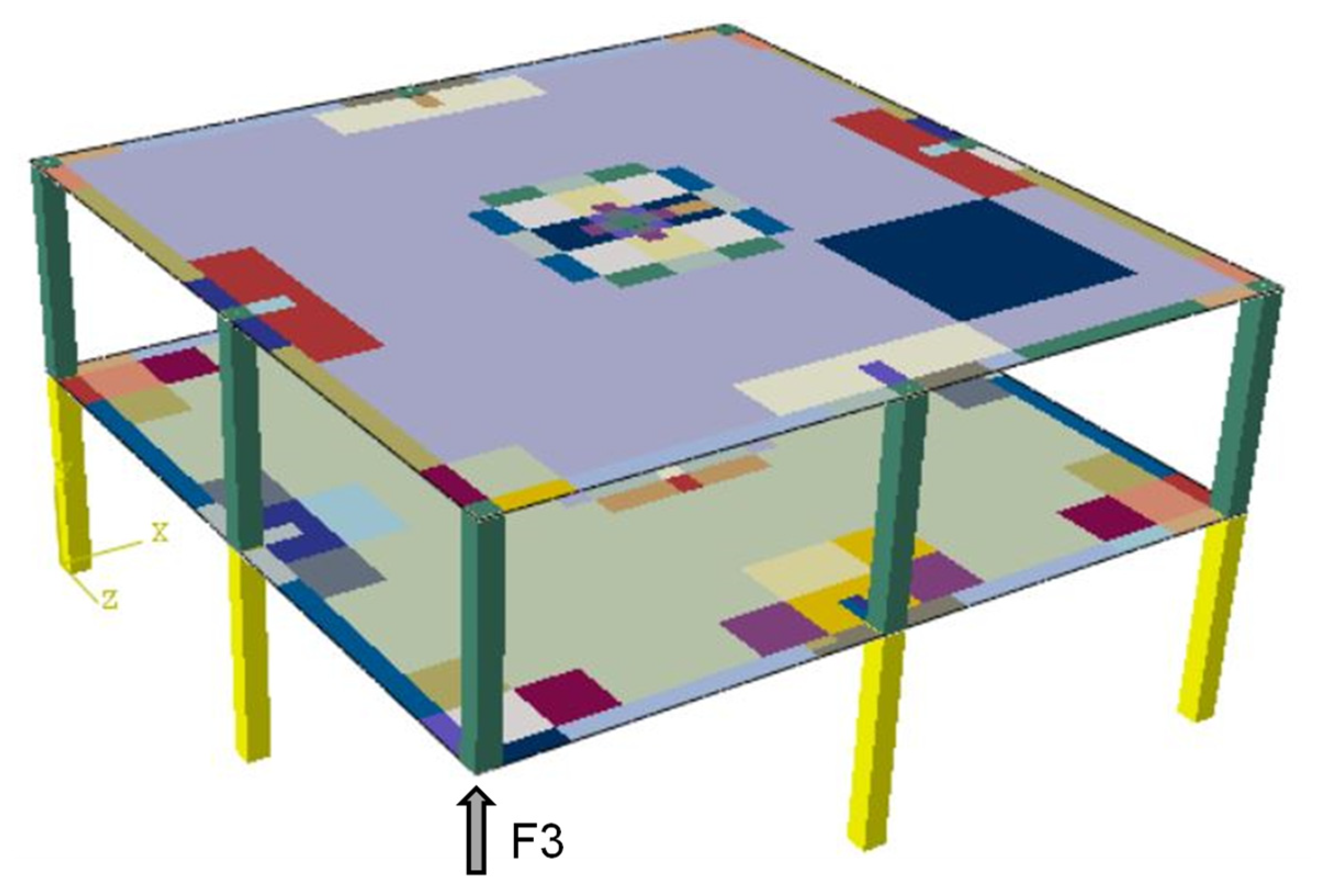
2.2. FE Model
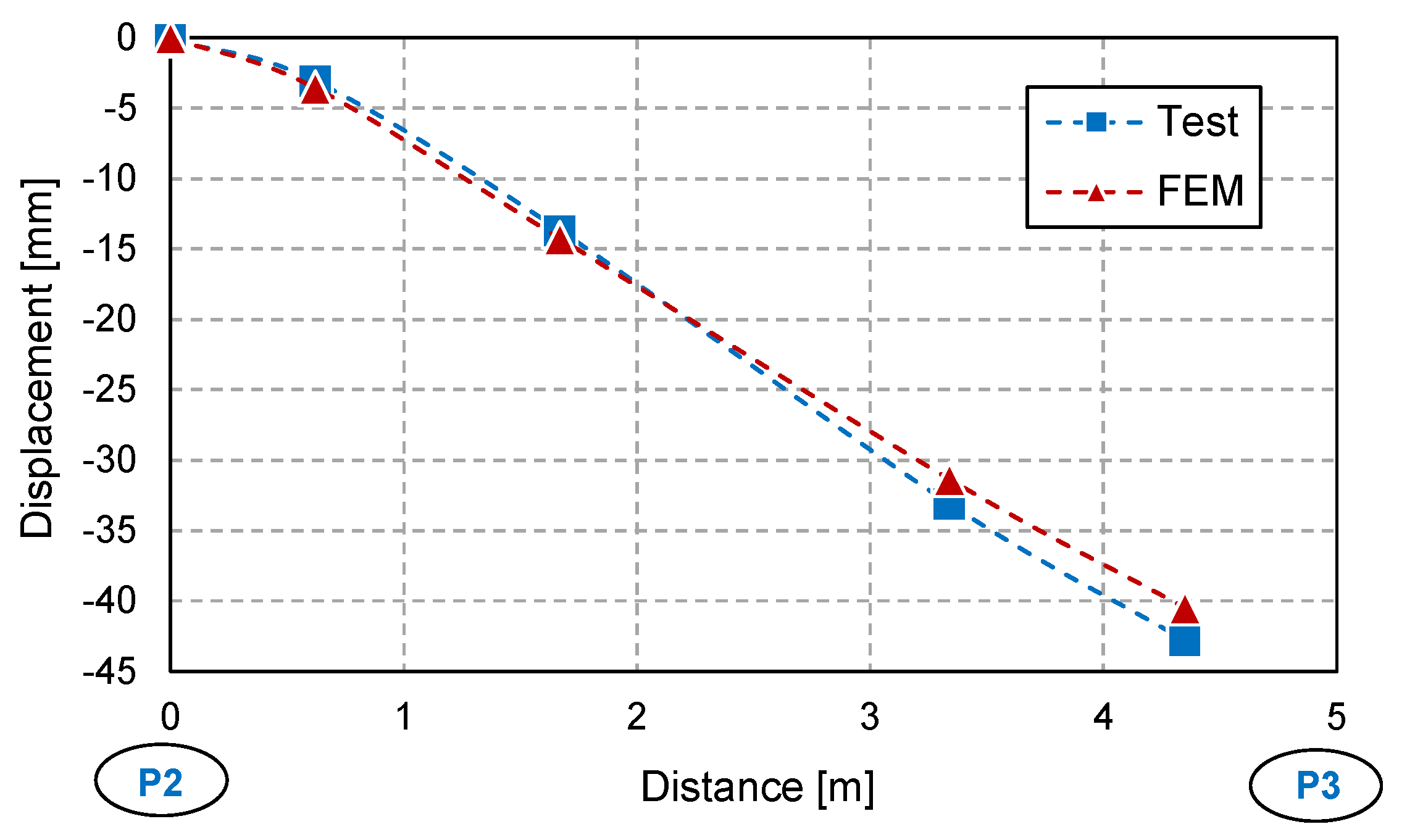
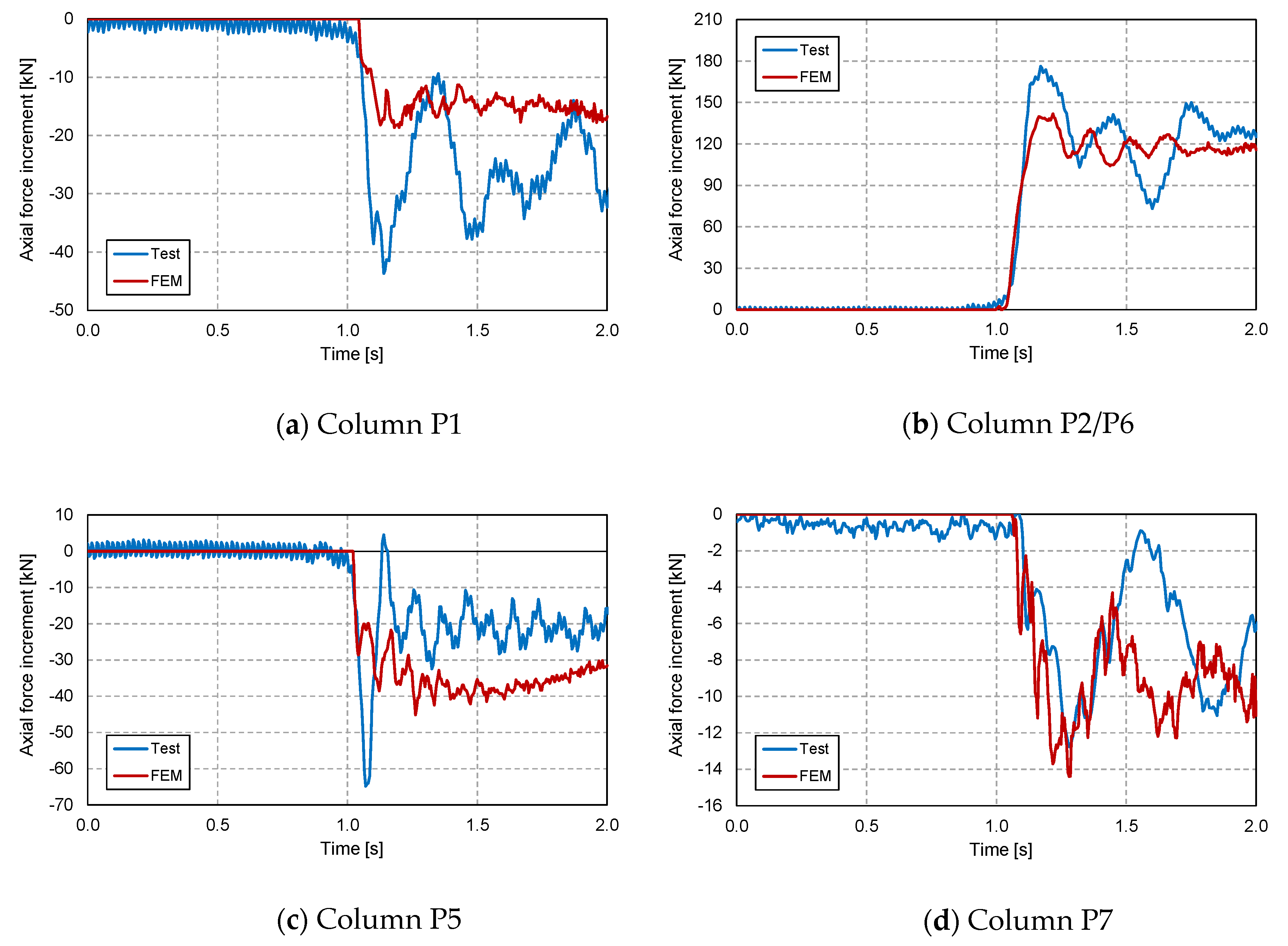
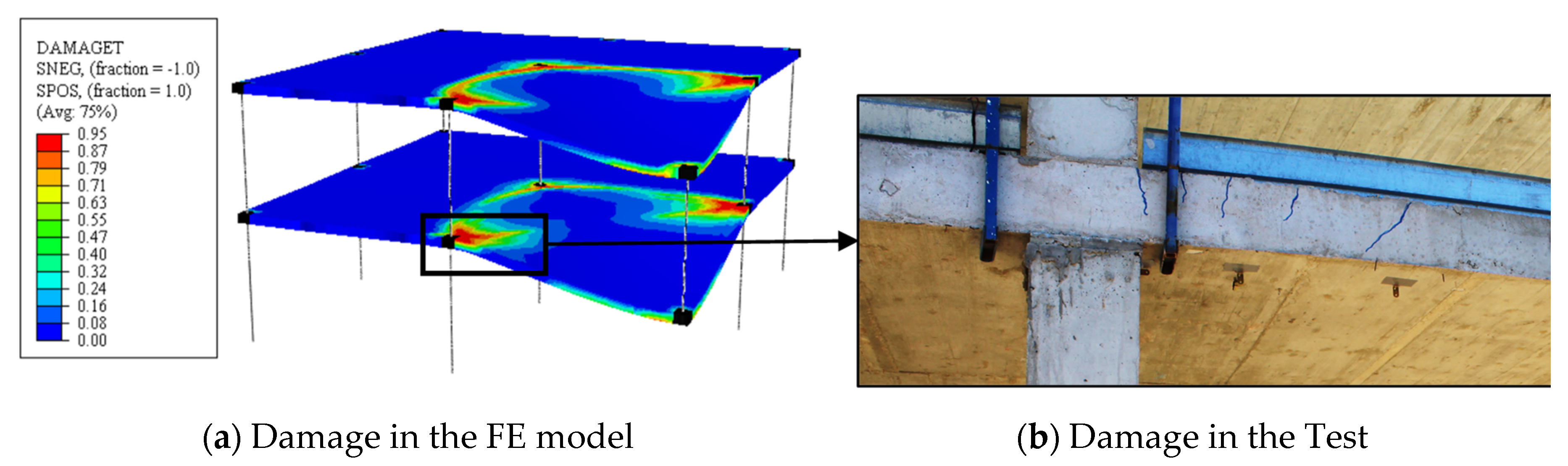
2.3. FE Model Validation
2.4. Parametric Study
3. Results
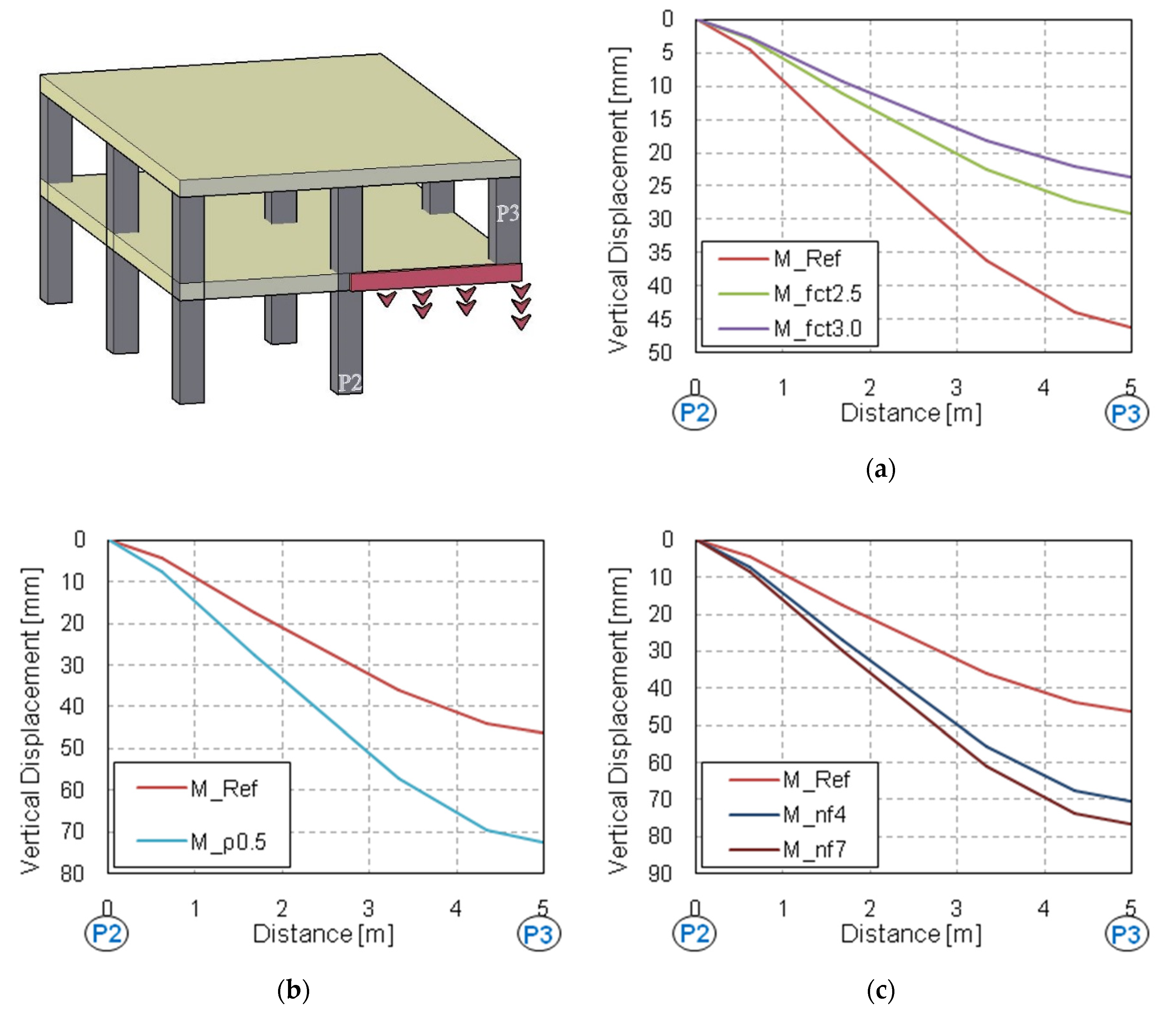
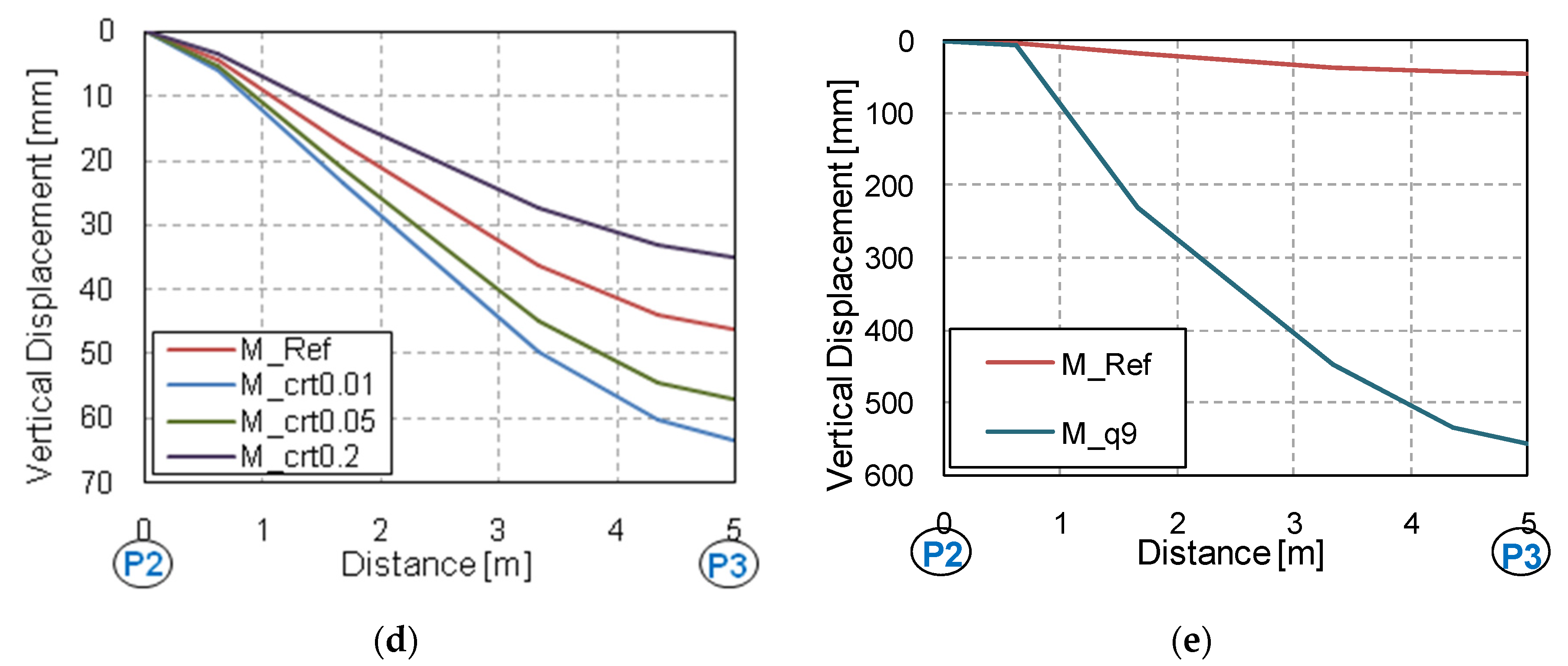
3.1. Vertical Displacement
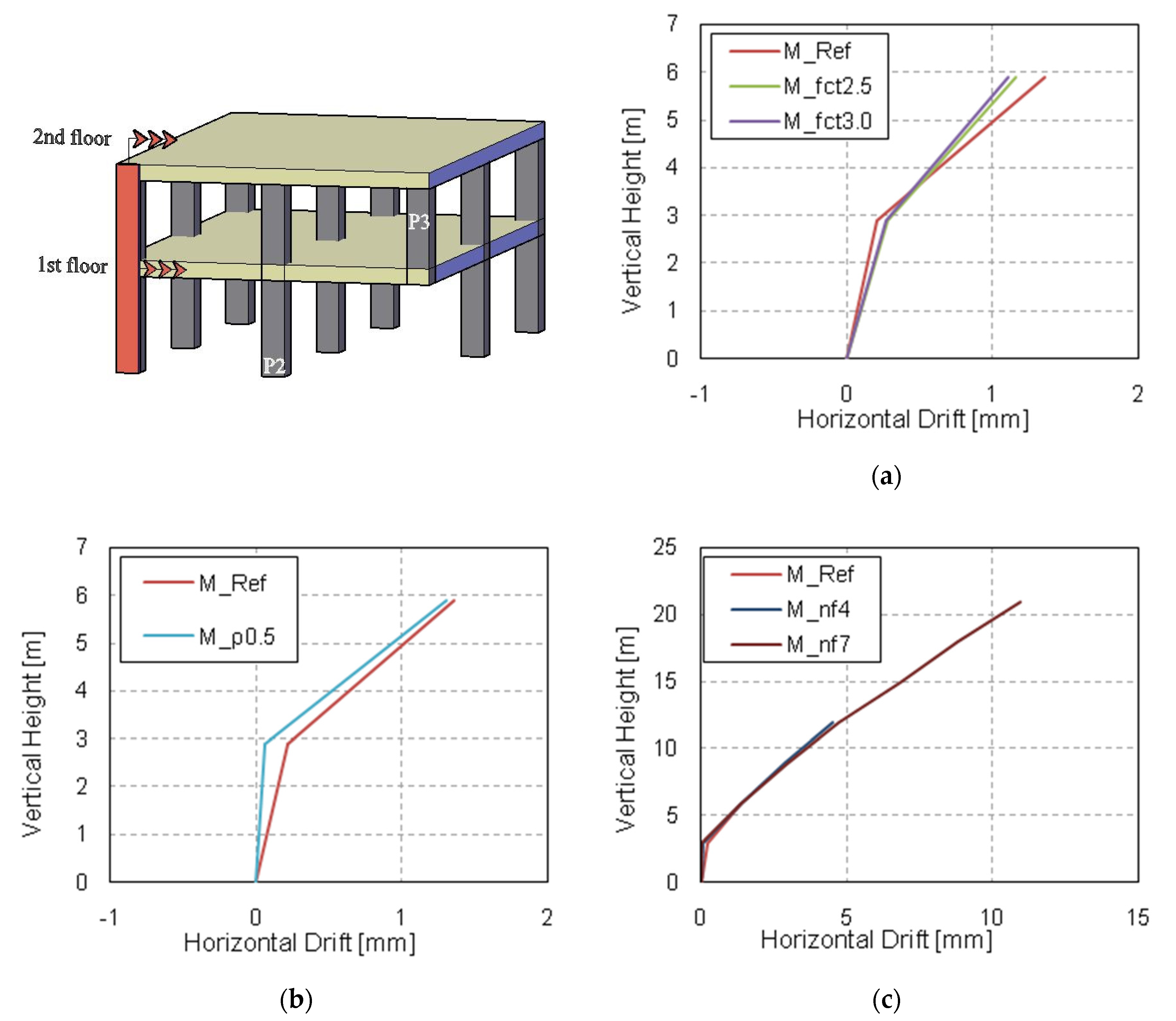
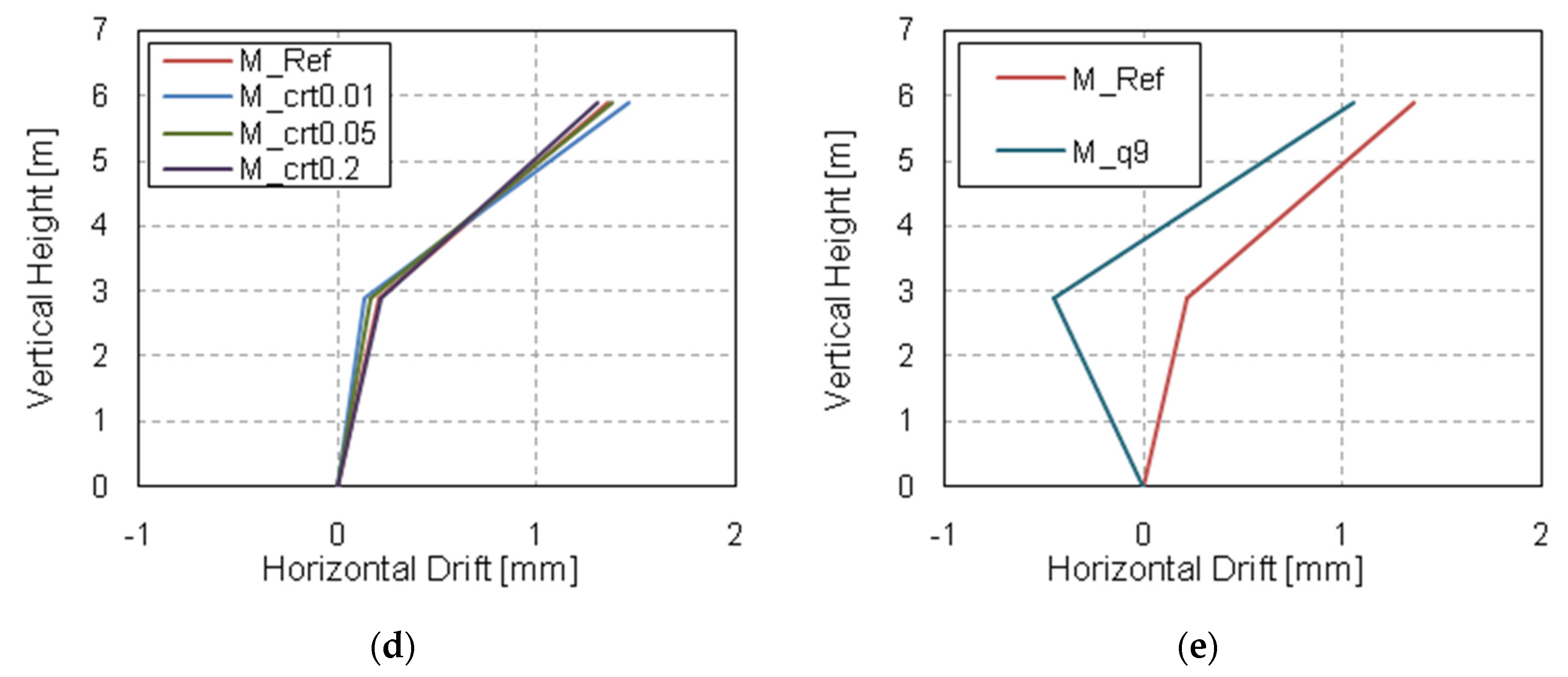
3.2. Drift
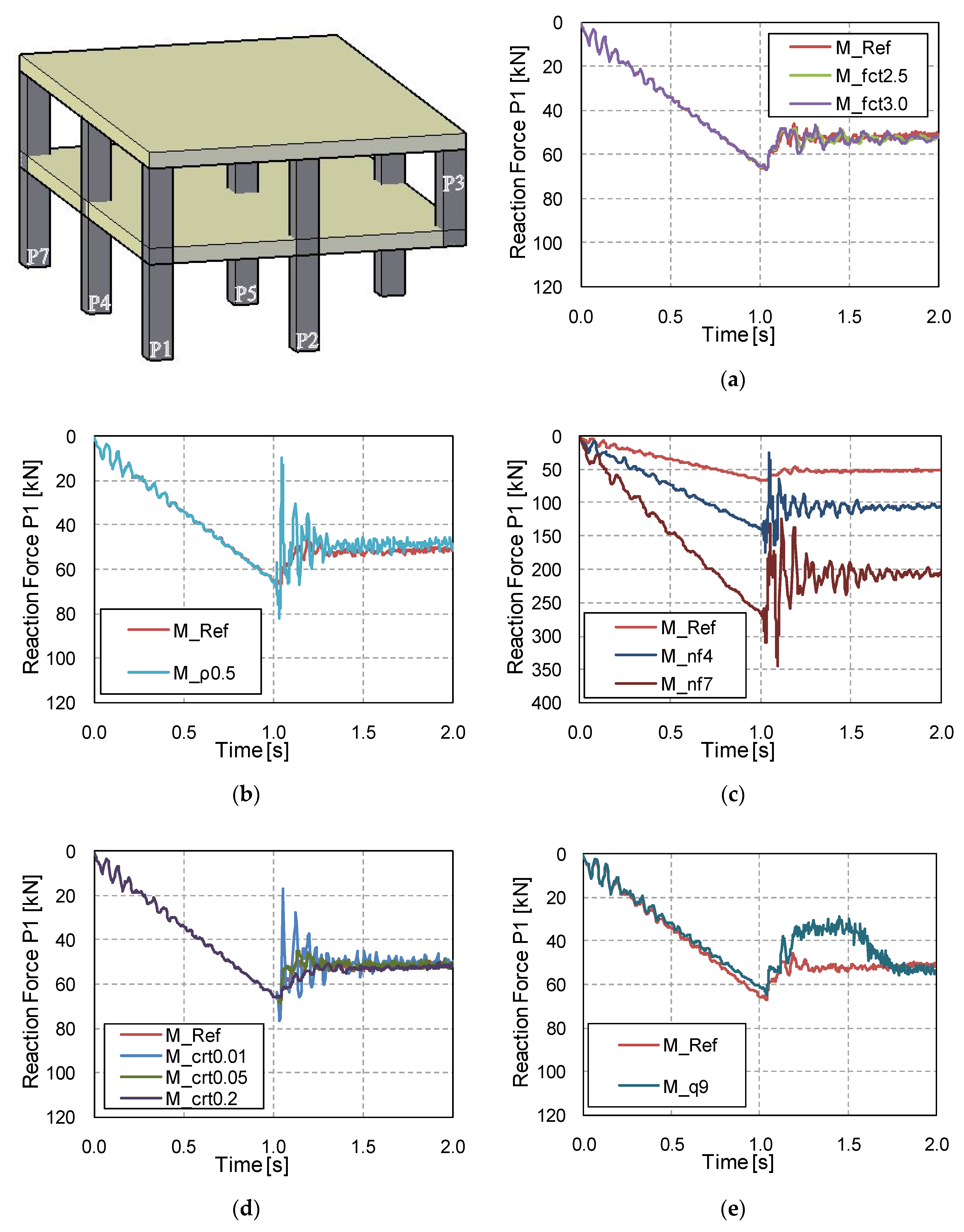
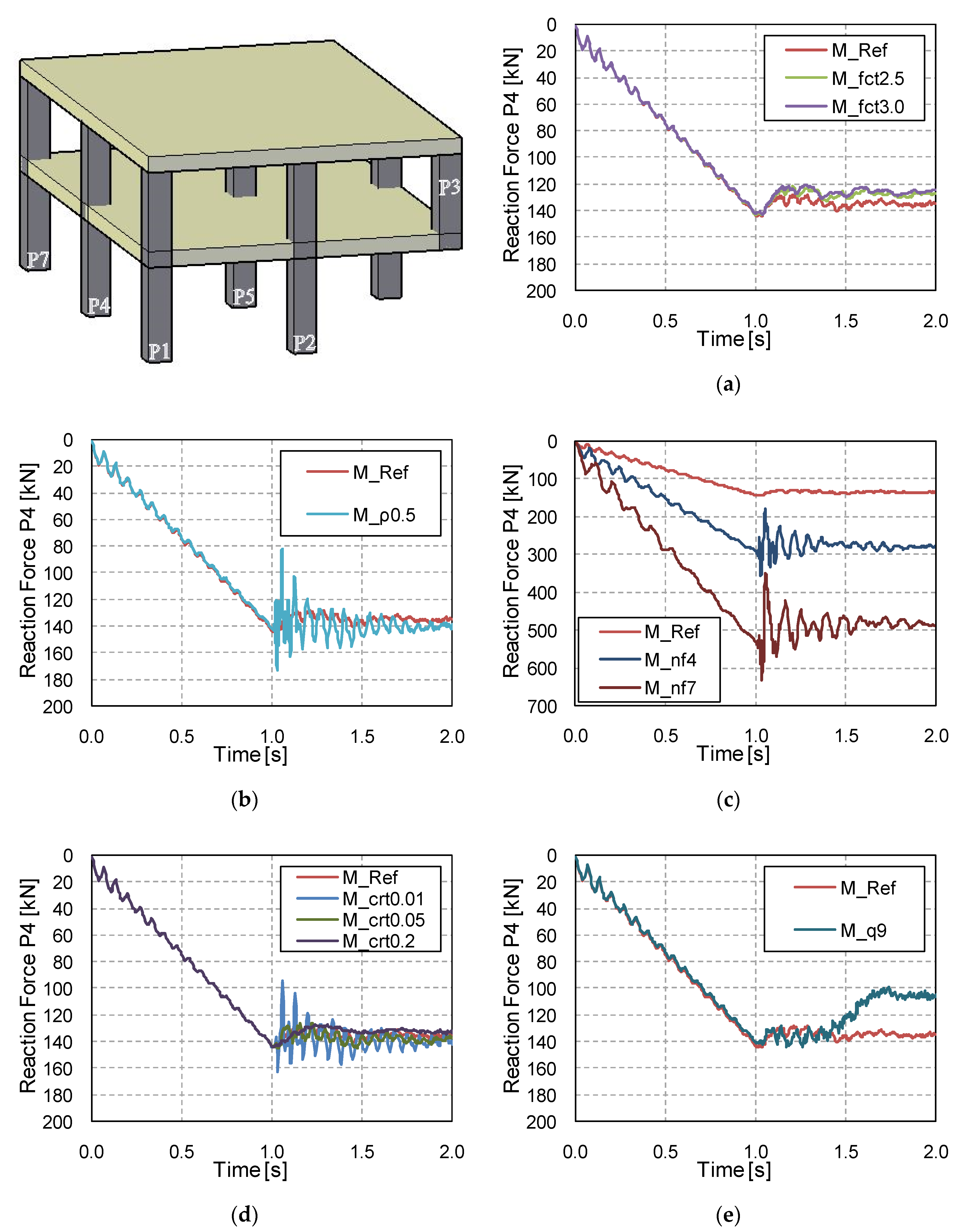
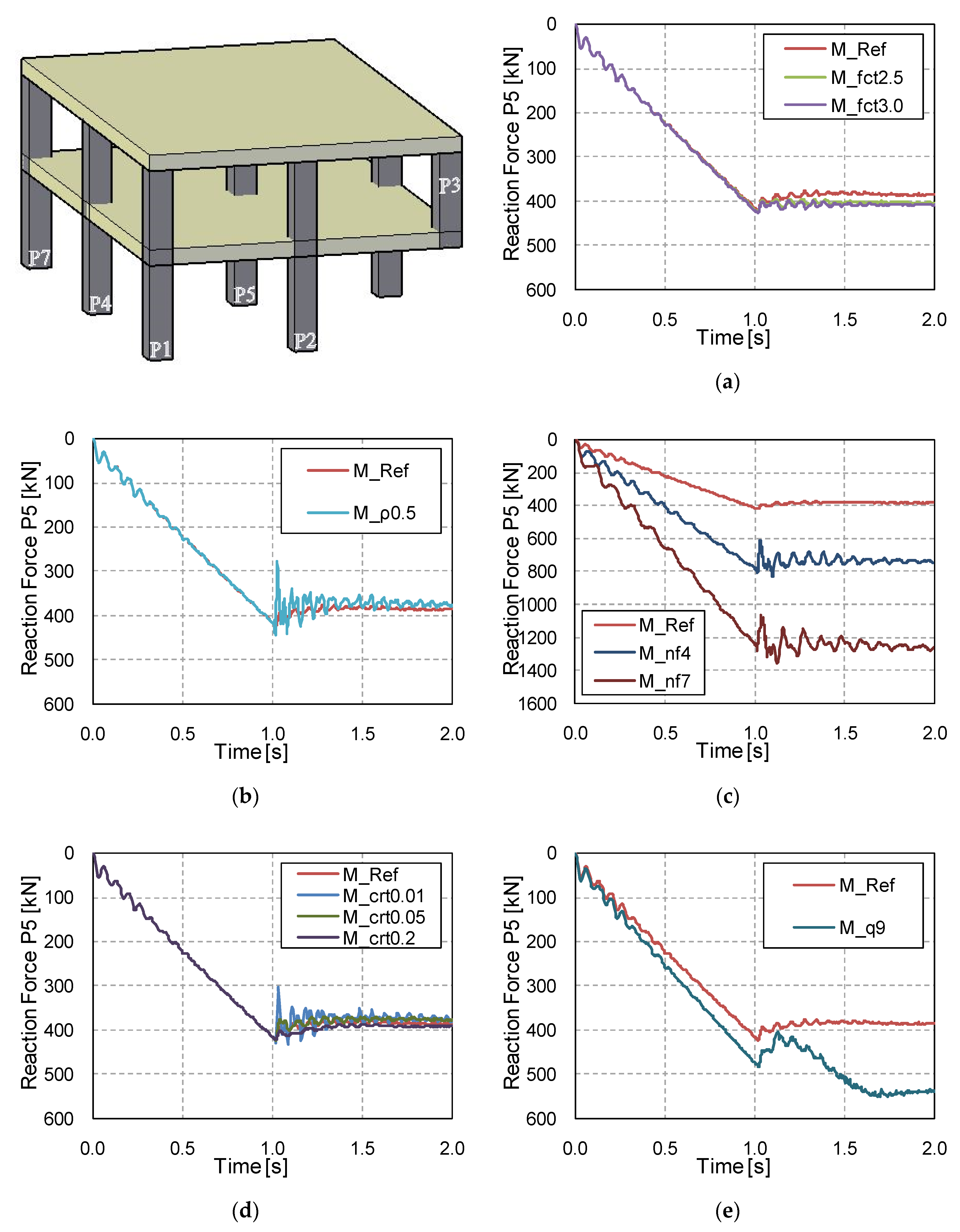
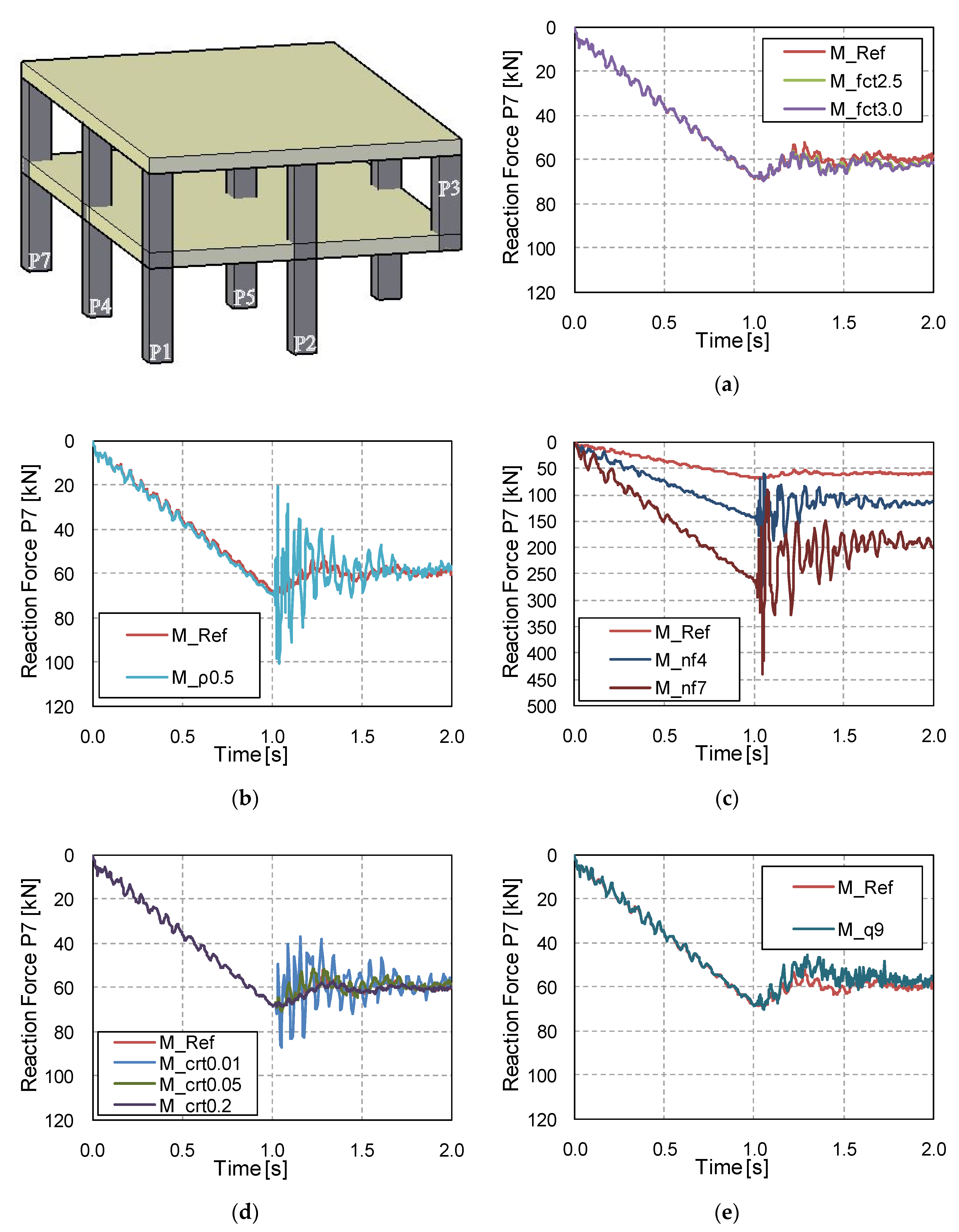
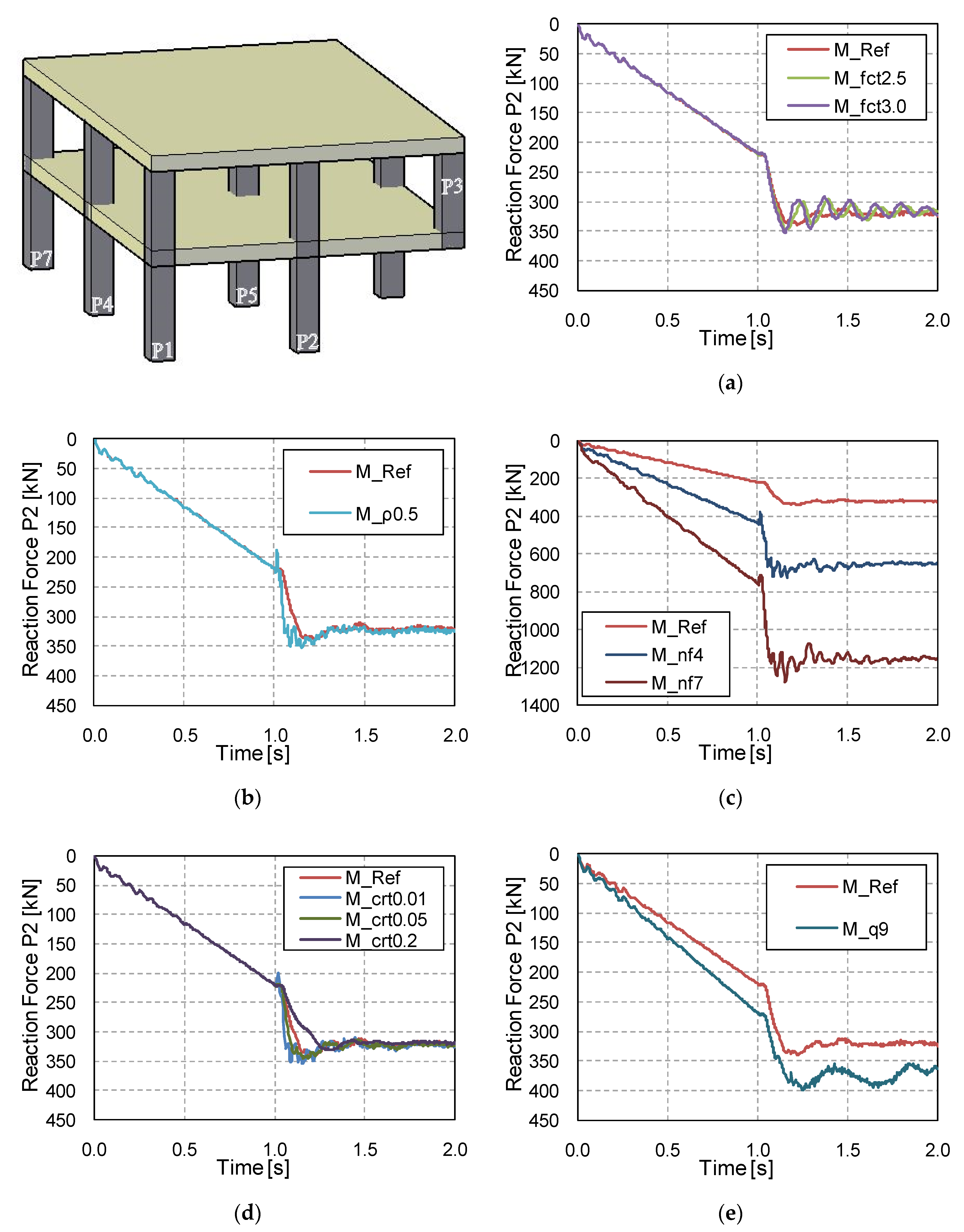
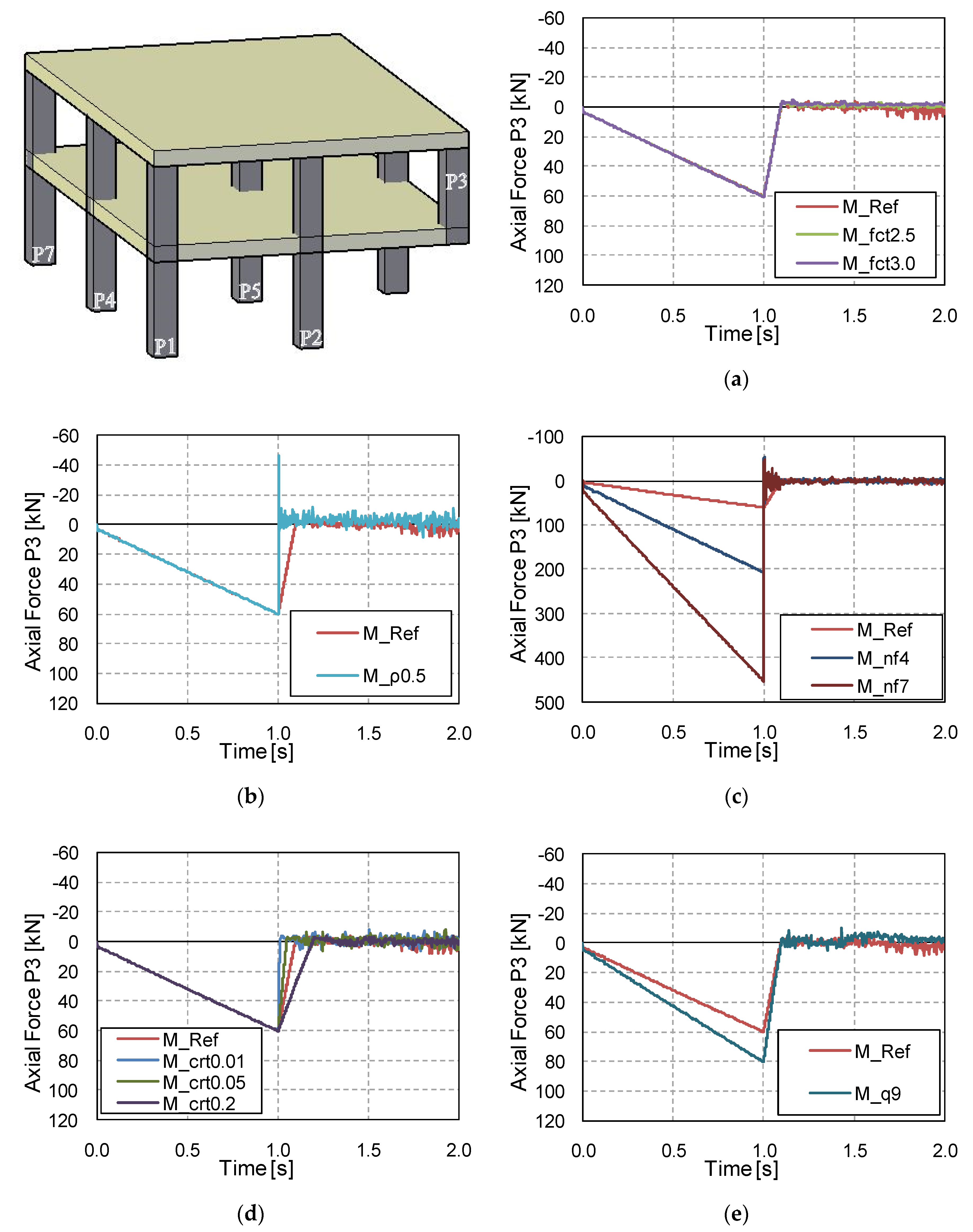
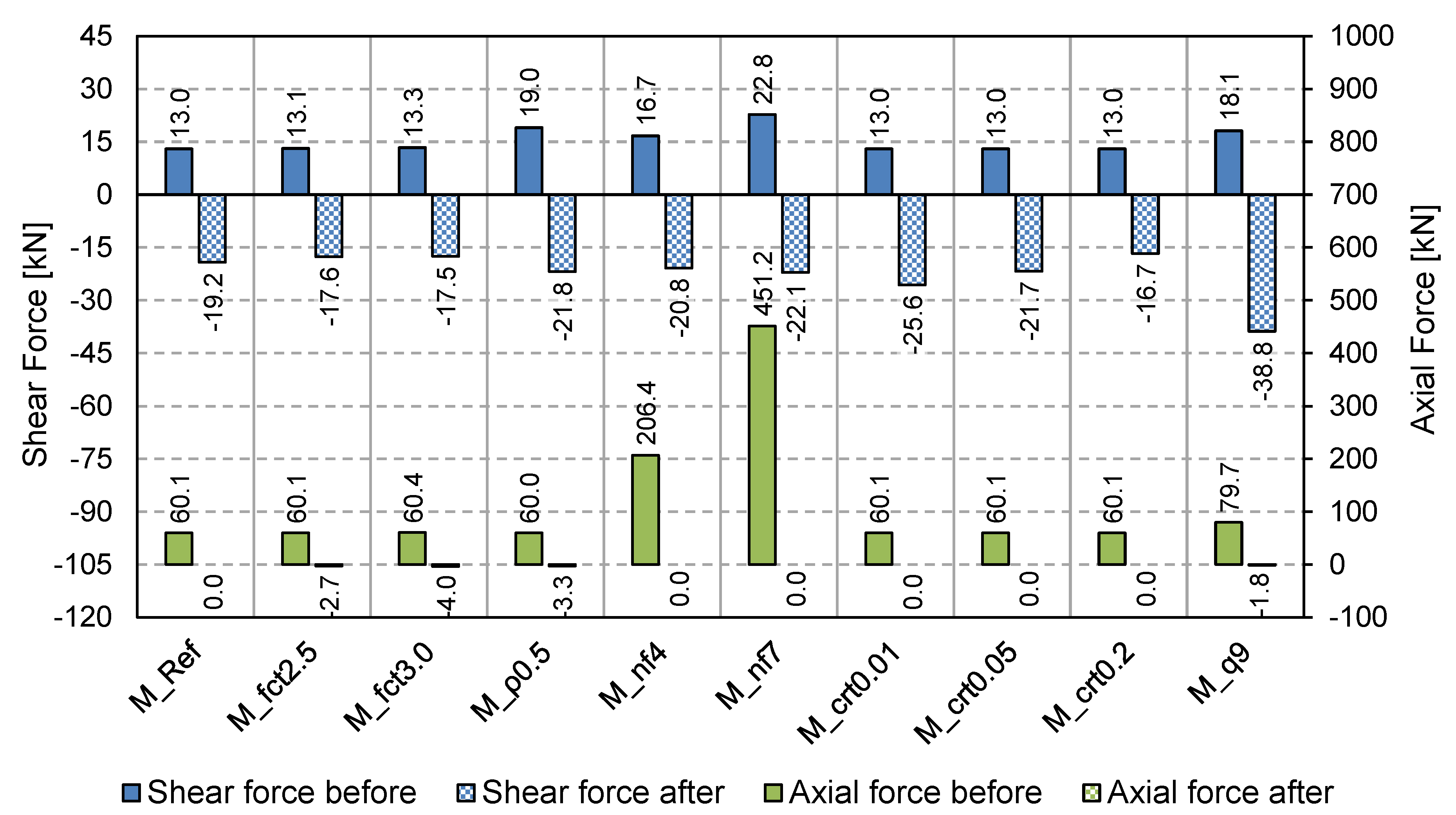
3.3. Vertical Reactions in the Adjacent Columns
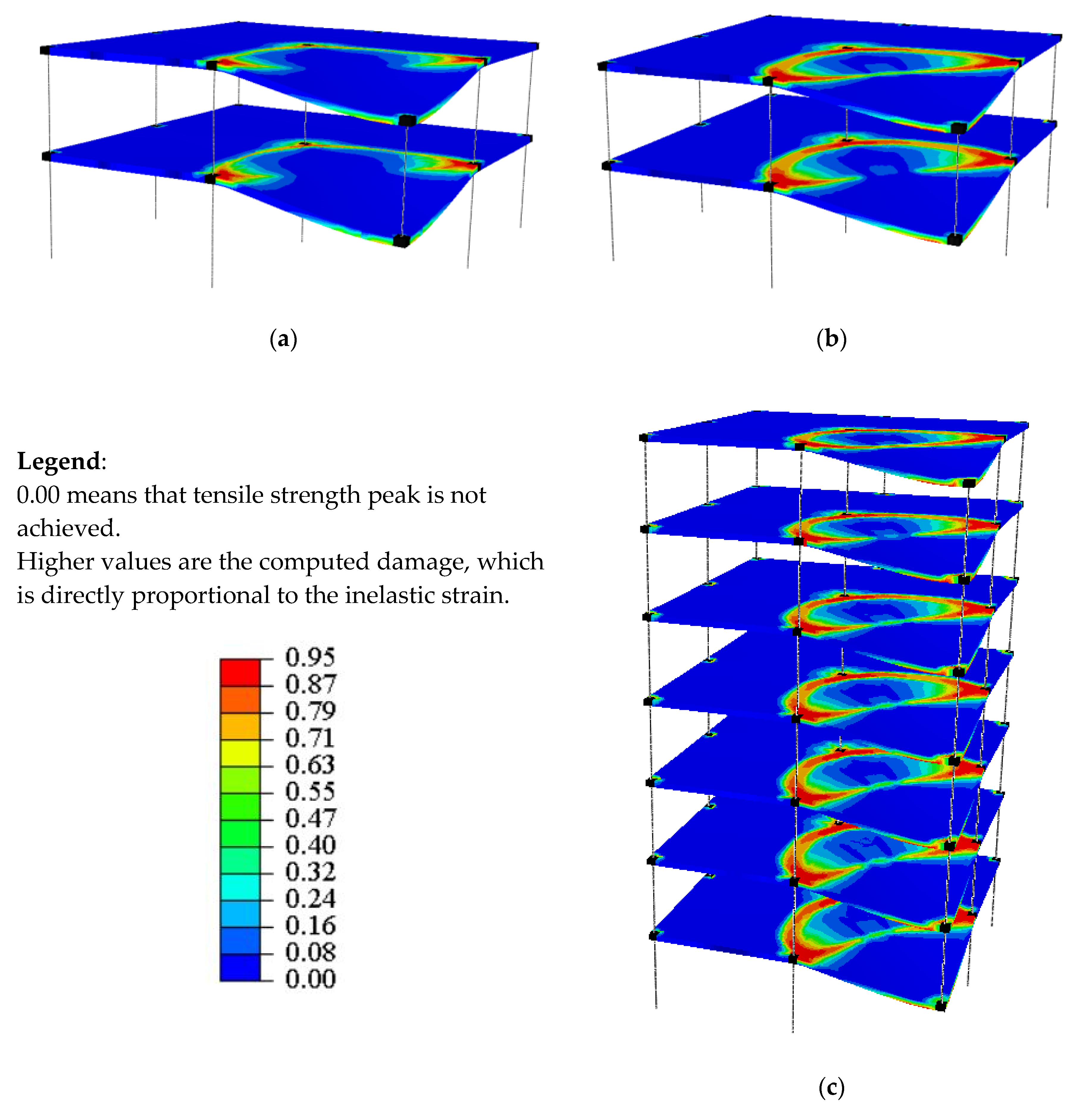
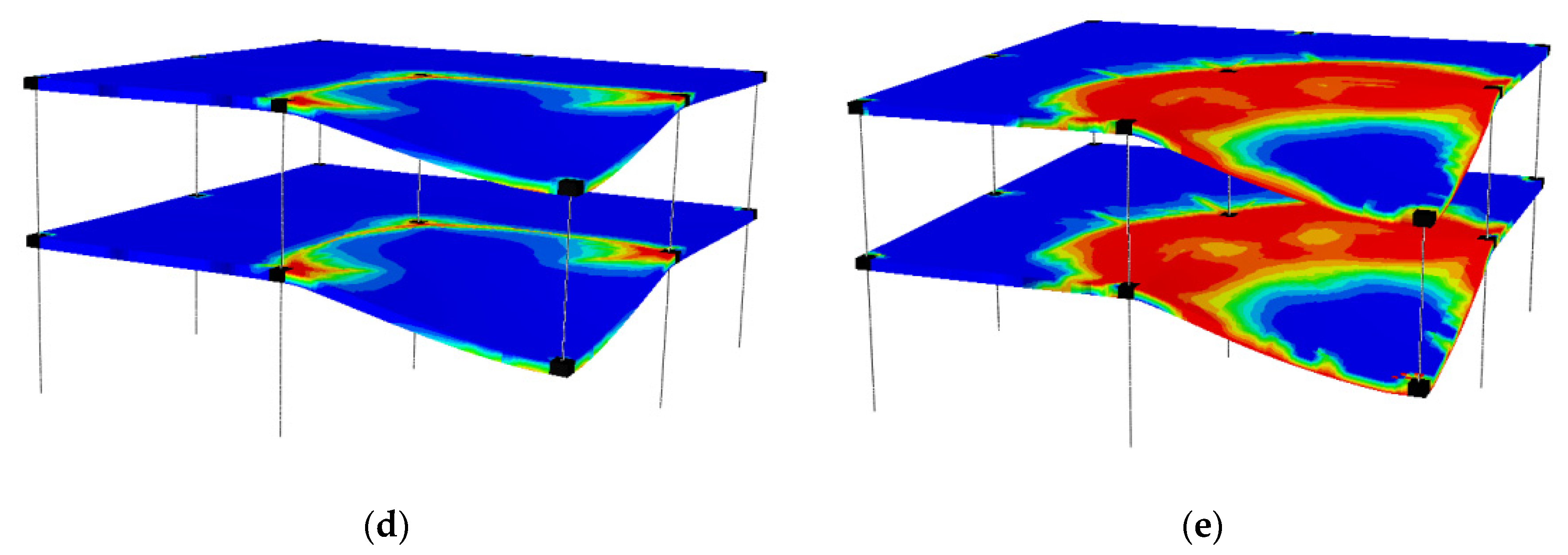
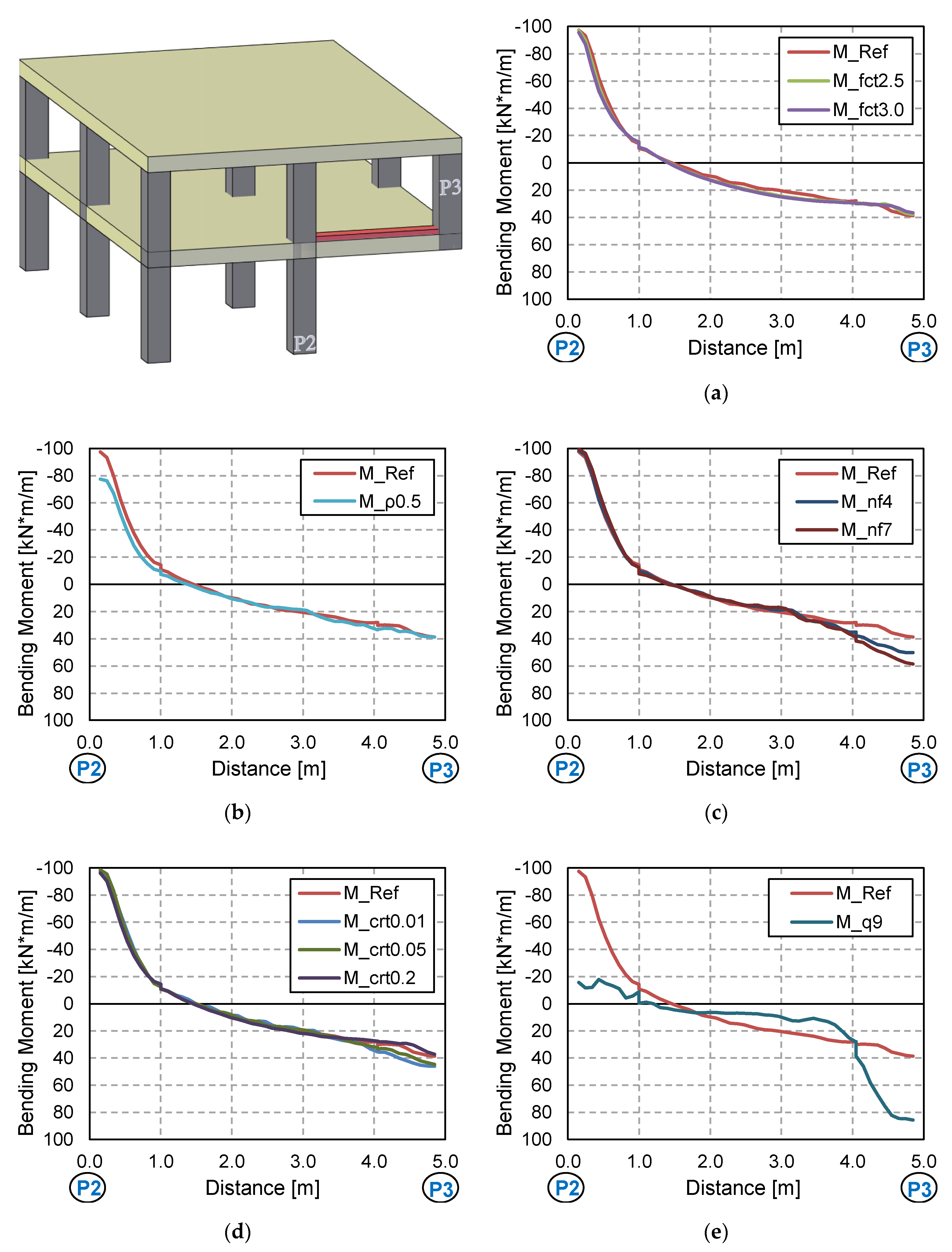
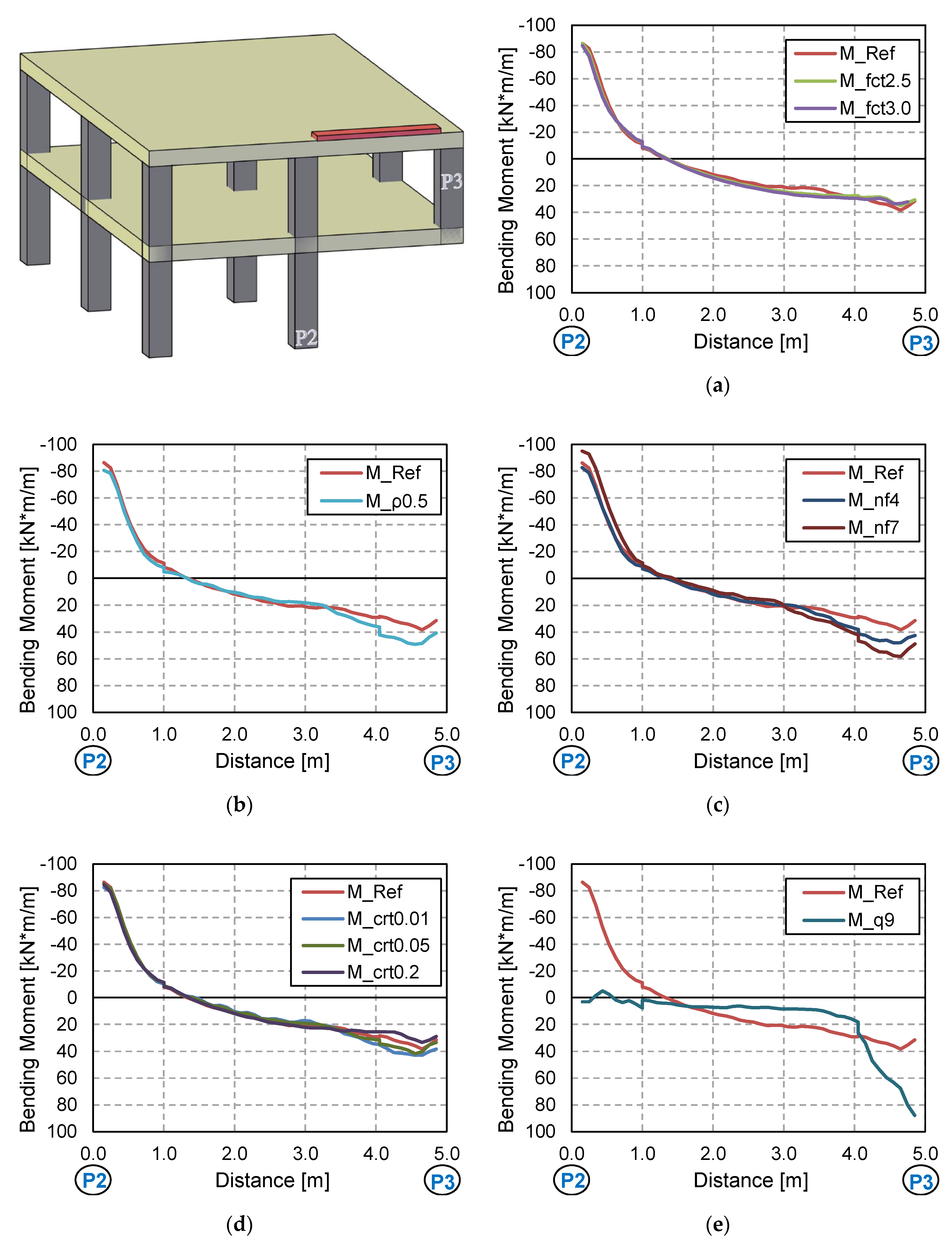
3.4. Computed Tensile Damage Maps
4. Discussion
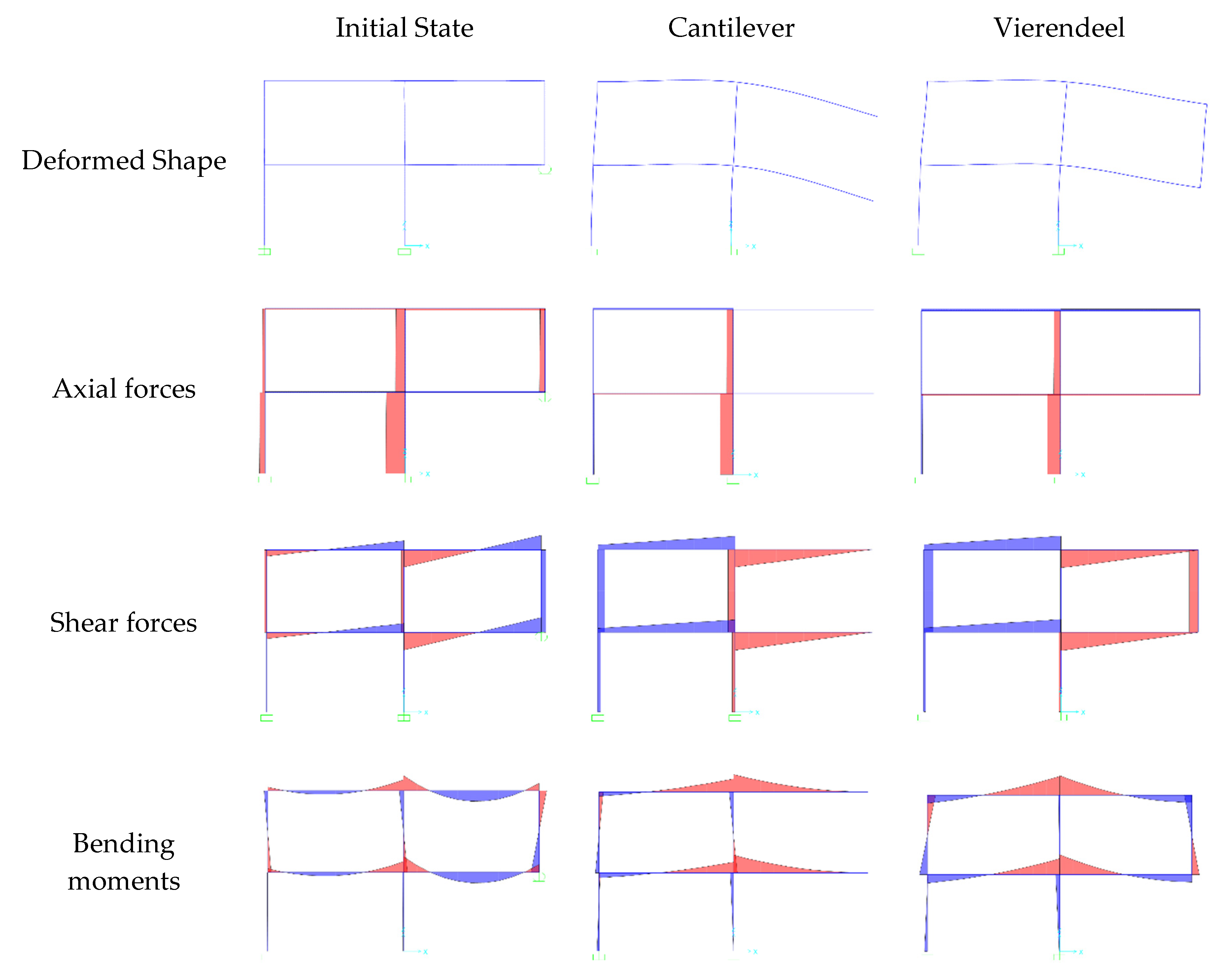
4.1. Activation of Alternative Load Paths (ALPs)
4.2. Dynamic Amplification and Load Increase Factors (DAFs and LIFs)
5. Conclusions
- The tensile concrete strength has a strong influence on the numerical predictions of displacements and structural damage. This affects the computed DAFLD, with low values of fct generally giving more realistic values of DAFLD. This parameter did not have a significant effect on the reactions/forces.
- The same conclusions can be drawn for the influence of the flexural reinforcement ratio, although in this case it also had a significant influence on the member reaction/force values. However, this influence is not transferred to the computed DAFLF, which is not significantly influenced by this parameter.
- The number of floors also has a clear influence on both vertical displacements and member reaction/forces. However, DAFLD and DAFLF are not influenced by this parameter.
- Column removal time has a strong influence on vertical displacements and bending moments, although it barely affects the reaction forces’ peak and residual force values. Due to the wide variation found, it is always recommended to assume the worst possible case at the limit of the GSA recommendations [36] to establish a column removal time equal to a tenth of the structure’s fundamental period without the missing column (T/10).
- The applied superimposed load had a strong influence on all the aspects studied. A comparison was made between a load combination for ULS and a common design accidental load. Results showed that considering a more aggressive scenario than a design accidental situation could result in making different and erroneous recommendations on the safe side, in some cases (e.g., excessive deflections or forces can be considered in a design accidental situation but this is a persistent and transient situation), but these recommendations would still be unsafe for the DAFLF (i.e., resulting in a lower value than in a design accidental situation).
- The test and FE models in this paper showed that Vierendeel action was the main ALP of the structure for the particular case investigated, i.e., without infill walls and subjected to a design compliant corner-column removal situation. The rest of the column above the removed one acts as a key element in effectively activating this ALP. However, for this ALP to be safe, a series of reinforcement details should be in the design phase of the structure.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Adam, J.M.; Parisi, F.; Sagaseta, J.; Lu, X. Research and practice on progressive collapse and robustness of building structures in the 21st century. Eng. Struct. 2018, 173, 122–149. [Google Scholar] [CrossRef]
- Kiakojouri, F.; De Biagi, V.; Chiaia, B.; Sheidaii, M.R. Progressive collapse of framed building structures: Current knowledge and future prospects. Eng. Struct. 2020, 206, 110061. [Google Scholar] [CrossRef]
- Stephen, D.; Lam, D.; Forth, J.; Ye, J.; Tsavdaridis, K.D. An evaluation of modelling approaches and column removal time on progressive collapse of building. J. Constr. Steel Res. 2019, 153, 243–253. [Google Scholar] [CrossRef]
- Eren, N.; Brunesi, E.; Nascimbene, R. Influence of masonry infills on the progressive collapse resistance of reinforced concrete framed buildings. Eng. Struct. 2019, 178, 375–394. [Google Scholar] [CrossRef]
- Zhang, L.; Li, H.; Wang, W. Retrofit strategies against progressive collapse of steel gravity frames. Appl. Sci. 2020, 10, 4600. [Google Scholar] [CrossRef]
- De Biagi, V.; Kiakojouri, F.; Chiaia, B.; Sheidaii, M.R. A simplified method for assessing the response of RC frame structures to sudden column removal. Appl. Sci. 2020, 10, 3081. [Google Scholar] [CrossRef]
- Yu, J.; Luo, L.; Li, Y. Numerical study of progressive collapse resistance of RC beam-slab substructures under perimeter column removal scenarios. Eng. Struct. 2018, 159, 14–27. [Google Scholar] [CrossRef]
- Bermejo, M.; Santos, A.P.; Goicolea, J.M. Development of Practical Finite Element Models for Collapse of Reinforced Concrete Structures and Experimental Validation. Shock Vib. 2017, 1–9. [Google Scholar] [CrossRef]
- Fu, Q.; Tan, K.-H. Numerical study on steel-concrete composite floor systems under corner column removal scenario. Structures 2019. [Google Scholar] [CrossRef]
- Kolchunov, V.; Fedorova, N.; Savin, S.; Kovalev, V.; Iliushchenko, T. Failure simulation of a RC multi-storey building frame with prestressed girders. Mag. Civ. Eng. 2019, 92, 155–162. [Google Scholar] [CrossRef]
- Mucedero, G.; Perrone, D.; Brunesi, E.; Monteiro, R. Numerical Modelling and Validation of the Response of Masonry Infilled RC Frames Using Experimental Testing Results. Buildings 2020, 10, 182. [Google Scholar] [CrossRef]
- Tohidi, M.; Janby, A. Finite-Element Modeling of Progressive Failure for Floor-to-Floor Assembly in the Precast Cross-Wall Structures. J. Struct. Eng. 2020, 146, 04020087. [Google Scholar] [CrossRef]
- Garzón-Roca, J.; Sagaseta, J.; Buitrago, M.; Adam, J.M. Dynamic punching assessment of edge columns after sudden corner column removal. ACI Struct. J. 2020. [Google Scholar]
- Olmati, P.; Sagaseta, J.; Cormie, D.; Jones, A.E.K. Simplified reliability analysis of punching in reinforced concrete flat slab buildings under accidental actions. Eng. Struct. 2017, 130, 83–98. [Google Scholar] [CrossRef]
- Buitrago, M.; Sagaseta, J.; Adam, J.M. Avoiding failures during building construction using structural fuses as load limiters on temporary shoring structures. Eng. Struct. 2020, 204, 109906. [Google Scholar] [CrossRef]
- Buitrago, M.; Sagaseta, J.; Adam, J.M. Effects of sudden failure of shoring elements in concrete building structures under construction. Eng. Struct. 2018, 172, 508–522. [Google Scholar] [CrossRef]
- Joshi, D.D.; Patel, P.V. Experimental study of precast dry connections constructed away from beam–column junction under progressive collapse scenario. Asian J. Civ. Eng. 2019, 20, 209–222. [Google Scholar] [CrossRef]
- Ma, F.; Gilbert, B.P.; Guan, H.; Xue, H.; Lu, X.; Li, Y. Experimental study on the progressive collapse behaviour of RC flat plate substructures subjected to corner column removal scenarios. Eng. Struct. 2019, 180, 728–741. [Google Scholar] [CrossRef]
- Yang, T.; Han, Z.; Deng, N.; Chen, W. Collapse responses of concrete frames reinforced with BFRP bars in middle column removal scenario. Appl. Sci. 2019, 9, 4436. [Google Scholar] [CrossRef]
- Faridmehr, I.; Baghban, M.H. An overview of progressive collapse behavior of steel beam-to-column connections. Appl. Sci. 2020, 10, 6003. [Google Scholar] [CrossRef]
- Qian, K.; Li, B. Strengthening and Retrofitting Precast Concrete Buildings to Mitigate Progressive Collapse Using Externally Bonded GFRP Strips. J. Compos. Constr. 2019, 23, 1–15. [Google Scholar] [CrossRef]
- Lin, K.; Lu, X.; Li, Y.; Guan, H. Experimental study of a novel multi-hazard resistant prefabricated concrete frame structure. Soil Dyn. Earthq. Eng. 2019, 119, 390–407. [Google Scholar] [CrossRef]
- Qian, K.; Liang, S.-L.; Feng, D.-C.; Fu, F.; Wu, G. Experimental and Numerical Investigation on Progressive Collapse Resistance of Post-Tensioned Precast Concrete Beam-Column Subassemblages. J. Struct. Eng. 2020, 146, 04020170. [Google Scholar] [CrossRef]
- Zhou, Y.; Hu, X.; Pei, Y.; Hwang, H.-J.; Chen, T.; Yi, W.; Deng, L. Dynamic load test on progressive collapse resistance of fully assembled precast concrete frame structures. Eng. Struct. 2020, 214, 110675. [Google Scholar] [CrossRef]
- Alshaikh, I.M.H.; Bakar, B.H.A.; Alwesabi, E.A.H.; Akil, H.M. Experimental investigation of the progressive collapse of reinforced concrete structures: An overview. Structures 2020, 25, 881–900. [Google Scholar] [CrossRef]
- Buitrago, M.; Bertolesi, E.; Calderón, P.A.; Adam, J.M. Robustness of steel truss bridges: Laboratory testing of a full-scale 21-metre bridge span. Structures 2021. [Google Scholar] [CrossRef]
- Buitrago, M.; Bertolesi, E.; Sagaseta, J.; Calderón, P.A.; Adam, J.M. Robustness of RC building structures with infill masonry walls: Tests on a purpose-built building. Eng. Struct. 2021, 226, 111384. [Google Scholar] [CrossRef]
- Adam, J.M.; Buitrago, M.; Bertolesi, E.; Sagaseta, J.; Moragues, J.J. Dynamic performance of a real-scale reinforced concrete building test under corner-column failure scenario. Eng. Struct. 2020, 210, 110414. [Google Scholar] [CrossRef]
- Osteraas, J.D. Murrah building bombing revisited: A qualitative assessment of blast damage and collapse patterns. J. Perform. Constr. Facil. 2006, 20, 330–335. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Le, J.-L.; Greening, F.R.; Benson, D.B. What Did and Did Not Cause Collapse of World Trade Center Twin Towers in New York? J. Eng. Mech. 2008, 134, 892–906. [Google Scholar] [CrossRef]
- Sasani, M.; Kazemi, A.; Sagiroglu, S.; Forest, S. Progressive Collapse Resistance of an Actual 11-Story Structure Subjected to Severe Initial Damage. J. Struct. Eng. 2011, 137, 893–902. [Google Scholar] [CrossRef]
- Pearson, C.; Delatte, N. Ronan Point Apartment Tower Collapse and its Effect on Building Codes. J. Perform. Constr. Facil. 2005, 19, 172–177. [Google Scholar] [CrossRef]
- Xiao, Y.; Kunnath, S.; Li, F.W.; Zhao, Y.B.; Lew, H.S.; Bao, Y. Collapse Test of Three-Story Half-Scale Reinforced Concrete Frame Building. ACI Struct. J. 2015, 112, 429–438. [Google Scholar] [CrossRef]
- Qian, K.; Weng, Y.H.; Li, B. Impact of two columns missing on dynamic response of RC flat slab structures. Eng. Struct. 2018, 177, 598–615. [Google Scholar] [CrossRef]
- Feng, P.; Qiang, H.; Ou, X.; Qin, W.; Yang, J. Progressive Collapse Resistance of GFRP-Strengthened RC Beam–Slab Subassemblages in a Corner Column–Removal Scenario. J. Compos. Constr. 2019, 23, 1–15. [Google Scholar] [CrossRef]
- GSA. Alternate Path Analysis & Design Guidelines for Progressive Collapse Resistance; General Services Administration: Washington, WA, USA, 2013.
- DoD. Design of Buildings to Resist Progressive Collapse (UFC 4-023-03); Department of Defense: Washington, WA, USA, 2009.
- EN 1991-1-7. Eurocode 1: Actions on Structures—Part 1-7: General Actions—Accidental Actions; CEN: Brussels, Belgium, 2006. [Google Scholar]
- EN 1990. Eurocode: Basis of Structural Design; CEN: Brussels, Belgium, 2002. [Google Scholar]
- EN 1992-1-1. Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings; CEN: Brussels, Belgium, 2004. [Google Scholar]
- ABAQUS v16.4. Theory Manual; Dassault Systèmes: París, French, 2016. [Google Scholar]
- Zhou, Y.; Chen, T.; Pei, Y.; Hwang, H.-J.; Hu, X.; Yi, W.; Deng, L. Static load test on progressive collapse resistance of fully assembled precast concrete frame structure. Eng. Struct. 2019, 200, 109719. [Google Scholar] [CrossRef]
- Gao, S.; Guo, L. Progressive collapse analysis of 20-storey building considering composite action of floor slab. Int. J. Steel Struct. 2015, 15, 447–458. [Google Scholar] [CrossRef]
- Wang, F.; Yang, J.; Shah, S. Effect of Horizontal Restraints on Progressive Collapse Resistance of Precast Concrete Beam-Column Framed Substructures. KSCE J. Civ. Eng. 2020, 24, 879–889. [Google Scholar] [CrossRef]
- Zhang, H.; Shu, G.; Pan, R. Failure Mechanism of Composite Frames Under the Corner Column-Removal Scenario. J. Fail. Anal. Prev. 2019, 19, 649–664. [Google Scholar] [CrossRef]
- LS-DYNA. Theory Manual; LSTC: Livermore, CA, USA, 2012. [Google Scholar]
- Micallef, K.; Sagaseta, J.; Fernández Ruiz, M.; Muttoni, A. Assessing punching shear failure in reinforced concrete flat slabs subjected to localised impact loading. Int. J. Impact Eng. 2014, 71, 17–33. [Google Scholar] [CrossRef]
- Chen, X.; Duan, J.; Li, Y. Mass proportional damping in nonlinear time-history analysis. In Proceedings of the 3rd International Conference on Material, Mechanical and Manufacturing Engineering (IC3ME), Guangzhou, China, 27–28 June 2015; pp. 567–571. [Google Scholar]
- SAP2000. Theory Manual; Computers & Structures Inc.: California, CA, USA, 2020. [Google Scholar]


| Mechanical Property | Element | Result [MPa] |
|---|---|---|
| Compressive strength(fc) | 1st slab | 30.5 |
| 2nd slab | 31.1 | |
| Tensile strength(fct) | 1st slab | 2.44 |
| 2nd slab | 1.83 | |
| Elastic Modulus(E) | Ground floor columns | 29,275 |
| 1st slab | 28,810 | |
| 1st floor columns | 29,403 | |
| 2nd slab | 33,119 |
| Component | Value | Test | FE Model | Error [mm] | |
|---|---|---|---|---|---|
| Maximum vertical displacement [mm] | Peak | −48.1 | −41.9 | 6.2 | |
| Residual | −42.8 | −40.5 | 2.3 | ||
| Drift [mm] | Floor 1 | Peak | 1.40 | 0.84 | 0.56 |
| Residual | 0.40 | 0.38 | 0.02 | ||
| Floor 2 | Peak | 4.80 | 2.34 | 2.46 | |
| Residual | 2.40 | 1.53 | 0.87 | ||
| Model | Parameters | ||||
|---|---|---|---|---|---|
| fct [MPa] 1 | ρ1 | nf | crt [s] | q [kN/m2] 1 | |
| Reference (M_Ref) | 2.0 | 0.8% | 2 | 0.1 | 5.3 |
| M_fct2.5 | 2.5 | 0.8% | 2 | 0.1 | 5.3 |
| M_fct3.0 | 3.0 | 0.8% | 2 | 0.1 | 5.3 |
| M_ρ0.5 | 2.0 | 0.5% | 2 | 0.1 | 5.3 |
| M_nf4 | 2.0 | 0.8% | 4 | 0.1 | 5.3 |
| M_nf7 | 2.0 | 0.8% | 7 | 0.1 | 5.3 |
| M_crt0.01 | 2.0 | 0.8% | 2 | 0.01 | 5.3 |
| M_crt0.05 | 2.0 | 0.8% | 2 | 0.05 | 5.3 |
| M_crt0.2 | 2.0 | 0.8% | 2 | 0.2 | 5.3 |
| M_q9 | 2.0 | 0.8% | 2 | 0.1 | 9.0 |
| Model | Distance [m] | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.62 | 1.67 | 3.33 | 4.35 | 5 | ||||||
| Peak | Residual | Peak | Residual | Peak | Residual | Peak | Residual | Peak | Residual | |
| M_Ref | 4.47 | 4.39 | 17.61 | 17.38 | 36.60 | 36.09 | 44.46 | 43.84 | 46.88 | 46.18 |
| M_fct2.5 | 3.14 | 2.97 | 11.84 | 11.17 | 24.10 | 22.51 | 29.33 | 27.33 | 31.32 | 29.02 |
| M_fct3 | 2.74 | 2.54 | 9.99 | 9.16 | 20.15 | 18.24 | 24.45 | 22.06 | 26.20 | 23.63 |
| M_ρ0.5 | 7.54 | 7.48 | 27.78 | 27.64 | 57.35 | 57.20 | 69.83 | 69.46 | 72.85 | 72.48 |
| M_nf4 | 7.209 | 7.17 | 26.96 | 26.78 | 56.09 | 55.53 | 68.09 | 67.53 | 71.23 | 70.41 |
| M_nf7 | 8.37 | 8.26 | 29.94 | 29.63 | 61.63 | 60.82 | 74.54 | 73.55 | 77.71 | 76.52 |
| M_crt0.01 | 6.05 | 6.00 | 23.70 | 23.60 | 50.14 | 49.72 | 60.45 | 60.13 | 63.42 | 63.32 |
| M_crt0.05 | 5.48 | 5.39 | 21.62 | 21.38 | 45.28 | 44.73 | 55.06 | 54.33 | 57.83 | 56.99 |
| M_crt0.2 | 3.44 | 3.39 | 13.44 | 13.27 | 27.61 | 27.23 | 33.50 | 33.03 | 35.62 | 35.11 |
| M_q9 | 5.32 | 5.32 | 230.7 | 230.7 | 446.80 | 446.80 | 533.54 | 533.54 | 556.30 | 556.30 |
| Model | Vertical Displacement in P3 [mm] | Increase/Decrease [%] |
|---|---|---|
| M_Ref | 46.18 | - |
| M_fct2.5 | 29.02 | −37.2% |
| M_fct3.0 | 23.63 | −48.8% |
| M_ρ0.5 | 72.48 | 57.0% |
| M_nf4 | 70.41 | 52.5% |
| M_nf7 | 76.52 | 65.7% |
| M_crt0.01 | 63.32 | 37.1% |
| M_crt0.05 | 56.99 | 23.4% |
| M_crt0.2 | 35.11 | −24.0% |
| M_q9 | 556.30 | 1104.7% |
| Model | Floor | |||
|---|---|---|---|---|
| 1st Floor | 2nd Floor | |||
| Peak | Residual | Peak | Residual | |
| M_Ref | 0.61 | 0.21 | 1.99 | 1.36 |
| M_fct2.5 | 0.73 | 0.28 | 1.85 | 1.16 |
| M_fct3 | 0.71 | 0.27 | 1.76 | 1.11 |
| M_ρ0.5 | 0.45 | 0.06 | 1.95 | 1.30 |
| M_nf4 | 0.41 | 0.07 | 2.05 | 1.37 |
| M_nf7 | 0.16 | 0.01 | 1.58 | 1.35 |
| M_crt0.01 | 0.63 | 0.14 | 2.14 | 1.46 |
| M_crt0.05 | 0.62 | 0.16 | 2.06 | 1.38 |
| M_crt0.2 | 0.53 | 0.22 | 1.70 | 1.30 |
| M_q9 | −0.74 | −0.46 | 1.57 | 1.05 |
| Model | Static Nonlinear | Static Linear | Dynamic Nonlinear | DAFLD | LIFLD | DAFLF | LIFLF | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Max. Disp. [mm] | Axial Force P2/P6 [kN] | Max. Disp. [mm] | Axial Force P2/P6 [kN] | Max. Disp. [mm] | Axial Force P2/P6 [kN] | |||||
| M_Ref | 25.6 | 317.4 | 14.1 | 317.3 | 46.9 | 340.1 | 1.83 | 3.33 | 1.07 | 1.07 |
| M_fct2.5 | 20.6 | 316.0 | 14.1 | 317.3 | 31.3 | 346.4 | 1.52 | 2.22 | 1.10 | 1.09 |
| M_fct3.0 | 18.4 | 316.1 | 14.1 | 317.3 | 26.2 | 351.4 | 1.42 | 1.86 | 1.11 | 1.11 |
| M_ρ0.5 | 26.9 | 317.9 | 14.1 | 317.2 | 72.7 | 350.6 | 2.70 | 5.16 | 1.10 | 1.11 |
| M_nf4 | 27.8 | 645.0 | 15.2 | 649.6 | 70.3 | 720.7 | 2.53 | 4.63 | 1.12 | 1.11 |
| M_nf7 | 30.7 | 1138.8 | 18.1 | 1152.1 | 77.7 | 1267.4 | 2.53 | 4.29 | 1.11 | 1.10 |
| M_crt0.01 | 25.6 | 317.4 | 14.1 | 317.3 | 63.4 | 352.6 | 2.48 | 4.56 | 1.11 | 1.11 |
| M_crt0.05 | 25.6 | 317.4 | 14.1 | 317.3 | 57.8 | 343.6 | 2.26 | 4.10 | 1.08 | 1.08 |
| M_crt0.2 | 25.6 | 317.4 | 14.1 | 317.3 | 35.6 | 330.5 | 1.39 | 2.52 | 1.04 | 1.04 |
| M_q9 | 76.3 | 411.4 | 18.7 | 399.3 | 556.8 | 398.6 | 7.30 | 29.78 | 0.97 | 1.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buitrago, M.; Bertolesi, E.; Garzón-Roca, J.; Sagaseta, J.; Adam, J.M. A Parametric Computational Study of RC Building Structures under Corner-Column Removal Situations. Appl. Sci. 2020, 10, 8911. https://doi.org/10.3390/app10248911
Buitrago M, Bertolesi E, Garzón-Roca J, Sagaseta J, Adam JM. A Parametric Computational Study of RC Building Structures under Corner-Column Removal Situations. Applied Sciences. 2020; 10(24):8911. https://doi.org/10.3390/app10248911
Chicago/Turabian StyleBuitrago, Manuel, Elisa Bertolesi, Julio Garzón-Roca, Juan Sagaseta, and José M. Adam. 2020. "A Parametric Computational Study of RC Building Structures under Corner-Column Removal Situations" Applied Sciences 10, no. 24: 8911. https://doi.org/10.3390/app10248911
APA StyleBuitrago, M., Bertolesi, E., Garzón-Roca, J., Sagaseta, J., & Adam, J. M. (2020). A Parametric Computational Study of RC Building Structures under Corner-Column Removal Situations. Applied Sciences, 10(24), 8911. https://doi.org/10.3390/app10248911






