The Role of Crystalline Orientation in the Formation of Surface Patterns on Solids Irradiated with Femtosecond Laser Double Pulses
Abstract
Featured Application
Abstract
1. Introduction
2. Theoretical Model
2.1. Ultrafast Dynamics
2.2. LSFL Formation
2.3. Fluid Transport. Ripples and Grooves
- The first pulse irradiates a flat surface which leads to the formation of a crater and small protrusions (humps) at the edges on the surface of the heated zone due to mass displacement [22,33]. Moreover, due to the high fluence value, some ablation also occurs. The first pulse irradiates a flat surface with no corrugations, therefore the formation of periodic structures is not expected to happen. It is noted that due to the axial symmetry of a Gaussian beam, for NP = 1, Equations (1)–(9) can be solved in 2D.
- The second pulse, then, irradiates the attained pattern and therefore the spatial symmetry breaks; as a result, 2D modelling can no longer be used. The coupling of the electric field of the incident beam with the induced surface-scattered wave produces a nonuniform, periodic distribution of the absorbed energy. The periodic variation of the absorbed energy, in turn, leads to a periodic excited electron density distribution [9]. It is noted, however, that the computation of the amount of the absorbed energy at each position requires the evaluation of the energy deposition on a curved surface (i.e., Equation (7) for reflectivity is valid for flat profiles). Therefore, appropriate computational schemes are used to compute the absorbed energy on each point of the curved surface [9]. The calculated spatially modulated electron energy distribution is transferred to the lattice system (through the second equation of Equation (1)) and subsequently, upon phase transition fluid transport and resolidification processes, LIPSS are formed.
- The above methodology is used to describe the formation of LIPSS for N2 (including a correction to the surface plasmon wavelength shift to smaller values with increasing depth of the profile following an increase in dose [13,32,39]); however, there is a resonance at which further excitation of surface plasmons stops being the driving force behind the induced surface profile and suprawavelength structures are produced. In a previous report, it was shown that if the surface profile becomes sufficiently deep (at large NP) normal thermocapillary waves which lead to regular LIPSS are not produced [8,23]. By contrast, another solution of NSE dominates, namely, hydrothermal waves that propagate between the wells of the ripples in a perpendicular direction to the laser beam polarisation [8]. Another important feature of these solutions is that, only, waves of a certain periodicity (i.e., larger than the laser wavelength) lead to stable structures upon solidification, which are orientated perpendicularly to the beam polarisation and they are termed grooves.
3. Experimental Protocol
4. Discussion
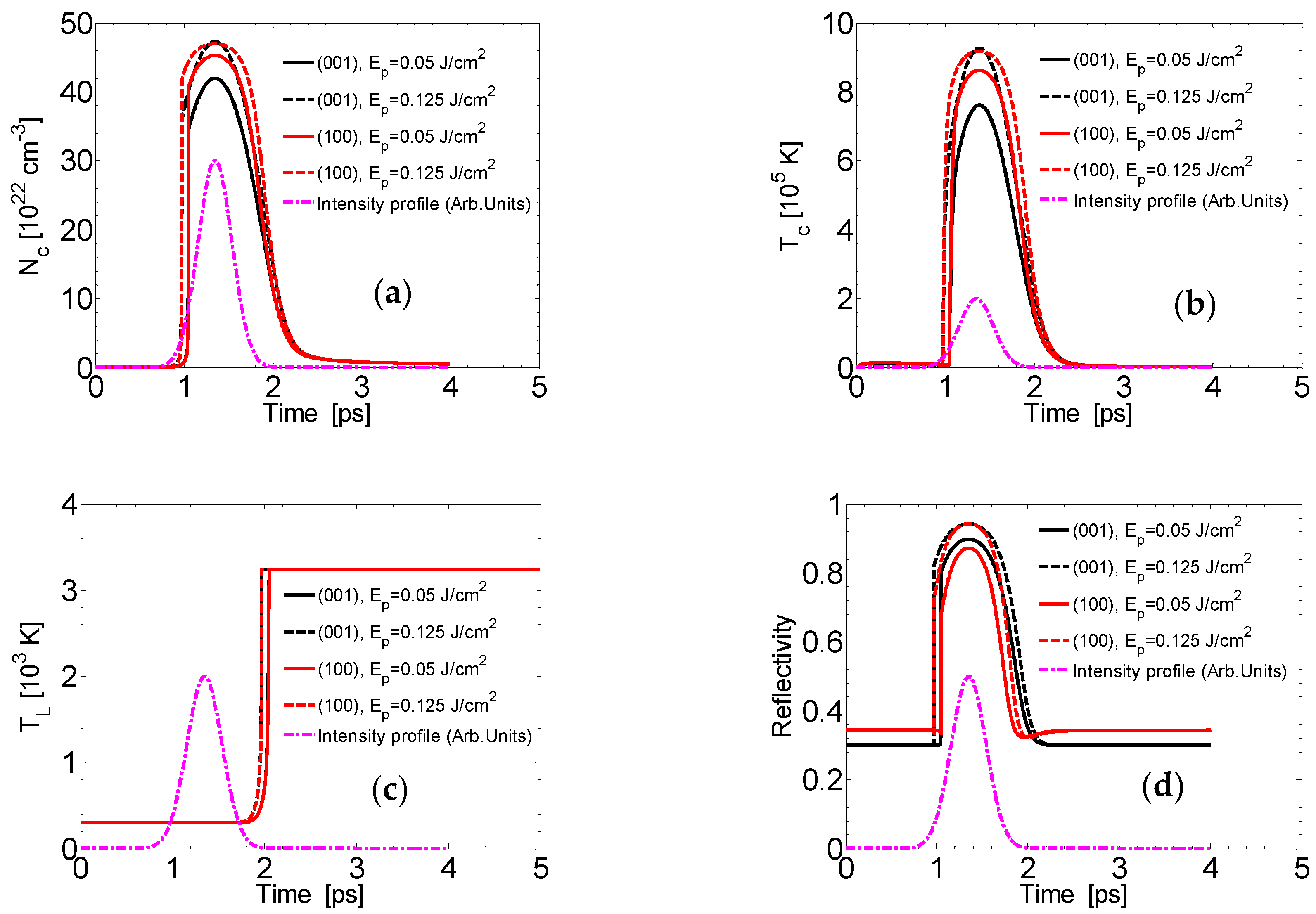
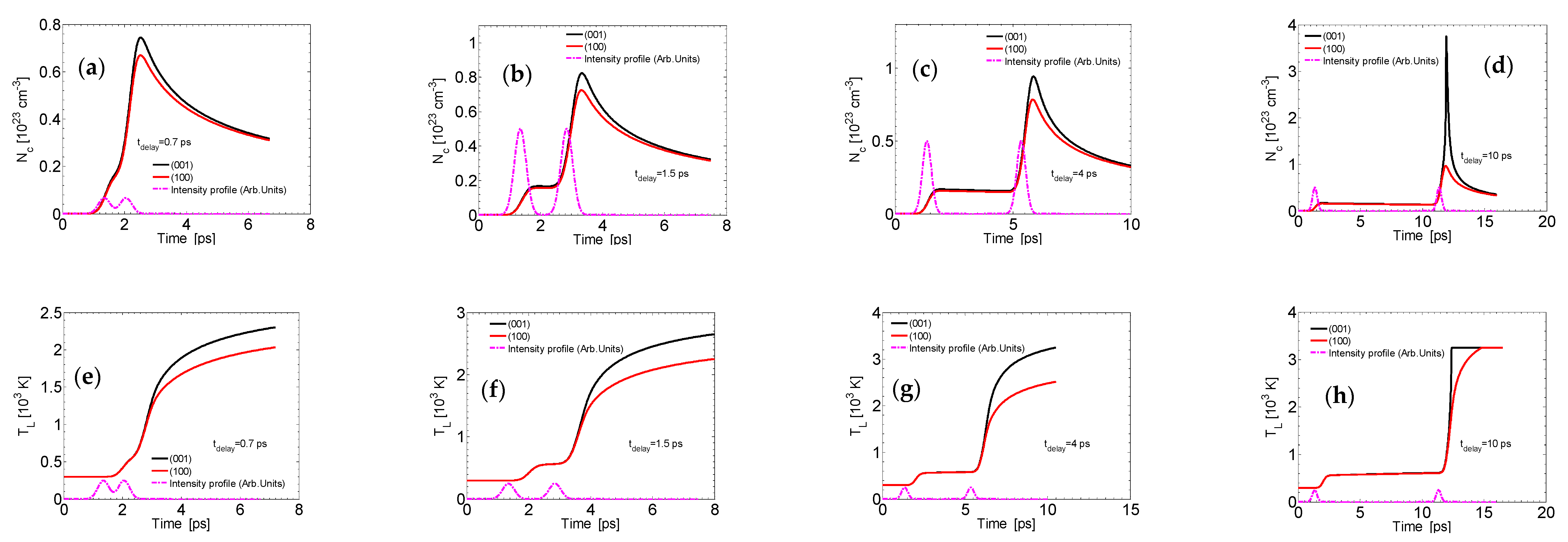
4.1. Single Pulse Excitation (tdelay = 0)
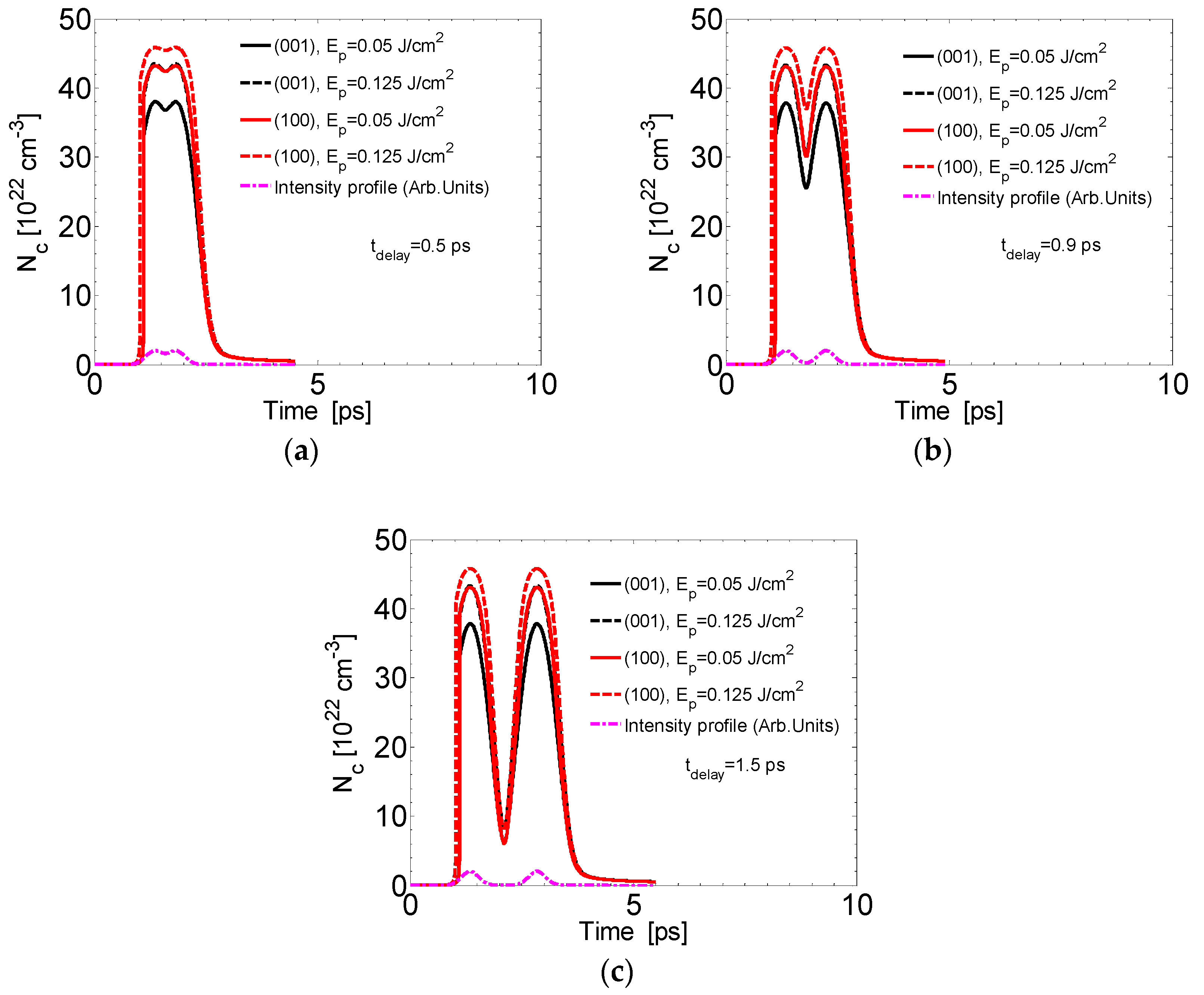
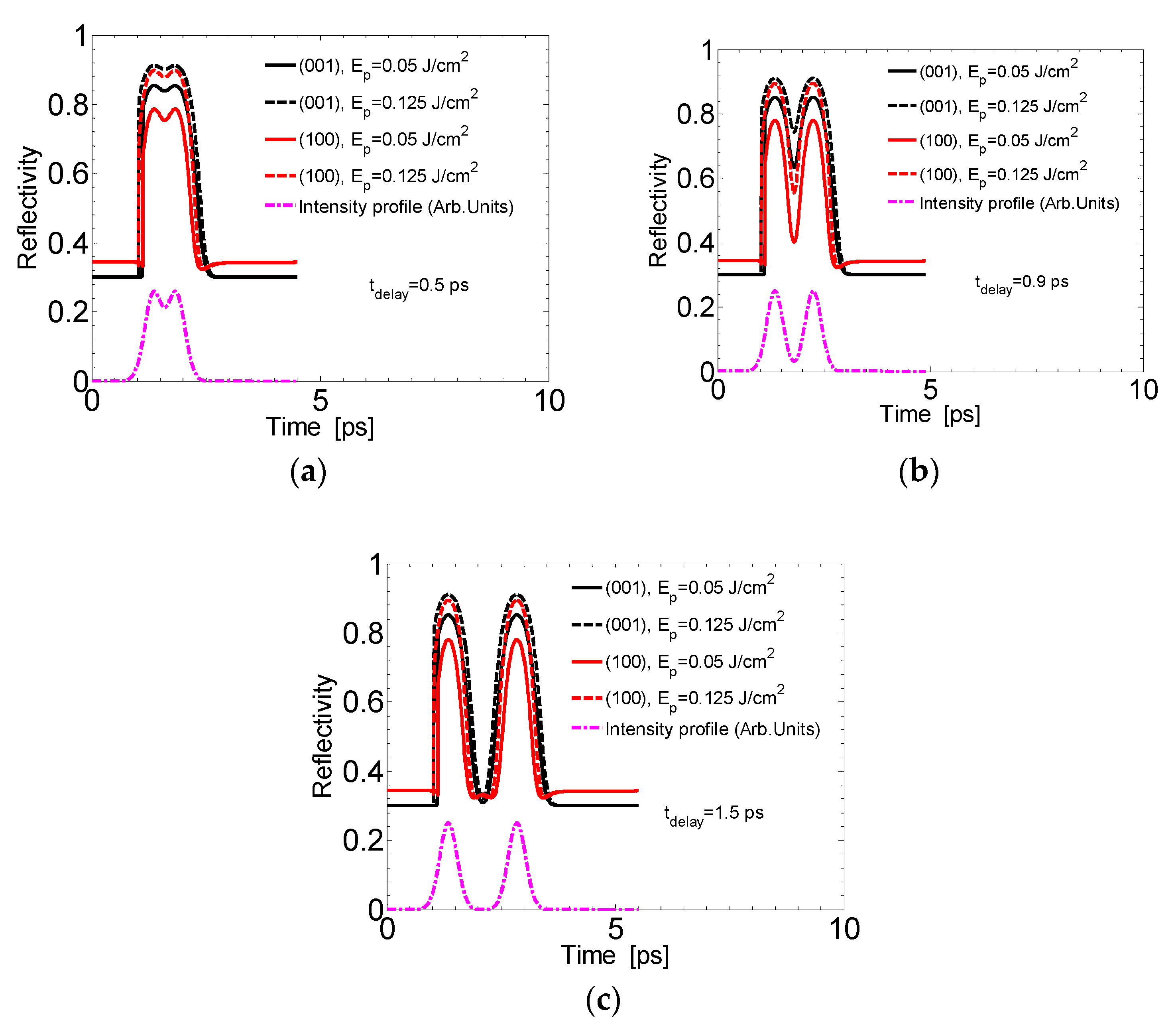
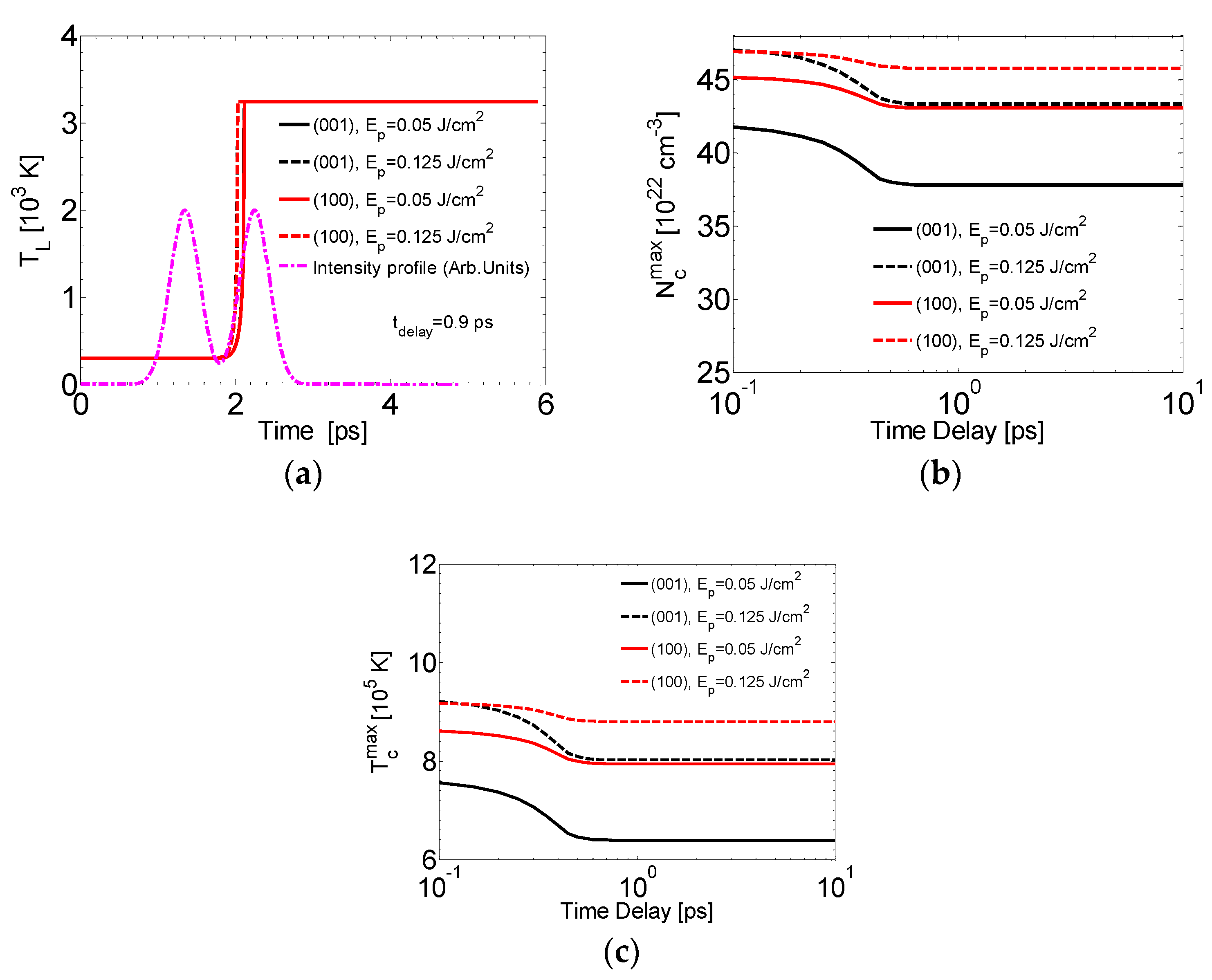
4.2. Double Pulse Excitation (tdelay ≠ 0)
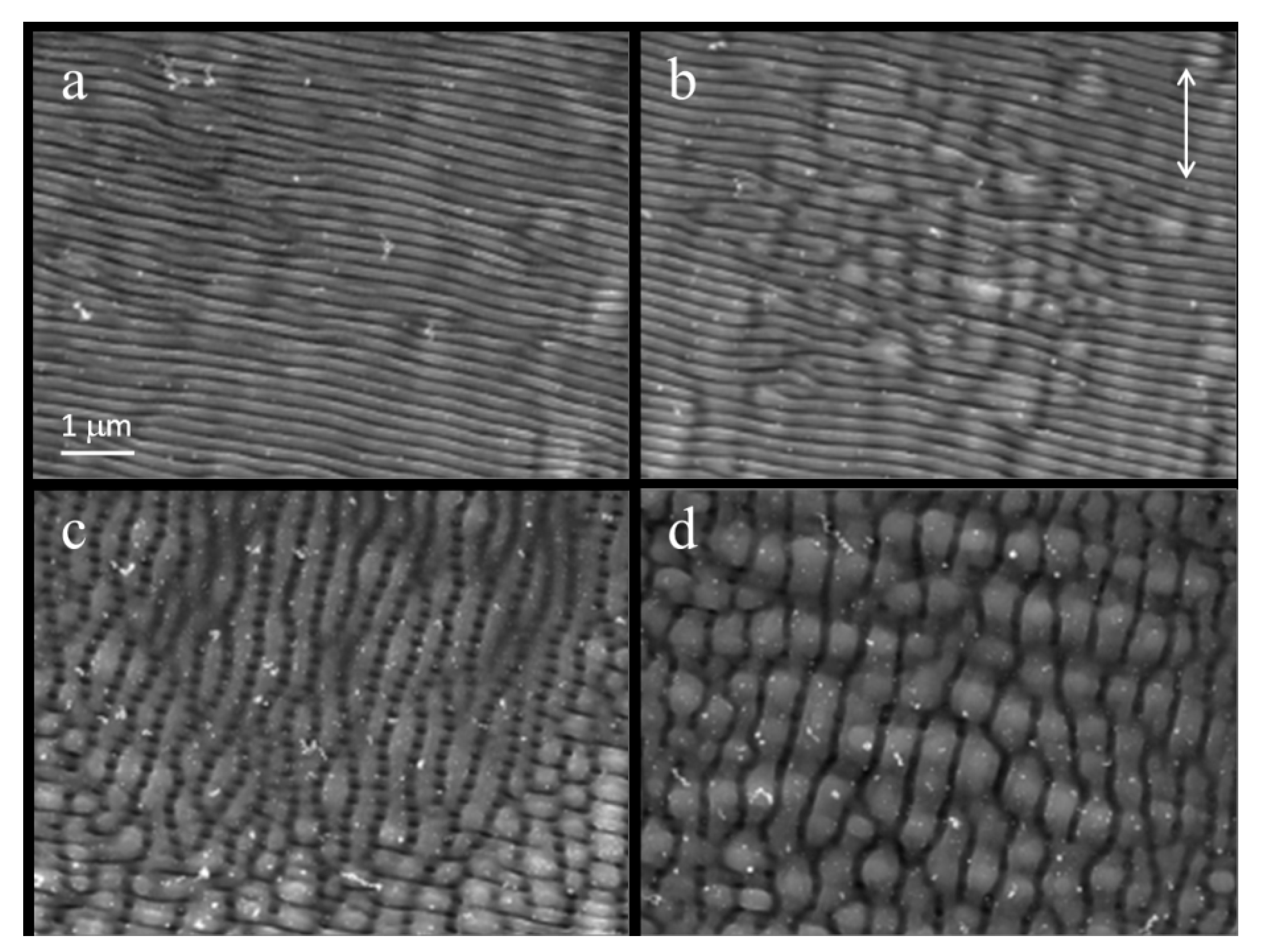
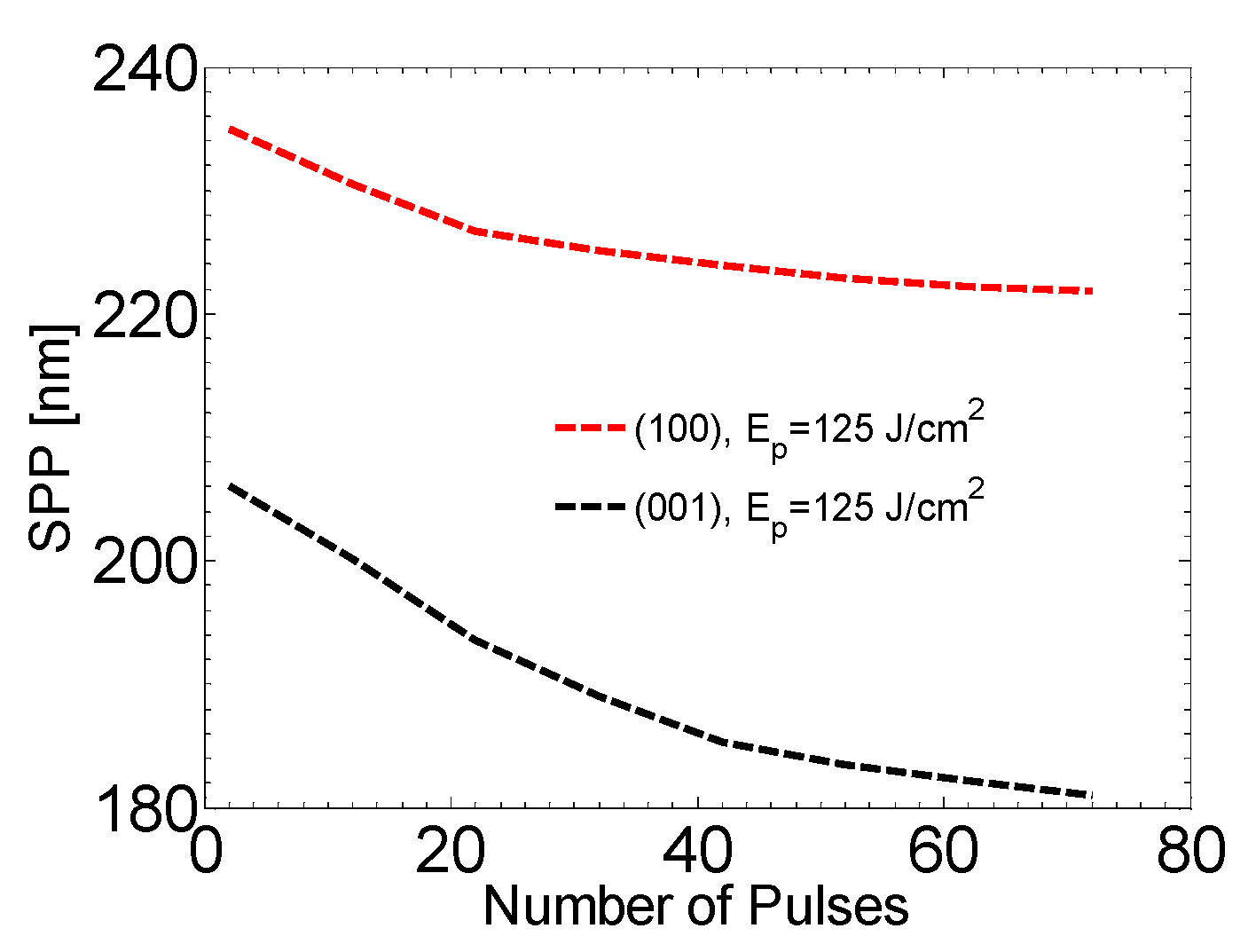
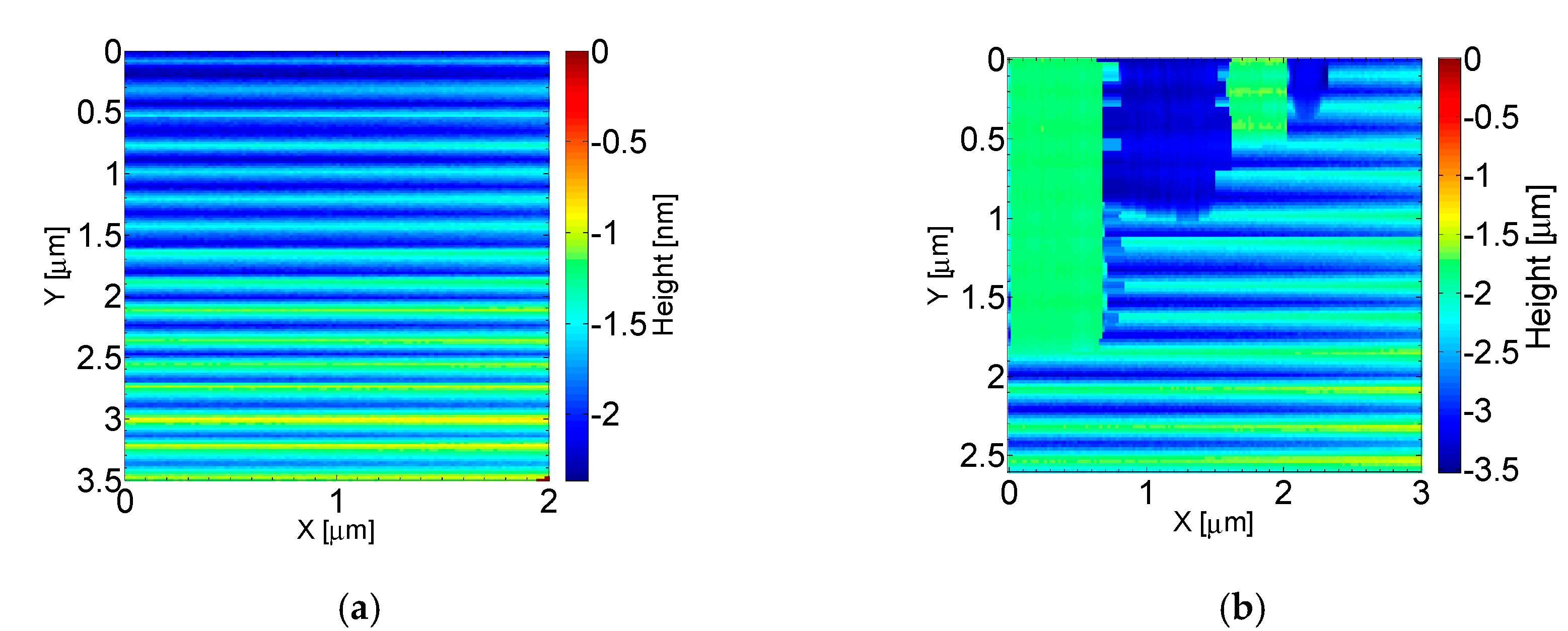
4.3. LIPSS Formation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
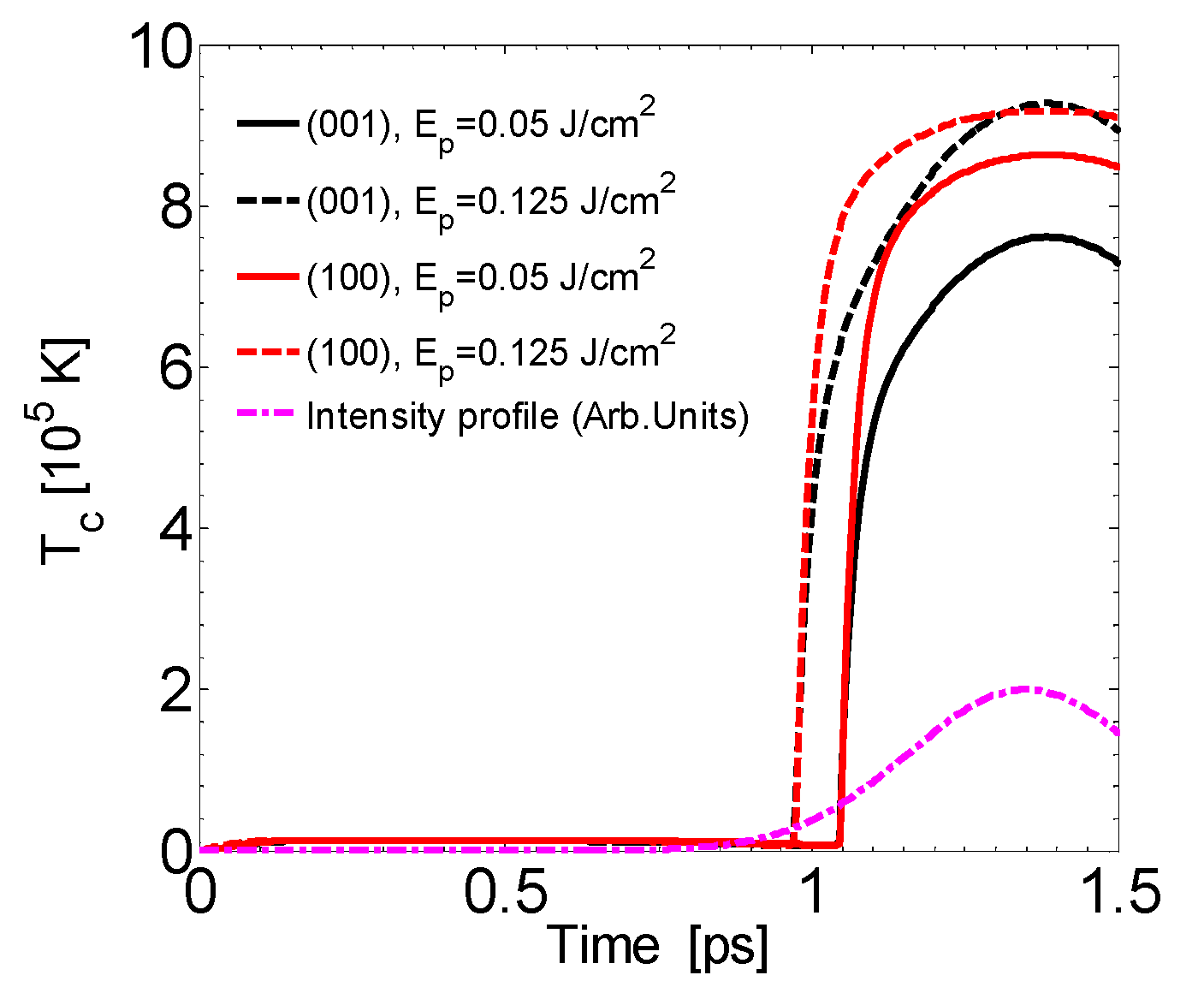
Appendix B
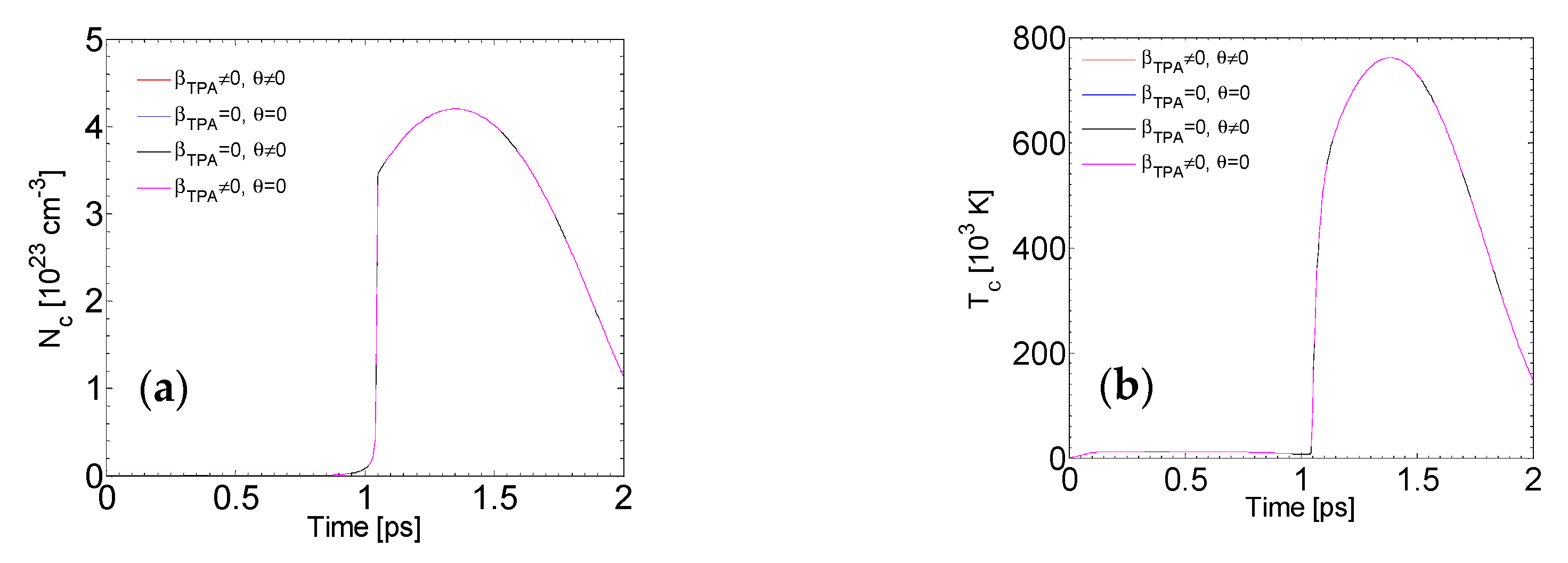
Appendix C
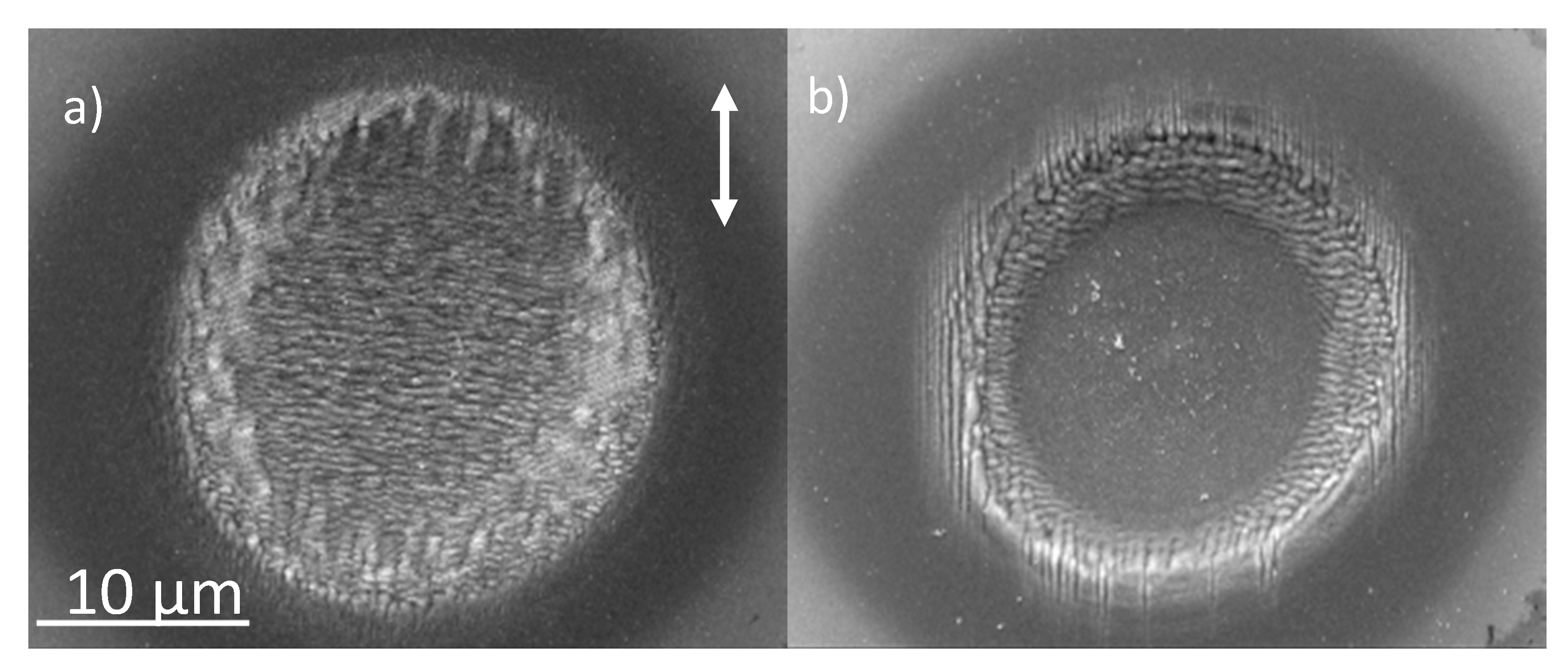
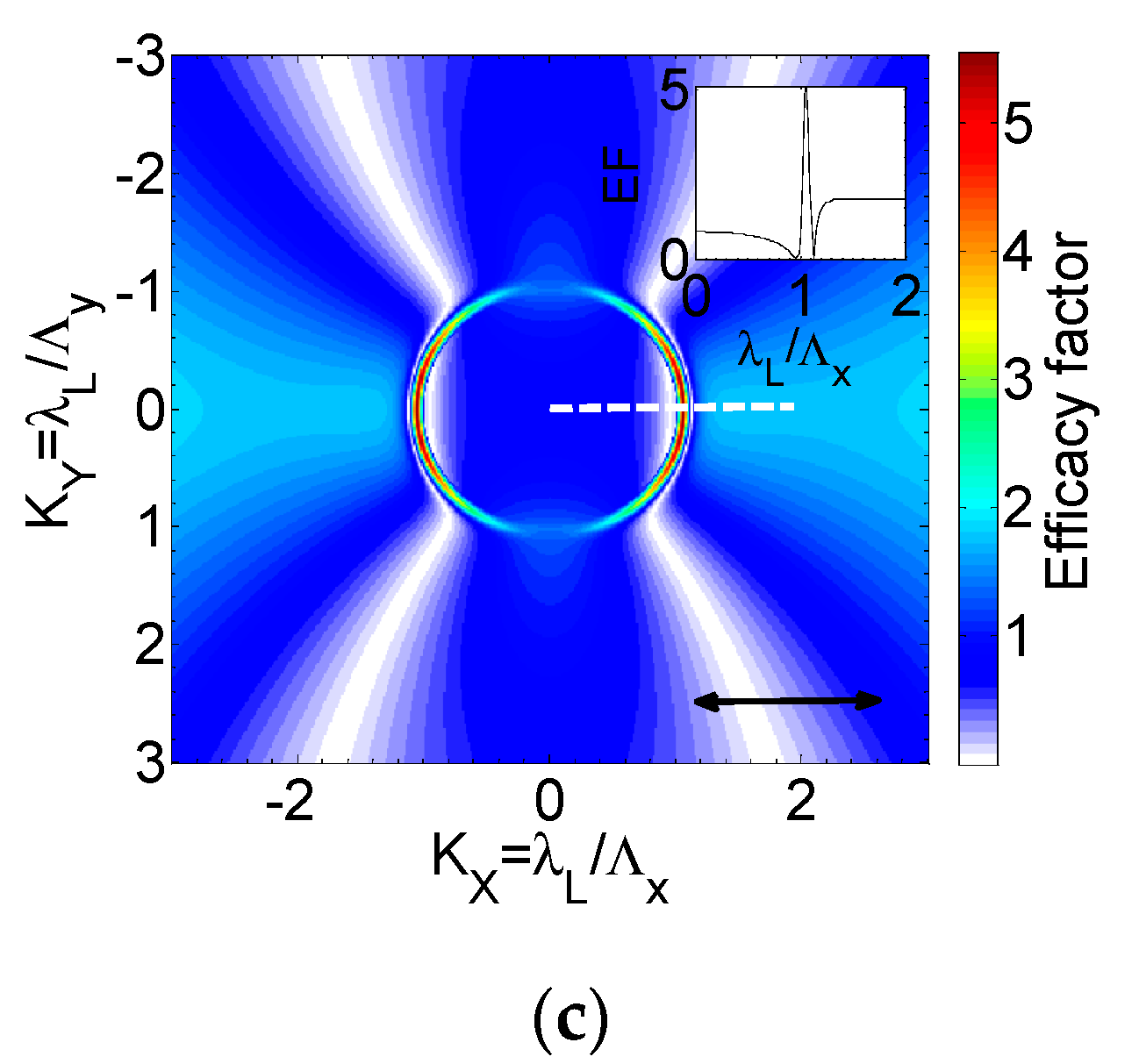
References
- Vorobyev, A.Y.; Guo, C. Direct femtosecond laser surface nano/microstructuring and its applications. Laser Photon. Rev. 2013, 7, 385–407. [Google Scholar] [CrossRef]
- Zorba, V.; Persano, L.; Pisignano, D.; Athanassiou, A.; Stratakis, E.; Cingolani, R.; Tzanetakis, P.; Fotakis, C. Making silicon hydrophobic: Wettability control by two-lengthscale simultaneous patterning with femtosecond laser irradiation. Nanotechnology 2006, 17, 3234–3238. [Google Scholar] [CrossRef]
- Zorba, V.; Stratakis, E.; Barberoglou, M.; Spanakis, E.; Tzanetakis, P.; Anastasiadis, S.H.; Fotakis, C. Biomimetic Artificial Surfaces Quantitatively Reproduce the Water Repellency of a Lotus Leaf. Adv. Mater. 2008, 20, 4049–4054. [Google Scholar] [CrossRef]
- Zimmer, K. Laser Processing and Chemistry. Z. Phys. Chem. 1999, 208, 291–292. [Google Scholar] [CrossRef]
- Diels, J.-C.; Rudolph, W. Ultrashort Laser Pulse Phenomena: Fundamentals, Techniques, and Applications on a Femtosecond Time Scale, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Papadopoulou, E.L.; Samara, A.; Barberoglou, M.; Manousaki, A.; Pagakis, S.N.; Anastasiadou, E.; Fotakis, C.; Stratakis, E. Silicon Scaffolds Promoting Three-Dimensional Neuronal Web of Cytoplasmic Processes. Tissue Eng. Part C Methods 2010, 16, 497–502. [Google Scholar] [CrossRef]
- Wang, Z.B.; Hong, M.H.; Lu, Y.F.; Wu, D.J.; Lan, B.; Chong, T.C. Femtosecond laser ablation of polytetrafluoroethylene (Teflon) in ambient air. J. Appl. Phys. 2003, 93, 6375–6380. [Google Scholar] [CrossRef]
- Böhme, R.; Pissadakis, S.; Ruthe, D.; Zimmer, K. Laser backside etching of fused silica with ultra-short pulses. Appl. Phys. A 2006, 85, 75–78. [Google Scholar] [CrossRef]
- Petrović, S.M.; Gakovic, B.M.; Peruško, D.; Stratakis, E.; Bogdanovicradovic, I.; Cekada, M.; Fotakis, C.; Jelenkovic, B.M. Femtosecond laser-induced periodic surface structure on the Ti-based nanolayered thin films. J. Appl. Phys. 2013, 114, 233108. [Google Scholar] [CrossRef]
- Stratakis, E.; Bonse, J.; Heitz, J.; Siegel, J.; Tsibidis, G.; Skoulas, E.; Papadopoulos, A.; Mimidis, A.; Joel, A.-C.; Comanns, P.; et al. Laser engineering of biomimetic surfaces. Mater. Sci. Eng. R Rep. 2020, 141, 100562. [Google Scholar] [CrossRef]
- Stratakis, E.; Ranella, A.; Fotakis, C. Biomimetic micro/nanostructured functional surfaces for microfluidic and tissue engineering applications. Biomicrofluidics 2011, 5, 013411. [Google Scholar] [CrossRef]
- Bonse, J.; Koter, R.; Hartelt, M.; Spaltmann, D.; Pentzien, S.; Höhm, S.; Rosenfeld, A.; Kruger, J. Femtosecond laser-induced periodic surface structures on steel and titanium alloy for tribological applications. Appl. Phys. A 2014, 117, 103–110. [Google Scholar] [CrossRef]
- Lu, Y.; Hua, M.; Liu, Z. The Biomimetic Shark Skin Optimization Design Method for Improving Lubrication Effect of Engineering Surface. J. Tribol. 2014, 136, 031703–3170313. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Y.-B.; Bai, F.; Wang, C.-W.; Zhao, Q.-Z. Angle-dependent lubricated tribological properties of stainless steel by femtosecond laser surface texturing. Opt. Laser Technol. 2016, 81, 60–66. [Google Scholar] [CrossRef]
- Simitzi, C.; Efstathopoulos, P.; Kourgiantaki, A.; Ranella, A.; Charalampopoulos, I.; Fotakis, C.; Athanassakis, I.; Stratakis, E.; Gravanis, A. Laser fabricated discontinuous anisotropic microconical substrates as a new model scaffold to control the directionality of neuronal network outgrowth. Biomaterials 2015, 67, 115–128. [Google Scholar] [CrossRef]
- Jiang, H.-B.; Zhang, Y.-L.; Liu, Y.; Fu, X.; Li, Y.; Liu, Y.-Q.; Li, C.-H.; Sun, H.-B. Bioinspired few-layer graphene prepared by chemical vapor deposition on femtosecond laser-structured Cu foil. Laser Photon. Rev. 2016, 10, 441–450. [Google Scholar] [CrossRef]
- Papadopoulos, A.; Skoulas, E.; Mimidis, A.; Perrakis, G.; Kenanakis, G.; Tsibidis, G.D.; Stratakis, E. Biomimetic Omnidirectional Antireflective Glass via Direct Ultrafast Laser Nanostructuring. Adv. Mater. 2019, 31, e1901123. [Google Scholar] [CrossRef]
- Bonse, J.; Hohm, S.; Kirner, S.V.; Rosenfeld, A.; Kruger, J. Laser-Induced Periodic Surface Structures—A Scientific Evergreen. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 1–15. [Google Scholar] [CrossRef]
- Skoulas, E.; Manousaki, A.; Fotakis, C.; Stratakis, E. Biomimetic surface structuring using cylindrical vector femtosecond laser beams. Sci. Rep. 2017, 7, 45114. [Google Scholar] [CrossRef]
- Nivas, J.J.J.; He, S.; Rubano, A.; Vecchione, A.; Paparo, D.; Marrucci, L.; Bruzzese, R.; Amoruso, S. Direct Femtosecond Laser Surface Structuring with Optical Vortex Beams Generated by a q-plate. Sci. Rep. 2015, 5, 17929. [Google Scholar] [CrossRef]
- Huang, M.; Zhao, F.; Cheng, Y.; Xu, N.; Xu, Z. Origin of Laser-Induced Near-Subwavelength Ripples: Interference between Surface Plasmons and Incident Laser. ACS Nano 2009, 3, 4062–4070. [Google Scholar] [CrossRef]
- Tsibidis, G.D.; Barberoglou, M.; Loukakos, P.A.; Stratakis, E.; Fotakis, C. Dynamics of ripple formation on silicon surfaces by ultrashort laser pulses in subablation conditions. Phys. Rev. B 2012, 86, 115316. [Google Scholar] [CrossRef]
- Bonse, J.; Kruger, J.; Höhm, S.; Rosenfeld, A. Femtosecond laser-induced periodic surface structures. J. Laser Appl. 2012, 24, 042006. [Google Scholar] [CrossRef]
- Rudenko, A.; Colombier, J.-P.; Höhm, S.; Rosenfeld, A.; Krüger, J.; Bonse, J.; Itina, T.E. Spontaneous periodic ordering on the surface and in the bulk of dielectrics irradiated by ultrafast laser: A shared electromagnetic origin. Sci. Rep. 2017, 7, 12306. [Google Scholar] [CrossRef]
- Tsibidis, G.D.; Fotakis, C.; Stratakis, E. From ripples to spikes: A hydrodynamical mechanism to interpret femtosecond laser-induced self-assembled structures. Phys. Rev. B 2015, 92, 041405. [Google Scholar] [CrossRef]
- Van Driel, H.M. Kinetics of high-density plasmas generated in Si by 1.06- and 0.53-μmpicosecond laser pulses. Phys. Rev. B 1987, 35, 8166–8176. [Google Scholar] [CrossRef]
- Sundaram, S.K.; Mazur, E. Inducing and probing non-thermal transitions in semiconductors using femtosecond laser pulses. Nat. Mater. 2002, 1, 217–224. [Google Scholar] [CrossRef]
- Knoesel, E.; Hotzel, A.; Wolf, M. Ultrafast dynamics of hot electrons and holes in copper: Excitation, energy relaxation, and transport effects. Phys. Rev. B 1998, 57, 12812–12824. [Google Scholar] [CrossRef]
- Derrien, T.J.Y.; Krüger, J.; Itina, T.E.; Höhm, S.; Rosenfeld, A.; Bonse, J. Rippled area formed by surface plasmon polaritons upon femtosecond laser double-pulse irradiation of silicon: The role of carrier generation and relaxation processes. Appl. Phys. A 2013, 117, 77–81. [Google Scholar] [CrossRef]
- Derrien, T.J.-Y.; Itina, T.E.; Torres, R.; Sarnet, T.; Sentis, M. Possible surface plasmon polariton excitation under femtosecond laser irradiation of silicon. J. Appl. Phys. 2013, 114, 083104. [Google Scholar] [CrossRef]
- Bonse, J.; Munz, M.; Sturm, H. Structure formation on the surface of indium phosphide irradiated by femtosecond laser pulses. J. Appl. Phys. 2005, 97, 013538. [Google Scholar] [CrossRef]
- Van Driel, H.; Young, J.F.; Sipe, J. Laser Induced Periodic Surface Structure. MRS Proc. 1982, 13, 1141–1154. [Google Scholar] [CrossRef]
- Tsibidis, G.D.; Skoulas, E.; Papadopoulos, A.; Stratakis, E. Convection roll-driven generation of supra-wavelength periodic surface structures on dielectrics upon irradiation with femtosecond pulsed lasers. Phys. Rev. B 2016, 94, 081305. [Google Scholar] [CrossRef]
- Bonse, J.; Rosenfeld, A.; Krueger, J. On the role of surface plasmon polaritons in the formation of laser-induced periodic surface structures upon irradiation of silicon by femtosecond-laser pulses. J. Appl. Phys. 2009, 106, 104910. [Google Scholar] [CrossRef]
- Cheng, K.; Liu, J.; Cao, K.; Chen, L.; Zhang, Y.; Jiang, Q.; Feng, D.; Zhang, S.; Su, Z.; Jia, T. Ultrafast dynamics of single-pulse femtosecond laser-induced periodic ripples on the surface of gold films. Phys. Rev. B 2018, 98, 184106. [Google Scholar] [CrossRef]
- Barberoglou, M.; Tsibidis, G.D.; Gray, D.; Magoulakis, E.; Fotakis, C.; Stratakis, E.; Loukakos, P.A. The influence of ultra-fast temporal energy regulation on the morphology of Si surfaces through femtosecond double pulse laser irradiation. Appl. Phys. A 2013, 113, 273–283. [Google Scholar] [CrossRef]
- Tsibidis, G.D.; Stratakis, E.; Loukakos, P.A.; Fotakis, C. Controlled ultrashort-pulse laser-induced ripple formation on semiconductors. Appl. Phys. A 2014, 114, 57–68. [Google Scholar] [CrossRef]
- Varlamova, O.; Costache, F.; Reif, J.; Bestehorn, M. Self-organized pattern formation upon femtosecond laser ablation by circularly polarized light. Appl. Surf. Sci. 2006, 252, 4702–4706. [Google Scholar] [CrossRef]
- Rudenko, A.; Colombier, J.-P.; Itina, T.E. From random inhomogeneities to periodic nanostructures induced in bulk silica by ultrashort laser. Phys. Rev. B 2016, 93, 075427. [Google Scholar] [CrossRef]
- Sipe, J.E.; Young, J.F.; Preston, J.S.; Van Driel, H.M. Laser-induced periodic surface structure. I. Theory. Phys.Rev.B. 1983, 27, 1141–1154. [Google Scholar] [CrossRef]
- Tsibidis, G.D. Ultrafast dynamics of non-equilibrium electrons and strain generation under femtosecond laser irradiation of Nickel. Appl. Phys. A 2018, 124, 311. [Google Scholar] [CrossRef]
- Tsibidis, G.D. The influence of dynamical change of optical properties on the thermomechanical response and damage threshold of noble metals under femtosecond laser irradiation. J. Appl. Phys. 2018, 123, 085903. [Google Scholar] [CrossRef]
- Chimier, B.; Utéza, O.; Sanner, N.; Sentis, M.; Itina, T.E.; Lassonde, P.; Légaré, F.; Vidal, F.; Kieffer, J.C. Damage and ablation thresholds of fused-silica in femtosecond regime. Phys. Rev. B 2011, 84, 094104. [Google Scholar] [CrossRef]
- Nathala, C.S.R.; Ajami, A.; Husinsky, W.; Farooq, B.; Kudryashov, S.I.; Daskalova, A.; Bliznakova, I.; Assion, A. Ultrashort laser pulse ablation of copper, silicon and gelatin: Effect of the pulse duration on the ablation thresholds and the incubation coefficients. Appl. Phys. A 2016, 122, 1–8. [Google Scholar] [CrossRef]
- Ionin, A.A.; Kudryashov, S.; Makarov, S.V.; Seleznev, L.V.; Sinitsyn, D.V. Electron dynamics and prompt ablation of aluminum surface excited by intense femtosecond laser pulse. Appl. Phys. A 2014, 117, 1757–1763. [Google Scholar] [CrossRef]
- Museur, L.; Tsibidis, G.D.; Manousaki, A.; Anglos, D.; Kanaev, A. Surface structuring of rutile TiO2(100) and (001) single crystals with femtosecond pulsed laser irradiation. J. Opt. Soc. Am. B 2018, 35, 2600–2607. [Google Scholar] [CrossRef]
- Breckenridge, R.G.; Hosler, W.R. Electrical Properties of Titanium Dioxide Semiconductors. Phys. Rev. 1953, 91, 793–802. [Google Scholar] [CrossRef]
- Ekuma, C.E.; Bagayoko, D. Ab-initio Electronic and Structural Properties of Rutile Titanium Dioxide. Jpn. J. Appl. Phys. 2011, 50, 101103. [Google Scholar] [CrossRef]
- Xiong, Q.-L.; Li, Z.; Kitamura, T. Effect of Crystal Orientation on Femtosecond Laser-Induced Thermomechanical Responses and Spallation Behaviors of Copper Films. Sci. Rep. 2017, 7, 1–14. [Google Scholar] [CrossRef]
- Hendry, E.; Koeberg, M.; Pijpers, J.; Bonn, M. Reduction of carrier mobility in semiconductors caused by charge-charge interactions. Phys. Rev. B 2007, 75. [Google Scholar] [CrossRef]
- Dou, M.; Persson, C. Comparative study of rutile and anatase SnO2 and TiO2: Band-edge structures, dielectric functions, and polaron effects. J. Appl. Phys. 2013, 113, 083703. [Google Scholar] [CrossRef]
- Kang, W.; Hybertsen, M.S. Quasiparticle and optical properties of rutile and anatase TiO2. Phys. Rev. B 2010, 82, 085203. [Google Scholar] [CrossRef]
- Yagi, E.; Hasiguti, R.R.; Aono, M. Electronic conduction above 4 K of slightly reduced oxygen-deficient rutile TiO2-x. Phys. Rev. B 1996, 54, 7945–7956. [Google Scholar] [CrossRef]
- Zajac, V.; Němec, H.; Kužel, P. Picosecond charge transport in rutile at high carrier densities studied by transient terahertz spectroscopy. Phys. Rev. B 2016, 94, 115206. [Google Scholar] [CrossRef]
- Itina, T.E.; Shcheblanov, N. Electronic excitation in femtosecond laser interactions with wide-band-gap materials. Appl. Phys. A 2010, 98, 769–775. [Google Scholar] [CrossRef]
- Chen, J.; Tzou, D.; Beraun, J. Numerical investigation of ultrashort laser damage in semiconductors. Int. J. Heat Mass Transf. 2005, 48, 501–509. [Google Scholar] [CrossRef]
- Rämer, A.; Osmani, O.; Rethfeld, B. Laser damage in silicon: Energy absorption, relaxation, and transport. J. Appl. Phys. 2014, 116, 053508. [Google Scholar] [CrossRef]
- Anisimov, S.I.; Kapeliovich, B.L.; Perel’man, T.L. Electron-emission from surface of metals induced by ultrashort laser pulses. J. Exp. Theor. Phys. 1974, 66, 776. [Google Scholar]
- De Ligny, D.; Richet, P.; Westrum, E.F., Jr.; Roux, J. Heat capacity and entropy of rutile (TiO2) and nepheline (NaAlSiO4). Phys. Chem. Miner. 2002, 29, 267–272. [Google Scholar] [CrossRef]
- Data. Available online: https://www.azom.com/properties.aspx?ArticleID=1179 (accessed on 4 February 2020).
- Jellison, G.E. Optical absorption of silicon between 1.6 and 4.7 eV at elevated temperatures. Appl. Phys. Lett. 1982, 41, 180. [Google Scholar] [CrossRef]
- Penzkofer, A.; Falkenstein, W. Direct determination of the intensity of picosecond light pulses by two-photon absorption. Opt. Commun. 1976, 17, 1–5. [Google Scholar] [CrossRef]
- Yamada, Y.; Kanemitsu, Y. Blue photoluminescence of highly photoexcited rutileTiO2: Nearly degenerate conduction-band effects. Phy. Rev. B 2010, 82, 113103. [Google Scholar] [CrossRef]
- Wu, A.Q.; Chowdhury, I.H.; Xu, X. Femtosecond laser absorption in fused silica: Numerical and experimental investigation. Phys. Rev. B 2005, 72, 085128. [Google Scholar] [CrossRef]
- Lee, S.H.; Lee, J.S.; Park, S.; Choi, Y.K. Numerical analysis on heat transfer characteristics of a silicon film irradiated by pico-to femtosecond pulse lasers. Numer. Heat Transf. Part A-Appl. 2003, 44, 833–850. [Google Scholar] [CrossRef]
- Sokolowski-Tinten, K.; Von Der Linde, D. Generation of dense electron-hole plasmas in silicon. Phys. Rev. B 2000, 61, 2643–2650. [Google Scholar] [CrossRef]
- Palik, E.D.; Ghosh, G. Handbook of Optical Constants of Solids; Academic Press: San Diego, CA, USA, 1998. [Google Scholar]
- Cardona, M.; Harbeke, G. Optical Properties and Band Structure of Wurtzite-Type Crystals and Rutile. Phys. Rev. 1965, 137, A1467–A1476. [Google Scholar] [CrossRef]
- Vos, K.; Krusemeyer, H.J. Reflectance and Electroreflectance of Tio2 Single-Crystals. 1. Optical-Spectra. J. Phys. C Solid State 1977, 10, 3893–3915. [Google Scholar] [CrossRef]
- Glassford, K.M.; Chelikowsky, J.R. Optical properties of titanium dioxide in the rutile structure. Phys. Rev. B 1992, 45, 3874–3877. [Google Scholar] [CrossRef]
- Tiwald, T.; Schubert, M. Measurement of Rutile TiO2 Dielectric Tensor from 0.148 to 33 um Using Generalized Ellipsometry; SPIE: Bellingham, WA, USA, 2000. [Google Scholar]
- Landmann, M.; Rauls, E.; Schmidt, W.G. The electronic structure and optical response of rutile, anatase and brookite TiO2. J. Phys. Condens. Matter 2012, 24, 195503. [Google Scholar] [CrossRef]
- Tsibidis, G.D.; Skoulas, E.; Stratakis, E. Ripple formation on nickel irradiated with radially polarized femtosecond beams. Opt. Lett. 2015, 40, 5172–5175. [Google Scholar] [CrossRef]
- Bonse, J. Quo Vadis LIPSS?—Recent and Future Trends on Laser-Induced Periodic Surface Structures. Nanomaterials 2020, 10, 1950. [Google Scholar] [CrossRef]
- Guosheng, Z.; Fauchet, P.M.; Siegman, A.E. Growth of spontaneous periodic surface structures on solids during laser illumination. Phys. Rev. B 1982, 26, 5366–5381. [Google Scholar] [CrossRef]
- Tsibidis, G.D.; Stratakis, E.; Aifantis, K.E. Thermoplastic deformation of silicon surfaces induced by ultrashort pulsed lasers in submelting conditions (Volume 111, 053502, 2012). J. Appl. Phys. 2012, 112, 089901. [Google Scholar] [CrossRef]
- Papadopoulos, A.; Skoulas, E.; Tsibidis, G.D.; Stratakis, E. Formation of periodic surface structures on dielectrics after irradiation with laser beams of spatially variant polarisation: A comparative study. Appl. Phys. A 2018, 124, 146. [Google Scholar] [CrossRef]
- Tsibidis, G.D.; Stratakis, E. Ripple formation on silver after irradiation with radially polarised ultrashort-pulsed lasers. J. Appl. Phys. 2017, 121, 163106. [Google Scholar] [CrossRef]
- Tsibidis, G.D.; Mimidis, A.; Skoulas, E.; Kirner, S.V.; Krüger, J.; Bonse, J.; Stratakis, E. Modelling periodic structure formation on 100Cr6 steel after irradiation with femtosecond-pulsed laser beams. Appl. Phys. A 2018, 124, 27. [Google Scholar] [CrossRef]
- Birnbaum, M. Semiconductor Surface Damage Produced by Ruby Lasers. J. Appl. Phys. 1965, 36, 3688–3689. [Google Scholar] [CrossRef]
- Zuhlke, C.A.; Tsibidis, G.D.; Anderson, T.; Stratakis, E.; Gogos, G.; Alexander, D.R. Investigation of femtosecond laser induced ripple formation on copper for varying incident angle. AIP Adv. 2018, 8, 015212. [Google Scholar] [CrossRef]
- Raether, P.D.H. Surface Plasmons on Smooth and Rough Surfaces and on Gratings; Springer Science and Business Media LLC.: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Tsibidis, G.D.; Stratakis, E. Ionisation processes and laser induced periodic surface structures in dielectrics with mid-infrared femtosecond laser pulses. Sci. Rep. 2020, 10, 1–13. [Google Scholar] [CrossRef]
- Fuentes-Edfuf, Y.; Sánchez-Gil, J.A.; Garcia-Pardo, M.; Serna, R.; Tsibidis, G.D.; Giannini, V.; Solis, J.; Siegel, J. Tuning the period of femtosecond laser induced surface structures in steel: From angled incidence to quill writing. Appl. Surf. Sci. 2019, 493, 948–955. [Google Scholar] [CrossRef]
- Höhm, S.; Rosenfeld, A.; Kruger, J.; Bonse, J. Femtosecond laser-induced periodic surface structures on silica. J. Appl. Phys. 2012, 112, 014901. [Google Scholar] [CrossRef]
- Pierre, P.D.S.S. A Note on the Melting Point of Titanium Dioxide. J. Am. Ceram. Soc. 1952, 35, 188. [Google Scholar] [CrossRef]
- Burakov, I.; Bulgakova, N.M.; Stoian, R.; Rosenfeld, A.; Hertel, I. Theoretical investigations of material modification using temporally shaped femtosecond laser pulses. Appl. Phys. A 2005, 81, 1639–1645. [Google Scholar] [CrossRef]
- Kelly, R.; Miotello, A. Comments on explosive mechanisms of laser sputtering. Appl. Surf. Sci. 1996, 96–98, 205–215. [Google Scholar] [CrossRef]
- Kerley, G.I.; Services, G.I.; Kerley, T. Equations of State for Titanium and Ti6A14V Alloy; Sandia National Laboratories: Albuquerque, NM, USA, 2003. [Google Scholar] [CrossRef]
- Alderman, O.L.G.; Skinner, L.B.; Benmore, C.J.; Tamalonis, A.; Weber, J. Structure of molten titanium dioxide. Phys. Rev. B 2014, 90, 094204. [Google Scholar] [CrossRef]
- Zhou, K.; Wang, H.P.; Chang, J.; Wei, B. Experimental study of surface tension, specific heat and thermal diffusivity of liquid and solid titanium. Chem. Phys. Lett. 2015, 639, 105–108. [Google Scholar] [CrossRef]
- Fletcher, C.A.J.; Srinivas, K. Computational Techniques for Fluid Dynamics, 2nd ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1991. [Google Scholar]
- Wang, Y.; Tsai, H.L. Impingement of filler droplets and weld pool dynamics during gas metal are welding process. Int. J. Heat Mass Transf. 2001, 44, 2067–2080. [Google Scholar] [CrossRef]
- Margiolakis, A.; Tsibidis, G.D.; Dani, K.M.; Tsironis, G.P. Ultrafast dynamics and sub-wavelength periodic structure formation following irradiation of GaAs with femtosecond laser pulses. Phys. Rev. B 2018, 98, 224103. [Google Scholar] [CrossRef]
- Petrakakis, E.; Tsibidis, G.D.; Stratakis, E. Modelling of the ultrafast dynamics and surface plasmon properties of silicon upon irradiation with mid-IR femtosecond laser pulses. Phys. Rev. B 2019, 99, 195201. [Google Scholar] [CrossRef]
- Tsibidis, G.D.; Mouchliadis, L.; Pedio, M.; Stratakis, E. Modeling ultrafast out-of-equilibrium carrier dynamics and relaxation processes upon irradiation of hexagonal silicon carbide with femtosecond laser pulses. Phys. Rev. B 2020, 101, 075207. [Google Scholar] [CrossRef]
- Derrien, T.J.-Y.; Krüger, J.; Itina, T.E.; Höhm, S.; Rosenfeld, A.; Bonse, J. Rippled area formed by surface plasmon polaritons upon femtosecond laser double-pulse irradiation of silicon. Opt. Express 2013, 21, 29643–29655. [Google Scholar] [CrossRef]
- Skolski, J.Z.P.; Römer, G.R.B.E.; Obona, J.V.; Ocelik, V.; Veld, A.J.H.I.; de Hosson, J.T.M. Laser-induced periodic surface structures: Fingerprints of light localization. Phys. Rev. B 2012, 85, 075320. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsibidis, G.D.; Museur, L.; Kanaev, A. The Role of Crystalline Orientation in the Formation of Surface Patterns on Solids Irradiated with Femtosecond Laser Double Pulses. Appl. Sci. 2020, 10, 8811. https://doi.org/10.3390/app10248811
Tsibidis GD, Museur L, Kanaev A. The Role of Crystalline Orientation in the Formation of Surface Patterns on Solids Irradiated with Femtosecond Laser Double Pulses. Applied Sciences. 2020; 10(24):8811. https://doi.org/10.3390/app10248811
Chicago/Turabian StyleTsibidis, George D., Luc Museur, and Andrei Kanaev. 2020. "The Role of Crystalline Orientation in the Formation of Surface Patterns on Solids Irradiated with Femtosecond Laser Double Pulses" Applied Sciences 10, no. 24: 8811. https://doi.org/10.3390/app10248811
APA StyleTsibidis, G. D., Museur, L., & Kanaev, A. (2020). The Role of Crystalline Orientation in the Formation of Surface Patterns on Solids Irradiated with Femtosecond Laser Double Pulses. Applied Sciences, 10(24), 8811. https://doi.org/10.3390/app10248811





