Double-Probe Ultrasonic Detection Method for Cracks in Steel Structure
Abstract
1. Introduction
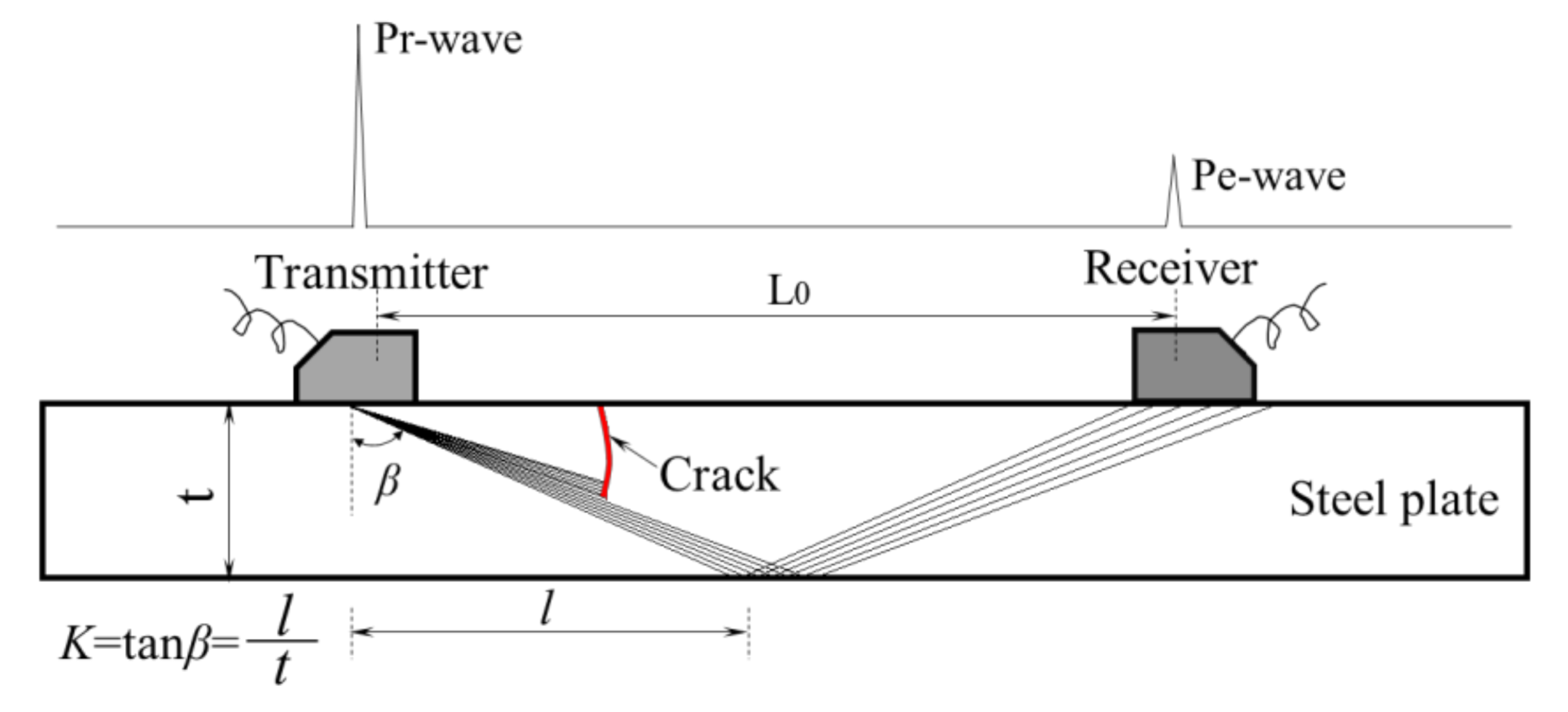
2. Ultrasonic Double-Probe Penetration Detection Method
3. General Situations of the Test
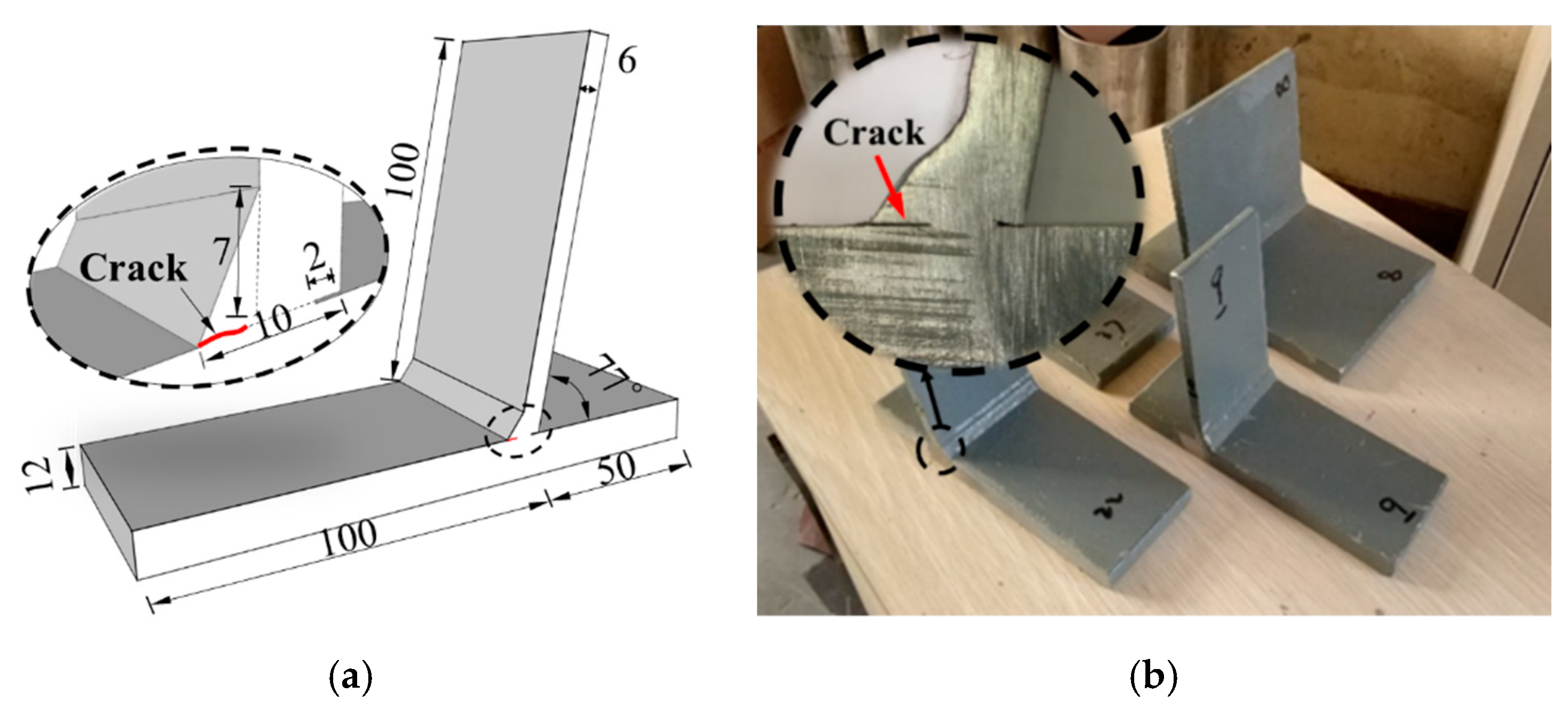
3.1. Specimens
3.2. Measurement of ωK
4. Influence of ωK
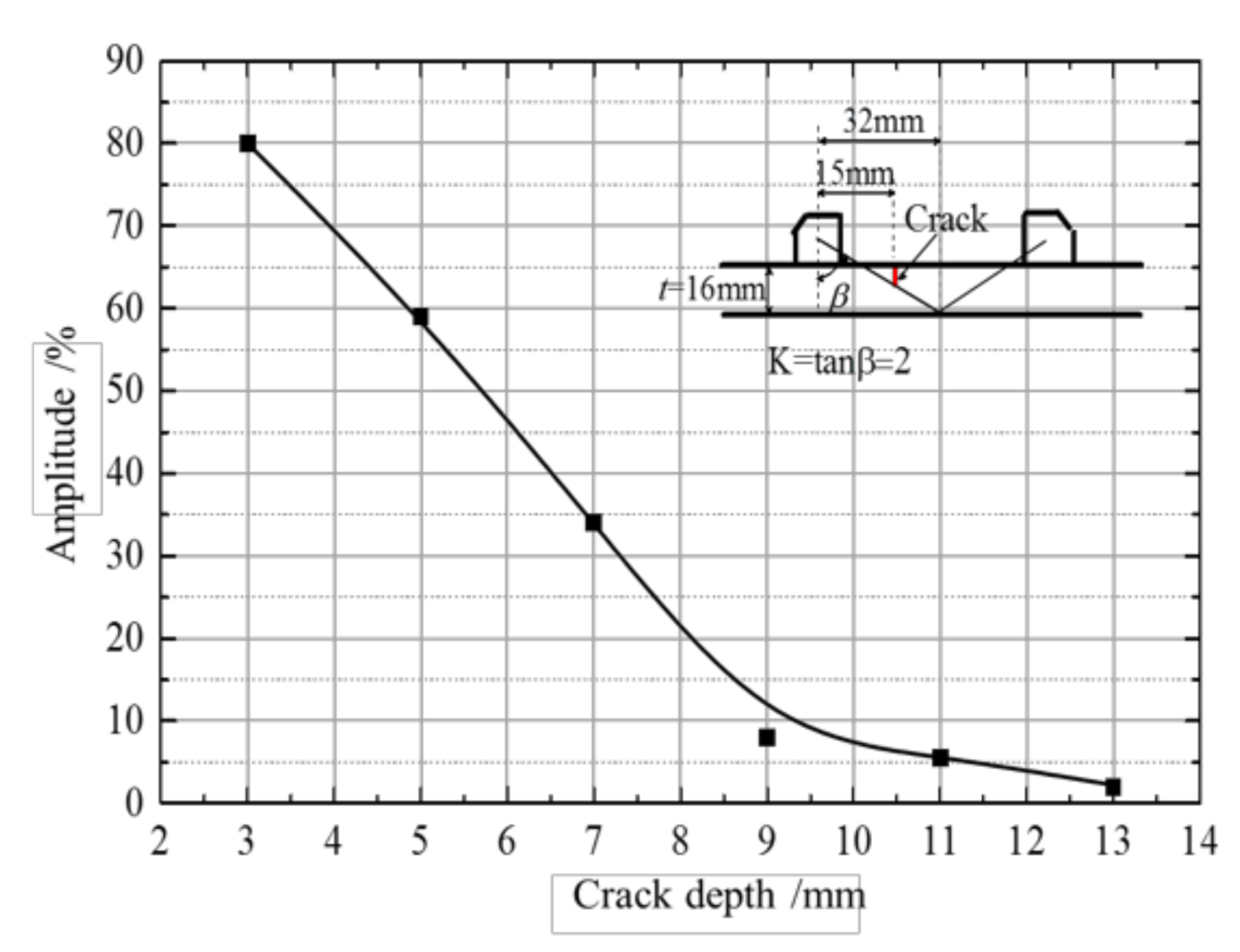
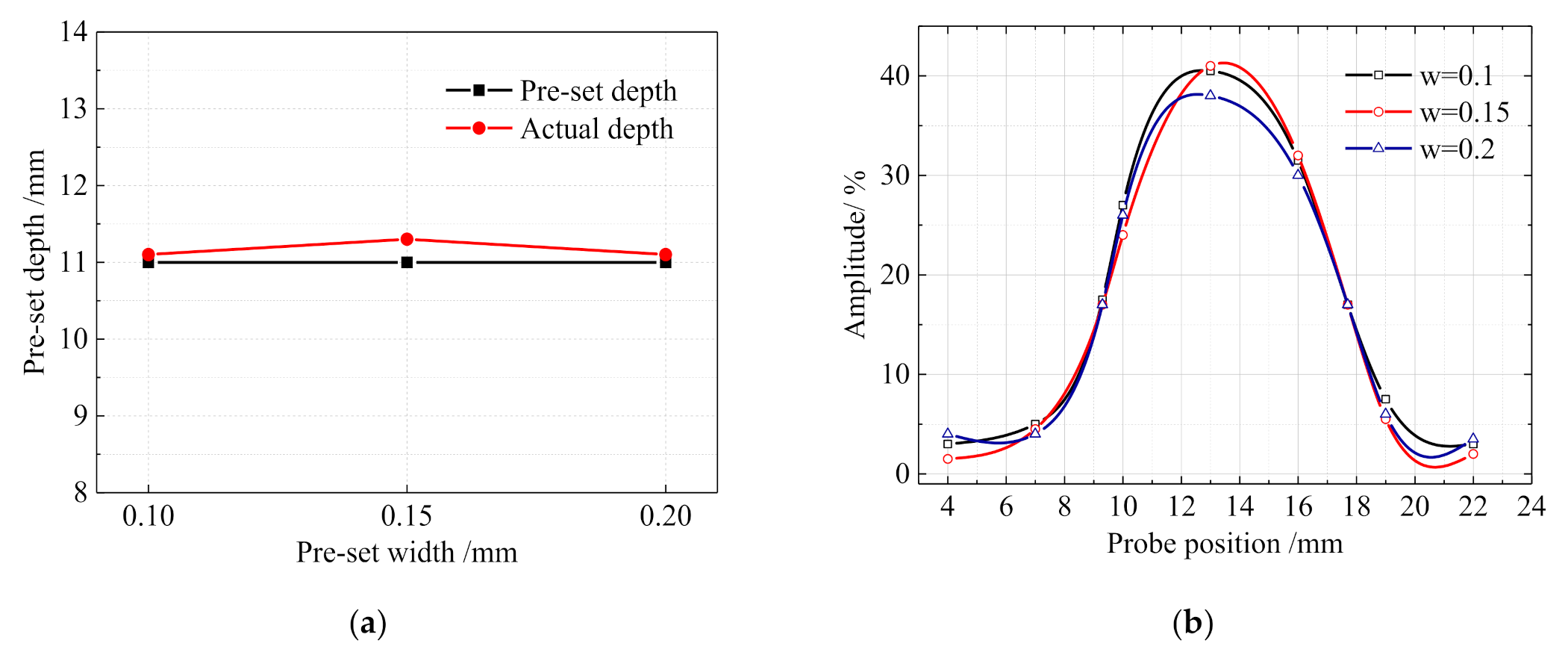
4.1. Crack Depth
4.2. Crack Width
4.3. Probe K Value
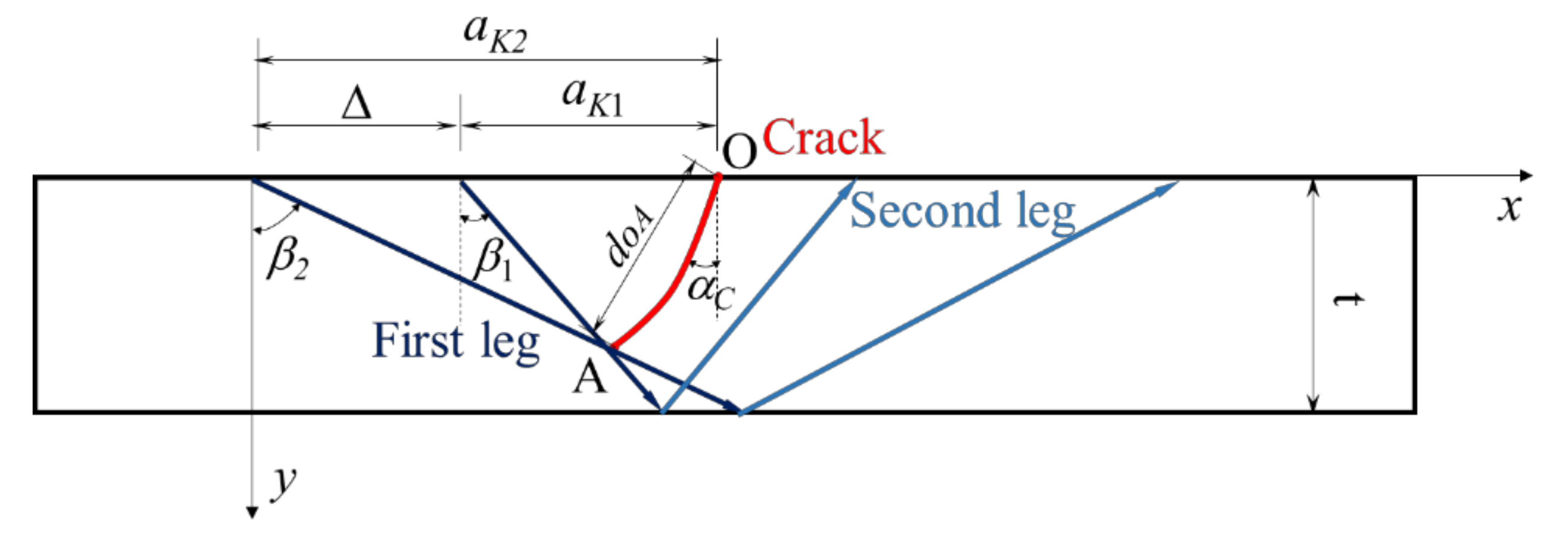
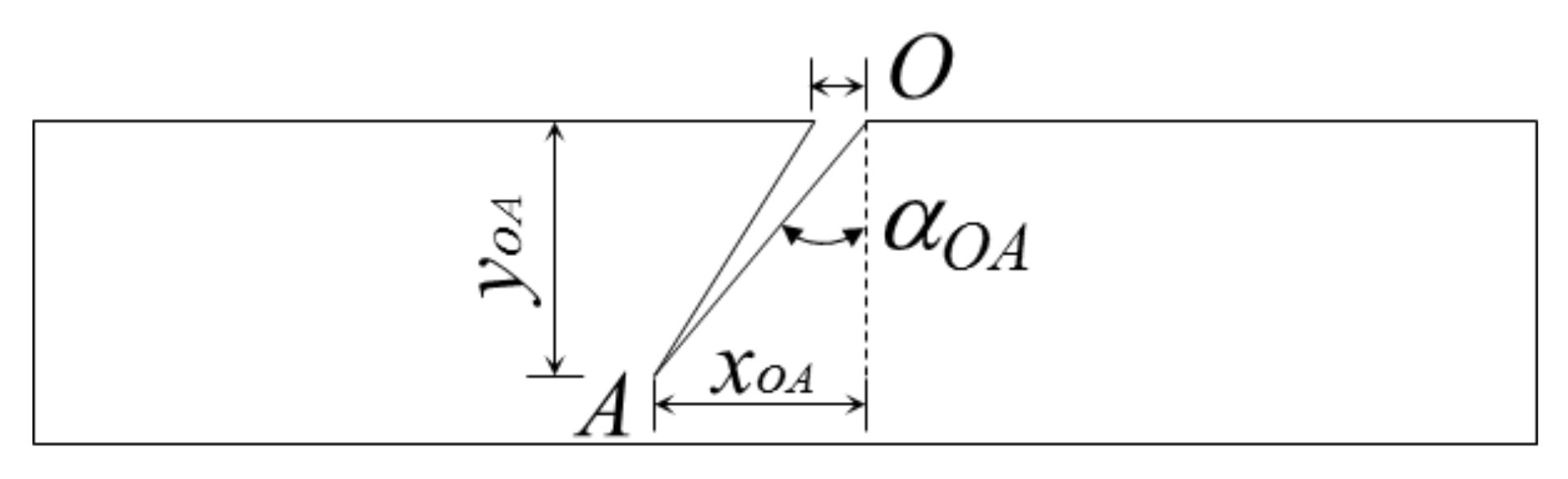
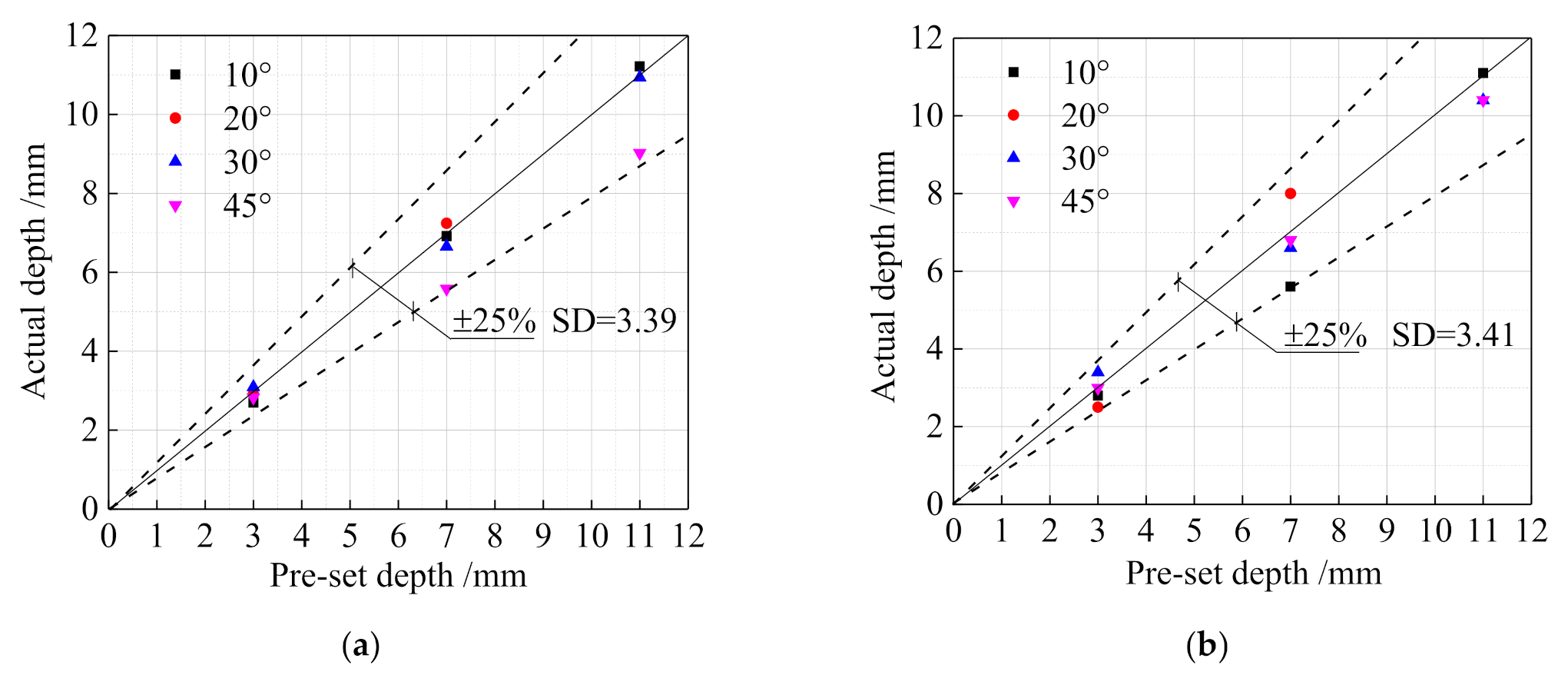
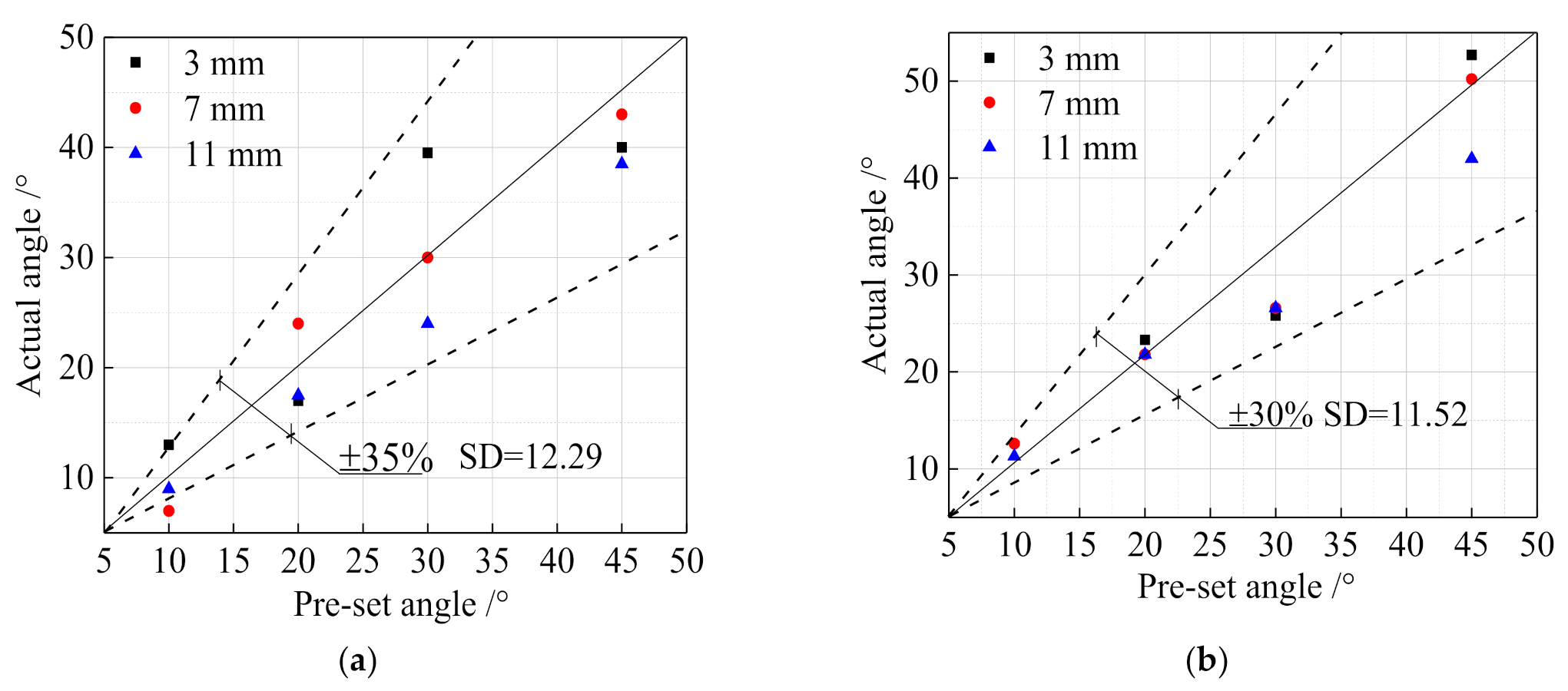
5. Error Analysis
5.1. Crack Parameters
5.2. Penetration Method and the Pulse Reflection Method
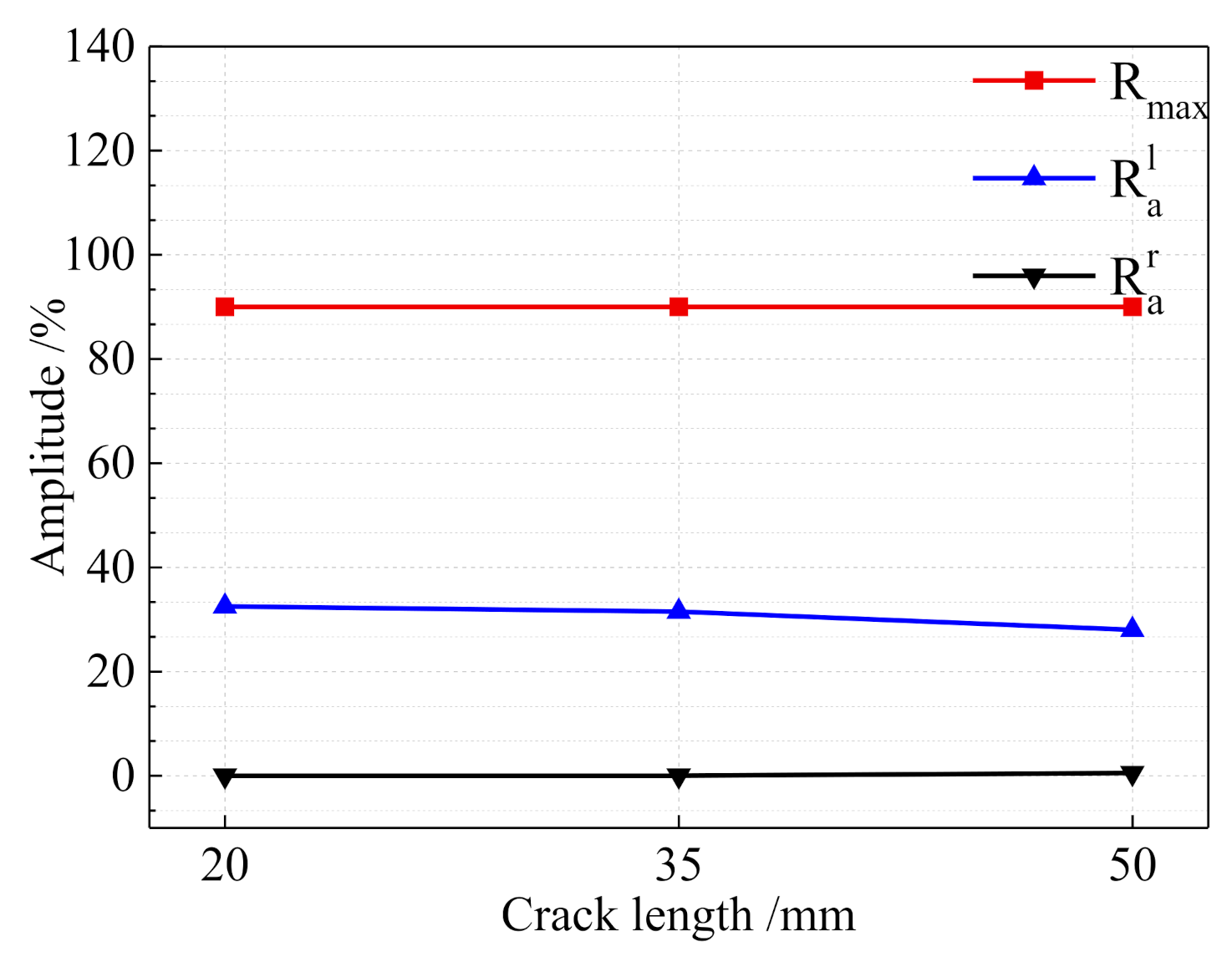
6. Weld Inspection Application
6.1. Feasibility Analysis
6.2. Experimental Verification
7. Conclusions
- (1)
- The ratio of wave height of crack tip to maximum wave height without a crack ωK was related to the K value of the chosen probe, while the influence of crack depth and width could be ignored.
- (2)
- The double-probe penetration method had high detection accuracy for the crack depth and angle. Compared with the single-probe pulse reflection method, the detection accuracy for crack angle was improved by nearly 5%, and the discreteness was reduced, which could meet the needs of engineering practice.
- (3)
- The finite element analysis shows that the double probe penetration method could be used to detect the rib-to-deck detail. The experimental testing results showed that the ωK value of the rib-to-deck weld was consistent with the test results from flat steel plate specimens, which verified the feasibility of the double-probe penetration method for crack detection around rib-to-deck weld details.
Author Contributions
Funding
Conflicts of Interest
References
- Guo, T.; Li, A.; Wang, H. Influence of ambient temperature on the fatigue damage of welded bridge decks. Int. J. Fatigue 2008, 30, 1092–1102. [Google Scholar] [CrossRef]
- Xiao, Z.G.; Yamada, K.; Ya, S.; Zhao, X.L. Stress analyses and fatigue evaluation of rib-deck joints in steel orthotropic decks. Int. J. Fatigue 2008, 30, 1387–1397. [Google Scholar] [CrossRef]
- Fu, Z.; Wang, Y.; Ji, B.; Jiang, F. Effects of multiaxial fatigue on typical details of orthotropic steel bridge deck. Thin Walled Struct. 2019, 135, 137–146. [Google Scholar] [CrossRef]
- Guo, T.; Liu, Z.; Correia, J.; de Jesus, A.M. Experimental study on fretting-fatigue of bridge cable wires. Int. J. Fatigue 2020, 131, 105321. [Google Scholar] [CrossRef]
- Dinda, S.K.; Warnett, J.M.; Williams, M.A.; Roy, G.G.; Srirangam, P. 3D imaging and quantification of porosity in electron beam welded dissimilar steel to Fe-Al alloy joints by X-ray tomography. Mater. Des. 2016, 96, 224–231. [Google Scholar] [CrossRef]
- Huggett, D.J.; Dewan, M.W.; Wahab, M.A.; Okeil, A.; Liao, T.W. Phased array ultrasonic testing for post-weld and online detection of friction stir welding defects. Res. Nondestruct. Eval. 2017, 28, 187–210. [Google Scholar] [CrossRef]
- Li, Z.; Haigh, A.; Soutis, C.; Gibson, A.; Sloan, R. A simulation-assisted non-destructive approach for permittivity measurement using an open-ended microwave Waveguide. J. Nondestruct. Eval. 2018, 37, 39. [Google Scholar] [CrossRef]
- Rashidyan, S.; Ng, T.T.; Maji, A. Practical aspects of nondestructive induction field testing in determining the depth of steel and reinforced concrete foundations. J. Nondestruct. Eval. 2019, 38, 19. [Google Scholar] [CrossRef]
- Hayes, C. The ABC′s of nondestructive weld examination. Weld. J. 1997, 76, 46–51. [Google Scholar]
- Cacciola, M.; Morabito, F.C.; Versaci, M. Ultrasonic and Advanced Methods for Nondestructive Testing and Material Characterization; World Scientific: Singapore, 2007. [Google Scholar]
- Wohlschlögel, M.; Gläßel, G.; Sanchez, D.; Schüßler, A.; Dillenz, A.; Saal, D.; Mayr, P. Characterization of Nitinol Laser-Weld Joints by Nondestructive Testing. J. Mater. Eng. Perform. 2015, 24, 4991–4996. [Google Scholar] [CrossRef]
- Lopez, A.B.; Santos, J.; Sousa, J.P.; Santos, T.G.; Quintino, L. Phased array ultrasonic inspection of metal additive manufacturing parts. J. Nondestruct. Eval. 2019, 38, 62. [Google Scholar] [CrossRef]
- Macias, G.G.R. Long Range Crack Detection in the Welded Girder-Diaphragm Connection. Ph.D. Thesis, New Mexico State University, Las Cruces, NM, USA, 1997. [Google Scholar]
- Ng, C.C. The Relationship between Ultrasonic Signal and Fatigue Crack Surface Contact in Mild Steel Plate Specimen. Ph.D. Thesis, University of Alberta, Edmonton, AB, Canada, 1998. [Google Scholar]
- Franklin, R. Innovative Ultrasonic Methodology for Fatigue Crack Detection in Steel Members. Ph.D. Thesis, West Virginia University, Morgantown, WV, USA, 1998. [Google Scholar]
- Harri, K.; Patrick, G.; Steve, V. On-line damage detection on a wing panel using transmission of multisine ultrasonic waves. NDT E Int. 2008, 41, 312–317. [Google Scholar] [CrossRef]
- Harara, W.; Ahmad, A. Attempt Towards the Replacement of Radiography with Phased Array Ultrasonic Testing of Steel Plate Welded Joints Performed on Bridges and Other Applications. Russ. J. Nondestruct. Test. 2018, 54, 335–344. [Google Scholar] [CrossRef]
- Shirahata, H.; Miki, C.; Yamaguchi, R.; Kinoshita, K.; Yaginuma, Y. Fatigue crack detection by the use of ultrasonic wave height change with crack tip opening. Weld. World 2014, 58, 681–690. [Google Scholar] [CrossRef]
- Bakker, M.C.M.; De Jong, F.B.P. Ultrasonic underside inspection for fatigue cracks in the deck plate of a steel orthotropic bridge deck. Heron Engl. Ed. 2003, 48, 277–296. [Google Scholar]
- An, Y.-K.; Homin, S.; Hoon, S. Wireless ultrasonic wavefield imaging via laser for hidden damage detection inside a steel box girder bridge. Smart Mater. Struct. 2014, 23, 095019. [Google Scholar] [CrossRef]
- Pahlavan, L.; Gerrit, B. Fatigue crack sizing in steel bridge decks using ultrasonic guided waves. NDT E Int. 2016, 77, 49–62. [Google Scholar] [CrossRef]




| Specimen | Crack Number | Depth d/mm | Angle α/° | Length L/mm | Width w/mm | xOA/mm | yOA/mm | Measured Depth dOA/mm | Measured Angle α/° |
|---|---|---|---|---|---|---|---|---|---|
| Plate | S-1-1 | 3 | 0 | 70 | 0.2 | - | - | - | - |
| S-1-2 | 5 | 0 | 70 | 0.2 | - | - | - | - | |
| S-1-3 | 7 | 0 | 70 | 0.2 | - | - | - | - | |
| S-1-4 | 9 | 0 | 70 | 0.2 | - | - | - | - | |
| S-1-5 | 11 | 0 | 70 | 0.2 | - | - | - | - | |
| S-1-6 | 13 | 0 | 70 | 0.2 | - | - | - | - | |
| S-2-1 | 11 | 0 | 70 | 0.1 | - | - | - | - | |
| S-2-2 | 11 | 0 | 70 | 0.15 | - | - | - | - | |
| S-2-3 | 11 | 0 | 70 | 0.2 | - | - | - | - | |
| S-3-1 | 3 | 10 | 70 | 0.2 | 5.3 | 2.6 | 2.8 | 16.7 | |
| S-3-2 | 7 | 10 | 70 | 0.2 | 10.0 | 4.9 | 5.6 | 12.6 | |
| S-3-3 | 11 | 10 | 70 | 0.2 | 22.1 | 10.9 | 11.1 | 11.3 | |
| S-3-4 | 3 | 20 | 70 | 0.2 | 0.8 | 0.4 | 2.2 | 23.3 | |
| S-3-5 | 7 | 20 | 70 | 0.2 | 14.9 | 7.4 | 8.0 | 21.8 | |
| S-3-6 | 11 | 20 | 70 | 0.2 | 23.6 | 11.7 | 12.5 | 21.8 | |
| S-3-7 | 3 | 30 | 70 | 0.2 | 6.8 | 3.4 | 3.7 | 25.8 | |
| S-3-8 | 7 | 30 | 70 | 0.2 | 12.0 | 5.9 | 6.6 | 26.6 | |
| S-3-9 | 11 | 30 | 70 | 0.2 | 18.9 | 9.4 | 10.4 | 26.6 | |
| S-3-10 | 3 | 45 | 70 | 0.2 | 2.2 | 1.1 | 3.0 | 52.7 | |
| S-3-11 | 7 | 45 | 70 | 0.2 | 8.8 | 4.4 | 6.8 | 50.2 | |
| S-3-12 | 11 | 45 | 70 | 0.2 | 15.3 | 7.6 | 10.4 | 42.0 | |
| Rib-to-deck | S-4-1 | Penetrated | 0 | 20 | 0.2 | - | - | - | - |
| S-4-2 | Penetrated | 0 | 35 | 0.2 | - | - | - | - | |
| S-4-3 | Penetrated | 0 | 60 | 0.2 | - | - | - | - |
| Group Number | The Number of Probe | Frequency/MHz | Size of Chip/mm | Calculated K Value | Real K Value | Length of Probe Frontier/mm |
|---|---|---|---|---|---|---|
| 1 | 1 (transmitting) | 5 | 4 × 4 | 0.8 | 0.78 | 4.55 |
| 2 (receiving) | 5 | 4 × 4 | 0.8 | 0.84 | 5.08 | |
| 2 | 3 (transmitting) | 5 | 8 × 9 | 2 | 1.92 | 9.65 |
| 4 (receiving) | 5 | 8 × 9 | 2 | 1.92 | 9.91 |
| Tests | Crack Depth/mm | |||||
|---|---|---|---|---|---|---|
| 3 | 5 | 7 | 9 | 11 | 13 | |
| Ra/% | 30 | 28 | 29 | 26 | 25 | 26 |
| Rmax/% | 83 | 84 | 86 | 80 | 80 | 82 |
| ωK | 0.361 | 0.342 | 0.346 | 0.325 | 0.315 | 0.315 |
| Tests | Crack Width/mm | ||
|---|---|---|---|
| 0.1 | 0.15 | 0.2 | |
| Ra/% | 26.5 | 25 | 25 |
| Rmax/% | 74.5 | 76 | 74 |
| ωK | 0.355 | 0.328 | 0.338 |
| Crack Depth/mm | K = 2 | K = 0.8 | ||||||
|---|---|---|---|---|---|---|---|---|
| Ra/% | Rmax/% | ωK | Average ωK | Ra/% | Rmax/% | ωK | Average ωK | |
| 3 | 30 | 83 | 0.361 | 0.34 | 18.5 | 45 | 0.409 | 0.43 |
| 5 | 28 | 84 | 0.342 | 17.6 | 44 | 0.400 | ||
| 7 | 29 | 86 | 0.346 | 18.2 | 44 | 0.414 | ||
| 9 | 26 | 80 | 0.325 | 18.2 | 40 | 0.456 | ||
| 11 | 25 | 80 | 0.315 | 15.4 | 35 | 0.440 | ||
| 13 | 26 | 82 | 0.315 | 17.9 | 36 | 0.497 | ||
| Crack Number | Crack Parameters | Test Results | Measurement Error | Relative Error | ||||
|---|---|---|---|---|---|---|---|---|
| Depth d/mm | Angle α/° | Depth d/mm | Angle α/° | d/mm | Δα/° | δd/% | δα/% | |
| S-3-1 | 3 | 10 | 2.8 | 16.7 | 0.2 | −6.7 | 6.67 | - |
| S-3-2 | 7 | 10 | 5.6 | 12.6 | 1.4 | −2.6 | 20.00 | 26.00 |
| S-3-3 | 11 | 10 | 11.1 | 11.3 | −0.1 | −1.3 | 0.91 | 13.00 |
| S-3-4 | 3 | 20 | 2.2 | 23.3 | 0.8 | −3.3 | - | 16.50 |
| S-3-5 | 7 | 20 | 8.0 | 21.8 | −1 | −1.8 | 14.29 | 9.00 |
| S-3-6 | 11 | 20 | 12.5 | 21.8 | −1.5 | −1.8 | 13.64 | 9.00 |
| S-3-7 | 3 | 30 | 3.7 | 21.8 | −0.7 | 5.8 | 23.33 | 19.33 |
| S-3-8 | 7 | 30 | 6.6 | 26.6 | 0.4 | 3.4 | 5.71 | 11.33 |
| S-3-9 | 11 | 30 | 10.4 | 26.6 | 0.6 | 3.4 | 5.45 | 11.33 |
| S-3-10 | 3 | 45 | 3.0 | 69.7 | 0 | −7.7 | 0.00 | 17.11 |
| S-3-11 | 7 | 45 | 6.8 | 50.2 | 0.2 | −5.2 | 2.86 | 11.56 |
| S-3-12 | 11 | 45 | 10.4 | 42.0 | 0.6 | 3 | 5.45 | 6.67 |
| Crack Number | Crack Width/mm | Crack Length/mm | Crack Depth/mm | Deck Width/mm |
|---|---|---|---|---|
| T-1 | 0.2 | 20 | Full cracking to weld root | 60 |
| T-2 | 0.2 | 35 | 120 | |
| T-3 | 0.2 | 50 | 120 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Ye, Z.; Xia, J.Y.; Wang, J.X.; Ji, B.H. Double-Probe Ultrasonic Detection Method for Cracks in Steel Structure. Appl. Sci. 2020, 10, 8436. https://doi.org/10.3390/app10238436
Chen X, Ye Z, Xia JY, Wang JX, Ji BH. Double-Probe Ultrasonic Detection Method for Cracks in Steel Structure. Applied Sciences. 2020; 10(23):8436. https://doi.org/10.3390/app10238436
Chicago/Turabian StyleChen, Xin, Zhi Ye, Jun Yuan Xia, Jie Xiu Wang, and Bo Hai Ji. 2020. "Double-Probe Ultrasonic Detection Method for Cracks in Steel Structure" Applied Sciences 10, no. 23: 8436. https://doi.org/10.3390/app10238436
APA StyleChen, X., Ye, Z., Xia, J. Y., Wang, J. X., & Ji, B. H. (2020). Double-Probe Ultrasonic Detection Method for Cracks in Steel Structure. Applied Sciences, 10(23), 8436. https://doi.org/10.3390/app10238436




