Interaction Strength Analysis to Model Retweet Cascade Graphs
Abstract
1. Introduction
Research Objective and Contributions
- We introduce the concept of interaction strength (IS), a metric that indicates the strength of the link between two users;
- We propose two novel approaches based on IS to generate retweet cascade graphs—ISN and ISN-AF;
- ISN aims to maximize IS values for each pair of nodes in the graph;
- ISN-AF is similar to ISN, but the first level in the retweet cascade graph is based on the list of followers of the root user;
- Both of the proposed approaches are mainly based on information contained in the users’ timelines, which can be conveniently retrieved through the free Twitter API service (compared to fetching the list of friends for each node as in the traditional approach, which is a substantially more time-consuming task);
- The source code is freely available on GitHub (https://github.com/paolazola/Interaction-strength-analysis-to-model-retweet-cascade-graphs).
2. Related Work
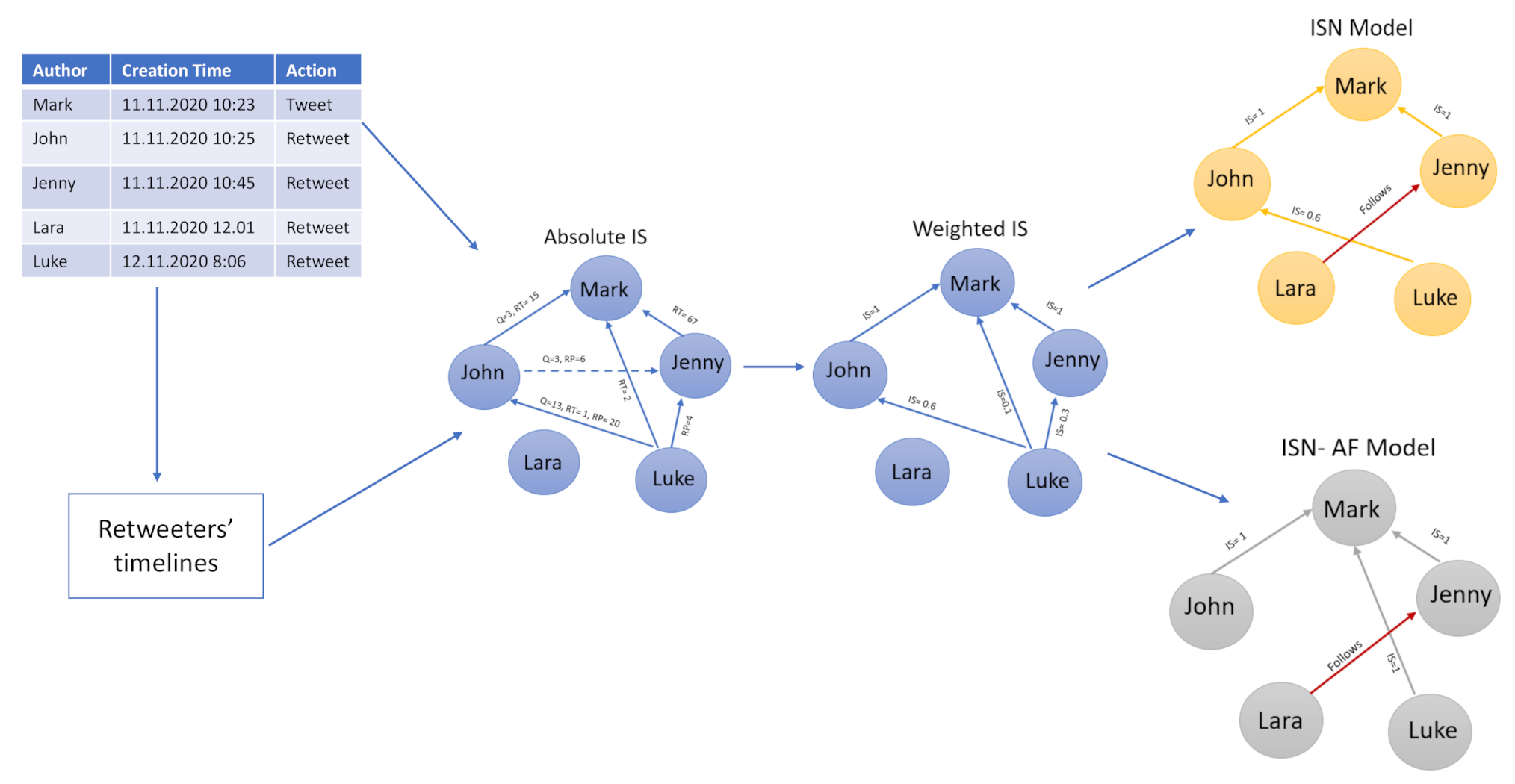
3. The Interaction Strength-Based Network (ISN) Approach to Generating Retweet Cascade Graphs
- The retweet’s creation time ;
- The interaction strength between each couple , which reflects the trust between users;
- The friend lists for the remaining nodes , for which no interactions were found (e.g., ).
3.1. Twitter User’s Interaction Strength
- The number of quotes that user u expressed to the node w;
- The number of replies that user u did to w;
- The number of retweets that user u did for w.
3.2. Interaction Weights for Retweet Cascade Graph
3.3. Users without Interactions and Sparse Nodes
4. Alternative Approach: Information Strength-Based Network with Author’s Followers Evaluation (ISN-AF)
5. Evaluation Metrics for Retweet Cascade Validation
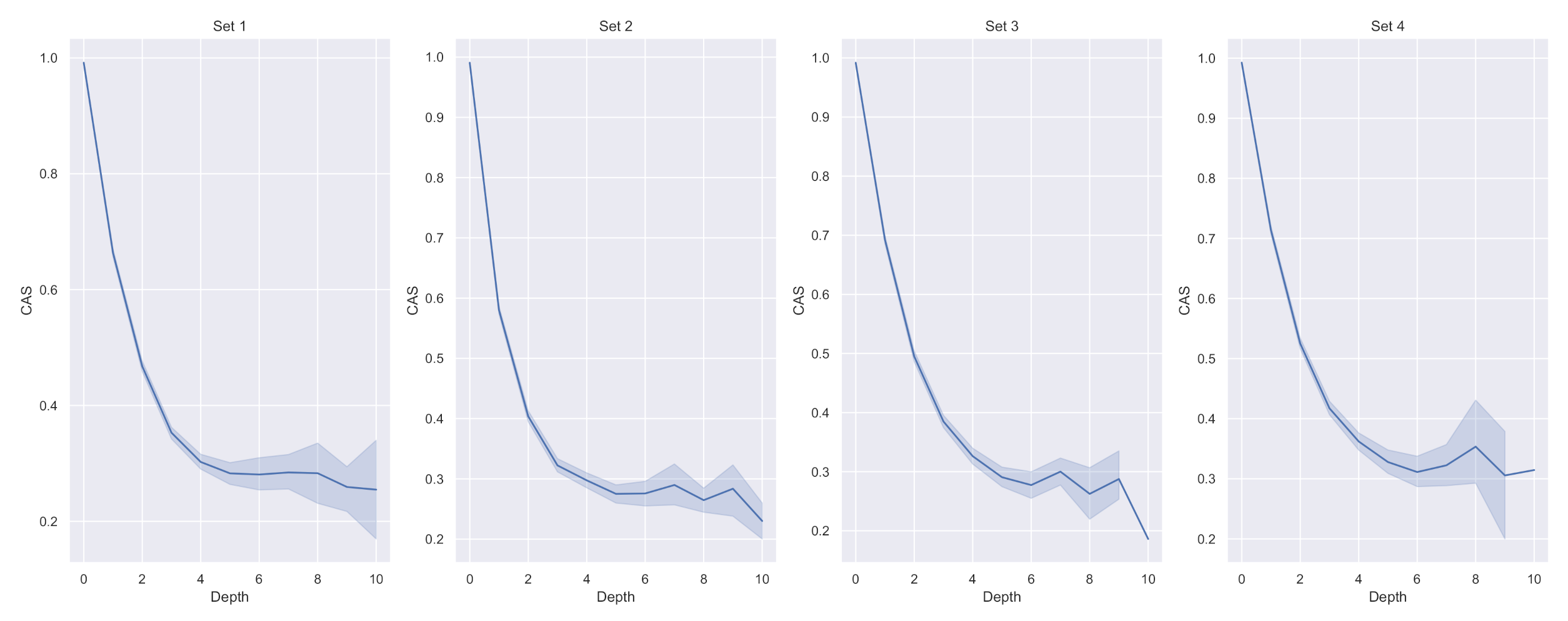
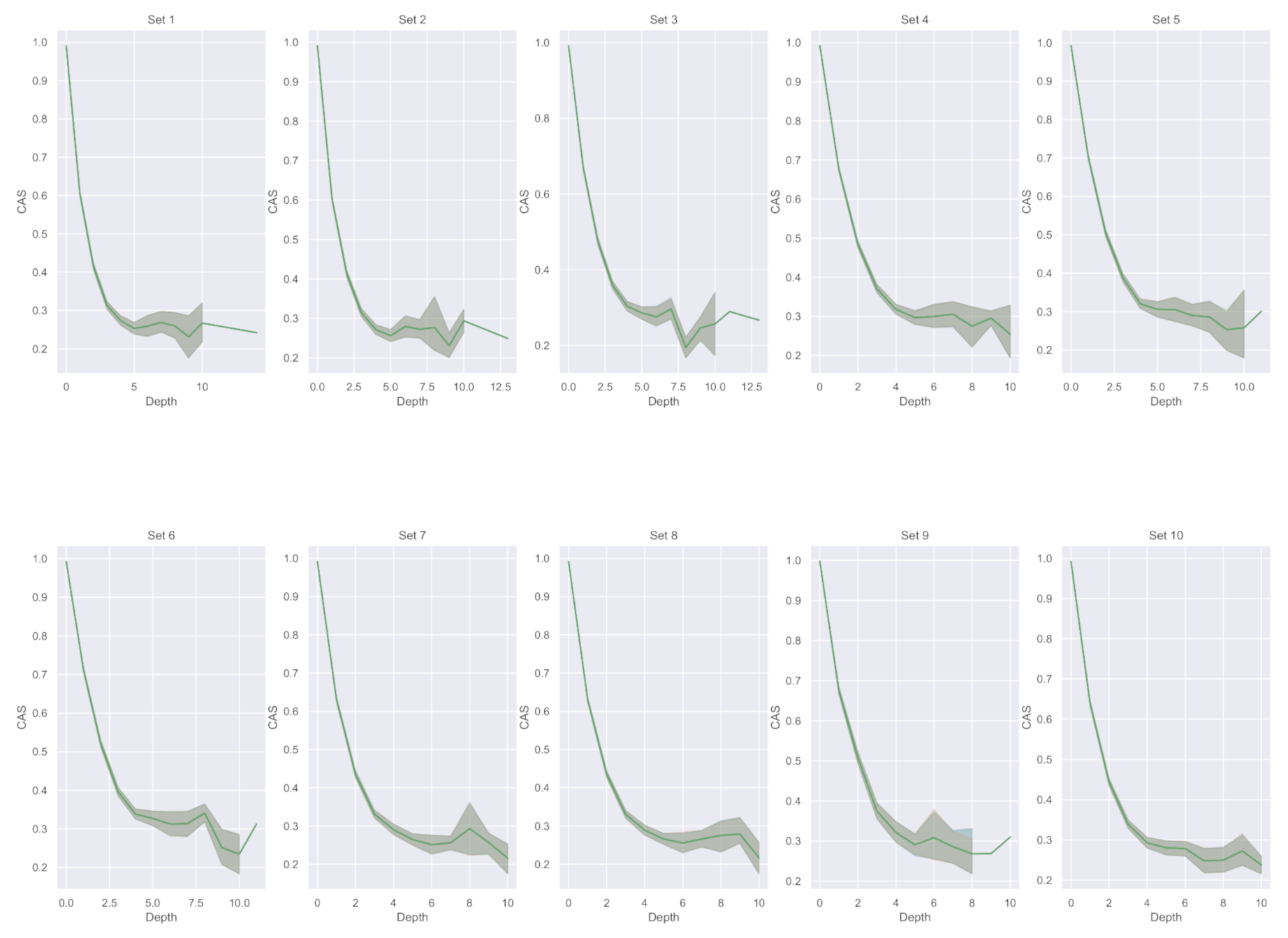
- Cascade average strength (CAS): given the assigned to each edge we derive the CAS as the average of the maximum IS between each pair of edges in such as:The aim is to maximise CAS for each cascade graph.
- Connected components count (CCC): returns the number of the connected components in the network. A connected component is a subgraph in which any two vertices are connected to each other by paths. This metric provide a description of the graph shape.
- Root fan ratio (RFR): it assesses whether there is a path to the from every other user. In other words, it measures the percentage of nodes directly or indirectly connected to the root. In the ISN-AF model, the RFR asses the percentage of followers. A higher RFR reflects a very concentrated graph around the determining the typical star shape of the cascade graph [25].
- Giant component size (GCS): the size, expressed in percentage of the cascade nodes, of the nodes present in the giant component (GC) which is the connected component with biggest size. The GCS is computed as follow:This metric provides a description of the graph shape in terms of node dispersion: The lower the GCS, the higher the dispersion of nodes in the graph, which can be sparse or connected. To further investigate the nodes’ dispersion we investigate the global reaching centrality and sparse node incidence.
- Global reaching centrality (GRC): It is the average over all nodes of the difference between the node local reaching centrality and the greatest local reaching centrality of any node in the graph. The local reaching centrality, , of node i is the proportion of all nodes in the graph that can be reached from node i via outgoing edges [35].
- Sparse node incidence (SNI): it measures the incidence (in percentage) of sparse nodes (i.e., nodes without links) with respect to the total number of nodes in the cascade. A lower SNI determines more connected and realistic retweet cascades.
6. Dataset
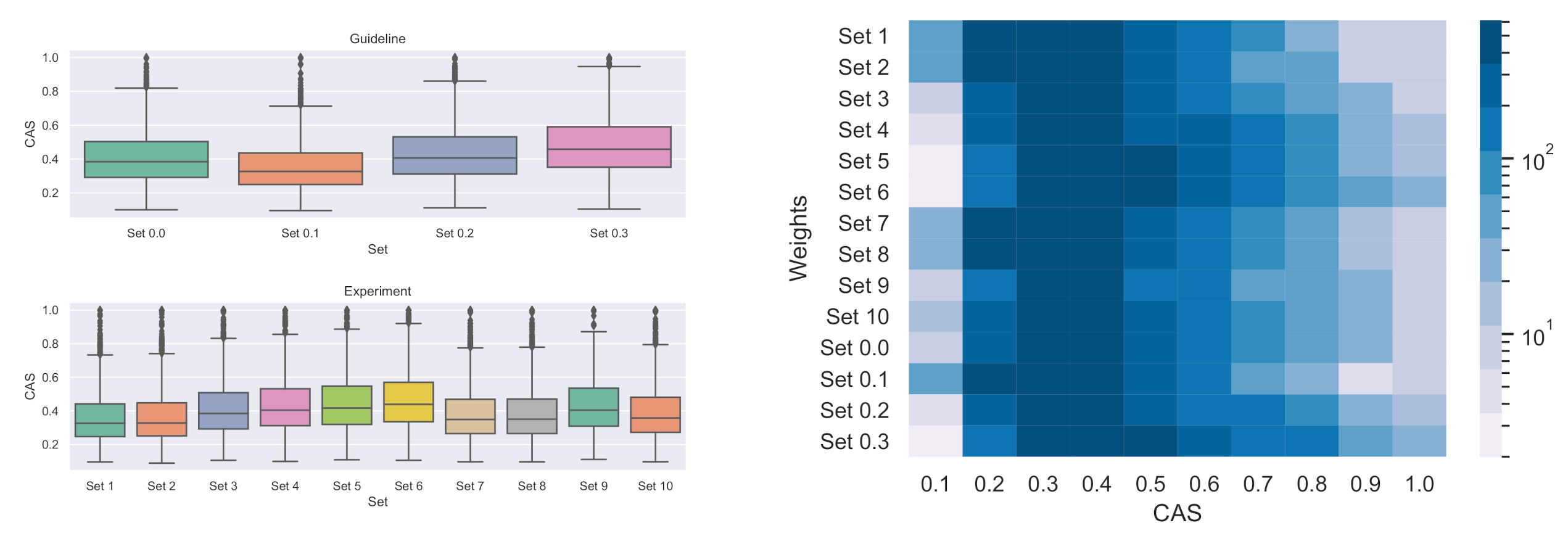
7. Evaluation of IS Weights
7.1. Experimental Results on the Entire Cascade Sample
7.2. Experimental Results on Cascades with at Least Five Nodes
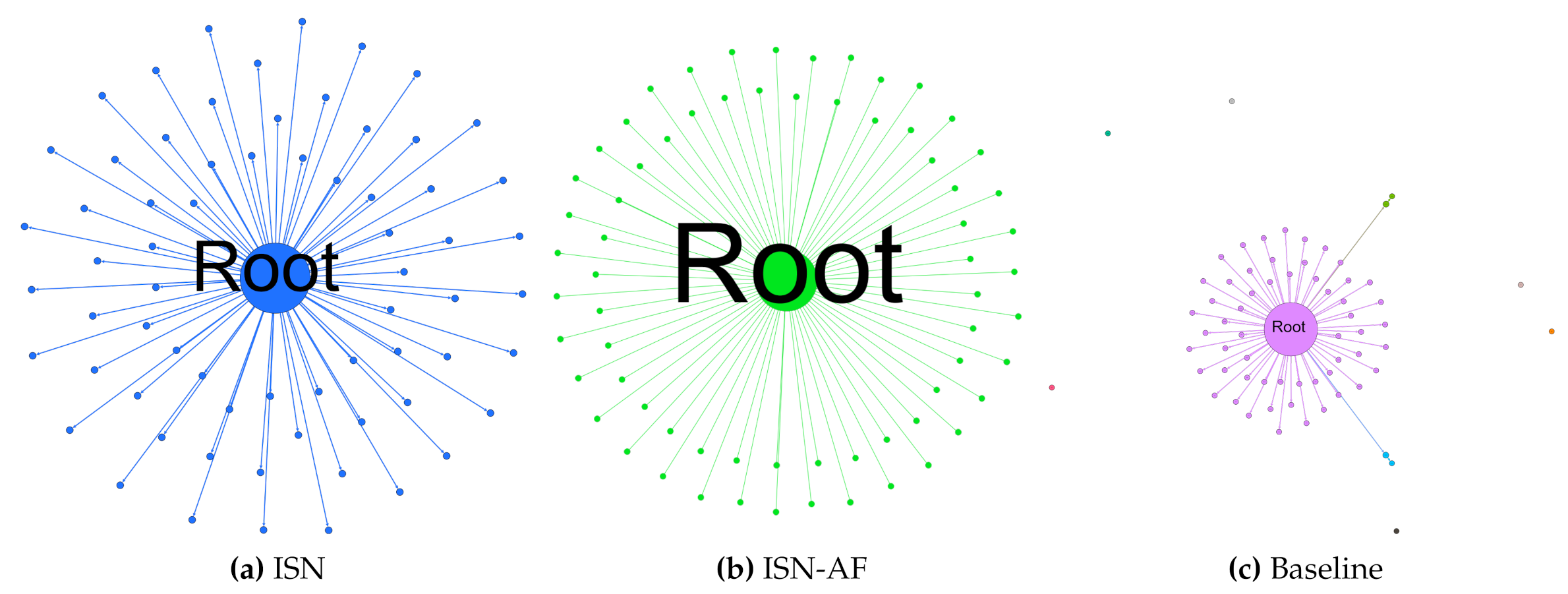
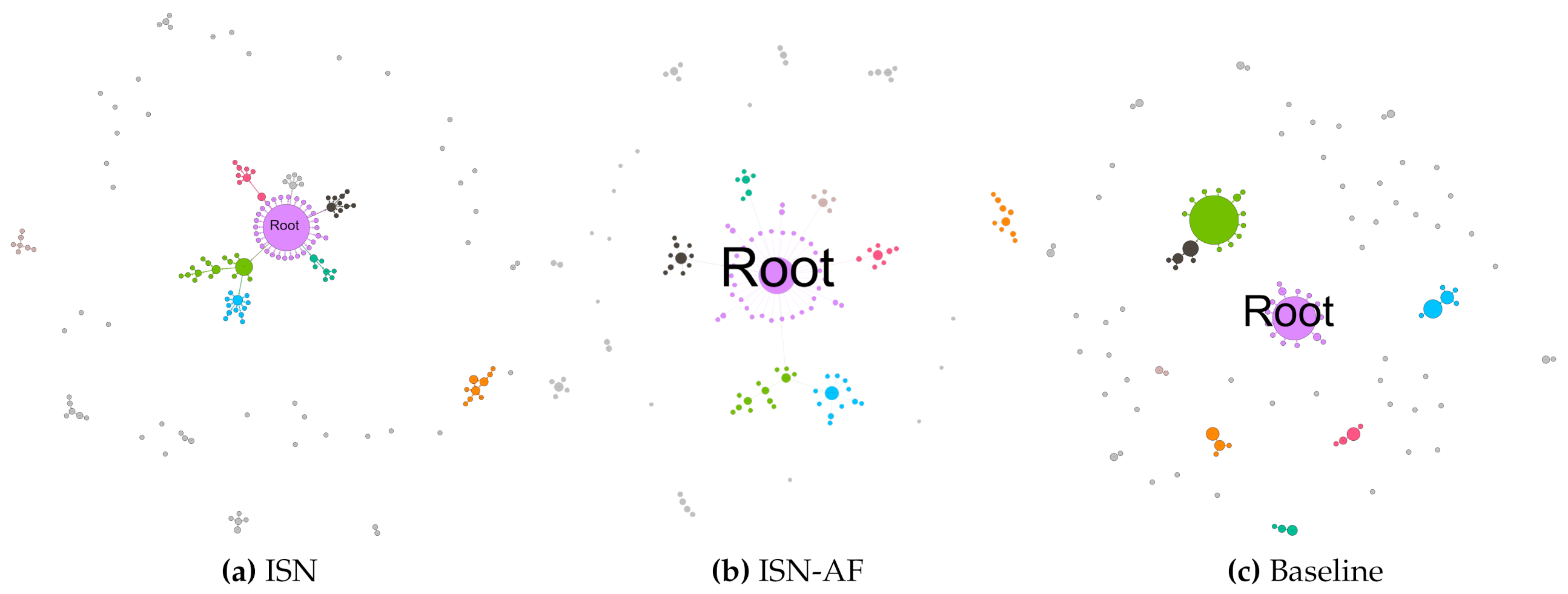
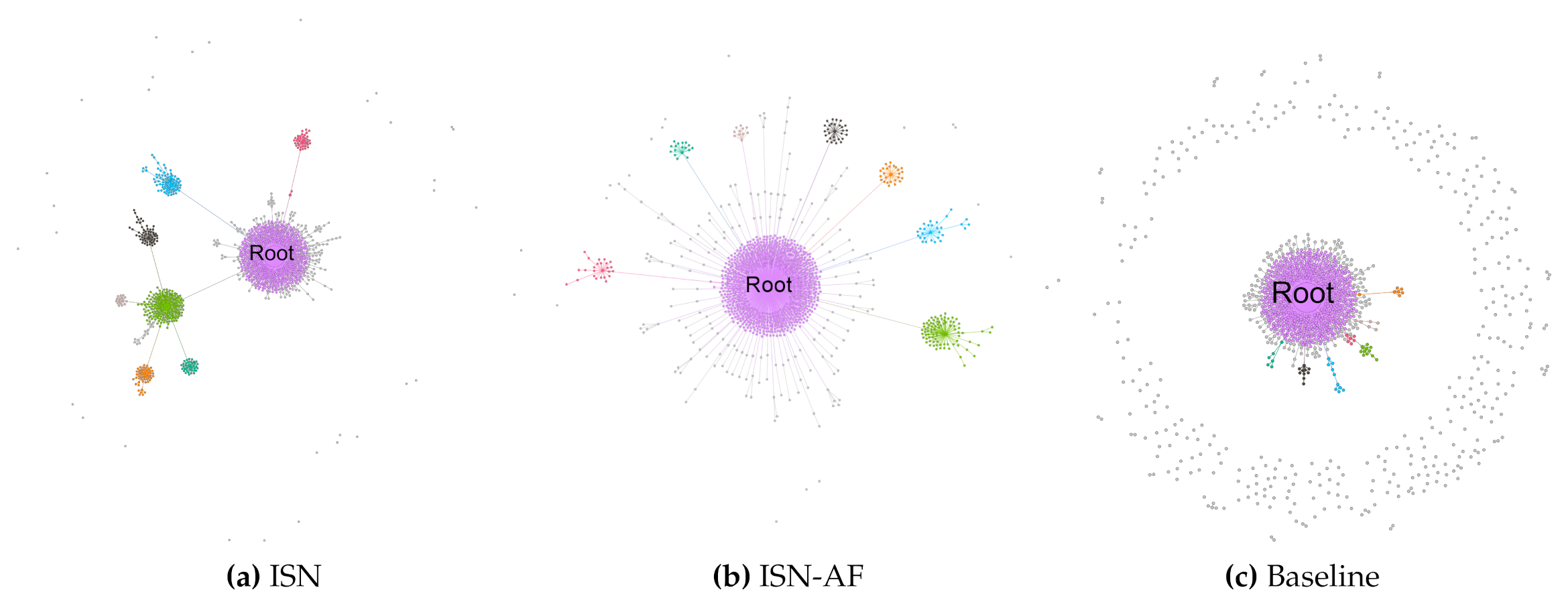
8. ISN, ISN-AF and Baseline Comparisons
Research Implications
9. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Avvenuti, M.; Cresci, S.; Marchetti, A.; Meletti, C.; Tesconi, M. Predictability or early warning: Using social media in modern emergency response. IEEE Internet Comput. 2016, 20, 4–6. [Google Scholar] [CrossRef]
- Zola, P.; Ragno, C.; Cortez, P. A Google Trends spatial clustering approach for a worldwide Twitter user geolocation. Inf. Process. Manag. 2020, 57, 102312. [Google Scholar] [CrossRef]
- Attia, A.M.; Aziz, N.; Friedman, B.; Elhusseiny, M.F. Commentary: The impact of social networking tools on political change in Egypt’s “Revolution 2.0”. Electron. Commer. Res. Appl. 2011, 10, 369–374. [Google Scholar] [CrossRef]
- Zola, P.; Cortez, P.; Brentari, E. Twitter alloy steel disambiguation and user relevance via one-class and two-class news titles classifiers. Neural Comput. Appl. 2020. [Google Scholar] [CrossRef]
- Myers, S.A.; Sharma, A.; Gupta, P.; Lin, J.J. Information network or social network? The structure of the twitter follow graph. In Proceedings of the 23rd International World Wide Web Conference, WWW ’14, Seoul, Korea, 7–11 April 2014; Companion Volume. ACM: New York, NY, USA, 2014; pp. 493–498. [Google Scholar] [CrossRef]
- Kwak, H.; Lee, C.; Park, H.; Moon, S.B. What is Twitter, a social network or a news media? In Proceedings of the 19th International Conference on World Wide Web, WWW 2010, Raleigh, NC, USA, 26–30 April 2010; ACM: New York, NY, USA, 2010; pp. 591–600. [Google Scholar] [CrossRef]
- Comarela, G.; Crovella, M.; Almeida, V.A.F.; Benevenuto, F. Understanding factors that affect response rates in Twitter. In Proceedings of the 23rd ACM Conference on Hypertext and Social Media, HT ’12, Milwaukee, WI, USA, 25–28 June 2012; ACM: New York, NY, USA, 2012; pp. 123–132. [Google Scholar] [CrossRef]
- Xiang, R.; Neville, J.; Rogati, M. Modeling relationship strength in online social networks. In Proceedings of the 19th international conference on World wide web 2010, Raleigh, NC, USA, 26–30 April 2010; pp. 981–990. [Google Scholar]
- Hoang, D.T.; Tran, V.C.; Hwang, D. Social network-based event recommendation. In Proceedings of the International Conference on Computational Collective Intelligence, Nicosia, Cyprus, 27–29 September 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 182–191. [Google Scholar]
- Guo, D.; Xu, J.; Zhang, J.; Xu, M.; Cui, Y.; He, X. User relationship strength modeling for friend recommendation on Instagram. Neurocomputing 2017, 239, 9–18. [Google Scholar] [CrossRef]
- Taxidou, I.; Fischer, P.M. Online analysis of information diffusion in Twitter. In Proceedings of the 23rd International World Wide Web Conference, WWW ’14, Seoul, Korea, 7–11 April 2014; Companion Volume. ACM: New York, NY, USA, 2014; pp. 1313–1318. [Google Scholar] [CrossRef]
- Szabó, G.; Huberman, B.A. Predicting the popularity of online content. Commun. ACM 2010, 53, 80–88. [Google Scholar] [CrossRef]
- Yang, J.; Counts, S. Predicting the Speed, Scale, and Range of Information Diffusion in Twitter. editor = William W. Cohen and Samuel Gosling, publisher = The AAAI Press, year = 2010, url = http://www.aaai.org/ocs/index.php/ICWSM/ICWSM10/paper/view/1468, timestamp =Wed, 01 Sep 2010 13:23:29 +0200, biburl = https://dblp.org/rec/conf/icwsm/YangC10a.bib, bibsource = dblp computer science bibliography, https://dblp.org. In Proceedings of the Fourth International Conference on Weblogs and Social Media, ICWSM 2010, Washington, DC, USA, 23–26 May 2010. [Google Scholar]
- Cogan, P.; Andrews, M.; Bradonjic, M.; Kennedy, W.S.; Sala, A.; Tucci, G. Reconstruction and analysis of twitter conversation graphs. In Proceedings of the First ACM International Workshop on Hot Topics on Interdisciplinary Social Networks Research, Beijing, China, 12–16 August 2012; pp. 25–31. [Google Scholar]
- Yang, C.; Harkreader, R.C.; Zhang, J.; Shin, S.; Gu, G. Analyzing spammers’ social networks for fun and profit: A case study of cyber criminal ecosystem on Twitter. In Proceedings of the 21st World Wide Web Conference 2012, WWW 2012, Lyon, France, 16–20 April 2012; ACM: New York, NY, USA, 2012; pp. 71–80. [Google Scholar] [CrossRef]
- Cazabet, R.; Pervin, N.; Toriumi, F.; Takeda, H. Information Diffusion on Twitter: Everyone Has Its Chance, However, All Chances Are Not Equal. In Proceedings of the Ninth International Conference on Signal-Image Technology & Internet-Based Systems, SITIS 2013, Kyoto, Japan, 2–5 December 2013; IEEE Computer Society: Washington, DC, USA, 2013; pp. 483–490. [Google Scholar] [CrossRef]
- Zaman, T.; Fox, E.B.; Bradlow, E.T. A Bayesian Approach for Predicting the Popularity of Tweets. Ann. Appl. Stat. 2014, 8, 1583–1611. [Google Scholar] [CrossRef]
- Pramanik, S.; Saha, A.; Mukherjee, P.; Patni, A.; Dan, S.; Mitra, B. Modelling Retweet Dynamics Using Hawkes Process—A Temporal Approach. 2015. Available online: http://aseempatni.com/docs/retweet.pdf (accessed on 13 October 2020).
- Yu, L.; Cui, P.; Wang, F.; Song, C.; Yang, S. From Micro to Macro: Uncovering and Predicting Information Cascading Process with Behavioral Dynamics. In Proceedings of the 2015 IEEE International Conference on Data Mining, ICDM 2015, Atlantic City, NJ, USA, 14–17 November 2015; IEEE Computer Society: Washington, DC, USA, 2015; pp. 559–568. [Google Scholar] [CrossRef]
- Zhao, Q.; Erdogdu, M.A.; He, H.Y.; Rajaraman, A.; Leskovec, J. SEISMIC: A Self-Exciting Point Process Model for Predicting Tweet Popularity. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, NSW, Australia, 10–13 August 2015; ACM: New York, NY, USA, 2015; pp. 1513–1522. [Google Scholar] [CrossRef]
- Gao, J.; Shen, H.; Liu, S.; Cheng, X. Modeling and Predicting Retweeting Dynamics via a Mixture Process. In Proceedings of the 25th International Conference on World Wide Web, WWW 2016, Montreal, QC, Canada, 11–15 April 2016; Companion Volume. ACM: New York, NY, USA, 2016; pp. 33–34. [Google Scholar] [CrossRef]
- Kobayashi, R.; Lambiotte, R. TiDeH: Time-Dependent Hawkes Process for Predicting Retweet Dynamics. In Proceedings of the Tenth International Conference on Web and Social Media, Cologne, Germany, 17–20 May 2016; AAAI Press: Palo Alto, CA, USA, 2016; pp. 191–200. [Google Scholar]
- Rodrigues, T.; Cunha, T.D.S.; Ienco, D.; Poncelet, P.; Soares, C. RetweetPatterns: Detection of Spatio-Temporal Patterns of Retweets. In New Advances in Information Systems and Technologies; Springer: Berlin/Heidelberg, Germany, 2016; pp. 879–888. [Google Scholar] [CrossRef]
- Cao, Q.; Shen, H.; Cen, K.; Ouyang, W.; Cheng, X. DeepHawkes: Bridging the Gap between Prediction and Understanding of Information Cascades. In Proceedings of the 2017 ACM on Conference on Information and Knowledge Management, CIKM 2017, Singapore, 6–10 November 2017; ACM: New York, NY, USA, 2017; pp. 1149–1158. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, B.; Sun, X.; Zheng, Q.; Liu, T. Analyzing and modeling dynamics of information diffusion in microblogging social network. J. Netw. Comput. Appl. 2017, 86, 92–102. [Google Scholar] [CrossRef]
- Stai, E.; Milaiou, E.; Karyotis, V.; Papavassiliou, S. Temporal Dynamics of Information Diffusion in Twitter: Modeling and Experimentation. IEEE Trans. Comput. Social Syst. 2018, 5, 256–264. [Google Scholar] [CrossRef]
- Bhowmick, A.K.; Gueuning, M.; Delvenne, J.; Lambiotte, R.; Mitra, B. Temporal Sequence of Retweets Help to Detect Influential Nodes in Social Networks. IEEE Trans. Comput. Social Syst. 2019, 6, 441–455. [Google Scholar] [CrossRef]
- Chen, G.; Kong, Q.; Xu, N.; Mao, W. NPP: A neural popularity prediction model for social media content. Neurocomputing 2019, 333, 221–230. [Google Scholar] [CrossRef]
- Liu, Y.; Bao, Z.; Zhang, Z.; Tang, D.; Xiong, F. Information cascades prediction with attention neural network. Hum. Centric Comput. Inf. Sci. 2020, 10, 1–16. [Google Scholar] [CrossRef]
- Kong, Q.; Rizoiu, M.A.; Xie, L. Modeling Information Cascades with Self-exciting Processes via Generalized Epidemic Models. In Proceedings of the 13th International Conference on Web Search and Data Mining, Houston, TX, USA, 3–7 February 2020; pp. 286–294. [Google Scholar]
- Wu, B.; Cheng, W.; Zhang, Y.; Cao, J.; Li, J.; Mei, T. Unlocking Author Power: On the Exploitation of Auxiliary Author-Retweeter Relations for Predicting Key Retweeters. IEEE Trans. Knowl. Data Eng. 2020, 32, 547–559. [Google Scholar] [CrossRef]
- Arnaboldi, V.; Gala, M.L.; Passarella, A.; Conti, M. Information diffusion in distributed OSN: The impact of trusted relationships. Peer Peer Netw. Appl. 2016, 9, 1195–1208. [Google Scholar] [CrossRef]
- Arnaboldi, V.; Passarella, A.; Tesconi, M.; Gazzè, D. Towards a Characterization of Egocentric Networks in Online Social Networks. On the Move to Meaningful Internet Systems: OTM 2011 Workshops—Confederated International Workshops and Posters: EI2N+NSF ICE, ICSP+INBAST, ISDE, ORM, OTMA, SWWS+MONET+SeDeS, and VADER 2011, Hersonissos, Crete, Greece, October 17–21, 2011. Proceedings. Springer, 2011, Vol. 7046. Lect. Notes Comput. Sci. 2011, 7046, 524–533. [Google Scholar] [CrossRef]
- Nies, T.D.; Taxidou, I.; Dimou, A.; Verborgh, R.; Fischer, P.M.; Mannens, E.; de Walle, R.V. Towards Multi-level Provenance Reconstruction of Information Diffusion on Social Media. In Proceedings of the 24th ACM International Conference on Information and Knowledge Management, CIKM 2015, Melbourne, VIC, Australia, 19–23 October 2015; ACM: New York, NY, USA, 2015; pp. 1823–1826. [Google Scholar] [CrossRef]
- Mones, E.; Vicsek, L.; Vicsek, T. Hierarchy measure for complex networks. PLoS ONE 2012, 7, e33799. [Google Scholar] [CrossRef] [PubMed]
- Mazza, M.; Cresci, S.; Avvenuti, M.; Quattrociocchi, W.; Tesconi, M. RTbust: Exploiting Temporal Patterns for Botnet Detection on Twitter. In Proceedings of the 11th ACM Conference on Web Science, WebSci 2019, Boston, MA, USA, 30 June–3 July 2019; ACM: New York, NY, USA, 2019; pp. 183–192. [Google Scholar] [CrossRef]



| Study | Target a | Dataset b | Dataset c Size | Dataset Collection Date | Topic Features | Text Features | Time Variable | Users Features | Users Interactions | Social Network | Location Features | Users Behaviour | Model d |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Szabo et al. [12] | REP | YT, D | YT: 7K, D: 850K U | 2007–2008 | - | - | X | - | - | LR | |||
| Yang et al. [13] | TIC-REP | TW | - | - | X | X | X | - | - | - | - | X | F+EM |
| Cogan [14] | TIC | TW | 33K T | 2012 | - | - | - | - | - | X | - | - | RCM |
| Comarela et al. [7] | RB | TW | 54M U | 2006–2009 | - | X | X | X | - | - | - | X | SVM, NB |
| Yang et al. [15] | RB | TW | 22M T | 2009 | X | - | X | - | - | - | - | - | CHR |
| Remy et al. [16] | TIC | TW | 362M T | 2011 | - | - | - | - | - | X | - | - | PL |
| Zaman et al. [17] | TIC-REP | TW | 52 | - | - | - | X | X | - | - | - | - | HB |
| Taxidou et al. [11] | TIC | TW | 11M T | 2012 | - | - | X | - | - | X | - | - | |
| Pramanik et al. [18] | TIC | TW | 55K | - | X | - | X | - | - | X | - | - | H |
| Yu et al. [19] | TIC-REP | TWB | 320M U | 2011 | - | - | X | X | - | - | - | X | NEWER |
| Zhao et al. [20] | REP | TW | 3.2B | 2011 | - | - | X | X | - | - | - | - | SEISMIC |
| Gao et al. [21] | TIC-REP | SW | 164 | - | - | - | X | - | - | - | - | - | RPP |
| Kobashy et al. [22] | TIC-REP | TW | 166K | 2011 | - | - | X | X | - | X | - | - | TiDeH |
| Rodrigues et al. [23] | TIC | TW | 17K | 2013 | - | X | X | - | - | X | X | - | GetMove |
| Cao et al. [24] | REP | SW, PC | 50K T, 35K P | 2016 | - | - | X | - | X | - | - | - | DH |
| Zhou et al. [25] | TIC-RB | SW | 69.4M | 2013–2014 | X | - | X | X | - | X | - | X | BN |
| Stai et al. [26] | TW | 35K | 2014–2016 | X | - | X | - | EpiM | |||||
| Bhowmick et al. [27] | TIC-KR | TW | 8M T | 2015–2018 | - | - | X | - | - | X | - | - | SmartInf |
| Chen et al. [28] | REP | TW | 20K | 2016 | - | X | X | - | - | - | - | - | NPP |
| Liu et al. [29] | TIC | TW, AM | 30K TW, 35K AM | 2016, 1996–2000 | - | - | X | - | - | - | - | - | ANN |
| Kong et al. [30] | TIC | TW | 210 K | - | - | - | X | - | - | X | - | - | EP+H |
| Wu et al. [31] | KR-TIC | SW | 50K M | - | - | - | X | X | X | - | X | RL2R | |
| in this work | TIC | TW | 16K T | 2020 | - | - | X | X | X | X | - | - | W-RCM |
| Set nr | Retweet Weight | Quote Weight | Reply Weight |
|---|---|---|---|
| 0.0 | 1.0 | 1.0 | 1.0 |
| 0.1 | 1.0 | 0.0 | 0.0 |
| 0.2 | 0.0 | 1.0 | 0.0 |
| 0.3 | 0.0 | 0.0 | 1.0 |
| Set nr | Retweet Weight | Quote Weight | Reply Weight |
|---|---|---|---|
| 1 | 0.0 | 0.3 | 0.6 |
| 2 | 0.0 | 0.6 | 0.3 |
| 3 | 0.3 | 0.0 | 0.6 |
| 4 | 0.3 | 0.6 | 0.0 |
| 5 | 0.6 | 0.0 | 0.3 |
| 6 | 0.6 | 0.3 | 0.0 |
| 7 | 0.1 | 0.4 | 0.5 |
| 8 | 0.1 | 0.5 | 0.4 |
| 9 | 0.2 | 0.3 | 0.5 |
| 10 | 0.2 | 0.5 | 0.3 |
| Full Dataset | Sampled Dataset | |
|---|---|---|
| Tweets Count | 506,147 | 16,304 |
| Unique Users Count | 102,468 | 41,592 |
| Retweets Count | 683,189 | 112,188 |
| Class | Set | Edge Count | CCC | GCS (%) | RFR (%) | GRC (%) | CAS (%) | Depth | SNI (%) |
|---|---|---|---|---|---|---|---|---|---|
| Guideline | 0.0 | 5.88 | 1.08 | 6.25 | 93.81 | 6.19 | 87.06 | 0.53 | 1.98 |
| Guideline | 0.1 | 5.88 | 1.08 | 6.29 | 93.75 | 6.18 | 85.39 | 0.53 | 2.05 |
| Guideline | 0.2 | 5.89 | 1.08 | 6.27 | 93.68 | 6.15 | 84.33 | 0.53 | 2.13 |
| Guideline | 0.3 | 5.89 | 1.08 | 6.29 | 93.68 | 6.15 | 84.32 | 0.53 | 2.11 |
| Set | Edge Count | CCC | GCS (%) | RFR (%) | GRC (%) | CAS (%) | Depth | SNI (%) |
|---|---|---|---|---|---|---|---|---|
| 1 | 5.88 | 1.08 | 6.27 | 93.61 | 6.12 | 83.53 | 0.53 | 2.04 |
| 2 | 5.89 | 1.08 | 6.25 | 93.59 | 6.12 | 82.93 | 0.53 | 2.01 |
| 3 | 5.89 | 1.08 | 6.29 | 93.77 | 6.17 | 86.32 | 0.53 | 2.08 |
| 4 | 5.89 | 1.08 | 6.25 | 93.81 | 6.19 | 87.23 | 0.52 | 1.98 |
| 5 | 5.80 | 1.08 | 6.20 | 93.77 | 6.06 | 84.63 | 0.52 | 2.03 |
| 6 | 5.80 | 1.08 | 6.20 | 93.74 | 6.06 | 84.21 | 0.52 | 2.04 |
| 7 | 5.80 | 1.08 | 6.22 | 93.78 | 6.07 | 84.80 | 0.52 | 2.11 |
| 8 | 5.88 | 1.08 | 6.28 | 93.62 | 6.15 | 83.45 | 0.53 | 1.98 |
| 9 | 5.88 | 1.08 | 6.29 | 95.73269 | 5.76 | 83.67 | 0.54 | 1.98 |
| 10 | 5.88 | 1.08 | 6.31 | 93.79 | 6.18 | 86.63 | 0.53 | 2.00 |
| Group | Weight | CAS | |||
|---|---|---|---|---|---|
| Set | Quotes | Replies | Mean | St Dev | |
| a | 0.2 | 1.0 | 0.0 | 0.28 | 0.06 |
| 0.3 | 0.0 | 1.0 | 0.32 * | 0.08 * | |
| b | 1 | 0.3 | 0.6 | 0.26 | 0.07 |
| 2 | 0.6 | 0.3 | 0.27 | 0.07 | |
| c | 3 | 0.0 | 0.6 | 0.28 | 0.07 |
| 4 | 0.6 | 0.0 | 0.30 * | 0.08 | |
| d | 5 | 0.0 | 0.3 | 0.29 | 0.07 |
| 6 | 0.3 | 0.1 | 0.31 | 0.08 | |
| e | 7 | 0.4 | 0.5 | 0.26 | 0.06 |
| 8 | 0.5 | 0.4 | 0.26 | 0.06 | |
| f | 9 | 0.3 | 0.5 | 0.28 | 0.09 |
| 10 | 0.5 | 0.3 | 0.26 | 0.05 | |
| g | 0 | 1.0 | 1.0 | 0.28 | 0.07 |
| 0.1 | 0.0 | 0.0 | 0.28 | 0.06 | |
| Set | Edge Count | CCC | GCS (%) | RFR (%) | GRC (%) | CAS (%) | Depth | SNI (%) |
|---|---|---|---|---|---|---|---|---|
| 0.0 | 46.17 | 1.54 | 41.96 | 60.76 | 32.84 | 46.77 | 2.37 | 16.33 |
| 0.1 | 46.17 | 1.56 | 42.31 | 60.29 | 32.71 | 41.45 | 2.37 | 16.96 |
| 0.2 | 46.21 | 1.56 | 42.09 | 59.78 | 32.54 | 38.34 | 2.40 | 17.56 |
| 0.3 | 46.21 | 1.55 | 42.28 | 59.80 | 32.58 | 38.46 | 2.40 | 17.43 |
| ine 1 | 46.17 | 1.55 | 42.13 | 59.37 | 32.35 | 36.09 | 2.43 | 16.81 |
| 2 | 46.21 | 1.52 | 41.92 | 59.43 | 32.27 | 35.90 | 2.43 | 16.54 |
| 3 | 46.21 | 1.55 | 42.28 | 60.51 | 32.65 | 43.65 | 2.39 | 17.14 |
| 4 | 46.21 | 1.52 | 41.95 | 60.70 | 32.82 | 48.31 | 2.36 | 16.33 |
| 5 | 46.15 | 1.56 | 42.16 | 59.75 | 32.56 | 38.80 | 2.39 | 16.96 |
| 6 | 46.15 | 1.56 | 42.09 | 59.58 | 32.54 | 37.71 | 2.39 | 17.08 |
| 7 | 46.15 | 1.56 | 42.31 | 59.83 | 32.58 | 39.34 | 2.39 | 17.64 |
| 8 | 46.17 | 1.55 | 42.20 | 59.48 | 32.53 | 36.39 | 2.41 | 16.35 |
| 9 | 46.17 | 1.55 | 42.12 | 55.36 | 31.12 | 45.43 | 2.37 | 16.43 |
| 10 | 46.17 | 1.55 | 42.46 | 60.63 | 32.73 | 44.74 | 2.38 | 16.47 |
| Edge Count | Depth | CCC | GCS (%) | RFR (%) | GRC (%) | CAS (%) | SNI (%) | |
|---|---|---|---|---|---|---|---|---|
| ISN (weight set 10) | 6.09 | 0.56 | 1.26 | 6.65 | 91.13 | 6.60 | 85.29 | 2.31 |
| ISN-AF (weight set 10) | 6.09 | 0.51 | 1.15 | 6.90 | 94.22 | 7.23 | 94.70 | 2.89 |
| Baseline | 5.49 | 0.37 | 2.25 | 4.99 | 92.23 | 6.32 | - | 6.66 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zola, P.; Cola, G.; Mazza, M.; Tesconi, M. Interaction Strength Analysis to Model Retweet Cascade Graphs. Appl. Sci. 2020, 10, 8394. https://doi.org/10.3390/app10238394
Zola P, Cola G, Mazza M, Tesconi M. Interaction Strength Analysis to Model Retweet Cascade Graphs. Applied Sciences. 2020; 10(23):8394. https://doi.org/10.3390/app10238394
Chicago/Turabian StyleZola, Paola, Guglielmo Cola, Michele Mazza, and Maurizio Tesconi. 2020. "Interaction Strength Analysis to Model Retweet Cascade Graphs" Applied Sciences 10, no. 23: 8394. https://doi.org/10.3390/app10238394
APA StyleZola, P., Cola, G., Mazza, M., & Tesconi, M. (2020). Interaction Strength Analysis to Model Retweet Cascade Graphs. Applied Sciences, 10(23), 8394. https://doi.org/10.3390/app10238394






