A Bio-Inspired Model of Picture Array Generating P System with Restricted Insertion Rules
Abstract
1. Introduction
2. Preliminaries
2.1. Basic Notions
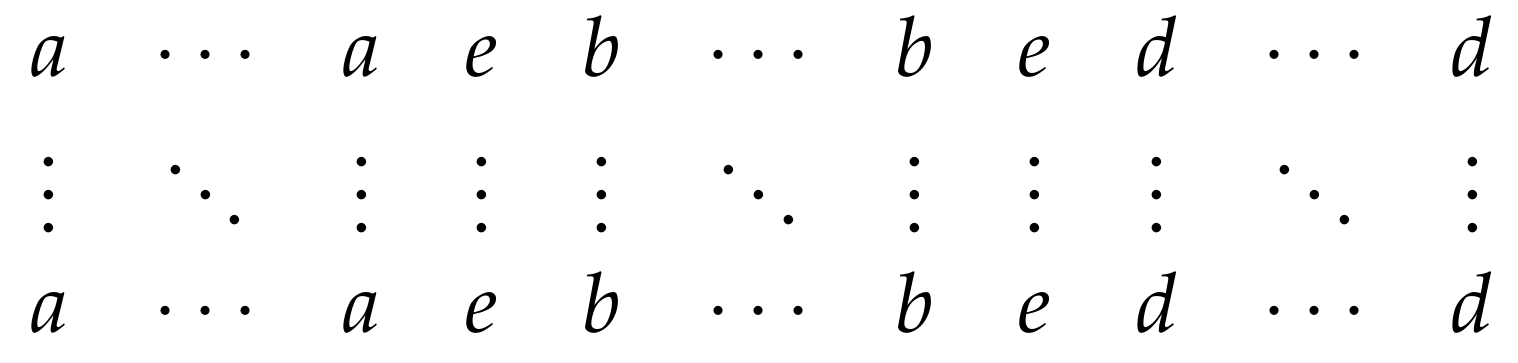
2.2. Picture-Insertion System
- (i)
- Σ is an alphabet;
- (ii)
- where called a column insertion table, is a finite set of column insertion rules with alphabetic contexts of the form such that for any two rules in , we have and either both the left contexts and are in Σ (likewise the right contexts and are in Σ) or both are λ;
- (iii)
- where called a row insertion table, is a finite set of row insertion rules with alphabetic contexts of the form such that for any two rules in , we have and either both the up contexts and are in Σ (likewise the down contexts and are in Σ) or both are λ;
- (iv)
- is a finite set of axiom arrays.
3. Array P System with Restricted Picture Insertion Rules
4. A Hierarchy between One Membrane and Two Membranes
5. Comparison with Pure 2D Context-Free Grammars
- 1.
- 2.
- 3.
- 4.
6. Comparison with Certain Standard 2D Grammar Models
7. An Application of the Model to “Kolam” Pattern Generation
8. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Păun, G. Membrane Computing: An Introduction; Springer: Berlin/Heidelbrg, Germany, 2000. [Google Scholar]
- Păun, G.; Rozenberg, G.; Salomaa, A. The Oxford Handbook of Membrane Computing; Oxford University Press Inc.: New York, NY, USA, 2010. [Google Scholar]
- Pan, L.; Păun, G.; Zhang, G. Foreword: Starting JMC. J. Membr. Comput. 2019, 1, 1–2. [Google Scholar] [CrossRef]
- Păun, G. Computing with membranes. J. Comp. System Sci. 2000, 61, 108–143. [Google Scholar] [CrossRef]
- Zhang, G.; Pérez-Jiménez, M.J.; Gheorghe, M. Real-life Applications with Membrane Computing. In Emergence, Complexity and Computation Series; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Wang, J.; Shi, P.; Peng, H. Membrane computing model for IIR filter design. Inf. Sci. 2016, 329, 164–176. [Google Scholar] [CrossRef]
- Zhang, G.; Rong, H.; Neri, F.; Pérez-Jiménez, M.J. An optimization spiking neural P system for approximately solving combinatorial optimization problems. Int. J. Neural Syst. 2014, 24, 1440006. [Google Scholar] [CrossRef]
- Zhang, G.; Gheorghe, M.; Pan, L.; Pérez-Jiménez, M.J. Evolutionary membrane computing: A comprehensive survey and new results. Inf. Sci. 2014, 279, 528–551. [Google Scholar] [CrossRef]
- Andreu-Guzmán, J.A.; Valencia-Cabrera, L. A novel solution for GCP based on an OLMS membrane algorithm with dynamic operators. J. Membr. Comput. 2019, 1, 1–13. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, G.; Neri, F.; Jiang, T.; Zhao, J.; Gheorghe, M.; Ipate, F.; Lefticaru, L. Design and implementation of membrane controllers for trajectory tracking of nonholonomic wheeled mobile robots. Integr. Comput. Aided Eng. 2016, 23, 15–30. [Google Scholar] [CrossRef]
- Perez-Hurtado, I.; Martınez-del-Amor, M.A.; Zhang, G.; Neri, F.; Pérez-Jiménez, M.J. A membrane parallel rapidly-exploring random tree algorithm for robotic motion planning. Integr. Comput. Aided Eng. 2020, 27, 121–138. [Google Scholar] [CrossRef]
- Buiu, C.; George, A. Membrane computing models and robot controller design, current results and challenges. J. Membr. Comput. 2019, 1, 262–269. [Google Scholar] [CrossRef]
- Peng, H.; Wang, J.; Ming, J.; Shi, P.; Pérez-Jiménez, M.J.; Yu, W.; Tao, C. Fault diagnosis of power systems using intuitionistic fuzzy spiking neural P systems. IEEE Trans. Smart Grid 2018, 9, 4777–4784. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, G.; Zhao, J.; He, Z.; Wang, J.; Pérez-Jiménez, M.J. Fault diagnosis of electric power systems based on fuzzy reasoning spiking neural P systems. IEEE Trans. Power Syst. 2015, 30, 1182–1194. [Google Scholar] [CrossRef]
- Rong, H.; Yi, K.; Zhang, G.; Dong, J.; Paul, P.; Huang, Z. Automatic implementation of fuzzy reasoning spiking neural P systems for diagnosing faults in complex power systems. Complexity 2019, 2019, 2635714. [Google Scholar] [CrossRef]
- Sánchez-Karhunen, E.; Valencia-Cabrera, L. Modelling complex market interactions using PDP systems. J. Membr. Comput. 2019, 1, 40–51. [Google Scholar] [CrossRef]
- Díaz-Pernil, D.; Gutiérrez-Naranjo, M.A.; Peng, H. Membrane computing and image processing: A short survey. J. Membr. Comput. 2019, 1, 58–73. [Google Scholar] [CrossRef]
- Peng, H.; Wang, J.; Shi, P.; Pérez-Jiménez, M.J.; Riscos-Núñez, A. An extended membrane system with active membrane to solve automatic fuzzy clustering problems. Int. J. Neural Syst. 2016, 26, 1–17. [Google Scholar] [CrossRef]
- Orellana-Martín, D.; Valencia-Cabrera, L.; Riscos-Núñez, A.; Pérez-Jiménez, M.J. P systems with proteins: A new frontier when membrane division disappears. J. Membr. Comput. 2019, 1, 29–39. [Google Scholar] [CrossRef]
- Jiang, Y.; Su, Y.; Luo, F. An improved universal spiking neural P system with generalized use of rules. J. Membr. Comput. 2019, 1, 270–278. [Google Scholar] [CrossRef]
- Freund, R. How derivation modes and halting conditions may influence the computational power of P systems. J. Membr. Comput. 2020, 2, 14–25. [Google Scholar] [CrossRef]
- Leporati, A.; Manzoni, L.; Mauri, G.; Porreca, A.E.; Zandron, C. A Turing machine simulation by P systems without charges. J. Membr. Comput. 2020, 2, 71–79. [Google Scholar] [CrossRef]
- Orellana-Martín, D.; Valencia-Cabrera, L.; Riscos-Núñez, A.; Pérez-Jiménez, M.J. Minimal cooperation as a way to achieve the efficiency in cell-like membrane systems. J. Membr. Comput. 2019, 1, 85–92. [Google Scholar] [CrossRef]
- Leporati, A.; Manzoni, L.; Mauri, G.; Porreca, A.E.; Zandron, C. Characterizing PSPACE with shallow non-confluent P systems. J. Membr. Comput. 2019, 1, 75–84. [Google Scholar] [CrossRef]
- Cooper, J.; Nicolescu, R. Alternative representations of P systems solutions to the graph colouring problem. J. Membr. Comput. 2019, 1, 112–126. [Google Scholar] [CrossRef]
- Sosík, P. P systems attacking hard problems beyond NP: A survey. J. Membr. Comput. 2019, 1, 198–208. [Google Scholar] [CrossRef]
- Calude, C.S.; Dinneen, M.J.; Hua, R. Quantum solutions for densest k-subgraph problems. J. Membr. Comput. 2020, 2, 26–41. [Google Scholar] [CrossRef]
- Buño, K.; Adorna, H. Distributed computation of a k P systems with active membranes for SAT using clause completion. J. Membr. Comput. 2020, 2, 108–120. [Google Scholar] [CrossRef]
- Chen, H.; Freund, R.; Ionescu, M.; Păun, G.; Pérez-Jiménez, M.J. On string languages generated by spiking neural P systems. Fundam. Inform. 2007, 75, 141–162. [Google Scholar]
- Ferretti, C.; Mauri, G.; Păun, G.; Zandron, C. On three variants of rewriting P systems. Theor. Comp. Sci. 2003, 301, 201–215. [Google Scholar] [CrossRef]
- Krithivasan, K.; Metta, V.P.; Garg, D. On string languages generated by spiking neural P systems with anti-spikes. Int. J. Found. Comput. Sci. 2011, 22, 15–27. [Google Scholar] [CrossRef]
- Cruz, R.T.A.D.L.; Cabarle, F.G.; Adorna, H.N. Generating context-free languages using spiking neural P systems with structural plasticity. J. Membr. Comput. 2019, 1, 161–177. [Google Scholar] [CrossRef]
- Ceterchi, R.; Mutyam, M.; Pǎun, G.; Subramanian, K.G. Array-rewriting P systems. Nat. Comput. 2003, 2, 229–249. [Google Scholar] [CrossRef]
- Subramanian, K.G. P systems and picture languages. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4664, pp. 99–109. [Google Scholar]
- Subramanian, K.G.; Sriram, S.; Song, B.; Pan, L. An Overview of 2D Picture Array Generating Models Based on Membrane Computing. In Reversibility and Universality. Emergence, Complexity and Computation; Adamatzky, A., Ed.; Springer: Berlin/Heidelberg, Germany, 2018; Volume 30, pp. 333–356. [Google Scholar]
- Fujioka, K. Morphic characterizations with insertion systems controlled by a context of length one. Theoret. Comput. Sci. 2013, 469, 69–76. [Google Scholar] [CrossRef]
- Haussler, D. Insertion languages. Inf. Sci. 1983, 31, 77–89. [Google Scholar] [CrossRef]
- Margenstern, M.; Păun, G.; Rogozhin, Y.; Verlan, S. Context-free insertion-deletion systems. Theor. Comp. Sci. 2005, 330, 339–348. [Google Scholar] [CrossRef]
- Kari, L.; Paun, G.; Thierrin, G.; Yu, S. At the crossroads of DNA computing and formal languages: Characterizing recursively enumerable languages using insertion-deletion systems. DIMACS Ser. Discret. Math. Theor. Comput. Sci. 1999, 48, 329–338. [Google Scholar]
- Păun, G.; Rozenberg, G.; Salomaa, A. DNA Computing: New Computing Paradigms; Springer: New York, NY, USA, 1998. [Google Scholar]
- Fujioka, K. A Two-Dimensional Extension of Insertion Systems. In Theory and Practice of Natural Computing (TPNC 2014); Dediu, A.H., Lozano, M., Martín-Vide, C., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2014; Volume 8890, pp. 181–192. [Google Scholar]
- Subramanian, K.G.; Ali, R.M.; Geethalakshmi, M.; Nagar, A.K. Pure 2D picture grammars and languages. Discret. Appl. Math. 2009, 157, 3401–3411. [Google Scholar] [CrossRef]
- Siromoney, G.; Siromoney, R.; Krithivasan, K. Array grammars and Kolam. Comput. Graph. Image Proc. 1974, 3, 63–82. [Google Scholar] [CrossRef]
- Samdanielthompson, G.; Nagar, A.K.; David, N.G.; Zhang, G.; Subramanian, K.G. Insertion Based Picture Array P systems. In Proceedings of the ACMC 2018, CDMTCS Research Report Series (CDMTCS-530), Auckland, New Zealand, 10–14 December 2018; Dinneen, M.J., Nicolescu, R., Eds.; University of Auckland: Auckland, New Zealand, 2018. [Google Scholar]
- Rozenberg, G.; Salomaa, A. Handbook of Formal Languages; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Giammarresi, D.; Restivo, A. Two-dimensional languages. In Handbook of Formal Languages; Rozenberg, G., Salomaa, G., Eds.; Springer: Berlin/Heidelberg, Germany, 1997; pp. 215–267. [Google Scholar]
- Morita, K. Two-dimensional languages. In Formal Languages and Applications. Series in Fuzziness and Soft Computing; Martin-Vide, C., Mitrana, V., Păun, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 148, pp. 426–437. [Google Scholar]
- Krivka, Z.; Martín-Vide, C.; Meduna, A.; Subramanian, K.G. A Variant of Pure Two-Dimensional Context-Free Grammars Generating Picture Languages. In IWCIA 2014, Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2014; Volume 8466, pp. 123–133. [Google Scholar]
- Subramanian, K.G.; Geethalakshmi, M.; David, N.G.; Nagar, A.K. Picture Array Generation Using Pure 2D Context-Free Grammar Rules. In IWCIA 2015 Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2015; Volume 4664, pp. 187–201. [Google Scholar]
- Siromoney, G.; Siromoney, R.; Krithivasan, K. Abstract families of matrices and picture languages. Comput. Graph. Image Proc. 1972, 1, 284–307. [Google Scholar] [CrossRef]
- Siromoney, R.; Subramanian, K.G.; Rangarajan, K. Parallel/sequential rectangular arrays with tables. Int. J. Comput. Math. 1977, 6, 143–158. [Google Scholar] [CrossRef]
- Head, T. Formal language theory and DNA: An analysis of the generative capacity of specific recombinant behaviours. Bull. Math. Biol. 1987, 49, 735–759. [Google Scholar] [CrossRef]
- Berstel, J.; Boasson, L.; Fagnot, I. Splicing systems and the Chomsky hierarchy. Theor. Comput. Sci. 2012, 436, 2–22. [Google Scholar] [CrossRef]
- Pan, L.; Nagar, A.K.; Subramanian, K.G.; Song, B. Picture Array Generation Using Flat Splicing Operation. J. Comput. Theoret. Nanosci. 2016, 13, 3568–3577. [Google Scholar] [CrossRef]
- Subramanian, K.G.; Van, D.L.; Helen Chandra, P.; Quyen, N.D. Array Grammars with Contextual Operations. Fundam. Inform. 2008, 83, 411–428. [Google Scholar]
- Nagata, S.; Robinson, T. Digitalization of Kolam Patterns and Tactile Kolam Tools. In Formal Models, Languages and Applications; Subramanian, K.G., Rangarajan, K., Madhavan, M., Eds.; World Scientific Publishing: Singapore, 2007; pp. 354–363. [Google Scholar]

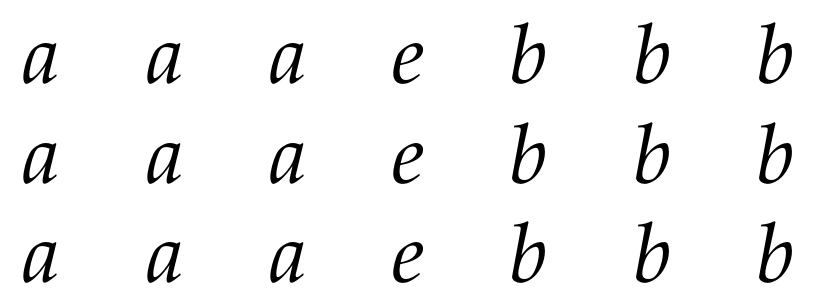






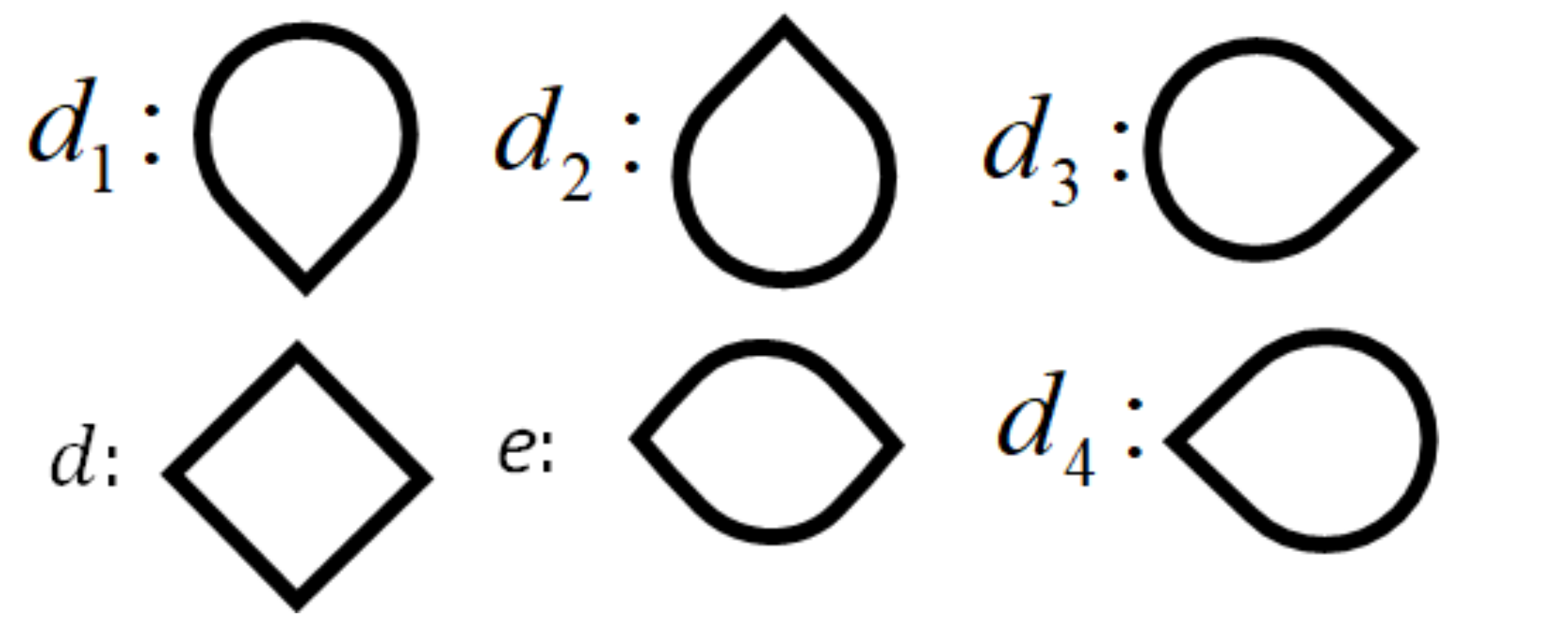
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Samdanielthompson, G.; David, N.G.; Nagar, A.K.; Subramanian, K.G. A Bio-Inspired Model of Picture Array Generating P System with Restricted Insertion Rules. Appl. Sci. 2020, 10, 8306. https://doi.org/10.3390/app10228306
Zhang G, Samdanielthompson G, David NG, Nagar AK, Subramanian KG. A Bio-Inspired Model of Picture Array Generating P System with Restricted Insertion Rules. Applied Sciences. 2020; 10(22):8306. https://doi.org/10.3390/app10228306
Chicago/Turabian StyleZhang, Gexiang, G. Samdanielthompson, N. Gnanamalar David, Atulya K. Nagar, and K.G. Subramanian. 2020. "A Bio-Inspired Model of Picture Array Generating P System with Restricted Insertion Rules" Applied Sciences 10, no. 22: 8306. https://doi.org/10.3390/app10228306
APA StyleZhang, G., Samdanielthompson, G., David, N. G., Nagar, A. K., & Subramanian, K. G. (2020). A Bio-Inspired Model of Picture Array Generating P System with Restricted Insertion Rules. Applied Sciences, 10(22), 8306. https://doi.org/10.3390/app10228306






