Acoustic Scattering Models from Rough Surfaces: A Brief Review and Recent Advances
Abstract
1. Introduction
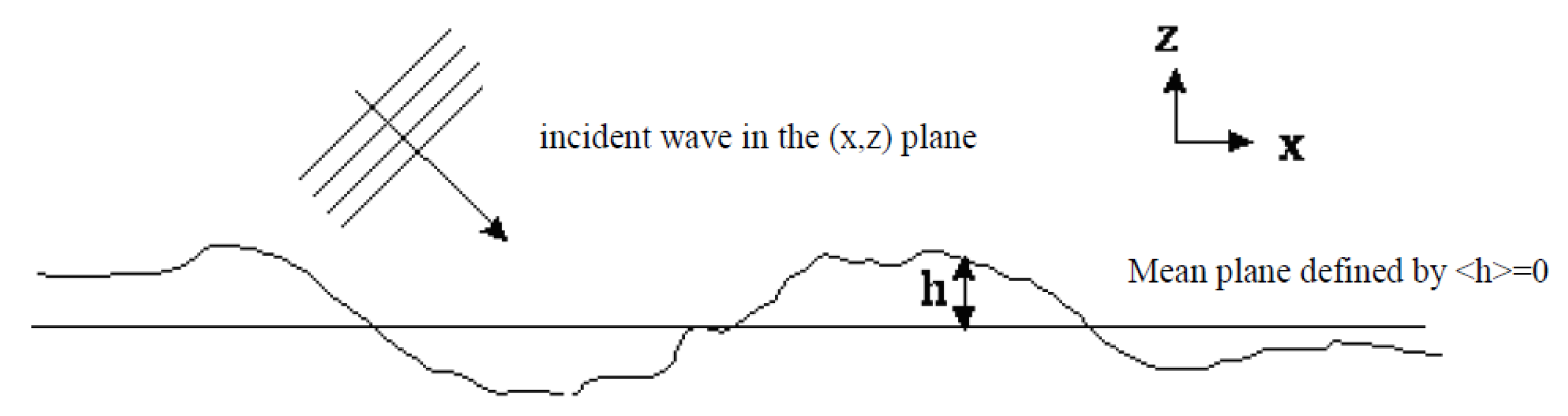
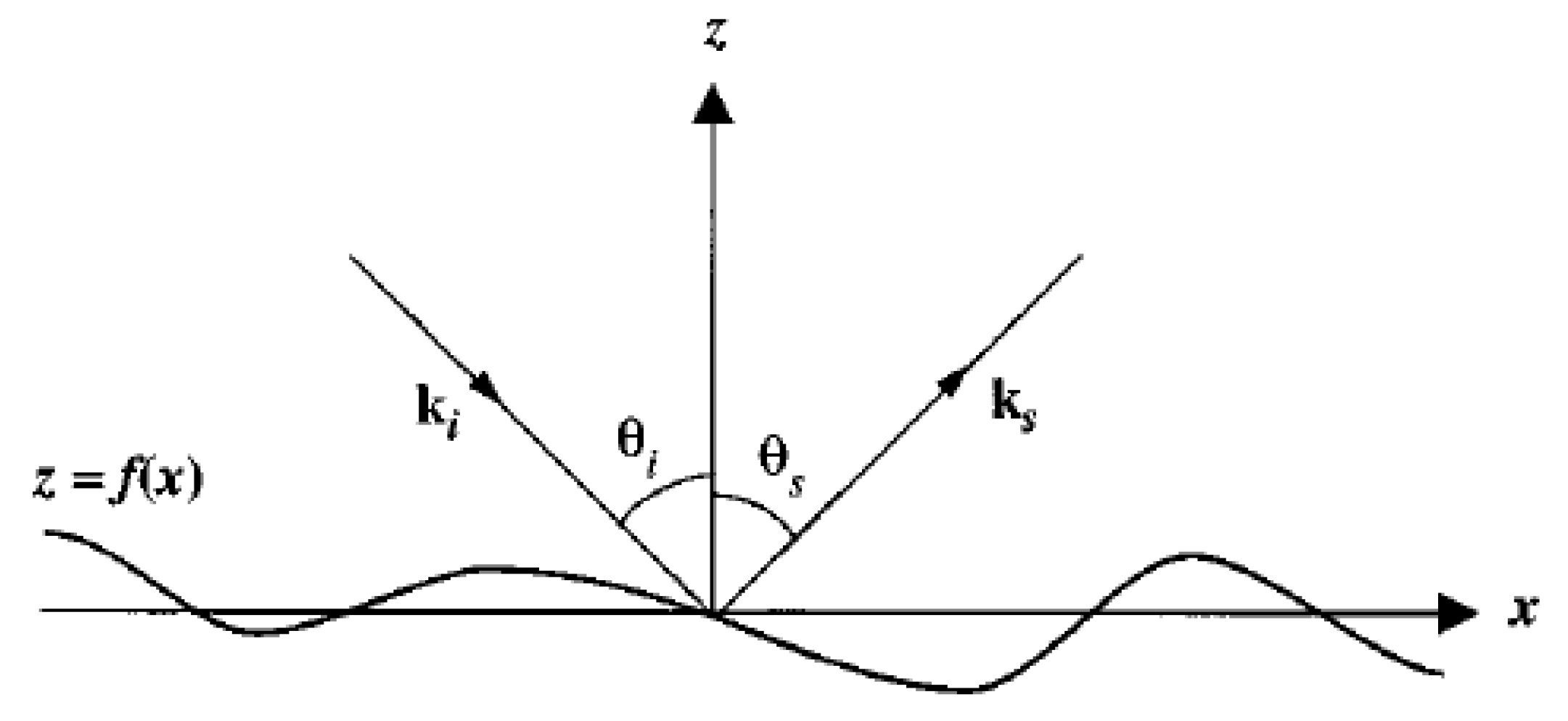
2. Rough Surfaces Parametrization
2.1. Statistical Properties
2.2. Generation Process of an Individual Gaussian Rough Surface
2.3. Implementation Example for Generation of an Individual Gaussian Rough Surface
- -
- The RMS surface height: . As the height is defined with zero mean ( = 0), the standard deviation of the height is equal to the RMS height : .
- -
- The correlation lengths, and , along the local axes x and y.
3. Historical Approximations
3.1. The Perturbation Theory
3.2. The Kirchhoff Approximation
3.2.1. Theory and History
- 1.
- Use of the Helmholtz equation: the scattered field is:
- 2.
- Boundary Conditions on the rough surface: Ogilvy [27] considered for instance Dirichlet boundary conditions (soft case) so that = 0. So one term in the previous Green integral disappears:
- 3.
- Kirchhoff approximation: the tangential plane approximation enables to approximate the value of inside the previous integral.
- 4.
- Far field approximation: the integrand value can be simplified by assuming >> 1, being the wave number.
- 5.
- Projection of integration on the rough surface on the smooth surface: this projection involves the gradients of the roughness.
- 6.
- Incorporation of a shadow function to approach auto-shadowing: Wagner [74] has proposed to incorporate a shadow function inside the Kirchhoff integral to take into account shadowing effects.
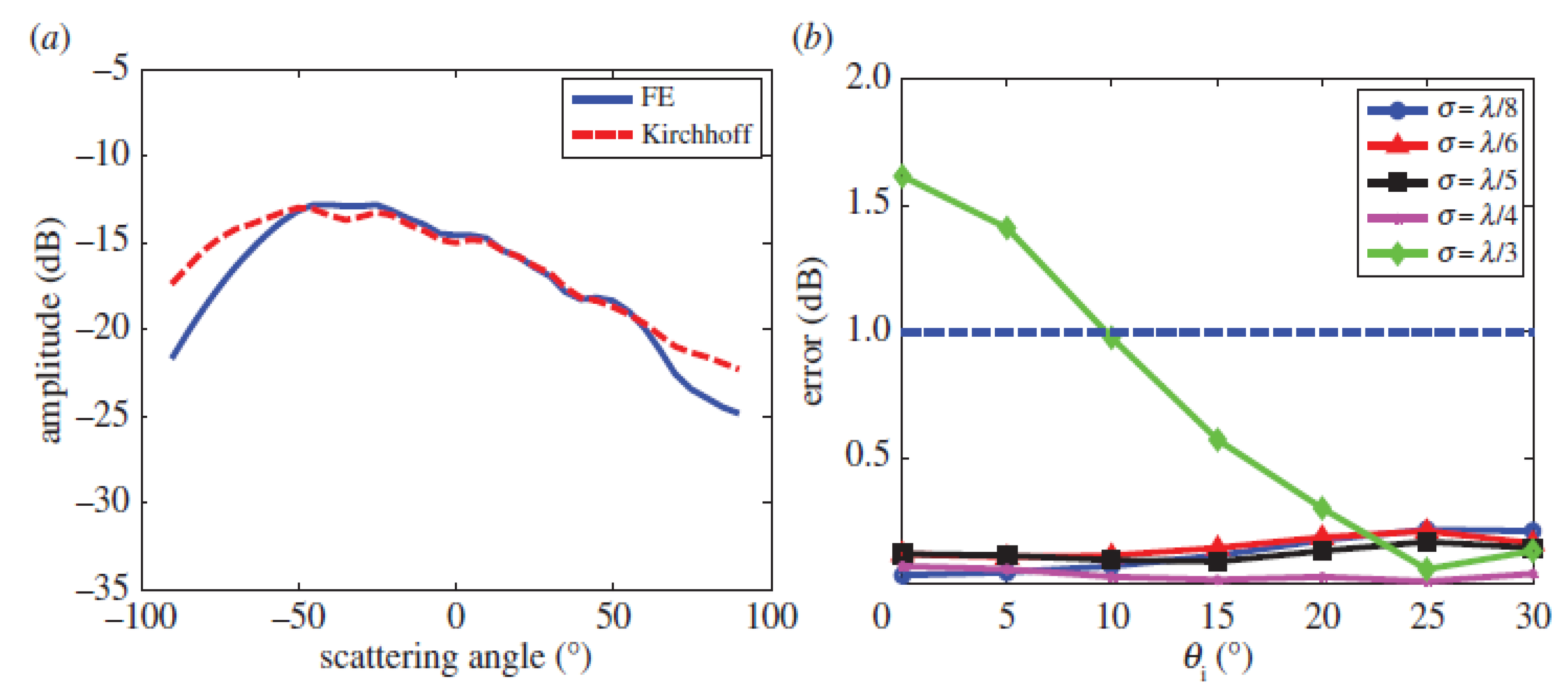
3.2.2. Validity
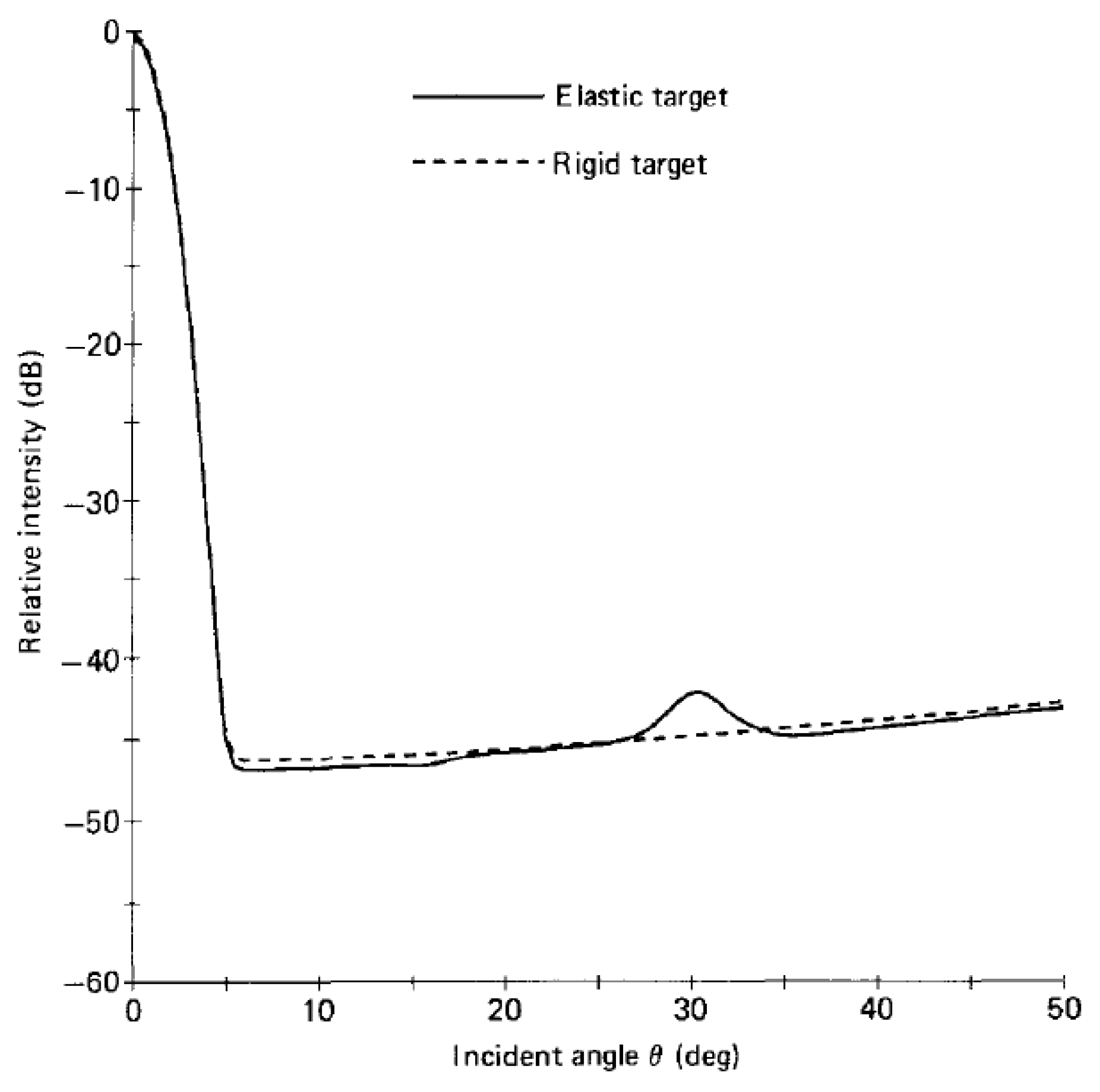
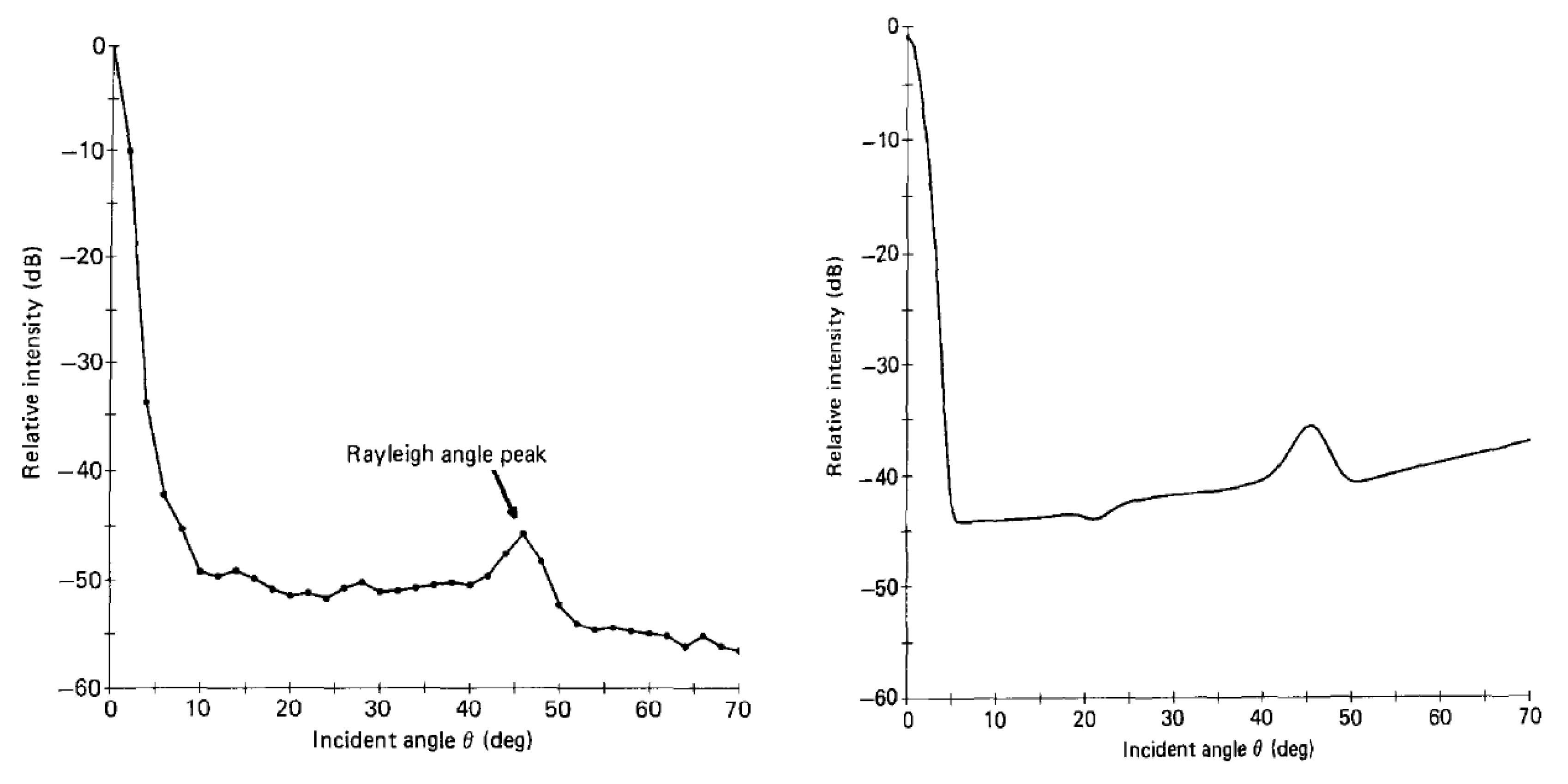
3.2.3. Elastic Targets and Applications
3.2.4. Periodic Surfaces
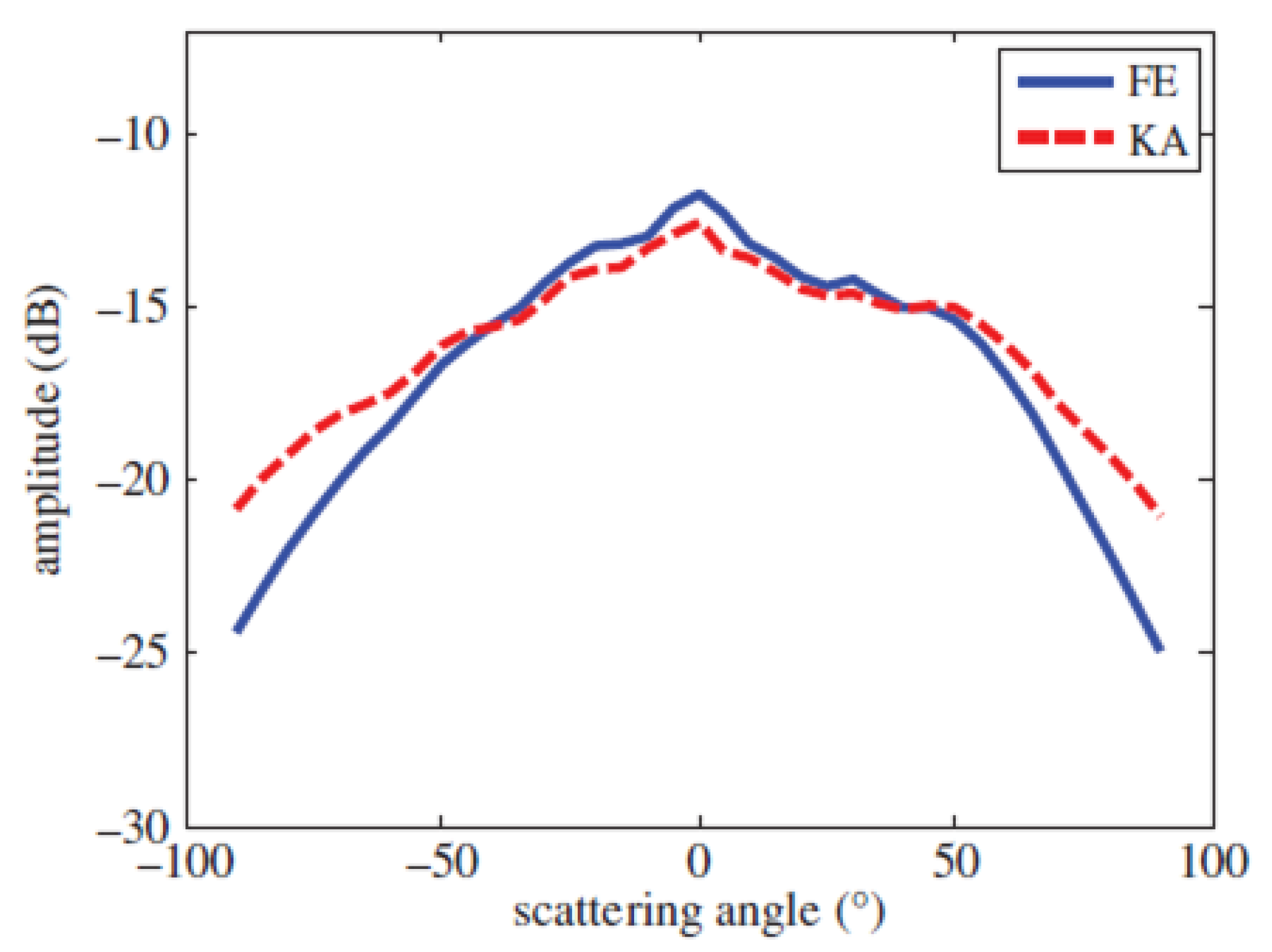
4. More Modern Approaches with Larger Domains of Validity
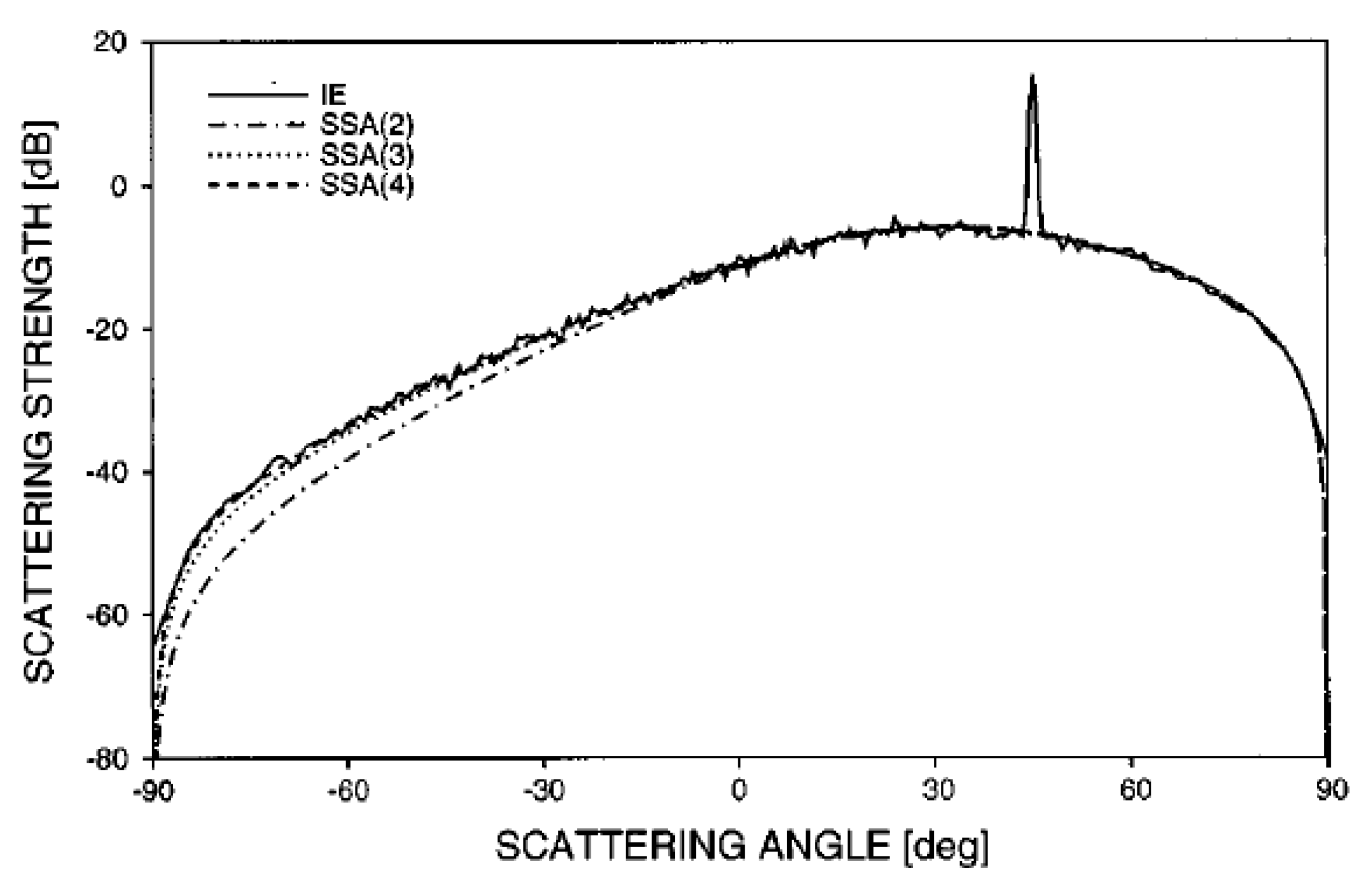
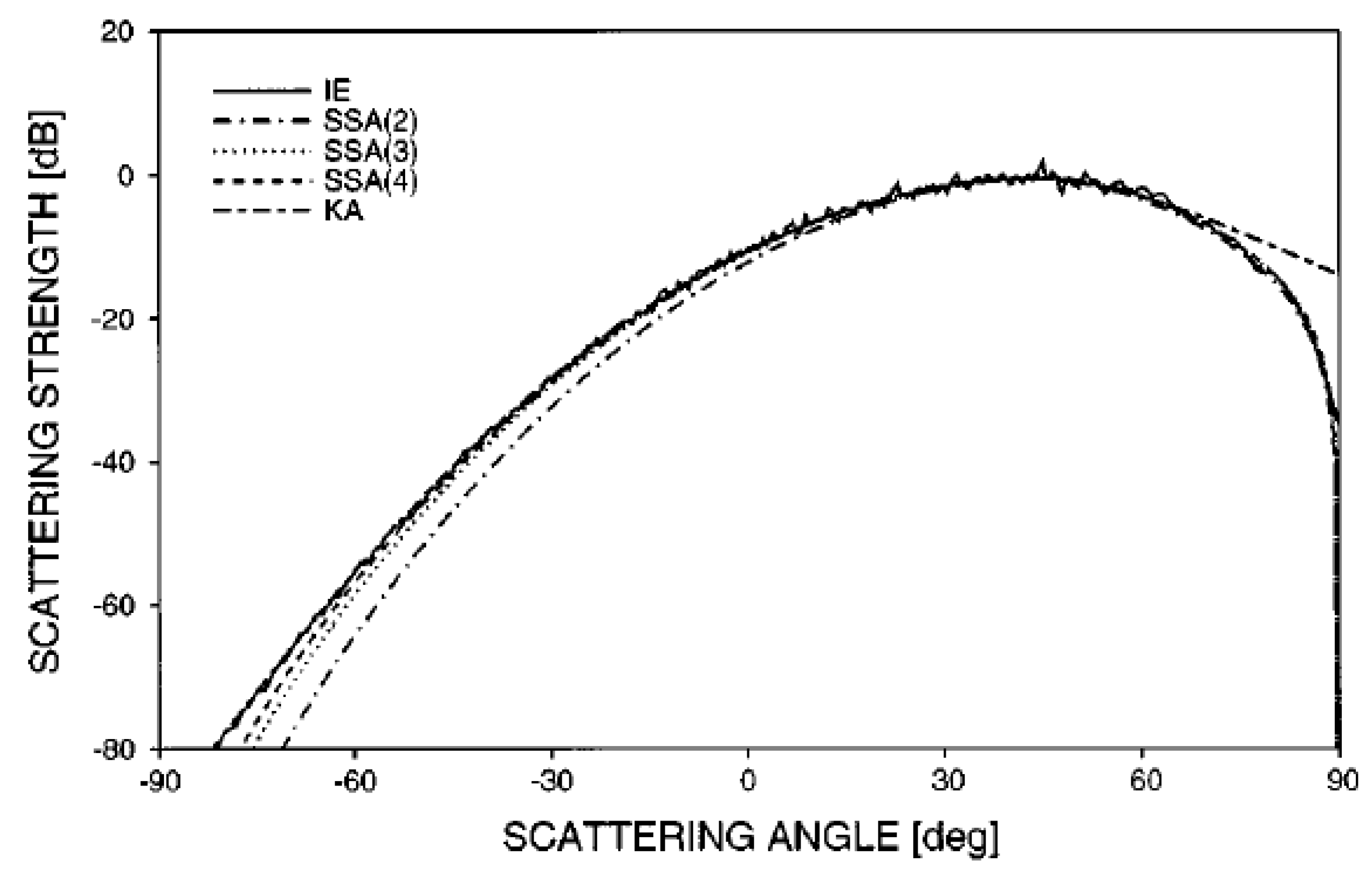
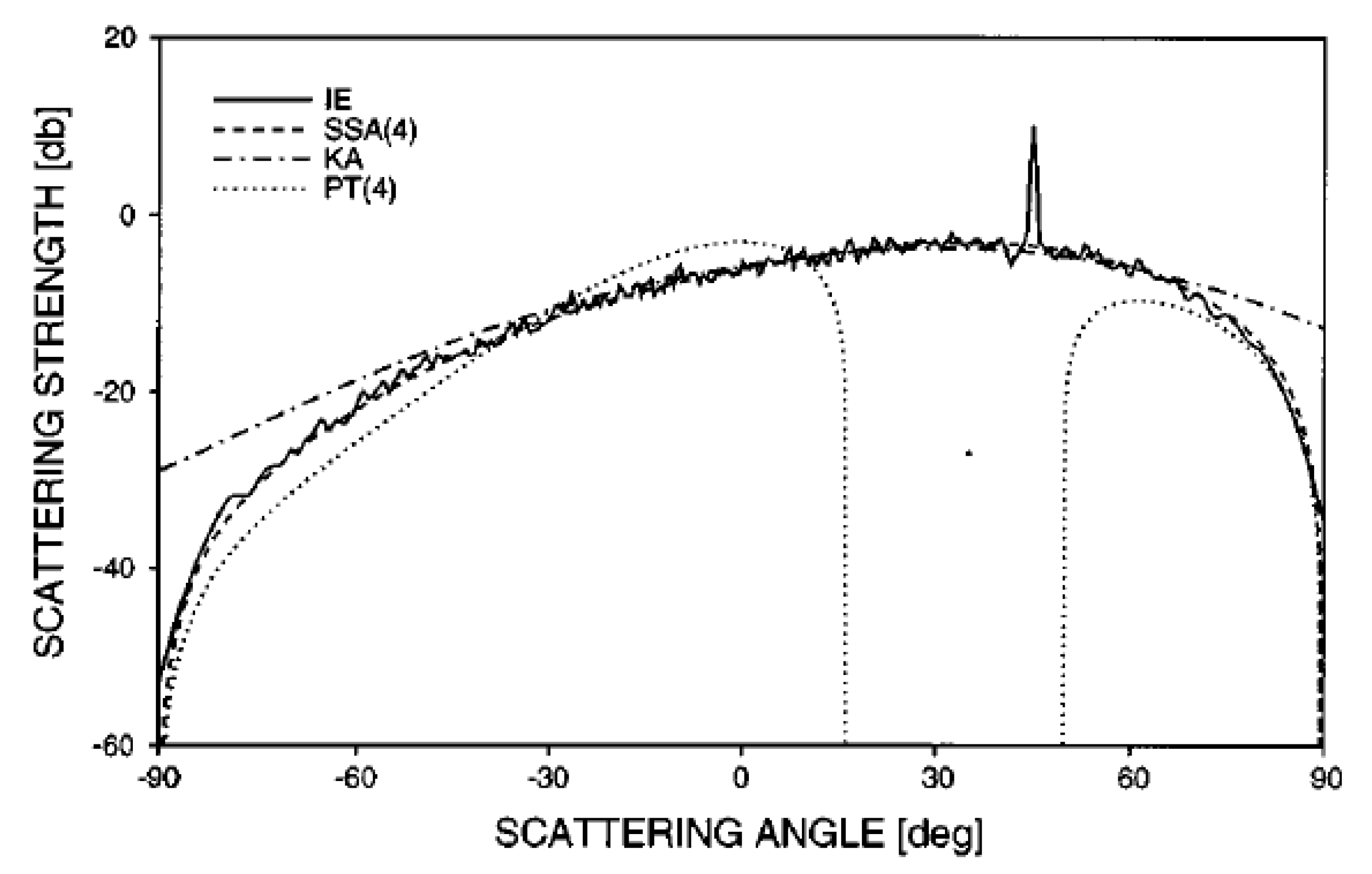
4.1. Small Slope Approximation (SSA)
4.2. Parabolic Equation (PE)
5. Summary, Discussion and Perspectives
Author Contributions
Funding
Conflicts of Interest
References
- Romanova, A.V.; Horoshenkov, K.V.; Krynkin, A. Dynamically Rough Boundary Scattering Effect on a Propagating Continuous Acoustical Wave in a Circular Pipe with Flow. Sensors 2018, 18, 1098. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Cui, X.; Ma, H.; Kang, Y.; Deng, Z. Effect of Surface Roughness on Ultrasonic Testing of Back-Surface Micro-Cracks. Appl. Sci. 2018, 8, 1233. [Google Scholar] [CrossRef]
- Dingler, J.R.; Boylls, J.C.; Lowe, R.L. A high-frequency sonar for profiling small-scale subaqueous bedforms. Mar. Geol. 1977, 24, 279–288. [Google Scholar] [CrossRef]
- Niu, L.; Qian, M.; Yang, W.; Meng, L.; Xiao, Y.; Wong, K.K.L.; Abbott, D.; Liu, X.; Zheng, H. Surface Roughness Detection of Arteries via Texture Analysis of Ultrasound Images for Early Diagnosis of Atherosclerosis. PLoS ONE 2013, 8, e76880. [Google Scholar] [CrossRef] [PubMed]
- Hériveaux, Y.; Nguyen, V.-H.; Biwa, S.; Haïat, G. Analytical modeling of the interaction of an ultrasonic wave with a rough bone-implant interface. Ultrasonics 2020, 108. [Google Scholar] [CrossRef]
- Ogilvy, J.A. Model for the ultrasonic inspection of rough defects. Ultrasonics 1989, 28, 69–79. [Google Scholar] [CrossRef]
- Ogilvy, J.A. Theoretical comparison of ultrasonic signal amplitudes from smooth and rough defects. NDT Int. 1986, 19, 371–385. [Google Scholar] [CrossRef]
- Ogilvy, J.A.; Culverwell, I.D. Elastic model for simulating ultrasonic inspection of smooth and rough defects. Ultrasonics 1991, 29, 490–496. [Google Scholar] [CrossRef]
- Nagy, P.B.; Adler, L. Surface roughness induced attenuation of reflected and transmitted ultrasonic waves. J. Acoust. Soc. Am. 1987, 82, 193–197. [Google Scholar] [CrossRef]
- Nagy, P.B.; Rose, J.H. Surface roughness and the ultrasonic detection of subsurface scatterers. J. Appl. Phys. 1993, 73, 566–580. [Google Scholar] [CrossRef]
- Nagy, P.B.; Adler, L.; Rose, J.H. Effects of Acoustic Scattering at Rough Surfaces on the Sensitivity of Ultrasonic Inspection. In Review of Progress in Quantitative Nondestructive Evaluation; Springer: Boston, MA, USA, 1993; pp. 1775–1782. ISBN 978-1-4613-6233-3. [Google Scholar]
- Bilgen, M. Effects of randomly rough surfaces on ultrasonic inspection. Retrosp. Theses Diss. 1993. [Google Scholar] [CrossRef]
- Ogilvy, J.A. Theory of Wave Scattering From Random Rough Surfaces; Taylor & Francis: Abingdon, UK, 1991; ISBN 978-0-7503-0063-6. [Google Scholar]
- Elfouhaily, T.M.; Guérin, C.-A. A critical survey of approximate scattering wave theories from random rough surfaces. Waves Random Media 2004, 14, R1–R40. [Google Scholar] [CrossRef]
- Ishimaru, A. Wave-Propagation and Scattering in Random-Media and Rough Surfaces. Proc. IEEE 1991, 79, 1359–1366. [Google Scholar] [CrossRef]
- Ticconi, F.; Pulvirenti, L.; Pierdicca, N. Models for Scattering from Rough Surfaces. Electromagn. Waves 2011. [Google Scholar] [CrossRef]
- Hermansson, P.; Forssell, G. A Review of Models for Scattering from Rough Surfaces. Available online: https://scholar.google.com/scholar?cluster=9344336395593944459&hl=fr&as_sdt=0,5&sciodt=0,5 (accessed on 25 March 2020).
- Ogilvy, J.A. Wave scattering from rough surfaces. Rep. Prog. Phys. 1987, 50, 1553–1608. [Google Scholar] [CrossRef]
- Brekhovskikh, L.M.; Lysanov, Y.P. Fundamentals of Ocean Acoustics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; ISBN 978-3-662-07328-5. [Google Scholar]
- Voronovich, A.G. Wave Scattering from Rough Surfaces; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; ISBN 978-3-642-59936-1. [Google Scholar]
- Thorsos, E.I. The validity of the Kirchhoff approximation for rough surface scattering using a Gaussian roughness spectrum. J. Acoust. Soc. Am. 1988, 83, 78–92. [Google Scholar] [CrossRef]
- Khenchaf, A.; Daout, F.; Saillard, J. The two-scale model for random rough surface scattering. In Proceedings of the OCEANS 96 MTS/IEEE Conference Proceedings. The Coastal Ocean-Prospects for the 21st Century, Fort Lauderdale, FL, USA, 23–26 September 1996; IEEE: Piscataway, NY, USA, 1996; Volume 2, pp. 887–891. [Google Scholar]
- Nayak, P.R. Random Process Model of Rough Surfaces. J. Lubr. Technol. 1971, 93, 398–407. [Google Scholar] [CrossRef]
- Johnson, K.L.; Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1987; ISBN 978-0-521-34796-9. [Google Scholar]
- Adler, R.J.; Firmin, D.; Kendall, D.G. A non-gaussian model for random surfaces. Philos. Trans. R. Soc. Lond. Ser. Math. Phys. Sci. 1981, 303, 433–462. [Google Scholar] [CrossRef]
- Pérez-Ràfols, F.; Almqvist, A. Generating randomly rough surfaces with given height probability distribution and power spectrum. Tribol. Int. 2019, 131, 591–604. [Google Scholar] [CrossRef]
- Ogilvy, J.A. Computer simulation of acoustic wave scattering from rough surfaces. J. Phys. Appl. Phys. 1988, 21, 260–277. [Google Scholar] [CrossRef]
- Civa Software Website. Available online: http://www.extende.com/ (accessed on 20 November 2020).
- Mahaut, S.; Chatillon, S.; Darmon, M.; Leymarie, N.; Raillon, R.; Calmon, P. An overview of ultrasonic beam propagation and flaw scattering models in the civa software. AIP Conf. Proc. 2010, 1211, 2133–2140. [Google Scholar] [CrossRef]
- Toullelan, G.; Raillon, R.; Chatillon, S.; Dorval, V.; Darmon, M.; Lonné, S. Results of the 2015 UT Modeling Benchmark Obtained with Models Implemented in Civa. AIP Conf. Proc. 2016. [Google Scholar] [CrossRef]
- Raillon-Picot, R.; Toullelan, G.; Darmon, M.; Calmon, P.; Lonné, S. Validation of CIVA ultrasonic simulation in canonical configurations. In Proceedings of the World Conference of Non Destructive Testing (WCNDT) 2012, Durban, South Africa, 16–20 April 2012. [Google Scholar]
- Raillon, R.; Bey, S.; Dubois, A.; Mahaut, S.; Darmon, M. Results of the 2010 ut modeling benchmark obtained with civa: Responses of backwall and surface breaking notches. AIP Conf. Proc. 2011, 1335, 1777–1784. [Google Scholar] [CrossRef]
- Raillon, R.; Bey, S.; Dubois, A.; Mahaut, S.; Darmon, M. Results of the 2009 ut modeling benchmark obtained with civa: Responses of notches, side-drilled holes and flat-bottom holes of various sizes. AIP Conf. Proc. 2010, 1211, 2157–2164. [Google Scholar] [CrossRef]
- Gilbert, F.; Knopoff, L. Seismic scattering from topographic irregularities. J. Geophys. Res. 1896–1977 1960, 65, 3437–3444. [Google Scholar] [CrossRef]
- Bass, F.G.; Fuks, I.M. Wave Scattering from Statistically Rough Surfaces; Pergamon Press: Oxford, UK, 1973. [Google Scholar]
- Blakemore, M. Blakemore Scattering of acoustic waves by the rough surface of an elastic solid. Ultrasonics 1993, 31, 161–174. [Google Scholar] [CrossRef]
- De Billy, M.; Quentin, G. Backscattering of acoustic waves by randomly rough surfaces of elastic solids immersed in water. J. Acoust. Soc. Am. 1982, 72, 591–601. [Google Scholar] [CrossRef]
- Kuperman, W.A.; Schmidt, H. Self-consistent perturbation approach to rough surface scattering in stratified elastic media. J. Acoust. Soc. Am. 1989, 86, 1511–1522. [Google Scholar] [CrossRef]
- Thorsos, E.I.; Jackson, D.R.; Williams, K.L. Modeling of subcritical penetration into sediments due to interface roughness. J. Acoust. Soc. Am. 1999, 107, 263–277. [Google Scholar] [CrossRef]
- Jackson, D.R.; Ivakin, A.N. Scattering from elastic sea beds: First-order theory. J. Acoust. Soc. Am. 1998, 103, 336–345. [Google Scholar] [CrossRef]
- Liu, J.Y.; Huang, C.F.; Hsueh, P.C. Acoustic plane-wave scattering from a rough surface over a random fluid medium. Ocean Eng. 2002, 29, 915–930. [Google Scholar] [CrossRef]
- Liu, J.Y.; Tsai, S.H.; Wang, C.C.; Chu, C.R. Acoustic wave reflection from a rough seabed with a continuously varying sediment layer overlying an elastic basement. J. Sound Vib. 2004, 275, 739–755. [Google Scholar] [CrossRef]
- Tang, D.; Jackson, D. A time-domain model for seafloor scattering. J. Acoust. Soc. Am. 2017, 142, 2968–2978. [Google Scholar] [CrossRef] [PubMed]
- Bjorno, L. Scattering of plane acoustic waves at elastic particles with rough surfaces. J. Acoust. Soc. Am. 2015, 137, 2439. [Google Scholar] [CrossRef]
- Neighbors, T.; Bradley, D. Applied Underwater Acoustics: Leif Bjørnø; Elsevier: Amsterdam, The Netherlands, 2017; ISBN 978-0-12-811247-2. [Google Scholar]
- Faran, J.J. Sound Scattering by Solid Cylinders and Spheres. J. Acoust. Soc. Am. 1951, 23, 405–418. [Google Scholar] [CrossRef]
- Flax, L.; Dragonette, L.R.; Überall, H. Theory of elastic resonance excitation by sound scattering. J. Acoust. Soc. Am. 1978, 63, 723–731. [Google Scholar] [CrossRef]
- Masood, F.; Amin, U.; Fiaz, M.A.; Ashraf, M.A. On relating the perturbation theory and random cylinder generation to study scattered field. Phys. Commun. 2020, 39, 101003. [Google Scholar] [CrossRef]
- Winebrenner, D.; Ishimaru, A. Investigation of a surface field phase perturbation technique for scattering from rough surfaces. Radio Sci. 1985, 20, 161–170. [Google Scholar] [CrossRef]
- Winebrenner, D.P.; Ishimaru, A. Application of the phase-perturbation technique to randomly rough surfaces. JOSA A 1985, 2, 2285–2294. [Google Scholar] [CrossRef]
- Broschat, S.L.; Tsang, L.; Ishimaru, A.; Thorsos, E.I. A Numerical Comparison of the Phase Perturbation Technique with the Classical Field Perturbation and Kirchhoff Approximations for Random Rough Surface Scattering. J. Electromagn. Waves Appl. 1988, 2, 85–102. [Google Scholar] [CrossRef]
- Broschat, S.L.; Thorsos, E.I.; Ishimaru, A. The Phase Perturbation Technique vs. an Exact Numerical Method for Random Rough Surface Scattering. J. Electromagn. Waves Appl. 2012. [Google Scholar] [CrossRef]
- Zhang, X.D.; Wu, Z.S.; Wu, C.K. A phase-perturbation technique for light scattering from randomly dielectric rough surfaces. Chin. Phys. Lett. 1997, 14, 32–35. [Google Scholar]
- Meecham, W.C. On the use of the Kirchhoff approximation for the solution of reflection problems. Eng. Res. Inst. Dep. Phys. Mich. Univ. 1955, 5, 323–334. [Google Scholar] [CrossRef][Green Version]
- Bouche, D.; Molinet, F.; Mittra, R. Asymptotic Methods in Electromagnetics; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Chungang, J.; Lixin, G.; Pengju, Y. Time-Domain Physical Optics Method for the Analysis of Wide-Band EM Scattering from Two-Dimensional Conducting Rough Surface. Available online: https://www.hindawi.com/journals/ijap/2013/584260/ (accessed on 21 September 2020).
- Dorval, V.; Chatillon, S.; Lu, B.; Darmon, M.; Mahaut, S. A general Kirchhoff approximation for echo simulation in ultrasonic NDT. AIP Conf. Proc. 2012, 1430, 193–200. [Google Scholar] [CrossRef]
- Darmon, M.; Leymarie, N.; Chatillon, S.; Mahaut, S. Modelling of Scattering of Ultrasounds by Flaws for NDT. In Ultrasonic Wave Propagation in Non Homogeneous Media; Springer: Berlin/Heidelberg, Germany, 2009; Volume 128, pp. 61–71. [Google Scholar]
- Lu, B.; Darmon, M.; Potel, C.; Zernov, V. Models Comparison for the scattering of an acoustic wave on immersed targets. J. Phys. Conf. Ser. 2012, 353, 012009. [Google Scholar] [CrossRef]
- Keller, J.B. Geometrical theory of diffraction. J. Opt. Soc. Am. 1962, 52, 116–130. [Google Scholar] [CrossRef]
- Darmon, M.; Chatillon, S.; Mahaut, S.; Fradkin, L.; Gautesen, A. Simulation of disoriented flaws in a TOFD technique configuration using GTD approach. In Proceedings of the 34th Annual Review of Progress in Quantitative Nondestructive Evaluation, Chicago, IL, USA, 20–25 July 2008; Volume 975, pp. 155–162. [Google Scholar]
- Chaffai, S.; Darmon, M.; Mahaut, S.; Menand, R. Simulations tools for TOFD inspection in Civa software. In Proceedings of the ICNDE 2007, Istanbul, Turkey, 15–20 April 2007. [Google Scholar]
- Darmon, M.; Ferrand, A.; Dorval, V.; Chatillon, S.; Lonné, S. Recent Modelling Advances for Ultrasonic TOFD Inspections. In AIP Conference Proceedings; AIP Publishing: College Park, MD, USA, 2015; Volume 1650, pp. 1757–1765. [Google Scholar]
- Chehade, S.; Kamta Djakou, A.; Darmon, M.; Lebeau, G. The spectral functions method for acoustic wave diffraction by a stress-free wedge: Theory and validation. J. Comput. Phys. 2019, 377, 200–218. [Google Scholar] [CrossRef]
- Chehade, S.; Darmon, M.; Lebeau, G. 2D elastic plane-wave diffraction by a stress-free wedge of arbitrary angle. J. Comput. Phys. 2019, 394, 532. [Google Scholar] [CrossRef]
- Ufimtsev, P.Y. Fundamentals of the Physical Theory of Diffraction; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Lü, B.; Darmon, M.; Fradkin, L.; Potel, C. Numerical comparison of acoustic wedge models, with application to ultrasonic telemetry. Ultrasonics 2016, 65, 5–9. [Google Scholar] [CrossRef]
- Zernov, V.; Fradkin, L.; Darmon, M. A refinement of the Kirchhoff approximation to the scattered elastic fields. Ultrasonics 2012, 52, 830–835. [Google Scholar] [CrossRef]
- Darmon, M.; Dorval, V.; Kamta Djakou, A.; Fradkin, L.; Chatillon, S. A system model for ultrasonic NDT based on the Physical Theory of Diffraction (PTD). Ultrasonics 2016, 64, 115–127. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Fradkin, L.J.; Darmon, M.; Chatillon, S.; Calmon, P. A semi-numerical model for near-critical angle scattering. J. Acoust. Soc. Am. 2016, 139, 141–150. [Google Scholar] [CrossRef] [PubMed]
- Djakou, A.K.; Darmon, M.; Fradkin, L.; Potel, C. The Uniform geometrical Theory of Diffraction for elastodynamics: Plane wave scattering from a half-plane. J. Acoust. Soc. Am. 2015, 138, 3272–3281. [Google Scholar] [CrossRef] [PubMed]
- Eckart, C. The Scattering of Sound from the Sea Surface. J. Acoust. Soc. Am. 1953, 25, 566–570. [Google Scholar] [CrossRef]
- Imbert, C. Visualisation Ultrasonore Rapide Sous Sodium Application Aux Reacteurs a Neutrons Rapides; INSA de Lyon: Villeurbanne, France, 1997. [Google Scholar]
- Wagner, R.J. Shadowing of Randomly Rough Surfaces. J. Acoust. Soc. Am. 1967, 41, 138–147. [Google Scholar] [CrossRef]
- Zverev, V.A.; Slavinskii, M.M. A method for calculating the acoustic field near a rough surface. Acoust. Phys. 1997, 43, 56–60. [Google Scholar]
- Chapman, D.M.F. An improved Kirchhoff formula for reflection loss at a rough ocean surface at low grazing angles. J. Acoust. Soc. Am. 1983, 73, 520–527. [Google Scholar] [CrossRef]
- Shi, F.; Choi, W.; Lowe, M.J.S.; Skelton, E.A.; Craster, R.V. The validity of Kirchhoff theory for scattering of elastic waves from rough surfaces. Proc. R. Soc. Math. Phys. Eng. Sci. 2015, 471, 20140977. [Google Scholar] [CrossRef]
- Haslinger, S.G. Elastic shear wave scattering by randomly rough surfaces. J. Mech. Phys. Solids 2020, 137, 103852. [Google Scholar] [CrossRef]
- Haslinger, S.G.; Lowe, M.J.S.; Huthwaite, P.; Craster, R.V.; Shi, F. Appraising Kirchhoff approximation theory for the scattering of elastic shear waves by randomly rough defects. J. Sound Vib. 2019, 460, 114872. [Google Scholar] [CrossRef]
- Opsal, J.L.; Visscher, W.M. Theory of elastic wave scattering: Applications of the method of optimal truncation. J. Appl. Phys. 1985, 58, 1102–1115. [Google Scholar] [CrossRef]
- Becache, E.; Joly, P.; Tsogka, C. An analysis of new mixed finite elements for the approximation of wave propagation problems. SIAM J. Numer. Anal. 2000, 37, 1053–1084. [Google Scholar] [CrossRef]
- Becache, E.; Joly, P.; Tsogka, C. Application of the fictitious domain method to 2D linear elastodynamic problems. J. Comput. Acoust. 2001, 9, 1175–1202. [Google Scholar]
- Huang, R.; Schmerr, L.W., Jr.; Sedov, A.; Gray, T.A. Kirchhoff approximation revisited—Some new results for scattering in isotropic and anisotropic elastic solids. Res. Nondestruct. Eval. 2006, 17, 137–160. [Google Scholar] [CrossRef]
- Darmon, M. Validity of the Kirchhoff Approximation for Small Flaws; CEA/DISC/LSMA: Saclay, France, 2014. [Google Scholar]
- Zhang, J.; Drinkwater, B.W.; Wilcox, P.D. Longitudinal Wave Scattering from Rough Crack-Like Defects. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 2171–2180. [Google Scholar] [CrossRef]
- Zernov, V.; Fradkin, L.; Gautesen, A.; Darmon, M.; Calmon, P. Wedge diffraction of a critically incident Gaussian beam. Wave Motion 2013, 50, 708–722. [Google Scholar] [CrossRef]
- Zernov, V.; Gautesen, A.; Fradkin, L.J.; Darmon, M. Aspects of diffraction of a creeping wave by a back-wall crack. J. Phys. Conf. Ser. 2012, 353, 012017. [Google Scholar] [CrossRef]
- Mahaut, S.; Huet, G.; Darmon, M. Modeling of Corner Echo in UT Inspection Combining Bulk and Head Waves Effect. In Proceedings of the 35th Annual Review of Progress in Quantitative Nondestructive Evaluation, 35th Annual Review of Progress in Quantitative Nondestructive Evaluation, Chicago, IL, USA, 20–25 July 2008; Volume 1096, pp. 73–80. [Google Scholar]
- Fradkin, L.J.; Djakou, A.K.; Prior, C.; Darmon, M.; Chatillon, S.; Calmon, P.-F. The Alternative Kirchhoff Approximation in Elastodynamics with Applications in Ultrasonic Nondestructive Testing. ANZIAM J. 2020, 1–17. [Google Scholar] [CrossRef]
- Ferrand, A.; Darmon, M.; Chatillon, S.; Deschamps, M. Modeling of ray paths of head waves on irregular interfaces in TOFD inspection for NDE. Ultrasonics 2014, 54, 1851–1860. [Google Scholar] [CrossRef]
- Bjorno, L.; Sun, S. Use of the Kirchhoff Approximation in Scattering from Elastic, Rough Surfaces. Acoust. Phys. 1995, 41, 637–648. [Google Scholar]
- Dacol, D.K. The Kirchhoff approximation for acoustic scattering from a rough fluid–elastic solid interface. J. Acoust. Soc. Am. 1998, 88, 978. [Google Scholar] [CrossRef]
- Gavrilov, A.L.; Dunin, S.Z.; Maskomov, G.A. Scattering of scalar fields by hard and soft rough surfaces. Angular distribution of intensity. Akust. Zhurnal 1992, 38, 861–873. [Google Scholar]
- Ploix, M.-A.; Kauffmann, P.; Chaix, J.-F.; Lillamand, I.; Baqué, F.; Corneloup, G. Acoustical properties of an immersed corner-cube retroreflector alone and behind screen for ultrasonic telemetry applications. Ultrasonics 2020, 106. [Google Scholar] [CrossRef] [PubMed]
- Darmon, M.; Chatillon, S. Main Features of a Complete Ultrasonic Measurement Model: Formal Aspects of Modeling of Both Transducers Radiation and Ultrasonic Flaws Responses. Open J. Acoust. 2013, 3, 36873. [Google Scholar] [CrossRef]
- Mahaut, S.; Darmon, M.; Chatillon, S.; Jenson, F.; Calmon, P. Recent advances and current trends of ultrasonic modelling in CIVA. Insight 2009, 51, 78–81. [Google Scholar] [CrossRef]
- Isakson, M.J.; Chotiros, N.P. Finite Element Modeling of Acoustic Scattering from Fluid and Elastic Rough Interfaces. IEEE J. Ocean. Eng. 2015, 40, 475–484. [Google Scholar] [CrossRef]
- Botten, L.C.; Cadilhac, M.; Derrick, G.H.; Maystre, D.; McPhedran, R.C.; Nevière, M.; Vincent, P. Electromagnetic Theory of Gratings; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 22. [Google Scholar]
- Richards, E.L.; Song, H.C.; Hodgkiss, W.S. Acoustic scattering comparison of Kirchhoff approximation to Rayleigh-Fourier method for sinusoidal surface waves at low grazing angles. J. Acoust. Soc. Am. 2018, 144, 1269–1278. [Google Scholar] [CrossRef]
- Williams, K.L.; Stroud, J.S.; Marston, P.L. High-frequency forward scattering from Gaussian spectrum, pressure release, corrugated surfaces. I. Catastrophe theory modeling. J. Acoust. Soc. Am. 1994, 96, 1687–1702. [Google Scholar] [CrossRef]
- Kur’yanov, B.F. The scattering of sound at a rough surface with two types of irregularity. Sov. Phys. Acoust. 1963, 8, 252–257. [Google Scholar]
- McDaniel, S.T.; Gorman, A.D. An examination of the composite-roughness scattering model. J. Acoust. Soc. Am. 1983, 73, 1476–1486. [Google Scholar] [CrossRef]
- Bachmann, W. A theoretical model for the backscattering strength of a composite-roughness sea surface. J. Acoust. Soc. Am. 2005, 54, 712. [Google Scholar] [CrossRef]
- Lemaire, D.; Sobieski, P.; Craeye, C.; Guissard, A. Two-scale models for rough surface scattering: Comparison between the boundary perturbation method and the integral equation method. Radio Sci. 2002, 37, 1–16. [Google Scholar] [CrossRef]
- Novarini, J.C.; Caruthers, J.W. The partition wavenumber in acoustic backscattering from a two-scale rough surface described by a power-law spectrum. IEEE J. Ocean. Eng. 1994, 19, 200–207. [Google Scholar] [CrossRef]
- Jones, A.D.; Sendt, J.S.; Duncan, A.J.; Zhang, Y.; Clarke, P.A.B. Modelling Acoustic Reflection Loss at the Ocean Surface—An Australian Study. Available online: /paper/Modelling-Acoustic-Reflection-Loss-at-the-Ocean-an-Jones-Sendt/697e50ae9aae2ed887353067e825c9b31bad19bc (accessed on 2 June 2020).
- Voronovich, A.G. Small slope approximation in wave scattering theory for rough surfaces. Zhurnal Eksp. Teor. Fiz. 1985, 89, 116–125. [Google Scholar]
- Voronovich, A. Small-slope approximation for electromagnetic wave scattering at a rough interface of two dielectric half-spaces. Waves Random Media 1994, 4, 337–367. [Google Scholar] [CrossRef]
- Voronovich, A.G. Non-local small-slope approximation for wave scattering from rough surfaces. Waves Random Media 1996, 6, 151–167. [Google Scholar] [CrossRef]
- McDaniel, S.T. A small-slope theory of rough surface scattering. J. Acoust. Soc. Am. 1994, 95, 1858–1864. [Google Scholar] [CrossRef]
- Thorsos, E.I.; Broschat, S.L. An investigation of the small slope approximation for scattering from rough surfaces. Part I. Theory. J. Acoust. Soc. Am. 1995, 97, 2082–2093. [Google Scholar] [CrossRef]
- Broschat, S.L.; Thorsos, E.I. An investigation of the small slope approximation for scattering from rough surfaces. Part II. Numerical studies. J. Acoust. Soc. Am. 1997, 101, 2615–2625. [Google Scholar] [CrossRef]
- Salin, M.B.; Dosaev, A.S.; Konkov, A.I.; Salin, B.M. Numerical simulation of Bragg scattering of sound by surface roughness for different values of the Rayleigh parameter. Acoust. Phys. 2014, 60, 442–454. [Google Scholar] [CrossRef]
- Yang, T.; Broschat, S.L. Acoustic scattering from a fluid–elastic-solid interface using the small slope approximation. J. Acoust. Soc. Am. 1994, 96, 1796–1804. [Google Scholar] [CrossRef]
- Berman, D.H. Simulations of rough interface scattering. J. Acoust. Soc. Am. 1991, 89, 623–636. [Google Scholar] [CrossRef]
- Jackson, D.; Olson, D.R. The small-slope approximation for layered, fluid seafloors. J. Acoust. Soc. Am. 2020, 147, 56–73. [Google Scholar] [CrossRef] [PubMed]
- Jackson, D. The small-slope approximation for layered seabeds. Proc. Meet. Acoust. 2013, 19, 070001. [Google Scholar] [CrossRef]
- Berrouk, A.; Dusseaux, R.; Afifi, S. Electromagnetic Wave Scattering from Rough Layered Interfaces: Analysis with the Small Perturbation Method and the Small Slope Approximation. Prog. Electromagn. Res. 2014, 57, 177–190. [Google Scholar] [CrossRef]
- Afifi, S.; Dusséaux, R.; Berrouk, A. Electromagnetic Scattering from 3D Layered Structures with Randomly Rough Interfaces: Analysis With the Small Perturbation Method and the Small Slope Approximation. IEEE Trans. Antennas Propag. 2014, 62, 5200–5208. [Google Scholar] [CrossRef]
- Dusséaux, R.; Afifi, S.; Dechambre, M. Scattering properties of a stratified air/snow/sea ice medium. Small slope approximation. Comptes Rendus Phys. 2016, 17, 995–1002. [Google Scholar] [CrossRef]
- Collins, M.D. A split-step Padé solution for the parabolic equation method. J. Acoust. Soc. Am. 1993, 93, 1736–1742. [Google Scholar] [CrossRef]
- Gao, Y.; Shao, Q.; Yan, B.; Li, Q.; Guo, S. Parabolic Equation Modeling of Electromagnetic Wave Propagation over Rough Sea Surfaces. Sensors 2019, 19, 1252. [Google Scholar] [CrossRef] [PubMed]
- Thorsos, E.I. Rough surface scattering using the parabolic wave equation. J. Acoust. Soc. Am. 1987, 82, S103. [Google Scholar] [CrossRef]
- Ramsurf Website. Available online: https://github.com/quiet-oceans/ramsurf (accessed on 17 October 2019).
- Modeling Reflection Loss of the Gaussian Rough Ocean Surface—IEEE Conference Publication. Available online: https://ieeexplore.ieee.org/document/8559454 (accessed on 11 October 2019).
- Jones, A.D.; Duncan, A.J.; Maggi, A.L.; Bartel, D.W.; Zinoviev, A. A Detailed Comparison between a Small-Slope Model of Acoustical Scattering from a Rough Sea Surface and Stochastic Modeling of the Coherent Surface Loss. IEEE J. Ocean. Eng. 2016, 41, 689–708. [Google Scholar] [CrossRef]
- Spivack, M.; Rath Spivack, O. Rough Surface Scattering via Two-Way Parabolic Integral Equation. Prog. Electromagn. Res. 2017, 56, 81–90. [Google Scholar] [CrossRef][Green Version]
- Huet, G.; Darmon, M.; Lhemery, A.; Mahaut, S. Modelling of Corner Echo Ultrasonic Inspection with Bulk and Creeping Waves. In 5th Meeting of the Anglo-French-Research-Group; Léger, A., Deschamps, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 128, pp. 217–226. [Google Scholar]
- Ferrand, A. Développement de Modèles Asymptotiques en Contrôle Non Destructif (CND) par Ultrasons: Interaction des Ondes Elastiques Avec des Irrégularités Géométriques et Prise en Compte des Ondes de Tête. Ph.D. Thesis, Université Sciences et Technologies, Bordeaux, France, 2014. [Google Scholar]
- Zhou, H.; Chen, X. Ray path of head waves with irregular interfaces. Appl. Geophys. 2010, 7, 66–73. [Google Scholar] [CrossRef]
- Olson, D.R. Numerical investigation of the two-scale model for rough surface scattering. J. Acoust. Soc. Am. 2019, 145, 1770. [Google Scholar] [CrossRef]
- Rath Spivack, O.; Spivack, M. Efficient boundary integral solution for acoustic wave scattering by irregular surfaces. Eng. Anal. Bound. Elem. 2017, 83, 275–280. [Google Scholar] [CrossRef]
- Li, C.; Campbell, B.K.; Liu, Y.; Yue, D.K.P. A fast multi-layer boundary element method for direct numerical simulation of sound propagation in shallow water environments. J. Comput. Phys. 2019, 392, 694–712. [Google Scholar] [CrossRef]
- Lee, S.; Pegues, J.W.; Shamsaei, N. Fatigue behavior and modeling for additive manufactured 304L stainless steel: The effect of surface roughness. Int. J. Fatigue 2020, 141, 105856. [Google Scholar] [CrossRef]
- Knezović, N.; Topić, A. Wire and Arc Additive Manufacturing (WAAM)—A New Advance in Manufacturing. In Lecture Notes in Networks and Systems; Springer International Publishing: New York, NY, USA, 2019; pp. 65–71. ISBN 978-3-319-90892-2. [Google Scholar]
- Gu, D.D.; Meiners, W.; Wissenbach, K.; Poprawe, R. Laser additive manufacturing of metallic components: Materials, processes and mechanisms. Int. Mater. Rev. 2012, 57, 133–164. [Google Scholar] [CrossRef]
- Gorsse, S.; Hutchinson, C.; Gouné, M.; Banerjee, R. Additive manufacturing of metals: A brief review of the characteristic microstructures and properties of steels, Ti-6Al-4V and high-entropy alloys. Sci. Technol. Adv. Mater. 2017, 18, 584–610. [Google Scholar] [CrossRef]
- Tian, H.; Lu, Z.; Li, F.; Chen, S. Predictive Modeling of Surface Roughness Based on Response Surface Methodology after WAAM; Atlantis Press: Paris, France, 2019; pp. 47–50. [Google Scholar]
- NUTALN. Finition de Surface de Pièces Produites par Fabrication. Additive. Available online: https://www.techniques-ingenieur.fr/base-documentaire/42687210-chaine-de-valeur-et-mise-en-uvre/download/bm7960/finition-de-surface-de-pieces-produites-par-fabrication-additive.html (accessed on 20 October 2020).
- Gharbi, M.; Peyre, P.; Gorny, C.; CARIN, M.; Morville, S.; LE MASSON, P.; CARRON, D.; Fabbro, R. Influence of various process conditions on surface finishes induced by the direct metal deposition laser technique on a Ti-6Al-4V alloy. J. Mater. Process. Technol. 2012, 213, 791–800. [Google Scholar] [CrossRef]
- Xiong, J.; Li, Y.-J.; Yin, Z.-Q.; Chen, H. Determination of Surface Roughness in Wire and Arc Additive Manufacturing Based on Laser Vision Sensing. Chin. J. Mech. Eng. 2018, 31, 74. [Google Scholar] [CrossRef]
- Sanviemvongsak, T.; Monceau, D.; Macquaire, B. High temperature oxidation of IN 718 manufactured by laser beam melting and electron beam melting: Effect of surface topography. Corros. Sci. 2018, 141, 127–145. [Google Scholar] [CrossRef]
- Taheri, H.; Koester, L.; Bigelow, T.; Bond, L.J. Finite element simulation and experimental verification of ultrasonic non-destructive inspection of defects in additively manufactured materials. AIP Conf. Proc. 2018, 1949, 020011. [Google Scholar] [CrossRef]
- Van Pamel, A.; Nagy, P.B.; Lowe, M.J.S. On the dimensionality of elastic wave scattering within heterogeneous media. J. Acoust. Soc. Am. 2016, 140, 4360–4366. [Google Scholar] [CrossRef] [PubMed]
- Ryzy, M.; Grabec, T.; Sedlák, P.; Veres, I.A. Influence of grain morphology on ultrasonic wave attenuation in polycrystalline media with statistically equiaxed grains. J. Acoust. Soc. Am. 2018, 143, 219–229. [Google Scholar] [CrossRef]
- Bai, X.; Tie, B.; Schmitt, J.-H.; Aubry, D. Comparison of ultrasonic attenuation within two- and three-dimensional polycrystalline media. Ultrasonics 2020, 100, 105980. [Google Scholar] [CrossRef]
- OUDAA, M.; Lhuillier, P.-E.; Guy, P.; Leclere, Q. Finite element modeling of ultrasonic attenuation within polycrystalline materials in two and three dimensions. In Proceedings of the 2019 International Congress on Ultrasonics, Bruges, Belgium, 3–6 September 2019. [Google Scholar]
- Komatitsch, D.; Tromp, J. Introduction to the spectral element method for three-dimensional seismic wave propagation. Geophys. J. Int. 1999, 139, 806–822. [Google Scholar] [CrossRef]
- Casadei, F.; Gabellini, E.; Fotia, G.; Maggio, F.; Quarteroni, A. A mortar spectral/finite element method for complex 2D and 3D elastodynamic problems. Comput. Methods Appl. Mech. Eng. 2002, 191, 5119–5148. [Google Scholar] [CrossRef]
- Imperiale, A.; Chatillon, S.; Darmon, M.; Leymarie, N.; Demaldent, E. UT simulation using a fully automated 3D hybrid model: Application to planar backwall breaking defects inspection. AIP Conf. Proc. 2018, 1949, 050004. [Google Scholar] [CrossRef]
- Yu, T.; Chaix, J.-F.; Audibert, L.; Komatitsch, D.; Garnier, V.; Henault, J.-M. Simulations of ultrasonic wave propagation in concrete based on a two-dimensional numerical model validated analytically and experimentally. Ultrasonics 2019, 92, 21–34. [Google Scholar] [CrossRef]
- Hériveaux, Y.; Nguyen, V.-H.; Haïat, G. Reflection of an ultrasonic wave on the bone-implant interface: A numerical study of the effect of the multiscale roughness. J. Acoust. Soc. Am. 2018, 144, 488–499. [Google Scholar] [CrossRef] [PubMed]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Darmon, M.; Dorval, V.; Baqué, F. Acoustic Scattering Models from Rough Surfaces: A Brief Review and Recent Advances. Appl. Sci. 2020, 10, 8305. https://doi.org/10.3390/app10228305
Darmon M, Dorval V, Baqué F. Acoustic Scattering Models from Rough Surfaces: A Brief Review and Recent Advances. Applied Sciences. 2020; 10(22):8305. https://doi.org/10.3390/app10228305
Chicago/Turabian StyleDarmon, Michel, Vincent Dorval, and François Baqué. 2020. "Acoustic Scattering Models from Rough Surfaces: A Brief Review and Recent Advances" Applied Sciences 10, no. 22: 8305. https://doi.org/10.3390/app10228305
APA StyleDarmon, M., Dorval, V., & Baqué, F. (2020). Acoustic Scattering Models from Rough Surfaces: A Brief Review and Recent Advances. Applied Sciences, 10(22), 8305. https://doi.org/10.3390/app10228305





