Abstract
To apply deep learning to estimate the three-dimensional interaction position of a Cherenkov detector, an experimental measurement of the true depth of interaction is needed. This requires significant time and effort. Therefore, in this study, we propose a direct annihilation position classification method based on deep learning using paired Cherenkov detectors. The proposed method does not explicitly estimate the interaction position or time-of-flight information and instead directly estimates the annihilation position from the raw data of photon information measured by paired Cherenkov detectors. We validated the feasibility of the proposed method using Monte Carlo simulation data of point sources. A total of 125 point sources were arranged three-dimensionally with 5 mm intervals, and two Cherenkov detectors were placed face-to-face, 50 mm apart. The Cherenkov detector consisted of a monolithic PbF2 crystal with a size of 40 × 40 × 10 mm3 and a photodetector with a single photon time resolution (SPTR) of 0 to 100 picosecond (ps) and readout pitch of 0 to 10 mm. The proposed method obtained a classification accuracy of 80% and spatial resolution with a root mean square error of less than 1.5 mm when the SPTR was 10 ps and the readout pitch was 3 mm.
1. Introduction
Clinical time-of-flight positron emission tomography (TOF-PET) scanners with 200–600 picosecond (ps) coincidence time resolution (CTR) have been developed [1,2,3]. In laboratory studies, CTR has approached ~30 ps at the detector level [4,5]. TOF information determines the annihilation position on the coincidence line connecting the two interaction positions of γ-rays with detectors, with the position uncertainty , where c is the speed of light and is the CTR. For example, if = 200 ps, = 30 mm. Although the position uncertainty of 30 mm is not comparable to the spatial resolution of clinical PET scanners (4–6 mm), the signal-to-noise ratio of the reconstructed image can be improved depending on the CTR and patient size using the TOF information in the reconstruction process [3]. If we could develop a TOF-PET detector with 26–40 ps CTR, corresponding to a position uncertainty of 4–6 mm, annihilation points could be determined event-by-event. Therefore, the image reconstruction process, which can amplify the noise of PET images, could be removed from the clinical PET.
Recently, Cherenkov radiation-based TOF-PET detectors have been developed [6,7,8]. Because the emission of the Cherenkov photon is as fast as a few ps, the detection of Cherenkov photons could potentially approach 10 ps CTR [9]. However, to stop the γ-ray using the Cherenkov radiator, such as a monolithic lead fluoride (PbF2) crystal with the same detection efficiency as a lutetium-based scintillator, thicker crystal is needed, for example, 20 mm. As the radiator thickness increases, the depth of interaction (DOI) of γ-rays causes timing errors because of the propagation speed difference between γ-rays and photons in crystals [10,11,12]. Thus, to achieve an extremely good CTR on the order of 10 ps, both TOF and DOI information will be needed. However, as fewer than 30 Cherenkov photons are produced by the 511 keV γ-ray [9,13], DOI estimation becomes challenging. Hence, DOI estimation methods based on machine learning have been developed for Cherenkov detectors [8,14]. Although the machine learning approach enables the Cherenkov detector to estimate DOI, it requires a dataset equipped with correct DOI. The measurement of the correct DOI for the Cherenkov detector requires substantial time and effort. Some methods that can be used to avoid this problem have been developed in detectors based on a monolithic scintillator [15,16,17,18]. However, these methods could not be applied to the monolithic Cherenkov detector. From a different point of view, the cause of the problem could be that we try to indirectly estimate the annihilation position from the TOF and DOI. If we can estimate the annihilation position directly from the spatial and temporal photon distribution measured by a pair of Cherenkov detectors, there would be no need to estimate the DOI in the first place.
In this study, we propose a direct annihilation position classification based on deep learning using paired Cherenkov detectors. We estimate the annihilation position directly from the photon information measured by paired Cherenkov detectors using deep learning instead of intermediate estimation of TOF and DOI. Deep learning is a powerful tool that has attracted the interest of researchers in the medical imaging field [19,20,21]. Recently, deep learning has been used to process raw data bypassing image reconstruction, such as ghost cytometry [22] or sinogram-space machine learning [23]. In the same spirit, we use deep learning to bypass the intermediate estimation of DOI and TOF and estimate the annihilation position directly from the raw data of photon information measured by paired Cherenkov detectors. We performed a Monte Carlo simulation with 125 point sources and trained a deep neural network (DNN) predicting the point source from which the γ-ray pair originated based on the photon information captured by paired Cherenkov detectors. We evaluated a classification accuracy and point spread function (PSF) over various single photon time resolutions (SPTR) and readout pitches. The point source position can be determined easily even in the experiment so that the above problem concerning the measurement of correct DOI is eliminated.
2. Materials and Methods
2.1. Paired Detectors
Figure 1 shows the paired Cherenkov detectors used in this study. The two Cherenkov detectors were placed face-to-face, 50 mm apart. The origin of the coordinate system, (x, y, z) = (0, 0, 0), was defined at the center of the detector plane for (x, y) and at the center between the pair of the detectors at the z-axis, as shown in Figure 1. For the Cherenkov radiator, we used a monolithic PbF2 crystal with a size of 40 × 40 × 10 mm3 in the (x, y, z) direction. The PbF2 crystal is appropriate as a Cherenkov radiator because it has a high density, high refractive index, and transparency toward the UV region, as shown in Table 1 [24,25]. Each photodetector was topped with 300-μm-thick protection resin (n = 1.5), and the photodetector array was connected to a radiator by 100-μm-thick grease, as shown in Figure 1. All crystal surfaces were painted black to reduce the number of reflections, except the surface where a photodetector array was coupled. As stated in the previous section, because the number of Cherekov photons is small, the position–time information of all photons should be read out individually to fully utilize limited information.
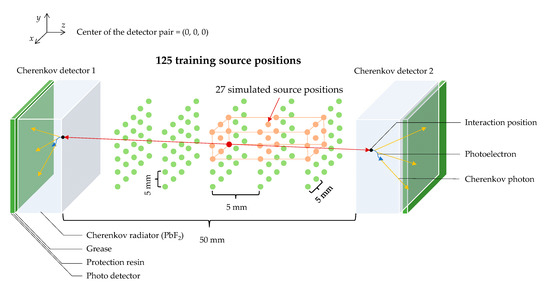
Figure 1.
Paired Cherenkov detectors and 125 training source positions. Two Cherenkov detectors were placed face-to-face, 50 mm apart. The origin of the coordinate system, (x, y, z) = (0, 0, 0), was defined at the center of the detector plane for (x, y) and at the center between the pair of the detectors at the z-axis. A monolithic PbF2 crystal with a 40 × 40 × 10 mm3 Cherenkov radiator was coupled to a photodetector array through 300-μm-thick protection resin (n = 1.5) with grease (n = 1.5).

Table 1.
Optical properties of PbF2 crystal.
For practical consideration, we modeled an SPTR of the photodetector as a Gaussian distribution of σ = 0 to 100 ps in intervals of 10 ps. The 10 ps SPTR is possible for MCP-PMT [26], but 50–100 ps is realistic for silicon photomultipliers (SiPM) [27]. Further, we changed the readout pitch of the photodetector in the range of 0 to 10 mm with an interval of 1 mm. The photodetection efficiency (PDE) was assumed to be 100 % for simplicity. The PDE does not affect whether the direct annihilation position classification is possible, although it affects the sensitivity of the system. The photon detection threshold was assumed to be five, except in the detection efficiency study, to confirm the feasibility of our proposed method under the same conditions as our previous studies [8,14], wherein the same photon detection threshold value was employed.
2.2. Simulation Dataset
A Monte Carlo simulation was performed to create a dataset using Geant4 [28] with the same physical parameters as in Ota et al. [8], except for the detector dimension. The Geant4 Livermore libraries were used for low-energy electromagnetic processes; both the photoelectric effect and Compton scattering were implemented according to Brunner et al. [29]. Geant4 has a maximum step length (MSL) parameter that balances the accuracy and computation time for particle tracking. For simulation with Cherenkov effects in the low-energy region, an appropriate setting of the MSL is important. We set the MSL to 1 μm. The optical properties of PbF2, for example, the transmittance, refractive index, and density, were determined based on the definition of Anderson et al. [24] and the Refractive Index Database [30].
Figure 1 shows a simulation setup of a paired Cherenkov detector and 125 training source positions. The two Cherenkov detectors were placed face-to-face, 50 mm apart. The origin of the coordinate system, (x, y, z) = (0, 0, 0), was defined at the center of the detector plane for (x, y) and at the center between the pair of the detectors at the z-axis, as shown in Figure 1. A total of 107 emissions of the γ-ray pair were performed at each source position, where x, y, and z were scanned from 0 to 10 mm in intervals of 5 mm. Thus, the 3 × 3 × 3 = 27 source positions in the first quadrant were simulated, as shown in the red rectangle of Figure 1. By utilizing symmetry, 98 source positions were replicated from those of the 27 source positions, as shown by the green dots in Figure 1. For example, by flipping the sign of x for the detected photon information, the simulation data of the source position (x, y, z) = (−5, 0, 0) can be generated from the simulation data of the source position (x, y, z) = (5, 0, 0). Thus, 125 (53) source positions were simulated in total. The momentum direction of the γ-ray pair was randomly determined against the polar and azimuth angles, which were varied from −π/4 to +π/4 and 0 to 2π, respectively.
In all simulations, we recorded the following information event-by-event.
- (xs, ys, zs): true source position.
- N, M, 5 ≤ N, 5 ≤ M: number of photons reaching the photodetector plane of Cherenkov detectors 1 and 2, respectively.
- (x1n, y1n, t1n), (x2m, y2m, t2m), 1 ≤ n ≤ N, 1 ≤ m ≤ M: xy position and time information for each photon reaching the photodetector plane of Cherenkov detectors 1 and 2, respectively, where the smaller of t11 and t21 is 0 s.
As the photon detection threshold was assumed to be five, a total of 227,005 coincidence events in which both detectors detected more than five Cherenkov photons were obtained. This number was only 0.02 % of all γ-ray pair emissions. We split this set to assign 75% for training and 25% for testing. To increase the number of coincidence events in the training dataset, we extracted the NC5 × MC5 events from coincidence events that were 6 ≤ N or 6 ≤ M. For example, in the case of N = 6 and M = 6, we could extract 36 coincidence events in which N = 5 and M = 5. For the test dataset, we extracted information for the first five photons from each single event, constructing the coincidence event that is 6 ≤ N or 6 ≤ M. It is known that if the number of data in each class is imbalanced, the performance of the classifier may deteriorate. Therefore, we applied the under-sampling technique [31]. The number of coincidence events for each source position was under-sampled to the minimum number of coincidence events between each source position. In the results, the training and testing datasets had 6,666,375 and 39,625 coincidence events, respectively.
To monitor the training, we considered 90% of the training dataset as an actual training dataset and 10% of the training dataset as the validation dataset.
2.3. Network Architecture
We propose the multilayer perceptron (MLP) architecture illustrated in Figure 2 for the direct classification of the annihilation position from the input data of paired Cherenkov detectors. The proposed MLP consists of an input layer, three hidden layers, and an output layer. The input layer receives the xy position and time information of each photon measured by Cherenkov detectors 1 and 2, respectively. In this study, as we assumed a photon detection threshold of five for each Cherenkov detector, the input layer has thirty units, as shown in Figure 2. The input units are affine transformed to a hidden layer with 256 units. Each unit of the hidden layer is normalized by batch-normalization [32] and activated by a rectified linear unit (ReLU) [33]. A similar process is repeated for each hidden layer. Finally, the final hidden layer is affine transformed to the output layer. The output units are activated by the soft-max function. We used cross-entropy as a loss function.
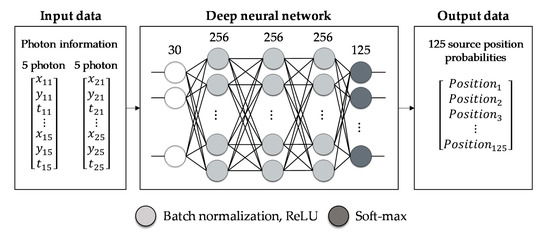
Figure 2.
Multi-layer perceptron (MLP) architecture for direct classification of annihilation position from photon information measured by paired Cherenkov detectors.
Training was performed on a computer running Ubuntu 16.04 with a graphical processing unit (NVIDIA GeForce GTX 1080 with 8 GB of memory) using a Chainer 6.0.0 [34]. Each variable of input data was standardized with zero mean and unit variance by a standard-scaler function of the sci-kit learn library [35]. We performed 100 epochs of training using the Adam method [36] and weight decay of 10−4 as regularization.
2.4. Evaluation Methods
2.4.1. Classification Accuracy
The classification accuracies defined below were measured for each SPTR and readout pitch.
where is the number of coincidence events in the test dataset and is the true label. In this study, was 39,625.
2.4.2. Confusion Matrix
To visualize how MLP performed misclassification, we summarized all predictions for the test dataset in the confusion matrix [37] defined below.
where is a predicted label. The confusion matrix represents the number of events predicted as . If all events were classified correctly, they were collected in the diagonal element of the confusion matrix. As we have 125 labels consisting of 5 (x) × 5 (y) × 5 (z), we created a 5 × 5 confusion matrix for each direction x, y, and z.
2.4.3. Point Spread Function
To visualize the PSF, we estimated the continuous-valued annihilation position as the center of gravity of the probability output by the MLP.
where (, , ) is the estimated continuous-valued annihilation position and Positions is the predicted probability that the coincidence event came from the source position (xs, ys, zs).
As a measure of spatial resolution, the root mean square errors (RMSE) of the x-, y-, and z-position estimation were calculated as those in Tabacchini et al. [38].
2.4.4. Detection Efficiency
To evaluate the system sensitivity, the γ-ray pair detection efficiency defined below was calculated.
where τ is the photon detection threshold and Nemission is the number of γ-ray pair emissions. In this study, Nemission was 1.25 × 109 (125 × 107).
3. Results
Figure 3 shows the training and validation loss curves at an SPTR of 0 ps and a readout pitch of 0 mm, and an SPTR of 10 ps and readout pitch of 3 mm, respectively. The differences between training and validation loss were small, so there was no overfitting of the MLP for each condition.
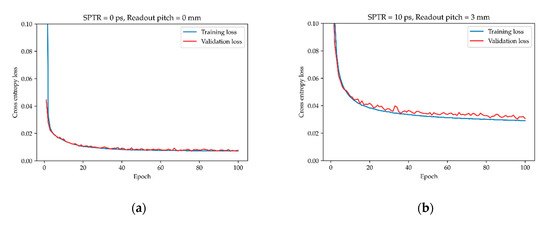
Figure 3.
Training and validation loss curves at an (a) single photon time resolution (SPTR) of 0 ps and readout pitch of 0 mm, and (b) SPTR of 10 ps and readout pitch of 3 mm, respectively.
3.1. Classification Accuracy
Figure 4 shows the classification accuracy relative to the SPTR and readout pitch. Table 2 shows the classification accuracy for the representative conditions.
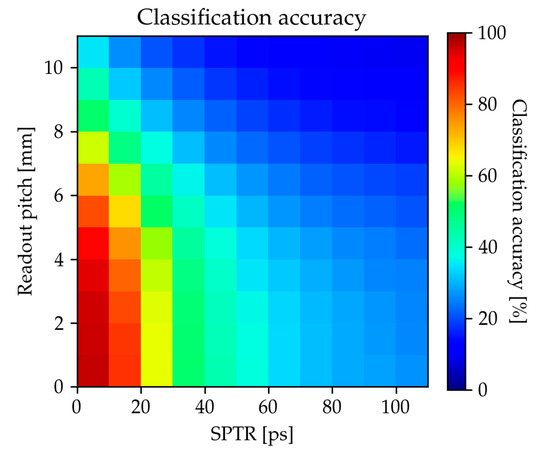
Figure 4.
Classification accuracy relative to SPTR and readout pitch.

Table 2.
Classification accuracy at representative conditions.
3.2. Confusion Matrix
Figure 5 shows the confusion matrix in the x- and z-directions. Figure 5a,b show the results at an SPTR of 10 ps and 100 ps, respectively. The results in the y-direction were omitted because of symmetry. The readout pitch was fixed at 3.0 mm. As the number of events in the test dataset was 39,625, the maximum number of events in diagonal elements was considered to be 7925. In the confusion matrix in the z-direction at an SPTR of 100 ps, the diagonal elements had expanded to nondiagonal elements.
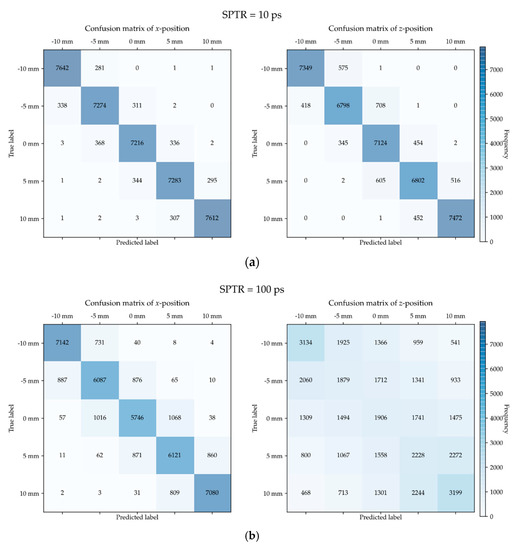
Figure 5.
Confusion matrix in the x- and z-directions at an SPTR of (a) 10 ps, and (b) 100 ps, respectively. Results in the y-direction were omitted because these were almost same as those in the x-direction. Readout pitch was fixed at 3 mm. As the number of events in the test dataset was 39,625, the maximum number of events in diagonal elements is considered to be 7925.
3.3. Point-Spread-Function
Figure 6a,b show the PSF as an error distribution of the estimated continuous-valued annihilation position at an SPTR of 10 ps and 100 ps, respectively. The readout pitch was fixed at 3 mm. Figure 6c,d show the projection of the PSF on the x- and z-axis, respectively. Results on the y-axis were omitted because they were very similar to those on the x-axis. There were side peaks at ±5 mm, as shown in Figure 6c. The PSF was blurred especially along the z-direction at an SPTR of 100 ps, as shown in Figure 6c.
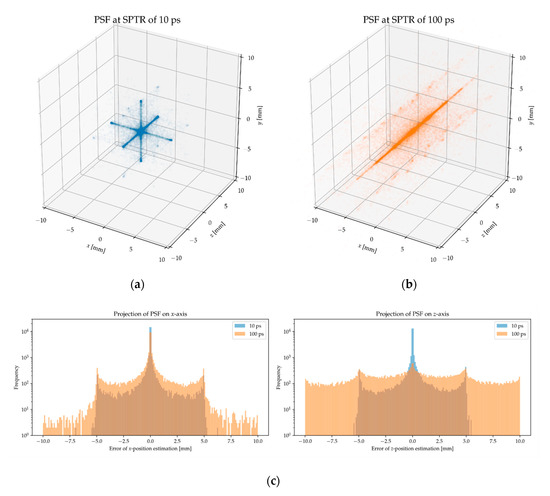
Figure 6.
Point spread function (PSF) as an error distribution between the true and estimated source position at an SPTR of (a) 10 ps and (b) 100 ps, respectively. (c) Projection of PSF on the x-and z-axes. Results on the y-axis were omitted because they were very similar to those on the x-axis. Readout pitch was fixed at 3 mm.
Figure 7a,b show the RMSE of the x-and z-position estimations, respectively, relative to the SPTR and readout pitch. The results of the y-position estimation were omitted because they were very similar to those of the x-position estimation. As shown in Figure 7a, the RMSE of the x-position estimation was almost the same for a readout pitch of 0 to 3 mm. As shown in Figure 7b, the RMSE of the z-position estimation was almost the same for all readout pitches. Table 3 shows the RMSE under representative conditions.
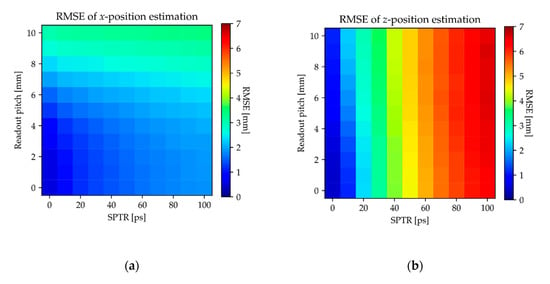
Figure 7.
Root mean square error (RMSE) of (a) x- and (b) z-position estimation, respectively, relative to the SPTR and readout pitch. The results of y-position estimation were omitted because these were very similar to those of x-position estimation.

Table 3.
RMSE at representative conditions.
3.4. Detection Efficiency
Figure 8 shows the detection efficiency for the γ-ray pair emission by the Cherenkov detector pair used in this study. For a photon detection threshold of 1, the detection efficiency was 4.3%.
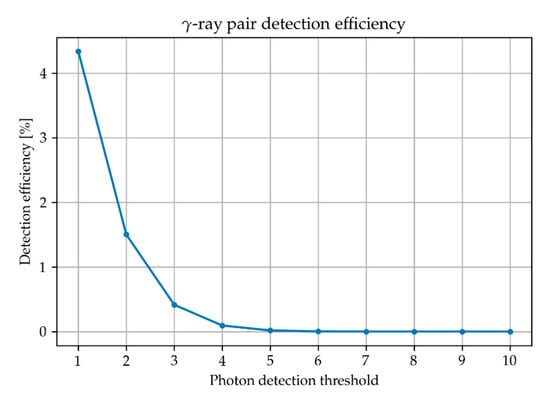
Figure 8.
Detection efficiency of the paired Cherenkov detectors for the γ-ray pair emission.
4. Discussion
We validated the feasibility of direct annihilation position classification based on DNNs from photon information measured by paired Cherenkov detectors. We used Monte Carlo simulation data of 125 point sources for validation. In addition, we evaluated the influence of the SPTR and readout pitch on the classification accuracy and spatial resolution.
The classification accuracy was 96% at ideal conditions where the SPTR was 0 ps and the readout pitch was 0 mm (Table 2). This indicates that the proposed method is feasible under ideal conditions. As the classification accuracies of the readout pitch of 0 to 3 mm were almost the same (Figure 4), a readout pitch of 3 mm was considered to be adequate. In contrast, the classification accuracies dropped rapidly as the SPTR worsened. To maintain a classification accuracy of 80%, the SPTR must be 10 ps or less (Figure 4). In addition, we evaluated the confusion matrix to determine whether the MLP made major mistakes, because classification accuracy as the figure of merit does not distinguish between major and minor mistakes. When the SPTR was 10 ps and the readout pitch was 3 mm, misclassification was concentrated on the adjacent positions (Figure 5a). This can be interpreted as evidence that the MLP rarely made major mistakes in these conditions. In contrast, as the SPTR worsened to 100 ps, the misclassification was broadly distributed in the z-direction (Figure 5b). These results indicate that an SPTR of 10 ps or less is preferable in view of the magnitude of misclassification.
To better understand the effects of the SPTR and readout pitch, we visualized the PSF by estimating the continuous-valued annihilation position as the center of gravity of the probability output by the MLP (Figure 6). When the SPTR was 10 ps and the readout pitch was 3 mm, the PSF was isotropic (Figure 6a). The magnitudes of misclassification in the x-, y-,and z-directions were almost equal and concentrated in adjacent positions. In contrast, as the SPTR worsened to 100 ps, the PSF was elongated in a bar shape along the z-direction (Figure 6b). This can be interpreted as an indication that the SPTR has a greater effect in the z-direction than in the x- and y-directions. The projections of the PSF on the x- and z-axis show that the shape of the PSF was sharp and had side peaks (Figure 6c). This means that Gaussian fitting is not adequate for analysis of the spatial resolution. Hence, we calculated the RMSE to determine spatial resolution as in Tabacchini et al. [38]. The RMSE of the x-position estimation was slightly affected by the readout pitch (Figure 7a). This was consistent with the results of 3-D interaction position estimation based on deep learning using the Cherenkov detector [14]. The RMSE of the z-position estimation was almost the same for all readout pitches and rapidly degraded as the SPTR worsened (Figure 7b). These results may indicate that the z-position was estimated using only time information. When the SPTR was 10 ps and the readout pitch was 3 mm, the proposed method obtained a σx of 1.12 mm and σz of 1.42 mm (Table 3).
The sensitivity of the proposed system was low (Figure 8). As we focused on whether direct annihilation position classification is possible in this study, we did not optimize the system to increase the sensitivity. In future studies, we aim to optimize the system parameters, for example, the distance between detectors, detector size, thickness, and surface treatment of the crystal, and the number of paired detectors, to improve the resolution and sensitivity. For example, Consuegra et al. optimized the thickness and surface treatment of PbF2 crystals of whole-body PbF2 TOF-PET scanners, using a figure of merit which was defined as the ratio between detection efficiency and CTR [39]. In addition, the photon detection threshold can be optimized to control the tradeoff between resolution and sensitivity. For example, when the SPTR was 0 ps and readout pitch was 0 mm, the proposed method obtained classification accuracies of 95% and 92% at photon detection thresholds of four and three, respectively (data not shown).
The limitation of this study is that the validation only used the simulation data of point sources. In future studies, we plan to experimentally validate the simulation results. For the experimental setup, a pair of Cherenkov detectors consisting of a position sensitive photodetector and a Cherenkov radiator would be used. In parallel, we will simulate a phantom to evaluate the image quality of the proposed system.
5. Conclusions
This study demonstrated the feasibility of direct annihilation position classification based on deep learning using paired Cherenkov detectors. In the Monte Carlo simulation, the proposed method obtained a classification accuracy of 80% and a spatial resolution of less than 1.5 mm (RMSE) when the SPTR was 10 ps and the readout pitch was 3 mm. As the classification accuracies for readout pitches of 0 to 3 mm were almost equal, a readout pitch of 3 mm could be sufficient. Furthermore, because the RMSE of the z-position estimation was almost equal for readout pitches from 0 to 10 mm, it may be that the z-position could be estimated from only time information. In future studies, we will optimize the system parameters to increase the sensitivity.
Author Contributions
Conceptualization, K.O., R.O., F.H., and T.H.; software/formal analysis; K.O. and R.O.; methodology/validation/investigation/resources/writing—original draft preparation/visualization, K.O.; writing—review and editing, R.O. and F.H.; supervision, T.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors would like to thank the staff of the Central Research Laboratory of Hamamatsu Photonics K.K.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Vandenberghe, S.; Mikhaylova, E.; D’Hoe, E.; Mollet, P.; Karp, J.S. Recent developments in time-of-flight PET. EJNMMI Phys. 2016, 3, 1–30. [Google Scholar] [CrossRef]
- Van Sluis, J.; De Jong, J.; Noordzij, W.; Van Snick, P.; Dierckx, R.; Borra, R.; Willemsen, A.; Boellaard, R. Performance characteristics of the digital biograph vision PET/CT system. J. Nucl. Med. 2019, 60, 1031–1036. [Google Scholar] [CrossRef] [PubMed]
- Conti, M.; Bendriem, B. The new opportunities for high time resolution clinical TOF PET. Clin. Transl. Imaging 2019, 7, 139–147. [Google Scholar] [CrossRef]
- Gundacker, S.; Turtos, R.M.; Kratochwil, N.; Pots, R.H.; Paganoni, M.; Lecoq, P.; Auffray, E. Experimental time resolution limits of modern SiPMs and TOF-PET detectors exploring different scintillators and Cherenkov emission. Phys. Med. Biol. 2020, 65, 025001. [Google Scholar] [CrossRef] [PubMed]
- Ota, R.; Nakajima, K.; Ogawa, I.; Tamagawa, Y.; Shimoi, H.; Suyama, M.; Hasegawa, T. Coincidence time resolution of 30 ps FWHM using a pair of Cherenkov-radiator-integrated MCP-PMTs. Phys. Med. Biol. 2019, 64, 07LT01. [Google Scholar] [CrossRef] [PubMed]
- Somlai-Schweiger, I.; Ziegler, S.I. CHERENCUBE: Concept definition and implementation challenges of a Cherenkov-based detector block for PET. Med. Phys. 2015, 42, 1825–1835. [Google Scholar] [CrossRef] [PubMed]
- Korpar, S.; Dolenec, R.; Križan, P.; Pestotnik, R.; Stanovnik, A. Study of TOF PET using Cherenkov light. Nucl. Instrum. Method Phys. Res. A 2011, 654, 532–538. [Google Scholar] [CrossRef]
- Ota, R.; Yamada, R.; Moriya, T.; Hasegawa, T. Cherenkov radiation-based three-dimensional position-sensitive PET detector: A Monte Carlo study. Med. Phys. 2018, 45, 1999–2008. [Google Scholar] [CrossRef] [PubMed]
- Gundacker, S.; Auffray, E.; Pauwels, K.; Lecoq, P. Measurement of intrinsic rise times for various L(Y)SO and LuAG scintillators with a general study of prompt photons to achieve 10 ps in TOF-PET. Phys. Med. Biol. 2016, 61, 2802–2837. [Google Scholar] [CrossRef] [PubMed]
- Moses, W.W.; Derenzo, S.E. Prospects for time-of-flight pet using LSO scintillator. IEEE Trans. Nucl. Sci. 1999, 46, 474–478. [Google Scholar] [CrossRef]
- Shibuya, K.; Nishikido, F.; Tsuda, T.; Kobayashi, T.; Lam, C.; Yamaya, T.; Yoshida, E.; Inadama, N.; Murayama, H. Timing resolution improvement using DOI information in a four-layer scintillation detector for TOF-PET. Nucl. Instrum. Method Phys. Res. A 2008, 593, 572–577. [Google Scholar] [CrossRef]
- Vinke, R.; Löhner, H.; Schaart, D.R.; Van Dam, H.T.; Seifert, S.; Beekman, F.J.; Dendooven, P. Time walk correction for TOF-PET detectors based on a monolithic scintillation crystal coupled to a photosensor array. Nucl. Instrum. Method Phys. Res. A 2010, 621, 595–604. [Google Scholar] [CrossRef]
- Lecoq, P. Development of new scintillators for medical applications. Nucl. Instrum. Method Phys. Res. A 2016, 809, 130–139. [Google Scholar] [CrossRef]
- Hashimoto, F.; Ote, K.; Ota, R.; Hasegawa, T. A feasibility study on 3D interaction position estimation using deep neural network in Cherenkov-based detector: A Monte Carlo simulation study. Biomed. Phys. Eng. Express 2019, 5, 035001. [Google Scholar] [CrossRef]
- Bruyndonckx, P.; Léonard, S.; Tavernier, S.; Lemaître, C.; Devroede, O.; Wu, Y.; Krieguer, M. Neural network-based position estimators for PET detectors using monolithic LSO blocks. IEEE Trans. Nucl. Sci. 2004, 51, 2520–2525. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, W.; Cheng, X.; Li, D. 3D position estimation using an artificial neural network for a continuous scintillator PET detector. Phys. Med. Biol. 2013, 58, 1375–1390. [Google Scholar] [CrossRef]
- Van Dam, H.T.; Seifert, S.; Vinke, R.; Dendooven, P.; Löhner, H.; Beekman, F.J.; Schaart, D.R. A practical method for depth of interaction determination in monolithic scintillator PET detectors. Phys. Med. Biol. 2011, 56, 4135–4145. [Google Scholar] [CrossRef]
- Pedemonte, S.; Pierce, L.; Van Leemput, K. A machine learning method for fast and accurate characterization of depth-of-interaction gamma cameras. Phys. Med. Biol. 2017, 62, 8376–8401. [Google Scholar] [CrossRef]
- Gong, K.; Berg, E.; Cherry, S.R.; Qi, J. Machine Learning in PET: From Photon Detection to Quantitative Image Reconstruction. Proc. IEEE 2020, 108, 51–68. [Google Scholar] [CrossRef]
- Suzuki, K. Overview of deep learning in medical imaging. Radiol. Phys. Technol. 2017, 10, 257–273. [Google Scholar] [CrossRef] [PubMed]
- Hashimoto, F.; Ohba, H.; Ote, K.; Teramoto, A.; Tsukada, H. Dynamic PET Image Denoising Using Deep Convolutional Neural Networks Without Prior Training Datasets. IEEE Access 2019, 7, 96594–96603. [Google Scholar] [CrossRef]
- Ota, S.; Horisaki, R.; Kawamura, Y.; Ugawa, M.; Sato, I.; Hashimoto, K.; Kamesawa, R.; Setoyama, K.; Yamaguchi, S.; Fujiu, K.; et al. Ghost cytometry. Science 2018, 360, 1246–1251. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Huang, C.; Yune, S.; Tajmir, S.H.; Kim, M.; Do, S. Machine Friendly Machine Learning: Interpretation of Computed Tomography Without Image Reconstruction. Sci. Rep. 2019, 9, 15540. [Google Scholar] [CrossRef] [PubMed]
- Anderson, D.F.; Kobayashi, M.; Woody, C.L.; Yoshimura, Y. Lead fluoride: An ultra-compact Cherenkov radiator for em calorimetry. Nucl. Instrum. Method Phys. Res. A 1990, 290, 385–389. [Google Scholar] [CrossRef]
- Miyata, M.; Tomita, H.; Watanabe, K.; Kawarabayashi, J.; Iguchi, T. Development of TOF-PET using cherenkov radiation. J. Nucl. Sci. Tech. 2006, 43, 339–343. [Google Scholar] [CrossRef]
- MCP-PMT R3809U-50. Available online: https://www.hamamatsu.com/jp/en/product/type/R3809U-50/index.html (accessed on 9 September 2020).
- Nemallapudi, M.V.; Gundacker, S.; Lecoq, P.; Auffray, E. Single photon time resolution of state of the art SiPMs. J. Instrum. 2016, 11, P10016. [Google Scholar] [CrossRef]
- Agostinelli, S.; Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. GEANT4-A simulation toolkit. Nucl. Instrum. Method Phys. Res. A 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Brunner, S.E.; Gruber, L.; Marton, J.; Suzuki, K.; Hirtl, A. Studies on the cherenkov effect for improved time resolution of TOF-PET. IEEE Trans. Nucl. Sci. 2014, 61, 443–447. [Google Scholar] [CrossRef]
- National Institute of Standards and Technology. Available online: https://physics.nist.gov/PhysRefData/Xcom/html/xcom1.html (accessed on 12 September 2020).
- Ali, A.; Shamsuddin, S.M.; Ralescu, A.L. Classification with class imbalance problem: A review. Int. J. Adv. Soft Comput. Appl. 2015, 7, 176–204. Available online: http://home.ijasca.com/data/documents/13IJASCA-070301_Pg176-204_Classification-with-class-imbalance-problem_A-Review.pdf (accessed on 1 October 2020).
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. Proceedings of International Conference on Machine Learning 2015. Available online: http://proceedings.mlr.press/v37/ioffe15.pdf (accessed on 14 September 2020).
- Glorot, X.; Bordes, A.; Bengio, Y. Deep sparse rectifier neural networks. J. Mach. Learn. Res. 2011, 15, 315–323. Available online: http://proceedings.mlr.press/v15/glorot11a/glorot11a.pdf (accessed on 14 September 2020).
- Tokui, S.; Okuta, R.; Akiba, T.; Niitani, Y.; Ogawa, T.; Saito, S.; Suzuki, S.; Uenishi, K.; Vogel, B.; Vincent, H.Y. Chainer: A deep learning framework for accelerating the research cycle. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2002–2011. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. Available online: https://jmlr.org/papers/volume12/pedregosa11a/pedregosa11a.pdf (accessed on 14 September 2020).
- Kingma, D.P.; Ba, J.L. Adam: A method for stochastic optimization. arXiv 2014, arXiv:14126980. Available online: https://arxiv.org/abs/1412.6980 (accessed on 26 September 2020).
- Stehman, S.V. Selecting and interpreting measures of thematic classification accuracy. Remote Sens. Environ. 1997, 62, 77–89. [Google Scholar] [CrossRef]
- Tabacchini, V.; Borghi, G.; Schaart, D.R. Time-based position estimation in monolithic scintillator detectors. Phys. Med. Biol. 2015, 60, 5513–5525. [Google Scholar] [CrossRef]
- Consuegra, D.; Korpar, S.; Križan, P.; Pestotnik, R.; Razdevšek, G.; Dolenec, R. Simulation study to improve the performance of a whole-body PbF2 Cherenkov TOF-PET scanner. Phys. Med. Biol. 2020, 65, 055013. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).