Optimizing Automatic Transmission Double-Transition Shift Process Based on Multi-Objective Genetic Algorithm
Abstract
1. Introduction
2. Modeling of DTS
2.1. Modeling of the Planetary Gear Sets Based on the Lagrange Method
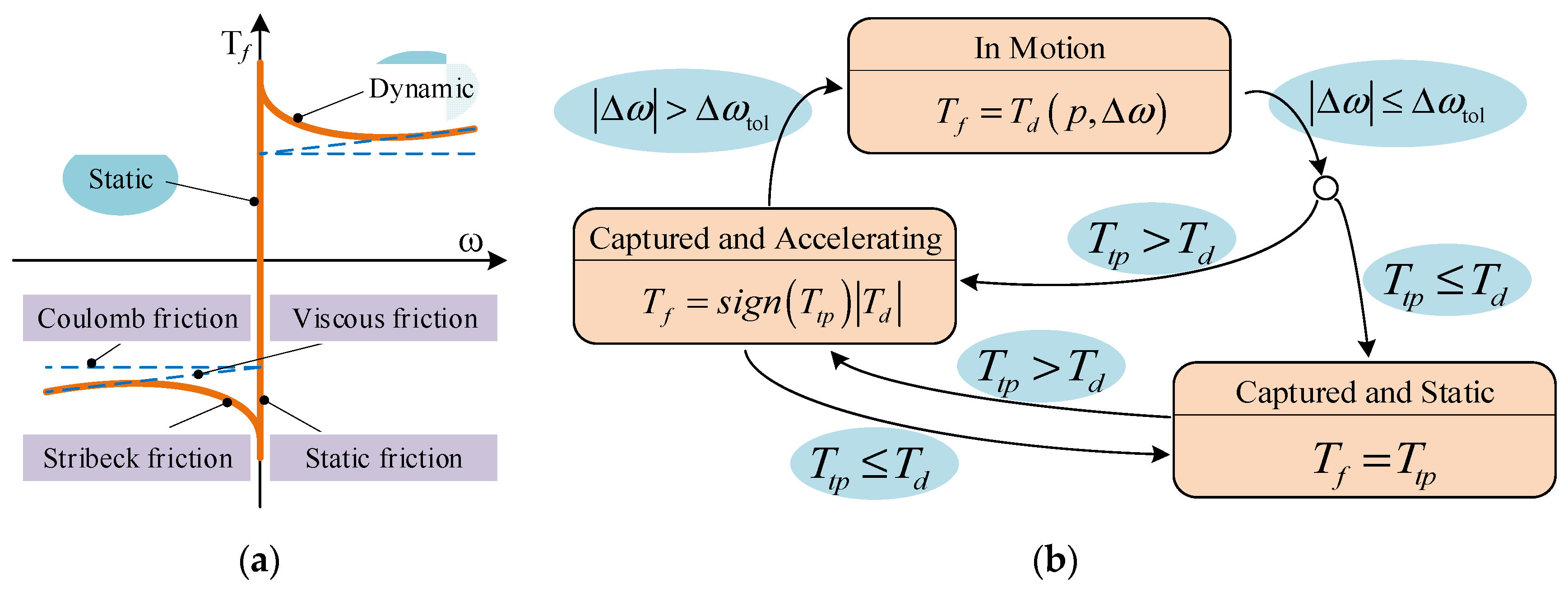
2.2. Modeling of Clutch Friction
2.3. Modeling of the Transmission Input Power
2.4. Modeling of the Transmission Output Power
3. Double-Transition Shift Process Analysis
3.1. BL and BM Power on Upshift Process Analysis
3.2. BS and CS Power on Downshift Process Analysis
4. Multi-Objective Optimization of DTS
4.1. Strategy One
4.2. Strategy Two
4.3. Strategy Three
4.4. Strategy Four
4.5. Strategy Five
5. Conclusions
- (1)
- In this paper, the Lagrange method is used to dynamically model the double-transition shift for heavy-duty mining truck automatic transmission. The vehicle powertrain system and the controller based on the multi-objective genetic algorithm are built-in Matlab/Simulink. The dynamic analysis of two sets of clutches for DTS is carried out.
- (2)
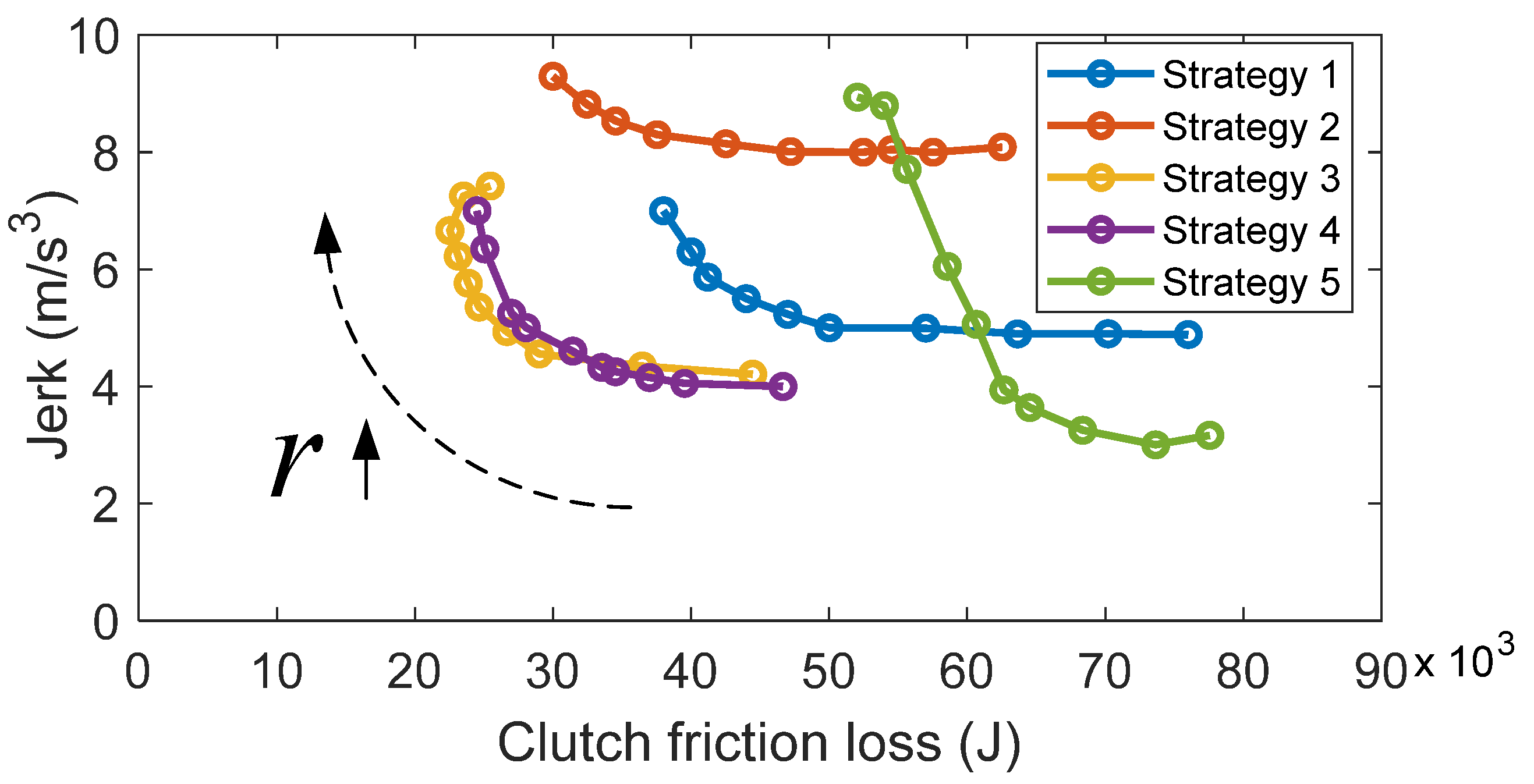
- Obtained in the multi-objective genetic algorithm, the Pareto optimal solution shows that the lowest root mean square of shift jerk and the energy loss of clutches are and , respectively.
- (3)
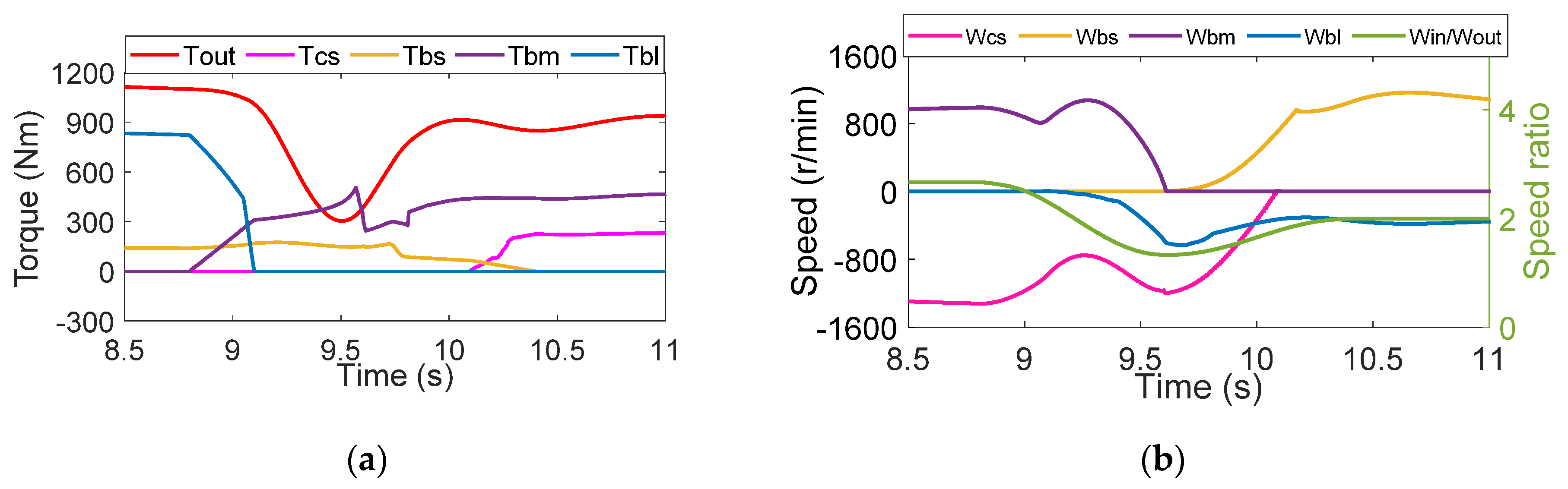
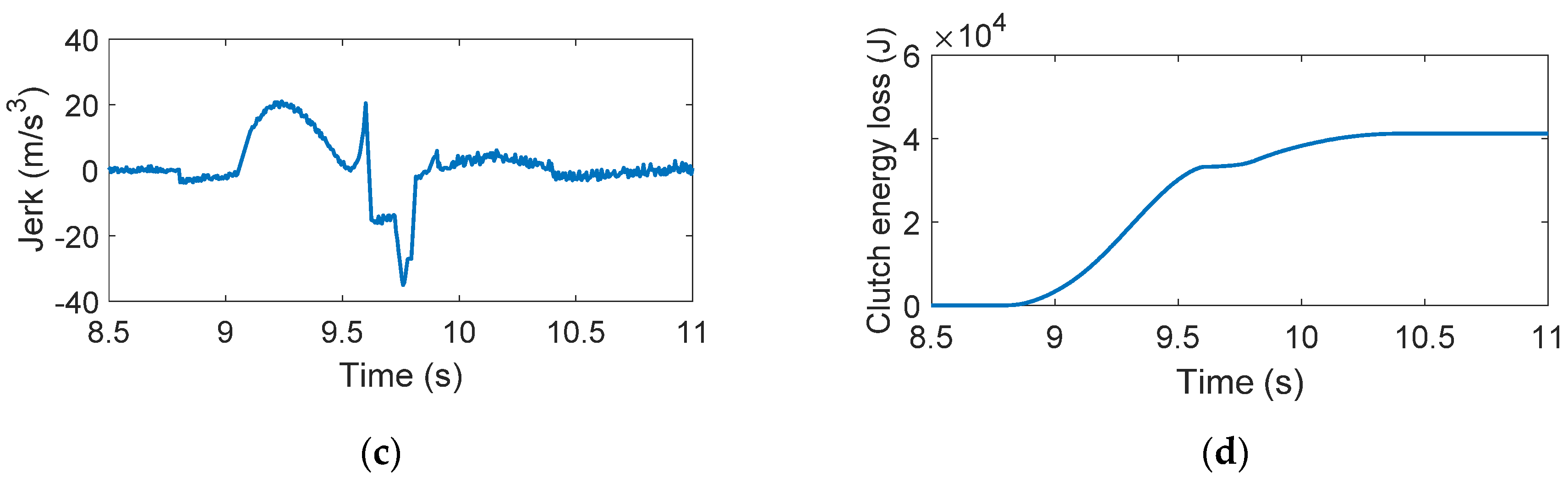
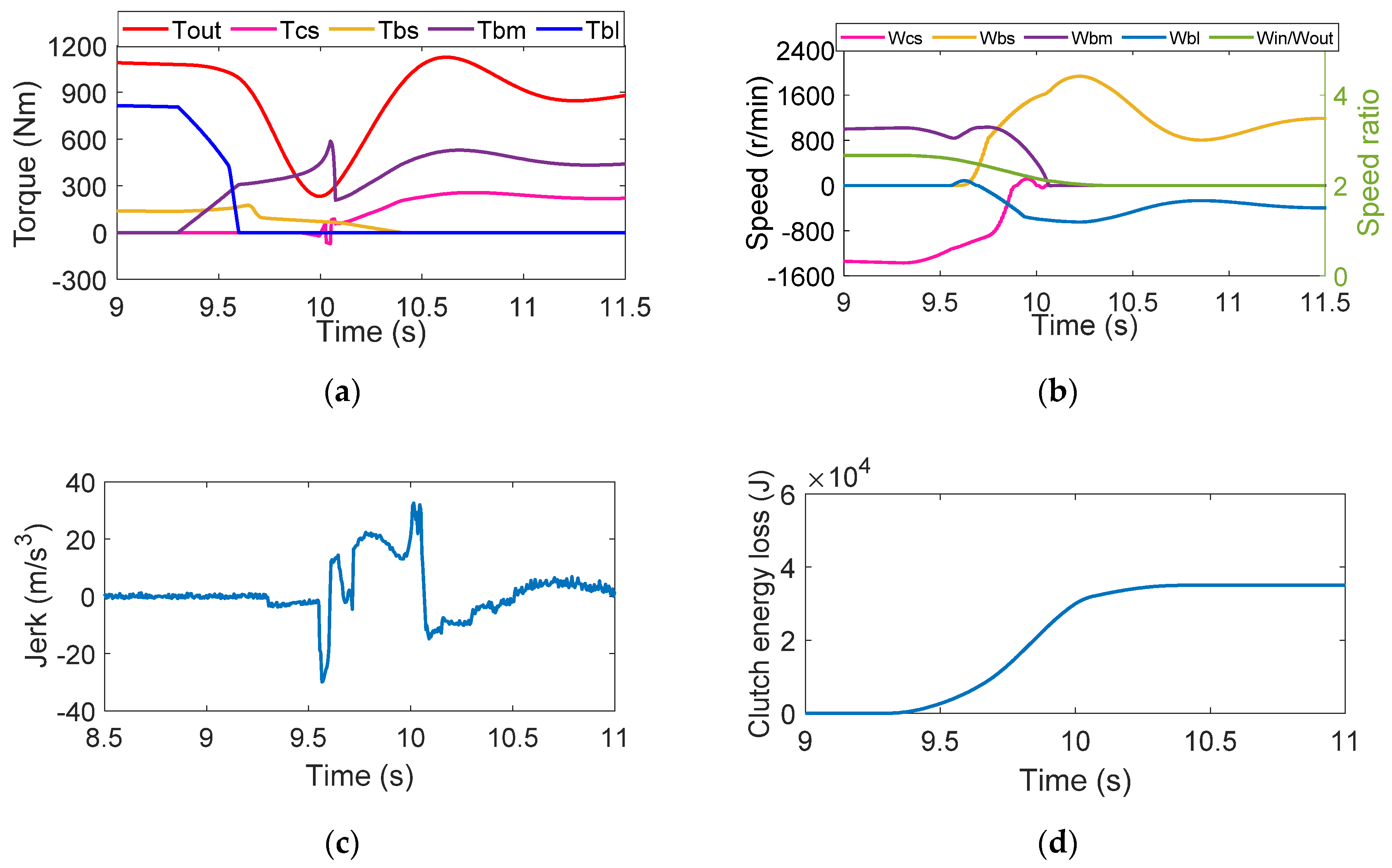
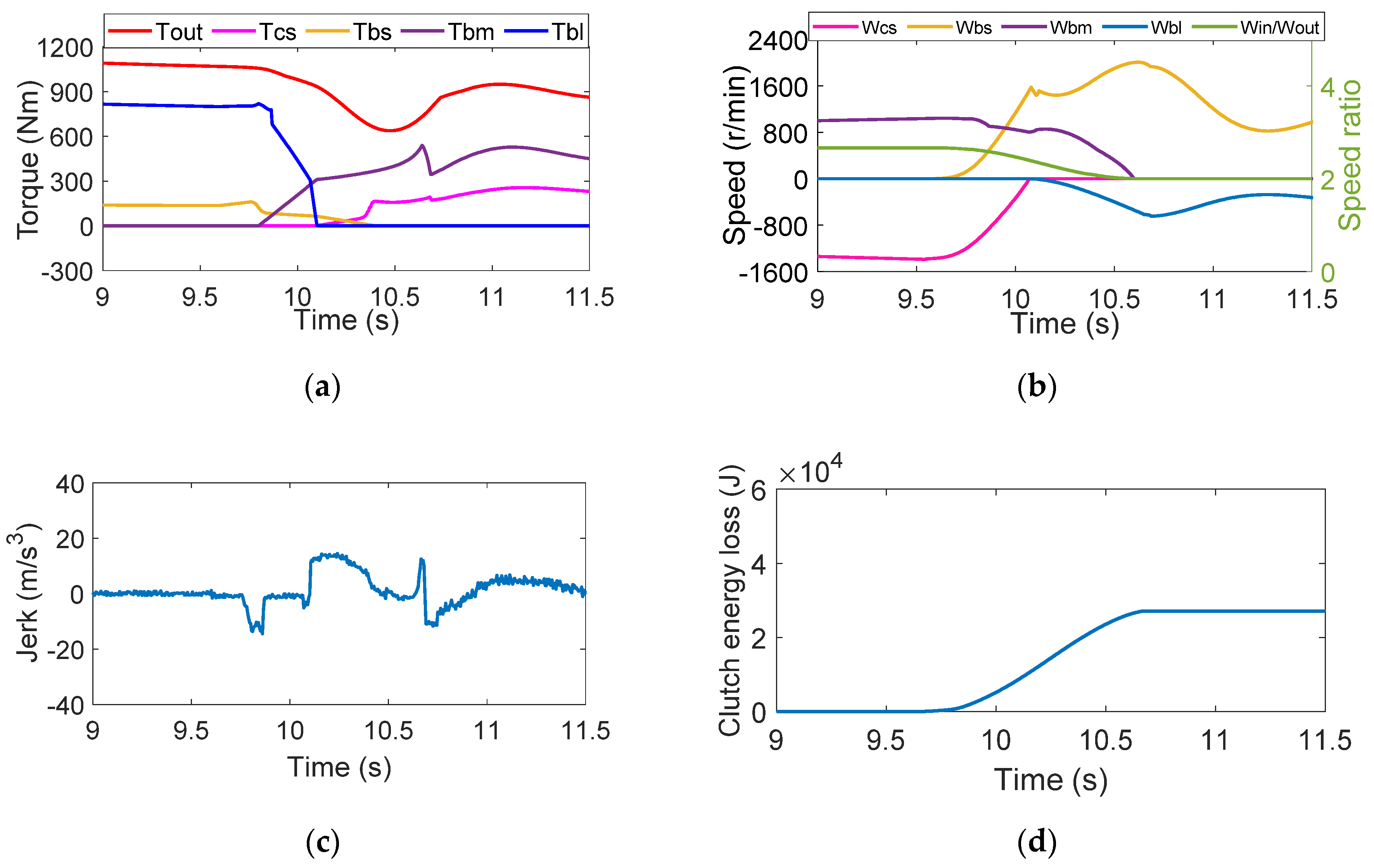
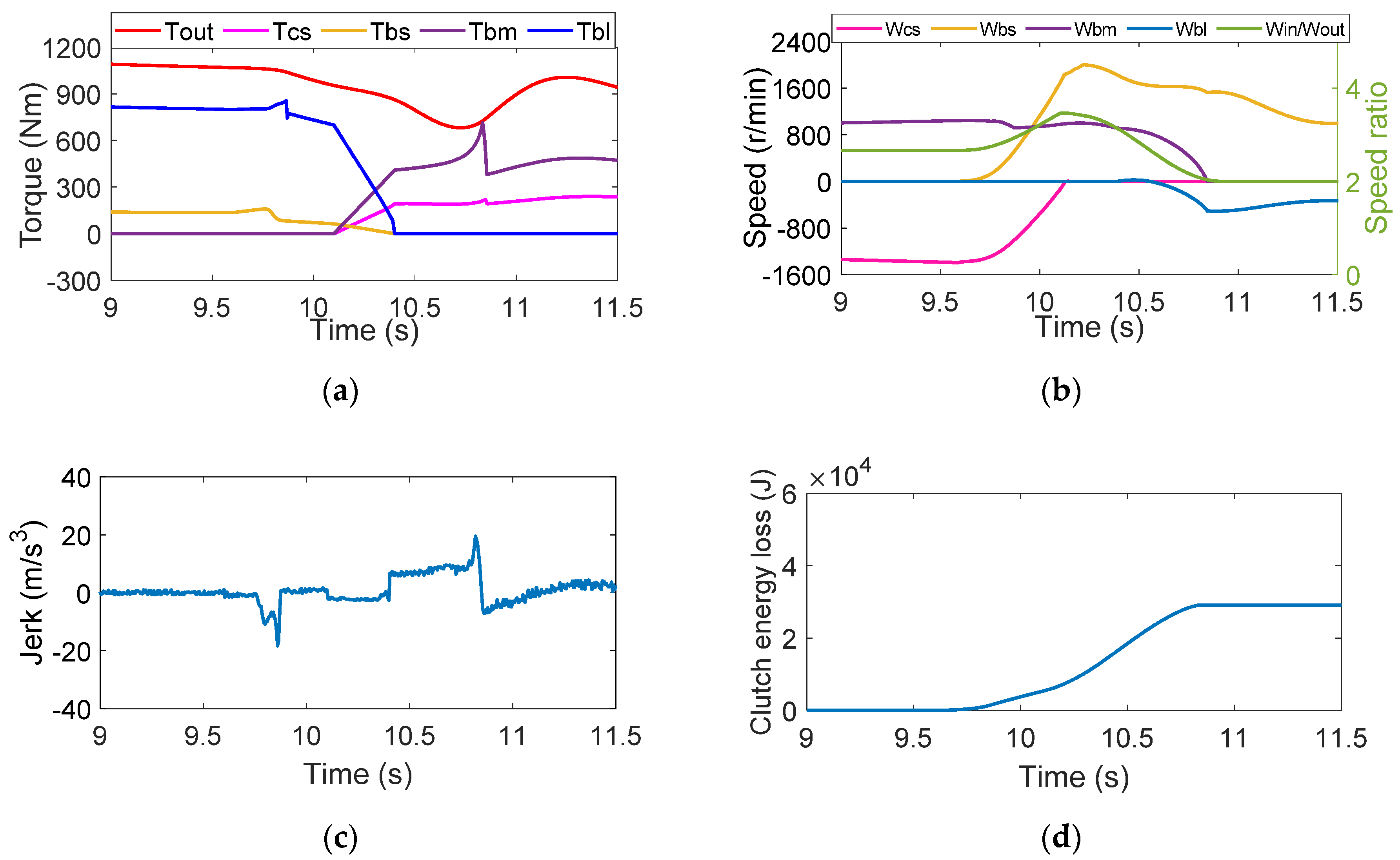
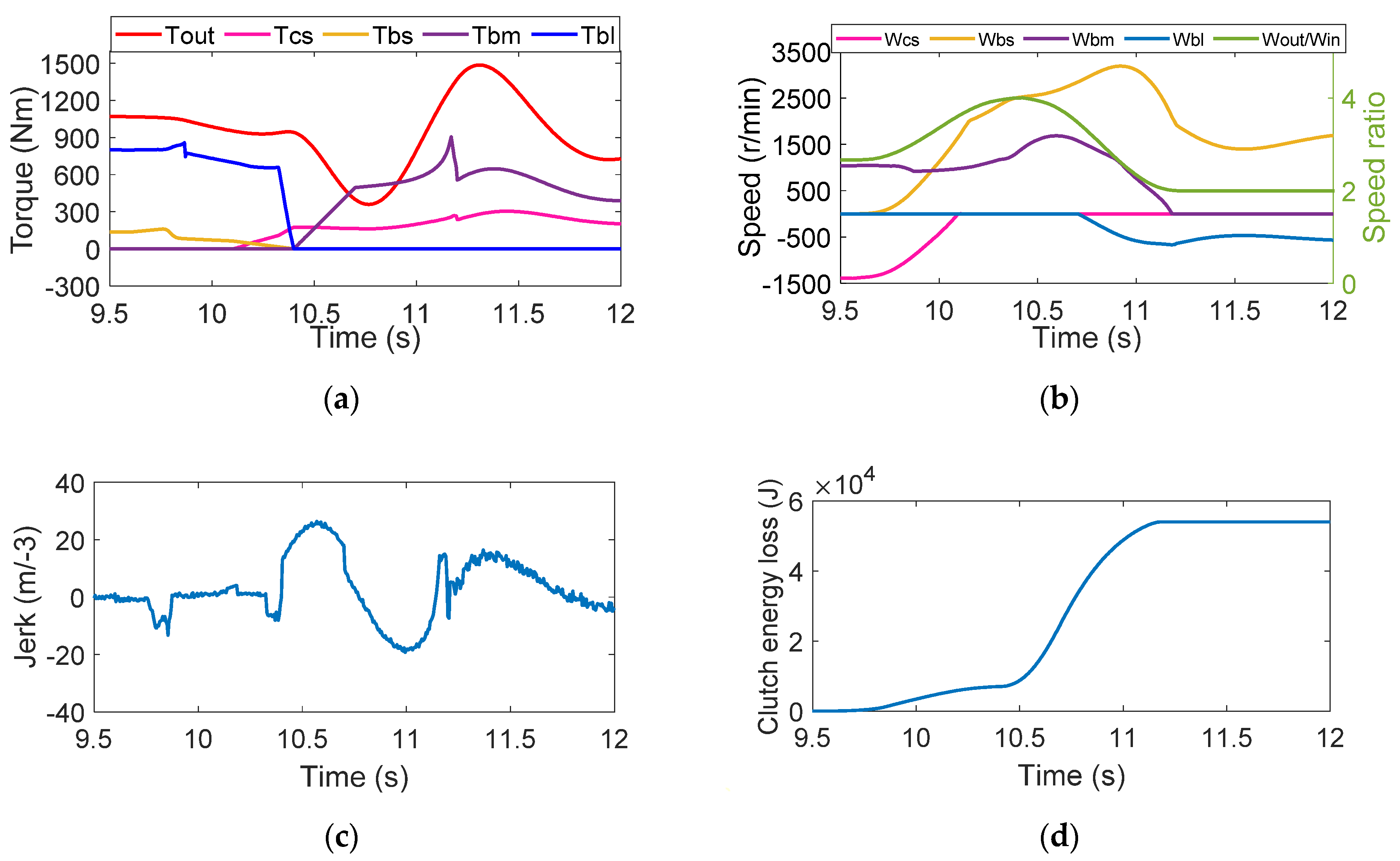
- The simulation results of five strategies of double-transition shift show that overlapping the inertia phases of both clutch groups will cause the fluctuation amplitude of the output torque to increase. On the contrary, the shift jerk can be more stable at , which is reduced by 56.3%, when the inertial phases are not overlapped. The torque phase overlaps with the inertia phase of another group of clutches, effectively reducing the shift time to about 1.1s and thus decreasing the clutch energy loss by 13.4%, which is .
Author Contributions
Funding
Conflicts of Interest
References
- Zhao, X.; Zhang, W.; Feng, Y.; Yang, Y. Optimizing Gear Shifting Strategy for Off-Road Vehicle with Dynamic Programming. Math. Probl. Eng. 2014, 2014, 1–9. [Google Scholar] [CrossRef]
- Meng, F.; Shi, P.; Karimi, H.R.; Zhang, H. Optimal design of an electro-hydraulic valve for heavy-duty vehicle clutch actuator with certain constraints. Mech. Syst. Signal. Process. 2016, 68, 491–503. [Google Scholar] [CrossRef]
- Ouyang, T.; Huang, G.; Li, S.; Chen, J.; Chen, N. Dynamic modelling and optimal design of a clutch actuator for heavy-duty automatic transmission considering flow force. Mech. Mach. Theory 2020, 145, 103716. [Google Scholar] [CrossRef]
- Gao, B.; Liang, Q.; Xiang, Y.; Guo, L.; Chen, H. Gear ratio optimization and shift control of 2-speed I-AMT in electric vehicle. Mech. Syst. Signal. Process. 2015, 615–631. [Google Scholar] [CrossRef]
- Cheng, Y.; Dong, P.; Yang, S.; Xu, X. Virtual Clutch Controller for Clutch-to-Clutch Shifts in Planetary-Type Automatic Transmission. Math. Probl. Eng. 2015, 2015, 1–16. [Google Scholar] [CrossRef]
- Ranogajec, V.; Deur, J.; Ivanović, V.; Tseng, H.E. Multi-objective parameter optimization of control profiles for automatic transmission double-transition shifts. Control. Eng. Pract. 2019, 93, 104183. [Google Scholar] [CrossRef]
- Čorić, M.; Ranogajec, V.; Deur, J.; Ivanovic, V.; Tseng, H.E. Optimization of Shift Control Trajectories for Step Gear Automatic Transmissions. J. Dyn. Syst. Meas. Control. 2017, 139, 061005. [Google Scholar] [CrossRef]
- Mishra, K.D.; Srinivasan, K. Robust control and estimation of clutch-to-clutch shifts. Control. Eng. Pract. 2017, 65, 100–114. [Google Scholar] [CrossRef]
- Oh, J.-Y.; Park, J.-Y.; Cho, J.-W.; Kim, J.-G.; Kim, J.-H.; Lee, G.-H. Influence of a clutch control current profile to improve shift quality for a wheel loader automatic transmission. Int. J. Precis. Eng. Manuf. 2017, 18, 211–219. [Google Scholar] [CrossRef]
- Sanada, K.; Gao, B.; Kado, N.; Takamatsu, H.; Toriya, K. Design of a robust controller for shift control of an automatic transmission. Proc. Inst. Mech. Eng. Part. D J. Automob. Eng. 2012, 226, 1577–1584. [Google Scholar] [CrossRef]
- Tsai, L.-W.; Norton, R. Mechanism Design: Enumeration of Kinematic Structures According to Function. Appl. Mech. Rev. 2001, 54, B85–B86. [Google Scholar] [CrossRef]
- Hsu, C.-H.; Hsu, J.-J. Epicyclic gear trains for automotive automatic transmissions. Proc. Inst. Mech. Eng. Part. D J. Automob. Eng. 2000, 214, 523–532. [Google Scholar] [CrossRef]
- Ranogajec, V.; Deur, J. A Bond Graph-Based Method of Automated Generation of Automatic Transmission Mathematical Model. Sae Int. J. Engines 2017, 10, 1367–1374. [Google Scholar] [CrossRef]
- Ranogajec, V.; Deur, J.; Čorić, M. Bond Graph Analysis of Automatic Transmission Shifts including Potential of Extra Clutch Control. Sae Int. J. Engines 2016, 9, 1929–1945. [Google Scholar] [CrossRef]
- Zhao, X.; Li, Z. Data-Driven Predictive Control Applied to Gear Shifting for Heavy-Duty Vehicles. Energies 2018, 11, 2139. [Google Scholar] [CrossRef]
- Song, X.; Sun, Z. Pressure-Based Clutch Control for Automotive Transmissions Using a Sliding-Mode Controller. IEEE Asme Trans. Mechatron. 2011, 17, 534–546. [Google Scholar] [CrossRef]
- Meng, F.; Tao, G.; Zhang, T.; Hu, Y.; Geng, P. Optimal shifting control strategy in inertia phase of an automatic transmission for automotive applications. Mech. Syst. Signal. Process. 2015, 742–752. [Google Scholar] [CrossRef]
- Wurm, A.; Bestle, D. Robust design optimization for improving automotive shift quality. Optim. Eng. 2015, 17, 421–436. [Google Scholar] [CrossRef]
- Wu, D.; Zhang, Y.; Chang, Y.-P.; Hebbale, K.; Kao, C.-K. Dynamic analysis and simulation of driveability and control of a double transition shifting system. 2009 IEEE Veh. Power Propuls. Conf. 2009, 348–353. [Google Scholar] [CrossRef]
- Wu, D.; Chang, Y.-P. Simulation and Studies on a Double Transition Shift Transmission. Sae Tech. Pap. Ser. 2010. [CrossRef]
- Ranogajec, V.; Ivanović, V.; Deur, J.; Tseng, H.E. Optimization-based assessment of automatic transmission double-transition shift controls. Control. Eng. Pract. 2018, 76, 155–166. [Google Scholar] [CrossRef]
- Patinya, S. Modeling and Control of Automatic Transmission with Planetary Gears for Shift Quality. Ph.D. Thesis, The University of Texas, Austin, TX, USA, 2012. [Google Scholar]
- Kim, J.; Choi, S.B. Design and Modeling of a Clutch Actuator System with Self-Energizing Mechanism. IEEE Asme Trans. Mechatron. 2010, 16, 953–966. [Google Scholar] [CrossRef]
- Hahn, J.-O.; Lee, K.-I. Nonlinear Robust Control of Torque Converter Clutch Slip System for Passenger Vehicles Using Advanced Torque Estimation Algorithms. Veh. Syst. Dyn. 2002, 37, 175–192. [Google Scholar] [CrossRef]
- Liang, J.; Zhang, J.; Zhang, H.; Yin, C. Fuzzy Energy Management Optimization for a Parallel Hybrid Electric Vehicle using Chaotic Non-dominated sorting Genetic Algorithm. Automatika 2015, 56, 149–163. [Google Scholar] [CrossRef]
- Saini, V.; Singh, S.; Nv, S.; Jain, H. Genetic Algorithm Based Gear Shift Optimization for Electric Vehicles. Sae Int. J. Altern. Powertrains 2016, 5, 348–356. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]


| Gears | CS | BS | CH | BM | BL | BR | Gear Ratio |
|---|---|---|---|---|---|---|---|
| 1 | √ | √ | 4.00 | ||||
| 2 | √ | √ | 2.67 | ||||
| 3 | √ | √ | 2.00 | ||||
| 4 | √ | √ | 1.33 | ||||
| 5 | √ | √ | 1.00 | ||||
| 6 | √ | √ | 0.67 | ||||
| R1 | √ | √ | −5.00 | ||||
| R2 | √ | √ | −3.33 |
| Time | BS and CS | BL and BM | ||||
|---|---|---|---|---|---|---|
| Strategy 1 | Strategy 2 | Strategy 3 | Strategy 4 | Strategy 5 | ||
| low gear | ||||||
| torque phase | low gear | |||||
| high gear | inertia phase | torque phase | low gear | |||
| inertia phase | high gear | inertia phase | torque phase | low gear | ||
| torque phase | high gear | inertia phase | torque phase | low gear | ||
| low gear | high gear | inertia phase | torque phase | |||
| high gear | inertia phase | |||||
| high gear | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Zhao, X.; Yang, J.; Zhang, W. Optimizing Automatic Transmission Double-Transition Shift Process Based on Multi-Objective Genetic Algorithm. Appl. Sci. 2020, 10, 7794. https://doi.org/10.3390/app10217794
Zhang H, Zhao X, Yang J, Zhang W. Optimizing Automatic Transmission Double-Transition Shift Process Based on Multi-Objective Genetic Algorithm. Applied Sciences. 2020; 10(21):7794. https://doi.org/10.3390/app10217794
Chicago/Turabian StyleZhang, Heng, Xinxin Zhao, Jue Yang, and Wenming Zhang. 2020. "Optimizing Automatic Transmission Double-Transition Shift Process Based on Multi-Objective Genetic Algorithm" Applied Sciences 10, no. 21: 7794. https://doi.org/10.3390/app10217794
APA StyleZhang, H., Zhao, X., Yang, J., & Zhang, W. (2020). Optimizing Automatic Transmission Double-Transition Shift Process Based on Multi-Objective Genetic Algorithm. Applied Sciences, 10(21), 7794. https://doi.org/10.3390/app10217794





