Next Article in Journal
Artificial Intelligence Prediction of Rutting and Fatigue Parameters in Modified Asphalt Binders
Next Article in Special Issue
Numerical Analysis-Based Blast Resistance Performance Assessment of Cable-Stayed Bridge Components Subjected to Blast Loads
Previous Article in Journal
Lengthening Transmission Distance of Continuous Variable Quantum Key Distribution with Discrete Modulation through Photon Catalyzing
Previous Article in Special Issue
Study on Dynamic Behavior of Bridge Pier by Impact Load Test Considering Scour
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 10
Issue 21
10.3390/app10217769
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Numerical Investigation of the Collapse of a Steel Truss Roof and a Probable Reason of Failure

by
Mertol Tüfekci
1,*,
Ekrem Tüfekci
2 and
Adnan Dikicioğlu
2
1
Department of Mechanical Engineering Imperial College London, Exhibition Road, London SW7 2AZ, UK
2
Faculty of Mechanical Engineering, Istanbul Technical University, Gumussuyu-Istanbul 34437, Turkey
*
Author to whom correspondence should be addressed.
Appl. Sci. 2020, 10(21), 7769; https://doi.org/10.3390/app10217769
Submission received: 6 October 2020 / Revised: 25 October 2020 / Accepted: 1 November 2020 / Published: 3 November 2020
(This article belongs to the Special Issue Buildings and Structures under Extreme Loads II)
Browse Figures
Versions Notes

Abstract

:
This study investigated the failure of the roof, with steel truss construction, of a factory building in Tekirdag in the northwestern part of Turkey. The failure occurred under hefty weather conditions including lightning strikes, heavy rain, and fierce winds. In order to interpret the reason for the failure, the effects of different combinations of factors on the design and dimensioning of the roof were studied. Finite element analysis, using the commercial software Abaqus (Dassault Systèmes, Vélizy-Villacoublay, France), was performed several times under different assumptions and considering different factors with the aim of determining the dominant factors that were responsible for the failure. Each loading condition gives out a characteristic form of failure. The scenario with the most similar form of failure to the real collapse is considered as the most likely scenario of failure. In addition, the factors included in this scenario are expected to be the responsible factors for the partial collapse of the steel truss structure.

1. Introduction

Engineers aim to make human life easier and to enhance life quality. Using mathematical calculations and experimentation, engineers try to predict the behaviour of a system and design it accordingly [1]. However, there have been cases that ended in structural failures, and some of these failures caused financial loss or even cost lives. Hadipriono studied nearly 150 major failures of structures around the world and determined that the major failures were due to lateral impact forces [2]. Moreover, Klasson published a survey covering failures of slender roofs [3]. Even the simplest structures, which have the most predictable behaviours, fail under unexpected conditions that exceed the designated safety margins [4,5].
Trusses are one of the most widely used and easy-to-design light structures [6]. They are able to carry very large loads relative to their own weights over very large spans. This is one of the main reasons that truss-type structures are preferred for building roofs and bridges. The possible loads are standardised to help engineers design structures in a very simple and straightforward way [7]. The standardised loads can be multiple times greater than the structures’ own weight. In the case of unexpectedly excessive loads of accumulated snow or rainwater, failure of the designed structure may be unavoidable [8,9]. Geis et al. studied more than 1000 snow-induced building failure incidents all over the world [10]. An accumulated mass may cause failure in various ways. Excessive weight loads acting on the structures lead to a different load distribution than that of the designed distribution due to some members entering the plastic region and/or buckling [11,12,13].
In addition, the loads caused by dynamic effects such as earthquakes could lead to failure [14,15,16]. Structures are more vulnerable to dynamic loads than they are to static loads [17,18,19]. A way to improve the performance of structures against dynamic loads is to add damping to the structure [20]. Earthquakes are not the only sources that cause dynamic loads on structures. One of the main dynamic effects that may lead to sudden or progressive collapses is wind [21,22,23,24]. The wind is a very significant factor that leads to lateral loads to which building structures are relatively more sensitive than they are to vertical loads [25].
A crucial dynamic effect that is a very complicated phenomenon is lightning strike [26]. A lightning strike can cause partial damage or complete failure of structures [27,28]. Specifically, there are cases where the main reason reported for structural failure is lightning strike [29,30,31,32]. In Australia, it is reported that 21% of insurance claims for damage to buildings are caused by lightning strikes [33]. A lightning strike can affect a structure in many different ways, with the two most dangerous processes being blast (local and rapid pressure oscillations) and heating [34]. Previous research proved the heating effects of the lightning strike phenomenon [35,36]. It is known that a lightning strike increases the temperature rapidly in a very short period of time [29,37]. The electric current that is caused by the lighting strike heats up the structure so that it can start fires [38]. Besides, fire alone can also be the main factor that leads to structural failure [39,40,41,42].
Lightning is one of the key points of this study. Of course, structures are not affected just by one of the consequences of the lightning strike phenomenon. Instead, the combination of these enumerated parameters creates a synergy effect, which increases the resultant influence of the factors so that the combination becomes greater than a superposition of these contributing load components [43]. The effects of a lightning strike can be even more dramatic on the structures when there is accumulated water on top of the structure, since the local blasts are amplified by the presence of the water and thermal changes influence the structure [34,44].
There are different types of failure mechanisms as well as different types of reasons for the collapse. Thus, it is possible to find possible reasons for the failure just from the mode/form of the failure. One of the most important types of failure mechanisms is fatigue [45]. Fatigue may lead to the progressive collapse of structures [46,47]. Progressive collapse may happen instantly following the changed load distribution of members due to buckling and/or failure of some members [48,49]. However, it does not have to happen at the time of the initial failure of individual members but can happen after a certain number of members have failed successively [50,51].
There has been experimental research focusing on the mechanical behaviour of some specific components and/or structures that are used in trusses [15,52,53,54,55]. In past studies by various researchers, real roof structures were put through experimental testing to analyse their mechanical behaviour [15,56,57]. However, experimentation is not always possible and/or feasible. Therefore, numerical studies are conducted to predict the mechanical behaviour as well as to predict plausible failures. For truss-type structures, the finite element method is usually employed since it is one of the most powerful tools in engineering [14,22,57,58]. Pieraccini et al. studied the collapse of a spatial truss roof of a gym building in North Italy during a moderate snowfall by using the finite element method [59]. They reported that the elements and connections made by ductile or brittle materials influenced the bearing capacity of the roof structures and created geometric imperfections.
On the other hand, not all the failures occur slowly. As mentioned earlier, some collapses occur suddenly under excessive, impulsive loadings. This study aimed to study a case in which a sudden partial failure of a steel truss roof of a factory built in July 2011 happened during heavy weather conditions on 22 October 2012 in Cerkezkoy Tekirdag in the northwestern part of Turkey [8]. The main focus was on developing a plausible theory for the failure by employing numerical analyses performed using the finite element method, which covers various loading conditions and their combinations. Not only the truss roof but also the combination of the truss roof with the column supports were analysed. Thus, the results of numerical analyses were used to compare the obtained failure modes to the real failure, considering different criteria for the failure. The extreme loads due to the ponding of rainfall or snow accumulation and the temperature shock due to the thunderstorm were considered in the analyses. Even under these potential mechanical overloads, the observed damage was different from the actual damage: The damage caused by these excessive loads occurred in different regions than those in which the actual damage occurred. While the studies in the literature mostly describe failures due to vertical loads caused by water/snow accumulation or horizontal loads caused by wind, this study showed that the critical regions created by temperature change are similar to the actual damaged zones.

2. Theory and Case Study

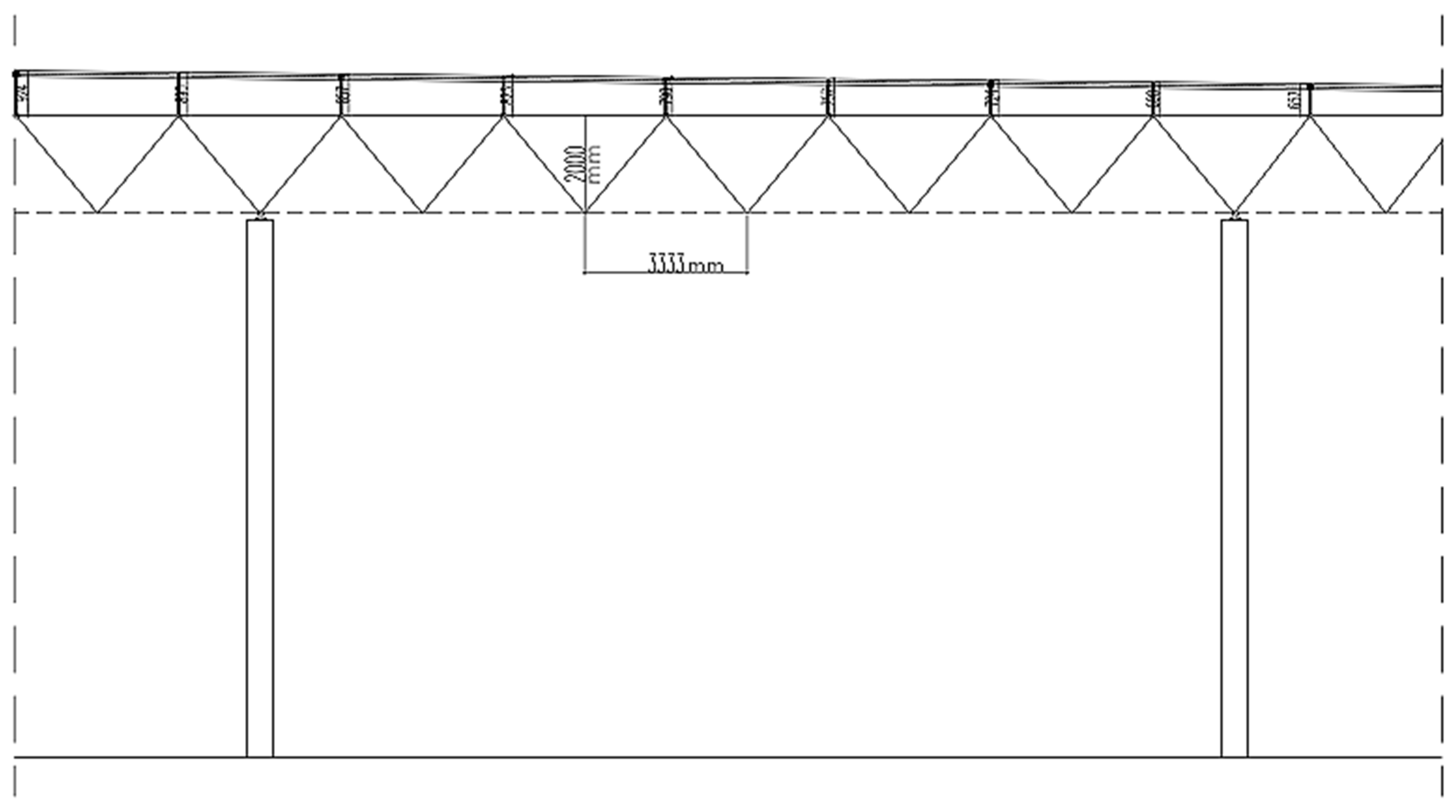
2.1. Overview of the Structure and the Case

The building consists of six partitions with different sizes and an administration office. The design and all the relevant details of the structure were provided by the company that undertook the design and the construction of the building. The steel truss roof structure, which is supported on steel-reinforced concrete columns, covers a total area of 30,180 m2.
The slope of the roof is 1% in each direction. The parapets of 15 and 25 cm heights surround the roof, which is equipped with a siphonic drainage system. The layout of the structure is presented schematically in Figure 1; the damaged parts are marked in white. The entire structure is made of seven partitions, including an administrative office and six halls where the industrial manufacturing took place.
The main dimensions of the unit truss system are presented in Figure 2. The steel carrier system consists of a double-layer truss with a depth of 2 m. The bars of this system have circular tube cross-sections with different wall thicknesses and diameters depending on their predicted loads. At both ends of the bars, screw threads are located to enable connecting those members to the mero system. The mero system includes steel spherical parts that have screw holes. It is noted that no eccentricity at the nodes is observed after the assembly of the individual members. The blocks are divided from each other with expansion joints.
The steel space truss roof structures are mounted on reinforced concrete columns that are 11 m tall with an 80 cm by 80 cm cross-section. The number of columns and their configuration can be seen in the plan view of the building, which is given in Figure 1. No failure, no deformation, and no cracks were observed on these columns during the investigations. Only some broken wings were observed on their top section, which was assumed to have happen during the collapse of the roof. Thus, it was concluded that the columns did not play a significant role in the collapse mechanism of this building. On top of the columns, the spherical joints are welded to the bearing plates. Figure 3 represents an overview of the real building structure, and Figure 4 shows the damaged roof of the space frame system on the night of the incident.
On the day of the incident, more than 500 lightning events were detected in the region by the British Meteorological Office’s (The Met Office) ATDnet (Arrival Time Difference Network) system and the Vaisala Global Lightning Dataset GLD360. It was determined that lightning struck the building and the lightning rods worked. Meteorological data indicate that the thunderstorms were rainy and the wind blew from 40 to 60 km/h from the north and northeast directions and up to 70 to 80 km/h locally. The rainfall was 22.6 mm during the collapse, although equally heavy local rainfalls had occurred several times in recent years. Around the roof, there are several siphonics at 5 cm height. The heights of the parapets on the roof are 15 cm and 25 cm. Although no scuppers are required to be used on such a shallow parapet, there are several scuppers of 15 cm height on the roof structure.

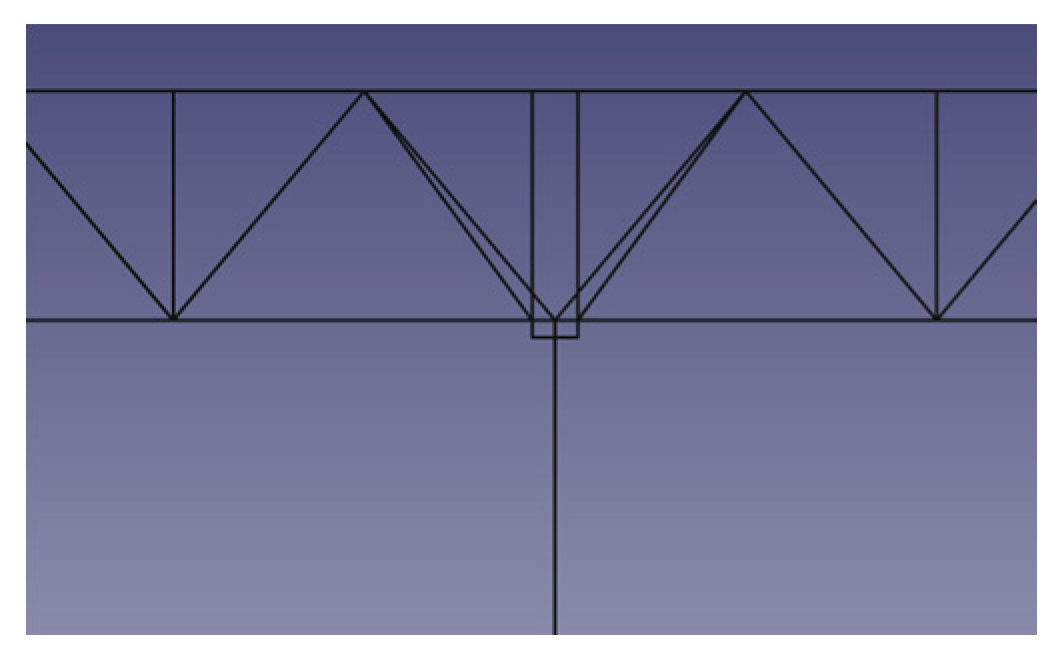
2.2. Structural Members

Members with steel tube sections of different diameters and thicknesses are used in the truss roof system. The pipe elements with screwed cone ends are connected to the hot forged steel spherical joints. These joints ensure that no eccentricity occurs and the only axial forces are developed in the bars of the truss system. The yield strength of the material (S235JR) of the bars and the cone parts at the ends of them (DIN 2458) is 235 MPa, ultimate tensile strength is 510 MPa, and the allowable stress is 144 MPa. The bolts used for mounting the bars to the spherical joints are made of 10.9 material quality. The tensile strength of the bolts is 1000 MPa, yield strength 900 MPa, and the allowable strength is 360 MPa, in which the safety factor is 2.5. The spherical joints used to connect the rods to each other and the supports are made of hot forged steel with a yield stress of 330 MPa and a tensile strength of 590 MPa. The strength values and the chemical decompositions of the materials used in the truss roof system were validated by Piroglu et al. [8].
The support spheres are fixed onto the concrete columns by using square or circular plates bolted to the columns. The supports are made of EN C45 steel, and Teflon plates are placed under the sliding supports to reduce friction. The details of the joints and supports are given in Figure 5.

3. Analysis

Two main groups of analyses were performed within the scope of this study. The first group was called the global analysis, where all the load-carrying members of the building were considered as beams and bars, while the second group considered the individual columns and supports.
The first group included multiple case scenarios with different combinations of loads. Only two major cases are presented in this study for the sake of simplicity.
The second group consisted of two stages. The first stage investigated the effective material properties of the concrete column reinforced with steel rods under uniaxial tensile strain conditions. Thus, the column was handled as a composite material. The second stage investigated the individual column support connection under the highest forces determined by the global model acting on an individual support.
All the simulations were conducted using the commercial software Abaqus (Dassault Systèmes, Vélizy-Villacoublay, France) under static loading assumptions.
The values of the three most important material properties, namely Young’s modulus (E), Poisson’s ratio (ν), and the thermal expansion coefficient (α) are shown in Table 1.

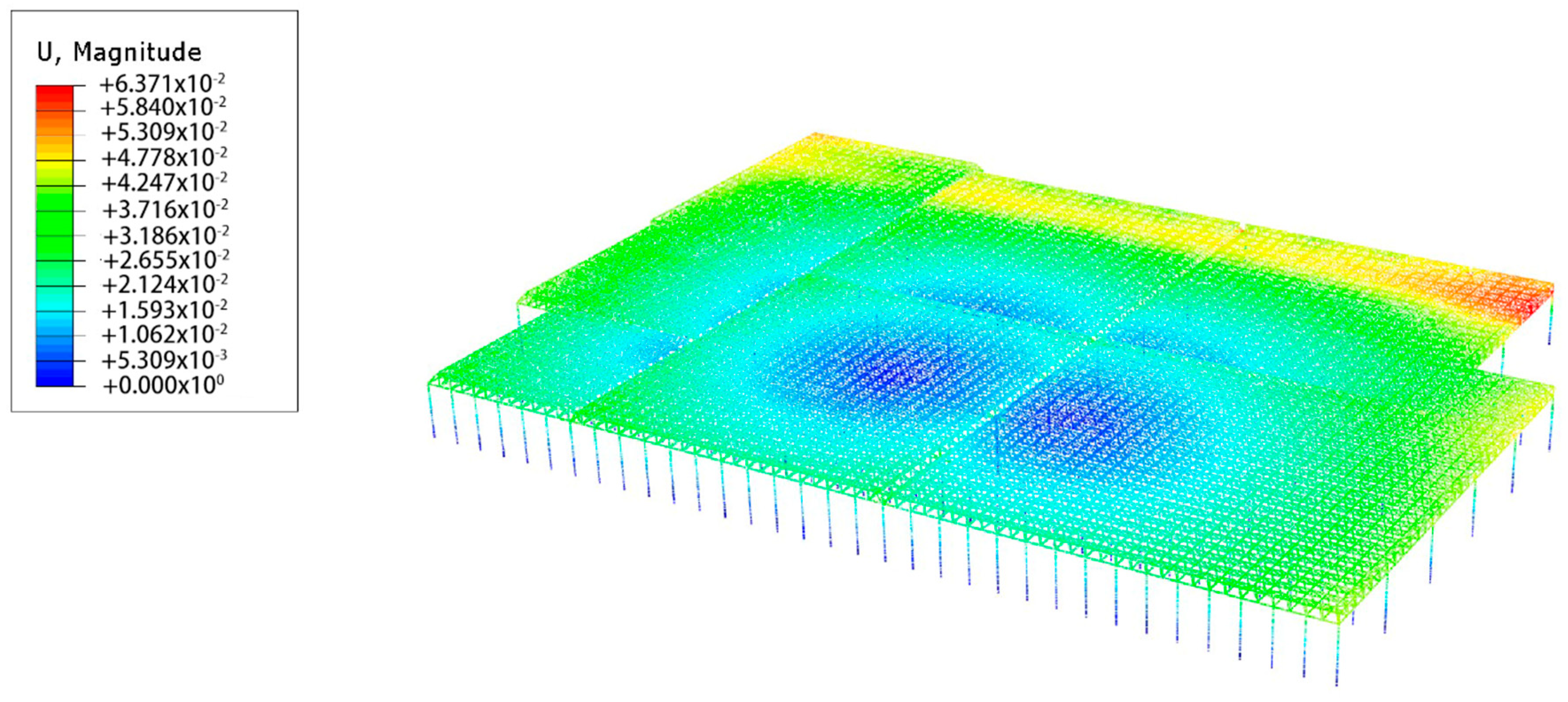
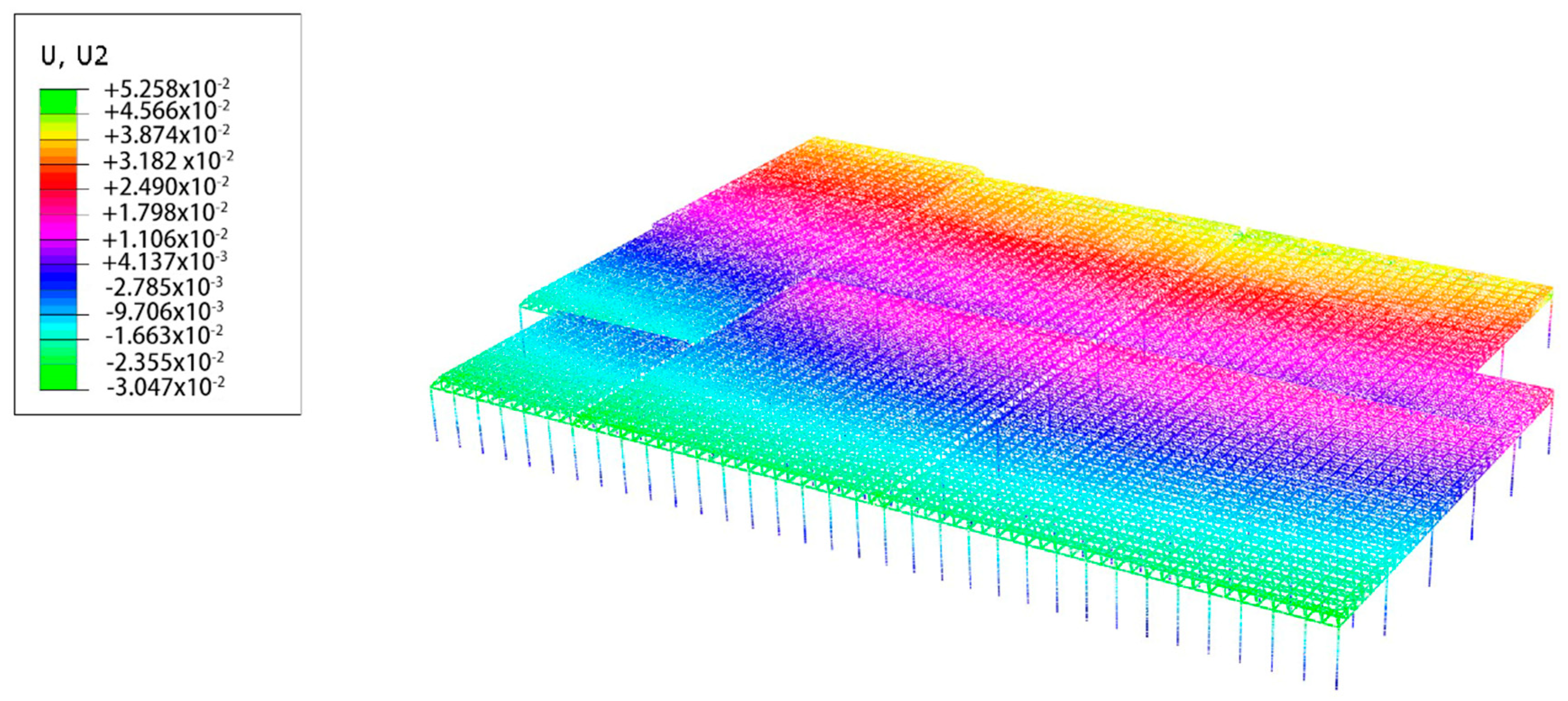
3.1. Global Analysis

The given design of the structure was recreated in a compatible computer aided design (CAD) format and was imported into the commercial finite element software mentioned above. The finite element model was used to simulate some assumptions and certain loading conditions with a consideration of geometric nonlinearities. The boundary conditions were defined as appropriate to the actual structure and the loads applied to the truss roof system were defined as given in Table 2, which are greater than the loads that are assumed for the design. So, the main purpose of this global analysis was to generate a better understanding of the mechanical behaviour of the roof and to predict the failure modes under different loads and assumptions. It is worthy of note that all the analyses were run in a static manner. Since the equivalent static loads are determined using the relevant Turkish standards, it is appropriate to use this simplification [8].
One of the most important aspects here is that the presented strength and elastic properties of the materials and members used were put through tests and experimental processes and were found to be consistent in general with the standards [8]. So, in the analyses performed for this study, the values that were presented in the reports of the company were mainly used.
Different dead, live, snow, temperature, and earthquake loads were considered in the design. Rain load caused by an excessive accumulation of water, especially on low-slope or flat roofs where the parapets are mounted around the roof, can cause partial or total destruction if they are not considered in the design. However,, rainfall ponding on the roof is considered in the design. The design code used gives wind loads for buildings of 20–90 m tall as 0.8 kN/m2 (pressure) on the windward and −0.4 kN/m2 (suction) on the leeward sides. For the seismic loads, the earthquake acceleration is taken as 0.3 g, where g is the gravitational acceleration, so the earthquake loads are overestimated [8].
The loads acting on the space truss system are to be transmitted to the bars over the spherical steel elements, called nodes. The weight of the space truss roof system is taken as 140 N/m2, the dead load from coatings and the installation is given in the design documents as 240 N/m2, but it was assumed to be 350 N/m2 in the analysis. The snow load is given in the design calculations as 1000 N/m2 and was taken as 2000 N/m2 in the analysis. The equivalent earthquake horizontal load is given as 180 N/m2 in the design calculations and was considered here as 200 N/m2. The equivalent earthquake vertical load was 950 N/m2 and the vertical wind load was 960 N/m2. Table 2 gives the loads used in the analyses.
The boundary conditions of the space truss system and the columns were arranged as the original design of the structure.
The bars of the space truss were modelled based on the standards of DIN S235 JR for quality linear elastic materials, and columns were modelled as C35 grade homogeneous and linear elastic steel-reinforced concrete with the elasticity modulus, which was determined using the homogenisation of the composite column analysis. The bar elements in the space truss system and the beam elements in the columns were assembled as a whole system of 160,133 elements and 461,847 nodes. Figure 6 displays the model for global analysis in a commercial finite element software. With this model, a static global analysis of the space truss system was performed with the above-mentioned loads being quite a bit larger than the design loads.

3.2. Analysis of the Columns and Supports

This section covers the analyses performed to gain more insights into the mechanical behaviour of the columns and the supports, which either were not very accurately represented in the global model or to increase the accuracy of the global model. The first stage of these analyses aimed to homogenise the composite column and the second stage investigates the mechanical behaviour of the column and support behaviour focusing on the stress/strength of the structure.

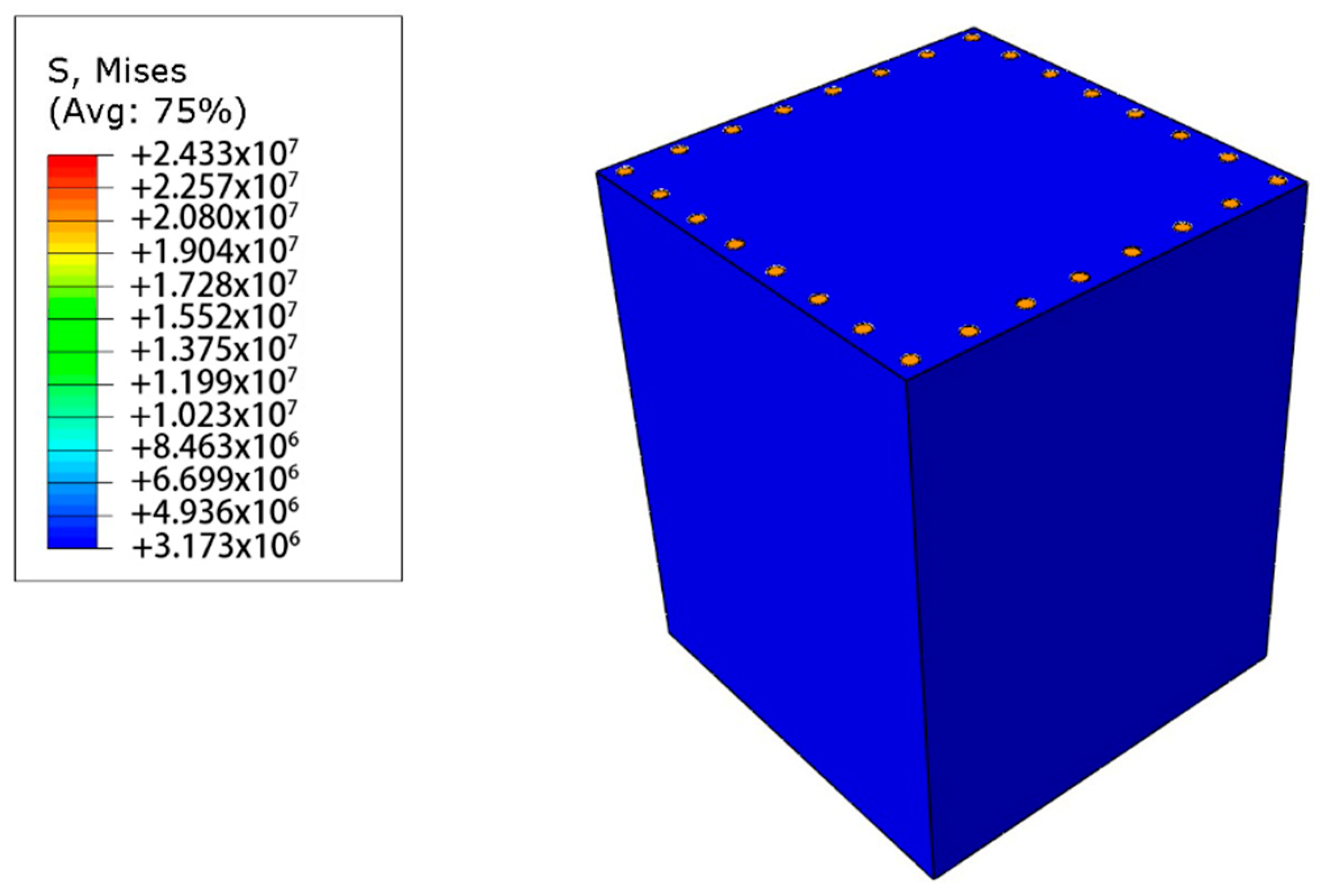
3.2.1. Analysis of the Steel-Reinforced Columns

The main purpose of this analysis was to understand the effective material properties of the steel-reinforced concrete columns by using three-dimensional finite elements. Here, the column was assumed to be a composite beam and its material properties were calculated with homogenisation. Thus, the aim was to obtain a more realistic global model. For this purpose, a model was created considering the steel reinforcement of the concrete columns. In this model, the column material was considered as a composite material with concrete and reinforcing steel rods. The steel rods were placed in the concrete as shown in Figure 7. The rods and the concrete were rigidly bonded to each other. According to the general theory of mechanics of composite materials, lateral reinforcement steel binders, which are predicted to have no significant effect on axial stiffness, were not included in the analysis for the sake of simplicity. The steel reinforcing rods were taken as given in the project and as described in the previous section.
To represent the behaviour, a cross-sectional face was subjected to axial displacement restrictions whereas the opposite face, which is the other cross-sectional face, was subjected to a uniform axial displacement. Using the results of the analysis, the effective Poisson’s ratio and Young’s modulus were determined. A similar procedure was also performed for the effective thermal expansion coefficient. The results of this analysis were used in the global analysis.

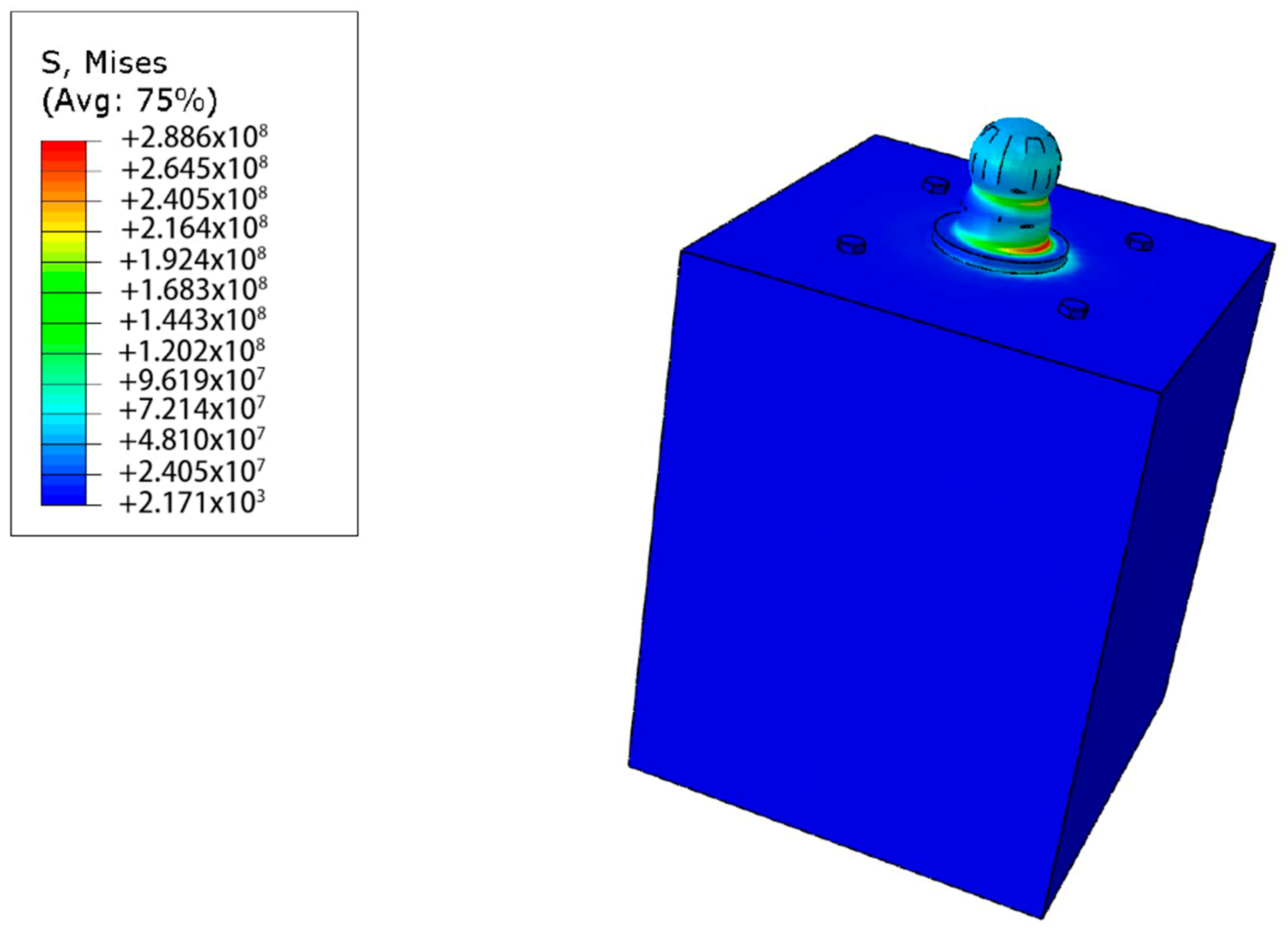
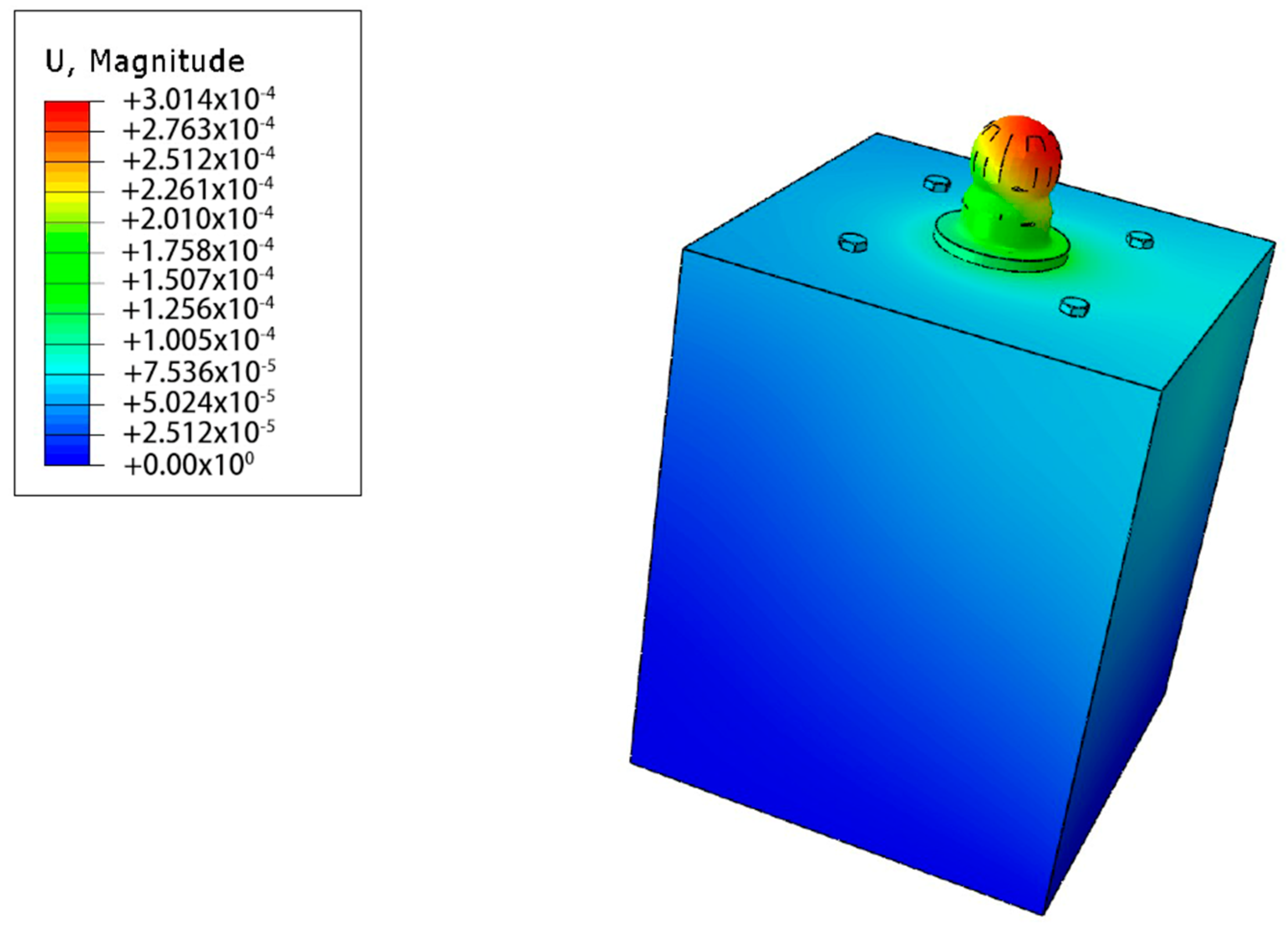
3.2.2. Analysis of the Spherical Support with Steel-Reinforced Columns

This part of the study was interested in the mechanical behaviour and safety of the column and spherical support structures. This study used the highest mechanical loads acting on a single truss-column connection node calculated in the global analysis. It is also important to note that this analysis considered only the mechanical loads and did not consider any thermal effects. The analysis of the column support connection was performed with a three-dimensional finite element model.
The column support connection was built such that the sphere was mounted on the support plate, which is embedded in the steel-reinforced concrete with a bolt connection. The structure of this model is given in Figure 8.
The contact interfaces between the steel rods and concrete were rigidly bonded and so too were the contact surfaces between the spherical support and the steel plate. The bolts were attached to the model with a standard preload and connected to the steel plate and concrete with friction.
The bottom cross-sectional face was connected to a grounded spring with 6 degrees of freedom and with the stiffness values of the rest of the column, to save computational time.

4. Results and Discussion

In this section, the results of the analyses are presented and discussed. Based on the interpretations of the results that match the actual failure form of the structure, a scenario, which is judged the most plausible, is described and discussed.

4.1. Analysis of the Steel-Reinforced Columns

The homogenisation study was conducted and the results are presented here. Figure 9 shows the equivalent stress distribution in the case of axial loading of the composite structure and Figure 10 shows displacement distribution. As a result of this analysis, the elasticity modulus and the resultant thermal expansion coefficient of the steel-reinforced concrete were calculated as 48 GPa and 12.8 μm/(m K), respectively. This axial elasticity modulus value was 50 GPa in the global analysis.

4.2. Global Analysis with Only Mechanical Loads

The displacements and the stresses occurring in the truss roof system were calculated by using the finite element analysis software. Figure 11 shows the vertical displacement (in meters) under the considered loads. The largest displacements of about 4.7 cm occurred in blocks A, C, and E, where the gap between the columns was the largest (28 m), as was expected. It should be noted here that due to the positive direction of the axis, which is upwards, blue colours are around zero and red is the largest in terms of absolute values. The region of the larger resultant displacements is not where the real damage happened. The deformations of the column structures are so small that they do not suggest any safety issues. The analyses demonstrate clearly that the system is safe and that the results are consistent with the results obtained by the engineering bureau.
Considering the stress analysis, the equivalent stresses using the von Mises criteria were calculated for all the structures. Figure 12 gives the von Mises stresses in the roof structure (in Pa). It can be seen that all stresses of the roof structure together with the columns are within the safety limits. The collapsed regions are also within the safety limits. As well as the displacements, the stresses occurring in the column structures are well below the safety limits. Although exaggerated loads are applied on the roof structure, the stresses and displacements in the beams and rods show that the structure would not fail under these combinations of excessive loads.
The greatest stresses occur at these “U” shaped connections shown in Figure 13; however, the displacements are not excessive. It is important to note that this connection structure does not exist in the real application. These connections are used in the CAD/FE model in order not to distort the dimensions of the truss structure. In reality, there are walls with certain thicknesses whereas the FE model used beam elements. To connect the trusses with the supports, such a “dummy” structure was used. Therefore, the stress values that were read at these connections were disregarded.

4.3. Analysis of the Spherical Support with Steel-Reinforced Columns

After concluding that the global structure is safe, the next step was to analyse an individual column support by using the finite element method. The results of the global analysis were used to determine the support reactions. At the most dangerous column support connection, the horizontal force was 95 kN and vertical force was 940 kN. The forces were taken as 120 kN in horizontal and 1000 kN in vertical directions.
The equivalent stress distribution obtained in this case is shown in Figure 14. As can be clearly seen from this figure, the stress levels are below the yield stress, even though extreme loads are applied. Figure 15 shows a post-damage image of one of the columns to which the space frame roof system was attached.
Figure 16 shows the distribution of the resultant displacement that occurs in the column support connection. Here, it can be seen that the maximum value of the displacement compounds of the spherical support was around 0.3 mm.

4.4. Global Analysis with Mechanical Loads and Thermal Effects

With these results obtained from the global analysis it was found that increasing horizontal forces may cause damage, various damage scenarios were investigated by changing the loads applied to the space frame system. As the first case, the vertical load was increased considerably and no damage was predicted in the real damaged zones A and F, as given in Figure 1. As the next case, the structure was tested by increasing the horizontal load. Although the horizontal load value was increased to a level that cannot be reached by wind and similar factors, the damage that occurred cannot be explained with these combinations of loads. However, the structure was found to be more sensitive and vulnerable to the horizontal loads. Finally, it was understood that the space frame system with the columns is safe against vertical loads (snow, water, etc.) and horizontal loads (wind, etc.).
It is obvious that different factors must have been present in order to explain the real damage in the structure. Therefore, considering the natural events occurring on the night of the event, their effects on the structure were considered. It was assumed that reasons such as heavy rain that leads to ponding on the roof with a slope of 1% and a plausibly clogged water discharging drainage system would not cause damage similar to that which occurred. Besides, around the rooftop surface there are several scuppers with 15 cm height. Even with the assumption of full ponding of the roof with 15 cm height, it can be confidently claimed that the chosen loads for the analysis were on the cautious side and led to conservative results, which do not point out any damage predictions similar to the real damage.
On the other hand, a large number of lightning strikes were detected on the night of the incident. The effects of lightning depend on the energy of the lightning itself. The energy of lightning, which is impossible to fully determine, depends on many parameters, such as the altitude of the cloud where the lightning originates. It is well known that this discharged energy heats up a considerable amount of air surrounding the core of the lightning. The temperature rise is so rapid and significant that it can start fires near the location where lightning strikes [37]. Furthermore, when lightning strikes a building, the electric current passes through the structure, which leads to a sudden heat generation and a rapid increase of temperature [29,37,38]. Besides, quite large shock forces occur due to the interaction of large masses of hot and cold air around it, and also due to the humidity of the air and the ground, which is called the blast effect. In addition, it is known that the presence of water amplifies the blast effect and interacts with the structure under electric current [34]. Therefore, it is thought that these great shock forces can cause instant damage.
Even though it is judged that the structure is heated, it is impossible to predict or evaluate the exact or even approximate rise of temperature. For the purpose of understanding the underlying factors that led to the damage shown in Figure 1, the effects of temperature change on the structure were investigated using a simplified approach. The space frame system was given a temperature increase of 50 °C. Lightning is most likely to cause a local thermal shock and not heat up the entire structure. However, it is impossible to know the number of lightning strikes, the generated heat, the temperature rise, generated blast, etc.
Based on these assumptions, a 50 °C temperature increase was applied to the global model alongside the external loads as described in the previous global analysis. A new static model was built and the results are given in Figure 17, Figure 18, Figure 19, Figure 20 and Figure 21. Figure 17 shows the equivalent stresses of von Mises occurring in the space truss systems and columns. It can be seen that the stresses coming out of this figure are quite safe. However, it has been found that the stress values in the support joints reach values exceeding the safety limits, and the supports reaching these values are concentrated in the areas where damage occurred. The reason for the great stress values in this global model is that the model is simple and gives a general idea. It would be appropriate to consider separately the situations in the supports with large stresses.
It is also to be noted that the “U” shaped connections between the steel truss structures and the supports on the walls display the greatest stresses, which is not realistic, as these connections do not exist in the real structures. Therefore, those stress values were disregarded.
Figure 18 shows the resultant displacements that occurred throughout the system. From this figure, it can be seen that displacements are suitable and larger displacements occurred in the regions where the damage occurred.
Furthermore, Figure 19 shows the displacements in the long-edge direction, x-direction. This figure clearly shows that there were large displacements in the areas where the damage occurred. Figure 20 shows the displacements in the direction of the short edge of the building, the so-called y-direction. It is to be noted that the larger displacements were observed in the direction along the shorter edge, whereas the larger displacements due to thermal expansion were expected in the direction of the long edge. The reason behind this can be explained with different stiffness levels of the structure in different directions and boundary conditions of the supports. As can be seen from Figure 6, the number of columns in the first two rows of the halls B, D, and F are much more intensively positioned than that seen in the rest of the building. Moreover, the intensity of the columns in the x-direction is greater than the intensity of columns in the y-direction. Therefore, the stiffness in the x-direction is expected to be greater than the stiffness in the y-direction. The sliding supports and the stiffness of the structure allow the structure to deform in the y-direction more than it can in the x-direction, even though the tendency to deform is more in the x-direction than in the y-direction. This leads to the storage of a larger amount of energy in the x-direction. Additionally, since, there was no damage in the spherical supports themselves, as can be seen in Figure 15, the excessive displacements caused larger stress values in the bolt connections between the spherical parts and the members. Therefore, it was found plausible that this mechanism caused the actual failure.
The displacements of the structure in the vertical direction are given in Figure 20. Comparing the vertical displacements of the previous global analysis and this one (Figure 11 and Figure 21), both cases display very similar distribution trends but the new one exhibits larger displacements. This is because there is a synergy effect based on the complex loading, and the thermal expansion leads to extra loading and elongation in horizontal directions.

5. Conclusions

The space truss roof structure, the columns, and the spherical steel supports of the factory building were put through several numerical analyses, and their behaviour was evaluated using the commercial software Abaqus (Dassault Systèmes, Vélizy-Villacoublay, France). These static stress analyses were performed using the finite element method and considering geometric nonlinearities. Based on the results of these simulations, the following conclusions about the real failure of the structure were drawn:
−
According to the global analysis, the structure is quite strong and insensitive to the vertical dead loads (rain, snow, etc.) even at some higher values, which are judged to be extreme and unrealistic. The most dangerous region of the space frame system in terms of vertical loads is the corridor with the largest column span in the A, C, and E blocks. However, this region is still safe, and the damage occurred somewhere else.
−
Using the results of the global analysis, the most critical support connection was individually investigated and found safe, although it is more sensitive to horizontal forces. However, in the analysis, all the effects that create lateral forces caused by the wind and similar homogeneous distributed loads could not make the structure exceed the safety limits and cause any damage in the locations where the real damage occurred.
−
It is judged that the thermal expansion of structural members increases the horizontal forces at the supports and the stresses at the members. The temperature change was assumed to be caused by lightning strikes. To investigate the effects of the temperature change, a simplified analysis with a uniform temperature rise was conducted and produced results that point out critical regions that are the same as the real damaged zones.
−
The significant change of temperature of the air surrounding the lightning channel and the electric current that passes through the structure may cause heating of the roof system rapidly and locally. The lightning at the scene may also cause a sudden pressure change that can be amplified by the presence of water on top of the structural surface. In addition to the thermal expansion, it is judged possible that the blast effect may have a significant role in the failure of the structure.
−
Testing the idea of temperature change, the damage prediction was found to be consistent with the real failure mode. It was concluded that the bolts and the bolted members attached to the supports in the real damaged regions of the space truss roof system were overloaded and damaged, as it can be seen in Figure 15.

Author Contributions

Conceptualization, E.T. and A.D.; methodology, E.T. and A.D.; software, M.T.; validation, E.T., A.D., and M.T.; formal analysis, M.T., E.T., and A.D.; investigation, M.T.; resources, A.D.; data curation, M.T.; writing—original draft preparation, M.T., E.T., and A.D.; writing—review and editing, M.T., E.T., and A.D.; visualization, M.T.; supervision, E.T. and A.D.; project administration, A.D.; All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Acknowledgments

The authors would like to thank İnci Pir for her support in visualizing the results.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Wu, Z.; Rong, J.; Liu, C.; Liu, Z.; Shi, W.; Xin, P.; Li, W. Dynamic analysis of spatial truss structures including sliding joint based on the geometrically exact beam theory and isogeometric analysis. Appl. Sci. 2020, 10, 1231. [Google Scholar] [CrossRef] [Green Version]
  2. Hadipriono, F.C. Analysis of Events in Recent Structural Failures. J. Struct. Eng. 1985, 111, 1468–1481. [Google Scholar] [CrossRef]
  3. Klasson, A.; Björnsson, I.; Crocetti, R.; Hansson, E.F. Slender Roof Structures—Failure Reviews and a Qualitative Survey of Experienced Structural Engineers. Structures 2018, 15, 174–183. [Google Scholar] [CrossRef]
  4. Deshpande, V.S.; Fleck, N.A. Collapse of truss core sandwich beams in 3-point bending. Int. J. Solids Struct. 2001, 38, 6275–6305. [Google Scholar] [CrossRef]
  5. Ballarini, R.; La Mendola, L.; Le, J.L.; Monaco, A. Computational study of failure of hybrid steel trussed concrete beams. J. Struct. Eng. 2017, 143, 1–13. [Google Scholar] [CrossRef] [Green Version]
  6. Wu, Y.; Xiao, Y. Steel and glubam hybrid space truss. Eng. Struct. 2018, 171, 140–153. [Google Scholar] [CrossRef]
  7. Sun, W.; Zhang, Q. Universal equivalent static wind loads of fluctuating wind loads on large-span roofs based on compensation of structural frequencies and modes. Structures 2020, 26, 92–104. [Google Scholar] [CrossRef]
  8. Piroglu, F.; Ozakgul, K.; Iskender, H.; Trabzon, L.; Kahya, C. Site investigation of damages occurred in a steel space truss roof structure due to ponding. Eng. Fail. Anal. 2014, 36, 301–313. [Google Scholar] [CrossRef]
  9. Goto, Y.; Kawanishi, N.; Honda, I. Dynamic stress amplification caused by sudden failure of tension members in steel truss bridges. J. Struct. Eng. 2011, 137, 850–861. [Google Scholar] [CrossRef]
  10. Geis, J.; Strobel, K.; Liel, A. Snow-Induced Building Failures. J. Perform. Constr. Facil. 2012, 26, 377–388. [Google Scholar] [CrossRef]
  11. Altunişik, A.C.; Ateş, Ş.; Hüsem, M. Lateral buckling failure of steel cantilever roof of a tribune due to snow loads. Eng. Fail. Anal. 2017, 72, 67–78. [Google Scholar] [CrossRef]
  12. Thai, H.T.; Kim, S.E. Nonlinear inelastic time-history analysis of truss structures. J. Constr. Steel Res. 2011, 67, 1966–1972. [Google Scholar] [CrossRef]
  13. Shivarudrappa, R.; Nielson, B.G.; Asce, M. Sensitivity of load distribution in light-framed wood roof systems due to typical modeling parameters. J. Perform. Constr. Facil. 2013, 27, 222–234. [Google Scholar] [CrossRef]
  14. Malla, R.B.; Nalluri, B.B. Dynamic effects of member failure on response of truss-type space structures. J. Spacecr. Rockets 1995, 32, 545–551. [Google Scholar] [CrossRef]
  15. Parisi, M.A.; Piazza, M. Seismic behavior and retrofitting of joints in traditional timber roof structures. Soil Dyn. Earthq. Eng. 2002, 22, 1183–1191. [Google Scholar] [CrossRef]
  16. Pollino, M.; Bruneau, M. Seismic testing of a bridge steel truss pier designed for controlled rocking. J. Struct. Eng. 2010, 136, 1523–1532. [Google Scholar] [CrossRef] [Green Version]
  17. Sosorburam, P.; Yamaguchi, E. Seismic retrofit of steel truss bridge using buckling restrained damper. Appl. Sci. 2019, 9, 2791. [Google Scholar] [CrossRef] [Green Version]
  18. Chou, C.C.; Chen, J.H. Seismic tests of post-tensioned self-centering building frames with column and slab restraints. Front. Archit. Civ. Eng. China 2011, 5, 323–334. [Google Scholar] [CrossRef]
  19. Zhao, H.; Ding, Y.; Nagarajaiah, S.; Li, A. Longitudinal displacement behavior and girder end reliability of a jointless steel-truss arch railway bridge during operation. Appl. Sci. 2019, 9, 2222. [Google Scholar] [CrossRef] [Green Version]
  20. Rezaei, S.; Akbari Hamed, A.; Basim, M.C. Seismic performance evaluation of steel structures equipped with dissipative columns. J. Build. Eng. 2020, 29. [Google Scholar] [CrossRef]
  21. Qu, W.L.; Chen, Z.H.; Xu, Y.L. Dynamic Analysis of Wind Excited Truss Tower With Friction Dampers. Comput. Struct. 2001, 79, 2817–2831. [Google Scholar] [CrossRef]
  22. Spyrakos, C.C.; Raftoyiannis, I.G.; Ermopoulos, J.C. Condition assessment and retrofit of a historic steel-truss railway bridge. J. Constr. Steel Res. 2004, 60, 1213–1225. [Google Scholar] [CrossRef]
  23. Zheng, H.D.; Fan, J. Analysis of the progressive collapse of space truss structures during earthquakes based on a physical theory hysteretic model. Thin-Walled Struct. 2018, 123, 70–81. [Google Scholar] [CrossRef]
  24. Maraveas, C.; Tsavdaridis, K.D. Assessment and retrofitting of an existing steel structure subjected to wind-induced failure analysis. J. Build. Eng. 2019, 23, 53–67. [Google Scholar] [CrossRef]
  25. Foraboschi, P. Lateral load-carrying capacity of steel columns with fixed-roller end supports. J. Build. Eng. 2019, 26. [Google Scholar] [CrossRef]
  26. Rakov, V.A. The physics of lightning. Surv. Geophys. 2013, 34, 701–729. [Google Scholar] [CrossRef]
  27. Hartono, Z.A.; Ibrahim, R. A database of lightning damage caused by bypasses of air terminals on buildings in Kuala Lumpur, Malaysia. In Proceedings of the VI International Symposium on Lightning Protection, Santos, Brazil, 19–23 November 2001. [Google Scholar]
  28. Bothma, J.G. Transmission line tower collapse investigation: A case study. In Proceedings of the IEEE Power and Energy Society Conference and Exposition in Africa: Intelligent Grid Integration of Renewable Energy Resources (PowerAfrica), Johannesburg, South Africa, 9–13 July 2012. [Google Scholar] [CrossRef]
  29. Mills, B.; Unrau, D.; Pentelow, L.; Spring, K. Assessment of lightning-related damage and disruption in Canada. Nat. Hazards 2010, 52, 481–499. [Google Scholar] [CrossRef]
  30. Zhang, W.; Meng, Q.; Ma, M.; Zhang, Y. Lightning casualties and damages in China from 1997 to 2009. Nat. Hazards 2011, 57, 465–476. [Google Scholar] [CrossRef]
  31. Krausmann, E.; Renni, E.; Campedel, M.; Cozzani, V. Industrial accidents triggered by earthquakes, floods and lightning: Lessons learned from a database analysis. Nat. Hazards 2011, 59, 285–300. [Google Scholar] [CrossRef]
  32. Patel, K. Effect of Lightning on Building and Its Protection Measures. Int. J. Eng. Adv. Technol. 2013, 2, 182. [Google Scholar]
  33. Blong, R. Residential building damage and natural perils: Australian examples and issues. Build. Res. Inf. 2004, 32, 379–390. [Google Scholar] [CrossRef]
  34. Shivalli, S. Lightning Phenomenon, Effects and Protection of Structures from Lightning Sanketa Shivalli. IOSR J. Electr. Electron. Eng. 2016, 11, 44–50. [Google Scholar]
  35. Zhivlyuk, Y.; Mandel’shtam, S. On the temperature of lightning and force of thunder. Sov. Phys. JETP 1961, 13, 338–340. [Google Scholar]
  36. Mu, Y.; Yuan, P.; Wang, X.; Dong, C. Temperature distribution and evolution characteristic in lightning return stroke channel. J. Atmos. Solar-Terrestrial Phys. 2016, 145, 98–105. [Google Scholar] [CrossRef]
  37. Elsom, D.M.; Webb, J.D.C. Lightning Impacts in the United Kingdom and Ireland. In Extreme Weather; Wiley-Blackwell: Hoboken, NJ, USA, 2016; pp. 195–207. [Google Scholar]
  38. Holle, R.L.; López, R.E.; Arnold, L.J.; Endres, J. Insured Lightning-Caused Property Damage in Three Western States. J. Appl. Meteorol. 1996, 35, 1344–1351. [Google Scholar] [CrossRef] [Green Version]
  39. Kmet, S.; Tomko, M.; Demjan, I.; Pesek, L.; Priganc, S. Analysis of a damaged industrial hall subjected to the effects of fire. Struct. Eng. Mech. 2016, 58, 757–781. [Google Scholar] [CrossRef]
  40. Usmani, A.S. Stability of the world trade center twin towers structural frame in multiple floor fires. J. Eng. Mech. 2005, 131, 654–657. [Google Scholar] [CrossRef]
  41. Behnam, B. Fire Structural Response of the Plasco Building: A Preliminary Investigation Report. Int. J. Civ. Eng. 2019, 17, 563–580. [Google Scholar] [CrossRef]
  42. Mwangi, S. Why Broadgate Phase 8 composite floor did not fail under fire: Numerical investigation using ANSYS® FEA code. J. Struct. Fire Eng. 2017, 8, 238–257. [Google Scholar] [CrossRef]
  43. Usmani, A.S.; Chung, Y.C.; Torero, J.L. How did the WTC towers collapse: A new theory. Fire Saf. J. 2003, 38, 501–533. [Google Scholar] [CrossRef] [Green Version]
  44. Meppelink, J. The Impact of a lightning Stroke on a Flat Roof When the Building is Filled with Water. In Proceedings of the ICLP ‘98, 24th International Conference on Lightning Protection, Birmingham, UK, 14–18 September 1998; pp. 826–831. [Google Scholar]
  45. Li, H.; Wu, G. Fatigue evaluation of steel bridge details integrating multi-scale dynamic analysis of coupled train-track-bridge system and fracture mechanics. Appl. Sci. 2020, 10, 3261. [Google Scholar] [CrossRef]
  46. Blandford, G.E. Progressive failure analysis of inelastic space truss structures. Comput. Struct. 1996, 58, 981–990. [Google Scholar] [CrossRef]
  47. Blandford, G.E. Review of Progressive Failure Analyses for Truss Structures. J. Struct. Eng. 1997, 123, 122–129. [Google Scholar] [CrossRef]
  48. Malla, R.B.; Agarwal, P.; Ahmad, R. Dynamic analysis methodology for progressive failure of truss structures considering inelastic postbuckling cyclic member behavior. Eng. Struct. 2011, 33, 1503–1513. [Google Scholar] [CrossRef]
  49. Machaly, E.S.B. Buckling contribution to the analysis of steel trusses. Comput. Struct. 1986, 22, 445–458. [Google Scholar] [CrossRef]
  50. Murtha-Smith, E. Alternate Path Analysis of Space Trusses for Progressive Collapse. J. Struct. Eng. 1999, 114, 1978–1999. [Google Scholar] [CrossRef]
  51. Astaneh-Asl, A. Progressive collapse of steel truss bridges, the case of I-35W collapse. In Proceedings of the International Conference on Steel Bridges, Guimarăes, Portugal, 4–6 June 2008; pp. 1–10. [Google Scholar]
  52. Tanzer, A. High school gymnasium roof truss support collapse. J. Fail. Anal. Prev. 2011, 11, 208–214. [Google Scholar] [CrossRef]
  53. Park, S.; Yun, C.B.; Roh, Y. Damage diagnostics on a welded zone of a steel truss member using an active sensing network system. NDT E Int. 2007, 40, 71–76. [Google Scholar] [CrossRef]
  54. Riasat Azim, M.; Gül, M. Damage Detection of Steel-Truss Railway Bridges Using Operational Vibration Data. J. Struct. Eng. 2020, 146, 1–12. [Google Scholar] [CrossRef]
  55. Wood, J.V.; Dawe, J.L. Full-scale test behavior of cold-formed steel roof trusses. J. Struct. Eng. 2006, 132, 616–623. [Google Scholar] [CrossRef]
  56. Fülöp, A.; Iványi, M. Experimentally analyzed stability and ductility behaviour of a space-truss roof system. Thin-Walled Struct. 2004, 42, 309–320. [Google Scholar] [CrossRef]
  57. Caglayan, O.; Yuksel, E. Experimental and finite element investigations on the collapse of a Mero space truss roof structure—A case study. Eng. Fail. Anal. 2008, 15, 458–470. [Google Scholar] [CrossRef]
  58. Piroglu, F.; Ozakgul, K. Partial collapses experienced for a steel space truss roof structure induced by ice ponds. Eng. Fail. Anal. 2016, 60, 155–165. [Google Scholar] [CrossRef]
  59. Pieraccini, L.; Palermo, M.; Trombetti, T.; Baroni, F. The role of ductility in the collapse of a long-span steel roof in North Italy. Eng. Fail. Anal. 2017, 82, 243–265. [Google Scholar] [CrossRef]
Applsci 10 07769 g001 550
Figure 1. Layout and damaged regions of the roof structure.
Figure 1. Layout and damaged regions of the roof structure.
Applsci 10 07769 g001
Applsci 10 07769 g002 550
Figure 2. Unit truss structure.
Figure 2. Unit truss structure.
Applsci 10 07769 g002
Applsci 10 07769 g003 550
Figure 3. Overview of the roof structure.
Figure 3. Overview of the roof structure.
Applsci 10 07769 g003
Applsci 10 07769 g004 550
Figure 4. Damage to the roof’s space truss system.
Figure 4. Damage to the roof’s space truss system.
Applsci 10 07769 g004
Applsci 10 07769 g005 550
Figure 5. View of the spherical joints and the supports.
Figure 5. View of the spherical joints and the supports.
Applsci 10 07769 g005
Applsci 10 07769 g006 550
Figure 6. Three-dimensional finite element model prepared for finite element (FE) analysis.
Figure 6. Three-dimensional finite element model prepared for finite element (FE) analysis.
Applsci 10 07769 g006
Applsci 10 07769 g007 550
Figure 7. CAD of a column with steel-reinforced concrete.
Figure 7. CAD of a column with steel-reinforced concrete.
Applsci 10 07769 g007
Applsci 10 07769 g008 550
Figure 8. CAD of the column support connection with steel-reinforced concrete.
Figure 8. CAD of the column support connection with steel-reinforced concrete.
Applsci 10 07769 g008
Applsci 10 07769 g009 550
Figure 9. Stress distribution in the case of axial stress on the steel-reinforced concrete column.
Figure 9. Stress distribution in the case of axial stress on the steel-reinforced concrete column.
Applsci 10 07769 g009
Applsci 10 07769 g010 550
Figure 10. Displacement distribution of the steel-reinforced concrete column in the case of axial stress.
Figure 10. Displacement distribution of the steel-reinforced concrete column in the case of axial stress.
Applsci 10 07769 g010
Applsci 10 07769 g011 550
Figure 11. Vertical displacement of the steel-reinforced concrete column system.
Figure 11. Vertical displacement of the steel-reinforced concrete column system.
Applsci 10 07769 g011
Applsci 10 07769 g012 550
Figure 12. Equivalent von Mises stress distribution of the steel-reinforced concrete columns.
Figure 12. Equivalent von Mises stress distribution of the steel-reinforced concrete columns.
Applsci 10 07769 g012
Applsci 10 07769 g013 550
Figure 13. Connections with the supports and steel truss at the block interfaces.
Figure 13. Connections with the supports and steel truss at the block interfaces.
Applsci 10 07769 g013
Applsci 10 07769 g014 550
Figure 14. Equivalent stress distribution of the column support connection.
Figure 14. Equivalent stress distribution of the column support connection.
Applsci 10 07769 g014
Applsci 10 07769 g015 550
Figure 15. Damage on the support to which the space truss roof system was attached.
Figure 15. Damage on the support to which the space truss roof system was attached.
Applsci 10 07769 g015
Applsci 10 07769 g016 550
Figure 16. Resultant displacement distribution of the column support connection.
Figure 16. Resultant displacement distribution of the column support connection.
Applsci 10 07769 g016
Applsci 10 07769 g017 550
Figure 17. Stresses due to load and thermal effects in the space frame and steel-reinforced concrete column system.
Figure 17. Stresses due to load and thermal effects in the space frame and steel-reinforced concrete column system.
Applsci 10 07769 g017
Applsci 10 07769 g018 550
Figure 18. Resultant displacements due to load and thermal effects in the space frame and steel-reinforced concrete column system.
Figure 18. Resultant displacements due to load and thermal effects in the space frame and steel-reinforced concrete column system.
Applsci 10 07769 g018
Applsci 10 07769 g019 550
Figure 19. Displacements in the long-edge direction caused by load and thermal effects in the space frame and steel-reinforced concrete column system.
Figure 19. Displacements in the long-edge direction caused by load and thermal effects in the space frame and steel-reinforced concrete column system.
Applsci 10 07769 g019
Applsci 10 07769 g020 550
Figure 20. Displacements in the short-edge direction caused by load and thermal effects in the space frame and steel-reinforced concrete column system.
Figure 20. Displacements in the short-edge direction caused by load and thermal effects in the space frame and steel-reinforced concrete column system.
Applsci 10 07769 g020
Applsci 10 07769 g021 550
Figure 21. Displacements in the vertical direction caused by the loads in the space frame and steel-reinforced concrete column system.
Figure 21. Displacements in the vertical direction caused by the loads in the space frame and steel-reinforced concrete column system.
Applsci 10 07769 g021
Table
Table 1. The material properties considered in the analyses.
Table 1. The material properties considered in the analyses.
PropertySteelConcrete
Young’s modulus (E)210 GPa32 GPa
Poisson’s ratio (ν)0.280.20
Thermal expansion coefficient (α)13 μm/(m K)11.5 μm/(m K)
Table
Table 2. The loads considered in the analyses.
Table 2. The loads considered in the analyses.
Load DescriptionValue
Weight of the space truss system140 N/m2
Dead loads350 N/m2
(240 N/m2 given in design calculations)
Snow load2000 N/m2
(1000 N/m2 given in design calculations.)
Vertical wind loads960 N/m2
Equivalent earthquake vertical load950 N/m2
Equivalent earthquake horizontal load200 N/m2
(180 N/m2 given in design calculations)
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Tüfekci, M.; Tüfekci, E.; Dikicioğlu, A. Numerical Investigation of the Collapse of a Steel Truss Roof and a Probable Reason of Failure. Appl. Sci. 2020, 10, 7769. https://doi.org/10.3390/app10217769

AMA Style

Tüfekci M, Tüfekci E, Dikicioğlu A. Numerical Investigation of the Collapse of a Steel Truss Roof and a Probable Reason of Failure. Applied Sciences. 2020; 10(21):7769. https://doi.org/10.3390/app10217769

Chicago/Turabian Style

Tüfekci, Mertol, Ekrem Tüfekci, and Adnan Dikicioğlu. 2020. "Numerical Investigation of the Collapse of a Steel Truss Roof and a Probable Reason of Failure" Applied Sciences 10, no. 21: 7769. https://doi.org/10.3390/app10217769

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop