Abstract
This paper proposes a novel controller, fast fractional-order terminal sliding mode control (FFOTSMC), for a seven-degree-of-freedom (7-DOF) robot manipulator with tracking control. The new controller applies the fractional-order derivative on both the sliding surface design and the sliding control/reaching law. Compared to previous research, which only applies the fractional-order derivative on the sliding surface design, the proposed controller has a faster convergence for reaching the sliding surface and maintaining stay on it because of the new fractional-order control law, which helps the tracking accuracy. To implement the controller on the robot with less chattering, a sliding perturbation observer (SPO) is used to estimate the disturbance and uncertainties. Stability analysis is analyzed using Lyapunov functions for fractional-order systems. The controller performance is evaluated by a simulation of a single-input and single-output (SISO) system in MATLAB Simulink and experiments on the robot manipulator.
1. Introduction
Sliding mode control (SMC) has been widely studied and applied to robot manipulators because of its simplicity of implementation, fast global convergence, high robustness to external variations, and insensitivity to modeling error and system parameter variations [1]. SMC includes a conventional linear sliding mode (LSM) control, which is asymptotically stable, and a terminal sliding mode (TSM) control with finite-time stability [2,3]. Typically, it includes two steps to design an SMC: the choice of sliding surface and the control/reaching law to reach the sliding surface and maintain stay on it.
TSM control (TSMC) utilizes a nonlinear sliding surface instead of a linear sliding surface in sliding surface design. It generates faster convergence, less tracking errors than LSM control (LSMC), and finite stability for reaching the equilibrium point. The control/reaching law in TSMC also contains a nonlinear term, which allows the sliding surface to be reached in finite time with fast convergence. Compared to the LSMC, TSMC shows various superior properties such as fast and finite-time convergence and few tracking errors. However, in TSMC, the first-order derivative of the nonlinear term in TSM causes a singularity problem. In recent years, many researchers have focused on solving the singularity [4,5]. Using fractional calculus can avoid this singularity because of the hereditary and memory property, such as fractional-order TSMC (FOTSMC) [6]. FOTSMC was proposed with a terminal sliding surface using the fractional-order derivative. It can help avoid the singularity, which exists by taking the first-order derivative to the sliding surface. In addition to this, compared to conventional TSMC, FOTSMC has a faster convergence speed.
The study on applying the fractional-order derivative to SMC techniques starts by applying it to the LSMC first. A fraction-order sliding mode control (FOSMC) was proposed based on LSM [7], and it exhibited better performance than the conventional LSMC (integer-order derivative-based). The reason has been roughly analyzed and discussed. In [8], researchers analyzed and found that the solution of a fractional-order (larger than zero and less or equal to one) differential equation could be presented as a Mittag-Leffler function. This mathematical solution explains why FOSMC exhibited a higher convergence speed than LSMC (see Appendix A). However, FOSMC is not globally faster than LSMC. It has slow convergence near the terminal where small values are, which is discussed in detail in Appendix A.
FOTSMC can compensate for the slow convergence drawback near the equilibrium of FOSMC because the terminal sliding surface has a faster convergence speed than the linear sliding surface, especially in the field of small values. Compared to TSMC and FOSMC, FOTSMC is a complementary method, the terminal sliding surface helps the slow convergence in the interval of small values, and the fractional-order derivative accelerates the convergence in other intervals.
Even though many researchers have demonstrated the performance of FOTSMC through real applications and simulations [9,10,11,12], the specific reason why FOTSMC performs better than FOSMC has not been introduced clearly, which is discussed in Appendix A. Additionally, all previous works on FOTSMC only focused on applying the fractional-order derivative on the sliding surface design, without paying attention to the design of the control/reaching law for reaching the sliding surface, e.g., FOTSMC in [9] only utilized the fractional calculus in designing the sliding surface. It applied a control law, obtained by taking the first-order derivative to the sliding surface with respect to time, to reach the sliding surface and maintain stay on it. The control input of FOTSMC was merely derived simply by the desired dynamics of the sliding surface.
In this research, the proposed controller, fast fractional-order terminal sliding mode control (FFOTSMC), uses the fractional-order derivative on both the sliding surface design and the control/reaching law. The new control law is conducive to reaching the sliding surface faster than the previously studied one (FOTSMC), designed using the integer-order derivative only. This fast reaching law is associated with fast convergence.
The controller is designed for a seven-degree-of-freedom (7-DOF) robot manipulator. Due to its complex dynamics, only using FFOTSMC is not enough to have an ideal performance. The high frequency switching in the control input of FFOTSMC can ensure the robustness of FFOTSMC; however, it could make the robot oscillate. In this research, we apply the sliding mode perturbation observer (SPO) [13] to estimate the perturbation. The estimated perturbation is used to compensate for the uncertainties and disturbances in the controller design. It reduces the switching gain of the control input of the FFOTSMC, which decreases the amplitude of chattering. SPO is efficient with high estimation accuracy for a low-frequency vibration, which has been demonstrated in electric motors and hydraulic cylinder actuated systems [14,15]. Through the compensation for the uncertainties and disturbances, the control precision is also improved.
The contributions of this paper are summarized as follows.
- (1)
- The new proposed controller, FFOTSMC, uses fractional-order derivatives on both sliding surface design and sliding control/reaching law. It has faster convergence and more outstanding tracking accuracy than FOTSMC, which has been researched previously.
- (2)
- The new controller FFOTSMC was designed to control a real 7-DOF robot manipulator for trajectory tracking. SPO is used to estimate the disturbance and uncertainties for reducing the chattering, ensuring the controller can be implemented in practice.
- (3)
- Stability is analyzed using the Lyapunov functions for fractional-order systems [16].
The paper is organized as follows. In Section 2, the 7-DOF robot manipulator modeling, fundamental definitions, two useful properties, and one lemma for proving the stability are presented. Section 3 describes the stability analysis of the new proposed FFOTSMC with SPO (FFOTSMCSPO). In Section 4, simulations using the proposed controller and four different controllers are compared in MATLAB for a single-input and single-output (SISO) system. Then, comparative experiments on the robot manipulator are discussed. The conclusion of this work is shown in Section 5.
2. Preliminaries
2.1. Mathematical Model for Robot Manipulators and Problem Formulation
Consider an n-links robotic manipulator is model as
where is the position state of the joints; is the velocity state vector and is the acceleration state vector; is the disturbance vector; is the torque vector acted on the joints; , and are the symmetric positive definite inertia matrix; the Coriolis and centrifugal matrix, and the gravitational matrix, respectively. After identifying system dynamics, the system in (1) can be rewritten with modeling parameters and uncertainties as
where and are identified dynamic parameters, and represents the perturbation, which contains the uncertainties of dynamics, the unknown gravitational term, and the disturbance as
where and represent the uncertainties of the inertia and the Coriolis and centrifugal term of dynamics, respectively. is assumed to have a boundary limited as . Hence, the new dynamics can be rewritten as follows
For trajectory tracking, the error state is defined as
where represents the desired position planning, and . The notation of the desired velocity state vector and the acceleration state vector are and , respectively.
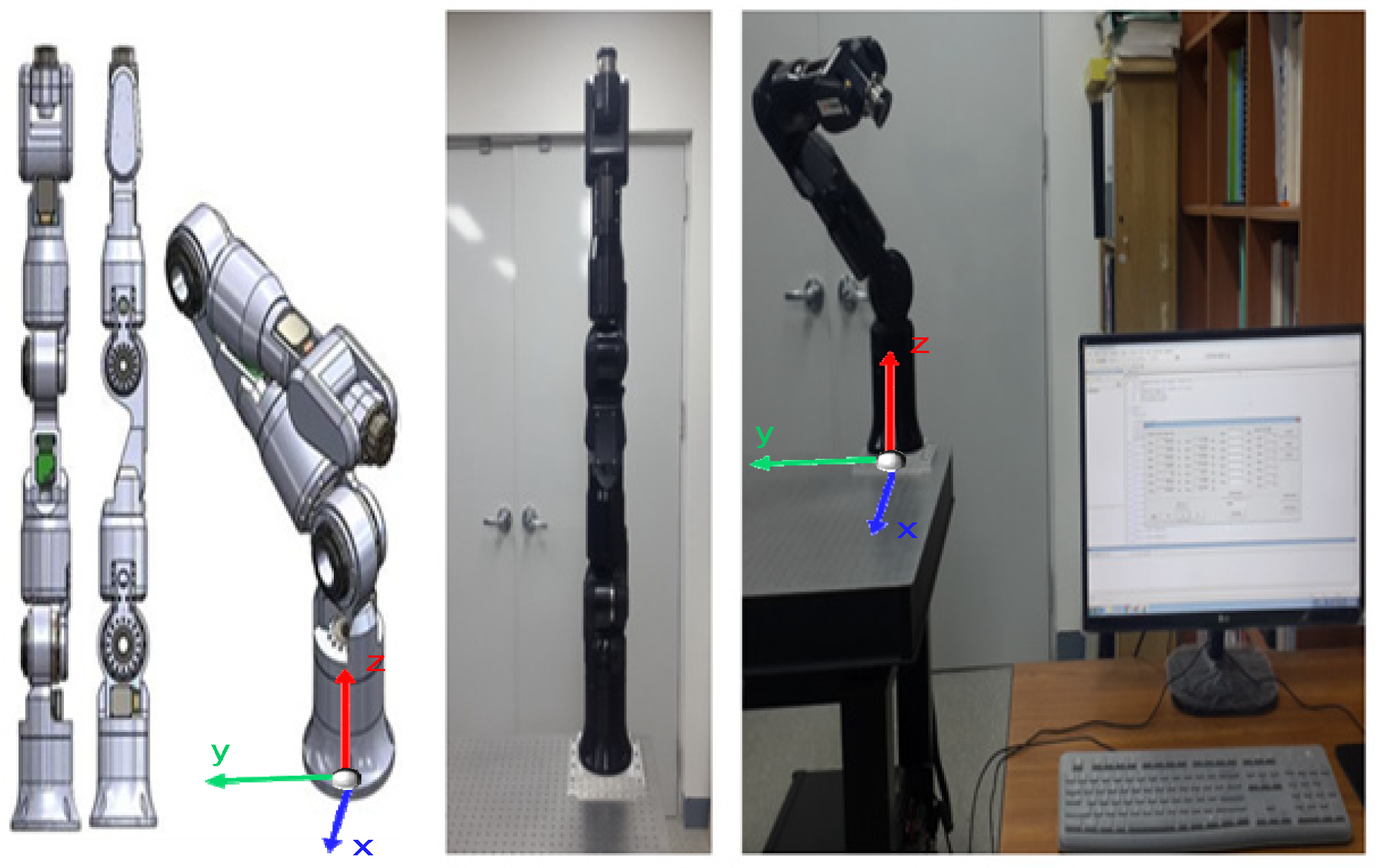
In this research, we aim to design a robust controller for a 7-DOF robot manipulator (n = 7), which is shown in Figure 1. All seven joints are rotary joints. The dynamic identification was finished in previous research [17] with a result of , .
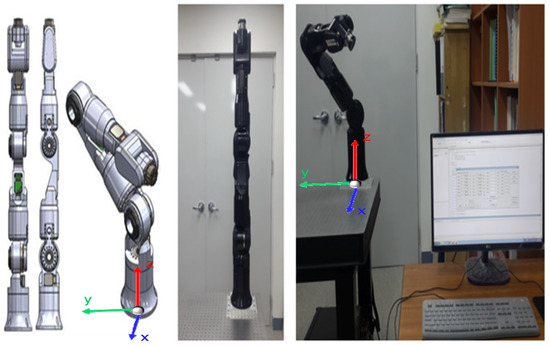
Figure 1.
Seven-axis robot manipulator.
The goal of the proposed controller is to guarantee the error states to reach the sliding manifold and then slide to the equilibrium point (i.e., ) despite .
2.2. Fractional Calculus
Fractional calculus defines the real number order for integral and derivative calculations. The Riemann–Liouville definition and the Caputo fractional derivative are adopted in this work.
Definition 1
[18].Theth-order Riemann–Liouville integral of function is given as
whereis the well-known Euler gamma function.is the initial time. The Riemann–Liouville integral has the semigroup property of. The Riemann–Liouville definition of theth-order derivative is
where. For convenience, the Riemann–Liouville derivative is abbreviated asin this article.
Definition 2
[8].Theth-order Caputo fractional derivative on the half axisfor a continuous function f(t) is defined as
in which.
Property 1
[8].If the Riemann–Liouville derivativeof a functionis integrable, then
Property 2
[18,19].The fractional-order Caputo fractional derivative has a relation to the Riemann–Liouville derivative.
2.3. Stabilities
Lemma 1
[16,20].The stability analysis for fractional-order systems is given as
If the following condition is satisfied
Thenis the equilibrium point, and the system (11) is asymptotically stable. Lemma 1 is proved by using the Lyapunov functions for fractional-order systems, which apply the fractional-order derivative to the Lyapunov function candidate as.
3. Controller Design
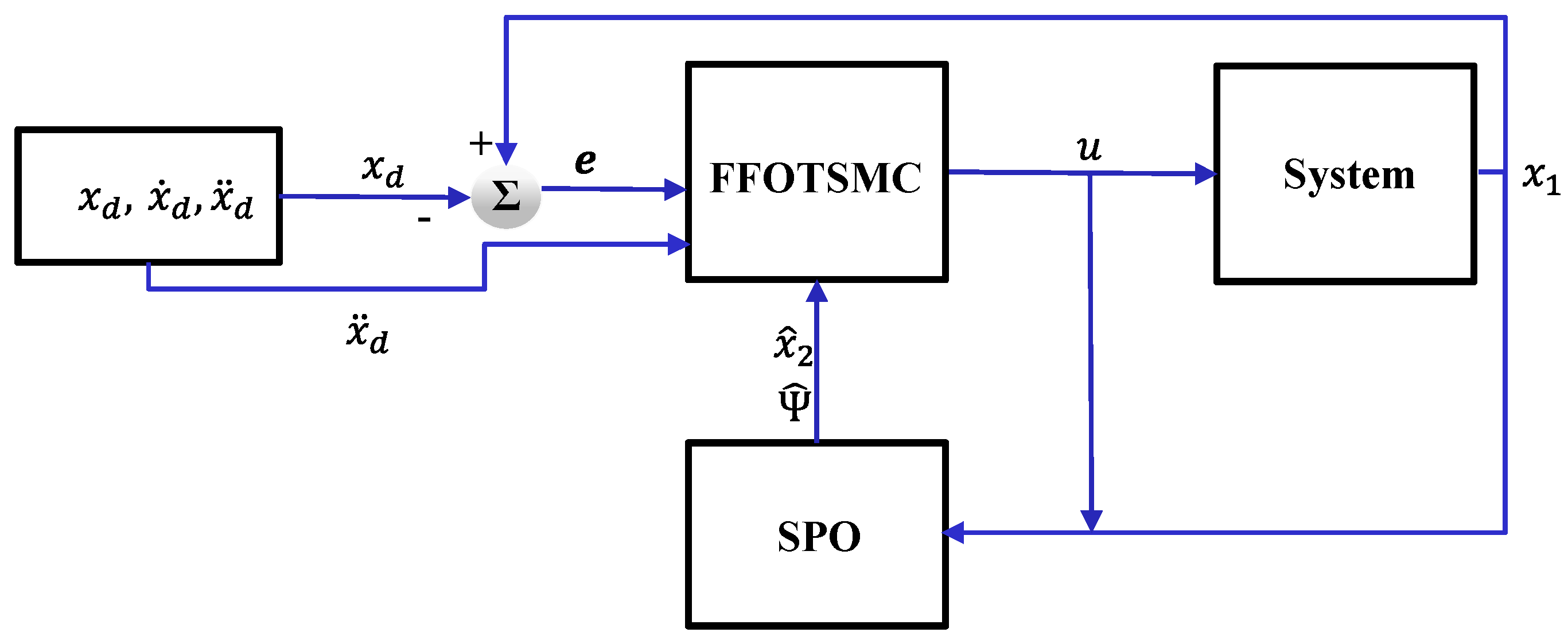
The controller FFOTSMC with SPO (FFOTSMCSPO) is proposed in this section. SPO is used to estimate the perturbation. Then, the estimated perturbation is transferred to the controller for compensation. The flow chart of the system and controller is shown in Figure 2. The usage of SPO is proposed first.
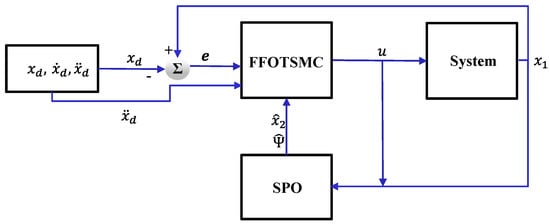
Figure 2.
Block diagram of the controller.
3.1. SPO
SPO estimates partial unknown states and perturbation. It helps the controller to reduce the chattering against uncertainties and disturbances. It is efficient in estimating perturbation in low-frequency vibration [13]. For the motor-driven robot, the main component of the perturbation is the external disturbance and gravity . The minor components include dynamic uncertainties and modeling errors.
The design of SPO is based on the state space. The state variables with a new state variable for the j-th () joint of the robot can be represented as:
where is a positive constant. is the new equivalent control input to separate the perturbation from dynamics as follows:
where . The new state variable is defined as:
The SPO for j-th joint is designed as follows:
where and are positive constants, and the notation means the estimation; means the estimation error, i.e., ; if , ; else, ; stands for the boundary layer of the estimation error.
The detailed stability analysis for the SPO has been proven in previous research [14]. Herein, we only use SPO to protect the controller against lesser uncertainties, which is reduced from to . The perturbation estimation error has a relation to the real perturbation [13], as shown in a Laplace transform as:
where estimation error , and (17) shows a high-pass filter from the real perturbation to the perturbation estimation error. It signifies that the SPO is effective for the system with a low-frequency variability.
3.2. FFOTSMCSPO
The proposed controller has a fractional-order terminal sliding surface and a fractional-order type control law. It has faster convergence in both reaching mode and sliding mode, which can guarantee precise tracking.
3.2.1. Fractional-Order Sliding Surface
The fractional-order sliding surface of FFOTSMC is designed as:
where , , , , and . Differentiating it using Caputo fractional-order derivative with β-th order yields
Depending on the definition of Caputo fractional derivative (8),
Applying the definition of Riemann–Liouville fractional derivative, we obtain
In practice, the trajectory tracking always commences with zero velocity error. Using Property 2 and assuming that the initial velocity error is zero.
Depending on the Definition 1 and 2, then
As the semigroup property of the fractional integral exists,
It yields
3.2.2. Fast Fractional-Order Sliding Control/Reaching Law
The control law of the new proposed controller is designed based on the fast-TSM-type [3]. It applies the fractional-order derivative to build the desired dynamics of the sliding surface as
where , , , and . is assumed as the boundary of perturbation estimation error for the j-th joint. can be estimated by using (17) with the assumption of real perturbation boundary . The order ( and ) of the fractional derivative is always selected from 0.7 to 0.9. The influence of the selection of fractional-orders on the sliding surface design and the reaching law design is discussed in Appendix A.
Compared to the control law of previous research such as FOTSMC [9], in designing the control law, the desired dynamics of the sliding surface is formed after a first-order derivative, i.e., ( in (26)). In FFOTSMC, the fast control law ( in (26)) adopts the fractional-order derivative. The fast control law results in a faster convergence speed to the sliding surface, which is the main contribution of this research.
Substituting by and using the dynamics (14), the control input of FFOTSCM with SPO is given as (see Appendix B)
Remark 1.
The singularity of conventional TSMC is avoided by the fractional calculus, which is discussed in the numerical method (see Section 3.4) for implementing the fractional-order derivative.
3.3. Stability Analysis
The asymptotic stability of reaching the sliding surface is proved by using Lemma 1 as follows. For the j-th joint, substituting the equivalent control input (27) to the dynamics (14) and (26), then applying yields (see Appendix B)
As
Additionally, for given parameters and , is a positive constant. As is a decreasing function of time , when is large. Hence, after a period of time ,
Depending on Lemma 1, the sliding manifold is asymptotically stable and can reach from any initial condition.
After reaching the sliding surface (i.e., )
only if . It satisfies the asymptotically stable condition in Lemma 1.
Remark 2.
The asymptotic stability of the reaching mode and sliding mode is proved. However, the finite reaching time has not been obtained in this research. An explicit solution of a fractional differential equation with a nonlinear term cannot be solved, neither can an analysis solution. Despite this, in the tracking control of a robot manipulator, the fast convergence is more critical than the finite-time stability. It ensures an overall small tracking error. The fast convergence of FFOTSMC is discussed and obtained by analyzing the convergence characteristics of FOSMC and TSMC in Appendix A.
3.4. Numerical Method
In order to implement the fractional-order derivative, the Grünwald–Letnikov fractional derivative is applied in this research. The Grünwald–Letnikov fractional derivative is derived from the limit definition for derivatives and equivalent to the Riemann–Liouville definition [18,19,21]. Thus, the equivalent control input of the sliding mode control (27), which uses the Riemann–Liouville derivative, was implemented using the Grünwald–Letnikov derivative. The Caputo derivative term in the sliding surface (18) was transferred to a Riemann–Liouville derivative with the initial error first using the properties mentioned. Then, it was implemented on the real system by the Grünwald–Letnikov derivative method. The th-order Grünwald–Letnikov fractional derivative for is
where is the sampling time. For the gamma function, the property is obtained as [18]
Thus, in (32) is rewritten as
The result of the Grünwald–Letnikov fractional derivative can be calculated using (34). When k is large (large t), a considerable amount of calculation is needed. As the term for , keeps decreasing. was assumed when . Thus, the fractional-order derivative was calculated in the real application as
Remark 3.
In the calculation of the fractional-order derivative with the numerical method, the singularity problem does not exist. Compared to the TSMC, the term in control input, such as, could have a singularity problem whenand.
4. Simulation and Experiment
4.1. Simulation
The designed controller, FFOTSMC with SPO (FFOTSMCSPO), was applied to a simple second-order SISO system simulated by MATLAB Simulink. It compared with four different controllers such as TSMC with SPO (TSMCSPO), LSMC with SPO (SMCSPO), FOSMC with SPO (FOSMCSPO) and FOTSMC with SPO (FOTSMCSPO). The advantages of using the fractional-order derivative and the terminal sliding surface were discussed via the simulation results. The dynamics of the second-order SISO system corresponding to the model (1) were defined as follows.
where , and . The given dynamics were used to assume a hydraulic servo system, whose frictional coefficient term has more impact than the moment of inertia . The control inputs of all controllers were calculated using (27) with different parameters, as shown in Table 1. The simulation simulated as a regulator () with the initial state .

Table 1.
Partial parameters of controllers.
Where determines whether the fractional-order derivative is used or not in the control law (27); represents the fractional/integer-order of the derivative in the sliding surface design; when it means the original first-order derivative. When selecting and , it means the fractional derivative is used. Selecting and closer to one, the fractional derivative is more similar to the first-order derivative. As the discussion in Appendix A shows, a smaller fractional-order (close to 0.5) results in a faster convergence speed in the beginning, leading to a short rising time in transient response; however, it causes a slow convergence in the terminal interval, resulting in a considerable settling time. is selected less than one when using the sliding surface of TSM; corresponding to the reaching law is associated with the fast control law in TSMC [3]. and can be viewed as terms to choose whether to approach linear control or discontinuous control between a linear control ( or ) and a discontinuous one ( or ). The discontinuous control input can generate faster convergence; however, the more discontinuous it is, the more chattering there is. The other parameters in (27) were selected as , and in all five controllers. Large can help a more accurate estimating of SPO; however, it is limited by the sampling time [13]. The sliding surface slope relates to the sliding manifold convergence speed, and it is also limited by the control input of the hardware limitation (maximum torque or voltage) in real applications. The reaching law gains (, and ) are associated with the reaching speed from to , and larger gains can generate a faster speed; however, chattering is also increased.
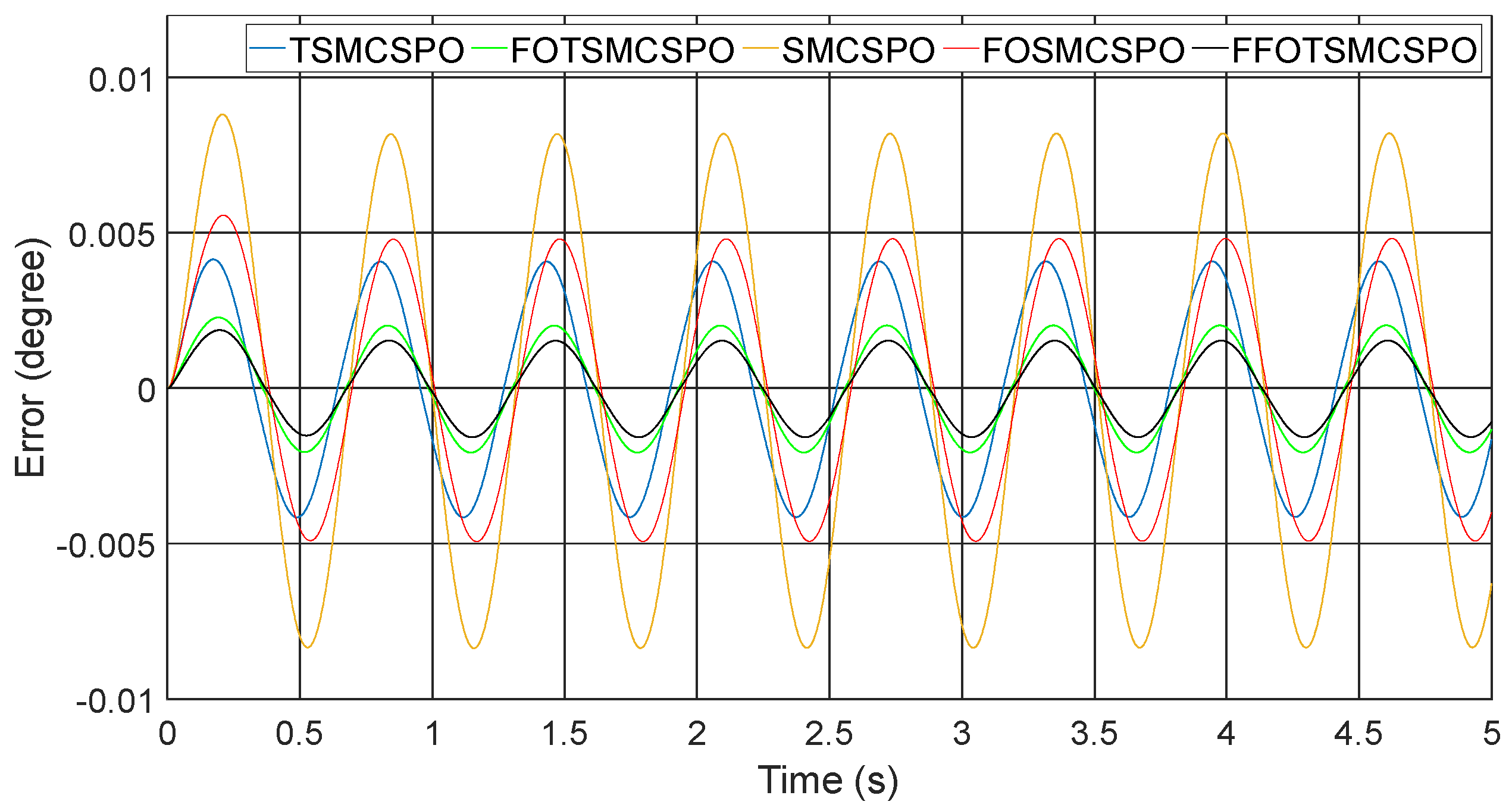
The simulation results for the SISO system are shown in Figure 3. Compared to SMCSPO, FOSMCSPO, and TSMCPO, FFOTSMCSPO exhibited the fewest errors, which means that both the fractional-order sliding surface and the TSM can generate a faster convergence. This was demonstrated by the result of the FOTSMCSPO, which applies the fractional-order derivative and terminal type in the sliding surface design. Compared to FOTSMCSPO, the proposed controller with a fast control law, FFOTSMCSPO exhibited a better tracking performance. Although an exact reaching time of FFOTSMCSPO cannot be solved, the simulation results demonstrate that applying fractional-order to the control law design allowed the controller to have fast convergence.
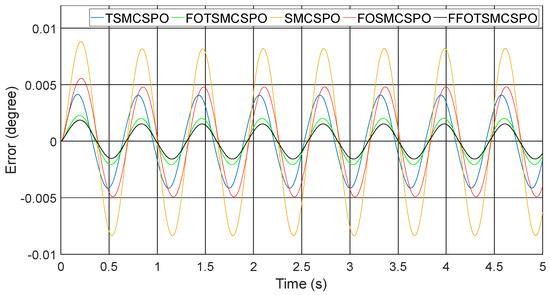
Figure 3.
Simulation result.
4.2. Experiment
The experiments on the 7-DOF robot (Figure 1) compared the controller FFOTSMCSPO with FOTSMCSPO, TSMCSPO, and SMCSPO and FOSMCSPO under the same testing conditions for comparison. The dynamic modeling and identified parameters were obtained from previous research [17]. Control input was calculated by (27) and (14).
4.2.1. Setting
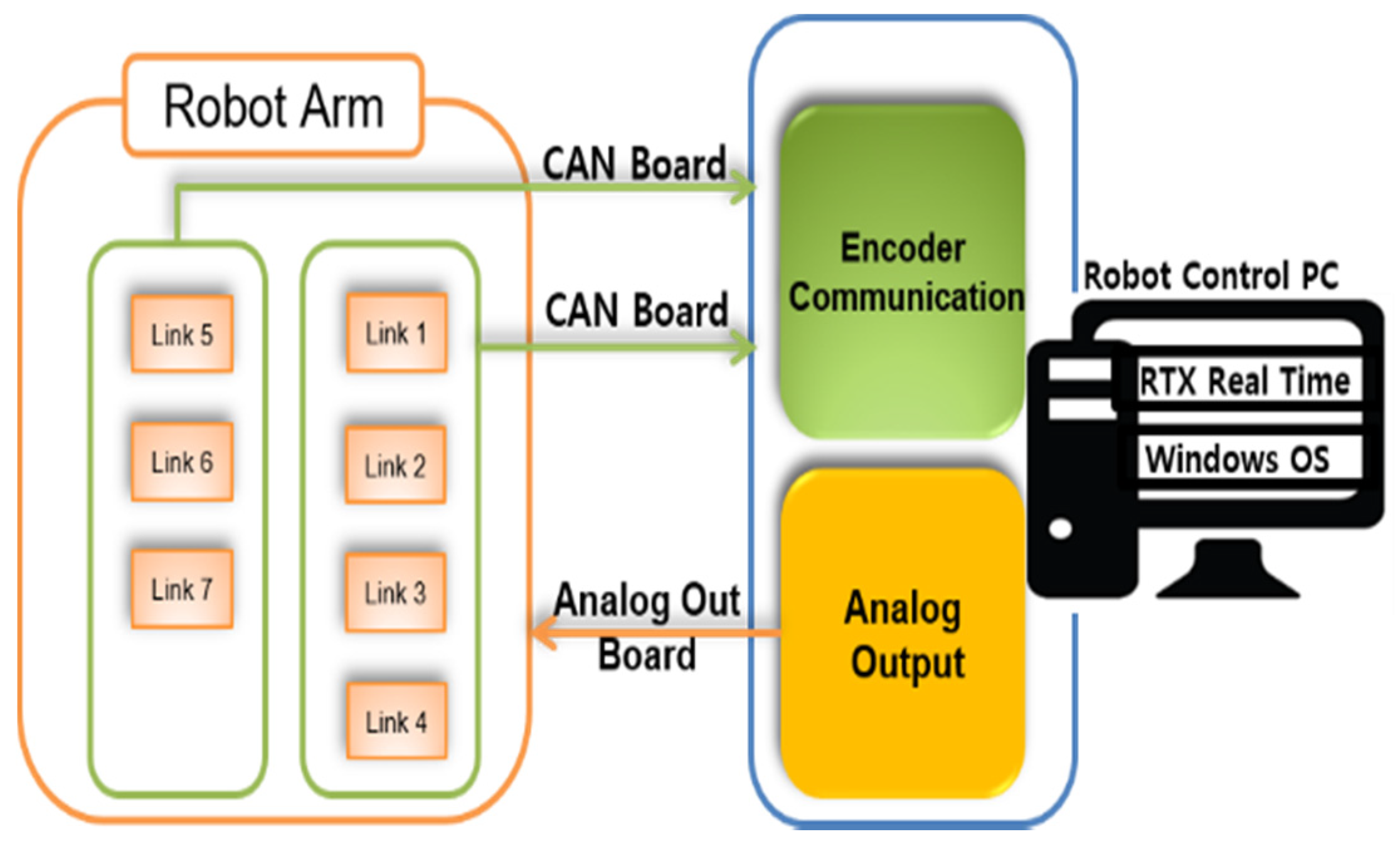
Figure 4 presents the configuration of the hardware and communication for the robot manipulator. The system uses a Windows operating system based PC for computation, IntervalZero RTX64 real-time extension to provide the real-time operation environment, two controller area network(CAN)-bus boards (each providing four channels) for the encoder data communication, and an eight-channel analog output board to provide the control input.
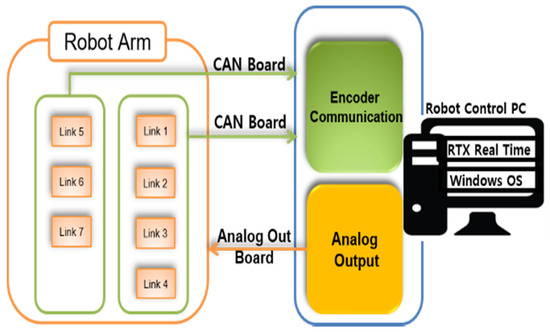
Figure 4.
Robot arm configuration.
Considering the limited communication speed of CAN-Bus and the data volumes of seven encoders, the system sampling time for receiving the rotary encoder data and transmitting the control input was set to 2 ms. According to (A12) in previous research [13], the parameter in SPO should be selected near 33.3. Thus, the controller parameters (27) for our proposed scheme are selected as , other parameters , , where . For FOTSMCSPO, SMCSPO, TSMCSPOP, and FOSMCSPO, the values of , , , and are set as the same as the simulations, which determine whether the controllers use the fraction-order derivative and TSM or not (Table 1).
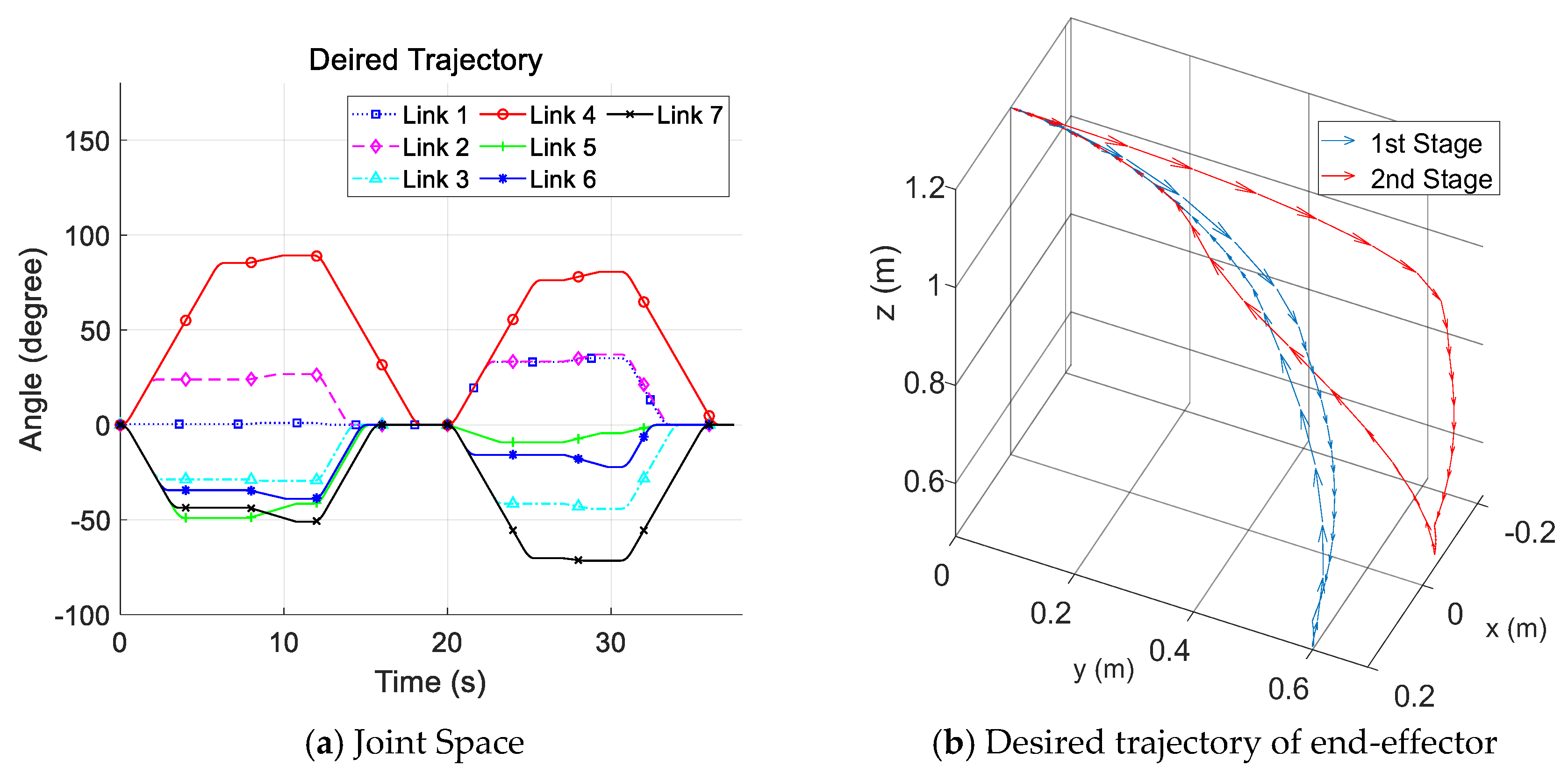
The desired trajectories are simulated assembly work on the end effector. They contain two stages of movement, the first stage simulated grabbing, picking up and homing; the second one simulated the movement that included moving to the assembled position and homing. The desired movement is shown in Figure 5a,b in joint space and the machine coordinate space (MCS), respectively (the base of the MCS is shown in Figure 1).
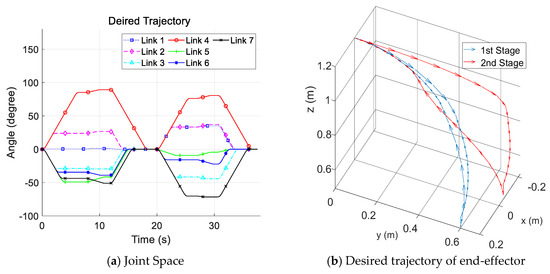
Figure 5.
Desired trajectory of 7 links.
4.2.2. Experimental Results
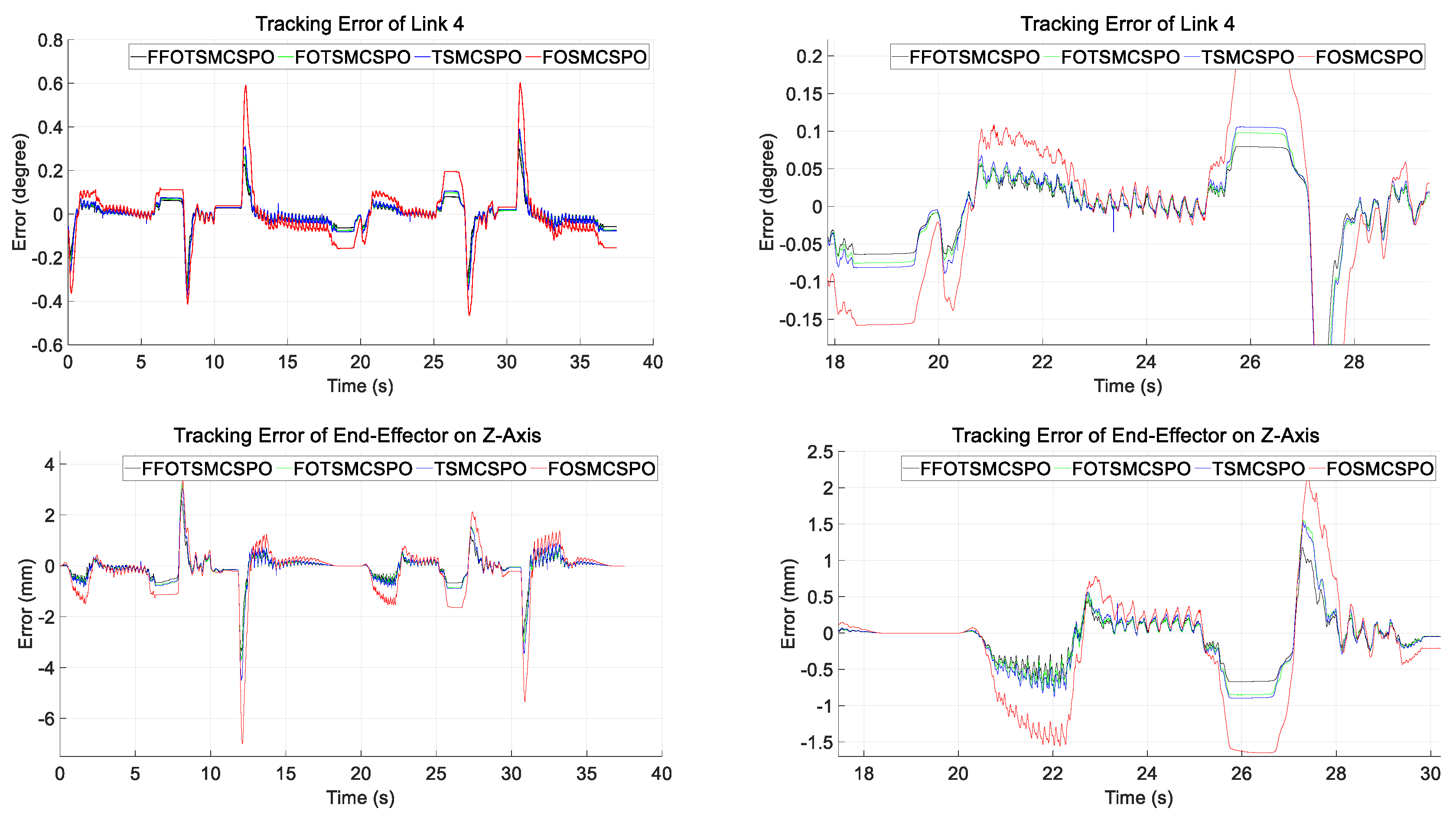
The trajectory tracking errors of the fourth link in joint space and the end effector tracking errors on the Z-axis in the Cartesian coordinate are plotted in Figure 6. The right side of Figure 6 shows the magnified figures to clarify the tracking error results. The results of SMCSPO are not plotted because they have the largest errors and can affect the readability of the figure. The errors of other links (except for the fourth link) and the end effector errors in X- and Y-axes in the Cartesian coordinate are shown in Figure A3 in Appendix C.
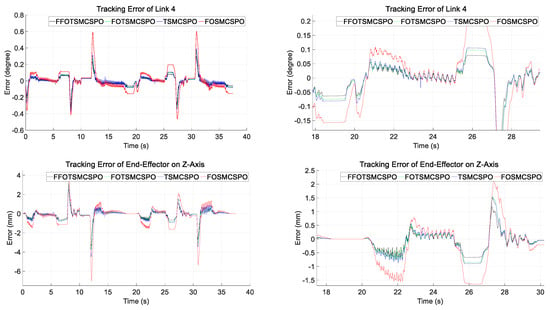
Figure 6.
Tracking error results of each joint and end effector.
The right side of Figure 6 shows that FFOTSMCSPO has the fewest tracking errors among the four controllers during the whole experiment interval. The controller of FOTSMCSPO using the fractional-order sliding surface showed fewer errors than TSMCSPO. This confirms that the fractional-order derivative improves control performance. The effect of TSMC can also be found by comparing the error result of FOTSMCSPO with FOSMCSPO. That is, it confirms that the FOTSMCSPO reduced more errors than FOSMCSPO.
The results in Figure 6 also show lesser chattering in all four controllers. This demonstrates that the approach of SPO in controllers is useful for reducing chattering and ensures the proposed controller will be applied in practice.
The numerical analysis of the experiment results is analyzed by comparing the mean absolute error (MAE). The MAE is calculated as
Table 2 shows the MAE results. In all seven links, the controller using fractional derivatives performed better with less MAE than the integer ones, FOTSMCSPO shows less MAE than TSMCSPO, and the results of FOSMCSPO are less than those using SMCSPO. Additionally, controllers using TSM show less errors than the conventional LSM ones, which is obtained from comparing FOTSMCSPO with FOSMCSPO, and TSMCSPO with SMCSPO. In the results of all five controllers, the new proposed controller FFOTSMCSPO, using the TSM and applying the fractional-order derivative in both the sliding surface design and the reaching law design, has the least MAE. It exhibits the fastest convergence and demonstrates the improvement. Comparing the results in FOSMCSPO with TSMCSPO, FOSMCSPO exhibits less MAE. This means that TSMCSPO is more efficient than FOSMCSPO.

Table 2.
Mean absolute error.
5. Conclusions
The proposed controller, FFOTSMC, applies fractional calculus on both the terminal sliding surface design and the control/reaching law for reaching the sliding surface and maintaining stay on it. This guarantees fast convergence and high trajectory tracking performance. FFOTSMC is used with SPO for less chattering, resisting the modeling error and disturbance from the environment. The stability of the controller is analyzed based on the Lyapunov stability theory for fractional-order systems. Both the comparative simulation in MATLAB and experiments on the seven links robot manipulator verified the excellent tracking performance of the proposed controller. The experimental results demonstrate the feasibility of the proposed controller, which shows a small error and less chattering against the high gravity effect in dynamics and modeling errors.
Even the finite-time stability of FFOTSMC (reaching the sliding surface and the equilibrium in finite time) cannot be proved in this research. The experimental results and simulation results have demonstrated the outstanding performance in tracking and improvement by applying the fractional-order derivative on the control/reaching law design. The finite-time stability problem will be investigated in the future.
Author Contributions
Conceptualization, J.W. and M.C.L.; methodology, J.W.; validation, J.W., J.H.K. and H.H.K.; writing—original draft, J.W.; writing—review and editing, J.W. and M.C.L.; supervision, M.C.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Smart Factory Development Support Program (20005055, Development of Integrated Control Technology supporting both control of four robots and PLCopen standard-based programmable logic controller(PLC) languages (five types) for SME’s smart factory) and the Technology Innovation Program (10073147, Development of Robot Manipulation Technology by Using Artificial Intelligence) funded by the Ministry of Trade, Industry and Energy (MOTIE, Korea).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The reason why FOTSMC provides benefits in terms of fast convergence is discussed here. Considering the sliding surface of FOSMC as
where is required to stabilize at the equilibrium point. When selecting the derivative order , (A1) is a simple first-order LSM sliding surface. After reaching the sliding surface (i.e., ), the solved solution in the form of the Mittag-Leffler function is [22]
where . When , the solution corresponds to the first integer-order LSM. Its solution is an exponential function as
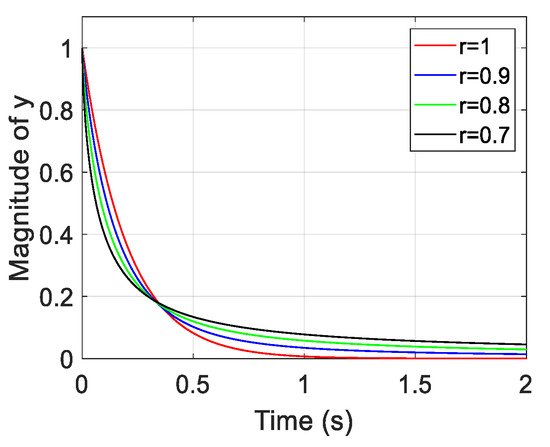
Figure A1.
Solution of the fractional-order differential Equation (A1) where (0 < r < 1), = 1 and A = −5.
Figure A1.
Solution of the fractional-order differential Equation (A1) where (0 < r < 1), = 1 and A = −5.
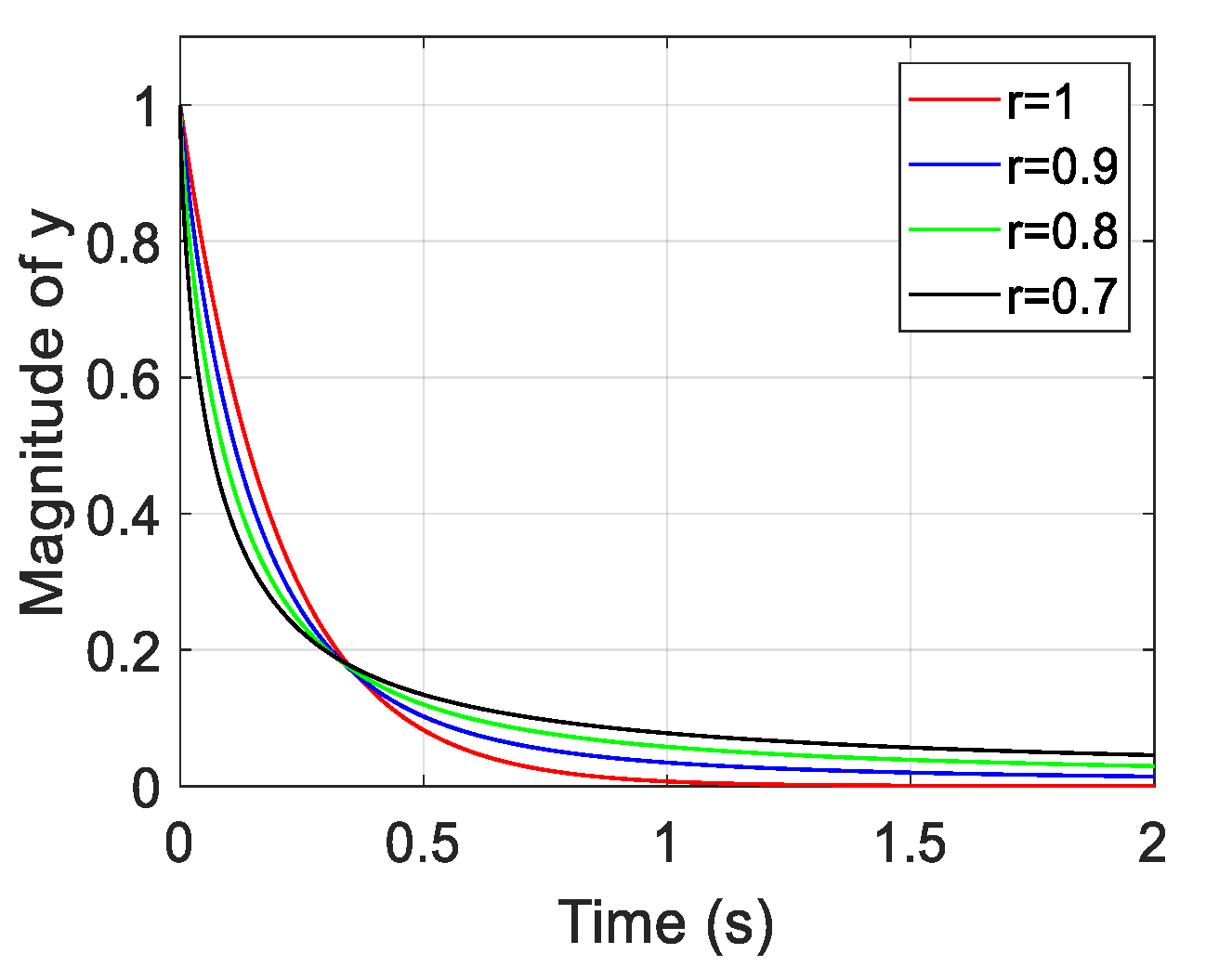
Figure A1 shows the result of the time response of FOSMC after reaching the sliding surface. The fractional-order one () has a faster decay than integer-order () in the interval at the beginning (transient response); however, the convergence near the steady-state becomes slow. In the beginning, fast convergence is observed. It has a more significant effect on trajectory tracking, which can reduce the relatively large error fast. It explains why the fractional-order derivative allows for a better control performance in SMC for robot manipulator trajectory tracking. However, drawbacks of FOSMC, such as a slow convergence in the terminal interval (i.e., long settling time), exist. In addition, the smaller is associated with faster convergence in the transient response part; however, extremely small would result in a considerable settling time. Hence, selecting the order of the derivative is a tradeoff problem.
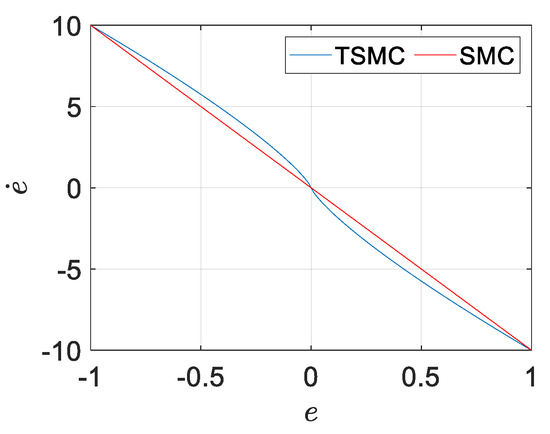
Figure A2.
corresponding with .
Figure A2.
corresponding with .
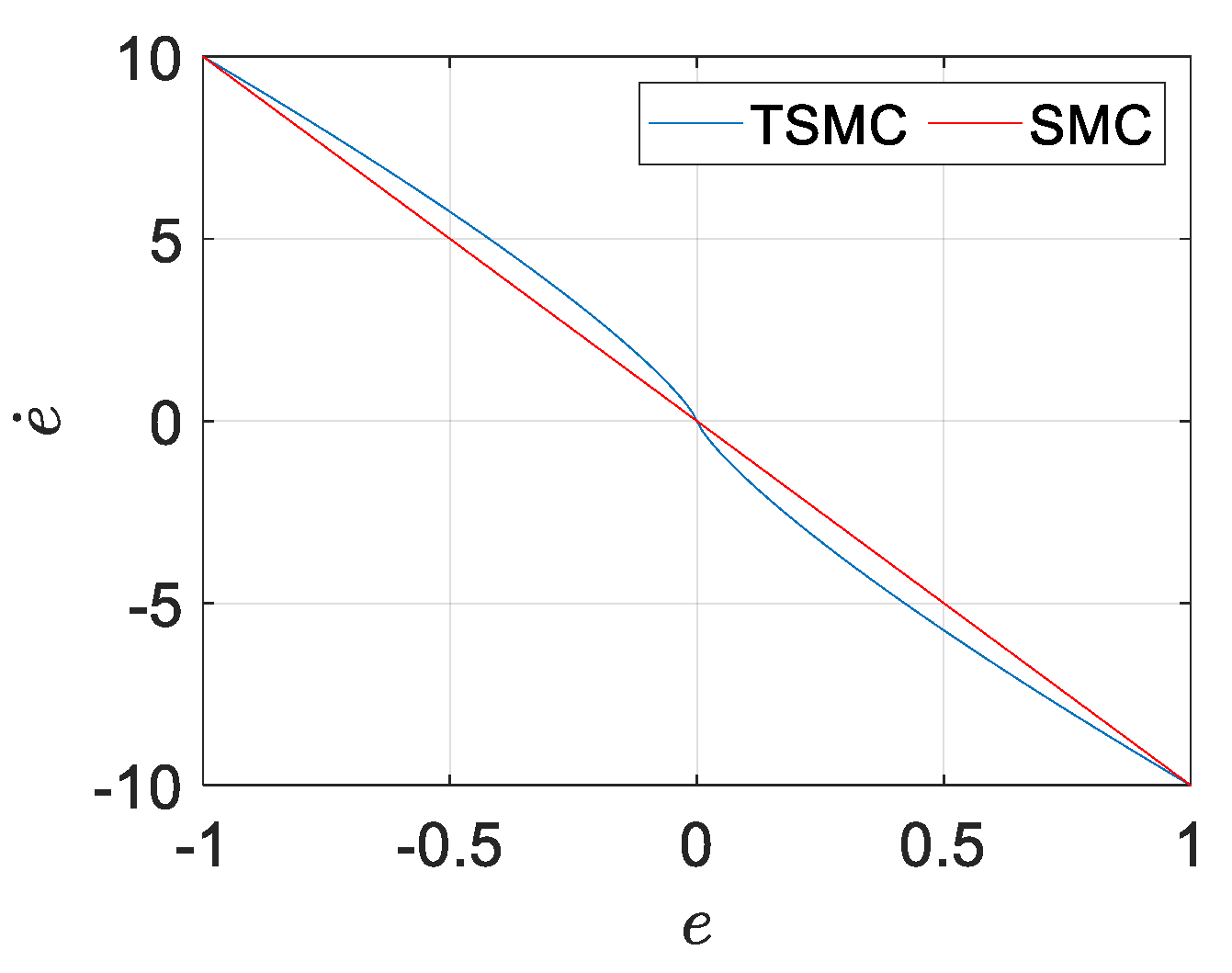
In order to compensate for the slow convergence in the interval of small values in FOSMC, TSM control is expected to be used because the nonlinear sliding surface in TSM affects convergence speed more efficiently in the interval of a small error. Considering a TSM sliding surface is
where and . After reaching the sliding surface, it yields
The in TSM (i.e., ) generates larger than using LSM (i.e., ). Moreover, the smaller results in a larger gradient, as shown in Figure A2. This signifies that the TSM has fast convergence benefits, especially in the small error field. This is useful to compensate for the drawbacks of FOSMC.
However, in the case of using TSM in FOSMC, FOTSMC, an explicit solution of the sliding surface, such as FOSMC shown in (A2), cannot be solved because of the nonlinear term in the TSM sliding surface. Thus, the finite time for reaching the sliding surface and the equilibrium has not been solved in this research.
Appendix B
The derivation of (27) and (28) are shown in this section. Using (25) and (26), we obtain
As , it yields
As the semigroup property of the Riemann–Liouville derivative is limited, such as [8], taking the fractional derivative on both sides of (A7) yields
As and , by substituting them for (A8), (27) is derived.
However, due to the limited semigroup property of the Riemann–Liouville derivative, using the equivalent control input (27) for the real dynamics of the sliding surface (25) cannot obtain the desired dynamics (26). This can be found after substituting (27) for (25) as
The term can be rewritten as follows, using Property 1.
With the assumption that the initial error of velocity and acceleration is zero, i.e., , the term in (A9) is simplified as
As the semigroup property of the Riemann–Liouville integral exists, by using the Definition 2, (A11) is derived as
Thus, substituting (A10) and (A12) for (A9), the dynamics of the sliding surface for the j-th element
are derived.
Appendix C
Partial results of experiments are shown here.
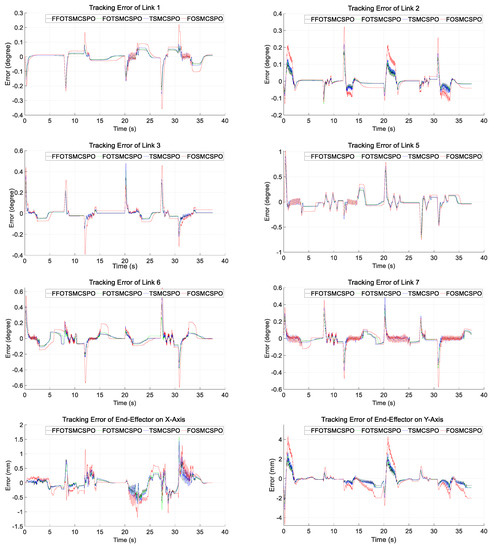
Figure A3.
Tracking error results of each joint and end effector.
Figure A3.
Tracking error results of each joint and end effector.
References
- Young, K.D.; Utkin, V.I.; Ozguner, U. A control engineer’s guide to sliding mode control. IEEE Trans. Control. Syst. Technol. 1999, 7, 328–342. [Google Scholar] [CrossRef]
- Zhihong, M.; Yu, X.H. Terminal sliding mode control of MIMO linear systems. In Proceedings of the 35th IEEE Conference on Decision and Control, Kobe, Japan, 13 December 1996; Volume 4, pp. 4619–4624. [Google Scholar]
- Yu, S.; Yu, X.; Shirinzadeh, B.; Man, Z. Continuous finite-time control for robotic manipulators with terminal sliding mode. Automatica 2005, 41, 1957–1964. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, X.; Man, Z. Non-singular terminal sliding mode control of rigid manipulators. Automatica 2002, 38, 2159–2167. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, X.; Han, F. On nonsingular terminal sliding-mode control of nonlinear systems. Automatica 2013, 49, 1715–1722. [Google Scholar] [CrossRef]
- Dadras, S.; Momeni, H.R. Fractional terminal sliding mode control design for a class of dynamical systems with uncertainty. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 367–377. [Google Scholar] [CrossRef]
- Zhang, B.T.; Pi, Y.G.; Luo, Y. Fractional order sliding-mode control based on parameters auto-tuning for velocity control of permanent magnet synchronous motor. ISA Trans. 2012, 51, 649–656. [Google Scholar] [CrossRef] [PubMed]
- Kilbas, A.A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier Science Limited: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Wang, Y.; Luo, G.; Gu, L.; Li, X. Fractional-order nonsingular terminal sliding mode control of hydraulic manipulators using time delay estimation. J. Vib. Control 2016, 22, 3998–4011. [Google Scholar] [CrossRef]
- Sun, G.; Ma, Z.; Yu, J. Discrete-time fractional order terminal sliding mode tracking control for linear motor. IEEE Trans. Ind. Electron. 2017, 65, 3386–3394. [Google Scholar] [CrossRef]
- Wang, Y.; Gu, L.; Xu, Y.; Cao, X. Practical tracking control of robot manipulators with continuous fractional-order nonsingular terminal sliding mode. IEEE Trans. Ind. Electron. 2016, 63, 6194–6204. [Google Scholar] [CrossRef]
- Jie, W.; Yudong, Z.; Bao, Y.; Kim, H.H.; Lee, M.C. Trajectory tracking control using fractional-order terminal sliding mode control with sliding perturbation observer for a 7-DOF robot manipulator. IEEE/ASME Trans. Mechatron. 2020, 25, 1886–1893. [Google Scholar] [CrossRef]
- Moura, J.T.; Elmali, H.; Olgac, N. Sliding mode control with sliding perturbation observer. J. Dyn. Syst. Meas. Control 1997, 119, 657–665. [Google Scholar] [CrossRef]
- Wang, J.; Lee, M.C.; Kallu, K.D.; Abbasi, S.J.; Ahn, S. Trajectory tracking control of a hydraulic system using tsmcspo based on sliding perturbation observer. Appl. Sci. 2019, 9, 1455. [Google Scholar] [CrossRef]
- Lee, M.C.; Kim, C.Y.; Yao, B.; Peine, W.J.; Song, Y.E. Reaction force estimation of surgical robot instrument using perturbation observer with SMCSPO algorithm. In Proceedings of the 2010 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Montreal, QC, Canada, 6–9 July 2010; pp. 181–186. [Google Scholar]
- Aguila-Camacho, N.; Duarte-Mermoud, M.A.; Gallegos, J.A. Lyapunov functions for fractional order systems. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2951–2957. [Google Scholar] [CrossRef]
- Jie, W.; Jamshed, S.; Kim, D.J.; Yulong, B.; Lee, M.C. Trajectory tracking control of a 7-axis robot arm using SMCSPO. In Proceedings of the 2019 International Conference on Intelligent Robotics and Applications, Shenyang, China, 8–11 August 2019; Springer: Cham, Switzerland, 2019; pp. 701–708. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Li, C.; Qian, D.; Chen, Y. On Riemann–Liouville and caputo derivatives. Discret. Dyn. Nat. Soc. 2011, 2011. [Google Scholar] [CrossRef]
- Deng, W.; Li, C.; Lü, J. Stability analysis of linear fractional differential system with multiple time delays. Nonlinear Dyn. 2007, 48, 409–416. [Google Scholar] [CrossRef]
- Scherer, R.; Kalla, S.L.; Tang, Y.; Huang, J. The Grünwald–Letnikov method for fractional differential equations. Comput. Math. Appl. 2011, 62, 902–917. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.Q.; Podlubny, I. Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag–Leffler stability. Comput. Math. Appl. 2010, 59, 1810–1821. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).