Observability Analysis and Navigation Filter Optimization of High-Orbit Satellite Navigation System Based on GNSS
Abstract
1. Introduction
- (1)
- We propose a new method for calculating the observable degree of a high-orbit satellite navigation system based on GNSS, which can simultaneously give the relative observability of each state component at each moment and the overall observability of the system;
- (2)
- We design an adaptive optimization method of navigation filter based on this observable degree, which maps the observable degree of the state component to a feedback weighting factor to improve the performance of the navigation filter;
- (3)
- Based on the GNSS navigation system, we combine the proposed observability calculation method as an adjustment factor of the adaptive filter for filter optimization. Numerical simulation shows that the method effectively improves the navigation filter accuracy of the navigation systems of the high-orbit satellite based on GNSS.
2. Navigation Model Based on GNSS
2.1. State Equation of the Navigation System
2.2. Measure Equation of the Navigation System
2.3. Model Linearization
3. Observability of the Navigation System
3.1. Observability Qualitative Analysis
3.2. Observable Degree Analysis
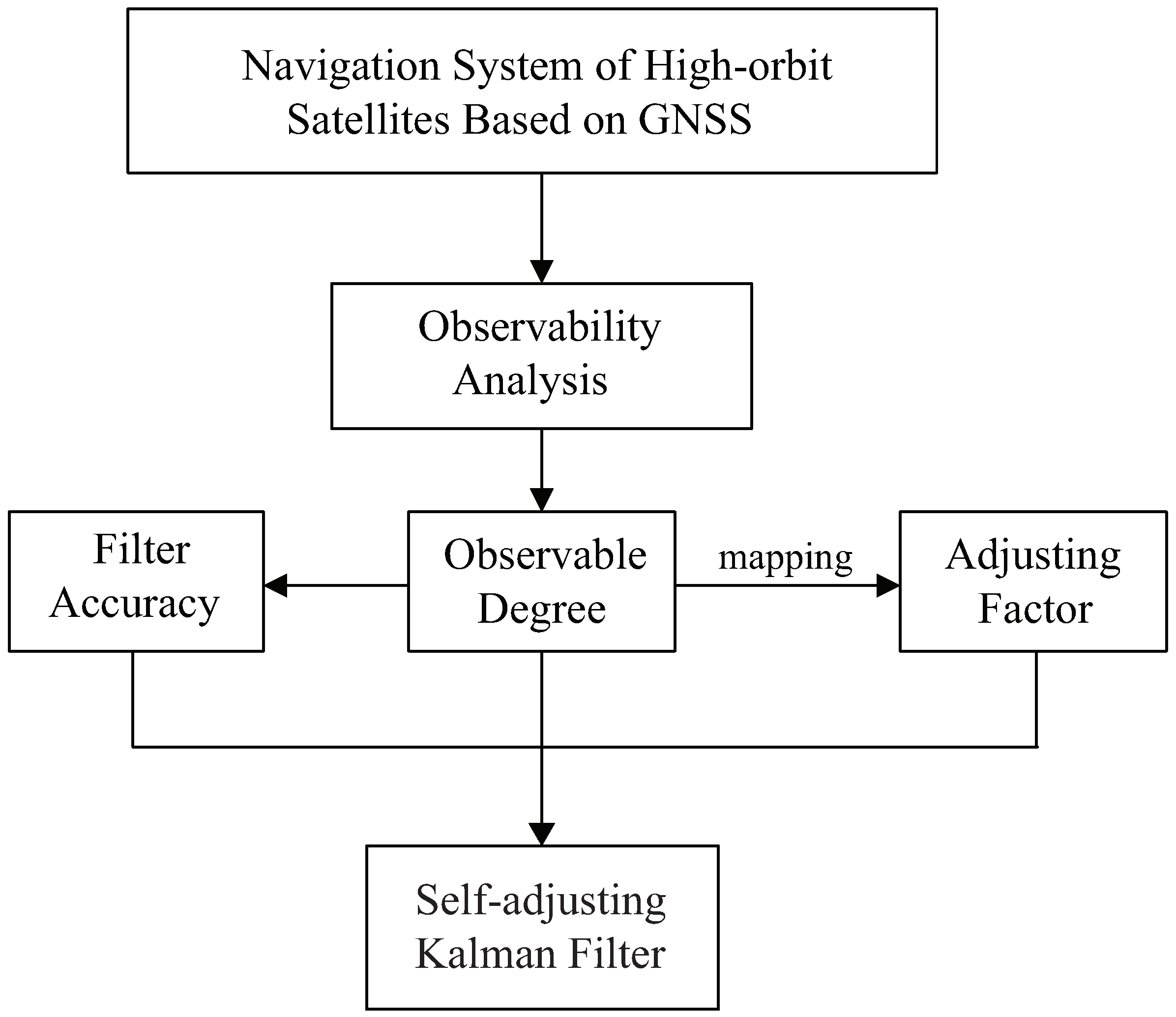
4. Optimized Filter Algorithm for Navigation System Based on the Observable Degree
| Algorithm 1 Adaptive Extend Kalman Filter |
| 1: Input: Optimal estimation of and covariance matrix in moment |
| 2: Output: Optimal estimation of and covariance matrix in moment k |
| Step 1: Calculate the state transition , measurement matrix and state covariance matrix by Equations (19)–(23) |
| Step 2: Repeat Step 1 and calculate the state transition matrix and measurement matrix at moment , written as . |
| Step 3: Use the in Step 1 and Step 2 then calculate the by Equation (18). |
| Step 4: Define a mapping function based on the criterion in Section 3 then calculate the by Equation (25). |
| Step 5: Calculate the new filter gain matrix by Equation (24). |
| Step 6: Calculate and and output them. |
5. Simulation Analysis
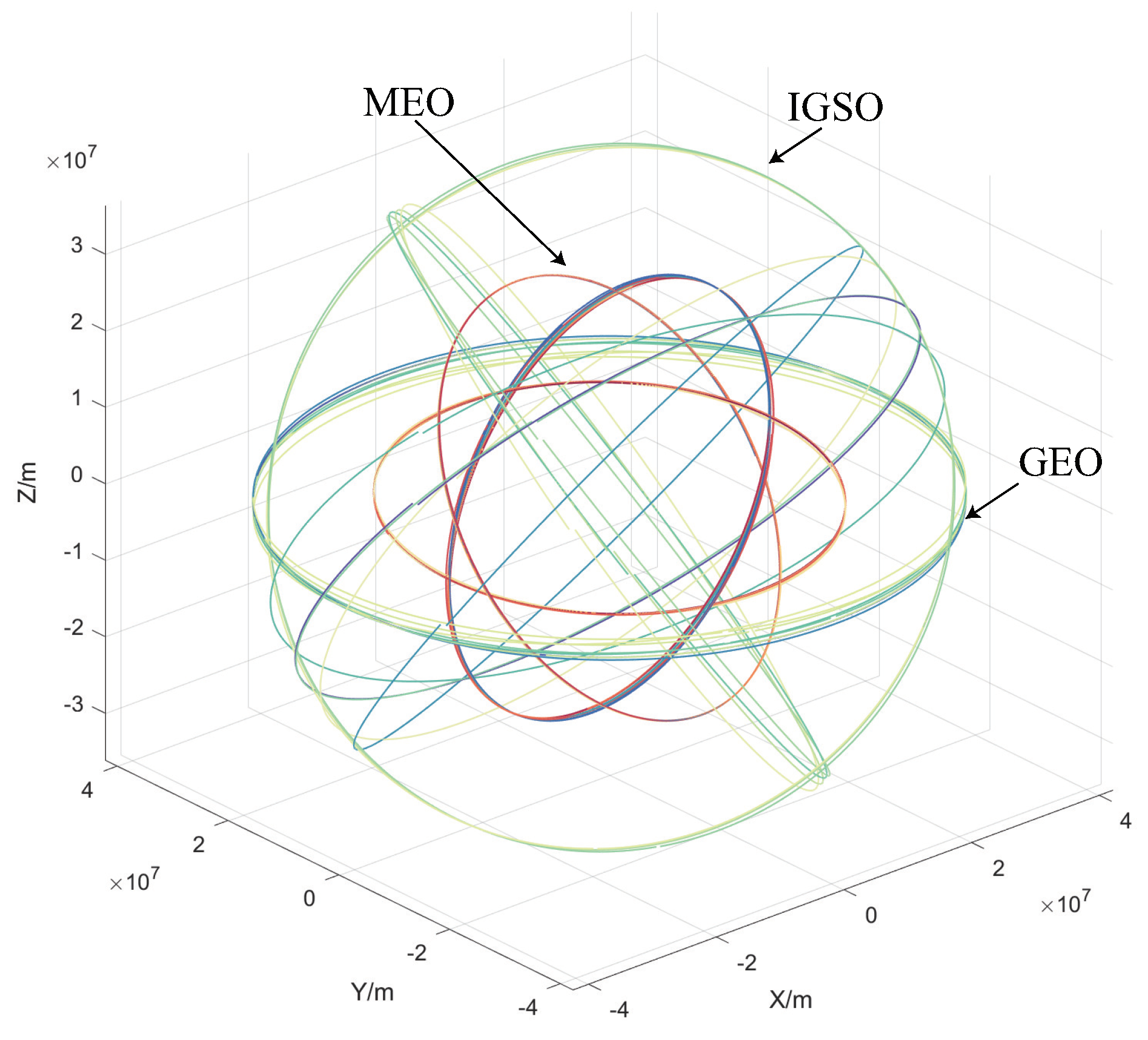
5.1. Simulation Conditions
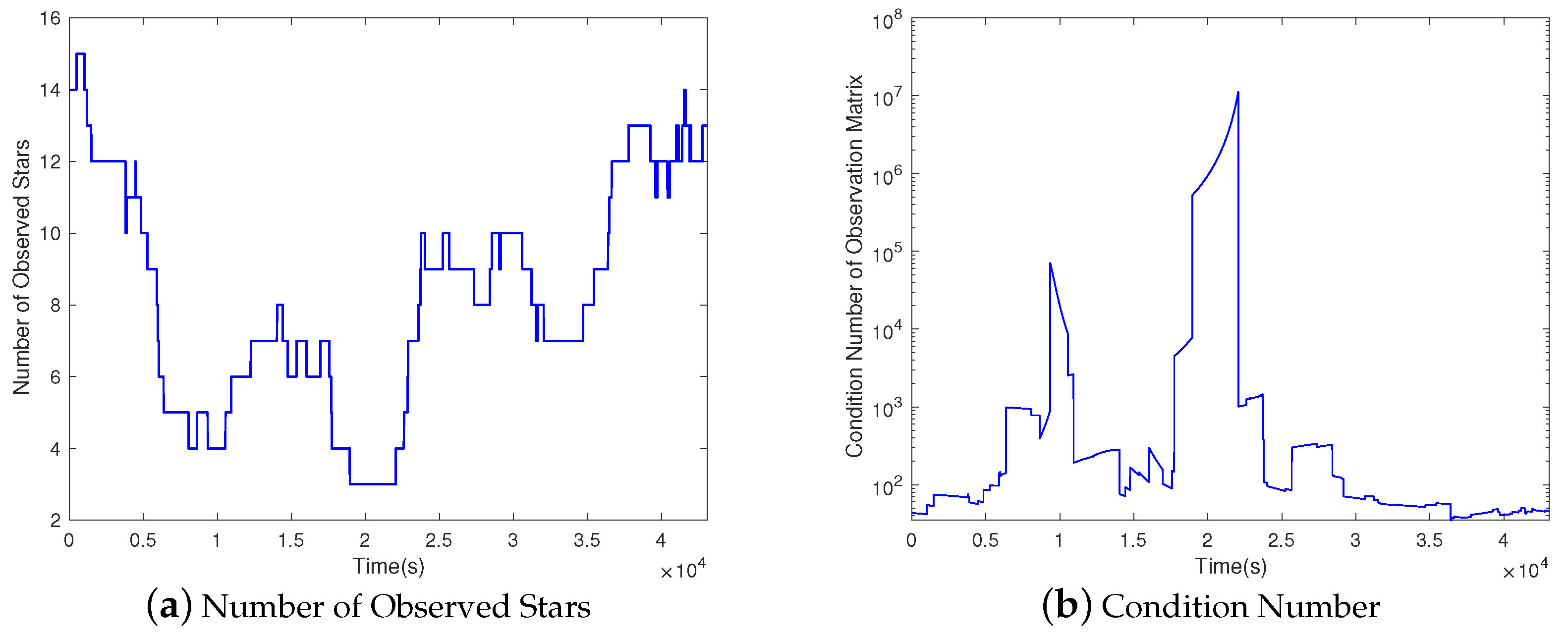
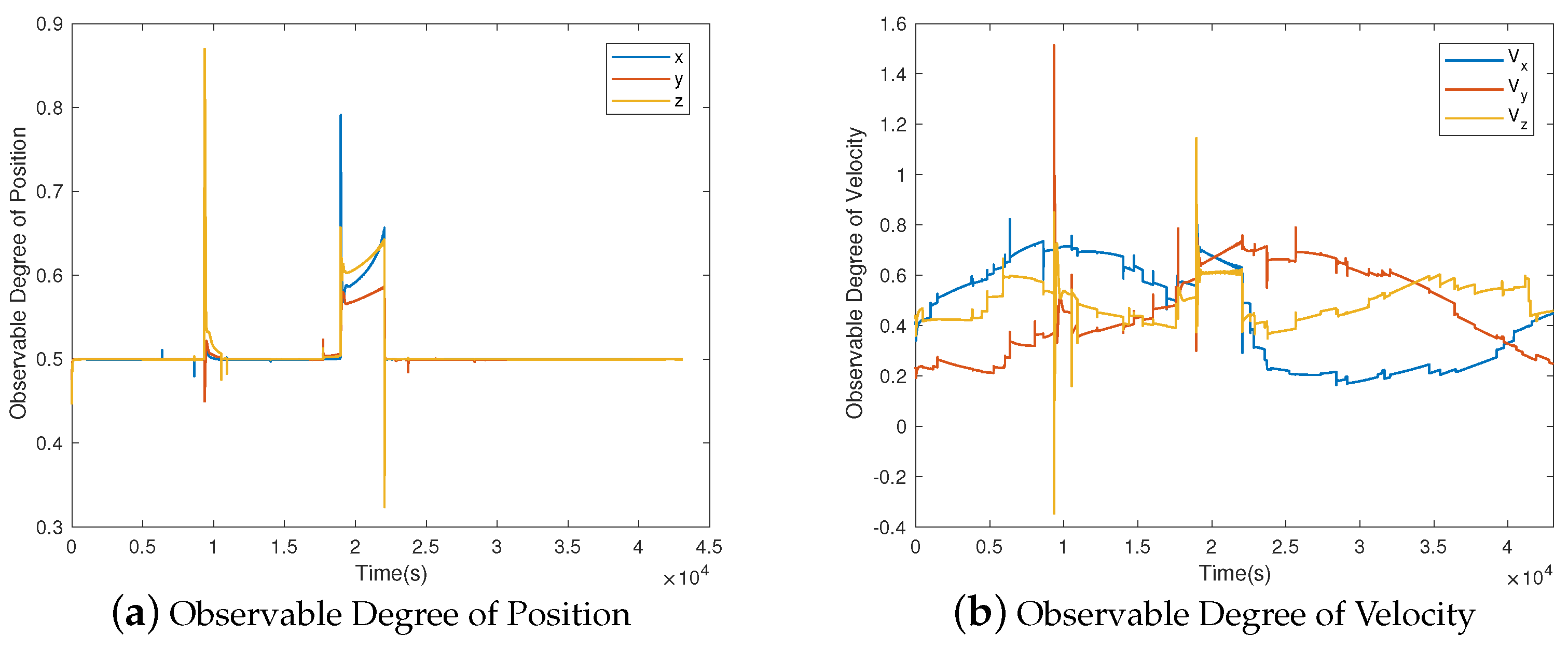
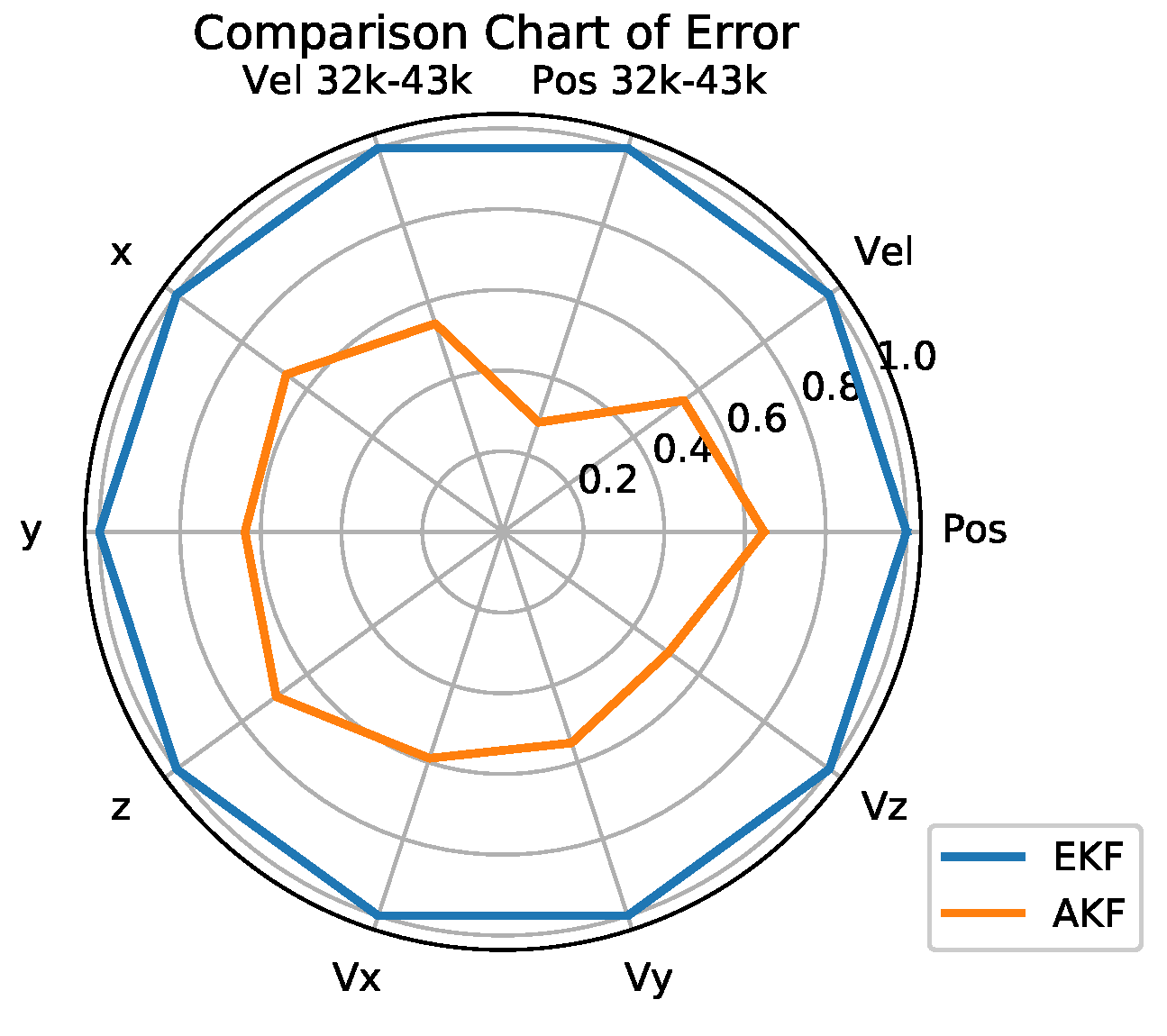
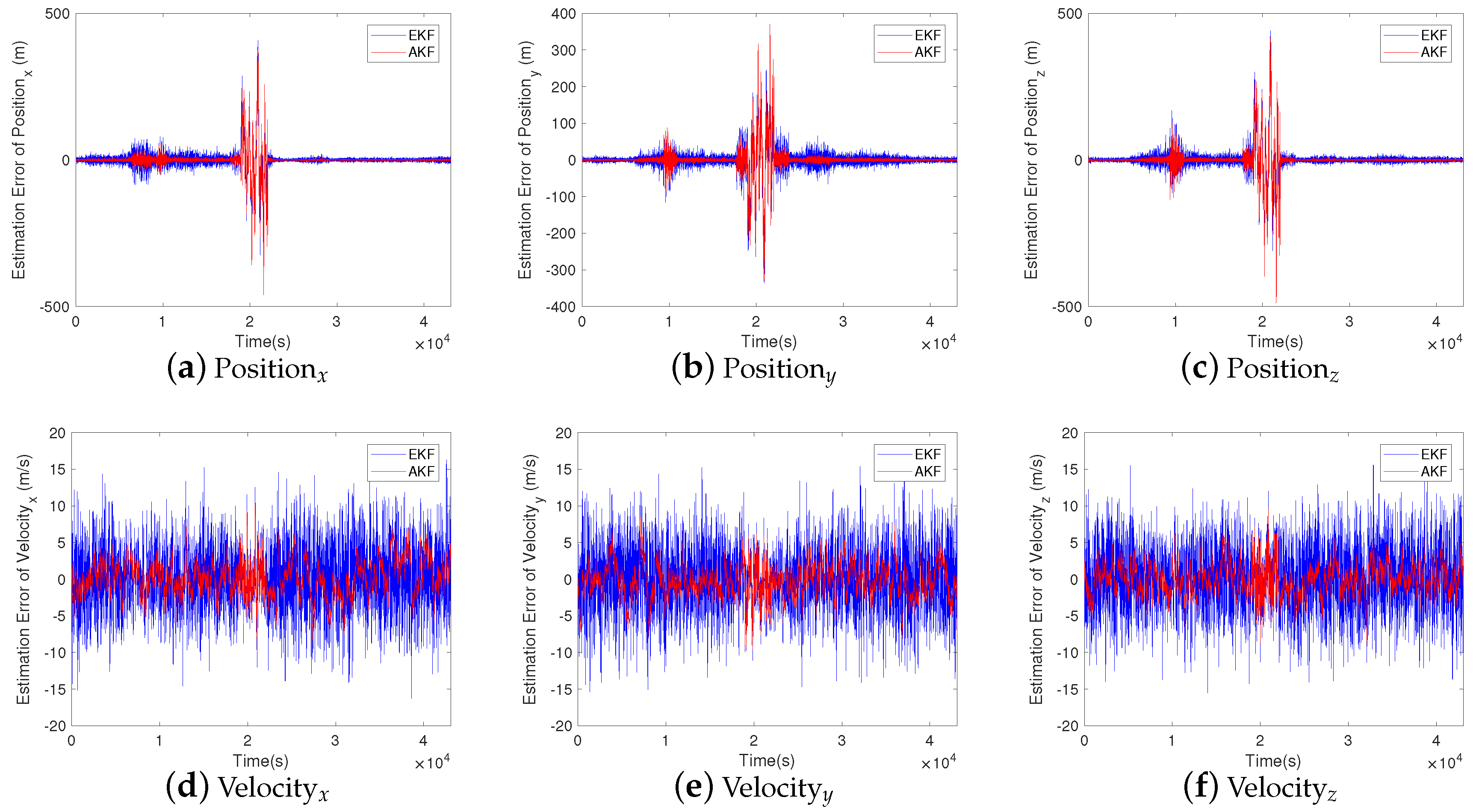
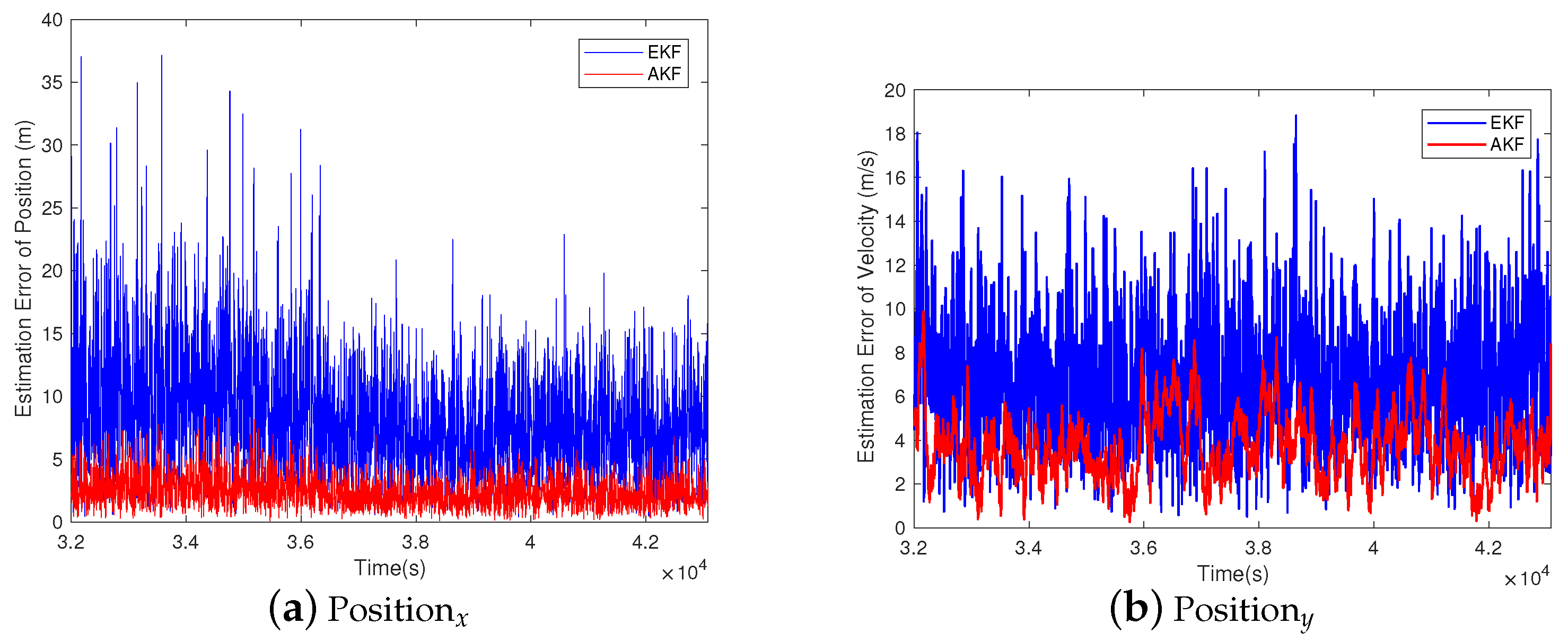
5.2. Simulation Results and Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| GNSS | Global Navigation Satellite System |
| EKF | Extend Kalman filter |
| AKF | adaptive Kalman filter |
| IGSO | inclined geo-synchronization orbit |
| UTC | Universal Time |
References
- Chory, M.A.; Hoffman, D.P.; Lemay, J.L. Satellite autonomous navigation—Status and history. In Office of Entific & Technical Information Technical Reports; Institute of Electrical and Electronics Engineers: New York, NY, USA, 1986; pp. 110–121. [Google Scholar]
- Moreau, M.C.; Axelrad, P.; Garrison, J.L.; Kelbel, D.; Long, A. GPS Receiver Architecture and Expected Performance for Autonomous Navigation in High Earth Orbits. Navigation 2000, 47, 190–204. [Google Scholar] [CrossRef]
- Rycroft, M.J. Understanding GPS: Principles and Applications. J. Atmos. Sol.-Terr. Phys. 1996, 59, 598–599. [Google Scholar] [CrossRef]
- Gao, W.; Zhang, Y.; Wang, J. A Strapdown Interial Navigation System/Beidou/Doppler Velocity Log Integrated Navigation Algorithm Based on a Cubature Kalman Filter. Sensors 2013, 14, 1511–1527. [Google Scholar] [CrossRef] [PubMed]
- Burdziakowski, P. A Novel Method for the Deblurring of Photogrammetric Images Using Conditional Generative Adversarial Networks. Remote Sens. 2020, 12, 2586. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, Q.; Niu, X. Estimate the Pitch and Heading Mounting Angles of the IMU for Land Vehicular GNSS/INS Integrated System. IEEE Trans. Intell. Trans. Syst. 2020, 1–13. [Google Scholar] [CrossRef]
- Paziewski, J.; Crespi, M. High-precision multi-constellation GNSS: Methods, selected applications and challenges. Meas. Technol. 2020, 31, 010101. [Google Scholar] [CrossRef]
- Specht, C.; Lewicka, O.; Specht, M.; Dbrowski, P.S.; Burdziakowski, P. Methodology for Carrying Out Measurements of the Tombolo Geomorphic Landform Using Unmanned Aerial and Surface Vehicles near Sopot Pier, Poland. J. Mar. Eng. 2020, 8, 384. [Google Scholar] [CrossRef]
- Specht, C.; Lewicka, O.; Specht, M.; Dbrowski, P.S.; Burdziakowski, P. Road Tests of the Positioning Accuracy of INS/GNSS Systems Based on MEMS Technology for Navigating Railway Vehicles. Energies 2020, 17, 4463. [Google Scholar] [CrossRef]
- Stateczny, A.; Burdziakowski, P.; Najdecka, K.; Domagalska-Stateczna, B. Accuracy of Trajectory Tracking Based on Nonlinear Guidance Logic for Hydrographic Unmanned Surface Vessels. Sensors 2020, 20, 832. [Google Scholar] [CrossRef]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Ge, Q.; Ma, J.; Chen, S.; Wang, Y.; Bai, L. Observable Degree Analysis to Match Estimation Performance for Wireless Tracking Networks. Asian J. Control 2017, 19, 1259–1270. [Google Scholar] [CrossRef]
- Wang, X.-M.; Cui, H.-T.; Cui, P.-Y. Robustness of observability of linear systems. J. Jilin Univ. (Eng. Technol. Ed.) 2019, 39, 286–290. [Google Scholar]
- Liu, Y.; Cui, P. Observability Analysis of Deep-space Autonomous Navigation System. In Proceedings of the Chinese Control Conference, Harbin, China, 7–11 August 2006. [Google Scholar]
- Bender, E.M.; Flickinger, D.; Oepen, S. The Grammar Matrix: An Open-Source Starter-Kit for the Rapid Development of Cross-Linguistically Consistent Broad-Coverage Precision Grammars. In Proceedings of the 2002 Workshop on Grammar Engineering and Evaluation; Association for Computational Linguistics: Stroudsburg, PA, USA, 2002; Volume 15, pp. 1–7. [Google Scholar]
- Wood, D. Bicolored digraph grammar systems. In Rairo Informatique Theorique et Applications/Theoretical Informatics & Applications; EDP SCIENCES S A: Les Ulis, France, 1973. [Google Scholar]
- Hermann, R.; Krener, A. Nonlinear controllability and observability. IEEE Trans. Automat. Contr. 1977, 22, 728–740. [Google Scholar] [CrossRef]
- Chen, Z. Local observability and its application to multiple measurement estimation. Ind. Electron. IEEE Trans. 1991, 38, 491–496. [Google Scholar] [CrossRef]
- Zhang, L.; Neusypin, K.A.; Selezneva, M.S. A New Method for Determining the Degree of Controllability of State Variables for the LQR Problem Using the Duality Theorem. Appl. Sci. 2020, 10, 5234. [Google Scholar] [CrossRef]
- Ham, F.M.; Brown, R.G. Observability, Eigenvalues, and Kalman Filtering. IEEE Trans. Aerosp. Electron. Syst. 1983, AES-19, 269–273. [Google Scholar] [CrossRef]
- Cheng, X.; Dejun, W. Study on Observability and Its Degree of Strapdown Inertial Navigation System. J. Southeast Univ. 1997, 27, 6–11. [Google Scholar]
- Baram, Y.; Kailath, T. Estimability and Regulability of Linear Systems. IEEE Trans. Autom. Control 1988, 33, 1116–1121. [Google Scholar] [CrossRef]
- Jauffret, C. Observability and fisher information matrix in nonlinear regression. Aerosp. Electron. Syst. IEEE Trans. 2007, 43, 756–759. [Google Scholar] [CrossRef]
- Sun, D.; Crassidis, J.L. Observability Analysis of Six-Degree-of-Freedom Configuration Determination Using Vector Observations. J. Guid. Control Dyn. 2002, 25, 1149–1152. [Google Scholar] [CrossRef]
- Tichavsky, P.; Muravchik, C.H.; Nehorai, A. Posterior Cramer-Rao bounds for discrete-time nonlinear. IEEE Trans. Signal Process. 1998, 46, 1386–1396. [Google Scholar] [CrossRef]
- Xiong, K.; Liu, L. Design of parallel adaptive extended Kalman filter for online estimation of noise covariance. Aircr. Eng. 2019, 91, 112–123. [Google Scholar] [CrossRef]
- Xiong, K.; Wei, C. Adaptive Iterated Extended KALMAN Filter for Relative Spacecraft Attitude and Position Estimation. Asian J. Control 2018, 20, 1595–1610. [Google Scholar] [CrossRef]
- Bermudez, J.; Valdés, R.M.A.; Comendador, V.F.G. Engineering Applications of Adaptive Kalman Filtering Based on Singular Value Decomposition (SVD). Appl. Sci. 2020, 10, 5168. [Google Scholar] [CrossRef]
- Tan, T.N.; Khenchaf, A.; Comblet, F.; Franck, P.; Champeyroux, J.M.; Reichert, O. Robust-Extended Kalman Filter and Long Short-Term Memory Combination to Enhance the Quality of Single Point Positioning. Appl. Sci. 2020, 10, 4335. [Google Scholar] [CrossRef]
- Alammari, A.; Alkahtani, A.; Riduan, M.; Noman, F.; Esa, M.R.M.; Muhammad, H.M.S.; Mohammad, S.A.; Salih Al-Khaleefa, A.; Kawasaki, Z.; Agelidis, V. Kalman Filter and Wavelet Cross-Correlation for VHF Broadband Interferometer Lightning Mapping. Appl. Sci. 2020, 10, 4238. [Google Scholar] [CrossRef]
- Liang, H.; Wang, D.D.; Mu, R.J. Adaptive filtering algorithm based on observable degree analysis of state parameters in carrier-aircraft transfer alignment. Zhongguo Guanxing Jishu Xuebao/J. Chin. Inert. Technol. 2014, 22, 58–62. [Google Scholar]
- Chu, Y.; Wang, D.; Huang, X. Observability Analysis Based Information Fusion Integrated Navigation. Aerosp. Control 2011, 29, 31–41. [Google Scholar]
- Ge, Q.; Ma, J.; He, H.; Li, H.; Zhang, G. A basic smart linear Kalman filter with online performance evaluation based on observable degree. Appl. Math. Comput. 2020, 367, 124603. [Google Scholar] [CrossRef]
- Filippi, H.; Gottzein, E.; Kuehl, C.; Mueller, C.; Barrios-Montalvo, A.; Dauphin, H. Feasibility of GNSS receivers for satellite navigation in GEO and higher altitudes. In Proceedings of the 5th ESA Workshop on Satellite Navigation Technologies and European Workshop on GNSS Signals and Signal Processing (NAVITEC), Noordwijk, The Netherlands, 8–10 December 2010; pp. 1–8. [Google Scholar]
- Dion, A.; Calmettes, V.; Bousquet, M.; Boutillon, E. Performances of a GNSS receiver for space-based applications. arXiv 2018, arXiv:1809.10086. [Google Scholar]
- Qiao, L.; Lim, S.; Liu, J. Autonomous GEO Satellite Navigation with Multiple GNSS Measurements. In Proceedings of the 22nd International Meeting of the Satellite Division of The Institute of Navigation, Savannah, GA, USA, 22–25 September 2009; pp. 2169–2177. [Google Scholar]
- Hong, S.; Chun, H.H.; Kwon, S.H.; Lee, M.H. Observability Measures and Their Application to GPS/INS. IEEE Trans. Veh. Technol. 2008, 57, 97–106. [Google Scholar] [CrossRef]
- Shang, Z.; Ma, X.; Liu, Y.; Ya, S. Adaptive hybrid Kalman filter based on the degree of observability. In Proceedings of the 34th Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015. [Google Scholar]
- Park, E.S.; Park, S.Y.; Roh, K.M.; Choi, K.H. Satellite orbit determination using a batch filter based on the unscented transformation. Aerosp. Sci. Technol. 2010, 14, 387–396. [Google Scholar] [CrossRef]
- Qiao, L.; Lim, S.; Rizos, C.; Liu, J. GNSS-Based Orbit Determination for Highly Elliptical Orbit Satellites. Earth 2009, 2, 3. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, Y.; Zhou, X.; Wang, J.; He, Z.; Zhou, H. Observability Analysis and Navigation Filter Optimization of High-Orbit Satellite Navigation System Based on GNSS. Appl. Sci. 2020, 10, 7513. https://doi.org/10.3390/app10217513
Xiao Y, Zhou X, Wang J, He Z, Zhou H. Observability Analysis and Navigation Filter Optimization of High-Orbit Satellite Navigation System Based on GNSS. Applied Sciences. 2020; 10(21):7513. https://doi.org/10.3390/app10217513
Chicago/Turabian StyleXiao, Yaqi, Xuanying Zhou, Jiongqi Wang, Zhangming He, and Haiyin Zhou. 2020. "Observability Analysis and Navigation Filter Optimization of High-Orbit Satellite Navigation System Based on GNSS" Applied Sciences 10, no. 21: 7513. https://doi.org/10.3390/app10217513
APA StyleXiao, Y., Zhou, X., Wang, J., He, Z., & Zhou, H. (2020). Observability Analysis and Navigation Filter Optimization of High-Orbit Satellite Navigation System Based on GNSS. Applied Sciences, 10(21), 7513. https://doi.org/10.3390/app10217513



