Generative Enhancement of 3D Image Classifiers
Abstract
1. Introduction
2. Related Work
3. Dataset
Preprocessing and Transformation
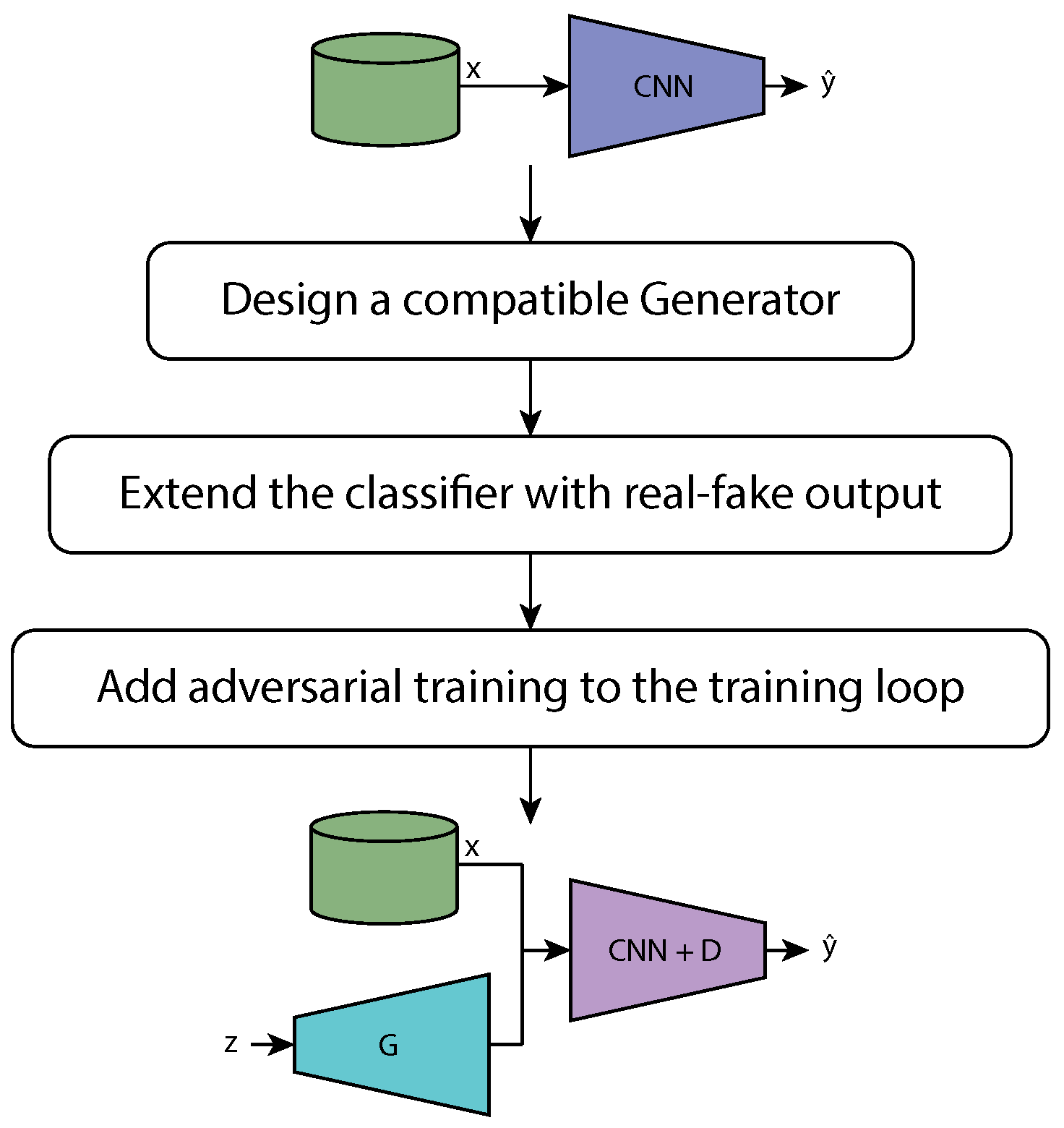
4. Generative Enhancement Methodology
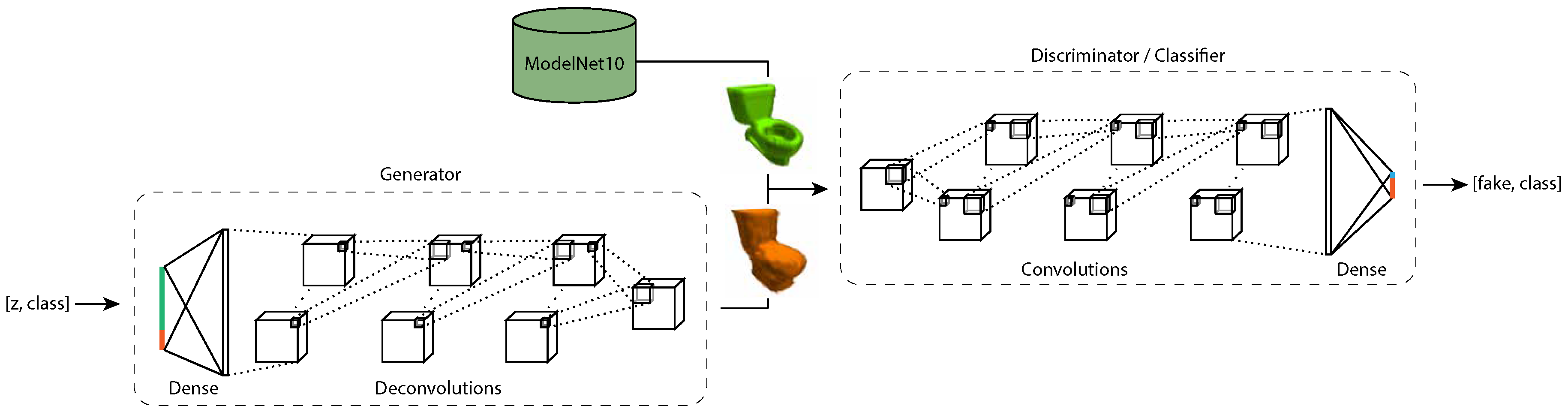
5. Models and Methods
5.1. 3D Convolutional Neural Network Classifiers
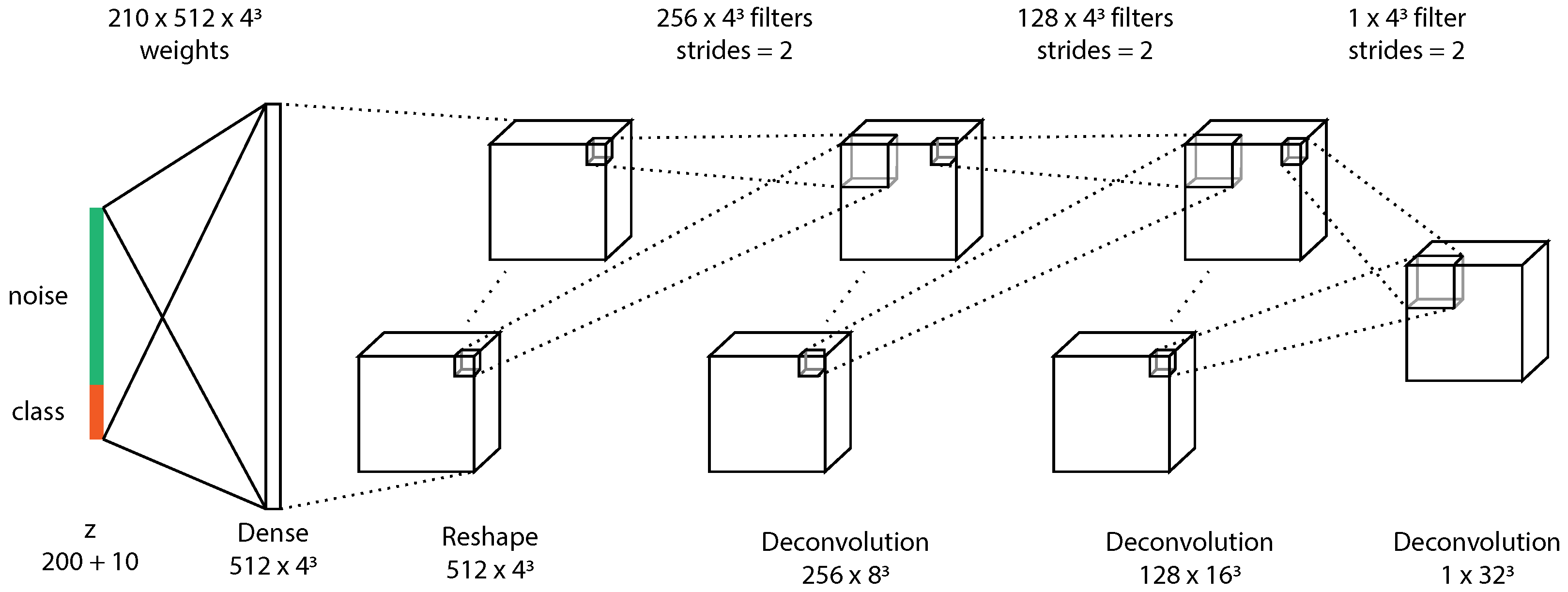
5.2. 3D Conditional Generative Adversarial Network
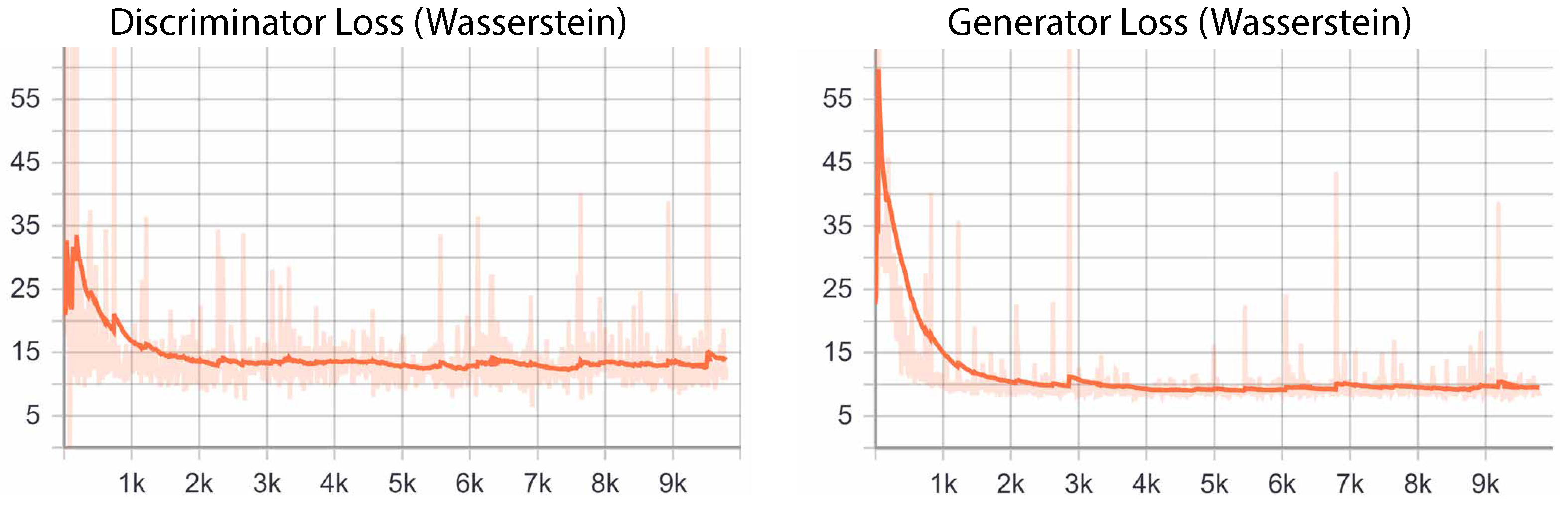
5.3. Training
6. Results and Discussion
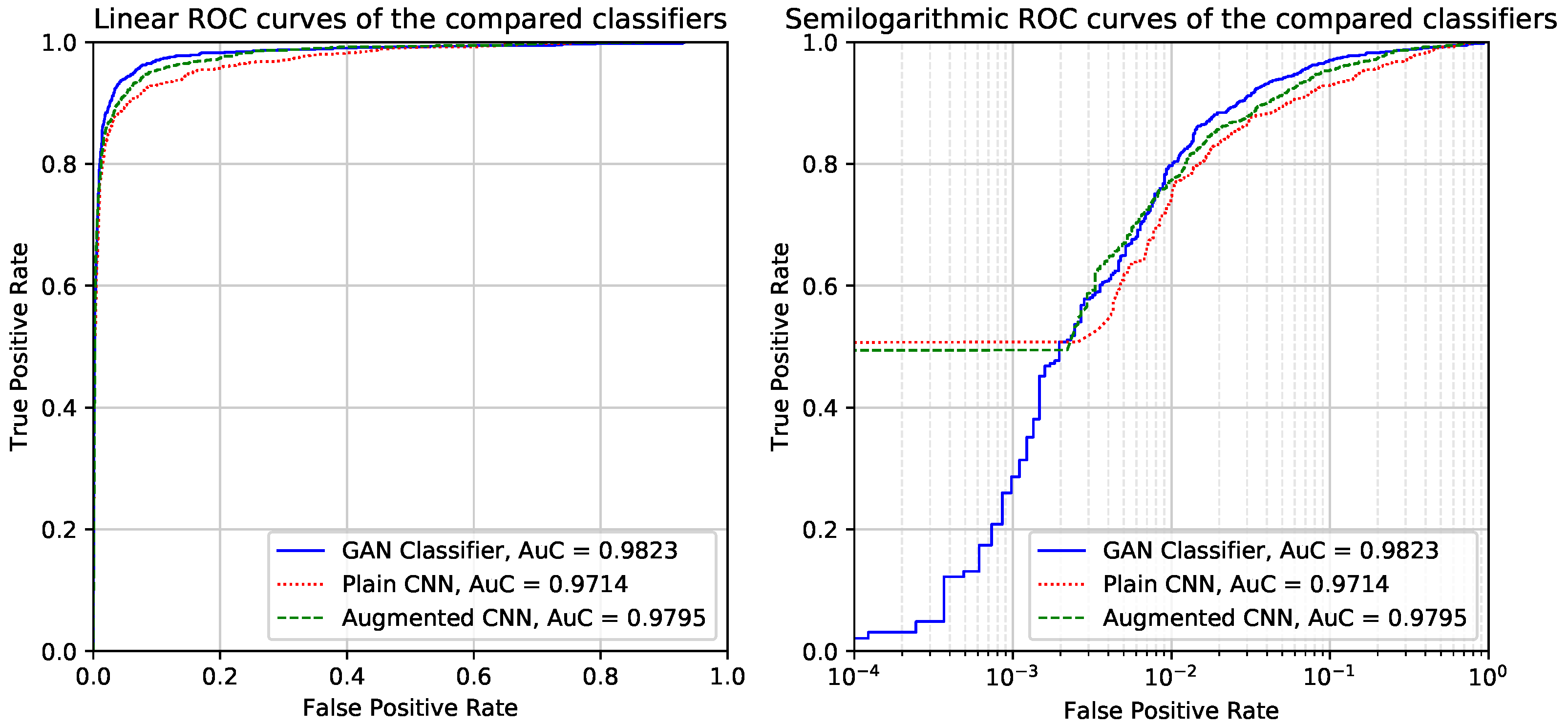
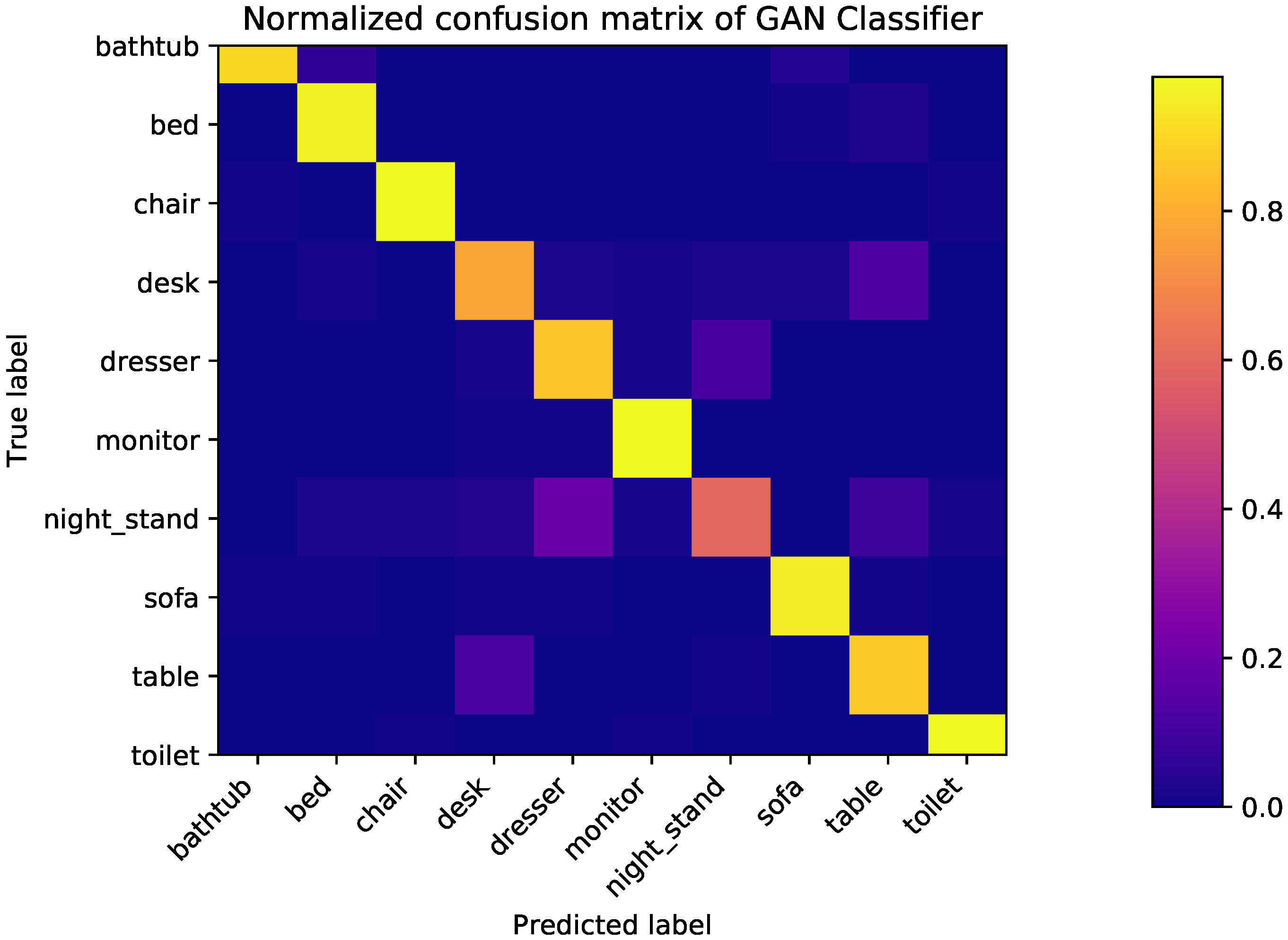
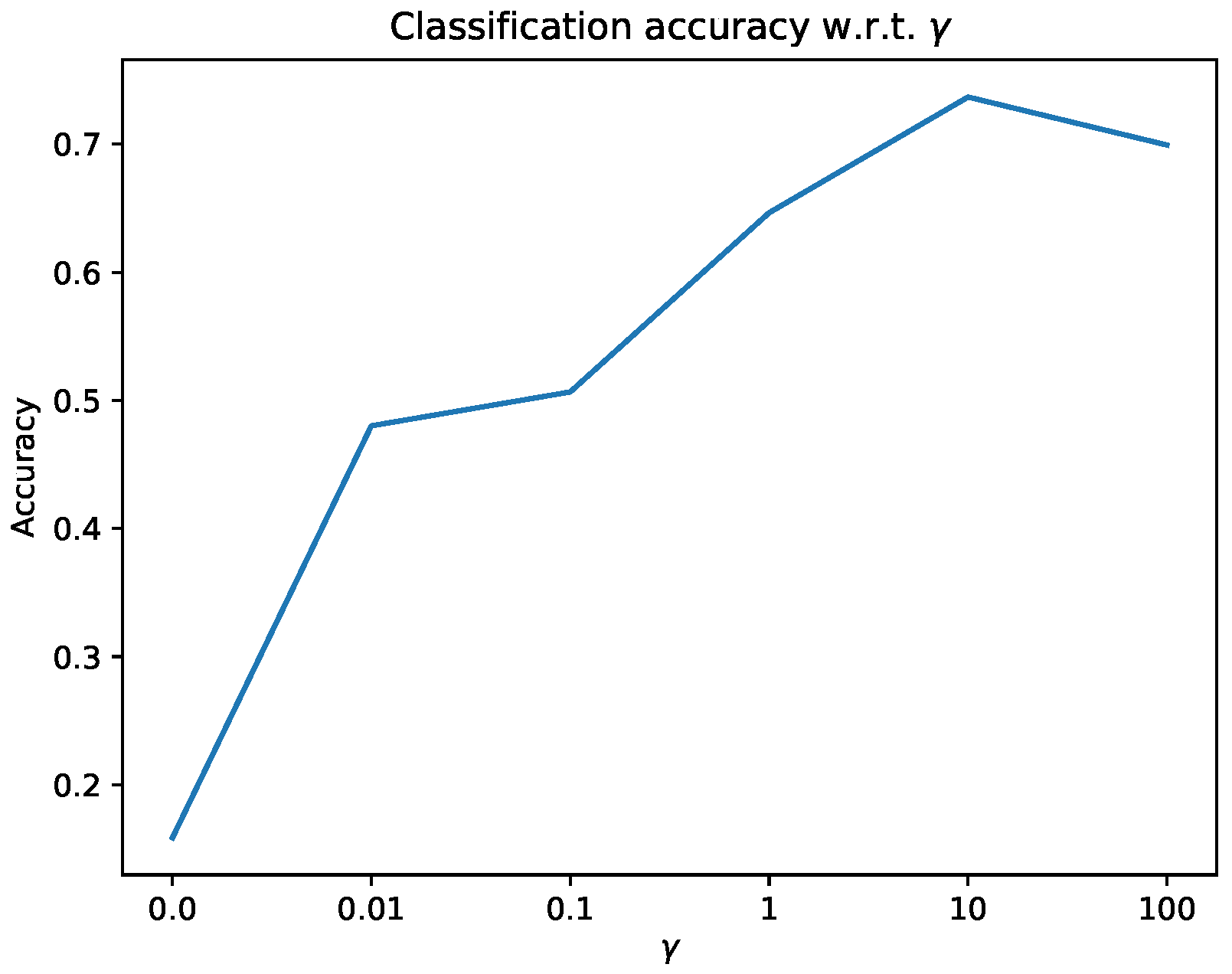
6.1. Classification
6.2. Object Generation
6.3. Performance and Timing
7. Conclusions and Future Work
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hartmann, K.G.; Schirrmeister, R.T.; Ball, T. EEG-GAN: Generative Adversarial Networks for Electroencephalograhic (EEG) Brain Signals. arXiv 2018, arXiv:1806.01875. [Google Scholar]
- Chen, L.; Dai, S.; Tao, C.; Zhang, H.; Gan, Z.; Shen, D.; Zhang, Y.; Wang, G.; Zhang, R.; Carin, L. Adversarial Text Generation via Feature-Mover’s Distance. In Proceedings of the Advances in Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018; pp. 4666–4677. [Google Scholar]
- Zhang, H.; Xu, T.; Li, H.; Zhang, S.; Wang, X.; Huang, X.; Metaxas, D.N. Stackgan: Text to Photo-Realistic Image Synthesis with Stacked Generative Adversarial Networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 5907–5915. [Google Scholar]
- Pascual, S.; Bonafonte, A.; Serra, J. SEGAN: Speech Enhancement Generative Adversarial Network. arXiv 2017, arXiv:1703.09452. [Google Scholar]
- Vondrick, C.; Pirsiavash, H.; Torralba, A. Generating Videos with Scene Dynamics. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 613–621. [Google Scholar]
- Wang, Y.; Tao, X.; Shen, X.; Jia, J. Wide-Context Semantic Image Extrapolation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 1399–1408. [Google Scholar]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]
- Jiang, Y.; Xu, J.; Yang, B.; Xu, J.; Zhu, J. Image Inpainting Based on Generative Adversarial Networks. IEEE Access 2020, 8, 22884–22892. [Google Scholar] [CrossRef]
- Tasse, F.P.; Dodgson, N. Shape2Vec: Semantic-Based Descriptors for 3D Shapes, Sketches and Images. ACM Trans. Graph. (TOG) 2016, 35, 208:1–208:12. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, C.; Xue, T.; Freeman, B.; Tenenbaum, J. Learning a Probabilistic Latent Space of Object Shapes via 3d Generative-Adversarial Modeling. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 82–90. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Advances in Neural Information Processing Systems 27; Ghahramani, Z., Welling, M., Cortes, C., Lawrence, N.D., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Palais des Congrès de Montréal, Montréal, QC, Canada, 2014; pp. 2672–2680. [Google Scholar]
- Odena, A. Semi-Supervised Learning with Generative Adversarial Networks. In Proceedings of the Workshop on Data-Efficient Machine Learning (ICML 2016), New York City, NY, USA, 19–24 June 2016. [Google Scholar]
- Brock, A.; Lim, T.; Ritchie, J.M.; Weston, N.J. Generative and Discriminative Voxel Modeling with Convolutional Neural Networks. In Proceedings of the Neural Inofrmation Processing Conference, Barcelona, Spain, 5–10 December 2016; pp. 1–9. [Google Scholar]
- Achlioptas, P.; Diamanti, O.; Mitliagkas, I.; Guibas, L. Learning Representations and Generative Models for 3D Point Clouds. In Proceedings of the International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 40–49. [Google Scholar]
- Khan, S.H.; Guo, Y.; Hayat, M.; Barnes, N. Unsupervised Primitive Discovery for Improved 3D Generative Modeling. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 9739–9748. [Google Scholar]
- Kanezaki, A.; Matsushita, Y.; Nishida, Y. RotationNet: Joint Object Categorization and Pose Estimation Using Multiviews from Unsupervised Viewpoints. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 5010–5019. [Google Scholar]
- Han, Z.; Wang, X.; Vong, C.M.; Liu, Y.S.; Zwicker, M.; Chen, C.P. 3DViewGraph: Learning Global Features for 3D Shapes from a Graph of Unordered Views with Attention. In Proceedings of the 2019 International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019. [Google Scholar]
- Han, Z.; Liu, X.; Liu, Y.S.; Zwicker, M. Parts4Feature: Learning 3D Global Features from Generally Semantic Parts in Multiple Views. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019. [Google Scholar]
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3d Shapenets: A Deep Representation for Volumetric Shapes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1912–1920. [Google Scholar]
- Salimans, T.; Goodfellow, I.; Zaremba, W.; Cheung, V.; Radford, A.; Chen, X. Improved Techniques for Training GANs. In Proceedings of the 30th International Conference on Neural Information Processing Systems; Curran Associates Inc.: Red Hook, NY, USA, 2016; NIPS’16; pp. 2234–2242. [Google Scholar]
- Chintala, S. How to Train a GAN? Tips and Tricks to Make GANs Work. 2019. Available online: https://github.com/soumith/ganhacks (accessed on 14 October 2020).
- Antoniou, A.; Storkey, A.; Edwards, H. Data Augmentation Generative Adversarial Networks. arXiv 2018, arXiv:1711.04340. [Google Scholar]
- Wang, J.; Perez, L. The Effectiveness of Data Augmentation in Image Classification Using Deep Learning. Convolutional Neural Netw. Vis. Recognit. 2017, 11, abs/1712.04621. [Google Scholar]
- Tanaka, F.H.K.d.S.; Aranha, C. Data Augmentation Using GANs. arXiv 2019, arXiv:1904.09135. [Google Scholar]
- Iqbal, T.; Ali, H. Generative Adversarial Network for Medical Images (MI-GAN). J. Med. Syst. 2018, 42, 231. [Google Scholar] [CrossRef] [PubMed]
- Židek, K.; Lazorík, P.; Pitel’, J.; Hošovskỳ, A. An Automated Training of Deep Learning Networks by 3D Virtual Models for Object Recognition. Symmetry 2019, 11, 496. [Google Scholar] [CrossRef]
- Odena, A.; Olah, C.; Shlens, J. Conditional Image Synthesis With Auxiliary Classifier GANs. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; Precup, D., Teh, Y.W., Eds.; PMLR: International Convention Centre, Sydney, Australia, 2017; Volume 70, pp. 2642–2651. [Google Scholar]
- Mariani, G.; Scheidegger, F.; Istrate, R.; Bekas, C.; Malossi, C. BAGAN: Data Augmentation with Balancing GAN. arXiv 2018, arXiv:1803.09655. [Google Scholar]
- Sutskever, I.; Jozefowicz, R.; Gregor, K.; Rezende, D.; Lillicrap, T.; Vinyals, O. Towards Principled Unsupervised Learning. arXiv 2015, arXiv:1511.06440. [Google Scholar]
- Springenberg, J.T. Unsupervised and Semi-Supervised Learning with Categorical Generative Adversarial Networks. In Proceedings of the 5th International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Shen, P.; Lu, X.; Li, S.; Kawai, H. Conditional Generative Adversarial Nets Classifier for Spoken Language Identification. In Proceedings of the INTERSPEECH 2017, Stockholm, Sweden, 20–24 August 2017. [Google Scholar] [CrossRef]
- Fan, H.; Su, H.; Guibas, L.J. A Point Set Generation Network for 3d Object Reconstruction from a Single Image. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 605–613. [Google Scholar]
- Ren, M.; Niu, L.; Fang, Y. 3D-A-Nets: 3D Deep Dense Descriptor for Volumetric Shapes with Adversarial Networks. arXiv 2017, arXiv:1711.10108. [Google Scholar]
- Wang, W.; Huang, Q.; You, S.; Yang, C.; Neumann, U. Shape Inpainting Using 3d Generative Adversarial Network and Recurrent Convolutional Networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2298–2306. [Google Scholar]
- Yi, L.; Zhao, W.; Wang, H.; Sung, M.; Guibas, L.J. Gspn: Generative Shape Proposal Network for 3d Instance Segmentation in Point Cloud. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 3947–3956. [Google Scholar]
- Wang, W.; Yu, R.; Huang, Q.; Neumann, U. Sgpn: Similarity Group Proposal Network for 3d Point Cloud Instance Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2569–2578. [Google Scholar]
- Varga, M.; Jadlovský, J. Evaluation of Depth Modality in Convolutional Neural Network Classification of RGB-D Images. Acta Electrotech. Inform. 2018, 18, 26–31. [Google Scholar] [CrossRef]
- Jiang, J.; Bao, D.; Chen, Z.; Zhao, X.; Gao, Y. MLVCNN: Multi-Loop-View Convolutional Neural Network for 3D Shape Retrieval. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 8513–8520. [Google Scholar]
- Bazrafkan, S.; Corcoran, P. Versatile Auxiliary Classifier with Generative Adversarial Network (Vac+ Gan), Multi Class Scenarios. arXiv 2018, arXiv:1806.07751. [Google Scholar]
- Varga, M.; Jadlovský, J. Contribution to Generative Modelling and Classification of 3D Images. In SCYR 2018: Proceedings from Conference; TUKE: Herl’any, Slovakia, 2018; pp. 61–62. [Google Scholar]
- Min, P. Binvox. 2004. Available online: http://www.patrickmin.com/binvox (accessed on 14 October 2020).
- Nooruddin, F.S.; Turk, G. Simplification and Repair of Polygonal Models Using Volumetric Techniques. IEEE Trans. Vis. Comput. Graph. 2003, 9, 191–205. [Google Scholar] [CrossRef]
- Varga, M.; Jadlovský, J. Contribution to 3D Voxel Generative Adversarial Networks. In SCYR 2019: Proceedings from Conference; TUKE: Herl’any, Slovakia, 2019; pp. 56–57. [Google Scholar]
- Campagnola, L. PyQtGraph. 2012. Available online: http://www.pyqtgraph.org (accessed on 14 October 2020).
- Mirza, M.; Osindero, S. Conditional Generative Adversarial Nets. arXiv 2014, arXiv:1411.1784. [Google Scholar]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein GAN. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; Precup, D., Teh, Y.W., Eds.; PMLR: International Convention Centre, Sydney, Australia, 2017; Volume 70, pp. 214–223. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference for Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Han, Z.; Shang, M.; Liu, Y.S.; Zwicker, M. View Inter-Prediction GAN: Unsupervised Representation Learning for 3D Shapes by Learning Global Shape Memories to Support Local View Predictions. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 8376–8384. [Google Scholar]
- Jadlovský, J.; Jadlovská, A.; Jadlovská, S.; Čerkala, J.; Kopčík, M.; Čabala, J.; Oravec, M.; Varga, M.; Vošček, D. Research Activities of the Center of Modern Control Techniques and Industrial Informatics. In Proceedings of the 2016 IEEE 14th International Symposium on Applied Machine Intelligence and Informatics (SAMI), Herl’any, Slovakia, 21–23 January 2016; pp. 279–285. [Google Scholar] [CrossRef]


| Accuracy [%] | Mean AP [%] | |
|---|---|---|
| VRN Ensemble [13] | 97.14 | |
| Achlioptas et al. [14] | 95.40 | |
| VIPGAN [48] | 94.05 | 90.69 |
| Primitive-GAN [15] | 92.20 | |
| 3D-GAN [10] | 91.00 | |
| Plain CNN (ours) | 83.04 | 83.75 |
| Augmented CNN (ours) | 84.58 | 86.31 |
| GAN Classifier (ours) | 89.21 | 89.18 |
| GAN Classifier no-fake (ours) | 87.11 | 90.04 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Varga, M.; Jadlovský, J.; Jadlovská, S. Generative Enhancement of 3D Image Classifiers. Appl. Sci. 2020, 10, 7433. https://doi.org/10.3390/app10217433
Varga M, Jadlovský J, Jadlovská S. Generative Enhancement of 3D Image Classifiers. Applied Sciences. 2020; 10(21):7433. https://doi.org/10.3390/app10217433
Chicago/Turabian StyleVarga, Michal, Ján Jadlovský, and Slávka Jadlovská. 2020. "Generative Enhancement of 3D Image Classifiers" Applied Sciences 10, no. 21: 7433. https://doi.org/10.3390/app10217433
APA StyleVarga, M., Jadlovský, J., & Jadlovská, S. (2020). Generative Enhancement of 3D Image Classifiers. Applied Sciences, 10(21), 7433. https://doi.org/10.3390/app10217433





