Abstract
Currently, the seismic designs of reinforced concrete (RC) bridges with tall piers are often accomplished following the ductility-based seismic design method. Though the collapses of the RC bridges with tall piers can be avoided, they are likely to experience major damage and loss of functionality when subjected to strong near-fault ground motions. The objectives of this study are to put forward an innovative design concept of a tall-pier system and its application in tall-pier bridges. The concept of the innovative tall-pier system is derived from the principle of earthquake-resilient structures, and is to improve the seismic performances of the tall-pier bridges under strong near-fault ground motions. The proposed tall-pier system has a box section and is composed of four concrete-filled steel tubular (CFST) columns and energy dissipating mild steel plates (EDMSPs). Trial design of a bridge with the new composite tall-pier system is performed based on a typical continuous rigid frame highway bridge with conventional RC box section tall piers. Both static analysis and nonlinear time history analysis of both the bridges with the new composite tall piers and conventional RC tall piers under the near-fault velocity pulse-type ground motions were conducted in Midas Civil2019 and ABAQUS. The results show that: under the design-based earthquake (DBE), the CFST columns and connecting steel beams remain elastic in the bridge with the new composite tall piers, while the damage is found in the replaceable EDMSPs which help dissipate the seismic input energy. The displacement responses of the new bridge are significantly smaller than those of the conventional bridge under DBE. It is concluded that the bridge with the new composite tall piers is seismic resilient under near-fault ground motions.
1. Introduction
When constructing an expressway or a railway in areas with high mountains and deep valleys, the total length of the route may be shortened by 200 m to 400 m as the height of pier increases 1 m [1]. Therefore, tall-pier bridges are the only design option most times. According to statistics, the number of tall-pier bridges with a pier height over 40 m accounts for more than 40% of the bridges in Western China [2]. However, a worldwide common definition of tall-pier bridge is lacking. AASHTO [3] does not directly provide the definition of the tall-pier bridge, but it regulates that the second-order effect should be considered when the slenderness of the pier is greater than 40. Chinese engineers usually regard the bridge with a pier height no less than 35 m as a tall-pier bridge [4]. This type of highway bridge was investigated in this study. In the middle of the 20th century, some countries, such as Europe and North America, began the construction of tall-pier bridges. In recent years, the construction quantity and technology of tall-pier bridges in China have developed rapidly. Many bridges in China, such as the Labajin bridge, Hezhang bridge, and so on have continuously broken the record of pier height. However, there are still some challenges and obstacles in the construction of tall-pier bridges.
First of all, compared with medium and short piers, the slenderness ratio of tall piers is significantly larger, resulting in instability problems and greater displacement at the top of the piers. To meet the requirements of stability and control the displacement of the piers, double thin-walled or hollow piers are commonly used [5]. These sections can effectively increase the sectional moment of inertia, reduce the slenderness ratio, cut the material consumption of concrete of the tall pier, and improve its stability.
Secondly, the methods such as gliding formwork, climbing formwork or turnover formwork [6] to pour concrete on site, are usually adopted in the construction of traditional RC tall piers. These construction methods generally have problems of long construction periods, high labor and site machinery costs, high altitude operations, and other high-risk factors. Furthermore, the seismic design of tall-pier bridges is more complicated than conventional bridges. The mass distribution, high-order modes and second-order effects play significant roles in the structural seismic response. However, there are few relating research on the seismic performance of tall-pier bridges.
The difference in the spectral components of different ground motions will result in a varying contribution of different mode in the structural responses. Hence, the ductility of tall piers is different when different ground motions are input. Freeman et al. [7] pointed out that the participation factor of higher-order modes in tall piers is too large to be neglected. Otherwise, it would lead to significant errors when performing the displacement-based design. Tubaldi et al. [8] employed the linear-elastic Euler–Bernoulli cantilever beam with a distributed mass and a concentrated mass at the top to simulate the tall pier. The analytical formulation regarding the dynamic behavior and seismic response is proposed, considering the influence of P-Δ effect and high-order modes on the dynamic characteristics and seismic response of the pier. The results showed that the mass participation factor of the first mode decreased significantly with the increase of pier height. Meanwhile, the seismic response was strongly influenced by second-order effects and higher modes contributions related to the distributed pier mass. Li et al. [9,10] found that the high-order modes significantly contributed to the seismic response of a tall-pier bridge. These modes would result in additional plastic hinges midway up the pier under strong ground motions. Mistakenly using the displacement-based seismic design method for tall piers may result in a seriously unsafe condition. Ceravolo et al. [11] focused on the effectiveness of the capacity design procedure in the design of a tall-pier bridge. The investigation showed that the positions of plastic hinges did not match with the common assumption, due to the contributions of the inertial forces of the piers.
Currently, due to the limited investigations and lack of suitable design codes or specifications, the seismic design of tall-pier bridges remains an aimless and casual design. In the Specifications for Seismic Design of Highway Bridges (JTG/T 2231-01-2020) [12], it is required that specified research needs to be conducted if the maximum pier height exceeds 40 m or the effective mass of the first mode of the pier is less than 60%. The AASHTO Guide Specifications for LRFD Seismic Bridge Design [3] and CALTRANS Seismic Design Criteria [13] are only appliable to regular bridges, whereas the tall-pier bridge belongs to the typical irregular bridges. In Eurocode 8 [14], for irregular bridges, the damping ratio of higher modes has a great influence on the calculated response spectrum so that the multi-degree-of-freedom model is usually employed. The difference between the tall pier and medium or short pier is not considered. In the specifications for highway bridges in Japan [15], there are no specified definitions for the tall, medium or short pier.
The above-mentioned research points out that the seismic design of regular bridges is not applicable to tall-pier bridges, which does not meet the definition of the regular bridge. Currently, the design method of regular medium to short pier is still applied in the design of tall-pier bridges, which is aimless and insufficient. During the Great Wenchuan Earthquake, the Miaoziping Bridge and Luzipingpu Bridge and other tall-pier bridges experienced severe damage and loss of function [16]. Compared with the far-fault ground motions, the characteristics of the near-fault ground motions are quite different. The ground motions are characterized by intense pulse, long pulse period and large fault displacement, which lead to the energy accumulation in a short time and thus damage the structures [17]. In the Imperial Valley earthquake (1979), the Northridge earthquake (1994), the Kobe earthquake (1995), and the Chi-Chi earthquake (1999), the damage and collapse of a large number of structures under near-fault ground motions caused the widespread concern among scholars. Anderson and Bertero [18] demonstrated that the relationship between the acceleration pulse duration and the fundamental period of the structure greatly affected the structural seismic performance. The results revealed that the more serious damage would occur when the pulse duration is much larger than the structural period. Somerville et al. [19] analyzed effects of rupture directivity on the amplitude and duration of strong ground motion. It is found that the elastic response spectrum of pulse-type ground motion was larger than that of non-pulse ground motion for periods longer than 0.6 s. Also, many other scholars concluded that near-fault ground motions with pulses greatly affected the seismic performance of the structures with a medium fundamental period. Kalkan and Kunnath [20] analyzed the influence of the dynamic response of a steel frame structure subjected to the near-fault earthquake. The results showed that compared with the far-fault ground motions, the velocity pulse in near-fault ground motions would cause the structure to dissipate considerable input energy in relatively few plastic cycles.
To sum up, structures will experience more serious damage when subjected to near-fault ground motions with pulses. Due to the lack of specialized seismic design concepts and design methods for RC tall-pier bridges, excessive displacement and deformation of the bridge may occur under near-fault ground motions, leading to severe structural damage, which requires costly and time-consuming repair, and even replacement [16,21]. How to improve the seismic performance of the tall-pier bridge under near-fault ground motion has become an urgent problem.
The isolation system and self-centering system are widely investigated [22,23,24,25] and proved to be effective in decreasing the seismic vulnerability and improving the seismic performance of bridges. Although these new tall-pier bridges have better seismic performance and some of them have been used in the engineering practice, the problem of complex construction, and time-cosuming repairment still exists, their seismic design concepts and design methods are not systematic and updated. In 2003, Bruneau et al. [26] put forward the conceptual framework of seismic resilience and aroused wide attention in the field of civil engineering. With the development of seismic technology and the resilient design concept of engineering structure, more and more effort are paid to the research of earthquake-resilient structures. In recent years, the seismic design concept of bridges has developed from earthquake-resistant to earthquake-resilient. Moreover, seismic resilience is the theme of the 16th World Earthquake Engineering (16WCEE, 2017) [27]. Based on the design concept of seismic resilience, considerable methods, such as rocking structure, self-centering structure, replaceable component and so on have been proposed and used in the engineering practice. Roeder and Popov [28] proposed the design concept of “structural fuse” when studying eccentrically braced steel frames. Tang et al. [29] firstly proposed the design concept of the replaceable steel main tower that consists of steel columns and beams when designing the east span of the new San Francisco-Oakland Bay Bridge. McDaniel and Seible [30] further concluded that the steel coupling beam served as a “structural fuse” and yielded while the tower column remained elastic under moderate and strong earthquakes. Since then, more and more experiments and theoretical research were conducted to develop the replaceable components in bridges. Some typical examples include the bi-steel columns with buckling restrained braces (BRB) and the bi-steel columns with steel energy dissipating coupling beams [31,32,33]. Currently, the research of replaceable component structure system in bridge engineering concentrates on multi-column pier with BRB and multi-column pier with steel plate shear link and they are mainly applied in the medium and short pier bridges. Bazaez and Dusicka [34] conducted quasi-static tests for RC bridge bents retrofitted using BRBs. The results demonstrated that the BRBs could be replaced immediately after large plastic deformation. Xiang and Alam [35] proposed a design procedure for bridge bents with BRBs; the authors pointed out that BRBs could reduce the vulnerability of bridge bents at various damage states under both near-fault and far-field motions.
However, the above research focused on short-to-mediate pier columns while few investigations on bridges with tall pier columns have been reported to date. The application of the replaceable component structure in bridge engineering remains an unsolved issue. Due to the “strong beam - weak column” principle in the seismic design of the bridge, pier columns are designed as ductile elements that may be damaged in a strong earthquake [36]. To improve the seismic performance and avoid the time-consuming repairment of the tall-pier bridge, especially under near-fault ground motions, a new type of tall pier, is firstly proposed in this study based on the design concept of seismic resilience. The newly proposed composite tall pier consists of four-limb concrete-filled steel tubular (CFST) columns and energy dissipating mild steel plates (EDMSPs). The vertical axial loads are mainly resisted by the CFST columns due to the sufficient bearing capicity. The EDMSPs serve as both energy-dissipating components and sacrificial components. Meanwhile, the I-shape steel beams are installed with some intervals to connect the four limbs of the CFST column. Figure 1 shows the sketch of the new composite tall pier.

Figure 1.
Design concept of the new composite tall pier. (a) longitudinal view, (b) transverse view, (c) cross section. CFST: column: concrete-filled steel tubular column.
2. Design Concept of New Composite Tall-Pier Bridge
The design concepts of the new composite tall-pier bridge are as follows:
- Under normal service conditions, the new composite tall pier provides sufficient flexural and torsional stiffness. Meanwhile, the I-shape steel beams are installed along the height of the pier to ensure the overall stability of the structure.
- Under the service level earthquakes (SLEs), the whole bridge is intentionally designed to remain essentially elastic.
- Under the design-based earthquakes (DBEs), the EDMSPs are intentionally designed for energy dissipation while CFST columns are designed to remain elastic. The seismic input energy is dissipated by the hysteretic behavior of the EDMSPs, which in return reduces the stiffness of the pier and mitigates the seismic damage. Only slight damage or inelastic states are allowed for I-shape steel beams.
In terms of load-carrying capacity design, the lateral and vertical load transferred from the superstructure are mainly resisted by the four-limb CFST columns under the basic load combination. Under the seismic load combination, both the lateral and vertical loads are mainly resisted by the four-limb CFST columns, while the EDMSPs and the I-shape steel beams participate in resisting part of the lateral load. Compared with the conventional RC tall-pier bridge, the advantages of the new composite tall-pier bridge are readily visible:
- The new composite tall piers are supposed to perform as well as the conventional RC box section tall piers subject to the static loads. Meanwhile, due to the vertical axial loads are mainly resisted by the CFST columns, the problem of local bulking in conventional steel pier can be avoided.
- During the earthquakes, the CFST columns are designed to remain elastic with the help of the energy dissipating devices. The EDMSPs yield and dissipate seismic energy and can be replaced quickly. The design concept of seismic resilience for tall-pier bridges can be achieved by proper design.
- The new composite tall piers have the same characteristic of rapid construction as the CFST lattice columns, such as segmental prefabrication, less volume of concrete, easy hoisting and installation. Compared with the construction of traditional RC tall piers, the construction equipment is simpler, and the construction speed can be significantly improved during the turnover and climbing formwork.
A conventional RC continuous rigid-frame bridge with box section tall piers located in the highway of the mountainous area is taken as the prototype. Then, the ptototype tall piers are replaced by the new composite tall piers. Meanwhile, the other parts of the bridge remain the same as the prototype. Both static and time history analyses of the new and conventional tall-pier bridges are conducted in Midas2019 and ABAQUS for comparing their seismic performances.
3. Design of New Composite Tall-Pier Bridge
3.1. Bridge Prototype
In this study, a tall-pier bridge located at the highway in the mountainous area is used as the prototype bridge as shown in Figure 2. The bridge has two side spans of 57.5 m and a main span of 105 m. The superstructure is a prestressed concrete continuous rigid girder, with a variable box section. C50 concrete with a compressive strength of 50 MPa is used in the girder. The height of the girder at the mid-support is 6.0 m. It reduces to 2.6 m at the mid-span and the end of the side span. The lower edge of the girder is a second-order parabola. The P2, P3 tall piers are RC box section piers with a wall thickness of 0.8 m and a height of 48 m. The P1, P4 piers are RC box section piers with a wall thickness of 0.8 m and a height of 30 m. The piers are constructed with C40 concrete. The width of the tall pier in the transverse direction is 6 m and the longitudinal width is 4.2 m. The GPZ(II)3DX and GPZ(II)3SX (“GPZ(II)” indicates a type of basin rubber bearing, “3” indicates the the bearing capacity is 3000 kN, “SX” and “DX” for single-directional bearing and bi-directional bearing, respectively) bearings are installed between the superstructure and the top of P1 and P4 piers.
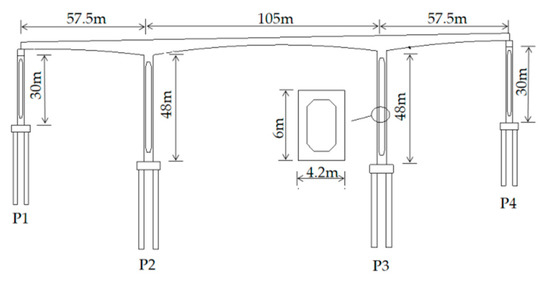
Figure 2.
Layout of the prototype bridge.
3.2. Design Procedure
To investigate the seismic performance of the new composite tall piers, the P2, P3 piers of the prototype bridge are replaced by the new composite tall piers. Meanwhile, the other parts of the bridge remain the same as the prototype. The following principles are followed when designing the new composite tall pier:
- The axial load-carrying capacity of the new composite tall pier is equivalent to the prototype pier.
- The height and stiffness in the longitudinal direction of the new composite tall pier are equivalent to the prototype one.
Based on the above design principles, the structural details of the new composite tall pier are determined as follows. The EDMSPs only connect with the CFST columns. Besides, some intervals are left between the steel beams and the EDMSPs to release the buckling deformation while resisting no vertical load. Therefore, the load-carrying capacity of the EDMSPs along the vertical direction can be neglected. The vertical axial loads are mainly resisted by the CFST columns. In terms of the lateral stiffness, the contribution of the EDMSPs is considered. To achieve similar mechanical properties with the prototype pier, and retain the prototype design of the pier cap, the sectional dimension of the new composite tall pier is kept same as the prototype pier (i.e., 6 m × 4.2 m). The four CFST columns are made of Q345 (“Q”indicates yield point, fy = 345 MPa) steel tube and C50 (fck = 50 MPa) concrete. And the EDMSPs between the CFST columns are made of LYP100 (low-yield point steel, fy = 100 MPa) steel plate. The mechanical properties of the LYP100 are shown in Table 1. In addition, the Q345 I-shaped steel beams with a sectional dimension of 400 mm × 146 mm × 16.5 mm are installed every 16 m along the height of the pier. Figure 3 shows the configuration of the new composite tall pier.

Table 1.
Mechanical properties of LYP100 steel.
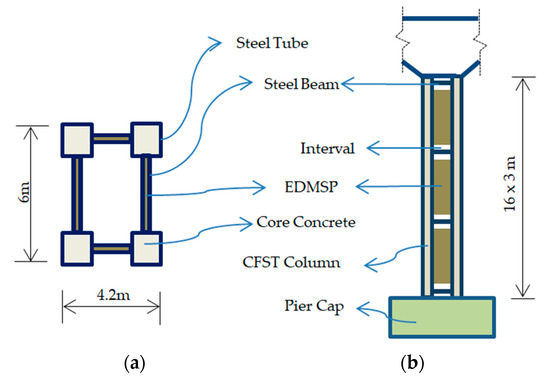
Figure 3.
Design of the new composite tall pier. (a)cross section, (b) longitudinal view.
According to the equivalent principle in terms of the vertical axial load-carrying capacity, the longitudinal and transverse dimensions of CFST columns, BL and BT, the thicknesses of steel tube t, can be obtained. Note that due to the numerous interrelated parameters, the values of these parameters are not unique. Therefore, a set of parameters is selected empirically. Then the longitudinal and transverse lengths of EDMSPs, WL and WT, the thicknesses of EDMSPs tM, are obtained based on the equivalent stiffness in the longitudinal direction as shown in Equation (1). Finally, the sectional parameters of the new composite tall pier are determined. The design procedure is presented in Figure 4.
where EC, ES, EM are the elastic modulus of the core concrete, steel tube and EDMSP, respectively. ICL, ISL, IML are the longitudinal moment of inertia of the core concrete, steel tube and EDMSP, respectively. L is the length of the composite tall pier. KN is the longitudinal stiffness of the composite tall pier.
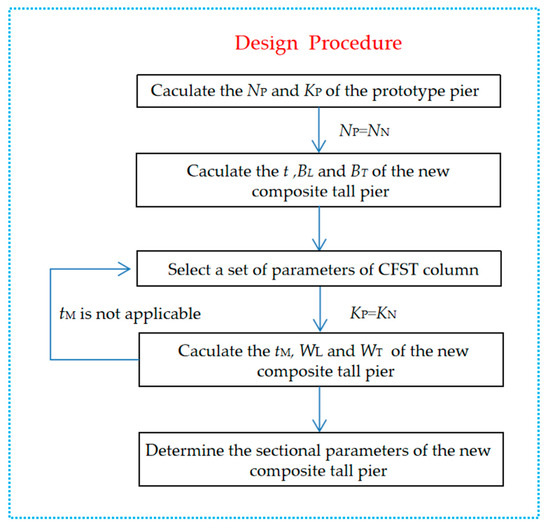
Figure 4.
Flow chart of the design program.
It is calculated that the axial compression ratios of the prototype and the new composite tall pier are 0.192 and 0.195, respectively. Hence, the axial compression ratio is considered to be identical for the two types of tall piers. Moreover, the longitudinal flexural stiffnesses of the prototype tall pier and the new composite tall pier are calculated as 27,045 kN/m and 28,483 kN/m, respectively. Therefore, the sectional properties of the new composite tall-pier bridge are similar to the prototype tall-pier bridge.
4. Static Performance Analysis
The static analysis of the new composite tall-pier bridge is implemented in Midas Civil2019. The P-Δ effects are incorporated into the analysis of the construction process.
According to the Technical Specification for Concrete-Filled Rectangular Steel Tubular Structures (CECS 159:2004) in China [37], the bending moments of the principal plane of a rectangular CFST column should meet the requirements of Equations (2) and (3) simultaneously:
where N represents the design value of the axial compressive force; M is the design value of the bending moment; αc is the working load factor of the concrete; Nun is the designed value of the sectional vertical load-bearing capacity; Mun is the design value of the sectional flexural capacity; γ is the importance coefficient, which is taken as 1.1. At the same time, Equation (4) should also be met to ensure the out-of-plane stability:
where is the compression stability coefficient; β is the equivalent bending moment coefficient.
Table 2 lists the design combination of the forces of the new composite tall pier under the basic load combination. The checking results, also shown in Table 2, indicate that the four-limb CFST columns meet the requirements of the load-carrying capacity and stability. According to the analysis results, the maximum Von Mises stress of the EDMSPs under the basic load combination is 67.6 MPa, which is less than the design yield stress of 100 MPa. Hence, the EDMSPs remain elastic.

Table 2.
Design internal forces and checks of CFST Columns.
5. Seismic Performance Analysis
5.1. Finite Element Model of the Bridges
The finite element models of the prototype bridge and the new composite tall-pier bridge are established in ABAQUS. For the prototype bridge, the superstructure and piers are simulated by the B31 elements(“B”indicates beam element, “3” is for three-dimensional beams, and “1” is for linear interpolation). The girder is assumed to remain elastic with C50 concrete(Ec = 30 GPa, fck = 50 MPa). The reinforcement is defined by the *rebar keyword (i.e., a method to define a integration point with different material fiber in the beam element section). The Kent-Scott-Park model [38] and the USteel01 model (kinematic hardening elastoplastic uniaxial constitutive model) in the PQ-Fiber subroutine developed by the Department of Civil Engineering of Tsinghua University are adopted for the constitutive models of C40(Ec = 30 GPa, fck = 40 MPa) unconfined concrete, and the HRB400 (Es = 210 GPa, fy = 400 MPa, and α = 0.01) reinforcement, as shown in Figure 5, respectively. The basin type bearings are simulated by the link elements. The stiffness is infinite along the fixed direction. In the active direction, the bidirectional elastoplastic model is adopted for the link element.
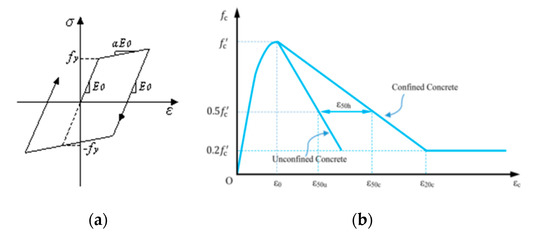
Figure 5.
Constitutive behaviors. (a) USteel01 model, (b) Kent-Scott-Park concrete model.
For the new composite tall-pier bridge, the superstructure and the basin type bearings adopt the same modeling strategy as the prototype bridge. The four-limb CFST columns and the I-shape steel beams are also modeled by the B31 element. The steel tube is simulated in fiber elements and defined by the *rebar keyword. The USteel01 material in the PQ-Fiber subroutine is adopted for the steel tube. Meanwhile, the confinement effect of the core C50 concrete is considered by the constitutive model proposed by Han [39]. The EDMSPs are modeled by the four-node reduced integrated shell elements (i.e., S4R elements). The bi-linear plastic material with the Von Mises yield criterion in ABAQUS is used for the Q345 I-shape steel beam and the LYP100 EDMSPs and the yield points are 345 MPa and 100 MPa, respectively. Both of the elastic modulus are 200 GPa. The steel beams and CFST columns are merged into a whole frame. Then, the connections between the EDMSPs and the frame are modeled using the “tie” command (i.e., a method to attach an element to the adjacent elements) Furthermore, the boundary condition is simplified as the fixed connection at the pier base. Besides, the effects of structural geometric nonlinearities are considered in the analyses.
5.2. Modal Analysis
The modal analyses are firstly conducted using the ‘eigen’ order to determine the natural periods and mode shapes of the bridge to compare the dynamic characteristic of the prototype tall-pier bridge and the new composite tall-pier bridge. The results are summarized in Figure 6 and Table 3. Both of the first modes are the transverse symmetrical bending. The second modal shapes of the two bridges are longitudinal bending. And the third modal shapes are the transverse antisymmetric bending deformations. It indicates that the two bridges have similar dynamic characteristics. The comparative results of the vibration periods of the three modes indicate the participation factor of higher-order modes in tall piers is too large to be neglected. Besides, it can be inferred from the natural periods that the response of the bridge in the transverse and longitudinal direction will be sensitive to the pulse-type near-fault ground motions. Thus, as a preliminary study, the ground motions are mainly applied in the transverse and longitudinal directions in this work.
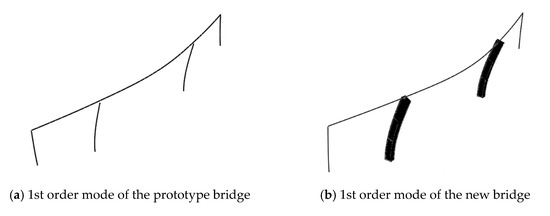
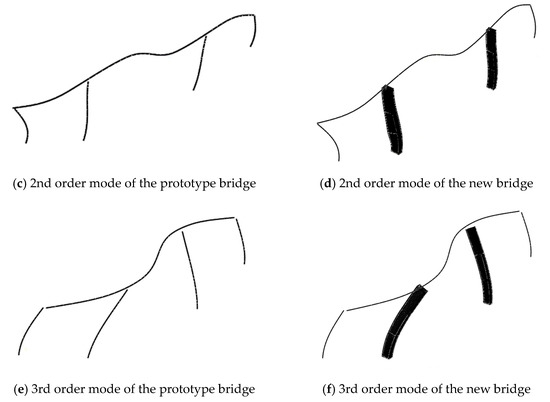
Figure 6.
Comparison of the vibration modes.

Table 3.
Comparison of the vibration modes.
5.3. Ground Motion Input
Near-fault ground motions are significantly different from the far-fault ground motions due to the effects of the fling-step and forward-directivity [40]. The ground motions are characterized by pulse-type wave shape, small fault distance d (i.e., less than 20 km), large peak ground velocity (PGV) and peak ground acceleration (PGA), and sometimes large permanent ground displacement. Based on the characteristics, near-fault pulse-type ground motion records are selected from the PEER database [41] and presented in Table 4. All the records contain the ground motions in longitudinal, transverse, and vertical directions. In the Eurocode 8 [42], the site is classified as A, B, C and D, according to the value of the average shear wave velocity, vS,30. Besides, the structures in seismic regions should be designed and constructed based on the following requirements: no-collapse requirement under the DBEs and damage limitation requirement under SLEs. The no-collapse requirement means the bridge should retain its structural integrity and a residual load-carrying capacity after the DBEs. Similarly, the occurrence of damage and the associated limitations of use is not allowed in the damage limitation requirement when the structure subjects to SLEs.

Table 4.
Near-fault velocity pulsed ground motion records.
Therefore, the largest peak ground accelerations among three directions of the selected ground motions are scaled to 0.1 g and 0.4 g, to consider the PGA of the SLE and DBE, respectively. Besides, the PGAs in the other directions are scaled in proportion. The ground motion records in three directions are input simultaneously.
5.4. Seismic Responses under the SLEs
For the prototype bridge, according to the bending moment-curvature analysis results, the yield curvatures of the main pier in longitudinal and transverse directions are 0.00056 and 0.00039, respectively. Under SLEs, the maximum curvature in the longitudinal direction equaling 0.00024 is observed at the top of the tall piers. The maximum curvature in the transverse direction of the bridge is 0.00002. Both of the curvature values are less than the yield curvatures. Therefore, the RC tall-pier bridge remains elastic when subject to SLEs.
For the new composite tall piers, under the SLEs, the maximum curvature at the top and bottom of the tall piers are 0.00082 and 0.00018, respectively. Both values are less than the yield curvature of 0.00240. Meanwhile, the maximum stress of the steel beams is 75 MPa, which is less than the yield stress of 345 MPa. Besides, the maximum stress of EDMSPs equals 81 MPa and is less than its yield stress. Therefore, the new composite tall-pier bridge is in the elastic state. Table 5 shows the average values of maximum displacements under different seismic actions. The results indicate that the lateral displacements of the new composite tall-pier bridge are close to the prototype bridge under the SLEs. Both the seismic responses of two bridges meet the requirements of damage limitation state when subject to the SLEs. Figure 7 compares the maximum displacement responses of the bridge under the SLEs. Although the maximum displacements of new composite tall-pier bridge are larger than the prototype one under some ground motions considering SLEs, the seismic performances of two bridges are similar. Both the prototype and the new bridges remain elastic without damage.

Table 5.
Comparison of average displacements under the SLEs.
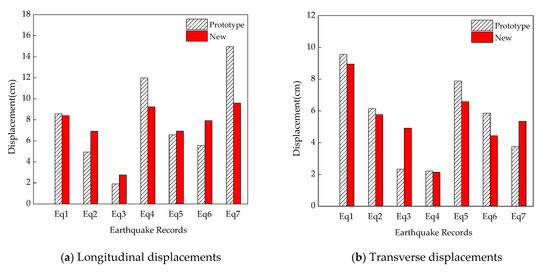
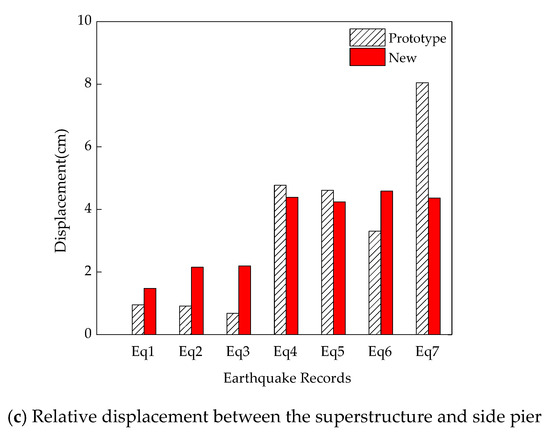
Figure 7.
Relative displacements at the pier tops under the SLEs.
5.5. Seismic Responses under the DBEs
Under the DBEs, damage is found in the prototype tall piers due to the exceedance of the yield curvature. In this study, the modified Park-Ang index is used to analyze the damage states of the bridge models. The modified Park-Ang index is defined as follow according to Kunnath et al. [43]:
where Φm, Φu, Φy, My indicate the maximum sectional curvature, the ultimate curvature, the yield curvature, yield flexural capacity of the component, respectively; β is the energy dissipation coefficient. For the component subject to compression and bending simultaneously, the accumulated hysteretic energy Eh can be obtained by integrating the bending moment over the curvature within the plastic hinge zones.
Based on the Park-Ang index, the damage states of the bridge models can be classified as no damage (D < 0.10), slight damage (0.10 ≤ D < 0.25), medium damage (0.25 ≤ D < 0.40), and significant damage (0.40 ≤ D < 1.0). Accordingly, the maximum modified Park-Ang indices and corresponding damage levels of the conventional RC tall-pier bridge under above-mentioned ground motions, are listed in Table 6. The result indicates that both the P2 and P3 tall piers suffer moderate or significant damage under the DBEs.

Table 6.
Damage indices and corresponding damage states of the piers in the prototype bridge.
For the new composite tall-pier bridge, under the DBEs, the maximum curvatures at the top and bottom of the CFST column in the tall piers are 0.00196 and 0.00170, respectively, which are less than the yield curvature of 0.00240. Therefore, the four-limb CFST columns remain elastic. The maximum Mises stress of the steel beams is 263 MPa, which is less than the yield stress of 345 MPa. Thus, the steel beams also remain elastic.
Furthermore, as shown Table 7, the average maximum displacements of the new composite tall-pier bridge is significantly less than the conventional one under the DBEs. The average values of maximum pier-top displacements in the longitudinal and transverse directions are reduced by 37.4% and 28.6%, respectively. And the average values of maximum relative displacement between the superstructure and the side pier is reduced by 21.9%. Figure 8 compares the maximum displacement responses of the bridge under the different ground motions. The results indicate that the lateral displacements of the new composite tall-pier bridge are apparently less than the conventional one under all the selected ground motions considering DBEs, indicating that the new bridge performs much better than the prototype under near-fault ground motions. Meanwhile, it should be noted that the CFST columns of the new bridge remain elastic with sufficient stiffness.

Table 7.
Comparison of maximum lateral displacements under the DBEs.
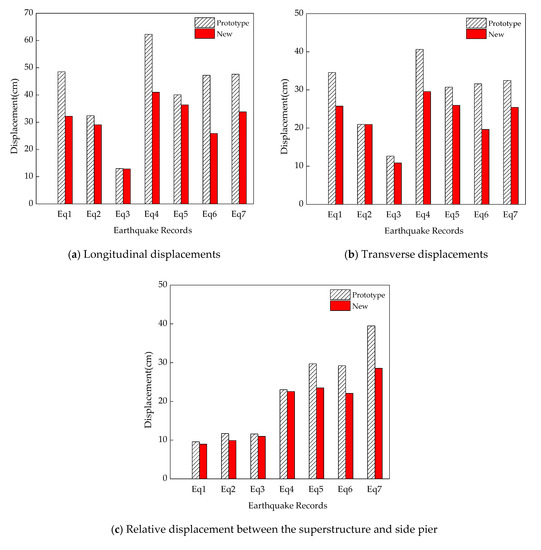
Figure 8.
Relative displacements at the pier tops under the DBEs.
As a typical example, the distributions of the yield EDMSPs under the Loma Prieta earthquake (Saratoga-Aloha Ave station) are presented in Figure 9 and Figure 10.
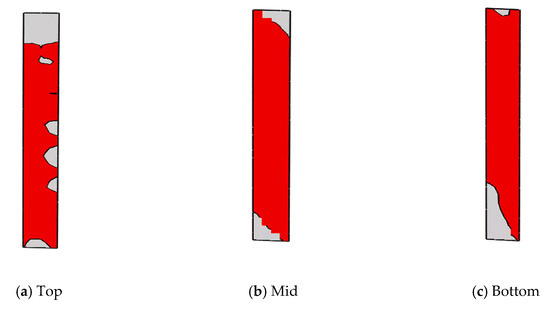
Figure 9.
Distribution of the yield EDMSPs in longitudinal direction.
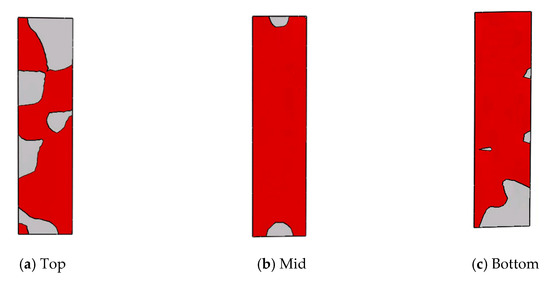
Figure 10.
Distribution of the yield EDMSPs in transverse direction.
The red parts and gray parts represent the yield parts and elastic parts of the EDMSPs, respectively. It is evident that the EDMSPs have yielded to a large extent and serve as the energy-dissipating components and sacrificial components. With similar static performances, the new composite tall-pier bridge shows better seismic performance under different strong near-fault ground motions. With the help of the hysteretic energy dissipation of the mild steel components, the displacement at the pier top under near-fault ground motion is greatly reduced. Meanwhile, no damage is found in the four-limb CFST columns of the new tall pier during the ground motion inputs. After the DBEs, the CFST columns remain elastic. The load-carrying capacities of the new composite tall piers do not decrease, which helps maintain the necessary function of the lifelines in the facilities.
6. Conclusions
The performance of the conventional RC hollow section tall-pier bridge is unsatisfactory under strong ground motions, especially near-fault ones. Many scholars have proposed different concept and method to improve the seismic performance. Although some of them can provide a satisfyting seismic responses subjected to moderate, even strong earthquake, there are still some unsolved problem subjected to the strong near-fault ground motions. Due to the lack of specialized seismic design concepts and design methods, the conventional RC tall pier is easy to be damaged, and difficult to repair.
This study proposed the structural design methods and principles of a new type of composite tall pier based on the concept of earthquake-resilient structures. Based on the piers of a typical tall-pier highway bridge, the new composite tall-pier system, which consists of the four-limb CFST columns, EDMSPs and steel beams, is proposed to improve the seismic performance of tall-pier bridges. Both static and time history analyses of the prototype tall-pier bridge and the new composite tall-pier bridge are conducted to compare their seismic performances.
The new composite tall piers can provide a satisfying load-carrying capacity and stability, and perform as well as the conventional RC tall piers under basic load combination. Under the SLEs, the new composite tall piers remain elastic and the lateral displacement is similar with the conventional RC tall piers. Both of the seismic performances of two bridges meet the requirements of the damage limitation as regulated in Eurocode 8. However, the conventional RC tall piers experience major damage and the stiffeness of the pier decrease sharply under near-fault ground motions considering DBEs. Meanwhile, no damage is found in the CFST column and steel beams during the ground motion inputs. For the new composite tall piers, only the EDMSPs yield to a large extent and serve as the energy-dissipating components and sacrificial components. Besides, the maximum lateral displacements of the new composite tall piers are significantly reduced compared to the conventional RC tall piers.
To sum up, the proposed composite tall pier has sufficient resistance and stiffness after the strong near-fault earthquakes. The resilient concept could be achieved by replacing the yield EDMSPs, which are made of the readily available materials, without interruption of service or time-consuming reinforcement maintenance after the strong near-fault earthquakes.
However, future work on the static and pseudo-static test of the proposed tall-pier system is still needed to validate the finite element models. More research is still required to address some potential design challenges, such as the manufacturing details of the connections between the columns and EDMSPs, the configurations of the EDMSPs and so on.
Author Contributions
Conceptualization, W.Z. and Y.S.; formal analysis, Z.C. and Z.W.; writing—review and editing, Z.C., K.L., W.Z. and Y.S.; supervision, K.L., W.Z. and Y.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 51878180, and the Fujian Provincial Transportation Science and Technology Development Project, grant number 201803.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, K. Seismic Research on Bridges, 2nd ed.; China Railway Press: Beijing, China, 2014. (In Chinese) [Google Scholar]
- Zong, Z.; Xia, J.; Xu, C. Seismic study of tall piers of large-span bridges: An overview and research development. J. Southeast. Univ. Nat. Sci. 2013, 43, 445–452. (In Chinese) [Google Scholar]
- AASHTO. Guide Specifications for LRFD Seismic Bridge Design; American Association of State Highway and Transportation Official: Washington, DC, USA, 2017. [Google Scholar]
- Liao, Z. Pier, Abutment and Foundation; China Communications Press: Beijing, China, 2013. (In Chinese) [Google Scholar]
- Chen, W.; Duan, L. Handbook of International Bridge Engineering; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Chen, W.; Duan, L. Bridge Engineering Handbook: Construction and Maintenance; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Freeman, S.A.; Nicolctti, J.P.; Tyrell, J.V. Evaluations of existing buildings for seismic risk-A ease study of Puget Sound Naval Shipyard. In Proceedings of the 1st U.S. National Conference on Earthquake Engineering, Ann Arbor, MI, USA, 18–20 June 1975. [Google Scholar]
- Tubaldi, E.; Tassotti, L.; Dall, A.A. Seismic response analysis of slender bridge piers. Earthq. Eng. Struct. D 2014, 43, 1503–1519. [Google Scholar] [CrossRef]
- Liang, Z. Study on Calculational Methods of Displacement Ductility Capacity of Tall Pier. Earthq. Resist. Eng. Retrofit. 2006, 27, 57–62. (In Chinese) [Google Scholar]
- Li, J. Investigation on Rational Analytical Model of a Tall Bridge Pier. J. Earthq. Eng. Eng. Vib. 2007, 27, 91–98. (In Chinese) [Google Scholar]
- Ceravolo, R.; Demarie, G.V.; Giordano, L.; Mancini, G.; Sabia, D. Problems in applying code specified capacity design procedures to seismic design of tall piers. Eng. Struct. 2009, 31, 1811–1821. [Google Scholar] [CrossRef]
- JTG/T 2231-01-2020. Specifications for Seismic Design of Highway Bridges; Ministry of Transport of the People’s Republic of China: Beijing, China, 2020. (In Chinese) [Google Scholar]
- Caltrans. Calrans Seismic Design Criteria Version 2.0; California Department of Transportation: Los Angles, USA, 2019. [Google Scholar]
- Eurocode 8. Design Provisions for Earthquake Resistance of Structures Part 2: Bridges; European Committee for Standardization: Brussels, Belgium, 2018. [Google Scholar]
- JRA. Specifications for Highway Bridge, Part V: Seismic Design; Japan Road Association: Tokyo, Japan, 2002. (In Japanese) [Google Scholar]
- Chen, L.; Zhuang, W.; Zhao, H. Reconnaissance of Highway Seismic Damage in Wenchuan Earthquake; China Communications Press: Beijing, China, 2012. (In Chinese) [Google Scholar]
- Alavi, B.; Krawinkler, H. Consideration of Near-Fault Ground Motion Effects in Seismic Design. In Proceedings of the 12th World Conference on Earthquake, Auckland, New Zealand, 30 January–4 February 2000. [Google Scholar]
- Anderson, J.C.; Bertero, V.V. Uncertainties in Establishing Design Earthquakes. J. Struct. Eng. 1987, 113, 1709–1724. [Google Scholar] [CrossRef]
- Somerville, P.G.; Smith, N.F.; Graves, R.W. Modification of empirical strong ground motion attenuation relations to include the amplitude and duration effects of rupture directivity. Seismol. Res. Lett. 1997, 68, 199–222. [Google Scholar] [CrossRef]
- Kalkan, E.; Kunnath, S.K. Effects of fling step and forward directivity on seismic response of buildings. Earthq. Spectr. 2006, 22, 367–390. [Google Scholar] [CrossRef]
- Shan, D.S.; Zhang, E.H.; Dong, J. Wenchuan ground motion attenuation characteristics and seismic responses of long-span and tall pier continuous rigid frame bridges. Chin. Civil. Eng. J. 2017, 50, 107–115. (In Chinese) [Google Scholar]
- Martelli, A.; Clemente, P. Anti-seismic systems: Worldwide application and conditions of their correct use. In Proceedings of the 16th World Conference on Earthquake, Santiago, MN, USA, 9–13 January 2017. [Google Scholar]
- Dicleli, M.; Buddaram, S. Effect of isolator and ground motion characteristics on the performance of seismic-isolated bridges. Earthq. Eng. Struct. D. 2006, 35, 233–250. [Google Scholar] [CrossRef]
- Shen, J.; Tsai, M.H.K.; Chang, K.C.; Lee, C.L. Performance of a seismically isolated bridge under near-fault earthquake ground motions. J. Struct. Eng. 2004, 130, 861–868. [Google Scholar] [CrossRef]
- Liao, W.; Loh, C.H.; Lee, B.H. Comparison of dynamic response of isolated and non-isolated continuous girder bridges subjected to near-fault ground motions. Eng. Struct. 2004, 26, 2173–2183. [Google Scholar] [CrossRef]
- Bruneau, M.; Chang, S.E.; Eguchi, R.T. A Framework to Quantitatively Assess and Enhance the Seismic Resilience of Communities. Earthq. Spectr. 2012, 19, 733–752. [Google Scholar] [CrossRef]
- Mahin, S. Resilience by design: A structural engineering perspective. In Proceedings of the 16th World Conference on Earthquake, Santiago, MN, USA, 9–13 January 2017. [Google Scholar]
- Roeder, C.; Popov, E. Inelastic Behavior of Eccentric Braced Steel Frames under Cyclic Loadings; Earthquake Engineering Research Center, University of California at Berkeley: Berkeley, CA, USA, 1978. [Google Scholar]
- Tang, M.; Manzanarez, R.; Nader, M.; Abbas, S.; Baker, G. Replacing the East Bay Bridge. Civil. Eng. 2000, 70, 38–43. [Google Scholar]
- McDaniel, C.C.; Seible, F. Influence of inelastic tower links on cable-supported bridge response. J. Bridge Eng. 2005, 10, 272–280. [Google Scholar] [CrossRef]
- El-Bahey, S.; Bruneau, M. Bridge piers with structural fuses and bi-steel columns. I: Experimental Testing. J. Bridge Eng. 2012, 17, 25–35. [Google Scholar] [CrossRef]
- El-Bahey, S.; Bruneau, M. Bridge piers with structural fuses and bi-steel columns. II: Analytical Investigation. J. Bridge Eng. 2012, 17, 39–42. [Google Scholar] [CrossRef]
- Wei, X.; Bruneau, M. Case study on applications of structural fuses in bridge bents. J. Bridge Eng. 2016, 21, 5–16. [Google Scholar] [CrossRef]
- Bazaez, R.; Dusicka, P. Cyclic behavior of reinforced concrete bridge bent retrofitted with buckling restrained braces. Eng. Struct. 2016, 119, 34–48. [Google Scholar] [CrossRef]
- Xiang, N.; Alam, M.S. Displacement-based seismic design of bridge bents retrofitted with various bracing devices and their seismic fragility assessment under near-fault and far-field ground motions. Soil. Dyn. Earthq. Eng. 2019, 119, 75–90. [Google Scholar] [CrossRef]
- Fan, L.; Zhuo, W. Seismic Design of Bridge Ductility; China Communication Press: Beijing, China, 2001. (In Chinese) [Google Scholar]
- CECS 159:2004. Technical Specification for Concrete-Filled Rectangular Steel Tubular Structures; China Engineering Construction Standardization: Beijing, China, 2004. (In Chinese) [Google Scholar]
- Scott, B.D.; Park, R.; Priestley, M.J.N. Stress-strain behavior of concrete confined by overlapping hoops at low and high strain rates. ACI Struct. J. 1982, 79, 13–27. [Google Scholar]
- Han, L. Concrete-Filled Steel Tube Structure: Theory and Practice, 2nd ed.; Science Press: Beijing, China, 2007. (In Chinese) [Google Scholar]
- Aki, K. Seismic displacements near a fault. J. Geophys. Res. 1968, 73, 5359–5376. [Google Scholar] [CrossRef]
- Pacific Earthquake Engineering Research Center Ground Motion Database. Available online: http://ngawest2.berkeley.edu/ (accessed on 3 August 2020).
- Eurocode 8. Design of Structures for Earthquake Resistance-Part 1: General Rules, Seismic Actions and Rules for Buildings; European Committee for Standardization: Brussels, Belgium, 2018. [Google Scholar]
- Kunnath, S.K.; Reinhorn, A.M.; Park, Y.J. Analytical Modeling of Inelastic Seismic Response of RC Structures. J. Struct. Eng. 1990, 116, 996–1017. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).