A Comparative Study of Random Forest and Genetic Engineering Programming for the Prediction of Compressive Strength of High Strength Concrete (HSC)
Abstract
1. Introduction
2. Research Methodology
2.1. Random Forest Regression
- Collection of trained regression trees using training set.
- Calculating average of the individual regression tree output.
- Cross-validation of the predicted data using validation set.
2.2. Gene Expression Programming
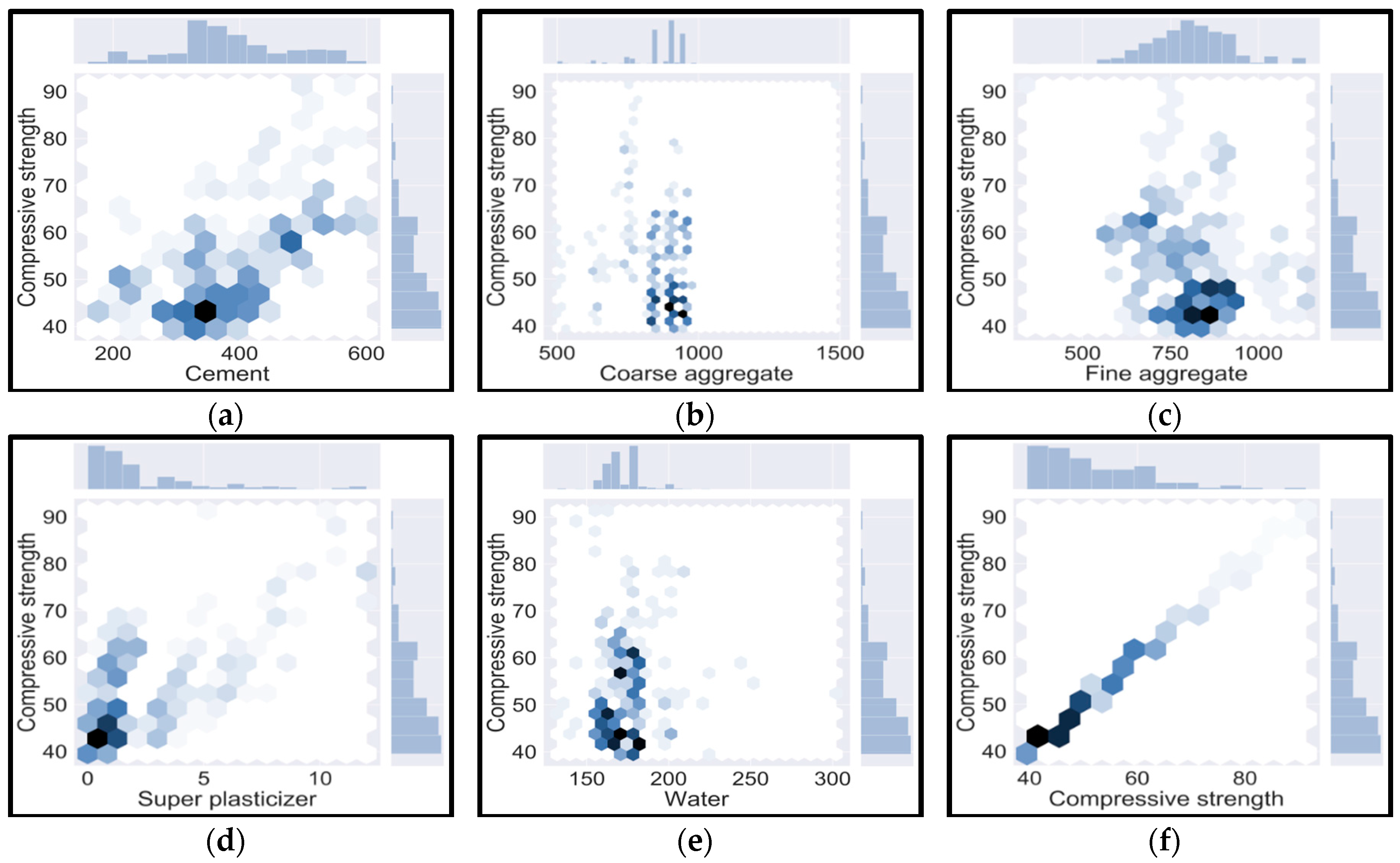
3. Experimental Database Representation
3.1. Dataset Used in Modeling Aspect
3.2. Programming-Based Presentation of Datasets
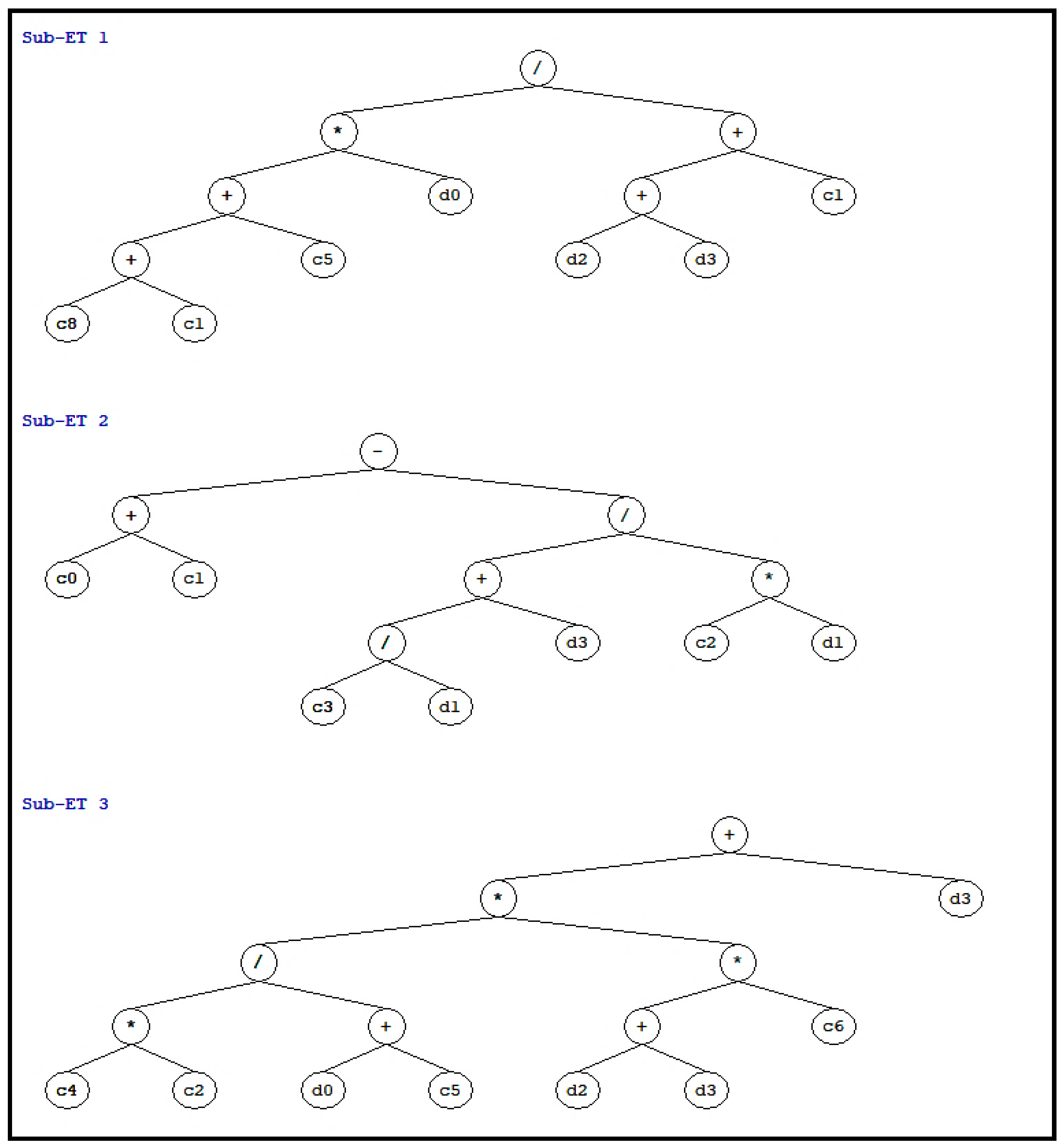
4. GEP Model Development
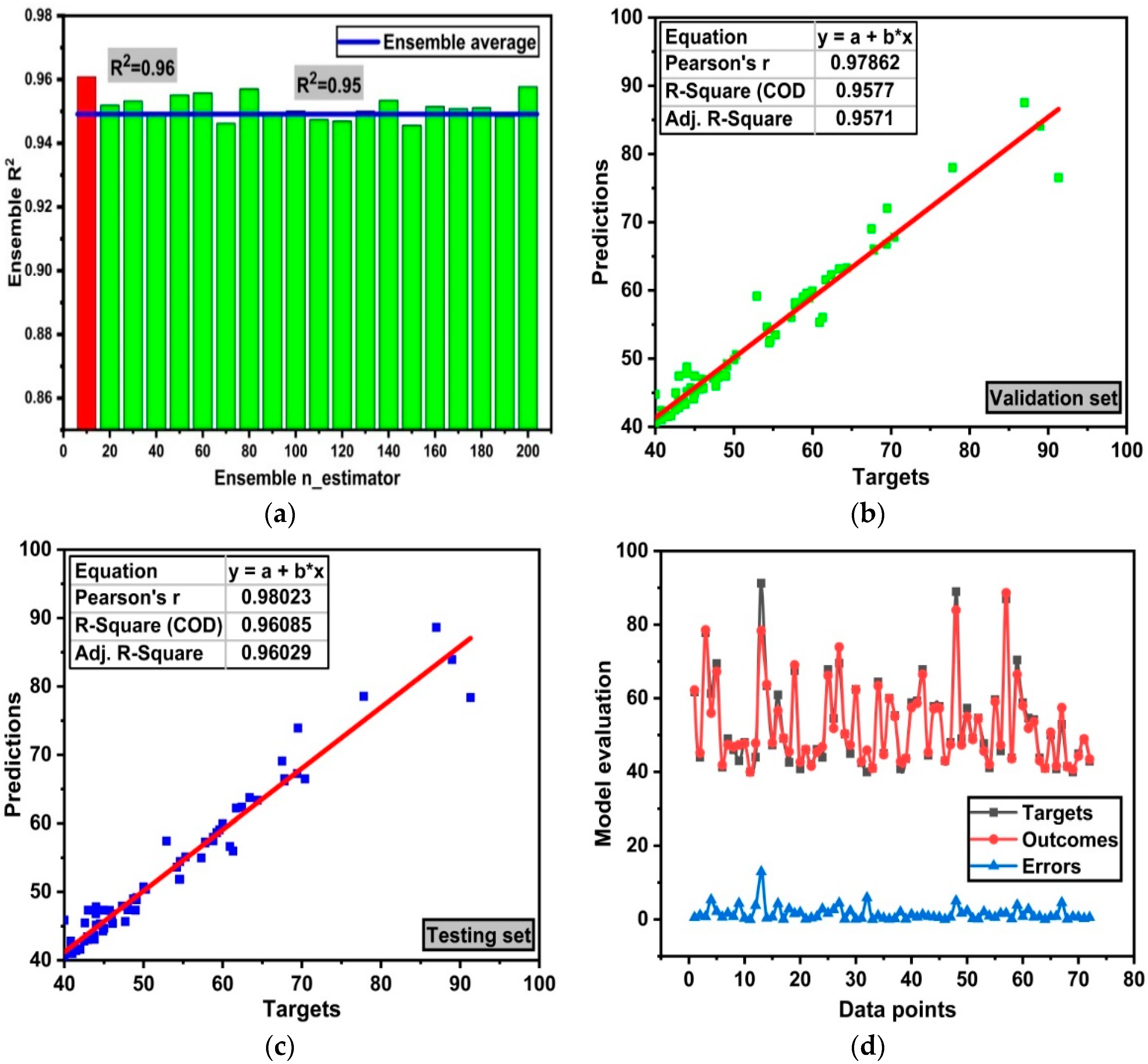
5. Model Performance Analysis
6. Results and Discussion
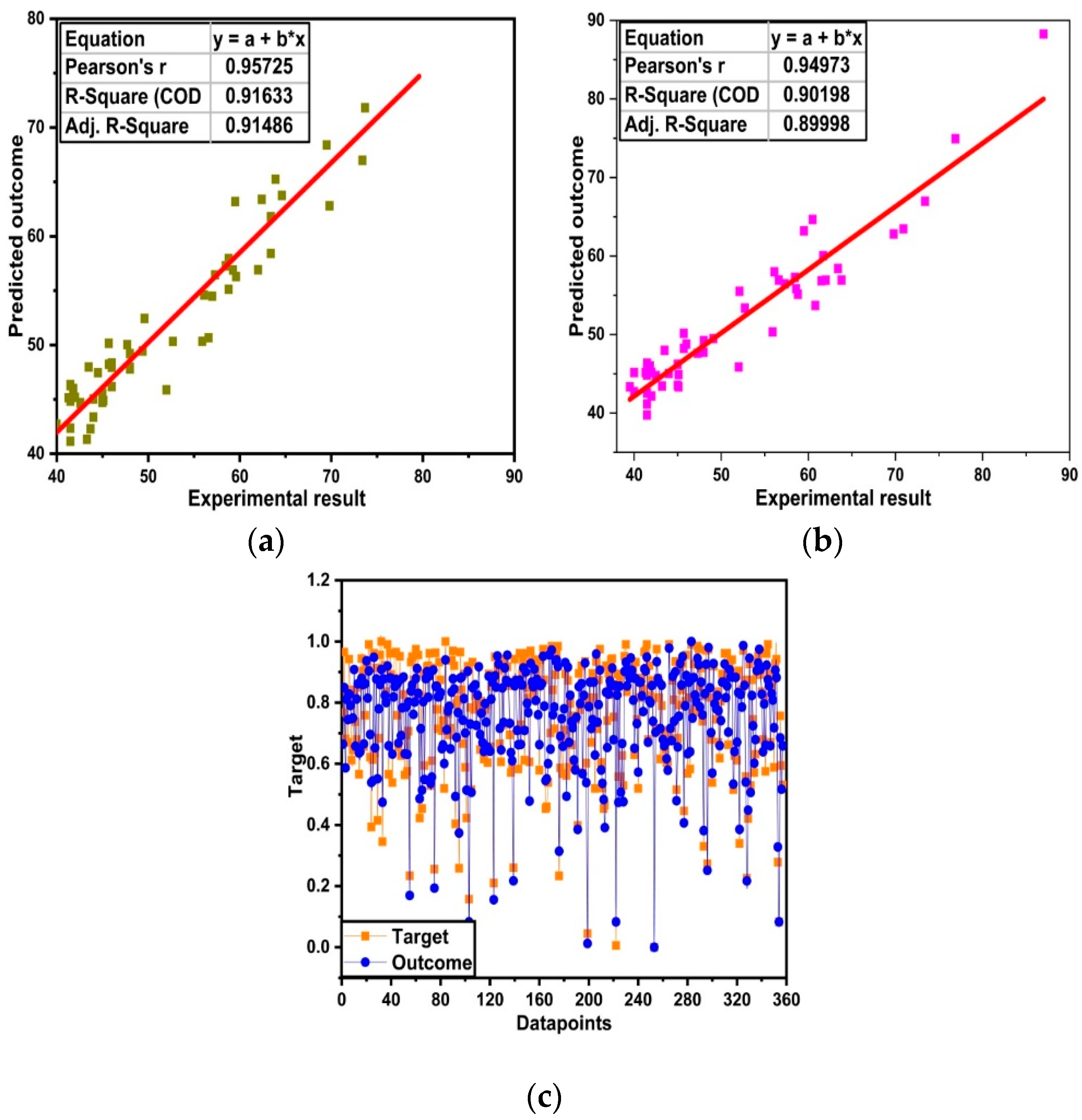
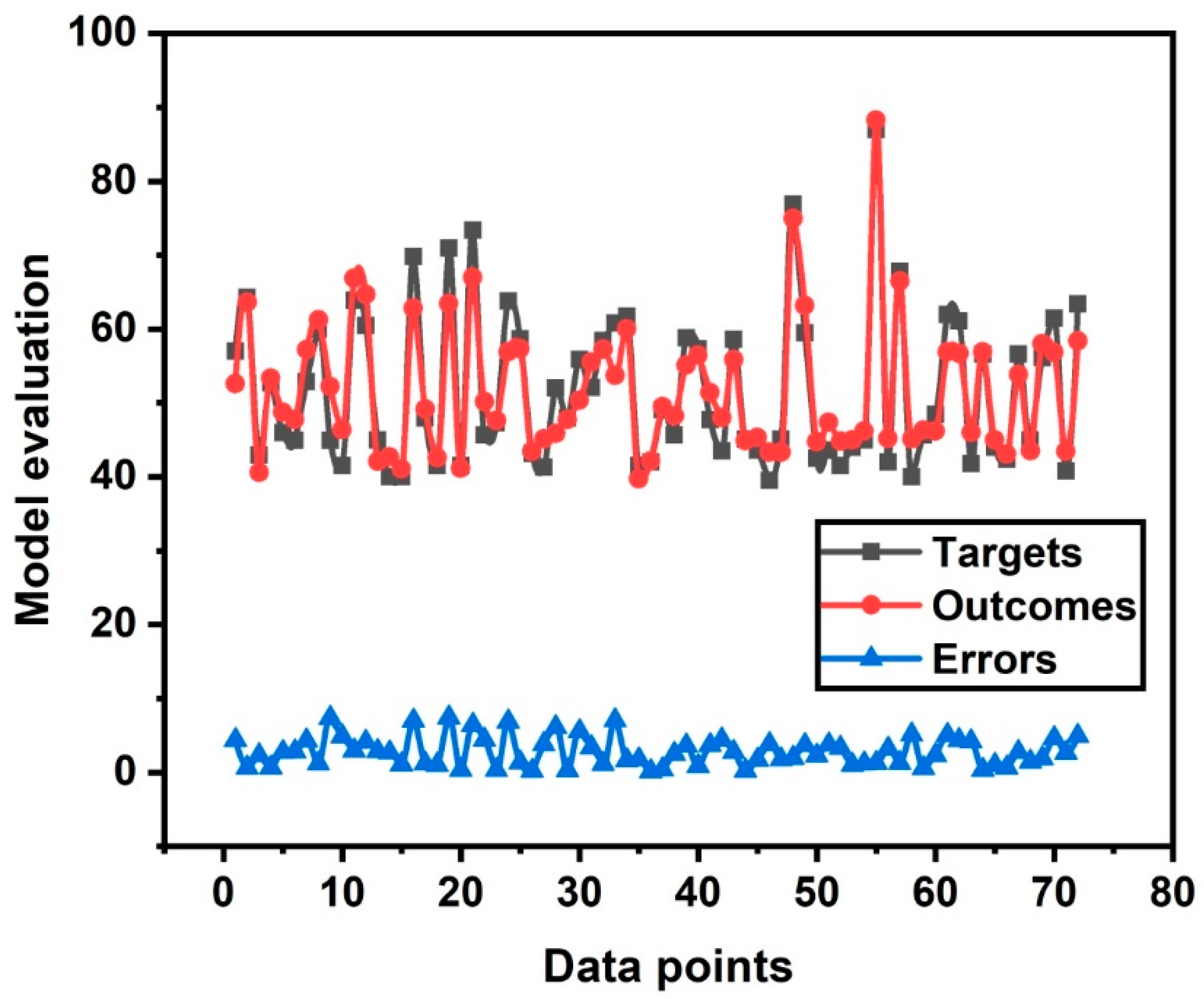
6.1. Random Forest Model Analysis
6.2. Empirical Relation of HSC Using the GEP Model
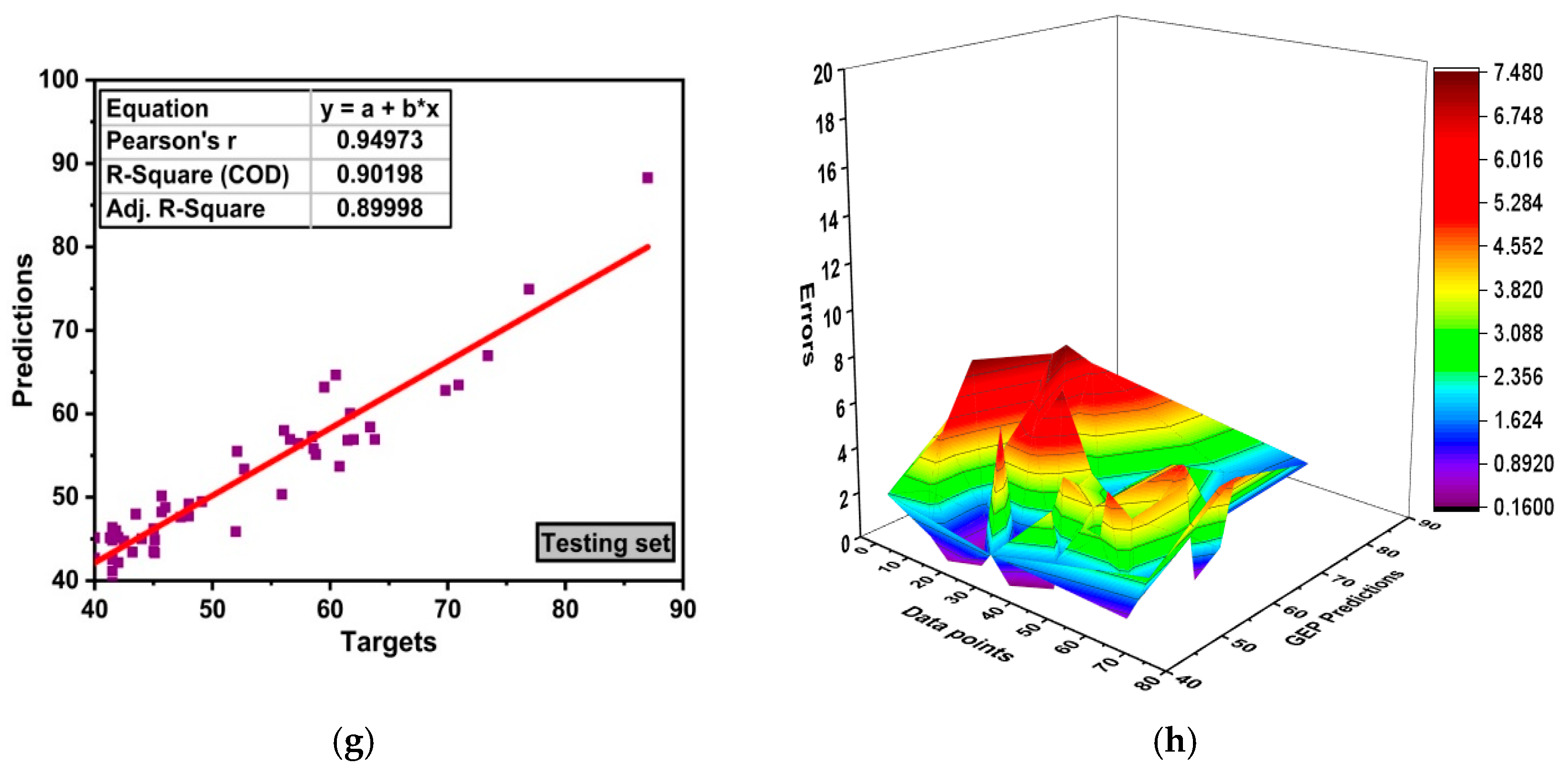
6.3. GEP Model Evaluation
7. Statistical Analysis Checks on RF and GEP Model
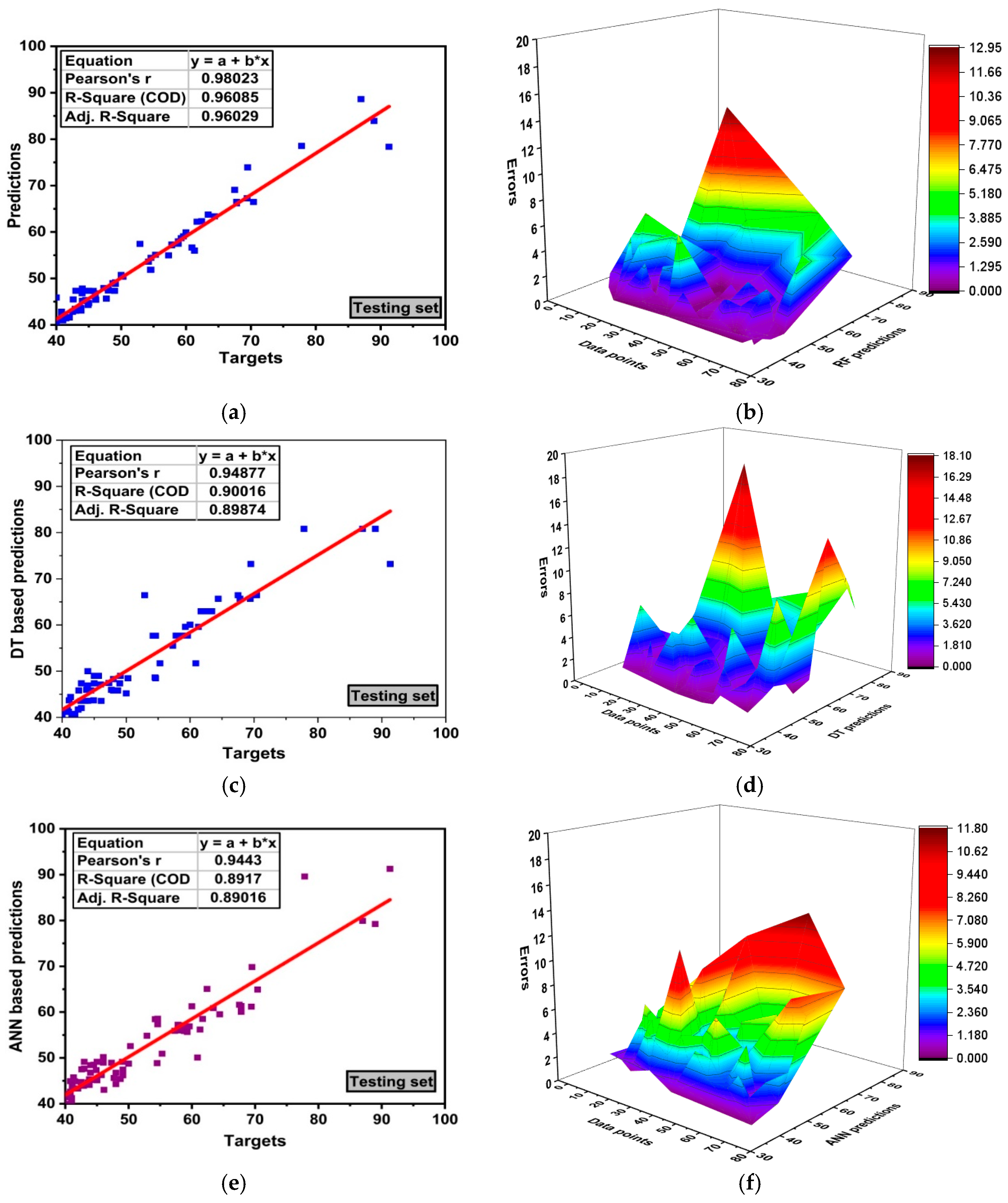
8. Comparison of Models with ANN and Decision Tree
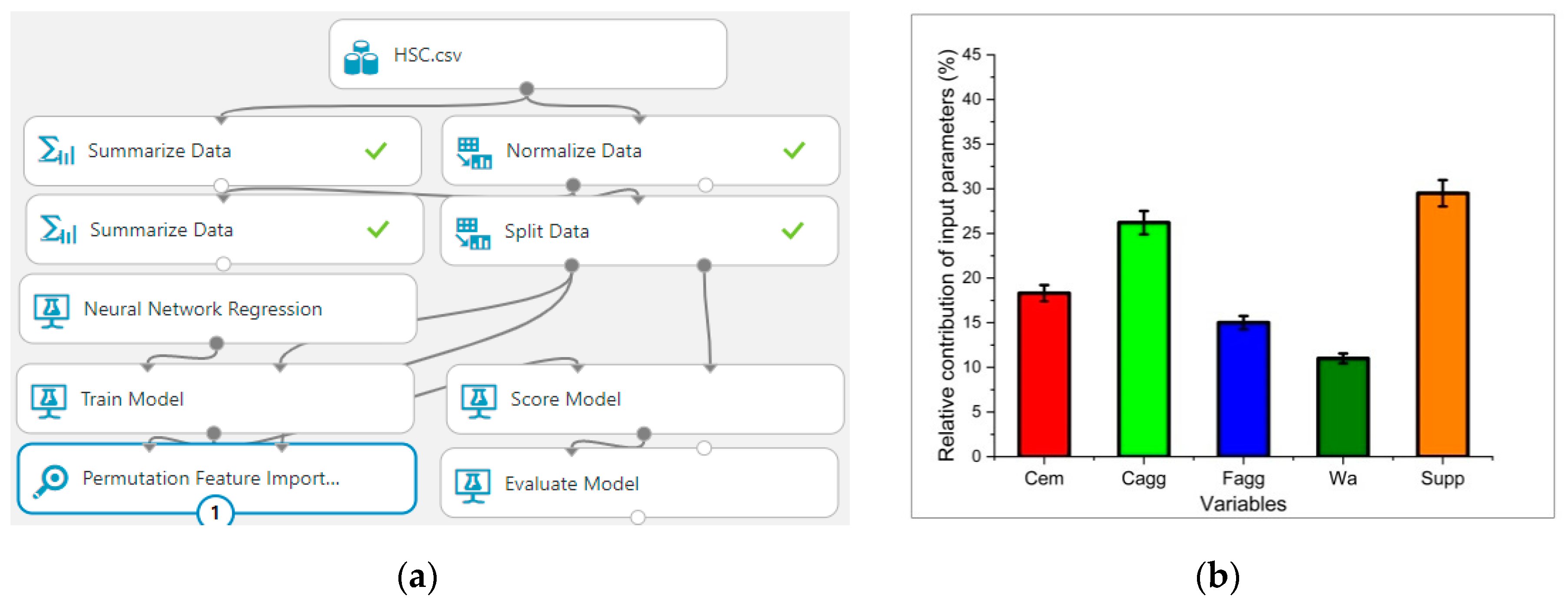
9. Permutation Feature Analysis (PFA)
10. Conclusions
- Random forest is an ensemble approach which gives adamant performance between observed and predicted value. It is due to incorporation of a weak learner as base learner (decision tree) and gives determination of coefficient R2 = 0.96.
- GEP is an individual model rather than an ensemble algorithm. It gives a good relation with the empirical relation. This relation can be used to predict the mechanical aspect of high strength concrete via hand calculation.
- Comparison of the RF and GEP models is made with ANN and DT. However, RF outbursts and gives an obstinate relation of R2 = 0.96. GEP model gives R2 = 0.90. ANN and DT models give 0.89 and 0.90, respectively. Moreover, RF gives less errors as compared to others individual algorithms. This is due to the bagging mechanism of RF.
- Permutation features give an influential parameter in HSC. This help us to check and know the most dominant variables in using experimental work; thus, all the variables have an effect on compressive strength.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, X.; Han, J. The effect of ultra-fine admixture on the rheological property of cement paste. Cem. Concr. Res. 2000, 30, 827–830. [Google Scholar] [CrossRef]
- Khaloo, A.; Mobini, M.H.; Hosseini, P. Influence of different types of nano-SiO2 particles on properties of high-performance concrete. Constr. Build. Mater. 2016, 113, 188–201. [Google Scholar] [CrossRef]
- Hooton, R.D.; Bickley, J.A. Design for durability: The key to improving concrete sustainability. Constr. Build. Mater. 2014, 67, 422–430. [Google Scholar] [CrossRef]
- Farooq, F.; Akbar, A.; Khushnood, R.A.; Muhammad, W.L.B.; Rehman, S.K.U.; Javed, M.F. Experimental investigation of hybrid carbon nanotubes and graphite nanoplatelets on rheology, shrinkage, mechanical, and microstructure of SCCM. Materials 2020, 13, 230. [Google Scholar] [CrossRef]
- Carrasquillo, R.; Nilson, A.; Slate, F.S. Properties of High Strength Concrete Subjectto Short-Term Loads. 1981. Available online: https://www.concrete.org/publications/internationalconcreteabstractsportal.aspx?m=details&ID=6914 (accessed on 27 September 2020).
- Mbessa, M.; Péra, J. Durability of high-strength concrete in ammonium sulfate solution. Cem. Concr. Res. 2001, 31, 1227–1231. [Google Scholar] [CrossRef]
- Baykasoǧlu, A.; Öztaş, A.; Özbay, E. Prediction and multi-objective optimization of high-strength concrete parameters via soft computing approaches. Expert Syst. Appl. 2009, 36, 6145–6155. [Google Scholar] [CrossRef]
- Demir, F. Prediction of elastic modulus of normal and high strength concrete by artificial neural networks. Constr. Build. Mater. 2008, 22, 1428–1435. [Google Scholar] [CrossRef]
- Demir, F. A new way of prediction elastic modulus of normal and high strength concrete-fuzzy logic. Cem. Concr. Res. 2005, 35, 1531–1538. [Google Scholar] [CrossRef]
- Yan, K.; Shi, C. Prediction of elastic modulus of normal and high strength concrete by support vector machine. Constr. Build. Mater. 2010, 24, 1479–1485. [Google Scholar] [CrossRef]
- Ahmadi-Nedushan, B. Prediction of elastic modulus of normal and high strength concrete using ANFIS and optimal nonlinear regression models. Constr. Build. Mater. 2012, 36, 665–673. [Google Scholar] [CrossRef]
- Safiuddin, M.; Raman, S.N.; Salam, M.A.; Jumaat, M.Z. Modeling of compressive strength for self-consolidating high-strength concrete incorporating palm oil fuel ash. Materials 2016, 9, 396. [Google Scholar] [CrossRef] [PubMed]
- Al-Shamiri, A.K.; Kim, J.H.; Yuan, T.F.; Yoon, Y.S. Modeling the compressive strength of high-strength concrete: An extreme learning approach. Constr. Build. Mater. 2019, 208, 204–219. [Google Scholar] [CrossRef]
- Aslam, F.; Farooq, F.; Amin, M.N.; Khan, K.; Waheed, A.; Akbar, A.; Javed, M.F.; Alyousef, R.; Alabdulijabbar, H. Applications of Gene Expression Programming for Estimating Compressive Strength of High-Strength Concrete. Adv. Civ. Eng. 2020, 2020, 1–23. [Google Scholar] [CrossRef]
- Samui, P. Multivariate adaptive regression spline (MARS) for prediction of elastic modulus of jointed rock mass. Geotech. Geol. Eng. 2013, 31, 249–253. [Google Scholar] [CrossRef]
- Gholampour, A.; Mansouri, I.; Kisi, O.; Ozbakkaloglu, T. Evaluation of mechanical properties of concretes containing coarse recycled concrete aggregates using multivariate adaptive regression splines (MARS), M5 model tree (M5Tree), and least squares support vector regression (LSSVR) models. Neural Comput. Appl. 2020, 32, 295–308. [Google Scholar] [CrossRef]
- Shahmansouri, A.A.; Bengar, H.A.; Ghanbari, S. Compressive strength prediction of eco-efficient GGBS-based geopolymer concrete using GEP method. J. Build. Eng. 2020, 31, 101326. [Google Scholar] [CrossRef]
- Javed, M.F.; Farooq, F.; Memon, S.A.; Akbar, A.; Khan, M.A.; Aslam, F.; Alyousef, R.; Alabduljabbar, H.; Rehman, S.K.U. New prediction model for the ultimate axial capacity of concrete-filled steel tubes: An evolutionary approach. Crystals 2020, 10, 741. [Google Scholar] [CrossRef]
- Sonebi, M.; Abdulkadir, C. Genetic programming based formulation for fresh and hardened properties of self-compacting concrete containing pulverised fuel ash. Constr. Build. Mater. 2009, 23, 2614–2622. [Google Scholar] [CrossRef]
- Rinchon, J.P.M. Strength durability-based design mix of self-compacting concrete with cementitious blend using hybrid neural network-genetic algorithm. IPTEK J. Proc. Ser. 2017, 3. [Google Scholar] [CrossRef]
- Kang, F.; Li, J.; Dai, J. Prediction of long-term temperature effect in structural health monitoring of concrete dams using support vector machines with Jaya optimizer and salp swarm algorithms. Adv. Eng. Softw. 2019, 131, 60–76. [Google Scholar] [CrossRef]
- Ling, H.; Qian, C.; Kang, W.; Liang, C.; Chen, H. Combination of support vector machine and K-fold cross validation to predict compressive strength of concrete in marine environment. Constr. Build. Mater. 2019, 206, 355–363. [Google Scholar] [CrossRef]
- Ababneh, A.; Alhassan, M.; Abu-Haifa, M. Predicting the contribution of recycled aggregate concrete to the shear capacity of beams without transverse reinforcement using artificial neural networks. Case Stud. Constr. Mater. 2020, 13, e00414. [Google Scholar] [CrossRef]
- Xu, J.; Chen, Y.; Xie, T.; Zhao, X.; Xiong, B.; Chen, Z. Prediction of triaxial behavior of recycled aggregate concrete using multivariable regression and artificial neural network techniques. Constr. Build. Mater. 2019, 226, 534–554. [Google Scholar] [CrossRef]
- Van Dao, D.; Ly, H.B.; Vu, H.L.T.; Le, T.T.; Pham, B.T. Investigation and optimization of the C-ANN structure in predicting the compressive strength of foamed concrete. Materials 2020, 13, 1072. [Google Scholar] [CrossRef]
- Han, Q.; Gui, C.; Xu, J.; Lacidogna, G. A generalized method to predict the compressive strength of high-performance concrete by improved random forest algorithm. Constr. Build. Mater. 2019, 226, 734–742. [Google Scholar] [CrossRef]
- Zounemat-Kermani, M.; Stephan, D.; Barjenbruch, M.; Hinkelmann, R. Ensemble data mining modeling in corrosion of concrete sewer: A comparative study of network-based (MLPNN & RBFNN) and tree-based (RF, CHAID, & CART) models. Adv. Eng. Inform. 2020, 43, 101030. [Google Scholar] [CrossRef]
- Zhang, J.; Li, D.; Wang, Y. Toward intelligent construction: Prediction of mechanical properties of manufactured-sand concrete using tree-based models. J. Clean. Prod. 2020, 258, 120665. [Google Scholar] [CrossRef]
- Vakhshouri, B.; Nejadi, S. Predicition of compressive strength in light-weight self-compacting concrete by ANFIS analytical model. Arch. Civ. Eng. 2015, 61, 53–72. [Google Scholar] [CrossRef]
- Dutta, S.; Murthy, A.R.; Kim, D.; Samui, P. Prediction of Compressive Strength of Self-Compacting Concrete Using Intelligent Computational Modeling Call for Chapter: Risk, Reliability and Sustainable Remediation in the Field OF Civil AND Environmental Engineering (Elsevier) View project Ground Rub. 2017. Available online: https://www.researchgate.net/publication/321700276 (accessed on 27 September 2020).
- Vakhshouri, B.; Nejadi, S. Prediction of compressive strength of self-compacting concrete by ANFIS models. Neurocomputing 2018, 280, 13–22. [Google Scholar] [CrossRef]
- Info, A. Application of ANN and ANFIS Models Determining Compressive Strength of Concrete. Soft Comput. Civ. Eng. 2018, 2, 62–70. Available online: http://www.jsoftcivil.com/article_51114.html (accessed on 27 September 2020).
- Iqbal, M.F.; Liu, Q.f.; Azim, I.; Zhu, X.; Yang, J.; Javed, M.F.; Rauf, M. Prediction of mechanical properties of green concrete incorporating waste foundry sand based on gene expression programming. J. Hazard. Mater. 2020, 384, 121322. [Google Scholar] [CrossRef]
- Trtnik, G.; Kavčič, F.; Turk, G. Prediction of concrete strength using ultrasonic pulse velocity and artificial neural networks. Ultrasonics 2009, 49, 53–60. [Google Scholar] [CrossRef] [PubMed]
- Shahmansouri, A.A.; Yazdani, M.; Ghanbari, S.; Bengar, H.A.; Jafari, A.; Ghatte, H.F. Artificial neural network model to predict the compressive strength of eco-friendly geopolymer concrete incorporating silica fume and natural zeolite. J. Clean. Prod. 2020, 279, 123697. [Google Scholar] [CrossRef]
- Javed, M.F.; Amin, M.N.; Shah, M.I.; Khan, K.; Iftikhar, B.; Farooq, F.; Aslam, F.; Alyousef, R.; Alabduljabbar, H. Applications of gene expression programming and regression techniques for estimating compressive strength of bagasse Ash based concrete. Crystals 2020, 10, 737. [Google Scholar] [CrossRef]
- Nour, A.I.; Güneyisi, E.M. Prediction model on compressive strength of recycled aggregate concrete filled steel tube columns. Compos. Part B Eng. 2019, 173. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, G.; Huang, Y.; Sun, J.; Aslani, F.; Nener, B. Modelling uniaxial compressive strength of lightweight self-compacting concrete using random forest regression. Constr. Build. Mater. 2019, 210, 713–719. [Google Scholar] [CrossRef]
- Sun, Y.; Li, G.; Zhang, J.; Qian, D. Prediction of the strength of rubberized concrete by an evolved random forest model. Adv. Civ. Eng. 2019. [Google Scholar] [CrossRef]
- Bingöl, A.F.; Tortum, A.; Gül, R. Neural networks analysis of compressive strength of lightweight concrete after high temperatures. Mater. Des. 2013, 52, 258–264. [Google Scholar] [CrossRef]
- Duan, Z.H.; Kou, S.C.; Poon, C.S. Prediction of compressive strength of recycled aggregate concrete using artificial neural networks. Constr. Build. Mater. 2013, 40, 1200–1206. [Google Scholar] [CrossRef]
- Chou, J.S.; Pham, A.D. Enhanced artificial intelligence for ensemble approach to predicting high performance concrete compressive strength. Constr. Build. Mater. 2013, 49, 554–563. [Google Scholar] [CrossRef]
- Chou, J.S.; Tsai, C.F.; Pham, A.D.; Lu, Y.H. Machine learning in concrete strength simulations: Multi-nation data analytics. Constr. Build. Mater. 2014, 73, 771–780. [Google Scholar] [CrossRef]
- Azim, I.; Yang, J.; Javed, M.F.; Iqbal, M.F.; Mahmood, Z.; Wang, F.; Liu, Q.f. Prediction model for compressive arch action capacity of RC frame structures under column removal scenario using gene expression programming. Structures 2020, 25, 212–228. [Google Scholar] [CrossRef]
- Pala, M.; Özbay, E.; Öztaş, A.; Yuce, M.I. Appraisal of long-term effects of fly ash and silica fume on compressive strength of concrete by neural networks. Constr. Build. Mater. 2007, 21, 384–394. [Google Scholar] [CrossRef]
- Anaconda Inc. Anaconda Individual Edition, Anaconda Website. 2020. Available online: https://www.anaconda.com/products/individual (accessed on 27 September 2020).
- Downloads, (n.d.). Available online: https://www.gepsoft.com/downloads.htm (accessed on 27 September 2020).
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Svetnik, V.; Liaw, A.; Tong, C.; Culberson, J.C.; Sheridan, R.P.; Feuston, B.P. Random forest: A classification and regression tool for compound classification and QSAR modeling. J. Chem. Inf. Comput. Sci. 2003, 43, 1947–1958. [Google Scholar] [CrossRef]
- Patel, J.; Shah, S.; Thakkar, P.; Kotecha, K. Predicting stock market index using fusion of machine learning techniques. Expert Syst. Appl. 2015, 42, 2162–2172. [Google Scholar] [CrossRef]
- Jiang, H.; Deng, Y.; Chen, H.S.; Tao, L.; Sha, Q.; Chen, J.; Tsai, C.J.; Zhang, S. Joint analysis of two microarray gene-expression data sets to select lung adenocarcinoma marker genes BMC Bioinform. BMC Bioinform. 2004, 5. [Google Scholar] [CrossRef]
- Prasad, A.M.; Iverson, L.R.; Liaw, A. Newer classification and regression tree techniques: Bagging and random forests for ecological prediction. Ecosystems 2006, 9, 181–199. [Google Scholar] [CrossRef]
- Ferreira, C. Gene Expression Programming: A New Adaptive Algorithm for Solving Problems. 2001. Available online: http://www.gene-expression-programming.com (accessed on 29 March 2020).
- Behnood, A.; Golafshani, E.M. Predicting the compressive strength of silica fume concrete using hybrid artificial neural network with multi-objective grey wolves. J. Clean. Prod. 2018, 202, 54–64. [Google Scholar] [CrossRef]
- Getahun, M.A.; Shitote, S.M.; Gariy, Z.C.A. Artificial neural network based modelling approach for strength prediction of concrete incorporating agricultural and construction wastes. Constr. Build. Mater. 2018, 190, 517–525. [Google Scholar] [CrossRef]
- Project Jupyter, Project Jupyter, Home. 2017. Available online: https://jupyter.org/ (accessed on 27 September 2020).
- Gholampour, A.; Gandomi, A.H.; Ozbakkaloglu, T. New formulations for mechanical properties of recycled aggregate concrete using gene expression programming. Constr. Build. Mater. 2017, 130, 122–145. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Babanajad, S.K.; Alavi, A.H.; Farnam, Y. Novel approach to strength modeling of concrete under triaxial compression. J. Mater. Civ. Eng. 2012, 24, 1132–1143. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Roke, D.A. Assessment of artificial neural network and genetic programming as predictive tools. Adv. Eng. Softw. 2015, 88, 63–72. [Google Scholar] [CrossRef]
- Frank, I.; Todeschini, R. The data analysis handbook. Data Handl. Sci. Technol. 1994, 14, 1–352. [Google Scholar] [CrossRef]
- Alavi, A.H.; Ameri, M.; Gandomi, A.H.; Mirzahosseini, M.R. Formulation of flow number of asphalt mixes using a hybrid computational method. Constr. Build. Mater. 2011, 25, 1338–1355. [Google Scholar] [CrossRef]
- Golbraikh, A.; Tropsha, A. Beware of q2! J. Mol. Graph. Model. 2002, 20, 269–276. [Google Scholar] [CrossRef]
- Öztaş, A.; Pala, M.; Özbay, E.; Kanca, E.; Çaǧlar, N.; Bhatti, M.A. Predicting the compressive strength and slump of high strength concrete using neural network. Constr. Build. Mater. 2006, 20, 769–775. [Google Scholar] [CrossRef]
- Singh, B.; Singh, B.; Sihag, P.; Tomar, A.; Sehgal, A. Estimation of compressive strength of high-strength concrete by random forest and M5P model tree approaches. J. Mater. Eng. Struct. JMES 2019, 6, 583–592. Available online: http://revue.ummto.dz/index.php/JMES/article/view/2020 (accessed on 21 August 2020).
| Properties | Data Points | Algorithm | References |
|---|---|---|---|
| Compressive strength, Slump test | 187 | ANN | [7] |
| Elastic modulus | 159 | ANN | [8] |
| Elastic modulus | 159 | FUZZY | [9] |
| Elastic modulus | 159 | SVM | [10] |
| Elastic modulus | 159 | ANFIS and nonlinear | [11] |
| Compressive strength | 20 | ANN | [12] |
| Compressive strength | 324 | ELM | [13] |
| Compressive strength | 357 | GEP | [14] |
| Parameters | Cement | Fine/Coarse Aggregate | Water | Superplasticizer |
|---|---|---|---|---|
| Mean | 384.34 | 0.96 | 173.56 | 2.34 |
| Standard Error | 4.92 | 0.01 | 0.82 | 0.14 |
| Median | 360 | 0.92 | 170 | 1.25 |
| Mode | 360 | 1.01 | 170 | 1 |
| Standard Deviation | 93.00 | 0.26 | 15.56 | 2.69 |
| Sample Variance | 8650.50 | 0.06 | 242.19 | 7.24 |
| Kurtosis | 0.36 | 6.45 | 15.59 | 2.88 |
| Skewness | 0.14 | 2.12 | 2.45 | 1.79 |
| Range | 440 | 1.86 | 170.08 | 12 |
| Minimum | 160 | 0.23 | 132 | 0 |
| Maximum | 600 | 2.1 | 302.08 | 12 |
| Sum | 137,212.84 | 344.07 | 61,963.8 | 837.61 |
| Count | 357 | 357 | 357 | 357 |
| Parameters | Cement | Fine/Coarse Aggregate | Water | Superplasticizer |
|---|---|---|---|---|
| Mean | 383.29 | 0.97 | 173.72 | 2.42 |
| Standard Error | 6.06 | 0.01 | 1.08 | 0.17 |
| Median | 360 | 0.92 | 170 | 1.37 |
| Mode | 320 | 1.01 | 170 | 1 |
| Standard Deviation | 95.95 | 0.27 | 17.17 | 2.74 |
| Sample Variance | 9206.57 | 0.07 | 295.07 | 7.54 |
| Kurtosis | 0.60 | 5.82 | 14.42 | 2.96 |
| Skewness | 0.19 | 2.08 | 2.48 | 1.82 |
| Range | 420 | 1.86 | 170.08 | 12 |
| Minimum | 180 | 0.23 | 132 | 0 |
| Maximum | 600 | 2.1 | 302.08 | 12 |
| Sum | 95,823.1 | 242.79 | 43,431.75 | 606.43 |
| Count | 250 | 250 | 250 | 250 |
| Parameters | Cement | Fine/Coarse aggregate | Water | Superplasticizer |
|---|---|---|---|---|
| Mean | 387.04 | 0.92 | 172.18 | 1.98 |
| Standard Error | 12.46 | 0.02 | 1.34 | 0.33 |
| Median | 400 | 0.90 | 170 | 1 |
| Mode | 360 | 0.75 | 170 | 1 |
| Standard Deviation | 95.76 | 0.18 | 10.35 | 2.55 |
| Sample Variance | 9170.56 | 0.03 | 107.25 | 6.55 |
| Kurtosis | 0.22 | 6.82 | 0.18 | 4.75 |
| Skewness | 0.17 | 1.66 | 0.33 | 2.19 |
| Range | 440 | 1.22 | 45.2 | 12 |
| Minimum | 160 | 0.58 | 154.8 | 0 |
| Maximum | 600 | 1.80 | 200 | 12 |
| Sum | 22,835.54 | 54.38 | 10,159.18 | 117.09 |
| Count | 54 | 54 | 54 | 54 |
| Parameters | Cement | Fine/Coarse Aggregate | Water | Superplasticizer |
|---|---|---|---|---|
| Mean | 390.52 | 0.90 | 173.07 | 2.10 |
| Standard Error | 12.58 | 0.02 | 1.21 | 0.34 |
| Median | 378 | 0.90 | 175 | 1 |
| Mode | 360 | 1.04 | 180 | 0.5 |
| Standard Deviation | 89.86 | 0.15 | 8.67 | 2.47 |
| Sample Variance | 8076.29 | 0.02 | 75.21 | 6.11 |
| Kurtosis | 1.08 | 0.52 | −0.18 | 2.17 |
| Skewness | 0.17 | 0.61 | −0.62 | 1.65 |
| Range | 440 | 0.73 | 38.32 | 10.5 |
| Minimum | 160 | 0.66 | 154 | 0 |
| Maximum | 600 | 1.39 | 192.32 | 10.5 |
| Sum | 19,916.87 | 46.34 | 8826.8 | 107.57 |
| Count | 55 | 55 | 55 | 55 |
| Parameters | Settings |
|---|---|
| General | |
| Genes | 4 |
| Chromosomes | 30 |
| Linking function | Addition |
| Head size | 10 |
| Function set | +, −, ×, ÷ |
| Numerical constants | |
| Constant per gene | 10 |
| Lower bound | −10 |
| Data type | Floating number |
| Upper bound | 10 |
| Genetic Operators | |
| Two-point recombination rate | 0.00277 |
| Gene transposition rate | 0.00277 |
| Model | RMSE | MAE | R2 | |||
|---|---|---|---|---|---|---|
| Fc | Validation | Testing | Validation | Testing | Validation | Testing |
| 1.22 | 1.42 | 0.475 | 0.495 | 0.967 | 0.041 | |
| RRMSE | RSE | P(row) | ||||
| Validation | Testing | Validation | Testing | Validation | Testing | |
| 0.0186 | 0.021 | 0.072 | 0.053 | 0.024 | 0.025 | |
| Model | RMSE | MAE | RSE | |||
|---|---|---|---|---|---|---|
| Fc | Validation | Testing | Validation | Testing | Validation | Testing |
| 1.42 | 1.62 | 0.575 | 0.595 | 0.092 | 0.023 | |
| RRMSE | R | P(row) | ||||
| Validation | Testing | Validation | Testing | Validation | Testing | |
| 0.0286 | 0.031 | 0.957 | 0.031 | 0.014 | 0.015 | |
| S.No | Equation | Condition | RF Model | GEP Model |
|---|---|---|---|---|
| 1 | 0.99 | 0.98 | ||
| 2 | 1.00 | 1.00 | ||
| 3 | 0.99 | 0.97 | ||
| 4 | 0.99 | 0.99 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farooq, F.; Nasir Amin, M.; Khan, K.; Rehan Sadiq, M.; Faisal Javed, M.; Aslam, F.; Alyousef, R. A Comparative Study of Random Forest and Genetic Engineering Programming for the Prediction of Compressive Strength of High Strength Concrete (HSC). Appl. Sci. 2020, 10, 7330. https://doi.org/10.3390/app10207330
Farooq F, Nasir Amin M, Khan K, Rehan Sadiq M, Faisal Javed M, Aslam F, Alyousef R. A Comparative Study of Random Forest and Genetic Engineering Programming for the Prediction of Compressive Strength of High Strength Concrete (HSC). Applied Sciences. 2020; 10(20):7330. https://doi.org/10.3390/app10207330
Chicago/Turabian StyleFarooq, Furqan, Muhammad Nasir Amin, Kaffayatullah Khan, Muhammad Rehan Sadiq, Muhammad Faisal Javed, Fahid Aslam, and Rayed Alyousef. 2020. "A Comparative Study of Random Forest and Genetic Engineering Programming for the Prediction of Compressive Strength of High Strength Concrete (HSC)" Applied Sciences 10, no. 20: 7330. https://doi.org/10.3390/app10207330
APA StyleFarooq, F., Nasir Amin, M., Khan, K., Rehan Sadiq, M., Faisal Javed, M., Aslam, F., & Alyousef, R. (2020). A Comparative Study of Random Forest and Genetic Engineering Programming for the Prediction of Compressive Strength of High Strength Concrete (HSC). Applied Sciences, 10(20), 7330. https://doi.org/10.3390/app10207330