1. Introduction
Transparent film, as an important industrial component, is widely used in modern optics, microelectronics, optical engineering, and other related scientific and technological fields. Various films produced by physical or chemical deposition methods can use interference effects to change optical properties, such as antireflection, filtering, and polarization. Meanwhile, their protection characteristics such as high-temperature resistance, corrosion, and abrasion play a decisive role in the quality of optical instruments in the fields of communication, display, storage, etc. [
1,
2] However, film preparation is affected by process parameters such as emission characteristics, relative position placement, and surface shape of the plated parts, resulting in uneven thickness distribution, which affects the barrier performance and tensile properties of subsequent applications [
3]. Therefore, the measurement and evaluation of film thickness are particularly important in the production process, especially for the thickness measurement of micron-grade industrial films. Limited by the irregular industrial environment, there is an urgent need for a fast, stable, and robust high-resolution film thickness measurement system.
Based on the characteristics of light absorption, reflection, and polarization, the optical measurement methods of film thickness can be divided into spectrophotometry [
4,
5], ellipsometry [
6,
7,
8], interferometry [
9,
10,
11], and multiple compound methods [
12,
13,
14]. Although the measurement methods based on ellipsometry and interferometry have high resolution and accuracy, the disadvantages of large system size, high price, and strict environmental conditions do not meet the rapid and stable application requirement of industrial measurement. The spectrophotometry is more widely used due to its simplicity and portability. Spectral reflectometry is an effective means to detect the thickness of the weakly absorbing film in spectrophotometry. Reflectometry has less affection than transmittance by extinction coefficient [
15] and can realize the compound assembly of the signal transmitter and receiver due to optical fiber technology, thus avoiding the alignment problem. The film thickness calculation methods based on the reflection spectrum can be subdivided into the envelope method [
5], the full-spectrum fitting method [
16], the turning point fitting method, etc. The above methods all use the reflectivity curve as the medium to obtain the film thickness indirectly. Therefore, the system is required to have a high stability light source or a high-precision reference sample. Second, these methods depend greatly on the reflectivity model, which means that non-ideal signals containing noise in actual measurements are prone to distortion. Among them, the envelope method, fitting the upper and lower envelope by the extreme points of the reflectivity curve, is easily affected by the baseline drift under temperature changes; for the full spectrum fitting method, the period and amplitude of the full-spectrum reflectance spectrum are matched at the same time, which may lead to over-fitting and low matching efficiency; only a very few wavelength data with an odd multiple of the optical thickness λ/4 is used in the turning point fitting method. The effective data segment needs to be selected manually, which makes it difficult to achieve automatic measurement.
According to the current research on thin-film thickness measurement, the existing methods still have disadvantages such as poor robustness, low efficiency, and high cost, which cannot meet the needs of industrial-grade rapid and stable measurement. Therefore, this paper built a miniaturized and rapid film thickness measurement system based on the principle of film low-coherence interference and confocal spectral imaging. A novel algorithm named phase power spectrum (PPS) analysis was proposed to calculate the film thickness by solving the power spectral density of the phase term. With no need for reference sample correction, the film thickness measurement system had the performance of a measurement range of 1–75 μm, measurement uncertainty of 0.1 μm, and measurement speed of 10 ms. The efficient and stable film thickness calculation of the standard films with micron-grade thickness, the film layer on the PCB chip, and the Germanium-based lens verified the feasibility of this method.
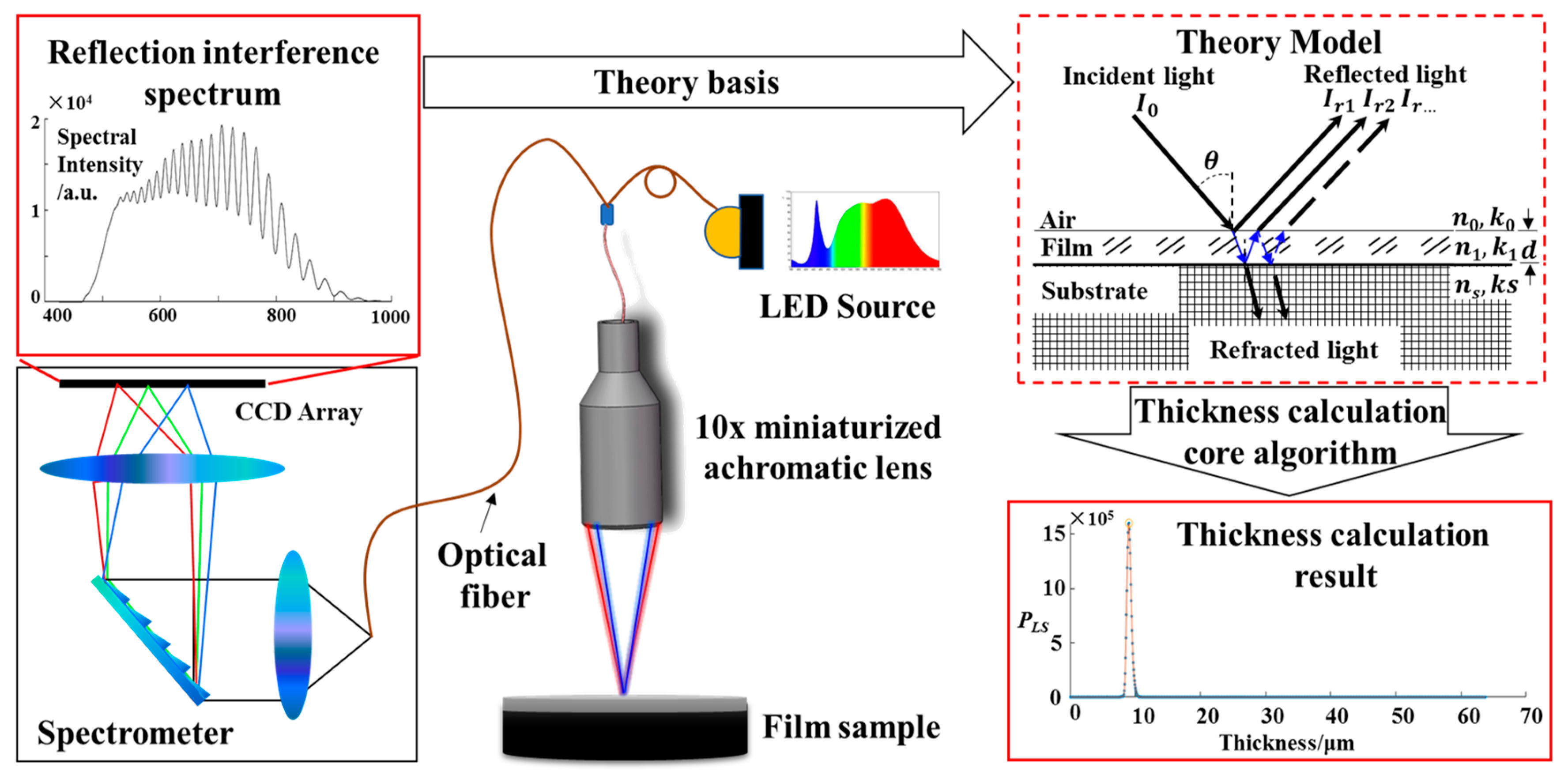
2. Measurement Scheme
Based on the principle of thin-film interference and confocal spectral imaging, this paper built a low-cost and fast-speed thin-film thickness measurement system to study the thickness calculation algorithm of the thin film. As shown in
Figure 1, a Light Emitting Diode (LED), a micro-spectrometer, and a self-designed confocal achromatic probe are used to realize the miniaturization of the measurement system.
The light intensity changes periodically in a coherent region with destructive and constructive phenomena. For dielectric films, if the absorption of light by the film is not considered, the total interference intensity of the reflected light beam incident on the film can be approximately expressed as
where λ is the wavelength and
ϕ0 is the additional phase.
R01 and
T01, respectively, represent the reflectance and transmittance from the air to the film.
R1s and
T10, respectively, represent the reflectance from the film to the substrate and the transmittance from the film to the air. For the case of normal incidence, the optical path difference
z = 2
n1 ×
d is determined by the film’s refractive index
n1 and thickness
d, where the refractive index is treated as a constant to improve computational efficiency.
The envelope of the spectral interference signal measured by the spectrometer is approximately a Gaussian distribution. The phase term 2πz/λ + ϕ0 caused by the optical path difference z determines the density of the interference fringes. As the core algorithm of the PPS analysis, Empirical Mode Decomposition (EMD) and Lomb–Scargle periodogram (LSP) process the high-frequency spectral interference information successively to extract the film thickness.
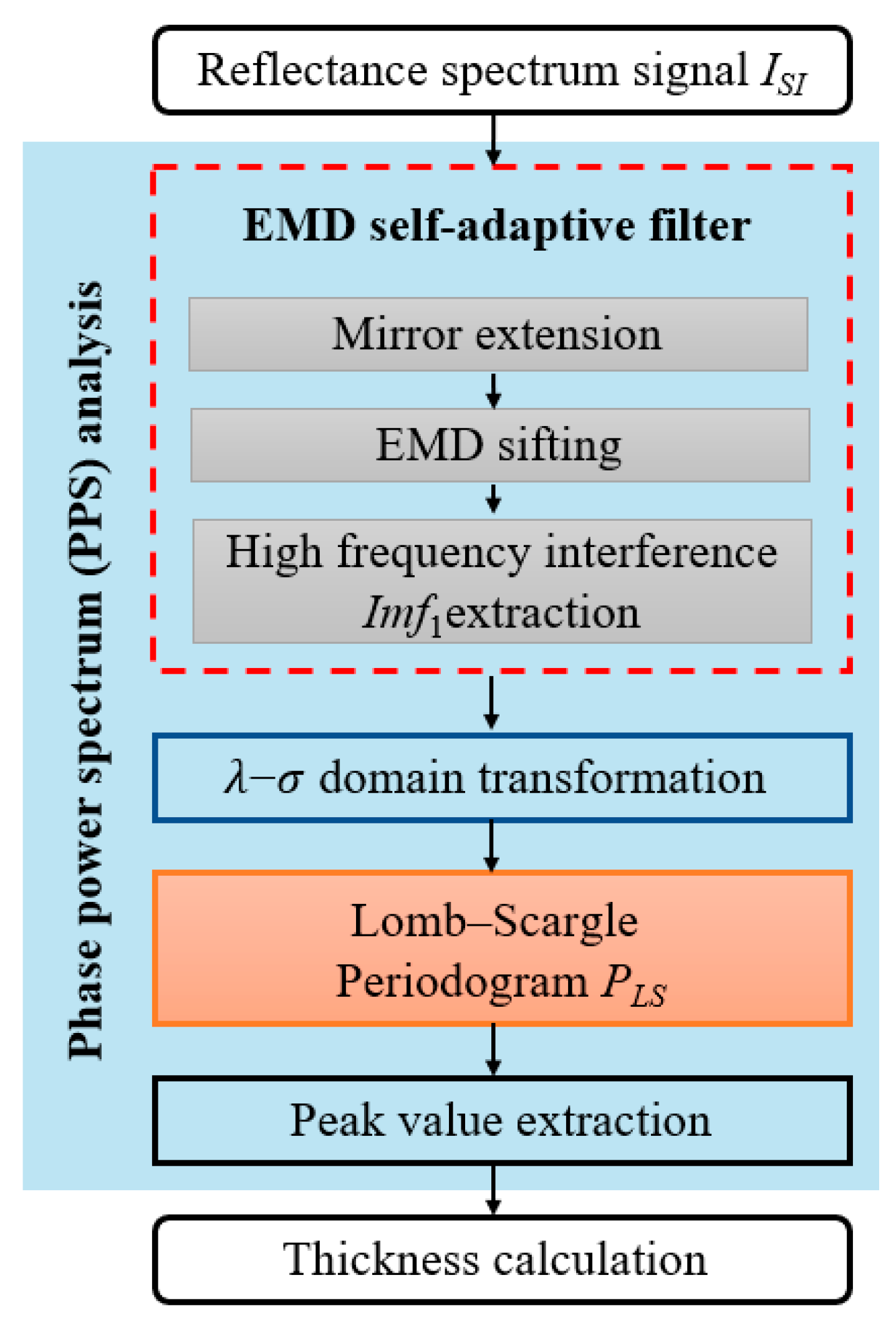
3. Film Thickness Calculation Algorithm
Figure 2 is the flow chart of the core algorithm in this paper. Firstly, aiming at the original interference signal collected by a spectrometer, EMD is used as a high-pass filter to extract high-frequency interference components, adaptively eliminating the influence of the non-uniform intensity distribution of the LED source. Second, to obtain the phase term introduced by film thickness, the interference component is transformed into the wavenumber σ domain through reciprocal of wavelength
λ. Third, through the spectral analysis method, we extract the phase term from the full spectrum to effectively avoid the interference of local noise. However, conventional spectral analysis methods, such as Fourier transform, cannot handle the problem of non-equal interval sampling of signals caused by the
λ−σ transformation. In this paper, the phase term is solved by the LSP spectrum analysis and illustrated by phase power spectral density distribution. Finally, the peak value of the power spectral density function is extracted by the maximum value method to calculate the film thickness. The detailed flow of the proposed algorithm is as follows.
EMD, as the preprocessing algorithm of Hilbert Huang Transform (HHT) [
17], can adaptively decompose the complex nonlinear and non-stationary signal into a limited number of Intrinsic Mode Function (IMF). In this paper, EMD is used as a high-pass filter [
18] to automatically filter out the high-frequency principal component of the reflectance spectrum signal. The mirror extending method [
19] assists in processing the endpoint data of the original signal to eliminate the boundary oscillation effect caused by the third-order spline interpolation in EMD.
The reflectance spectrum signal
ISI is a discrete function of the uniform sampled pixels for being collected by Charge Coupled Device (CCD) array in a micro spectrometer. After EMD filtering,
ISI is disassembled into a set of IMF components
Imfk,
k = 1, 2, …,
m of different frequency ranges, and a monotonic trend function
Res, as shown in
Figure 3b.
Imf1 is the first component to be filtered out with the highest signal frequency. In the case with no high-frequency noise,
Imf1 is the film interference principal component. Then, according to the corresponding relationship between the pixel index and the wavelength of CCD array in the spectrometer, the intensity
Ii of each σ
i,
i = 1, 2, …,
N, is obtained by converting
Imf1 from the
λ to the σ domain.
N is the number of pixels of the spectrometer.
Due to the wavelength drift of the spectrometer and the reciprocal transformation from the λ to the σ domain, the non-uniform sampled characteristic of σ
i made
Ii unable to be directly analyzed by the conventional spectral analysis method. Therefore, it is necessary to preprocess
Ii before performing spectral analysis to obtain film thickness information We adopt the cubic spline interpolation combined fast Fourier transform (CIFFT) and LSP [
20,
21] as two representative methods to process
Ii, and finally choose the LSP after comparing the solution results. In particular, inspired by the time-frequency domain (
t−
f) transformation [
22], we rewrite the LSP function into the wavenumber-phase factor domain (σ−z) transformation form, as Equations (2) and (3).
where δ is specified for each
z to ensure time-shift invariance,
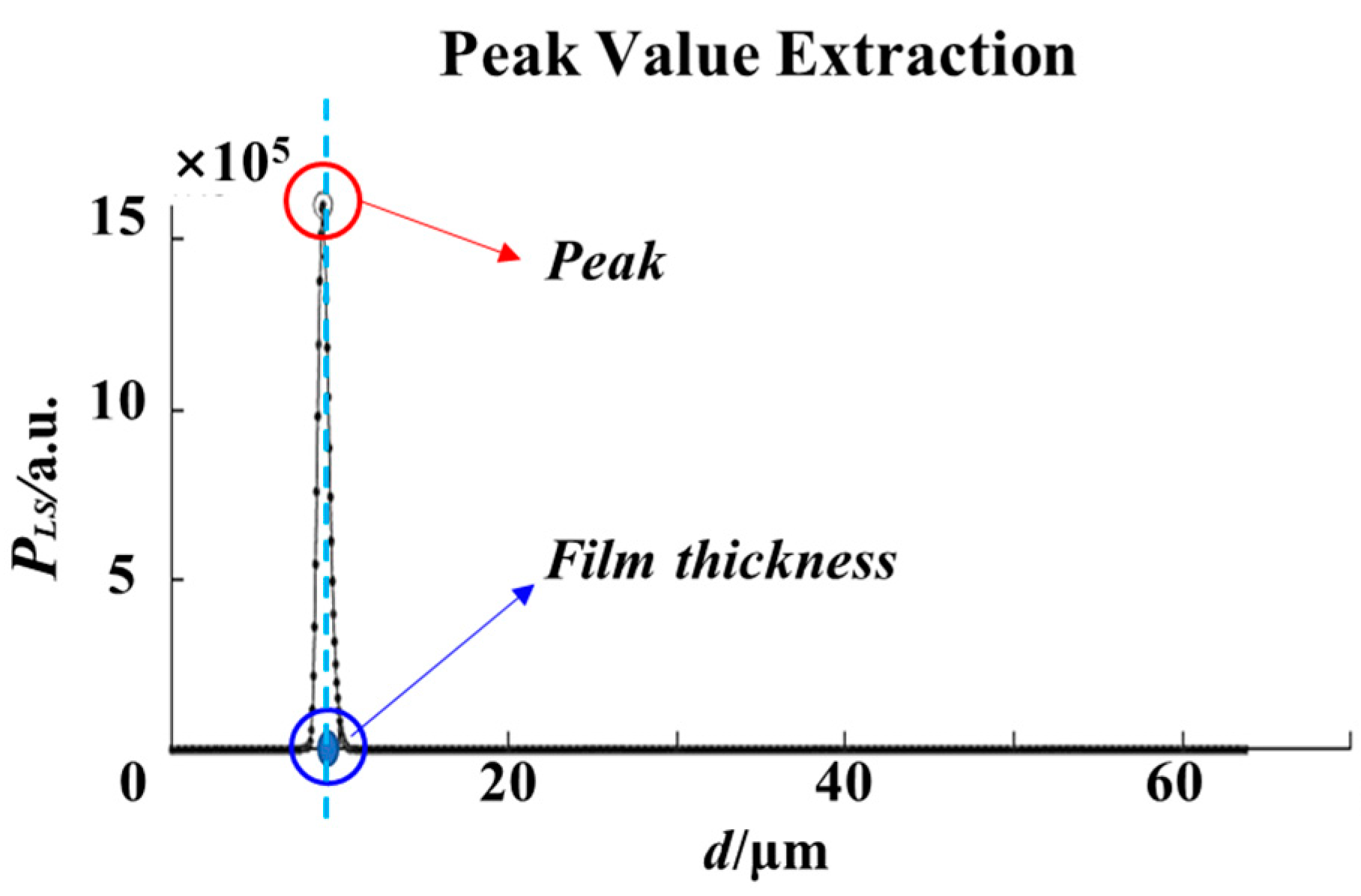
Under normal circumstances, the full width at half maximum of the single-layer film interference spectrum after LSP transformation is small (30–50 nm) as shown in
Figure 4. Therefore, the peak value
zpeak can be directly extracted by the maximum value method. The built-in false alarm probability of LSP evaluates the significance of the peak value to further ensure the correct extraction. If
n1 is the refractive index of the film, the film thickness
d is
In the PPS algorithm, EMD as a self-adaptive high-pass filter realizes the non-destructive extraction of spectral interference terms. While expanding the measurement range of the film, it effectively reduces the influence of the non-uniform distribution of the light source spectrum. The essence of LSP is to fit the data with a single sine function
y =
acos (
ωt) +
bsin (
ωt) with the same frequency [
20], which implicitly requiring the mean value of the measurement data to be zero. The IMF components after EMD filtering approximately meet this requirement, thus the combination of EMD and LSP can obtain a significant deterministic solution. Besides, LSP uses full range spectrum data and thus can better correct the gross errors introduced by local spectral noise. At the same time, using the built-in statistical tool of LSP to evaluate the reliability of the solution can greatly eliminate the false frequency interference caused by environmental noise and improve the stability of the system.
4. Simulation
The following problems have been found in the actual measurement of various types of films. (1) The absorption and reflection coefficients varying with film materials, which results in different fringe contrast of the actual film interference signal; (2) the influence of external stray light causes local noise in the reflected spectrum signal, which have an impact on the film thickness calculation. Besides, to clarify the effective range, inherent error, and the feasibility of this system, we conduct a simulation analysis based on the thin-film interference model. By adjusting the fringe contrast, the thickness, and the noise of the interference signal, we clarify the error influence of different measurement conditions, thus verify the robustness of the algorithm.
4.1. Verification of the Thin-Film Interference Model
We use the thin-film interference model
Ir (
z,
λ) of Equation (1) for simulation, where
A =
R01 +
T01R1sT10,
B = 2
,
A,
B∈(0,1], and suppose the light source intensity distribution conforms to the Gaussian distribution
G(
λ;
μ,
η2) with mathematical expectation
μ and standard variance
η2,
The reflected spectrum signal can be abbreviated as below, where
C is the maximum intensity amplitude of the light spectrum,
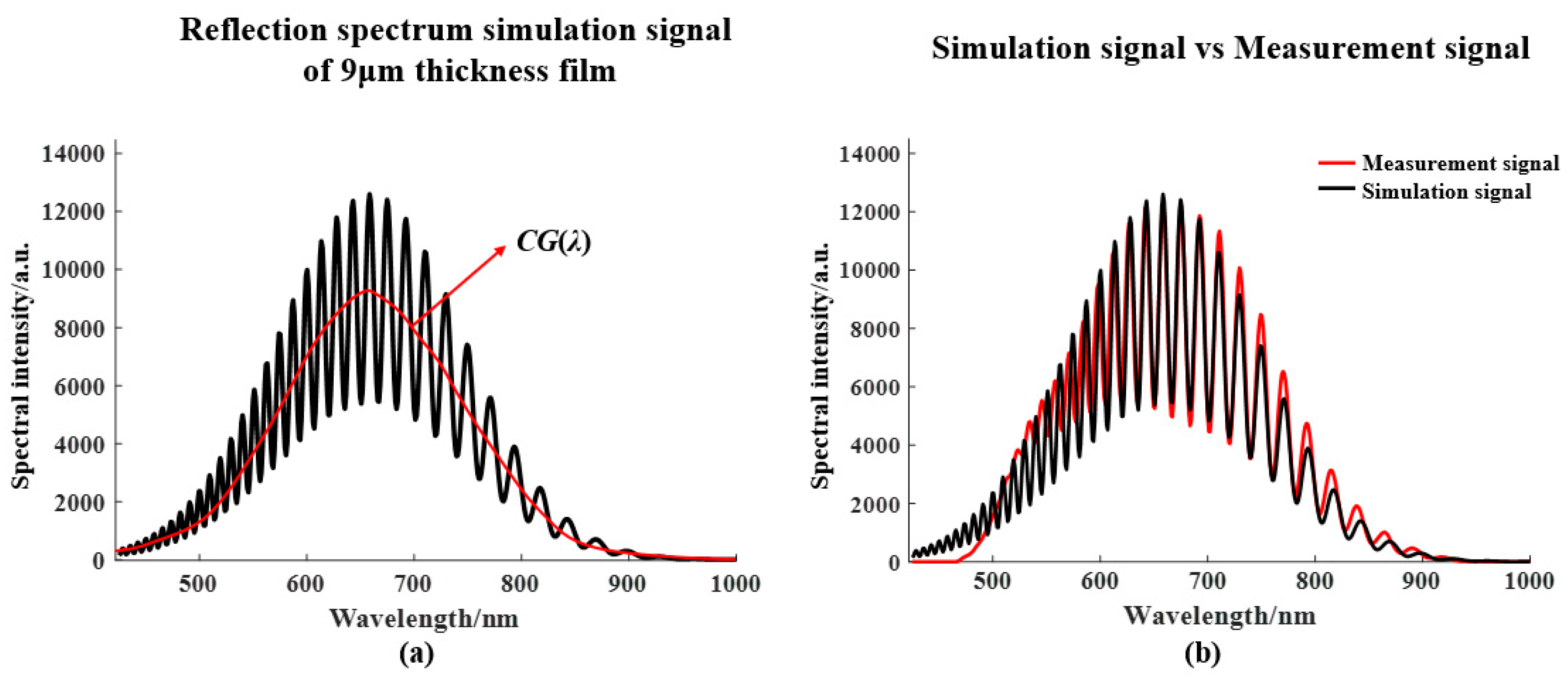
We take
A = 0.5,
B = 0.2,
C = 18000,
μ = 660 nm,
η = 80 nm,
ϕ0 =
π, and
z = 9 μm. The simulated interference spectrum is shown in
Figure 5a and compared with the measured data in
Figure 5b. The simulation signal is consistent with the actual measurement signal, which verifies the correctness of the simulation model.
4.2. Correlation Analysis of Influencing Factors
4.2.1. Influence of Thin-Film Thickness
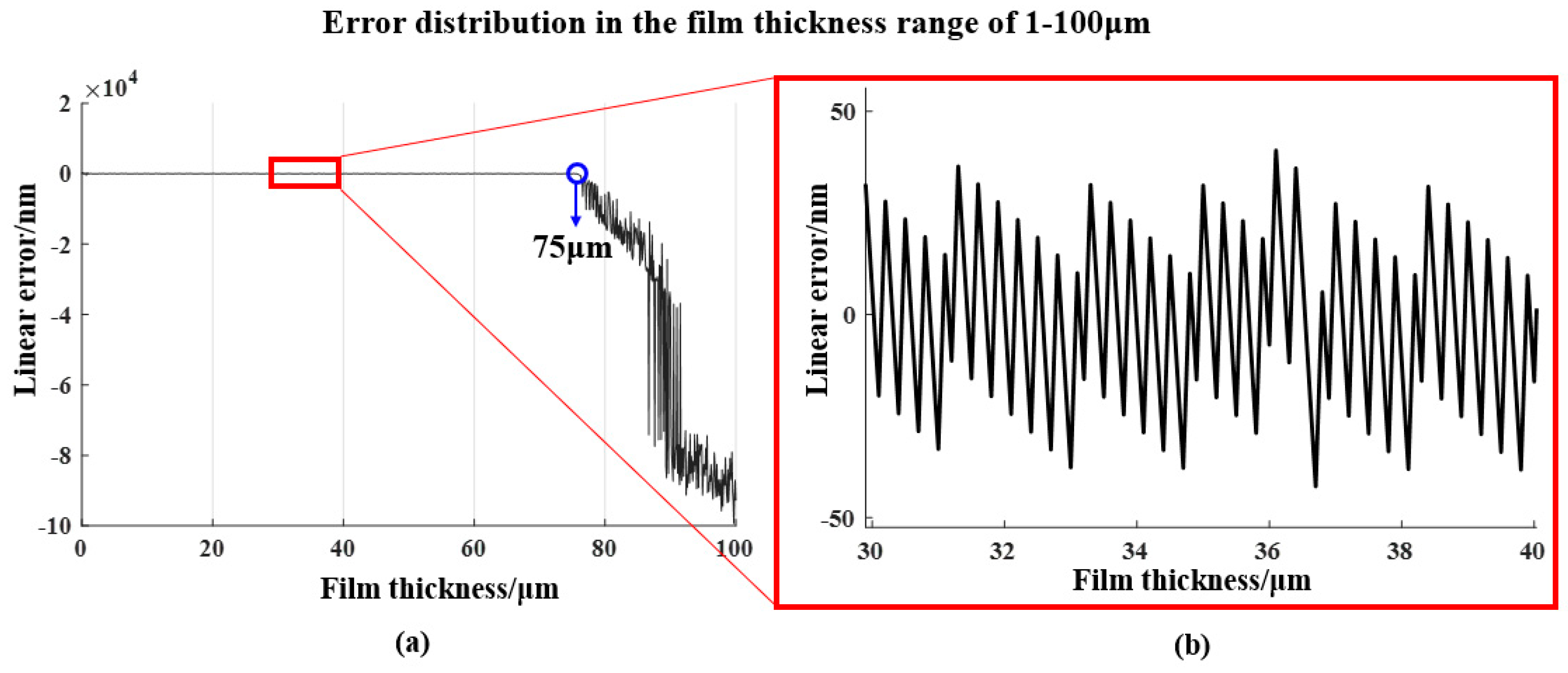
Using 0.1 μm as the interval of thickness value in
Ir (
z,
λ) to simulate the reflection spectrum of 1–100 μm film. The simulation result in
Figure 6 shows the inherent error of the algorithm changes periodically within ±50 nm in the effective range of 1–75 μm. The current measurement range is also limited by the wavelength resolution of the spectrometer, resulting in the failure calculation of the film thickness over 75 μm.
4.2.2. Influence of Thin-Film Materials
Based on the simulation signal of
Ir (
z,
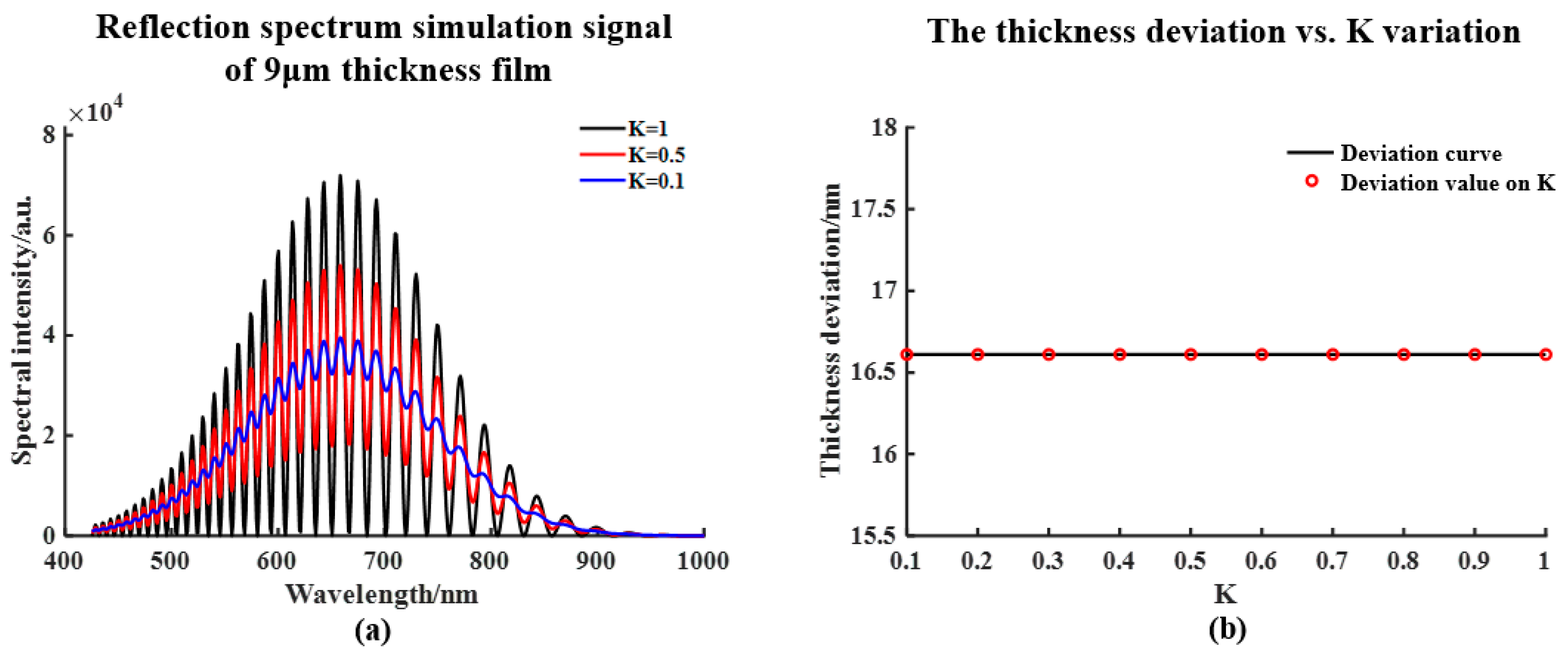
λ), we change signal contrast
K =
B/
A to analyze the influence caused by various absorption and reflection coefficients under different film materials.
Figure 7a illustrates the reflection spectrum signals with of 0.1, 0.5, and 1, respectively. For a particular thickness, the amplitude of the signal gets higher when contrast increases, while the period remains nearly constant. The thickness calculation deviations under different contrasts are shown in
Figure 7b. The deviations keep the value of 16.61 nm, which proves that the interference signal contrast does not relate to the thickness calculation deviation.
4.2.3. Influence of Noise
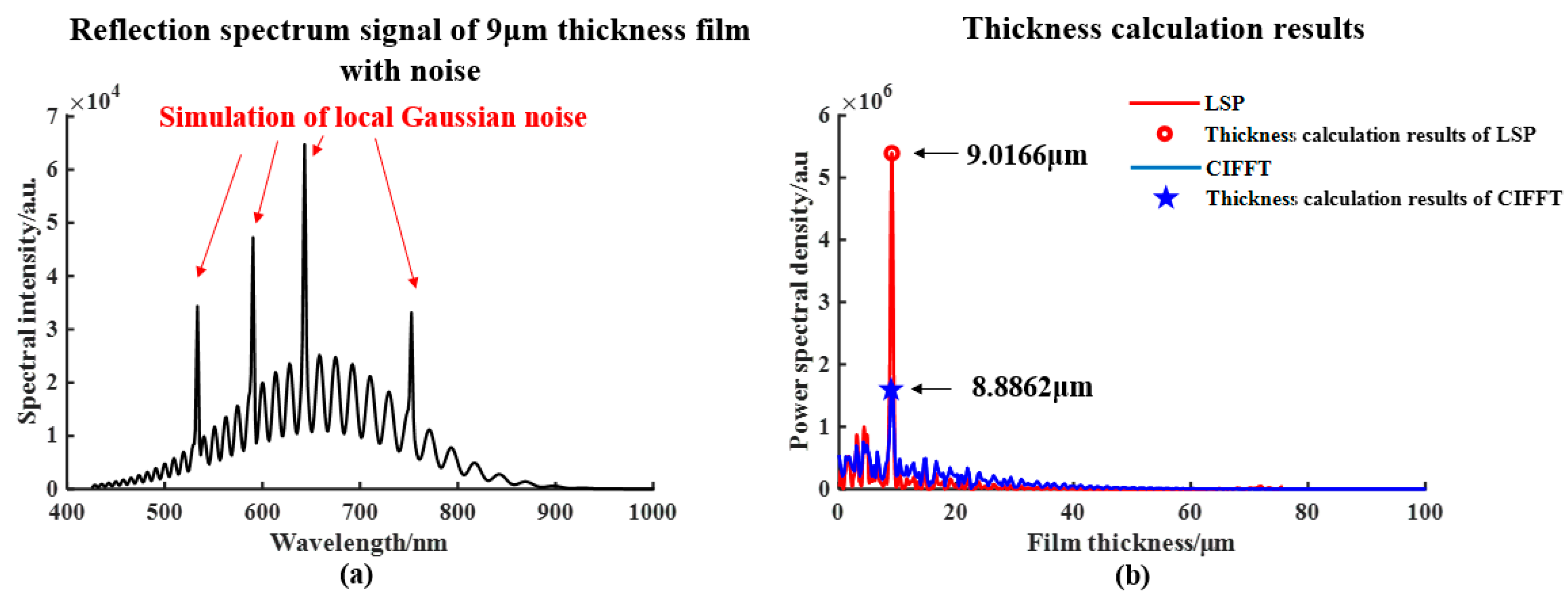
Irregular local Gaussian noise is added to the basic interference signal based on
Ir (
z,
λ) to simulate the noise introduced by CCD pixel data packet loss or environmental vibration to verify the robustness of the algorithm. As shown in
Figure 8b, the calculation result of LSP is closer to the true value of the thickness than CIFFT. Although the noise components are still contained in power spectrum density, whose density is much smaller compared to the peak value especially after LSP. Therefore, the combination of EMD and LSP has sufficient robustness by reducing the misjudgment rate.
6. Conclusions
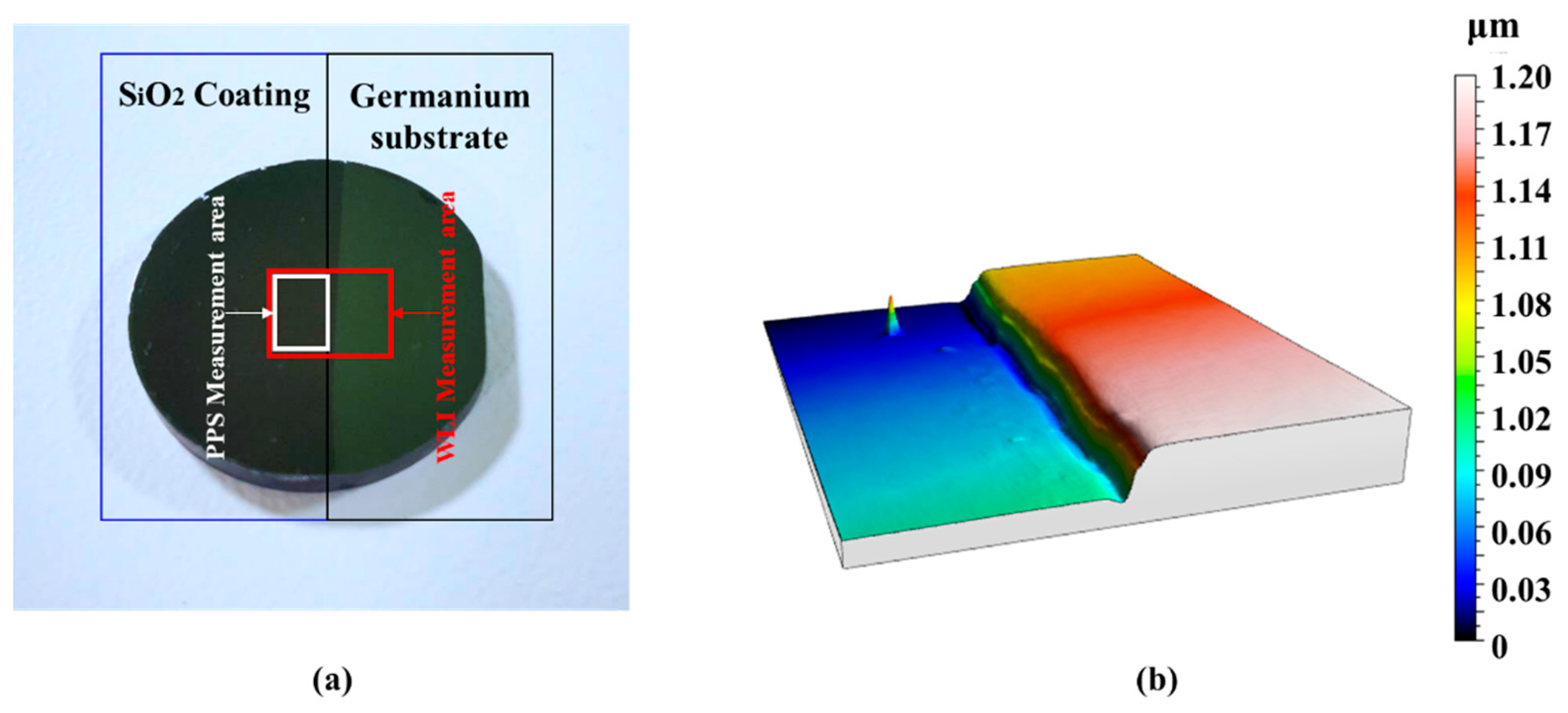
Based on the reflection spectrum interference theory, this paper built a low-cost and miniaturized thin-film thickness measurement system with the measurement range of 1–75 μm, an angle of ±5°, and an uncertainty of 0.1 μm. The measurement speed of 10 ms and no need of focusing within millimeter working distance met the efficient and convenient requirements of industrial-grade measurement. The validity of the system was verified by experiments of the standard PVC films, the micron-grade film layer on PCB chip, and Germanium-based SiO2 film. In the proposed phase power spectrum analysis method, the high-frequency spectral interference term was extracted adaptively from the full spectrum data through loop iterations, avoiding the use of the reference sample. For single-layer film thickness measurement, power spectrum analysis resolved the film thickness from the spectral interference term and corrected the gross error caused by local spectral noise, thereby ensuring the stability of the algorithm.
It is also clear that the industrial film thickness measurement results in this article need to be further optimized due to the lack of hardware performance. In the following work, the measurement range can be increased by selecting a high-resolution spectrometer. We can continue to optimize the algorithm model and the probe design to further improve the uncertainty of the measurement system.