A Deep Learning-Based Solution for Large-Scale Extraction of the Secondary Road Network from High-Resolution Aerial Orthoimagery
Abstract
1. Introduction
- We contrast the performance of state-of-the-art segmentation architectures and proposed hybrid segmentation models trained for the road extraction task and analyse the effect of the interaction between the architectures and the base networks (backbones).
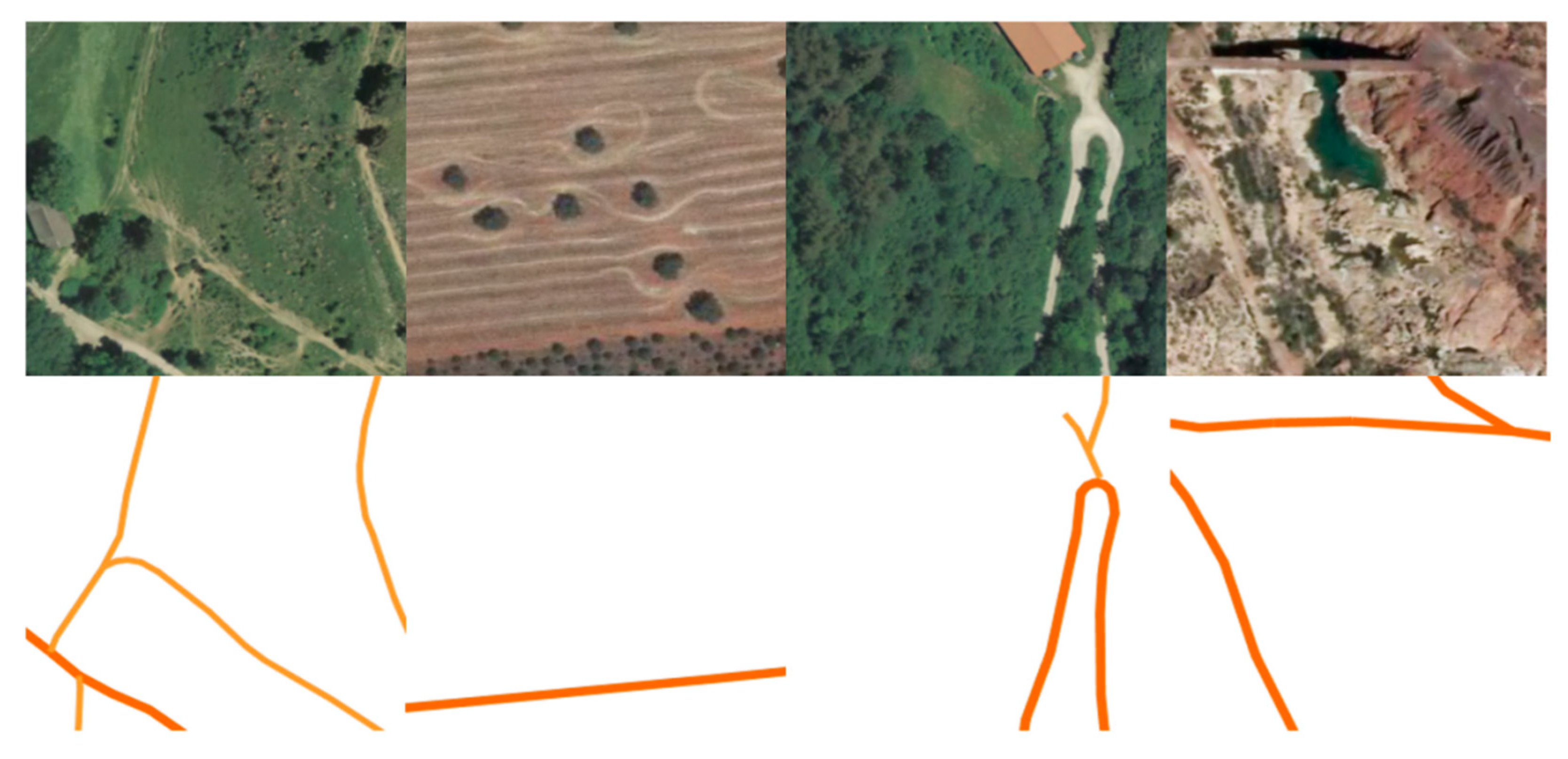
- Different from previous works, we focus on challenging scenes where shadows and occlusions are present, and take into account roads present on a variety of soil types, that are easily confused with the surroundings (secondary routes), further complicating the object’s extraction.
- We carry out the experiments on a new dataset composed of tiles with a spatial resolution of 0.50 m and their corresponding annotated reference masks covering representative areas of the Spanish national territory.
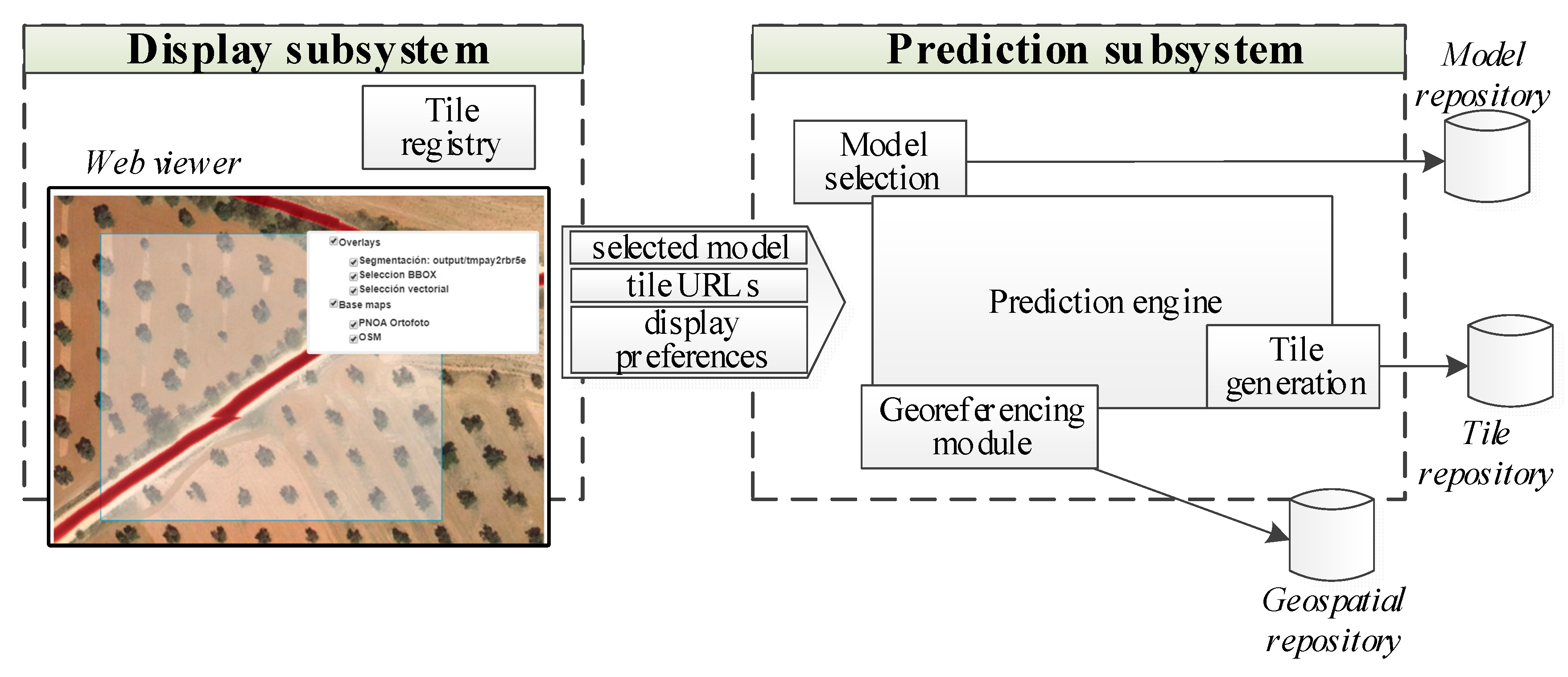
- To visually check the validity of our contributions, we built a system that combines the model’s predictions with existing data. The web platform allows the users to assess the quality of the segmentation results and naturally detect the limitations of the study, in order to propose future directions.
2. Related Work
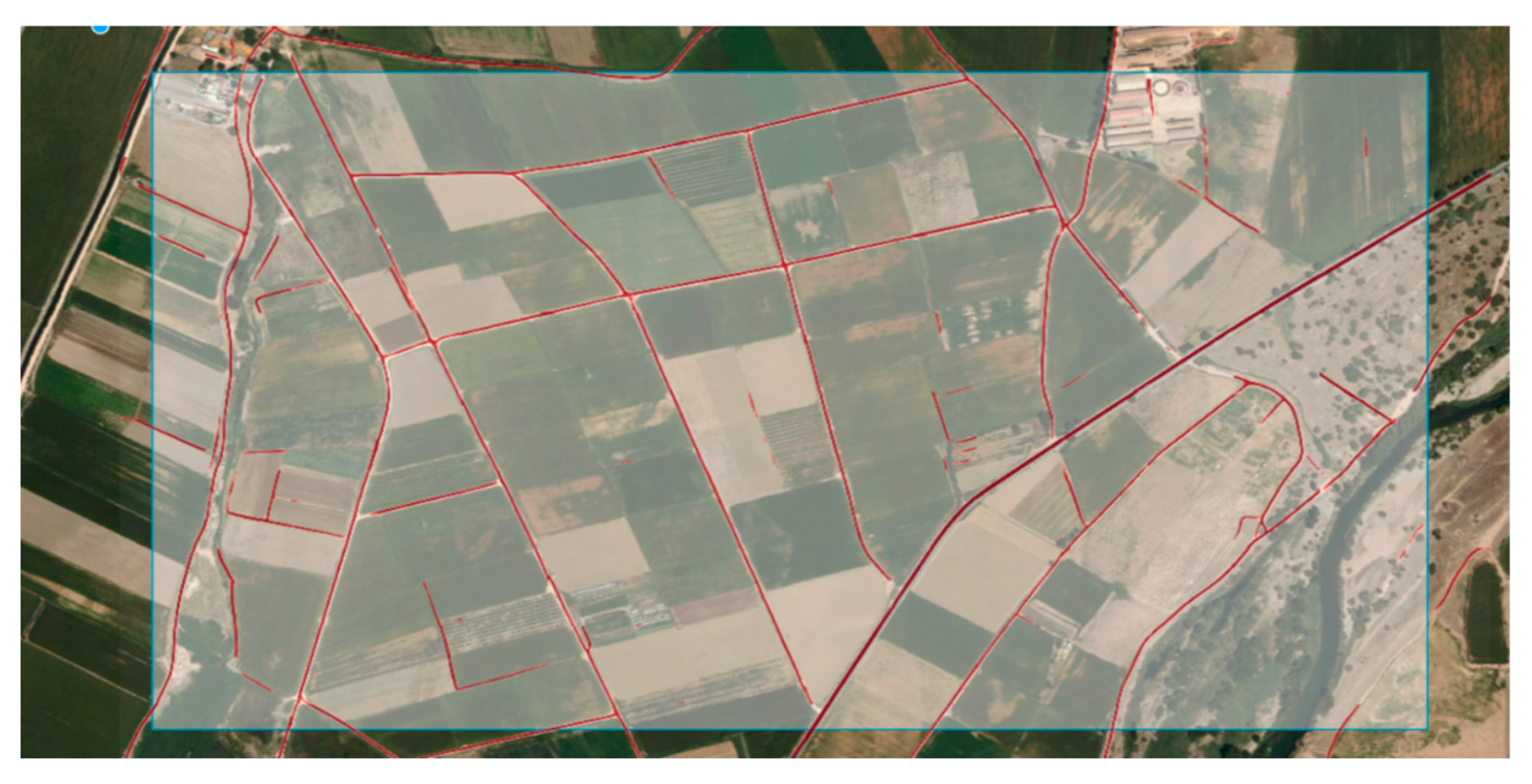
3. Dataset
- Firstly, the needed imagery was obtained from PNOA [39] (National Plan of Aerial Orthophotography, Spanish: “Plan Nacional de Ortofotografía Aérea”) and has a spatial resolution of 0.50 m and a planimetric RMSE (root-mean-square error) ≤ 1 m. The photograms were acquired in optimal meteorological conditions at a low flight altitude using calibrated photogrammetric cameras equipped with 3-band RGB sensors (8 bits per band). The imagery was orthorectified, radiometrically corrected and has topographic corrections applied using ground points measured with accurate GPS systems.
- Secondly, the segmentation masks containing the correspondent geographic information were obtained from the National Topographic Map [40] (Spanish: “Mapa Topográfico Nacional”) in vectorial format at a scale of 1:25,000. These road vectors were rasterized to create segmentation masks in image format, the resulting masks representing our training labels. One thing worth noting is that the rasterized vectors do not always align completely with the imagery due to the distinct criteria used for tagging (variations in width and contour, depending on the road’s importance), due to the error-prone conversion of a vector to a raster or due to human errors. However, as stated in the introduction, we wanted to focus on very challenging instances, with irregular geometries, different spectral signatures of the materials used for pavement, and where obstructions from objects are present. The intuition is that by training the models with real data, they will be better prepared to handle difficult scenarios and will offer an intuition about their expected behaviour in large-scale applications.
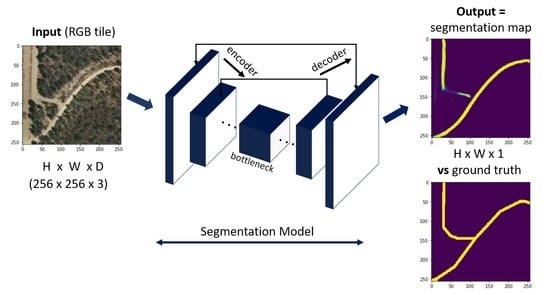
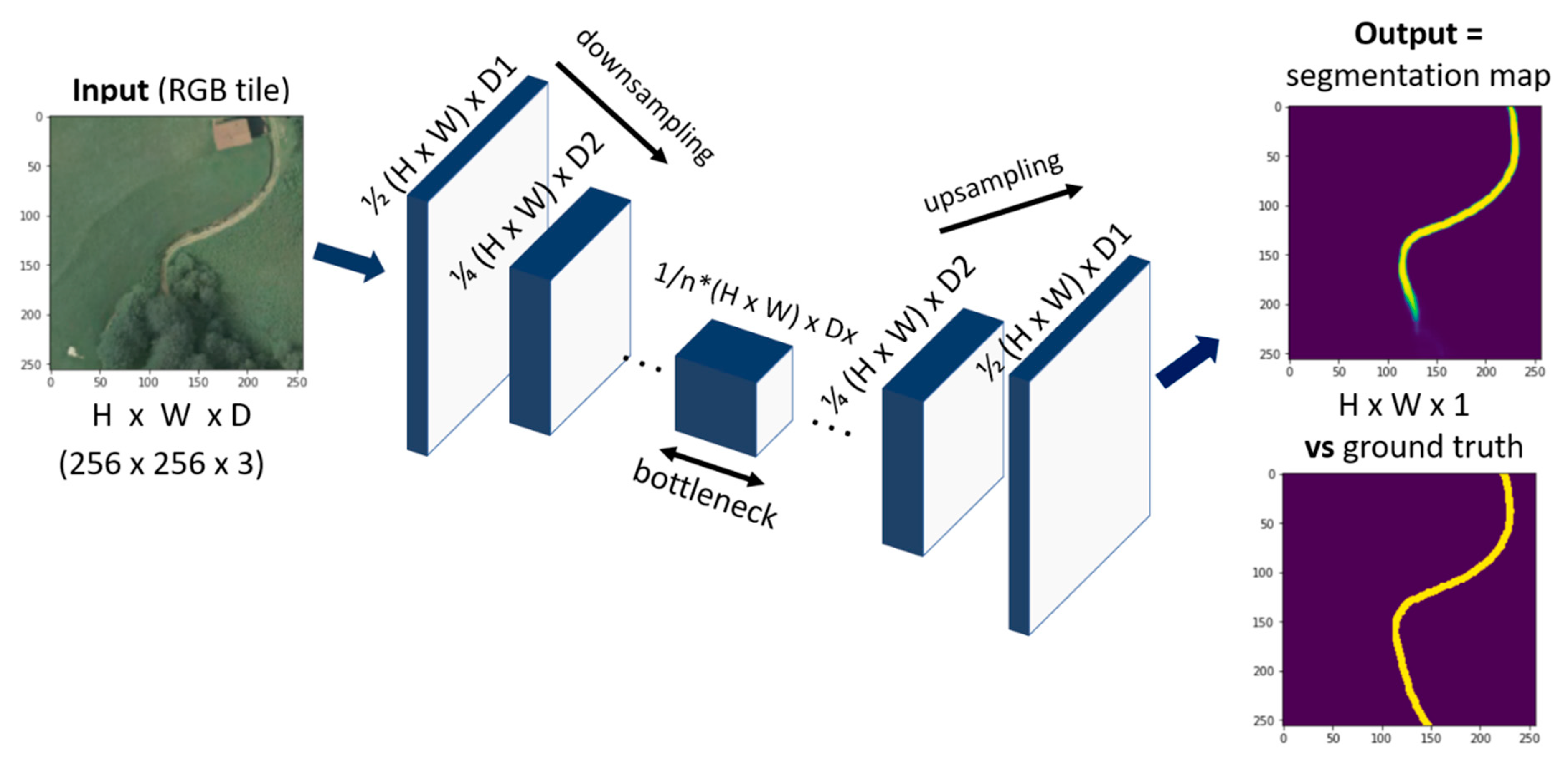
4. Methodology and Experiments
- A full training set of 6200 tiles and their corresponding segmentation maps (80% of the data) and five training subsets containing 90% of the training set (5580 tiles and segmentation maps) to perform the weights initialization. The five additional subsets represent variations of the training population and are used to statistically analyse the performance of the proposed networks and study the effect of the interaction effect between architectures and backbones.
- A test set (20% of the data) formed by 1550 sets of tiles and their segmentation maps for tuning the model’s hyperparameters and evaluating the model’s predictive performance.
5. Results and Discussions
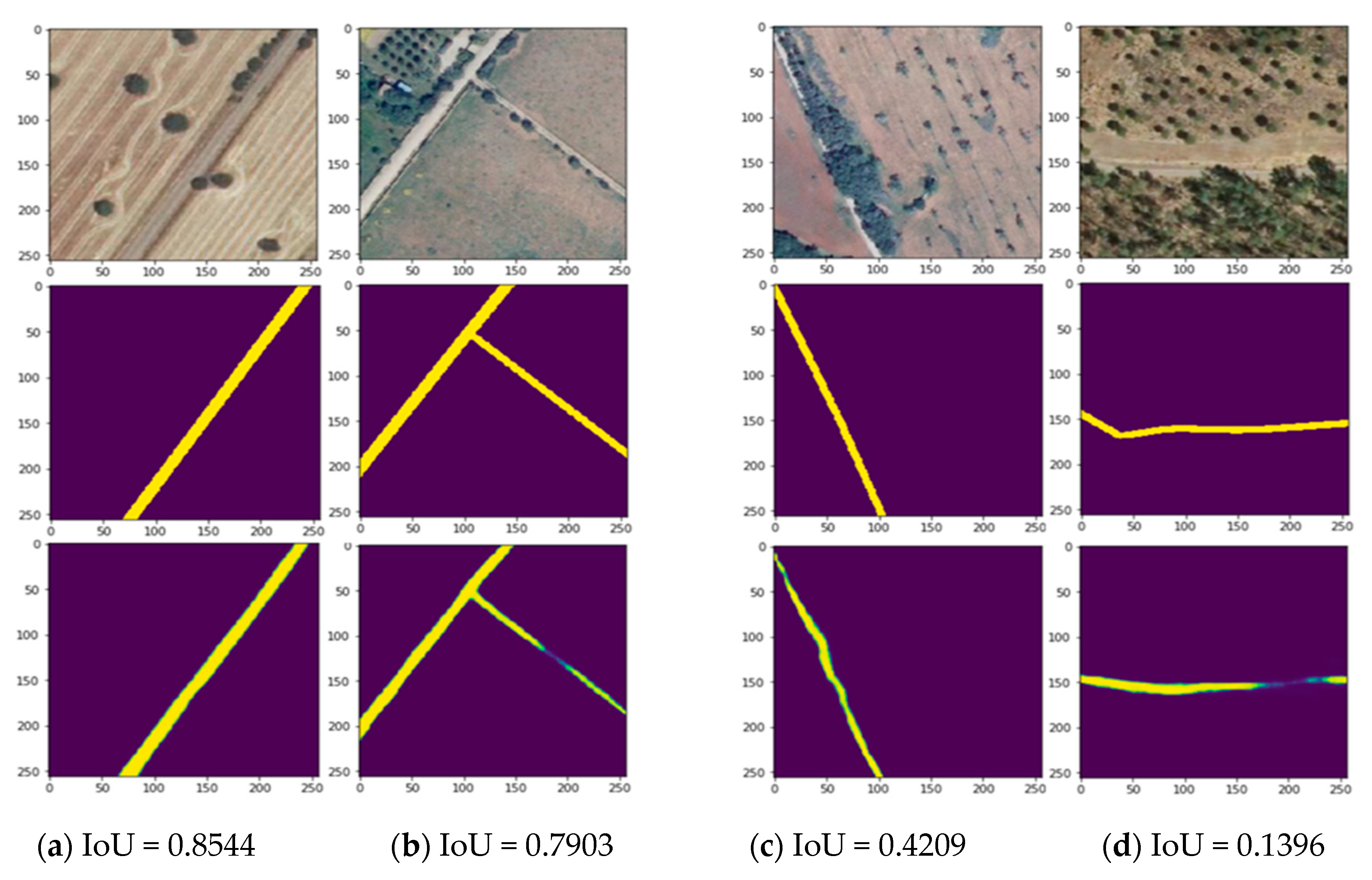
6. Visualization, Limitations and Future Directions
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Catálogo y Evolución de la Red de Carreteras|Ministerio de Transportes, Movilidad y Agenda Urbana. Available online: https://www.mitma.gob.es/carreteras/catalogo-y-evolucion-de-la-red-de-carreteras (accessed on 27 January 2020).
- Pritt, M.; Chern, G. Satellite Image Classification with Deep Learning. In Proceedings of the 2017 IEEE Applied Imagery Pattern Recognition Workshop (AIPR), Washington, DC, USA, 10–12 October 2017; IEEE: Washington, DC, USA, 2017; pp. 1–7. [Google Scholar]
- Tuia, D.; Persello, C.; Bruzzone, L. Domain Adaptation for the Classification of Remote Sensing Data: An Overview of Recent Advances. IEEE Geosci. Remote Sens. Mag. 2016, 4, 41–57. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Tuia, D.; Bruzzone, L.; Benediktsson, J.A. Advances in Hyperspectral Image Classification: Earth Monitoring with Statistical Learning Methods. IEEE Signal Process. Mag. 2014, 31, 45–54. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; IEEE: Boston, MA, USA, 2015; pp. 3431–3440. [Google Scholar]
- Everingham, M.; Eslami, S.M.A.; Van Gool, L.; Williams, C.K.I.; Winn, J.; Zisserman, A. The Pascal Visual Object Classes Challenge: A Retrospective. Int. J. Comput. Vis. 2015, 111, 98–136. [Google Scholar] [CrossRef]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. ImageNet Large Scale Visual Recognition Challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Forczmański, P. Performance Evaluation of Selected Thermal Imaging-Based Human Face Detectors. In Proceedings of the 10th International Conference on Computer Recognition Systems CORES 2017, Polanica Zdroj, Poland, 22–24 May 2017; Kurzynski, M., Wozniak, M., Burduk, R., Eds.; Springer International Publishing: Cham, Switzerland, 2018; Volume 578, pp. 170–181, ISBN 978-3-319-59161-2. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified Linear Units Improve Restricted Boltzmann Machines. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–24 June 2010; Fürnkranz, J., Joachims, T., Eds.; Omnipress: Madison, WI, USA, 2010; pp. 807–814. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, Munich, Germany, 5–9 October 2015; Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Chaurasia, A.; Culurciello, E. LinkNet: Exploiting Encoder Representations for Efficient Semantic Segmentation. In Proceedings of the 2017 IEEE Visual Communications Image Processing (VCIP), St. Petersburg, FL, USA, 10–13 December 2017; pp. 1–4. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; IEEE: Las Vegas, NV, USA, 2016; pp. 770–778. [Google Scholar]
- Lin, T.-Y.; Dollar, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature Pyramid Networks for Object Detection. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; IEEE: Honolulu, HI, USA, 2017; pp. 936–944. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015; 1409. Available online: https://arxiv.org/abs/1409.1556 (accessed on 16 October 2020).
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the Inception Architecture for Computer Vision. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; IEEE: Las Vegas, NV, USA, 2016; pp. 2818–2826. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.-C. MobileNetV2: Inverted Residuals and Linear Bottlenecks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; IEEE: Salt Lake City, UT, USA, 2018; pp. 4510–4520. [Google Scholar]
- Tan, M.; Le, Q.V. EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks. In Proceedings of the 36th International Conference on Machine Learning, ICML 2019, Long Beach, CA, USA, 9–15 June 2019; pp. 6105–6114. Available online: http://proceedings.mlr.press/v97/tan19a.html (accessed on 16 October 2020).
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-Excitation Networks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; IEEE: Salt Lake City, UT, USA, 2018; pp. 7132–7141. [Google Scholar]
- Xie, S.; Girshick, R.; Dollar, P.; Tu, Z.; He, K. Aggregated Residual Transformations for Deep Neural Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; IEEE: Honolulu, HI, USA, 2017; pp. 5987–5995. [Google Scholar]
- Woźniak, M.; Damaševičius, R.; Maskeliūnas, R.; Malūkas, U. Real Time Path Finding for Assisted Living Using Deep Learning. JUCS J. Univ. Comput. Sci. 2018. [Google Scholar] [CrossRef]
- Liu, J.; Qin, Q.; Li, J.; Li, Y. Rural Road Extraction from High-Resolution Remote Sensing Images Based on Geometric Feature Inference. ISPRS Int. J. Geo-Inf. 2017, 6, 314. [Google Scholar] [CrossRef]
- Mattyus, G.; Wang, S.; Fidler, S.; Urtasun, R. Enhancing Road Maps by Parsing Aerial Images Around the World. In Proceedings of the Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; IEEE Computer Society: Columbia, DC, USA, 2015; pp. 1689–1697. [Google Scholar]
- Dong, R.; Li, W.; Fu, H.; Gan, L.; Yu, L.; Zheng, J.; Xia, M. Oil palm plantation mapping from high-resolution remote sensing images using deep learning. Int. J. Remote Sens. 2020, 41, 2022–2046. [Google Scholar] [CrossRef]
- Alshaikhli, T.; Liu, W.; Maruyama, Y. Automated Method of Road Extraction from Aerial Images Using a Deep Convolutional Neural Network. Appl. Sci. 2019, 9, 4825. [Google Scholar] [CrossRef]
- Alshehhi, R.; Marpu, P.R.; Woon, W.L.; Mura, M.D. Simultaneous extraction of roads and buildings in remote sensing imagery with convolutional neural networks. ISPRS J. Photogramm. Remote Sens. 2017, 130, 139–149. [Google Scholar] [CrossRef]
- Kestur, R.; Farooq, S.; Abdal, R.; Mehraj, E.; Narasipura, O.; Mudigere, M. UFCN: A fully convolutional neural network for road extraction in RGB imagery acquired by remote sensing from an unmanned aerial vehicle. J. Appl. Remote Sens. 2018, 12, 1. [Google Scholar] [CrossRef]
- Henry, C.; Azimi, S.M.; Merkle, N. Road Segmentation in SAR Satellite Images with Deep Fully-Convolutional Neural Networks. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1867–1871. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Q.; Wang, Y. Road Extraction by Deep Residual U-Net. IEEE Geosci. Remote Sens. Lett. 2018, 15, 749–753. [Google Scholar] [CrossRef]
- Liu, Y.; Yao, J.; Lu, X.; Xia, M.; Wang, X.; Liu, Y. RoadNet: Learning to Comprehensively Analyze Road Networks in Complex Urban Scenes from High-Resolution Remotely Sensed Images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2043–2056. [Google Scholar] [CrossRef]
- Sujatha, C.; Selvathi, D. Connected component-based technique for automatic extraction of road centerline in high resolution satellite images. EURASIP J. Image Video Process. 2015, 2015. [Google Scholar] [CrossRef]
- Wang, Q.; Gao, J.; Yuan, Y. Embedding Structured Contour and Location Prior in Siamesed Fully Convolutional Networks for Road Detection. IEEE Trans. Intell. Transp. Syst. 2018, 19, 230–241. [Google Scholar] [CrossRef]
- Panboonyuen, T.; Jitkajornwanich, K.; Lawawirojwong, S.; Srestasathiern, P.; Vateekul, P. Road Segmentation of Remotely-Sensed Images Using Deep Convolutional Neural Networks with Landscape Metrics and Conditional Random Fields. Remote Sens. 2017, 9, 680. [Google Scholar] [CrossRef]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
- Xu, Y.; Xie, Z.; Feng, Y.; Chen, Z. Road Extraction from High-Resolution Remote Sensing Imagery Using Deep Learning. Remote Sens. 2018, 10, 1461. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; van der Maaten, L.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2017, Honolulu, HI, USA, 21–26 July 2017; IEEE Computer Society: Columbia, DC, USA, 2017; pp. 2261–2269. [Google Scholar]
- Hu, F.; Xia, G.-S.; Hu, J.; Zhang, L. Transferring Deep Convolutional Neural Networks for the Scene Classification of High-Resolution Remote Sensing Imagery. Remote Sens. 2015, 7, 14680–14707. [Google Scholar] [CrossRef]
- Luque, B.; Morros, J.R.; Ruiz-Hidalgo, J. Spatio-temporal Road Detection from Aerial Imagery using CNNs. In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications, Port, Portugal, 27 February–1 March 2017; SCITEPRESS—Science and Technology Publications: Porto, Portugal, 2017; pp. 493–500. [Google Scholar]
- Bonafilia, D.; Gill, J.; Basu, S.; Yang, D. Building High Resolution Maps for Humanitarian Aid and Development with Weakly- and Semi-Supervised Learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, CVPR Workshops 2019, Long Beach, CA, USA, 16–20 June 2019; pp. 1–9. Available online: https://openaccess.thecvf.com/content_CVPRW_2019/html/cv4gc/Bonafilia_Building_High_Resolution_Maps_for_Humanitarian_Aid_and_Development_with_CVPRW_2019_paper.html (accessed on 16 October 2020).
- Instituto Geográfico Nacional Plan Nacional de Ortofotografía Aérea. Available online: https://pnoa.ign.es/caracteristicas-tecnicas (accessed on 25 November 2019).
- Instituto Geográfico Nacional Centro de Descargas del CNIG (IGN). Available online: http://centrodedescargas.cnig.es (accessed on 3 February 2020).
- Gómez-Barrón, J.P.; Alcarria, R.; Manso-Callejo, M.-Á. Designing a Volunteered Geographic Information System for Road Data Validation. Proceedings 2019, 19, 7. [Google Scholar] [CrossRef]
- Li, F.-F.; Johnson, J.; Yeung, S. Lecture 11: Detection and Segmentation. 95. Available online: http://cs231n.stanford.edu/slides/2017/cs231n_2017_lecture11.pdf (accessed on 16 October 2020).
- Jordan, J. An Overview of Semantic Image Segmentation. Available online: https://www.jeremyjordan.me/semantic-segmentation/ (accessed on 4 February 2020).
- Yakubovskiy, P. Segmentation Models; GitHub: California, CA, USA, 2019; Available online: https://github.com/qubvel/segmentation_models (accessed on 16 October 2020).
- Chollet, F. Keras. 2015. Available online: https://github.com/fchollet/keras (accessed on 16 October 2020).
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A system for large-scale machine learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation, Savannah, GA, USA, 2–4 November 2016; p. 21. [Google Scholar]
- Cira, C.-I.; Alcarria, R.; Manso-Callejo, M.-Á.; Serradilla, F. Evaluation of Transfer Learning Techniques with Convolutional Neural Networks (CNNs) to Detect the Existence of Roads in High-Resolution Aerial Imagery. In Applied Informatics; Florez, H., Leon, M., Diaz-Nafria, J.M., Belli, S., Eds.; Springer International Publishing: Cham, Switzerland, 2019; Volume 1051, pp. 185–198. ISBN 978-3-030-32474-2. [Google Scholar]
- Zhu, X.; Vondrick, C.; Fowlkes, C.C.; Ramanan, D. Do We Need More Training Data? Int. J. Comput. Vis. 2016, 119, 76–92. [Google Scholar] [CrossRef]
- Cira, C.-I.; Alcarria, R.; Manso-Callejo, M.-Á.; Serradilla, F. A Framework Based on Nesting of Convolutional Neural Networks to Classify Secondary Roads in High Resolution Aerial Orthoimages. Remote Sens. 2020, 12, 765. [Google Scholar] [CrossRef]
- Sharma, S.; Ball, J.E.; Tang, B.; Carruth, D.W.; Doude, M.; Islam, M.A. Semantic Segmentation with Transfer Learning for Off-Road Autonomous Driving. Sensors 2019, 19, 2577. [Google Scholar] [CrossRef] [PubMed]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015; Available online: http://arxiv.org/abs/1412.6980 (accessed on 16 October 2020).
- Chen, X.; Liu, S.; Sun, R.; Hong, M. On the Convergence of a Class of Adam-Type Algorithms for Non-Convex Optimization. In Proceedings of the 7th International Conference on Learning Representations, ICLR 2019, New Orleans, LA, USA, 6–9 May 2019; Available online: https://openreview.net/pdf?id=H1x-x309tm (accessed on 16 October 2020).
- Garcia-Garcia, A.; Orts-Escolano, S.; Oprea, S.; Villena-Martinez, V.; Martinez-Gonzalez, P.; Garcia-Rodriguez, J. A survey on deep learning techniques for image and video semantic segmentation. Appl. Soft Comput. 2018, 70, 41–65. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, Z.; Sun, L.; Qin, W. One for All: A Mutual Enhancement Method for Object Detection and Semantic Segmentation. Appl. Sci. 2019, 10, 13. [Google Scholar] [CrossRef]
- Gupta, S.; Girshick, R.B.; Arbeláez, P.A.; Malik, J. Learning Rich Features from RGB-D Images for Object Detection and Segmentation. In Proceedings of the Computer Vision—ECCV 2014—13th European Conference, Zurich, Switzerland, 6–12 September 2014; pp. 345–360. [Google Scholar] [CrossRef]
- Ye, Y.; Yilmaz, A. An automatic pipeline for mapping roads from aerial images. In Proceedings of the 1st ACM SIGSPATIAL Workshop on High-Precision Maps and Intelligent Applications for Autonomous Vehicles—AutonomousGIS’17, Redondo Beach, CA, USA, 7 November 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Open Source Geospatial Foundation. GDAL/OGR contributors GDAL/OGR Geospatial Data Abstraction software Library. 2020. Available online: https://gdal.org/index.html (accessed on 30 March 2020).
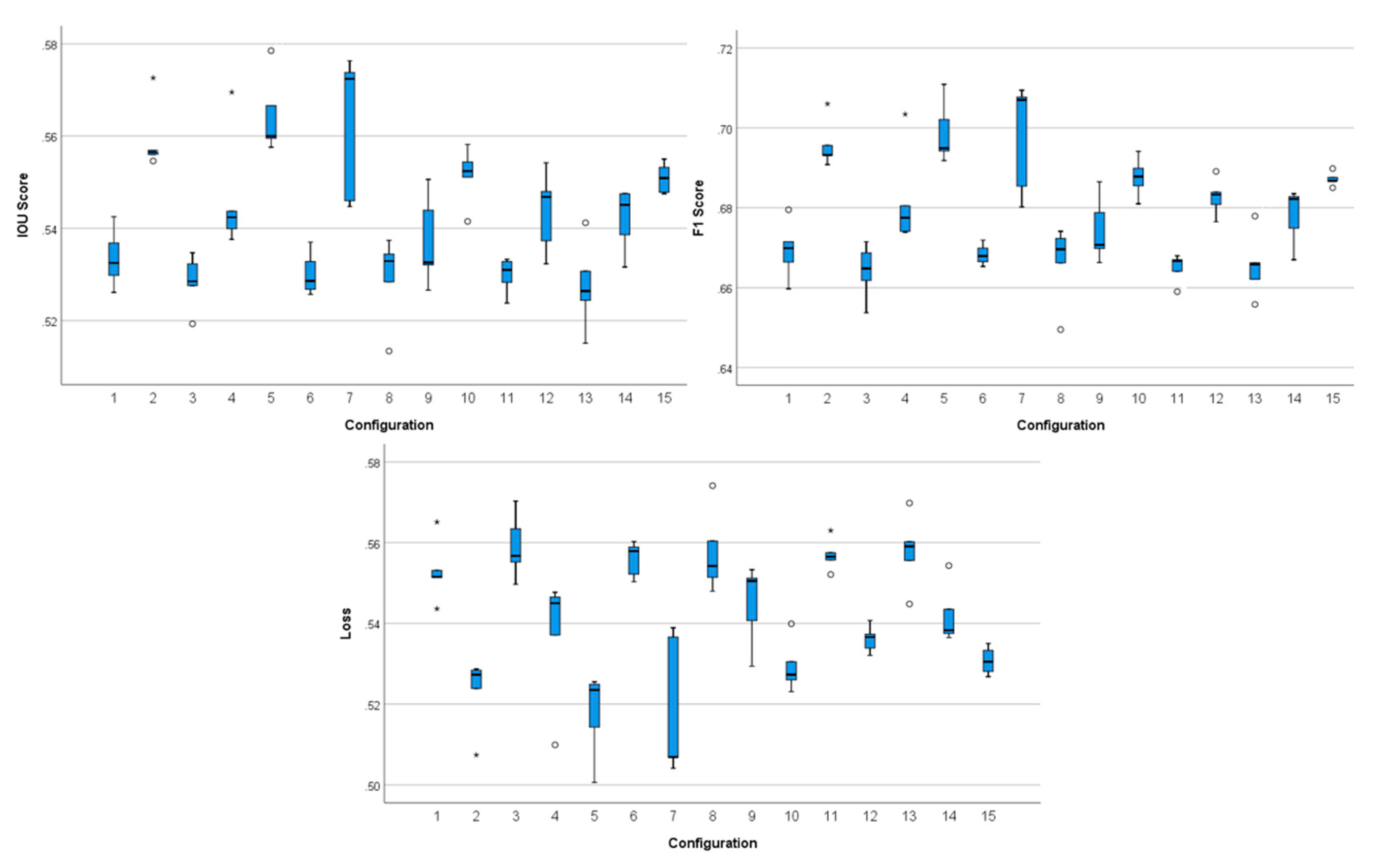
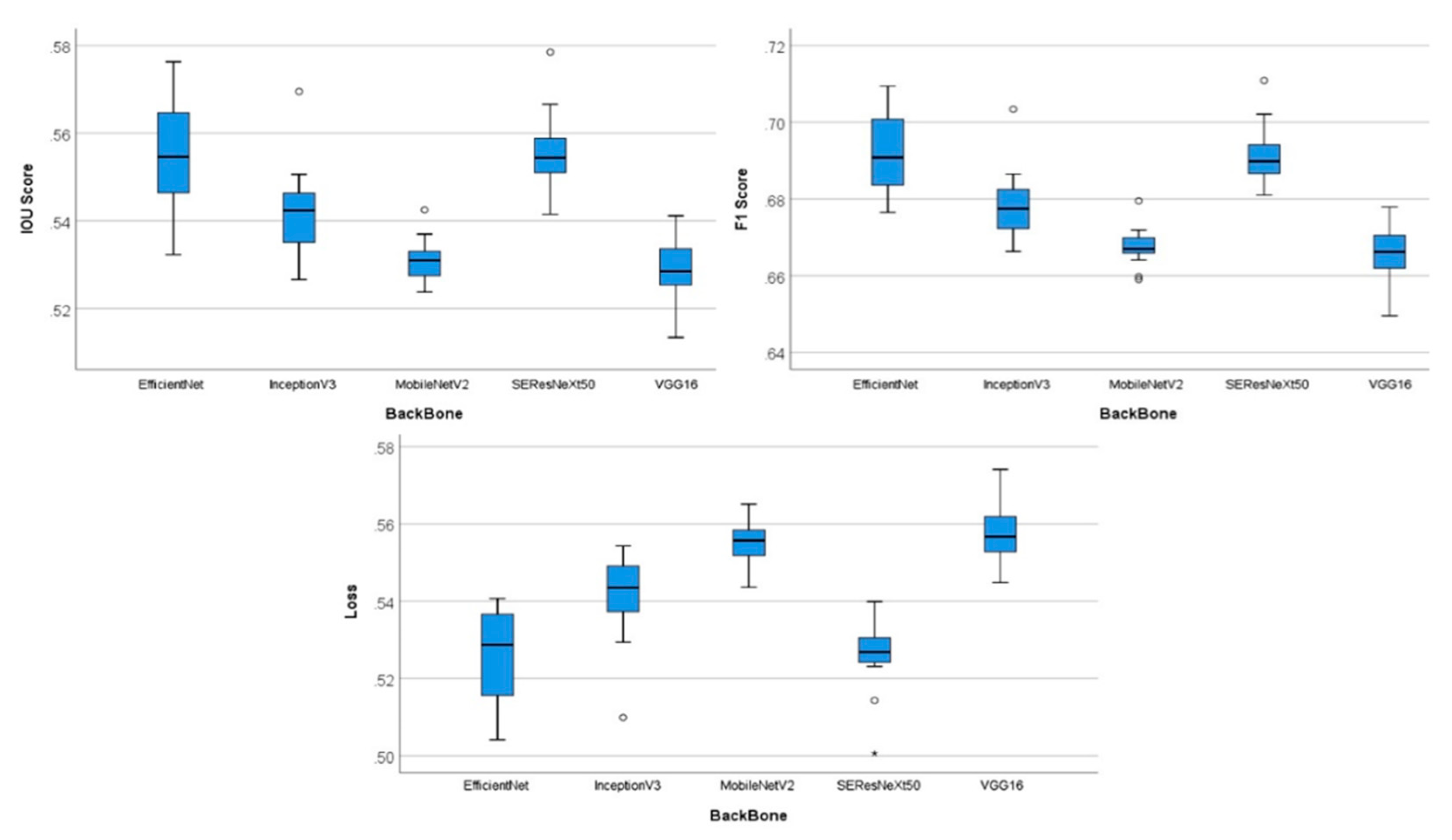
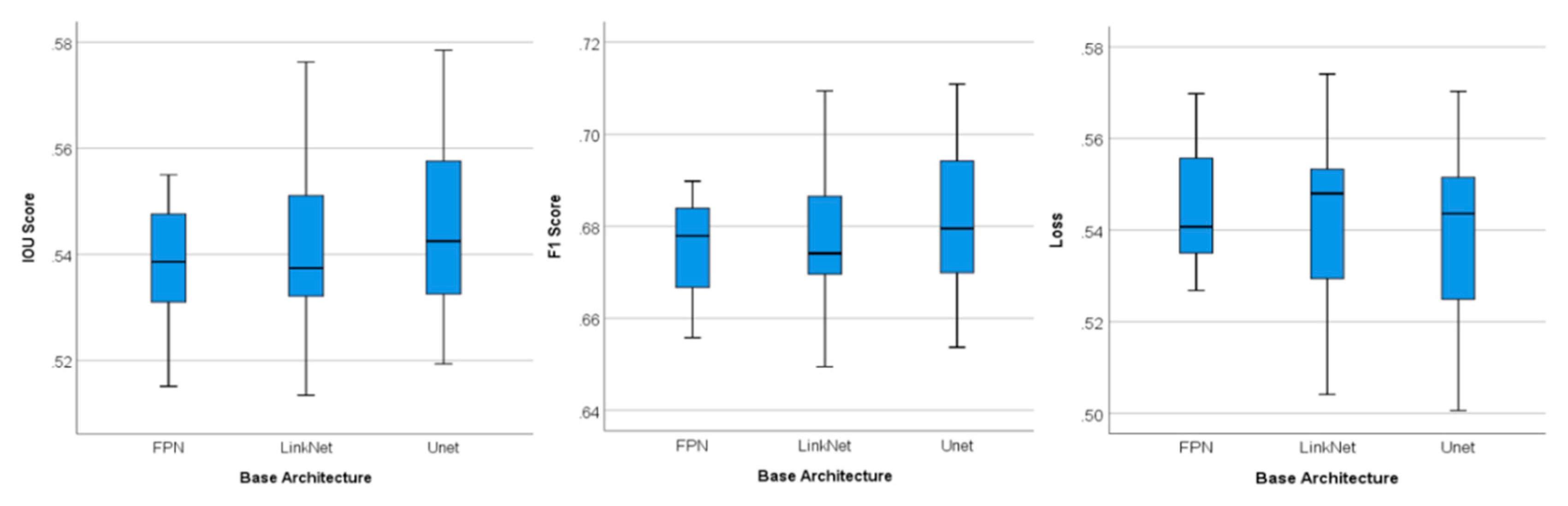

| Configuration | IoU Score | F1 Score | Loss | |||
|---|---|---|---|---|---|---|
| M | SD | M | SD | M | SD | |
| 1 | 0.5335 | 0.0064 | 0.6694 | 0.0072 | 0.5529 | 0.0077 |
| 2 | 0.5593 | 0.0075 | 0.6958 | 0.0060 | 0.5231 | 0.0090 |
| 3 | 0.5028 | 0.0059 | 0.6641 | 0.0069 | 0.5591 | 0.0080 |
| 4 | 0.5466 | 0.0130 | 0.6819 | 0.0123 | 0.5372 | 0.0158 |
| 5 | 0.5644 | 0.0086 | 0.6988 | 0.0078 | 0.5178 | 0.0106 |
| Standard U-Net | 0.5299 | 0.0087 | 0.6638 | 0.0044 | 0.5588 | 0.0055 |
| 6 | 0.5302 | 0.0047 | 0.6683 | 0.0026 | 0.5559 | 0.0044 |
| 7 | 0.5626 | 0.0159 | 0.6979 | 0.0140 | 0.5187 | 0.0175 |
| 8 | 0.5293 | 0.0095 | 0.6663 | 0.0099 | 0.5576 | 0.0103 |
| 9 | 0.5372 | 0.0098 | 0.6744 | 0.0082 | 0.5450 | 0.0100 |
| 10 | 0.5515 | 0.0062 | 0.6877 | 0.0049 | 0.5294 | 0.0065 |
| Standard LinkNet | 0.5184 | 0.0080 | 0.6552 | 0.0094 | 0.5687 | 0.0088 |
| 11 | 0.5298 | 0.0039 | 0.6650 | 0.0036 | 0.5570 | 0.0039 |
| 12 | 0.5437 | 0.0088 | 0.6827 | 0.0046 | 0.5361 | 0.0033 |
| 13 | 0.5276 | 0.0095 | 0.6656 | 0.0081 | 0.5579 | 0.0090 |
| 14 | 0.5421 | 0.0069 | 0.6781 | 0.0071 | 0.5420 | 0.0074 |
| 15 | 0.5509 | 0.0033 | 0.6871 | 0.0018 | 0.5307 | 0.0034 |
| Standard FPN | 0.5233 | 0.0093 | 0.6621 | 0.0075 | 0.5641 | 0.0105 |
| F-Statistic | 11.344 | 13.119 | 12.886 0.000 | |||
| p-value | 0.000 | 0.000 | ||||
| Config. No. | Homogeneous Subsets | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| 13 | 0.5276 | ||||
| 3 | 0.5285 | ||||
| 8 | 0.5293 | ||||
| 11 | 0.5298 | ||||
| 6 | 0.5302 | ||||
| 1 | 0.5335 | 0.5335 | |||
| 9 | 0.5372 | 0.5372 | |||
| 14 | 0.5421 | 0.5421 | 0.5421 | ||
| 12 | 0.5437 | 0.5437 | 0.5437 | 0.5437 | |
| 4 | 0.5466 | 0.5466 | 0.5466 | 0.5466 | 0.5466 |
| 15 | 0.5509 | 0.5509 | 0.5509 | 0.5509 | |
| 10 | 0.5515 | 0.5515 | 0.5515 | 0.5515 | |
| 2 | 0.5593 | 0.5593 | 0.5593 | ||
| 7 | 0.5626 | 0.5626 | |||
| 5 | 0.5644 | ||||
| Sig. | 0.055 | 0.092 | 0.127 | 0.059 | 0.098 |
| Dependent Variable | Source | Sum of Squares | Degrees of Freedom | Mean Square | F | Sig. |
|---|---|---|---|---|---|---|
| IoU score | Backbone | 0.0099 | 4 | 0.0025 | 33.367 | 0.000 |
| Base Architecture | 0.0007 | 2 | 0.0004 | 4.978 | 0.010 | |
| Backbone and Base Architecture | 0.0011 | 8 | 0.0001 | 1.924 | 0.073 | |
| Error | 0.0044 | 60 | 7.41 × 10−5 | |||
| Total | 0.0162 | 74 | ||||
| F1 score | Backbone | 0.0096 | 4 | 0.0024 | 40.382 | 0.000 |
| Base Architecture | 0.0005 | 2 | 0.0002 | 4.166 | 0.020 | |
| Backbone and Base Architecture | 0.0008 | 8 | 0.0001 | 1.726 | 0.111 | |
| Error | 0.0036 | 60 | 5.94 × 10−5 | |||
| Total | 0.0140 | 74 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cira, C.-I.; Alcarria, R.; Manso-Callejo, M.-Á.; Serradilla, F. A Deep Learning-Based Solution for Large-Scale Extraction of the Secondary Road Network from High-Resolution Aerial Orthoimagery. Appl. Sci. 2020, 10, 7272. https://doi.org/10.3390/app10207272
Cira C-I, Alcarria R, Manso-Callejo M-Á, Serradilla F. A Deep Learning-Based Solution for Large-Scale Extraction of the Secondary Road Network from High-Resolution Aerial Orthoimagery. Applied Sciences. 2020; 10(20):7272. https://doi.org/10.3390/app10207272
Chicago/Turabian StyleCira, Calimanut-Ionut, Ramón Alcarria, Miguel-Ángel Manso-Callejo, and Francisco Serradilla. 2020. "A Deep Learning-Based Solution for Large-Scale Extraction of the Secondary Road Network from High-Resolution Aerial Orthoimagery" Applied Sciences 10, no. 20: 7272. https://doi.org/10.3390/app10207272
APA StyleCira, C.-I., Alcarria, R., Manso-Callejo, M.-Á., & Serradilla, F. (2020). A Deep Learning-Based Solution for Large-Scale Extraction of the Secondary Road Network from High-Resolution Aerial Orthoimagery. Applied Sciences, 10(20), 7272. https://doi.org/10.3390/app10207272